Журнал вычислительной математики и математической физики, 2022, T. 62, № 6, стр. 1007-1015

1. ВВЕДЕНИЕ

Задача о движении обтекаемой стенки по потоку или против потока в стационарном пограничном слое является частным случаем нестационарного отрыва пограничного слоя вязкой несжимаемой жидкости при больших числах Рейнольдса. Широкий класс плоских отрывных ламинарных течений вязкой несжимаемой жидкости описан в [1], где, в частности, изложены основы асимптотической теории отрыва стационарного и нестационарного пограничных слоев и подробно описан случай стенки, движущейся вниз по потоку. В деталях изложено формирование особенности Мура–Рота–Сирса в решении уравнений пограничного слоя при воздействии на него неблагоприятного, тормозящего градиента давления. Похожая задача была рассмотрена и в [2], где величину неблагоприятного градиента давления можно было регулировать. При изменении величины действующего на пограничный слой давления поток тормозился внутри слоя вплоть до нулевого значения в некоторой точке. Причем удалось найти решение задачи с более слабой особенностью “кромочного” типа, нежели особенность Мура–Рота–Сирса, далее которой вниз по потоку решение не существует. Течение около стенки, движущейся вверх по потоку, в сверхзвуковом пограничном слое было исследовано численно в [3]. Применение асимптотических “многопалубных” разложений при исследовании задач гидродинамической устойчивости подробно описано в [4]. В [5] изучено воздействие скачка уплотнения, движущегося вверх по потоку (а в системе координат, движущейся со скачком, стенка соответственно движется вниз по потоку), на ламинарный пограничный слой. Исследование [3] повторено в работе [6] в несколько более широких рамках. Анализ отрывных течений в канале с подвижной стенкой с использованием метода сращиваемых асимптотических разложений выполнен в [7]. Численный расчет полных уравнений Навье–Стокса для чисел Маха больше единицы в случае подвижного скачка уплотнения, падающего на пограничный слой вязкого совершенного газа, выполнен в работе [8]. Подобные расчеты являются убедительным средством проверки и подтверждения результатов применения асимптотических теорий. Дальнейшее развитие теории отрывных течений на подвижной стенке было предложено в [9], где также рассматривалась поверхность, движущаяся вверх по потоку.

В настоящей работе рассматривается ламинарное течение несжимаемой вязкой жидкости в пограничном слое около стенки, движущейся вверх по потоку. А именно, изучено влияние заданных малых внешних возмущений давления на пограничный слой, содержащий противотоки. Предполагается, что на пограничный слой действует возмущение давления, источник которого является локальным, регулируется по величине и движется вниз по потоку.

2. ПОСТАНОВКА ЗАДАЧИ

В качестве базового течения в исследовании рассматривается двумерное ламинарное обтекание плоской пластины потоком вязкой несжимаемой жидкости при больших числах Рейнольдса. На расстоянии $\hat {L}$ от передней кромки пластины и на высоте ${{\hat {l}}_{d}} = \hat {L} \cdot l$ выше обтекаемой поверхности расположено малое тело, движущееся вниз по потоку с заданной постоянной скоростью ${{\hat {V}}_{d}} = {{\hat {V}}_{\infty }}{{u}_{W}}$, где ${{\hat {V}}_{\infty }}$ – скорость внешнего потока (фиг. 1).

Малое тело, создающее возмущение давления в потоке и соответственно на обтекаемой поверхности, заменим потенциальным диполем интенсивности $\hat {d} = {{\hat {V}}_{\infty }}{{\hat {L}}^{2}}m$. Комплексный потенциал w такого течения хорошо известен и имеет вид

$w = {{\hat {V}}_{\infty }}\hat {z} + \frac{{\hat {d}}}{{\hat {z} - (\hat {L} + i{{{\hat {l}}}_{d}})}} + \frac{{\hat {d}}}{{\hat {z} - (\hat {L} - i{{{\hat {l}}}_{d}})}}$, $\hat {z} = \hat {x} + i\hat {y}$.

А выражение для давления на обтекаемой поверхности пластины, введенное по формуле $\hat {p} = {{\hat {p}}_{\infty }} + \rho \hat {V}_{\infty }^{2}\bar {p}$, в безразмерных координатах $\left\{ {\bar {x},\bar {y}} \right\} = \left\{ {{{\hat {x}} \mathord{\left/ {\vphantom {{\hat {x}} {\hat {L}}}} \right. \kern-0em} {\hat {L}}},\,{{\hat {y}} \mathord{\left/ {\vphantom {{\hat {y}} {\hat {L}}}} \right. \kern-0em} {\hat {L}}}} \right\}$ следует из уравнения Бернулли

Далее в работе будем изучать режимы течения при малых высотах диполя над пластиной $l \to 0$, но, конечно, выше пограничного слоя, развивающегося вдоль обтекаемой поверхности вследствие действия сил вязкости. Если задать интенсивность диполя $m = {{l}^{{8/3}}}{{m}_{1}}$ такую, чтобы влияние возмущения давления было сопоставимо с вязкими и инерционными эффектами в вязком пристенном подслое пограничного слоя, и задать высоту положения диполя над поверхностью, бо́льшей по сравнению с размерами области взаимодействия ${{\operatorname{Re} }^{{ - {3 \mathord{\left/ {\vphantom {3 8}} \right. \kern-0em} 8}}}} \ll l \ll 1,$ $\operatorname{Re} = \hat {\rho }{{\hat {V}}_{\infty }}\hat {L}{\text{/}}\mu \to \infty $ (область 3, фиг. 1), то индуцированным давлением, обусловленным вытеснением вязкого подслоя, можно пренебречь и считать возмущение давления заданным исключительно диполем

В (2.1) введена новая нормированная продольная координата $\tilde {x}$, связанная с исходной по формуле $\bar {x} = 1 + l\tilde {x}$, а также из разложения давления отброшены члены более высокого порядка малости по параметру $l$.

При переходе в систему координат, движущуюся вместе с диполем вниз по потоку с малой постоянной скоростью ${{u}_{W}}$, заданное распределение давления (2.1) не изменится в главном приближении, так как нестационарные поправки к нему окажутся малыми. Однако при этом давление (2.1) будет воздействовать уже на вязкий пристенный подслой (область 1, фиг. 1), развивающийся на стенке, которая движется против потока со скоростью $ - {{u}_{W}}$. При ненулевой интенсивности диполя наблюдатель, движущийся вместе с ним, увидит вблизи обтекаемой стенки стационарное возмущенное течение с противотоками, качественно изображенное на фиг. 2.

Асимптотика решения уравнений Навье–Стокса в вязком подслое 1a–1b на дне пограничного слоя Блазиуса вблизи точки $\bar {x} = 1,$ $u_{{BLAS}}^{'}(0) = \lambda $ ищется при $l \to 0,$ $\operatorname{Re} \to \infty $ в виде

В результате подстановки (2.2) в уравнения Навье–Стокса задача в вязком подслое (область 1, фиг. 1) будет иметь следующий вид:

Задача (2.3) содержит два независимых параметра: $M$ – интенсивность диполя, ${{U}_{W}}$– скорость стенки. Искомая функция $A(\tilde {x})$ – это второй член координатного разложения решения при $\tilde {у} \to + \infty $ (называемый толщиной вытеснения вязкого подслоя), а $\tilde {p}$ – давление, заданное диполем. Уравнения вязкого подслоя (2.3) являются уравнениями параболического типа, однако из-за наличия противотоков начальные условия должны быть заданы с двух сторон: при $\tilde {x} \to + \infty $ и $\tilde {x} \to - \infty $. Соответственно использовать традиционный метод для решения системы (2.3) не удается.

3. МЕТОД РЕШЕНИЯ НЕЛИНЕЙНОЙ ЗАДАЧИ С ПРОТИВОТОКАМИ

Обозначим через $\tilde {y} = S(\tilde {x})$ заранее неизвестную кривую, в каждой точке которой горизонтальная скорость принимает нулевое значение. Таким образом, кривая $S(\tilde {x})$ делит исходную область на две подобласти 1a и 1b (см. фиг. 2), причем в области 1а, $\tilde {y} \in \left[ {0;S(\tilde {x})} \right]$, поток движется только в отрицательном направлении оси $O\tilde {x}$, а в области 1b, $\tilde {y} \in \left[ {S(\tilde {x}); + \infty } \right)$, – только в положительном направлении. В результате в случае заданного давления и известной функции $S(\tilde {x})$ можно сформулировать следующие краевые задачи в каждой из введенных областей по отдельности:

1а: $\tilde {u}\frac{{\partial{ \tilde {u}}}}{{\partial{ \tilde {x}}}} + \tilde {v}\frac{{\partial{ \tilde {u}}}}{{\partial{ \tilde {y}}}} = - \frac{{d\tilde {p}}}{{d\tilde {x}}} + \frac{{{{\partial }^{2}}\tilde {u}}}{{\partial {{{\tilde {y}}}^{2}}}}$, $\frac{{\partial{ \tilde {u}}}}{{\partial{ \tilde {x}}}} + \frac{{\partial{ \tilde {v}}}}{{\partial{ \tilde {y}}}} = 0$,

1b: $\tilde {u}\frac{{\partial{ \tilde {u}}}}{{\partial{ \tilde {x}}}} + \tilde {v}\frac{{\partial{ \tilde {u}}}}{{\partial{ \tilde {y}}}} = - \frac{{d\tilde {p}}}{{d\tilde {x}}} + \frac{{{{\partial }^{2}}\tilde {u}}}{{\partial {{{\tilde {y}}}^{2}}}}$, $\frac{{\partial{ \tilde {u}}}}{{\partial{ \tilde {x}}}} + \frac{{\partial{ \tilde {v}}}}{{\partial{ \tilde {y}}}} = 0$,

где ${{\tilde {v}}^{ - }}(\tilde {x},S(\tilde {x}))$ − вертикальная скорость на линии раздела, найденная из расчета течения в области 1a. Отметим, что на линии $\tilde {y} = S(\tilde {x})$ справедливо дополнительное краевое условие, связывающее касательные напряжения снизу и сверху от искомой кривой (в нашем случае имеет место равенство этих величин, поскольку иначе на данной линии будет приложена касательная сила, что не физично). В выбранных переменных указанное краевое условие имеет вид Задача (2.3) при нулевой интенсивности диполя ($M = 0$) допускает точное решение вида $\tilde {u} = - {{U}_{W}} + \tilde {y},$ $\tilde {v} = \tilde {p} = S - {{U}_{W}} = A = 0$. Если диполь имеет отличную от нуля малую интенсивность, то он слабо возмущает само течение и границу между областями 1a и 1b. Далее построим решение линеаризованной задачи при условии малой интенсивности диполя. Такое решение может быть выписано в замкнутом аналитическом виде и, таким образом, является удобным для проверки численного решения нелинейной задачи.

Введем функцию тока $\Psi $: $\tilde {u} = {{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial{ \tilde {y}}}}} \right. \kern-0em} {\partial{ \tilde {y}}}}$, $\tilde {v} = - {{\partial \Psi } \mathord{\left/ {\vphantom {{\partial \Psi } {\partial{ \tilde {x}}}}} \right. \kern-0em} {\partial{ \tilde {x}}}}$ и в качестве первого шага построим решение задачи с диполем малой интенсивности при $M \to 0$. Функция тока $\Psi $ представляется в виде ряда по $M$, а скорость движения стенки ${{U}_{W}}$ фиксирована. В случае решения линейной задачи граница раздела противотоков $\tilde {y} = S(\tilde {x})$ сносится на линию $\tilde {y} = {{U}_{W}}$, и задача сильно упрощается, позволяя применить для решения операционный метод

Подставив (3.4) в уравнения и граничные условия (2.3) и отбросив квадратичные по M члены, получим следующую линейную задачу:

где поправка ${{S}_{1}}(\tilde {x})$ находится из условия равенства нулю горизонтальной скорости на линии раздела противотоков. Линейную задачу (3.5) будем решать методом преобразования Фурье. Применяя это преобразование и обозначая фурье-образы искомых функций через

${{\hat {\Psi }}_{1}}(\alpha ,\tilde {y}) = {1 \mathord{\left/ {\vphantom {1 {\sqrt {2\pi } }}} \right. \kern-0em} {\sqrt {2\pi } }}\int_{ - \infty }^{ + \infty } {{{\Psi }_{1}}(\tilde {x},\tilde {y})} \,{{e}^{{ - i\,\alpha \tilde {x}}}}d\tilde {x}$   и   ${{\tilde {S}}_{1}}(\alpha ) = {1 \mathord{\left/ {\vphantom {1 {\sqrt {2\pi } }}} \right. \kern-0em} {\sqrt {2\pi } }}\int_{ - \infty }^{ + \infty } {{{S}_{1}}(\tilde {x})} \,{{e}^{{ - i\,\alpha \tilde {x}}}}d\tilde {x}$,

получим краевую задачу в областях 1а и 1b

Решая ее, находим искомые фурье-образы функций тока и скоростей по формулам В (3.7), (3.8) использованы следующие вспомогательные функции и константы: Здесь $Ai(z)$ – функция Эйри (см. [10]), а через ${{\tilde {P}}_{1}},\,\,{{\tilde {S}}_{1}},\,\,{{\tilde {A}}_{1}}$ обозначены образы возмущений давления, границы противотоков и толщины вытеснения. Применение обратного преобразования Фурье к (3.7), (3.8) позволит получить линейные возмущения решения, удобные для проверки точности численного метода.

4. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНОЙ ЗАДАЧИ

Выполним следующие преобразования координат и искомых скоростей, которые упрощают численное решение рассматриваемой задачи (3.1)–(3.3):

После преобразований (4.1) структура областей в вязком подслое существенно упрощается, так как граница раздела разнонаправленных потоков (областей 1a и 1b) в новых координатах проходит по прямой линии $Y = 1$, а задача (3.1)–(3.3) принимает следующий вид:

В вязком подслое была введена равномерная прямоугольная сетка с координатами $\{ {{x}_{i}} \in [ - 20;20],\;i = 1,...,Nx;\;{{Y}_{j}} \in [0;1],\;j = 1,...,N{{y}_{a}}\} $ в области 1a и $\{ {{x}_{i}} \in [ - 20;20],\;i = 1,...,Nx;$ ${{Y}_{j}} \in [1;11],\;j = 1,...,N{{y}_{b}}\} $ в области 1b. Для некоторой заданной сеточной функции формы границы раздела $\{ {{S}_{i}},\;i = 1,...,Nx\} $ численное решение задачи (4.2)–(4.4) проводилось в два этапа. На первом этапе решалась краевая задача (4.2) в области 1a, где поток направлен в отрицательном направлении вдоль оси $Ox$. Для ее решения использовалась разностная схема, аналогичная предложенной в [11]:

Начальные условия для (4.5) задавались в сечениях $x = {{x}_{{Nx}}}$ и $x = {{x}_{{Nx - 1}}}$: $U_{N}^{j} = - {{S}_{N}}{{U}_{W}} + S_{N}^{2}{{Y}_{j}}$, $U_{{N - 1}}^{j} = - {{S}_{{N - 1}}}{{U}_{W}} + S_{{N - 1}}^{2}{{Y}_{j}}$, $j = 2,...,N{{y}_{a}} - 1$, затем решение искалось маршевым способом, используя метод Ньютона в каждом сечении $x = {{x}_{i}}$. Производная $S_{i}^{'}$ аппроксимировалась с помощью центральных разностей со вторым порядком точности.

Далее полученные из решения задачи (4.5) значения вертикальной скорости на границе раздела $Y = 1$ $\{ \,V_{i}^{{{{N}_{{ya}}}}},\,\,i = 1,...,Nx\,\} $ использовались в качестве граничных условий для численного решения задачи (4.3) в области 1b, где поток направлен в положительном направлении вдоль оси $Ox$. Для решения краевой задачи (4.3) применялся маршевый метод слева направо, использующий аналогичную разностную схему из [11]:

Начальные условия для задачи (4.6) задавались в сечениях $x = {{x}_{1}}$ и $x = {{x}_{2}}$:$U_{1}^{j} = - {{S}_{1}}{{U}_{W}} + S_{1}^{2}{{Y}_{j}},$ $U_{2}^{j} = - {{S}_{2}}{{U}_{W}} + S_{2}^{2}{{Y}_{j}},$ $j = 2,...,N{{y}_{b}} - 1$.

После решения задач (4.5) и (4.6) при заданной форме границы можно вычислить значения касательных напряжений ниже и выше границы раздела противотоков $Y = 1$ и их невязку:

Из условия непрерывности касательного напряжения на границе раздела противотоков (4.4) следует, что величина (4.8) должна обращаться в нуль в каждой точке сетки. В результате в качестве второго этапа расчета можно сформулировать систему неявных уравнений для нахождения искомой формы границы $\{ {{S}_{i}},i = 3,...,Nx - 2\} $:

Для того чтобы решить систему нелинейных неявных уравнений (4.9) методом Ньютона, возникает нетривиальный вопрос о способе вычисления матрицы Якоби. В работе предлагается поточечно возмущать границу ${{S}_{i}}$ малым возмущением $\delta $ и для каждой возмущенной в одной точке границы вычислять вектор невязки (4.9). Разница между возмущенным вектором невязки и невозмущенным вектором невязки (4.9), деленная на $\delta $, даст столбец матрицы Якоби. Повторение указанной операции для всех $i$ позволит полностью заполнить матрицу Якоби на текущей итерации метода Ньютона. При описанном выше способе итерационная формула метода Ньютона будет иметь вид

где ${{\bar {S}}^{{(k)}}} = {{[\,S_{3}^{{(k)}},\,\,...,\,\,S_{{Nx - 2}}^{{(k)}}\,]}^{{\text{т}}}}$ − вектор значений сеточной функции формы границы на k-й итерации метода Ньютона, $\Delta {{\bar {S}}^{{(k)}}} = {{\bar {S}}^{{(k + 1)}}} - {{\bar {S}}^{{(k)}}}$, $\bar {F}({{\bar {S}}^{{(k)}}}) = {{[{{F}_{3}}({{\bar {S}}^{{(k)}}}),...,{{F}_{{Nx - 2}}}({{\bar {S}}^{{(k)}}})]}^{{\text{т}}}}$− вектор значений невязок (4.8) , $W({{\bar {S}}^{{(k)}}})$ − матрица Якоби. Компоненты матрицы Якоби $W({{\bar {S}}^{{(k)}}})$ вычислялись следующим образом: где ${{F}_{{2 + n}}}(\,{{\bar {S}}^{{(k)}}}\,)$ − значение невязки в точке $x = {{x}_{{2 + n}}}$ для невозмущенной границы ${{\bar {S}}^{{(k)}}} = {{[S_{3}^{{(k)}},..,S_{{2 + m}}^{{(k)}},..,S_{{Nx - 2}}^{{(k)}}]}^{{\text{т}}}}$ из (4.8), ${{F}_{{2 + n}}}(\,\bar {S}_{{2 + m}}^{{(k)}}\,)$ − значение невязки в точке $x = {{x}_{{2 + n}}}$, вычисленное для формы границы, возмущенной в точке $x = {{x}_{{2 + m}}}$: $\bar {S}_{{2 + m}}^{{(k)}} = {{[S_{3}^{{(k)}},...,S_{{2 + m}}^{{(k)}} + \delta ,...,S_{{Nx - 2}}^{{(k)}}]}^{{\text{т}}}}$.

5. РЕЗУЛЬТАТЫ РАСЧЕТОВ

С помощью предложенной схемы были выполнены расчеты для различных значений параметра $M$. Сравнение численного решения для $M = 0.01$ с решением линейной задачи (3.8) показало хорошее совпадение результатов (фиг. 3).

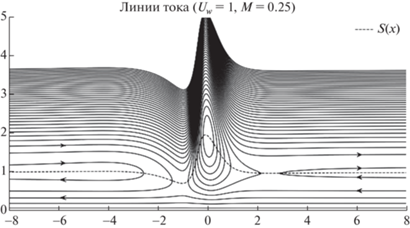
Также была проведена серия расчетов для значений параметров $M = 0.1$, 0.15, 0.25, 0.35, проявляющих нелинейный режим течения. Были построены картины линий тока в вязком подслое (область 1), на которых вблизи линии нулевой скорости видны замкнутая и две разомкнутые висячие отрывные зоны (фиг. 4). Из расчетов следует, что поперечный размер замкнутой висячей зоны отрыва существенно нарастает с увеличением значения параметра $M$.

Кроме того, численное решение показало заметное уменьшение касательного напряжения и увеличение значения вертикальной скорости в некоторой точке на линии раздела противотоков $\tilde {y} = S(\tilde {x})$ с ростом интенсивности диполя $M$ (фиг. 5). В этой же точке заметно нарастала производная функции $\tilde {y} = S(\tilde {x})$, а сама точка формировалась на фоне падающего давления, что свидетельствует о формировании особенности нового типа.

6. ВЫВОДЫ

Исследована детальная структура течения в вязком подслое с противотоками при заданном градиенте давления. Получены картины висячей замкнутой и двух разомкнутых отрывных зон для всех рассчитанных режимов. В отличие от течений на неподвижной стенке, в которых отрывы присоединены к поверхности, линия нулевой продольной скорости в изученных режимах находится внутри потока и, как следствие, отрывные зоны висячие. Отметим, что для любого $M > 0$ топологическая картина линий тока неизменна и отлична от невозмущенного течения, что подтверждается решением линейной задачи.

Обнаружен значительный вертикальный рост замкнутой зоны отрыва при увеличении заданного давления. Выявлено формирование сингулярности в картине течения вблизи точки минимума напряжения на границе раздела противотоков: с ростом заданного давления, вертикальная скорость заметно возрастает, наклон границы раздела противотоков также заметно возрастает, напряжение трения убывает до малых величин. Заданный градиент давления имеет отрицательную величину в изучаемой точке, что предполагает формирование особенности нового типа. Эта особенность, по-видимому, отлична от сингулярностей, исследованных Гольдштейном и Рубаном.