Журнал вычислительной математики и математической физики, 2023, T. 63, № 2, стр. 317-326

Коэффициент аналогии Рейнольдса в продольной цилиндрической задаче Куэтта: от режима сплошной среды до свободномолекулярного

А. А. Абрамов¹, В. Ю. Александров¹, А. В. Бутковский^1, *

¹ ЦАГИ
140180 М.о., Жуковский, ул. Жуковского, 1, Россия

Поступила в редакцию 26.07.2022
После доработки 26.07.2022
Принята к публикации 10.10.2022

EDN: BRDVJQ
DOI: 10.31857/S0044466923020023

Аннотация

Рассмотрено течение Куэтта газа для цилиндрической геометрии ограничивающих поверхностей, движущихся в продольном направлении относительно их оси симметрии. Для одноатомного газа исследована связь (аналогия Рейнольдса) между напряжением трения и потоком энергии, передаваемым обтекаемой поверхности. В случае течения сплошной среды и в случае свободномолекулярного течения в явном виде получены простые аналитические выражения для коэффициента аналогии Рейнольдса, зависящие только от числа Эккерта и не зависящие от отношения радиусов цилиндров. Для различных значений числа Кнудсена с помощью метода прямого статистического моделирования (DSMC) изучен переходный режим течения. Показано, что в этом случае коэффициент аналогии Рейнольдса при фиксированных значениях отношения радиусов и числа Кнудсена зависит от относительной скорости и температур поверхностей главным образом через число Эккерта. Найдено соотношение ме-жду погонными потоками энергии, передаваемой цилиндрическим поверхностям. Библ. 17. Фиг. 7.

Ключевые слова: аналогия Рейнольдса, продольное цилиндрическое течение Куэтта, число Эккерта, число Кнудсена, прямое статистическое моделирование.

1. ВВЕДЕНИЕ

Для плоского течения Куэтта, описываемого в рамках уравнений Навье–Стокса, связь между напряжением трения и потоком энергии, передаваемых пластине (аналогия Рейнольдса) хорошо известна при любом соотношении температур пластин [1], [2]. В случае одинаковых температур пластин этот результат означает, что потоки энергии, передаваемые пластинам, равны друг другу и равны половине произведения напряжения сдвига и относительной скорости пластин [1–3]. В настоящее время с развитием нанотехнологий возрастает интерес к передаче тепла в микроканалах [4–7]. В этой связи представляют интерес и исследования аналогии Рейнольдса для течений разреженного газа. Аналогия Рейнольдса при сверхзвуковом обтекании пластины потоком разреженного газа рассматривалась в [8], [9], а при обтекании затупленного тела в [10]. Аналогия Рейнольдса для течения Рэлея разреженного газа исследовалась в [11]. Плоское течение Куэтта разреженного газа рассматривалось в работе [12], в которой численно (с точностью до статистической флуктуации) показано, что единственными параметрами подобия для коэффициента аналогии Рейнольдса во всех рассмотренных случаях являются числа Эккерта Ec и Кнудсена Kn. В данной работе анализируются различные режимы течения продольного цилиндрического течения Куэтта. Целью статьи является исследование свойств аналогии Рейнольдса и свойств отношений величин погонных потоков энергий, передаваемых граничным поверхностям.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается установившееся течение Куэтта разреженного одноатомного газа между двумя соосными цилиндрами. Внутренний цилиндр радиуса ${{r}_{{\text{1}}}}$ и температуры ${{T}_{{\text{1}}}}$ находится в покое. Внешний цилиндр радиуса ${{r}_{{\text{2}}}}$ и температуры ${{T}_{{\text{2}}}}$ движется со скоростью ${{u}_{{{\text{rel}}}}}$ параллельной оси z. Средняя плотность газа и средняя числовая плотность газа равны соответственно ρ_av и n_av.

Для рассматриваемой конфигурации течение газа описывается уравнением Больцмана для функции распределения молекул по скоростям f, записанным в цилиндрической системе координат (r, φ, z):

(1)

${{{v}}_{r}}\frac{{\partial f}}{{\partial r}} + \frac{{{v}_{\varphi }^{2}}}{r}\frac{{\partial f}}{{\partial {{{v}}_{r}}}} - \frac{{{{{v}}_{r}}{{{v}}_{\varphi }}}}{r}\frac{{\partial f}}{{\partial {{{v}}_{\varphi }}}} = J(f,f{\kern 1pt} '),$

где r – расстояние от оси z, φ – азимутальная координата, а z-ось цилиндрической системы координат совпадает с общей осью цилиндров. Считаем, что молекулы отражаются от поверхностей диффузно с температурой, равной температуре поверхности:

(2)

$f = {{f}_{1}} = {{n}_{1}}{{(2\pi {{R}_{{{\text{gas}}}}}{{T}_{1}})}^{{ - 3/2}}}\exp \left[ { - \frac{{{v}_{r}^{2} + {{{v}}_{\varphi }}^{2} + {v}_{z}^{2}}}{{2{{R}_{{{\text{gas}}}}}{{T}_{1}}}}} \right],\quad {{{v}}_{r}} > 0,\quad r = {{r}_{1}},$

(3)

$f = {{f}_{2}} = {{n}_{2}}{{(2\pi {{R}_{{{\text{gas}}}}}{{T}_{2}})}^{{ - 3/2}}}\exp \left[ { - \frac{{{v}_{r}^{2} + {{{v}}_{\varphi }}^{2} + {{{({{{v}}_{z}} - {{u}_{{rel}}})}}^{2}}}}{{2{{R}_{{{\text{gas}}}}}{{T}_{2}}}}} \right],\quad {{{v}}_{r}} < 0,\quad r = {{r}_{2}}.$

Здесь J(f, f') – интеграл столкновений молекул [13]; ${{{v}}_{r}}$, ${{{v}}_{\varphi }}$, и ${{{v}}_{z}}$ – компоненты скоростей молекул в цилиндрической системе координат; ${{R}_{{{\text{gas}}}}}$ – газовая постоянная, параметры функции распределения n₁и n₂ находятся из условий баланса между падающими и отраженными молекулами. Используется молекулярная модель “твердые сферы”. Для этой модели средняя длина свободного пробега молекул $\lambda = {{(\sqrt 2 {{n}_{{{\text{av}}}}}{{\sigma }_{{{\text{sp}}}}})}^{{ - 1}}}$, где ${{\sigma }_{{{\text{sp}}}}}$ – сечение столкновения. Изучается поведение напряжения трения и потока энергии ${{P}_{{z{\kern 1pt} r}}}(r)$, $E(r)$:

${{P}_{{z{\kern 1pt} r}}}\left( r \right) = \int {m{{{v}}_{z}}{{{v}}_{r}}} f({\mathbf{v}},r)d{\mathbf{v}},\quad E(r) = \int {{{{v}}_{r}}} \frac{{m({v}_{r}^{2} + {v}_{\varphi }^{2} + {v}_{z}^{2})}}{2}f({\mathbf{v}},r)d{\mathbf{v}},$

где $d{\mathbf{v}} = d{{{v}}_{r}}d{{{v}}_{\varphi }}d{{{v}}_{z}}$, m – масса молекулы.

3. ВЗАИМОСВЯЗЬ МЕЖДУ ГИДРОДИНАМИЧЕСКИМИ ПЕРЕМЕННЫМИ

Напряжения сдвига ${{P}_{{zn{\text{1}}}}}(r),$ ${{P}_{{zn{\text{2}}}}}(r)$ и потоки энергии, передаваемые цилиндрам E₁, E₂ равны:

(4)

${{P}_{{zn{\text{1}}}}} = - {{P}_{{zr}}}({{r}_{1}}),\quad {{P}_{{zn{\text{2}}}}} = {{P}_{{zr}}}({{r}_{2}}),$

(5)

${{E}_{1}} = - E({{r}_{1}}),\quad {{E}_{2}} = \int {{{{v}}_{r}}\frac{{m[{v}_{r}^{2} + {{{v}}_{\varphi }}^{2} + {{{({{{v}}_{z}} - {{u}_{{{\text{rel}}}}})}}^{2}}]}}{2}} f({\mathbf{v}},{{r}_{2}})d{\mathbf{v}}.$

Величина потока энергии зависит от выбора системы координат. Здесь и далее под “потоком энергии, передаваемым цилиндру”, как и в [14], понимается поток энергии в системе координат, связанной с цилиндром. Это значение совпадает со скоростью изменения внутренней энергии цилиндра на единицу площади, если другая сторона поверхности цилиндра термически изолирована.

Взяв моменты в уравнении Больцмана, можно получить уравнения баланса для продольного импульса и энергии:

(6)

$\frac{d}{{dr}}\left( {r{{P}_{{rz}}}(r)} \right) = 0,$

(7)

$\frac{d}{{dr}}\left( {rE} \right) = 0.$

Интегрируя (6), находим с учетом (4), что напряжение сдвига на внешнем цилиндре пропорционально напряжению сдвига на внутреннем цилиндре:

(8)

${{P}_{{zn{\text{2}}}}} = - {{P}_{{zn{\text{1}}}}}{\text{/}}\beta ,$

где β = r₂/r₁.

Используя условие непроницаемости, легко убедиться, что

$\begin{gathered} \int {{{{v}}_{r}}\frac{{m[{v}_{r}^{2} + {v}_{\varphi }^{2} + {v}_{z}^{2}]}}{2}} f({\mathbf{v}},{{r}_{2}})d{\mathbf{v}} = \int {{{{v}}_{r}}\frac{{m[{v}_{r}^{2} + {v}_{\varphi }^{2} + {{{({{{v}}_{z}} - {{u}_{{{\text{rel}}}}})}}^{2}}]}}{2}} f({\mathbf{v}},{{r}_{2}})d{\mathbf{v}} + \\ \, + {{u}_{{{\text{rel}}}}}\int {m{{{v}}_{r}}{{{v}}_{z}}f({\mathbf{v}},{{r}_{2}})d{\mathbf{v}}} - mu_{2}^{2}\int {{{{v}}_{r}}f({\mathbf{v}},{{r}_{2}}} )d{\mathbf{v}} = {{E}_{2}} + {{P}_{{nz2}}}{{u}_{{{\text{rel}}}}}. \\ \end{gathered} $

Интегрируя (7), находим, что

$\int {{{{v}}_{r}}\frac{{m[{v}_{r}^{2} + {v}_{\varphi }^{2} + {v}_{z}^{2}]}}{2}} f({\mathbf{v}},{{r}_{2}})d{\mathbf{v}} = \beta \int {{{{v}}_{r}}\frac{{m({v}_{r}^{2} + {v}_{\varphi }^{2} + {v}_{z}^{2})}}{2}} f({\mathbf{v}},{{r}_{2}})d{\mathbf{v}}.$

Таким образом, с учетом (5) получаем

(9)

${{E}_{2}} = - \frac{{{{E}_{1}}}}{\beta } + \frac{{{{P}_{{zn1}}}}}{\beta }{{u}_{{{\text{rel}}}}}.$

Далее исследуется коэффициент аналогии Рейнольдса для внутреннего цилиндра, определяемый по формуле:

$R = \frac{{{{E}_{{\text{1}}}}}}{{{{P}_{{zn{\text{1}}}}}{{u}_{{{\text{rel}}}}}}}.$

Используя соотношения (8) и (9), можно легко выразить через $R$ аналогичный коэффициент аналогии Рейнольдса для внешнего цилиндра.

4. РЕЖИМ СПЛОШНОЙ СРЕДЫ И СВОБОДНОМОЛЕКУЛЯРНЫЙ РЕЖИМ

В режиме сплошной среды (${\text{Kn}} \to {\text{0}}$) краевая задача для уравнения Больцмана (1)–(3) сводится к краевой задаче для уравнений Навье-Стокса:

(10)

$\frac{{dp}}{{dr}} = 0,$

(11)

$\frac{d}{{dr}}\left( {r\mu \frac{{du}}{{dr}}} \right) = 0,$

(12)

$\frac{d}{{dr}}\left( {rk\frac{{dT}}{{dr}} + ru\mu \frac{{du}}{{dr}}} \right) = 0$

с граничными условиями прилипания на цилиндрах

(13)

$u({{r}_{1}}) = 0;\quad u({{r}_{2}}) = {{u}_{{{\text{rel}}}}}.$

Здесь $u$, $p$ и $T$ – скорость, давление и температура газа соответственно; μ – коэффициент динамической вязкости, $k$ – коэффициент теплопроводности.

Коэффициент аналогии Рейнольдса для плоского течения Куэтта получен в [1], [2]. После несложных преобразований соответствующее соотношение из [1], [2] принимает вид

$R = \frac{1}{2} - \frac{1}{{\Pr {\text{Ec}}}}.$

Здесь $\Pr = \mu {{c}_{p}}{\text{/}}k$ – число Прандтля; ${{c}_{p}}$ – теплоемкость при постоянном давлении. Для одноатомного газа ${{c}_{p}} = 5R{\text{/}}2$, $\Pr = 0.661$; ${\text{Ec}} = u_{{{\text{rel}}}}^{2}{\text{/}}[{{c}_{p}}({{T}_{1}} - {{T}_{2}})]$ – число Эккерта.

Результаты [1], [2] легко обобщаются на случай продольного цилиндрического течения Куэтта. Действительно, из (12), (13) следует, что

(14)

$k\frac{{dT}}{{dr}} + \mu u\frac{{du}}{{dr}} = \frac{{{{r}_{{\text{1}}}}{{E}_{{\text{1}}}}}}{r}.$

Так как число Прандтля постоянно, из (14) следует, что

(15)

$k\frac{{dT}}{{dr}} + \mu u\frac{{du}}{{dr}} = \mu \frac{d}{{dr}}\left( {\frac{{{{c}_{p}}T}}{{\Pr }} + \frac{{{{u}^{2}}}}{2}} \right) = \frac{{{{r}_{{\text{1}}}}{{E}_{{\text{1}}}}}}{r}.$

Интегрируя (15) по радиусу от ${{r}_{{\text{1}}}}$ до ${{r}_{{\text{2}}}}$, получаем

${{c}_{p}}\left( {{{T}_{2}} - {{T}_{1}}} \right) + \frac{{\Pr u_{{{\text{rel}}}}^{{\text{2}}}}}{2} = \Pr {{r}_{1}}{{E}_{1}}\int\limits_{{{r}_{1}}}^{{{r}_{2}}} {\frac{{dr}}{{\mu (T(r))r}}} .$

Принимая во внимание, что

${{u}_{{{\text{rel}}}}} = {{r}_{1}}{{P}_{{zn1}}}\int\limits_{{{r}_{1}}}^{{{r}_{2}}} {\frac{{dr}}{{\mu (T(r))r}}} ,$

находим

${{c}_{p}}\left( {{{T}_{2}} - {{T}_{1}}} \right) + \frac{{\Pr u_{{{\text{rel}}}}^{2}}}{2} = \frac{{\Pr {{u}_{{{\text{rel}}}}}{{E}_{1}}}}{{{{P}_{{zn1}}}}}.$

В результате получаем, что:

(16)

$R = \frac{1}{2} - \frac{1}{{\Pr }}\frac{1}{{{\text{Ec}}}}.$

Свободномолекулярное продольное цилиндрическое течение Куэтта изучалось в [15]. Из результатов [15], для коэффициента аналогии Рейнольдса следует формула:

(17)

$R = \frac{1}{2} - \frac{{\kappa + 1}}{{2\kappa }}\frac{1}{{{\text{Ec}}}},$

где $\kappa $ – показатель адиабаты. Для одноатомного газа $\kappa = 5{\text{/}}3$.

Таким образом, для продольного цилиндрического течения Куэтта коэффициент аналогии Рейнольдса, как в режиме сплошной среды, так и в свободномолекулярном режиме, не зависит от величины отношения радиусов цилиндров $\beta $ и совпадает с соответствующим значением коэффициента аналогии Рейнольдса для плоского течения Куэтта.

5. ПЕРЕХОДНЫЙ РЕЖИМ

Из анализа размерностей следует, что коэффициент аналогии Рейнольдса зависит не более чем от трех безразмерных переменных:

$t = \frac{{{{T}_{1}}}}{{{{T}_{2}}}},\quad U = \frac{{{{u}_{{{\text{rel}}}}}}}{с},\quad {\text{Kn}} = \frac{\lambda }{L},\quad {\text{где}}\quad c = \sqrt {2{{R}_{{{\text{gas}}}}}{{T}_{2}}} ,\quad L = {{r}_{2}} - {{r}_{1}}.$

Как показано в разд. 4, в режиме сплошной среды и свободномолекулярном режиме ${{T}_{1}},\,\,{{T}_{2}}$ и ${{u}_{{{\text{rel}}}}}$ влияют на коэффициент аналогии Рейнольдса только через число Эккерта. В [12] численно показано, что это же свойство справедливо (с точностью до статистических флуктуаций) и во всех рассмотренных в [12] случаях переходного режима плоского течения Куэтта. Выясним, в какой мере обладает этим свойством продольное цилиндрическое течение Куэтта.

Для этого численно методом прямого статистического моделирования [14] решим задачу Куэтта (1)–(3) при разных значениях ${{T}_{1}},\,\,{{T}_{2}}$, ${{u}_{{{\text{rel}}}}}$, но при одних и тех же числах Эккерта. Мы используем схему Берда [14], [16]. Пространство между цилиндрическими поверхностями разбивается на ячейки. Размер ячеек варьируется от $\lambda t{\text{/}}(6U)$ для $U > 1,$ $t < 1$, до $\lambda {\text{/}}6$ при $U \leqslant 1,$ $t \geqslant 1$. Число моделирующих молекул в ячейке варьируется от 100 до 1000. Шаг по времени варьируется от $\lambda t{\text{/}}(6Uc)$ для $U > 1,$ $t < 1$ до $\lambda {\text{/}}(6c)$ при $U \leqslant 1,$ $t \geqslant 1$. Количество отражений молекул от внутреннего цилиндра составляет 64 000 000. Погрешность вычислений в основном менее 1%. Расчеты проводились на персональном компьютере Intel Core i7, 3.5 ГГц. Время расчета зависит от местного числа Кнудсена вблизи внешнего цилиндра и обычно варьируется от получаса до суток.

Фиг. 1.

Схема продольного цилиндрического течения Куэтта.

Рассмотрим вначале важный случай равных температур, т.е. ${{T}_{1}} = {{T}_{2}}$. Как видно из (16) и (17), в свободномолекулярном пределе, также как и в навье-стоксовом $R = 1{\text{/}}2$, при любом $\beta $. Зависимости коэффициента аналогии Рейнольдса от числа Кнудсена в диапазоне от 0.01 до 100 для $t = 1$ и различных $U$ и $\beta $ приведены на фиг. 2. Аналогия Рейнольдса близка к 1/2 для всех рассмотренных $\beta $, но, в отличие от плоского случая ($\beta = 1$), она не равна 1/2. По мере увеличения $\beta $ значение $R$ уменьшается.

Фиг. 2.

Зависимость коэффициента аналогии Рейнольдса R от числа Кнудсена в случае одинаковых температур цилиндрических поверхностей для различных значений скорости U и отношения радиусов β.

Зависимости $R$ от Kn показаны на фиг. 3, 4 для различных значений $U$ и $t$. Величины $R$ для одноатомного газа описываемого уравнениями Навье-Стокса показаны отрезками сплошной линии. Штриховые отрезки соответствуют значениям $R$ для свободномолекулярного течения. Коэффициент аналогии Рейнольдса $R$ может быть положительным при всех Kn, отрицательным при всех Kn, или даже, как функция Kn, может менять знак при некоторых значениях Kn (см. фиг. 4). Последнее обусловлено эффектом перемены знака потока энергии в течении Куэтта разреженного газа [17].

Фиг. 3.

Зависимость коэффициента аналогии Рейнольдса R от числа Кнудсена при различных температурах и скоростях для $\left| {{\text{Ec}}} \right| = 0.5$ и $\left| {{\text{Ec}}} \right| = 1$.

Фиг. 4.

Зависимость коэффициента аналогии Рейнольдса R от числа Кнудсена при различных температурах и скоростях для $\left| {{\text{Ec}}} \right| = 2$.

Из фиг. 2–4 видно, что во всех рассмотренных случаях относительная скорость и температуры поверхностей влияют на коэффициент аналогии Рейнольдса в основном через число Эккерта. Поэтому естественно сделать предположение, что коэффициент аналогии Рейнольдса является функцией, главным образом, трех независимых параметров ($\beta $, Kn, Ec), а не четырех ($\beta $, Kn, $t$_,$U$).

Исходя из результатов расчетов, представленных на фиг. 2, 4 , можно заключить, что отношение радиусов цилиндров, число Эккерта и число Кнудсена являются основными независимыми параметрами подобия для коэффициента аналогии Рейнольдса в продольной цилиндрической задаче Куэтта.

Из данных на фиг. 3, 4 видно, что для всех рассмотренных параметров коэффициент аналогии Рейнольдса находится между его свободномолекулярным и его навье-стоксовым значением:

$\min \left[ {\left( {\frac{1}{2} - \frac{1}{{\Pr }}\frac{1}{{{\text{Ec}}}}} \right),\;\left( {\frac{1}{2} - \frac{{\kappa + 1}}{{2\kappa }}\frac{1}{{{\text{Ec}}}}} \right)} \right] < R < \max \left[ {\left( {\frac{1}{2} - \frac{1}{{\Pr }}\frac{1}{{{\text{Ec}}}}} \right),\;\left( {\frac{1}{2} - \frac{{\kappa + 1}}{{2\kappa }}\frac{1}{{{\text{Ec}}}}} \right)} \right].$

Результаты, представленные на фиг. 2–4 , позволяют модифицировать коэффициент аналогии Рейнольдса R путем его нормализации, введя величину

${{R}_{m}} = \left( {\frac{1}{2} - \frac{{\kappa + 1}}{{2\kappa }}\frac{1}{{{\text{Ec}}}} - \frac{{{{E}_{{\text{1}}}}}}{{{{p}_{{zn1}}}{{u}_{{{\text{rel}}}}}}}} \right){\text{Ec}}\,{\text{.}}$

В дальнейшем ${{R}_{m}}$ будем называть модифицированным коэффициентом аналогии Рейнольдса. Зависимости ${{R}_{m}}$ от Kn показаны на фиг. 5 для различных значений ${\text{Ec}}$ и $\beta $.

Фиг. 5.

Зависимость модифицированного коэффициента аналогии Рейнольдса ${{R}_{{\text{m}}}}$ от числа Кнудсена при различных значениях числа Эккерта и различных отношениях радиусов: a – для $\beta = 2$; б – для $\beta = 4$.

Как видно из фиг. 5, модифицированный коэффициент аналогии Рейнольдса зависит в основном от величин $\beta $ и Kn для всех рассмотренных чисел Эккерта. Естественно предположить, что отношение радиусов и число Кнудсена являются основными параметрами подобия для модифицированного коэффициента аналогии Рейнольдса для продольной цилиндрической задачи Куэтта. В силу вышесказанного, для всех рассмотренных значений U, $t$ и Kn

(18)

$\frac{{{{E}_{1}}}}{{{{p}_{{zn1}}}{{U}_{r}}}} \approx \frac{1}{2} - \frac{{\kappa + 1}}{{2\kappa }}\frac{1}{{{\text{Ec}}}} - \frac{{{{R}_{m}}({\text{Kn,}}\beta )}}{{{\text{Ec}}}}.$

Таким образом, введение модифицированного коэффициента аналогии Рейнольдса позволяет разделить влияние числа Эккерта и числа Кнудсена на коэффициент аналогии Рейнольдса при заданном отношении радиусов цилиндров.

Из (18) получаем еще одно свойство коэффициента аналогии Рейнольдса для течения Куэтта:

(19)

$R({\text{Ec}},{\text{Kn,}}\beta ) + R( - {\text{Ec}},{\text{Kn,}}\beta ) \approx 1.$

6. ОТНОШЕНИЕ ПОГОННЫХ ПОТОКОВ ЭНЕРГИЙ

Отношение значений погонных потоков энергий, передаваемых поверхностям, дается выражением $Q = {{E}_{{\text{2}}}}\beta {\text{/}}{{E}_{{\text{1}}}}$. Погонный поток энергии – это количество энергии, подводимой к поверхности цилиндра в единицу времени на единицу длины в продольном направлении.

Легко убедиться, что в свободномолекулярном режиме

(20)

$Q({\text{Ec}}) = - 1 + \frac{{2{\text{Ec}}}}{{1 + {{\kappa }^{{ - 1}}} + {\text{Ec}}}},$

а в режиме сплошной среды имеем

(21)

$Q({\text{Ec}}) = - 1 + \frac{{2{\text{Ec}}}}{{2{{{\Pr }}^{{ - 1}}} + {\text{Ec}}}}.$

Таким образом, отношение погонных потоков энергий, передаваемых поверхностям, как в режиме сплошной среды, так и в свободномолекулярном режиме продольного цилиндрического течения Куэтта зависит только от числа Эккерта (Pr и $\kappa $ фиксированы) и совпадает с отношением потоков энергии, передаваемых пластинам в соответствующей плоской задаче Куэтта. По мере увеличения числа ${\text{Ec}} \geqslant {\text{0}}$, отношения (20) и (21) монотонно изменяются от –1 (${\text{Ec = 0}}$ (случай неподвижных цилиндров)) до 1 (${\text{Ec}} \to \infty $ (случай равных температур)), см. фиг. 6.

Фиг. 6.

Зависимость отношения величин погонных потоков энергий, передаваемых цилиндрическим поверхностям, от числа Эккерта ${\text{Ec}} > 0$ для свободномолекулярного течения (1) и течения сплошной среды (2).

Из (9) следует, что

$Q({\text{Ec}},{\text{Kn,}}\beta ) = \frac{{1 - R({\text{Ec}},{\text{Kn,}}\beta )}}{{R({\text{Ec}},{\text{Kn,}}\beta )}}.$

Принимая во внимание (19), находим, что

$Q( - {\text{Ec}},{\text{Kn,}}\beta ) \approx \frac{{R({\text{Ec}},{\text{Kn,}}\beta )}}{{1 - R({\text{Ec}},{\text{Kn,}}\beta )}}.$

Отсюда за исключением случаев $R \ll 1$ и $R \approx 1$ получаем

(22)

$Q({\text{Ec}},{\text{Kn,}}\beta )Q( - {\text{Ec}},{\text{Kn,}}\beta ) \approx 1.$

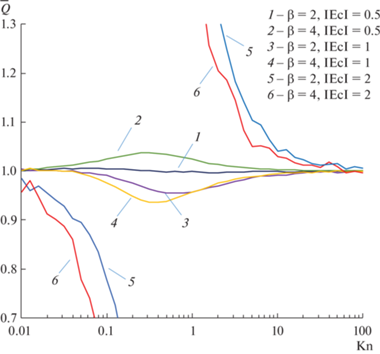
Для режима сплошной среды и свободномолекулярного режима, соотношения (18), (19), (22) выполняются точно ($R \ne 1$ и $R \ne 0$). Для переходного режима при $\beta = 1$ и любых ${\text{Kn}}$ они выполняются точно в случае, если ${{u}_{{{\text{rel}}}}}$ одно и то же ($R \ne 1$ и $R \ne 0$), а также в случае ${{T}_{1}} = {{T}_{2}}$. Функция $\bar {Q}((\left| {{\text{Ec}}} \right|,\;{\text{Kn,}}\,\beta ){\text{)}} = Q({\text{Ec}},\;{\text{Kn,}}\,\beta )Q( - {\text{Ec}},\;{\text{Kn,}}\,\beta )$ для различных значений ${\text{Ec}}$ и $\beta $ изображена на фиг. 7. Как видно из приведенных данных, соотношение (22) выполняется с точностью до 4% для $\left| {{\text{Ec}}} \right| = 0.5$ и до 6% для $\left| {{\text{Ec}}} \right| = 1$. Однако, для $\left| {{\text{Ec}}} \right| = 2$, соотношение (22) нарушается для чисел Кнудсена, соответствующих переходному режиму, потому что в этом случае мы имеем $R \ll 1$ или $R \approx 1$, см. фиг. 4.

Фиг. 7.

Зависимость произведения отношений погонных потоков энергий для двух течений c одинаковыми по модулю, но различными по знаку числами Эккерта от числа Кнудсена Kn.

7. ЗАКЛЮЧЕНИЕ

Рассмотрено продольное цилиндрическое течение Куэтта одноатомного газа. Исследована связь между потоком энергии, передаваемой цилиндрической поверхности, и напряжением трения на ней (аналогия Рейнольдса). Для режима сплошной среды и свободномолекулярного режима аналитически показано, что коэффициент аналогии Рейнольдса не зависит от отношения радиусов цилиндров, а зависит только от числа Эккерта. Таким образом, коэффициент аналогии Рейнольдса для продольного цилиндрического течения Куэтта совпадает в этих случаях с коэффициентом аналогии Рейнольдса для плоского течения Куэтта [1], [2], [12]. Методом DSMC показано, что в переходном режиме, в отличие от случая сплошной среды и свободномолекулярного течения, отношение радиусов влияет на коэффициент аналогии Рейнольдса. Обнаружено, что во всех рассмотренных случаях коэффициент аналогии Рейнольдса для одноатомного газа зависит от относительных скоростей и температур поверхностей, главным образом, через число Эккерта. Для разделения влияния числа Эккерта и числа Кнудсена на коэффициент аналогии Рейнольдса введен модифицированный коэффициент аналогии Рейнольдса. Для всех рассмотренных чисел Эккерта модифицированный коэффициент аналогии Рейнольдса зависит, главным образом, от числа Кнудсена и от отношения радиусов. На основе полученных численных результатов предложена приближенная формула для коэффициента аналогии Рейнольдса, в которую входят число Эккерта и модифицированный коэффициент аналогии Рейнольдса. Отношение погонных потоков энергий, передаваемых граничным поверхностям, выражается через коэффициент аналогии Рейнольдса и имеет те же параметры подобия, что и коэффициент аналогии Рейнольдса. Используя свойства коэффициента аналогии Рейнольдса, показано, что произведение отношений погонных потоков энергий, переданных граничным поверхностям, для двух разных течений Куэтта c одинаковыми по модулю, но различными по знаку числами Эккерта приблизительно, а в некоторых случаях, точно равно единице.

Список литературы

Liepmann H.W., Roshko A. Elements of Gasdynamics. New York: Willey, 1957. Перевод Липман Г.В., Рожко А. Элементы газовой динамики. М.: Иностр. лит., 1960.
Illingworth C.R. Some solutions of the equations of flow of a viscous compressible fluid // Math. Proc. of the Cambridge Philosophical Society. 1950. V. 46. P. 469.
Perlmutter M. Analysis of Couette flow and heat transfer between parallel plates enclosing rarefied gas by Monte Carlo // Proc. of 5th Internat. Symposium on Rarefied Gas Dynamics, edited by C. L. Brundin. New York: -Academic Press, 1967. V. 1. P. 455.
Sharipov F., Kalempa D. Oscillatory Couette flow at arbitrary oscillation frequency over the whole range of the Knudsen number // Microfluid Nanofluid. 2008. V. 4. P. 363.
Roy S., Chakraborty S. Near-wall effects in micro scale Couette flow and heat transfer in the Maxwell-slip regimes // Microfluid and Nanofluid. 2007. V. 3. P. 437.
Zahid W.A., Yin Y., Zhu K.Q. Couette–Poiseuille flow of a gas in long microchannels // Microfluidics and Nanofluidics. 2007. V. 3. P. 55.
Deng Z., Chen Y., Shao C. Gas flow through rough microchannels in the transition flow regime / Phys. Rev. E. 2016. V. 93. P. 013128-1.
Chen X.X., Wang Z.H., Yu Y.L. “Nonlinear Shear and Heat Transfer in Hypersonic Rarefied Flows Past Flat Plates // AIAA Journal. 2015. V. 53. P. 413.
Abramov A.A., Butkovskii A.V. Reynolds analogy for the fluid flow past a flat plate at different regimes // Phys. Fluids. 2021. V. 33. P. 017101-1.
Chen X.X., Wang Z.H., Yu Y.L. General Reynolds analogy for blunt-nosed bodies in hypersonic flows // AIAA J. 2015. V. 53. P. 2410.
Abramov A., Butkovskii A. Extended Reynolds analogy for the rarefied Rayleigh problem: Similarity parameters // 31st Internat. Symposium on Rarefied Gas Dynamics, AIP Conf. Proc. 2019. V. 2132. 180013-1.
Abramov A.A., Butkovskii A.V. The extended Reynolds analogy for the Couette problem: Similarity parameters // Internat. J. Heat Mass Transf. 2018. V. 117. P. 313.
Коган М.Н. Динамика разреженного газа. М.: Наука,1969.
Bird G.A. Molecular Gas Dynamics. Oxford, Clarendon Press, 1976. Перевод: Берд Г. Молекулярная газовая динамика. М.: Мир, 1981.
Abramov A.A., Alexandrov V.Yu., Butkovskii A.V. The longitudinal cylindrical Couette problem for rarefied gas: Energy fluxes maximums // Internat. J. Heat Mass Transf. 2017. V. 111. P. 608.
Bird G.A. Molecular Gas Dynamics and Direct Simulation of Gas Flows. Oxford, Oxford University Press, 1994.
Abramov A.A., Butkovsky A.V. The sign change effect of the energy flux and other effects in the transitional regime for the Couette problem // AIP Conf. Proc. 2012. V. 1501. P. 123.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал