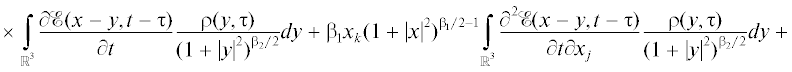Журнал вычислительной математики и математической физики, 2023, T. 63, № 2, стр. 282-316
Локальная разрешимость, разрушение и гёльдеровская регулярность решений некоторых задач Коши для нелинейных уравнений теории волн в плазме. II. Теория потенциала
М. О. Корпусов 1, *, Е. А. Овсянников 1, **
1 МГУ им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
* E-mail: korpusov@gmail.com
** E-mail: evg.bud@yandex.ru
Поступила в редакцию 29.11.2021
После доработки 04.07.2022
Принята к публикации 04.07.2022
- EDN: BOJJQG
- DOI: 10.31857/S0044466923020102
Аннотация
В статье рассматриваются объемный и поверхностный потенциалы, возникающие в задачах Коши для нелинейных уравнений из теории ионно-звуковых и дрейфовых волн в плазме, и изучаются их свойства. Для объемного потенциала выводится некоторая оценка. На ее основе доказываются одна априорная оценка типа Шаудера и оценки типа Шаудера для потенциалов с весом. Библ. 5.
Ключевые слова: объемный потенциал, поверхностный потенциал, априорные оценки типа Шаудера.
1. ОБЪЕМНЫЙ И ПОВЕРХНОСТНЫЙ ПОТЕНЦИАЛЫ В ПРОСТРАНСТВАХ ГЁЛЬДЕРА
Стоит отметить, что настоящая статья является логическим продолжением работы [1], в ней продолжаются исследования, начатые ранее в [1].
Рассмотрим следующие объемный и поверхностный потенциалы:
(1.1)
$U(x,t) = U[\rho ](x,t) = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$(1.2)
${{V}_{k}}(x,t) = {{V}_{k}}[\mu ](x,t) = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{k}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t)}}{{\partial {{t}^{k}}}}\mu (y){\kern 1pt} dy,\quad k \in \mathbb{N} \cup \{ 0\} ,$(1.3)
${{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t) = \frac{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\mathcal{E}(x - y,t),\quad {{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,$Теорема 1. Если $\rho (x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}))$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,$ то
и справедлива следующая оценка:
$\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{{{\partial }^{k}}U[{{\rho }_{1}}](x,t)}}{{\partial {{t}^{k}}}} - \frac{{{{\partial }^{k}}U[{{\rho }_{2}}](x,t)}}{{\partial {{t}^{k}}}}} \right|}_{{2 + \alpha }}}\;\leqslant \;T{{d}_{k}}(T)\mathop {\sup }\limits_{t \in [0,T]} {{\left| {{{\rho }_{1}}(x,t) - {{\rho }_{2}}(x,t)} \right|}_{\alpha }}$
для любых ${{\rho }_{j}}(x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}))$ при $j = 1,2,$ где ${{d}_{k}} = {{d}_{k}}(T) > 0$ при $k = 0,1,2$ является монотонно неубывающей, ограниченной на компактах.
Доказательство.
Шаг 1: $U(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$ Пусть $\rho (x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}))$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0.$ Объемный потенциал $U(x,t)$ можно представить в следующем виде:
(1.4)
$U(x,t) = \int\limits_0^t \,H(x,t,\tau ){\kern 1pt} d\tau ,\quad H(x,t,\tau ) = \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy.$
$({{x}^{j}},{{t}^{j}},{{\tau }^{j}}) \in {{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ,$
причем пусть ${{R}_{1}} > 0$ настолько велико, что
Тогда справедливо следующее неравенство:
(1.5)
$\begin{gathered} \left| {H({{x}^{1}},{{t}^{1}},{{\tau }^{1}}) - H({{x}^{2}},{{t}^{2}},{{\tau }^{2}})} \right|\;\leqslant \;\left| {{{H}_{1}}({{x}^{1}},{{t}^{1}},{{\tau }^{1}})} \right| + \left| {{{H}_{1}}({{x}^{2}},{{t}^{2}},{{\tau }^{2}})} \right| + \\ \, + \left| {{{H}_{2}}({{x}^{1}},{{t}^{1}},{{\tau }^{1}})} \right| + \left| {{{H}_{2}}({{x}^{2}},{{t}^{2}},{{\tau }^{2}})} \right| + \left| {{{H}_{3}}({{x}^{1}},{{t}^{1}},{{\tau }^{1}}) - {{H}_{3}}({{x}^{2}},{{t}^{2}},{{\tau }^{2}})} \right|, \\ \end{gathered} $
${{H}_{1}}({{x}^{j}},{{t}^{j}},{{\tau }^{j}}) = \int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}^{j}},{{R}_{\delta }})} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}({{x}^{j}},y,{{t}^{j}} - {{\tau }^{j}})\rho (y,{{\tau }^{j}}){\kern 1pt} dy,$
${{H}_{2}}({{x}^{j}},{{t}^{j}},{{\tau }^{j}}) = \int\limits_{O({{x}^{j}},{{r}_{\delta }})} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}({{x}^{j}},y,{{t}^{j}} - {{\tau }^{j}})\rho (y,{{\tau }^{j}}){\kern 1pt} dy,$
${{H}_{3}}({{x}^{j}},{{t}^{j}},{{\tau }^{j}}) = \int\limits_{O({{x}^{j}},{{R}_{\delta }})\backslash O({{x}^{j}},{{r}_{\delta }})} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}({{x}^{j}},y,{{t}^{j}} - {{\tau }^{j}})\rho (y,{{\tau }^{j}}){\kern 1pt} dy,\quad j = 1,2.$
Пусть $\delta > 0$ – произвольное фиксированное. Тогда найдется такое достаточно большое ${{R}_{\delta }},$ ${{R}_{\delta }}\; \geqslant \;{{R}_{0}} > 0$, и достаточно малое ${{r}_{\delta }},$ ${{R}_{0}}\; \geqslant \;{{r}_{\delta }} > 0$, и тогда, в силу оценок (6.7) и (6.9) работы [1], будут справедливы следующие оценки:
$\begin{gathered} \left| {{{H}_{1}}({{x}^{j}},{{t}^{j}},{{\tau }^{j}})} \right|\;\leqslant \;\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {\text{|}}\rho (x,t){\text{|}}{{(1 + R_{1}^{2})}^{{{{\beta }_{1}}/2}}}{{M}_{1}}(T,\varepsilon ,{{R}_{0}}) \times \\ \times \;\int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}^{j}},{{R}_{\delta }})} \frac{{\exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}{{x}^{j}} - y{\kern 1pt} {\text{|}})}}{{{\text{|}}{{x}^{j}} - y{\kern 1pt} {\text{|}}}}\frac{1}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy\;\leqslant \;{{M}_{2}}(T,\varepsilon ,{{R}_{0}},{{R}_{1}})\int\limits_{{{R}_{\delta }}}^{ + \infty } \rho \exp ( - (1 - \varepsilon )\rho ){\kern 1pt} d\rho < \frac{\delta }{3}, \\ \end{gathered} $
$\begin{gathered} \left| {{{H}_{2}}({{x}^{j}},{{t}^{j}},{{\tau }^{j}})} \right|\;\leqslant \;{{(1 + R_{1}^{2})}^{{{{\beta }_{1}}/2}}}\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {\text{|}}{{M}_{3}}(T,\varepsilon ,{{R}_{0}}) \times \\ \times \;\int\limits_{O({{x}^{j}},{{r}_{\delta }})} \frac{1}{{{\text{|}}{{x}^{j}} - y{\kern 1pt} {\text{|}}}}\frac{1}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy\;\leqslant \;{{M}_{4}}(T,\varepsilon ,{{R}_{0}},{{R}_{1}})\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {\text{|}}\frac{{r_{\delta }^{2}}}{2} < \frac{\delta }{3}. \\ \end{gathered} $
На этом моменте мы зафиксируем ${{R}_{\delta }}$ и ${{r}_{\delta }}$. Тогда справедливы следующие неравенства:
(1.6)
$\begin{gathered} \left| {{{H}_{3}}({{x}^{1}},{{t}^{1}},{{\tau }^{1}}) - {{H}_{3}}({{x}^{2}},{{t}^{2}},{{\tau }^{2}})} \right|\;\leqslant \\ \leqslant \;\int\limits_{O(0,{{R}_{\delta }})\backslash O(0,{{r}_{\delta }})} \left| {\frac{{{{{(1\; + \;{\text{|}}{{x}^{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1\; + \;{\text{|}}z + {{x}^{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\mathcal{E}(z,{{t}^{1}} - {{\tau }^{1}}) - \frac{{{{{(1\; + \;{\text{|}}{{x}^{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1\; + \;{\text{|}}z + {{x}^{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\mathcal{E}(z,{{t}^{2}} - {{\tau }^{2}})} \right|dz < \frac{\delta }{3} \\ \end{gathered} $(1.7)
$\left| {({{x}^{1}},{{t}^{1}},{{\tau }^{1}}) - ({{x}^{2}},{{t}^{2}},{{\tau }^{2}})} \right| < \eta (\delta )$
$\left| {H({{x}^{1}},{{t}^{1}},{{\tau }^{1}}) - H({{x}^{2}},{{t}^{2}},{{\tau }^{2}})} \right| < \delta .$
Таким образом, $H(x,t,\tau ) \in \mathbb{C}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} )$. Докажем теперь, что $H(x,t,\tau ) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times $ $ \times \;\{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} )$. Действительно, из (1.3) и (1.4) вытекает следующая цепочка неравенств:
(1.8)
$\begin{gathered} \left| {H(x,t,\tau )} \right|\;\leqslant \;\left( {\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {\text{|}}} \right)\left( {{{I}_{1}} + {{I}_{2}}} \right), \\ {{I}_{1}} = (1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{0}})} \frac{{\left| {\mathcal{E}(x - y,t - \tau )} \right|}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy,\quad {{I}_{2}} = (1\; + \;{\text{|}}x{{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\int\limits_{O(x,{{R}_{0}})} \frac{{\left| {\mathcal{E}(x - y,t - \tau )} \right|}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy. \\ \end{gathered} $
$\begin{gathered} {{I}_{1}} = (1\; + \;{\text{|}}x{{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}{{B}_{0}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{0}})} \frac{{\exp ( - (1 - \varepsilon ){\text{|}}x - y{\text{|}})}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}\frac{1}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = \\ = {{B}_{0}}{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,{{R}_{0}})} \frac{{\exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}z{\text{|}}}}\frac{1}{{{{{(1\; + \;{\text{|}}x - z{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dz\;\leqslant \;{{M}_{5}}(T,{{R}_{0}},\varepsilon )\frac{1}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\;\leqslant \;{{M}_{5}}(T,{{R}_{0}},\varepsilon ), \\ \end{gathered} $
где мы воспользовались оценкой (10.20) из [1] и тем, что по условию ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0.$ Для того, чтобы оценить интеграл ${{I}_{2}}$, заметим, что при ${{\beta }_{1}}\; \geqslant \;0$ справедлива следующая оценка:
(1.9)
${{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\;\leqslant \;{{2}^{{{{\beta }_{1}}/4}}}{{(1\; + \;{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}.$(1.10)
${{I}_{2}}\;\leqslant \;{{M}_{6}}(T,{{R}_{0}},\varepsilon )\int\limits_{O(x,{{R}_{0}})} \frac{{{{{(1\; + \;{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}\frac{1}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy\;\leqslant \;{{M}_{7}}(T,{{R}_{0}},\varepsilon ) < + \infty .$
$\mathop {\sup }\limits_{(x,\tau ,t) \in {{\mathbb{R}}^{3}} \times \{ 0\leqslant \tau \leqslant t\leqslant T\} } {\text{|}}H(x,t,\tau ){\kern 1pt} {\text{|}} < + \infty .$
Итак,
$H(x,t,\tau ) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$
Но тогда из (1.4) получаем, что
Шаг 2: ${{U}_{{{{x}_{j}}}}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$ Докажем, что
(1.11)
$\frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$(1.12)
$\frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}} = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy.$(1.13)
$H(x,t,\tau ) = \int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,2{{R}_{0}})} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )\rho (y,\tau ){\kern 1pt} dy + \int\limits_{O(0,2{{R}_{0}})} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )\rho (y,\tau ){\kern 1pt} dy = {{J}_{1}} + {{J}_{2}}.$(1.14)
$\frac{{\partial {{J}_{2}}}}{{\partial {{x}_{j}}}}\int\limits_{O(0,2{{R}_{0}})} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )}}{{\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy.$
${\text{|}}x - y{\kern 1pt} {\text{|}}\; \geqslant \;{\text{|}}y{\kern 1pt} {\text{|}}\; - \;{\text{|}}x{\kern 1pt} {\text{|}}\; \geqslant \;2{{R}_{0}} - {{R}_{0}} = {{R}_{0}} > 0.$
Пусть ${{x}_{h}} = ({{x}_{1}}, \ldots ,{{x}_{{j - 1}}},{{x}_{j}} + h,{{x}_{{j + 1}}}, \ldots ,{{x}_{3}})$. Справедлива следующая цепочка равенств:
${{J}_{3}} = \frac{{{{J}_{1}}({{x}_{h}},y,t - \tau ) - {{J}_{1}}(x,y,t - \tau )}}{h} - \int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,2{{R}_{0}})} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )}}{{\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy = $
$ = \int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,2{{R}_{0}})} \left[ {\frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x{\kern 1pt} *,t,t - \tau )}}{{\partial {{x}_{j}}}} - \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )}}{{\partial {{x}_{j}}}}} \right]\rho (y,\tau ){\kern 1pt} dy = $
$ = \int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,N{{R}_{0}})} \left[ {\frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x{\kern 1pt} *,t,t - \tau )}}{{\partial {{x}_{j}}}} - \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )}}{{\partial {{x}_{j}}}}} \right]\rho (y,\tau ){\kern 1pt} dy + $
$\, + \int\limits_{O(0,N{{R}_{0}})\backslash O(0,2{{R}_{0}})} \left[ {\frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x{\kern 1pt} *,t,t - \tau )}}{{\partial {{x}_{j}}}} - \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )}}{{\partial {{x}_{j}}}}} \right]\rho (y,\tau ){\kern 1pt} dy = {{J}_{{31}}} + {{J}_{{32}}},$
где $x{\kern 1pt} * \in {\text{|}}x,{{x}_{h}}{\kern 1pt} {\text{|}}$. Пусть $\delta > 0$ – произвольное фиксированное. Несложно заметить, что при достаточно большом $N \in \mathbb{N}$ имеет место оценка
Фиксируем это $N \in \mathbb{N}$. Тогда при достаточно малом ${\text{|}}h{\text{|}} > 0$ справедлива оценка
Таким образом, из (1.15) и (1.16) вытекает, что
и поэтому справедливо поточечное равенство
(1.17)
$\frac{{\partial {{J}_{1}}}}{{\partial {{x}_{j}}}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,2{{R}_{0}})} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,t,t - \tau )}}{{\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy.$(1.18)
$\mathop {\sup }\limits_{(x,\tau ,t) \in {{\mathbb{R}}^{3}} \times \{ 0\leqslant \tau \leqslant t\leqslant T\} } \left| {\frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}}} \right| < + \infty .$(1.19)
$\frac{{\partial U(x,t)}}{{\partial {{x}_{j}}}} = \int\limits_0^t \frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}}{\kern 1pt} d\tau .$(1.20)
$\begin{gathered} {{J}_{4}} = \frac{{U({{x}_{h}},t) - U(x,t)}}{h} - \int\limits_0^t \frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}}{\kern 1pt} d\tau = \int\limits_0^t \left[ {\frac{{H({{x}_{h}},t,\tau ) - H(x,t,\tau )}}{h} - \frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}}} \right]{\kern 1pt} d\tau = \\ \, = \int\limits_0^t \left[ {\frac{{\partial H(x{\kern 1pt} *,t,\tau )}}{{\partial {{x}_{j}}}} - \frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}}} \right]{\kern 1pt} d\tau \quad {\text{при}}\quad x{\kern 1pt} * \in {\text{|}}x,{{x}_{h}}{\text{|}}. \\ \end{gathered} $
${{J}_{4}} \to 0\quad {\text{при}}\quad h \to 0\quad {\text{для}}\;{\text{каждого}}\quad t \in [0,T].$
Таким образом, справедливо поточечное равенство (1.19), из которого с учетом (1.11)
и (1.18) приходим к выводу о том, что
(1.21)
$\frac{{\partial U(x,t)}}{{\partial {{x}_{j}}}} = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$Шаг 3: ${{U}_{t}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$
Докажем, что
$\frac{{\partial H(x,t,\tau )}}{{\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$
Сначала докажем поточечное равенство
(1.22)
$\frac{{\partial H(x,t,\tau )}}{{\partial t}} = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy.$
$H(x,t,\tau )\int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,2{{R}_{0}})} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy + \int\limits_{O(0,2{{R}_{0}})} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy = {{P}_{1}}(x,t,\tau ) + {{P}_{2}}(x,t,\tau ).$
Рассуждая точно так же, как при доказательстве леммы 4.1 из [2], несложно доказать, что
$\frac{{\partial {{P}_{2}}(x,t,\tau )}}{{\partial t}} = \int\limits_{O(0,2{{R}_{0}})} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy.$
При ${\text{|}}y{\kern 1pt} {\text{|}}\; \geqslant \;2{{R}_{0}}$ и ${\text{|}}x{\kern 1pt} {\text{|}} < {{R}_{0}}$ справедливо неравенство
Справедлива следующая цепочка равенств:
${{H}_{1}} = \frac{{{{P}_{1}}(x,t + h,\tau ) - {{P}_{1}}(x,t,\tau )}}{h} - \int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,2{{R}_{0}})} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy = $
(1.23)
$\begin{gathered} = \int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,2{{R}_{0}})} \left[ {\frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t{\kern 1pt} * - \;\tau )}}{{\partial t}} - \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right]\rho (y,\tau ){\kern 1pt} dy,\quad t{\kern 1pt} * \in {\text{|}}t,t + h{\kern 1pt} {\text{|,}} \\ {{H}_{1}} = \int\limits_{O(x,N{{R}_{0}})\backslash O(x,2{{R}_{0}})} \left[ {\frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t{\kern 1pt} * - \;\tau )}}{{\partial t}} - \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right]\rho (y,\tau ){\kern 1pt} dy + \\ \end{gathered} $
$ + \;\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,N{{R}_{0}})} \left[ {\frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t{\kern 1pt} * - \tau )}}{{\partial t}} - \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right]\rho (y,\tau ){\kern 1pt} dy = {{H}_{{11}}} + {{H}_{{12}}}.$
Для любого $\eta > 0$ найдется такое $N \in \mathbb{N},$ что справедлива следующая цепочка неравенств:
$\begin{gathered} {\text{|}}{{H}_{{12}}}{\kern 1pt} {\text{|}}\;\leqslant \;{{M}_{{11}}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {\text{|}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,N{{R}_{0}})} \frac{{{{{(1\; + \;{\text{|}}x - y{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1\; + \;{\text{|}}y{{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\frac{{\exp \left( { - (1 - \varepsilon ){\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}} \right)}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}{\kern 1pt} dy\;\leqslant \\ \leqslant \;{{M}_{{12}}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {\text{|}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O(0,N{{R}_{0}})} {{(1\; + \;{\text{|}}z{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{\exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}z{\kern 1pt} {\text{|}}}}{\kern 1pt} dz < \frac{\eta }{3}, \\ \end{gathered} $
где мы воспользовались неравенством (1.9), а также оценкой (6.9) из [1]. Фиксируем это $N \in \mathbb{N}$. Тогда для любого $\eta > 0$ найдется такое $\mu = \mu (\eta ) > 0,$ что при $\left| h \right| < \eta $ справедлива цепочка неравенств
(1.24)
${\text{|}}{{H}_{{11}}}{\kern 1pt} {\text{|}}\;\leqslant \;\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {\text{|}}\rho (x,t){\text{|}}\int\limits_{O(x,N{{R}_{0}})\backslash O(x,\delta )} \left| {\frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t{\kern 1pt} * - \;\tau )}}{{\partial t}} - \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}} \right|dy < \frac{\eta }{3},$Рассуждая точно так же, как на шаге 1, с учетом оценок (6.7) и (6.9) статьи [1], а также оценки интеграла (10. 20) из [1] мы можем доказать, что
(1.25)
$\frac{{\partial H(x,t,\tau )}}{{\partial t}} = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ),$(1.26)
$\mathop {\sup }\limits_{(x,t,\tau ) \in {{\mathbb{R}}^{3}} \times \{ 0\leqslant \tau \leqslant t\leqslant T\} } \left| {\frac{{\partial H(x,t,\tau )}}{{\partial t}}} \right| < + \infty .$(1.27)
$\frac{{\partial U(x,t)}}{{\partial t}} = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$(1.28)
$\frac{{\partial U(x,t)}}{{\partial t}} = \int\limits_0^t \frac{{\partial H(x,t,\tau )}}{{\partial t}}{\kern 1pt} d\tau .$(1.29)
$\begin{gathered} {{U}_{1}} = \frac{{U(t + h,x) - U(t,x)}}{h} - \int\limits_0^t \frac{{\partial H(x,t,\tau )}}{{\partial t}}{\kern 1pt} d\tau = \frac{1}{h}\int\limits_0^{t + h} H(x,t + h,\tau ){\kern 1pt} d\tau - \frac{1}{h}\int\limits_0^t H(x,t,\tau ){\kern 1pt} d\tau = \\ = \frac{1}{h}\int\limits_t^{t + h} H(x,t + h,\tau ){\kern 1pt} d\tau + \int\limits_0^t \left[ {\frac{{H(x,t + h,\tau ) - H(x,t,\tau )}}{h} - \frac{{\partial H(x,t,\tau )}}{{\partial t}}} \right]{\kern 1pt} d\tau = {{U}_{{11}}} + {{U}_{{12}}}. \\ \end{gathered} $
${{U}_{{11}}} = \frac{1}{h}\int\limits_t^{t + h} \left[ {H(x,t + h,\tau ) - H(x,t,t)} \right]{\kern 1pt} d\tau + H(x,t,t) = {{U}_{{111}}} + {{U}_{{112}}}.$
Ранее на шаге 1 было доказано, что $H(x,t,\tau ) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,t])$ для любого $t \in [0,T]$. Поэтому имеет место предельное свойство
Заметим, что из явного вида (5.6), см. [1], вытекает, что
${{U}_{{112}}} = H(x,t,t) = \int\limits_{{{\mathbb{R}}^{3}}} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,0)\rho (y,t){\kern 1pt} dy = 0.$
В силу (1.25) имеют место следующие соотношения:
(1.30)
${{U}_{{12}}} = \int\limits_0^t \left[ {\frac{{\partial H(x,t*,\tau )}}{{\partial t}} - \frac{{\partial H(x,t,\tau )}}{{\partial t}}} \right]{\kern 1pt} d\tau \to 0\quad {\text{при}}\quad h \to 0,$Шаг 4: ${{U}_{{{{x}_{j}}t}}}(x,t) = {{U}_{{t{{x}_{j}}}}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T])$.
Из поточечного равенства (1.21), рассуждая точно так же, как на шаге 3, можно доказать, что справедливо поточечное равенство
(1.31)
$\begin{gathered} \frac{{{{\partial }^{2}}U(x,t)}}{{\partial t\partial {{x}_{j}}}} = \int\limits_0^t \frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}}}{\kern 1pt} d\tau = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau , \\ \frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ), \\ \end{gathered} $
$\frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}}} = \frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial t}}.$
Из поточечного равенства (1.27), рассуждая точно так же, как на шаге 2, можно доказать,
что справедливо поточечное равенство
(1.32)
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial t}} = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{x}_{j}}\partial t}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau .$
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial t\partial {{x}_{j}}}},\;\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]),$
и поэтому в силу известного результата математического анализа производные коммутируют
(1.33)
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial t\partial {{x}_{j}}}} = \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$Шаг 5: ${{U}_{{tt}}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T])$.
Используя доказанное на шаге 3 поточечное равенство (1.27), точно так же, как на шаге 3, можно доказать, что справедливо следующее поточечное равенство:
(1.34)
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}} = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\rho (y,t){\kern 1pt} dy + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau .$
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$
Шаг 6: ${{U}_{{{{x}_{j}}{{x}_{k}}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T])$.
Поскольку $\rho (x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})),$ то с учетом (3.1) и (4.8) справедливо поточечное равенство
$\frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} = \left[ {{{\beta }_{1}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{kj}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{k}}{{x}_{j}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right] \times $
(1.35)
$\begin{gathered} \times \;\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + {{\beta }_{1}}{{x}_{k}}{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial {{x}_{j}}}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \, + {{\beta }_{1}}{{x}_{j}}{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial {{x}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
$ + \;{{({\kern 1pt} 1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = {{L}_{1}} + {{L}_{2}} + {{L}_{3}} + {{L}_{4}},$
причем для любых ${{R}_{\delta }} > {{r}_{\delta }} > 0$ справедливо равенство
$\begin{gathered} {{L}_{4}} = (1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = \\ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}((1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
(1.36)
$ + \int\limits_{O(x,{{R}_{\delta }})\backslash O(x,{{r}_{\delta }})} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + $
$\begin{gathered} + \int\limits_{O(x,{{r}_{\delta }})} \frac{{{{\partial }^{2}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\mathcal{E}(x - y,t - \tau )\left[ {\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}} - \frac{{\rho (x,\tau )}}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]{\kern 1pt} dy + \\ + \;\frac{{\rho (x,\tau )}}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\int\limits_{\partial O(x,{{r}_{\delta }})} \frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial {{y}_{k}}}}\cos ({{n}_{y}},{{e}_{j}}){\kern 1pt} d{{S}_{y}} = {{L}_{{41}}} + {{L}_{{42}}} + {{L}_{{43}}} + {{L}_{{44}}} + {{L}_{{45}}}. \\ \end{gathered} $
Точно так же, как на шаге 1, можно доказать, что
(1.37)
${{L}_{1}}(x,t,\tau ) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$(1.38)
${{L}_{2}}(x,t,\tau ),\;{{L}_{3}}(x,t,\tau ) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$(1.39)
$\begin{gathered} \frac{{\left| {{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}\;\leqslant \;3{{\beta }_{1}},\quad {{\beta }_{1}} \in [0,1], \\ \frac{{\left| {{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|}}{{{\text{|}}x - y{\kern 1pt} {\kern 1pt} {\text{|}}}}\;\leqslant \;3{{\beta }_{1}}{{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1\; + \;{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}},\quad {{\beta }_{1}} > 1. \\ \end{gathered} $
${\text{|}}x - y{\kern 1pt} {\text{|}}\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}$
справедливы следующие оценки при любом ${{R}_{0}} > 0$:
${\text{|}}x - y{\kern 1pt} {\text{|}}\left| {\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}} \right|\;\leqslant \;\frac{{{{A}_{4}}(T,{{R}_{0}},\varepsilon )}}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}}}}\quad {\text{при}}\quad {\text{|}}x - y{\kern 1pt} {\text{|}}\;\leqslant \;{{R}_{0}},$
${\text{|}}x - y{\kern 1pt} {\text{|}}\left| {\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}} \right|\;\leqslant \;{{B}_{4}}(T,{{R}_{0}},\varepsilon )\exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )\quad {\text{при}}\quad {\text{|}}x - y{\kern 1pt} {\text{|}} > {{R}_{0}}.$
Кроме того, в силу свойства гладкости (6.6) из [1] фундаментального решения $\mathcal{E}(x,t)$ имеем
(1.40)
${\text{|}}x{\kern 1pt} {\text{|}}\frac{{{{\partial }^{2}}\mathcal{E}(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} \in {{\mathbb{C}}^{{(m + n)}}}({{\mathbb{R}}^{3}}{{\backslash }}\{ 0\} \times [0, + \infty ))\quad {\text{для}}\;{\text{всех}}\quad m,n \in \mathbb{N} \cup \{ 0\} .$(1.41)
${{L}_{{41}}}(x,t,\tau ) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$(1.42)
$\begin{gathered} {\text{|}}{{L}_{{43}}}{\text{|}}\;\leqslant \;\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}} \times [0,T]} {{M}_{{13}}}(T,{{R}_{0}},\varepsilon )\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \frac{{\exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}{\kern 1pt} dy\;\leqslant \\ \leqslant \;{{M}_{{14}}}(T,{{R}_{0}},\varepsilon )\int\limits_{{{R}_{\delta }}}^{ + \infty } {\kern 1pt} \rho \exp ( - (1 - \varepsilon )\rho ){\kern 1pt} d\rho < \frac{\delta }{4}, \\ \end{gathered} $(1.43)
$\begin{gathered} {\text{|}}{{L}_{{44}}}{\kern 1pt} {\text{|}}\;\leqslant \;{{\left[ {\frac{{\rho (x,t)}}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}} - {{\beta }_{1}}}}}}}} \right]}_{\alpha }}\int\limits_{O(x,{{r}_{\delta }})} {\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{\alpha }}\left| {\frac{{{{\partial }^{2}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\mathcal{E}(x - y,t - \tau )} \right|{\kern 1pt} dy\;\leqslant \\ \leqslant \;{{M}_{{15}}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\rho (x,t)} \right|}_{\alpha }}\int\limits_{O(x,{{r}_{\delta }})} \frac{1}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{{3 - \alpha }}}}}{\kern 1pt} dy\;\leqslant \;{{M}_{{16}}}(T,{{R}_{0}},\varepsilon )r_{\delta }^{\alpha } < \frac{\delta }{4}. \\ \end{gathered} $(1.44)
${{L}_{{42}}}(x,t,\tau ) + {{L}_{{43}}}(x,t,\tau ) + {{L}_{{44}}}(x,t,\tau ) + {{L}_{{45}}}(x,t,\tau ) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$
$\begin{gathered} {\text{|}}{{L}_{{42}}}{\kern 1pt} {\text{|}}\;\leqslant \;{{M}_{{17}}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}}} {\text{|}}\rho (x,t){\kern 1pt} {\text{|}}\left[ {\int\limits_{O(x,2{{R}_{0}})\backslash O(x,{{R}_{0}})} \frac{{\exp ( - (1 - \varepsilon ){\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}{\kern 1pt} dy + \int\limits_{O(x,{{R}_{0}})\backslash O(x,{{R}_{0}}/2)} \frac{1}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{3}}}}{\kern 1pt} dy} \right]\;\leqslant \\ \leqslant \;{{M}_{{18}}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}}} {\text{|}}\rho (x,t){\kern 1pt} {\text{|}}, \\ \end{gathered} $
${\text{|}}{{L}_{{45}}}{\text{|}}\;\leqslant \;{{M}_{{19}}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{(x,t) \in {{\mathbb{R}}^{3}}} {\text{|}}\rho (x,t){\text{|}}.$
Таким образом, соотношение (1.44) доказано. Следовательно, из (1.41)–(1.44), а также
из (1.37), (1.38) вытекает, что
(1.45)
$\frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$(1.46)
$\frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{k}}\partial {{x}_{j}}}}.$
$\frac{{\partial U(x,t)}}{{\partial {{x}_{j}}}} = \int\limits_0^t \frac{{\partial H(x,t,\tau )}}{{\partial {{x}_{j}}}}{\kern 1pt} d\tau .$
В силу (1.11) и (1.45) точно так же, как на шаге 2 (см. цепочку равенств (1.20)),
получим следующее поточечное равенство:
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{k}}\partial {{x}_{j}}}} = \int\limits_0^t \frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{k}}\partial {{x}_{j}}}}{\kern 1pt} d\tau ,$
из которого в силу (1.45), как и на предыдущих шагах, приходим к выводу о том, что
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{k}}\partial {{x}_{j}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T])$
и, кроме того, в силу (1.46) справедливо поточечное равенство
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{k}}\partial {{x}_{j}}}}.$
Шаг 7: ${{U}_{{t{{x}_{j}}{{x}_{k}}}}}(x,t) = {{U}_{{{{x}_{j}}t{{x}_{k}}}}}(x,t) = {{U}_{{{{x}_{j}}{{x}_{k}}t}}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$
Прежде всего заметим, что справедливо поточечное равенство (1.22)
$\frac{{\partial H(x,t,\tau )}}{{\partial t}} = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$
Заметим, что поскольку $\rho (x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})),$ то в силу равенства (4.9) приходим к следующему равенству:
$\frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} = \left[ {{{\beta }_{1}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{kj}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{k}}{{x}_{j}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right] \times $
(1.47)
$\begin{gathered} \times \;\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + {{\beta }_{1}}{{x}_{k}}{{(1\; + \;{\text{|}}x{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{x}_{j}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \, + {{\beta }_{1}}{{x}_{j}}{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{x}_{k}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
$\, + {{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy,$
причем для любых ${{R}_{\delta }} > {{r}_{\delta }} > 0$ справедливо равенство
$\begin{gathered} {{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = \\ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial t}}((1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1\; + \;{\text{|}}y{\text{|}}{{{\kern 1pt} }^{2}})}^{{{{\beta }_{1}}/2}}})\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
(1.48)
$ + \;\int\limits_{O(x,{{R}_{\delta }})\backslash O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + $
$\begin{gathered} + \;\int\limits_{O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial t}}\left[ {\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}} - \frac{{\rho (x,\tau )}}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]{\kern 1pt} dy + \\ \, + \frac{{\rho (x,\tau )}}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\int\limits_{\partial O(x,{{r}_{\delta }})} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{k}}\partial t}}\cos ({{n}_{y}},{{e}_{j}}){\kern 1pt} d{{S}_{y}}. \\ \end{gathered} $
Точно так же, как на шаге 6, используя представление (1.47), можно доказать следующие
равенства:
(1.49)
$\begin{gathered} \frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ), \\ \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} = \int\limits_0^t \frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}{\kern 1pt} d\tau = \int\limits_0^t \frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]). \\ \end{gathered} $
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial t\partial {{x}_{k}}}}.$
Теперь наша задача доказать, что
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$
С этой целью воспользуемся равенствами (1.35) и (1.36). Точно так же, как на шаге
3, можно получить следующие поточечные равенства:
$\frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} = \left[ {{{\beta }_{1}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{kj}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{k}}{{x}_{j}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right] \times $
$\begin{gathered} + \;{{\beta }_{1}}{{x}_{j}}{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial t\partial {{x}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ + \;{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{3}}}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy, \\ \end{gathered} $
причем для любых ${{R}_{\delta }} > {{r}_{\delta }} > 0$ справедливо равенство
${{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{3}}}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = $
$ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial t\partial {{y}_{j}}\partial {{y}_{k}}}}((1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + $
$ + \;\int\limits_{O(x,{{R}_{\delta }})\backslash O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial t\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial t\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + $
$ + \;\int\limits_{O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}}}{{\partial t\partial {{y}_{j}}\partial {{y}_{k}}}}\mathcal{E}(x - y,t - \tau )\left[ {\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}} - \frac{{\rho (x,\tau )}}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]{\kern 1pt} dy + $
$ + \;\frac{{\rho (x,\tau )}}{{{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\int\limits_{\partial O(x,{{r}_{\delta }})} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial t\partial {{y}_{k}}}}\cos ({{n}_{y}},{{e}_{j}}){\kern 1pt} d{{S}_{y}}.$
Поскольку для фундаментального решения $\mathcal{E}(x,t)$ справедлива лемма 6.1 из [1], то можно доказать следующие равенства:
$\frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} = \left[ {{{\beta }_{1}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{kj}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{k}}{{x}_{j}}{{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right] \times $
(1.50)
$\begin{gathered} \, \times \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t - \tau )}}{{\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + {{\beta }_{1}}{{x}_{k}}{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{x}_{j}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \, + {{\beta }_{1}}{{x}_{j}}{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{x}_{k}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
$ + \;{{(1\; + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{3}}}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1\; + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy,$
причем для любых ${{R}_{\delta }} > {{r}_{\delta }} > 0$ справедливо равенство
$\begin{gathered} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{3}}}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = \\ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial t}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
(1.51)
$ + \;\int\limits_{O(x,{{R}_{\delta }})\backslash O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial t}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + $
$\begin{gathered} + \;\int\limits_{O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial t}}\mathcal{E}(x - y,t - \tau )\left[ {\frac{{\rho (y,\tau )}}{{{{{(1 + \,{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}} - \frac{{\rho (x,\tau )}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]{\kern 1pt} dy + \\ \, + \frac{{\rho (x,\tau )}}{{{{{(1 + \,{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\int\limits_{\partial O(x,{{r}_{\delta }})} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{k}}\partial t}}\cos ({{n}_{y}},{{e}_{j}}){\kern 1pt} d{{S}_{y}}. \\ \end{gathered} $
Из сравнения равенств (1.47) и (1.48) с равенствами (1.50) и (1.51) приходим к следующим
поточечным равенствам:
(1.52)
$\frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} = \int\limits_0^t \frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}{\kern 1pt} d\tau ,\quad \frac{{{{\partial }^{2}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$
Поэтому справедливо следующее равенство:
(1.53)
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{2}}H(x,t,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}}} + \int\limits_0^t \frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}}{\kern 1pt} d\tau ,$
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} = \int\limits_0^t \frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}}{\kern 1pt} d\tau = \int\limits_0^t \frac{{{{\partial }^{3}}H(x,t,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}{\kern 1pt} d\tau = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$
Кроме того, в силу (1.33) справедливы поточечные равенства
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial t\partial {{x}_{k}}}} = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}}.$
Шаг 8: ${{U}_{{{{x}_{j}}tt}}}(x,t) = {{U}_{{t{{x}_{j}}t}}}(x,t) = {{U}_{{tt{{x}_{j}}}}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T])$.
Точно так же, как на шаге 2, используя равенство (1.34), с учетом оценок (6.7) и (6.10) статьи [1] можно получить поточечное равенство
$\begin{gathered} \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{t}^{2}}}} = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\rho (y,t){\kern 1pt} dy + \\ \, + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]). \\ \end{gathered} $
С одной стороны, используя оценки (6.7) и (6.10) статьи [1], можно доказать в точности так же, как на шагах 4 и 5, поточечное равенство
(1.54)
$\begin{gathered} \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{t}^{2}}\partial {{x}_{j}}}} = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\rho (y,t){\kern 1pt} dy + \\ \, + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{2}}\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]). \\ \end{gathered} $
$\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{2}}\partial {{x}_{j}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$
из которого и из (1.54) вытекают равенства
$\begin{gathered} \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{t}^{2}}\partial {{x}_{j}}}} = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\rho (y,t){\kern 1pt} dy + \\ \, + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}. \\ \end{gathered} $
Заметим, что в силу результата шага 4 справедливо поточечное равенство
(1.55)
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{t}^{2}}\partial {{x}_{j}}}} = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial t}}.$(1.56)
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{t}^{2}}\partial {{x}_{j}}}} = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial t}} = \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{t}^{2}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$Шаг 9: ${{U}_{{{{x}_{j}}{{x}_{k}}tt}}}(x,t) = {{U}_{{{{x}_{j}}t{{x}_{k}}t}}}(x,t) = $ ${{U}_{{{{x}_{j}}tt{{x}_{k}}}}} = {{U}_{{t{{x}_{j}}{{x}_{k}}t}}}(x,t) = {{U}_{{t{{x}_{j}}t{{x}_{k}}}}}(x,t) = $ ${{U}_{{tt{{x}_{j}}{{x}_{k}}}}}(x,t) \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T])$.
Из формулы (1.34), используя оценки (6.7)–(6.11) статьи [1], точно так же, как на шаге 7, можно доказать поточечное равенство
(1.57)
$\begin{gathered} \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}} = - \frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\rho (y,t){\kern 1pt} dy + \\ \, + \int\limits_0^t \frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau , \\ \end{gathered} $
$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\rho (y,t){\kern 1pt} dy = \\ \, = \left[ {{{\beta }_{1}}{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{kj}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{k}}{{x}_{j}}{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right] \times \\ \end{gathered} $
(1.58)
$ \times \;\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + {{\beta }_{1}}{{x}_{k}}{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \left( {\frac{\partial }{{\partial {{x}_{j}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + $
$\begin{gathered} \, + {{\beta }_{1}}{{x}_{j}}{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \left( {\frac{\partial }{{\partial {{x}_{k}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \, + {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\text{|}}x - y{\kern 1pt} {\text{|}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy, \\ \end{gathered} $
$\begin{gathered} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = \\ = \int\limits_{{{\mathbb{R}}^{3}}} \left( {\frac{{{{\partial }^{2}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
(1.59)
$\begin{gathered} + \;\int\limits_{O(x,{{R}_{\delta }})\backslash O(x,{{r}_{\delta }})} \left( {\frac{{{{\partial }^{2}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \\ \, + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \left( {\frac{{{{\partial }^{2}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\text{|}}{\kern 1pt} }}} \right)\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
$\begin{gathered} + \;\int\limits_{O(x,{{r}_{\delta }})} \left( {\frac{{{{\partial }^{2}}}}{{\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\left[ {\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}} - \frac{{\rho (x,\tau )}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]{\kern 1pt} dy + \\ \, + \frac{{\rho (x,\tau )}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\int\limits_{\partial O(x,{{r}_{\delta }})} \left( {\frac{\partial }{{\partial {{y}_{k}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}} \right)\cos ({{n}_{y}},{{e}_{j}}){\kern 1pt} d{{S}_{y}}, \\ \end{gathered} $
$\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy = \left[ {{{\beta }_{1}}{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{kj}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{k}}{{x}_{j}}{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right] \times $
(1.60)
$\begin{gathered} \times \;\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + {{\beta }_{1}}{{x}_{k}}{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \, + {{\beta }_{1}}{{x}_{j}}{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{x}_{k}}\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
$ + \;{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy,$
$\begin{gathered} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = \\ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial {{t}^{2}}}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
(1.61)
$ + \;\int\limits_{O(x,{{R}_{\delta }})\backslash O(x,{{r}_{\delta }})} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + $
$\begin{gathered} \, + \int\limits_{O(x,{{r}_{\delta }})} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{j}}\partial {{y}_{k}}\partial {{t}^{2}}}}\left[ {\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}} - \frac{{\rho (x,\tau )}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]{\kern 1pt} dy + \\ + \;\frac{{\rho (x,\tau )}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\int\limits_{\partial O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{y}_{k}}\partial {{t}^{2}}}}\cos ({{n}_{y}},{{e}_{j}}){\kern 1pt} d{{S}_{y}},\quad {{R}_{\delta }} > {{r}_{\delta }} > 0, \\ \end{gathered} $
причем из (1.58) и (1.59) получаем, что справедливы соотношения
(1.62)
$\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\rho (y,t){\kern 1pt} dy \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]),$(1.63)
$\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times \{ 0\;\leqslant \;\tau \;\leqslant \;t\;\leqslant \;T\} ).$
$\frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$
Теперь из поточечного равенства (1.35) точно так же, как на шаге 7, с учетом оценок
(6.7)–(6.11) из [1] фундаментального решения $\mathcal{E}(x,t)$ можно аналогично шагу 5 доказать следующее поточечное равенство:
$\frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{t}^{2}}\partial {{x}_{j}}\partial {{x}_{k}}}} = - \frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\rho (y,t){\kern 1pt} dy + \int\limits_0^t \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$
где для первого слагаемого справедливы формулы (1.58) и (1.59), а для второго слагаемого имеют место следующие формулы:
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )\rho (y,\tau ){\kern 1pt} dy = \left[ {{{\beta }_{1}}{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{kj}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{k}}{{x}_{j}}{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right] \times $
(1.64)
$\begin{gathered} \times \;\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + {{\beta }_{1}}{{x}_{k}}{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}\partial {{x}_{j}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \, + {{\beta }_{1}}{{x}_{j}}{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}\partial {{x}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
$ + \;{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy,$
$\begin{gathered} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t - \tau )\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy = \\ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}\partial {{y}_{j}}\partial {{y}_{k}}}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy + \\ \end{gathered} $
(1.65)
$ + \;\int\limits_{O(x,{{R}_{\delta }})\backslash O(x,{{r}_{\delta }})} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{\delta }})} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}\partial {{y}_{j}}\partial {{y}_{k}}}}\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}{\kern 1pt} dy + $
$\begin{gathered} \, + \int\limits_{O(x,{{r}_{\delta }})} \frac{{{{\partial }^{4}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}\partial {{y}_{j}}\partial {{y}_{k}}}}\left[ {\frac{{\rho (y,\tau )}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}} - \frac{{\rho (x,\tau )}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]{\kern 1pt} dy + \\ + \;\frac{{\rho (x,\tau )}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}\int\limits_{\partial O(x,{{r}_{\delta }})} \frac{{{{\partial }^{3}}\mathcal{E}(x - y,t - \tau )}}{{\partial {{t}^{2}}\partial {{y}_{k}}}}\cos ({{n}_{y}},{{e}_{j}}){\kern 1pt} d{{S}_{y}},\quad {{R}_{\delta }} > {{r}_{\delta }} > 0. \\ \end{gathered} $
Используя результат леммы 6.1 из [1], можно доказать, что правые части равенств (1.60) и (1.64), (1.61) и (1.65) совпадают.
Поэтому сразу же получаем то, что справедливы соотношения
(1.66)
$\frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{t}^{2}}\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$(1.67)
$\begin{gathered} \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{t}^{2}}\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial t\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial t\partial {{x}_{k}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}, \\ \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t\partial t}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial t\partial {{x}_{k}}\partial t}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial t\partial t\partial {{x}_{k}}}}. \\ \end{gathered} $
$\frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t\partial t}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial t\partial {{x}_{k}}\partial t}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial t\partial t\partial {{x}_{k}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial t\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial t\partial {{x}_{k}}}} = \frac{{{{\partial }^{4}}U(x,t)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} \in {{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}} \times [0,T]).$
Итак, из результатов шагов 1–9 вытекает промежуточная
Лемма 1.1. Если $\rho (x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}))$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,$ то потенциал $U(x,t) \in \mathbb{C}_{b}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T])$.
Шаг 10: $U(x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})).$
Из теоремы 8 для каждого $t \in [0,T]$ и $\alpha \in (0,1)$ справедливы соотношения
(1.68)
$\begin{gathered} U(x,t) \in {{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}), \\ \frac{{\partial U(x,t)}}{{\partial t}} = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial {{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial t}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau \in {{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}). \\ \end{gathered} $(1.69)
$U(x,{{t}_{2}}) - U(x,{{t}_{1}}) = \int\limits_{{{t}_{1}}}^{{{t}_{2}}} \frac{{\partial U(x,t)}}{{\partial t}}{\kern 1pt} dt\quad {\text{для}}\;{\text{всех}}\quad 0\;\leqslant \;{{t}_{1}}\;\leqslant \;{{t}_{2}}\;\leqslant \;T.$(1.70)
${{\left| {U(x,{{t}_{2}}) - U(x,{{t}_{1}})} \right|}_{{2 + \alpha }}}\;\leqslant \;\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {{\left| {\frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{{2 + \alpha }}}{\kern 1pt} dt\quad {\text{для}}\;{\text{всех}}\quad 0\;\leqslant \;{{t}_{1}}\;\leqslant \;{{t}_{2}}\;\leqslant \;T,$
$\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{{2 + \alpha }}}\;\leqslant \;{{b}_{1}}(T)\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\rho (x,t)} \right|}_{\alpha }},$
из которой и из (1.70) получаем неравенство
${{\left| {U(x,{{t}_{2}}) - U(x,{{t}_{1}})} \right|}_{{2 + \alpha }}}\;\leqslant \;{{b}_{1}}(T)\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\rho (x,t)} \right|}_{\alpha }}{\text{|}}{{t}_{2}} - {{t}_{1}}{\text{|}} \to + 0\quad {\text{при}}\quad {\text{|}}{{t}_{2}} - {{t}_{1}}{\text{|}} \to + 0.$
Следовательно,
Шаг 11: $U(x,t) \in {{\mathbb{C}}^{{(1)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}))$.
Заметим, что справедливо равенство (1.34), которое можно переписать в следующем виде:
(1.72)
$\begin{gathered} W(x,t) = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\rho (y,t){\kern 1pt} dy, \\ {{U}_{2}}(x,t) = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{2}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau . \\ \end{gathered} $(1.74)
$\mathop {\sup }\limits_{t \in [0,T]} {\text{|}}W(x,t){\kern 1pt} {{{\text{|}}}_{{2 + \alpha }}}\;\leqslant \;{{b}_{2}}\mathop {\sup }\limits_{t \in [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {{{\text{|}}}_{\alpha }},$(1.75)
$\mathop {\sup }\limits_{t \in [0,T]} {\text{|}}{{U}_{2}}(x,t){\kern 1pt} {{{\text{|}}}_{{2 + \alpha }}}\;\leqslant \;{{b}_{3}}(T)\mathop {\sup }\limits_{t \in [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {{{\text{|}}}_{\alpha }}.$(1.76)
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}} \in {{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})\quad {\text{для}}\;{\text{всех}}\quad t \in [0,T].$
$\frac{{\partial U(x,{{t}_{2}})}}{{\partial t}} - \frac{{\partial U(x,{{t}_{1}})}}{{\partial t}} = \int\limits_{{{t}_{1}}}^{{{t}_{2}}} \frac{{{{\partial }^{2}}U(x,\tau )}}{{\partial {{\tau }^{2}}}}{\kern 1pt} d\tau $
для всех $0\;\leqslant \;{{t}_{1}}\;\leqslant \;{{t}_{2}}\;\leqslant \;T,$ из которого с учетом (1.68) и (1.76) получаем неравенства
$\begin{gathered} {{\left| {\frac{{\partial U(x,{{t}_{2}})}}{{\partial t}} - \frac{{\partial U(x,{{t}_{1}})}}{{\partial t}}} \right|}_{{2 + \alpha }}}\;\leqslant \;\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {{\left| {\frac{{{{\partial }^{2}}U(x,\tau )}}{{\partial {{\tau }^{2}}}}} \right|}_{{2 + \alpha }}}{\kern 1pt} d\tau \;\leqslant \;\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}}} \right|}_{{2 + \alpha }}}{\text{|}}{{t}_{2}} - {{t}_{1}}{\text{|}}\;\leqslant \\ \leqslant \;{{b}_{4}}(T)\mathop {\sup }\limits_{t \in [0,T]} {\text{|}}\rho (x,t){\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{t}_{2}} - {{t}_{1}}{\text{|}} \to + 0 \\ \end{gathered} $
при ${\text{|}}{{t}_{2}} - {{t}_{1}}{\text{|}} \to + 0.$ Следовательно,
$\frac{{\partial U(x,t)}}{{\partial t}} \in \mathbb{C}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})).$
Докажем, что
где символом $dU{\text{/}}dt$ мы обозначили сильную производную по времени в смысле банахова пространства ${{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})$. Действительно, справедливы следующие соотношения:
${{\left| {\frac{{U(x,t + h) - U(x,t)}}{h} - \frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{{2 + \alpha }}} = {{\left| {\frac{{U(x,t + h) - U(x,t)}}{h} - \frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{0}} + $
$ + \;\sum\limits_{j = 1}^3 {{\left| {\frac{{{{U}_{{{{x}_{j}}}}}(x,t + h) - {{U}_{{{{x}_{j}}}}}(x,t)}}{h} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial t}}} \right|}_{0}} + \sum\limits_{j,k = 1,1}^{3,3} {{\left| {\frac{{{{U}_{{{{x}_{j}}{{x}_{k}}}}}(x,t + h) - {{U}_{{{{x}_{j}}{{x}_{k}}}}}(x,t)}}{h} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}} \right|}_{\alpha }}\;\leqslant $
$\leqslant \;{{\left| {\frac{{\partial U(x,t{\kern 1pt} *)}}{{\partial t}} - \frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{0}} + \sum\limits_{j = 1}^3 {{\left| {\frac{{{{\partial }^{2}}U(x,t{\kern 1pt} *{\kern 1pt} *)}}{{\partial t\partial {{x}_{j}}}} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial t}}} \right|}_{0}} + $
(1.78)
$ + \;\sum\limits_{j,k = 1,1}^{3,3} {{\left| {\frac{{{{\partial }^{3}}U(x,t{\kern 1pt} *{\kern 1pt} *{\kern 1pt} *)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}} \right|}_{\alpha }}\;\leqslant \;\mathop {\sup }\limits_{s \in |t,t + h|} {{\left| {\frac{{\partial U(x,s)}}{{\partial t}} - \frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{0}} + $
$ + \;\sum\limits_{j = 1}^3 \,\mathop {\sup }\limits_{s \in |t,t + h|} {{\left| {\frac{{{{\partial }^{2}}U(x,s)}}{{\partial t\partial {{x}_{j}}}} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial t}}} \right|}_{0}} + \sum\limits_{j,k = 1,1}^{3,3} \,\mathop {\sup }\limits_{s \in |t,t + h|} {{\left| {\frac{{{{\partial }^{3}}U(x,s)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}}} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}} \right|}_{\alpha }} = $
$ = \mathop {\sup }\limits_{s \in |t,t + h|} {{\left| {\frac{{\partial U(x,s)}}{{\partial t}} - \frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{0}} + \sum\limits_{j = 1}^3 \,\mathop {\sup }\limits_{s \in |t,t + h|} {{\left| {\frac{{{{\partial }^{2}}U(x,s)}}{{\partial {{x}_{j}}\partial t}} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{x}_{j}}\partial t}}} \right|}_{0}} + $
$ + \;\sum\limits_{j,k = 1,1}^{3,3} \,\mathop {\sup }\limits_{s \in |t,t + h|} {{\left| {\frac{{{{\partial }^{3}}U(x,s)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}} \right|}_{\alpha }} = {{I}_{1}} + {{I}_{2}} + {{I}_{3}},$
где мы воспользовались коммутационными соотношениями, которые справедливы в силу результата
леммы 1.1. В силу этой же леммы справедливы предельные свойства
(1.79)
${{I}_{1}} \to 0,\quad {{I}_{2}} \to 0\quad {\text{при}}\quad {\text{|}}h{\kern 1pt} {\text{|}} \to + 0.$(1.80)
$\frac{{{{\partial }^{3}}U(x,s)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} = \int\limits_{|s,t|} \frac{{{{\partial }^{4}}U(x,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{\tau }^{2}}}}{\kern 1pt} d\tau ,$(1.81)
$\frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}},\quad \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}} \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})\quad {\text{для}}\;{\text{любого}}\quad t \in [0,T].$
${{\left| {\frac{{{{\partial }^{3}}U(x,s)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}} \right|}_{\alpha }}\;\leqslant \;\int\limits_{|s,t|} {{\left| {\frac{{{{\partial }^{4}}U(x,\tau )}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{\tau }^{2}}}}} \right|}_{\alpha }}{\kern 1pt} d\tau \;\leqslant \;\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial t}}} \right|}_{\alpha }}{\text{|}}t - s{\text{|}}\;\leqslant \;{{b}_{5}}(T)\mathop {\sup }\limits_{t \in [0,T]} {\text{|}}\rho (x,t){{{\text{|}}}_{\alpha }}{\text{|}}t - s{\text{|}},$
из которой вытекает, что
Таким образом, из (1.78) с учетом (1.79) и (1.82) приходим к выводу о том, что
${{\left| {\frac{{U(x,t + h) - U(x,t)}}{h} - \frac{{\partial U(x,t)}}{{\partial t}}} \right|}_{{2 + \alpha }}} \to + 0\quad {\text{при}}\quad {\text{|}}h{\text{|}} \to + 0.$
Следовательно, доказано (1.77), и поэтому вместе с результатом шага 10 приходим к
выводу, что
$U(x,t) \in {{\mathbb{C}}^{{(1)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}))\quad {\text{при}}\quad \alpha \in (0,1).$
Шаг 12: $U(x,t) \in {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}))$.
Заметим, что справедливо равенство (1.71). При этом в силу оценки (3.77) и соотношения (1.73) имеют место следующие соотношения:
(1.83)
$\begin{gathered} W(x,t) \in {{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})\quad {\text{для}}\;{\text{всех}}\quad t \in [0,T],\quad \alpha \in (0,1), \\ {{\left| {W(x,{{t}_{2}}) - W(x,{{t}_{1}})} \right|}_{{2 + \alpha }}}\;\leqslant \;{{b}_{2}}(T){{\left| {\rho (x,{{t}_{2}}) - \rho (x,{{t}_{1}})} \right|}_{\alpha }} \to + 0 \\ \end{gathered} $
$W(x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}))\quad {\text{при}}\quad \alpha \in (0,1).$
Теперь рассмотрим потенциал ${{U}_{2}}(x,t),$ определенный равенством (1.72). Точно так же, как при доказательстве равенства (1.71)
на шаге 5, используя результат леммы 5.1 [1], можно доказать поточечное равенство
$\frac{{\partial {{U}_{2}}(x,t)}}{{\partial t}} = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{3}}{{G}_{{{{\beta }_{1}},{{\beta }_{2}}}}}(x,y,t - \tau )}}{{\partial {{t}^{3}}}}\rho (y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau .$
Теперь, используя оценки (6.7)–(6.11) из [1], можно доказать, что
(1.84)
$\frac{{\partial {{U}_{2}}(x,t)}}{{\partial t}} \in \mathbb{C}_{b}^{{(2 + 0)}}({{\mathbb{R}}^{3}} \times [0,T]).$(1.85)
$\frac{{\partial {{U}_{2}}(x,t)}}{{\partial t}} \in \mathbb{C}_{b}^{{(2 + 1)}}({{\mathbb{R}}^{3}} \times [0,T]),$(1.86)
$\frac{{\partial {{U}_{2}}(x,t)}}{{\partial t}} \in {{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})\quad {\text{для}}\;{\text{всех}}\quad t \in [0,T].$(1.87)
$\frac{{{{\partial }^{2}}U(x,{{t}_{2}})}}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}U(x,{{t}_{1}})}}{{\partial {{t}^{2}}}} = W(x,{{t}_{2}}) - W(x,{{t}_{1}}) + \int\limits_{{{t}_{1}}}^{{{t}_{2}}} \frac{{\partial {{U}_{2}}(x,t)}}{{\partial t}}{\kern 1pt} dt,$(1.88)
$\begin{gathered} {{\left| {\frac{{{{\partial }^{2}}U(x,{{t}_{2}})}}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}U(x,{{t}_{1}})}}{{\partial {{t}^{2}}}}} \right|}_{{2 + \alpha }}}\;\leqslant \;{{\left| {W(x,{{t}_{2}}) - W(x,{{t}_{1}})} \right|}_{{2 + \alpha }}} + \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {{\left| {\frac{{\partial {{U}_{2}}(x,t)}}{{\partial t}}} \right|}_{{2 + \alpha }}}{\kern 1pt} dt, \\ \mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{\partial {{U}_{2}}(x,t)}}{{\partial t}}} \right|}_{{2 + \alpha }}}\;\leqslant \;{{b}_{3}}(T)\mathop {\sup }\limits_{t \in [0,T]} {{\left| {\rho (x,t)} \right|}_{\alpha }}. \\ \end{gathered} $
${{\left| {\frac{{{{\partial }^{2}}U(x,{{t}_{2}})}}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}U(x,{{t}_{1}})}}{{\partial {{t}^{2}}}}} \right|}_{{2 + \alpha }}}\;\leqslant \;{{b}_{4}}(T)\left( {{{{\left| {\rho (x,{{t}_{2}}) - \rho (x,{{t}_{1}})} \right|}}_{\alpha }} + \mathop {\sup }\limits_{t \in [0,T]} {{{\left| {\rho (x,t)} \right|}}_{\alpha }}{\text{|}}{{t}_{2}} - {{t}_{1}}{\text{|}}} \right) \to + 0$
при ${\text{|}}{{t}_{2}} - {{t}_{1}}{\text{|}} \to + 0$ для любых $0\;\leqslant \;{{t}_{1}}\;\leqslant \;{{t}_{2}}\;\leqslant \;T$. Следовательно,
$\frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}} \in \mathbb{C}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}))\quad {\text{при}}\quad \alpha \in (0,1).$
Учитывая, что на предыдущем шаге нами было доказано, что
то теперь наша задача доказать, что в смысле банахова пространства ${{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})$ справедливо равенство
$\frac{d}{{dt}}\frac{{\partial U(x,t)}}{{\partial t}} = \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}}.$
Справедлива следующая цепочка соотношений:
${{\left| {\frac{{{{U}_{t}}(x,t + h) - {{U}_{t}}(x,t)}}{h} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}}} \right|}_{{2 + \alpha }}} = {{\left| {\frac{{{{U}_{t}}(x,t + h) - {{U}_{t}}(x,t)}}{h} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}}} \right|}_{0}} + $
$\, + \sum\limits_{j = 1}^3 {{\left| {\frac{{{{U}_{{{{x}_{j}}t}}}(x,t + h) - {{U}_{{{{x}_{j}}t}}}(x,t)}}{h} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}} \right|}_{0}} + \sum\limits_{j,k = 1,1}^{3,3} {{\left| {\frac{{{{U}_{{{{x}_{j}}{{x}_{k}}t}}}(x,t + h) - {{U}_{{{{x}_{j}}{{x}_{k}}t}}}(x,t)}}{h} - \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}}} \right|}_{\alpha }} = $
$\, = {{\left| {\frac{{{{\partial }^{2}}U(x,t{\kern 1pt} *)}}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}}} \right|}_{0}} + \sum\limits_{j = 1}^3 {{\left| {\frac{{{{\partial }^{3}}U(x,t{\kern 1pt} *{\kern 1pt} *)}}{{\partial t\partial {{x}_{j}}\partial t}} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}} \right|}_{0}} + \sum\limits_{j,k = 1,1}^{3,3} {{\left| {\frac{{{{\partial }^{4}}U(x,t{\kern 1pt} *{\kern 1pt} *{\kern 1pt} *)}}{{\partial t\partial {{x}_{j}}\partial {{x}_{k}}\partial t}} - \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}}} \right|}_{\alpha }} = $
$\, = {{\left| {\frac{{{{\partial }^{2}}U(x,t{\kern 1pt} *)}}{{\partial {{t}^{2}}}} - \frac{{{{\partial }^{2}}U(x,t)}}{{\partial {{t}^{2}}}}} \right|}_{0}} + \sum\limits_{j = 1}^3 {{\left| {\frac{{{{\partial }^{3}}U(x,t{\kern 1pt} *{\kern 1pt} *)}}{{\partial {{x}_{j}}\partial {{t}^{2}}}} - \frac{{{{\partial }^{3}}U(x,t)}}{{\partial {{x}_{j}}\partial {{t}^{2}}}}} \right|}_{0}} + \sum\limits_{j,k = 1,1}^{3,3} {{\left| {\frac{{{{\partial }^{4}}U(x,t{\kern 1pt} *{\kern 1pt} *{\kern 1pt} *)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}} - \frac{{{{\partial }^{4}}U(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{t}^{2}}}}} \right|}_{\alpha }} = $
$\, = {{J}_{1}} + {{J}_{2}} + {{J}_{3}},\quad t{\kern 1pt} *,\;t{\kern 1pt} *{\kern 1pt} *,\;t{\kern 1pt} *{\kern 1pt} *{\kern 1pt} * \in {\text{|}}t,t + h{\text{|}},$
где мы воспользовались коммутационными соотношениями, поскольку в силу леммы 1.1 имеем
$U(x,t) \in \mathbb{C}_{b}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T])$. Далее, рассуждая точно так же, как на шаге 11, в силу (1.85), (1.86) и (1.88) можно
доказать, что
${{J}_{1}},\;{{J}_{2}},\;{{J}_{3}} \to + 0\quad {\text{при}}\quad {\text{|}}h{\kern 1pt} {\text{|}} \to + 0.$
Таким образом, в силу результатов шагов 10–12 справедливо основное утверждение настоящей
теоремы
$U(x,t) \in {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}}))\quad {\text{при}}\quad \alpha \in (0,1).$
Теорема доказана полностью.
Справедлива следующая
Теорема 2. Если $\mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$, то для любого $k \in \mathbb{N} \cup \{ 0\} $ имеем
${{V}_{k}}(x,t) \in {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})),$
где потенциал ${{V}_{k}}(x,t)$ определен равенством (1.2).
Доказательство. Утверждение фактически доказано при доказательстве теоремы 1.
Введем следующие потенциалы:
(1.89)
${{U}_{0}}(x,t) = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t - \tau ){{\rho }_{0}}(y,\tau ){\kern 1pt} dy{\kern 1pt} d\tau ,$
${{V}_{{00}}}(x,t) = \int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t){{\mu }_{0}}(y){\kern 1pt} dy,$
(1.90)
${{V}_{{01}}}(x,t) = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial t}}{{\mu }_{1}}(y){\kern 1pt} dy,$(1.91)
${{\rho }_{0}}(x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{\gamma /2}}};{{\mathbb{R}}^{3}}),$(1.92)
$\begin{gathered} {{\mu }_{0}}(x) \in {{\mathbb{C}}^{\alpha }}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}};{{\mathbb{R}}^{3}}), \\ {{\mu }_{0}}(x) \in {{\mathbb{C}}^{\alpha }}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{3}}/2}}};{{\mathbb{R}}^{3}}) \\ \end{gathered} $(1.93)
${{U}_{0}}(x,t) = \frac{{U(x,t)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}},\quad \rho (x,t) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{\gamma /2}}}{{\rho }_{0}}(x,t),$
${{V}_{{00}}}(x,t) = \frac{{{{V}_{0}}(x,t)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}},\quad \mu (x) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}}{{\mu }_{0}}(x),$
(1.94)
${{V}_{{01}}}(x,t) = \frac{{{{V}_{1}}(x,t)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}},\quad \mu (x) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{3}}/2}}}{{\mu }_{1}}(x).$Теорема 3. Если выполнены соотношения (1.91),(1.92), то при $\alpha \in (0,1)$ и $\min \{ \gamma ,{{\beta }_{2}},{{\beta }_{3}}\} \; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$ справедливы соотношения
${{U}_{0}}(x,t) \in {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})) \cap \mathbb{C}_{b}^{{(2 + 2)}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}};{{\mathbb{R}}^{3}} \times [0,T]),$
${{V}_{{00}}}(x,t),{\kern 1pt} {{V}_{{01}}}(x,t) \in {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})) \cap \mathbb{C}_{b}^{{(2 + 2)}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}};{{\mathbb{R}}^{3}} \times [0,T]).$
Доказательство. Теорема является следствием равенств (1.93), (1.94) и теорем 1, 2.
Справедлива следующая
Лемма 1.2. Если ${{u}_{0}}(x),\;{{u}_{1}}(x) \in \mathbb{C}_{b}^{{(2)}}({{\mathbb{R}}^{3}}),$ то справедливы следующие равенства:
(1.95)
$\frac{{\partial {{V}_{{00}}}[\Delta {{u}_{1}} - {{u}_{1}}]}}{{\partial t}}(x,0) = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\left[ {\Delta {{u}_{1}}(y) - {{u}_{1}}(y)} \right]{\kern 1pt} dy = {{u}_{1}}(x),$(1.96)
${{V}_{{01}}}[\Delta {{u}_{0}} - {{u}_{0}}](x,0) = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\left[ {\Delta {{u}_{0}}(y) - {{u}_{0}}(y)} \right]{\kern 1pt} dy = {{u}_{0}}(x),$(1.97)
$\begin{gathered} {{U}_{{00}}}(x,0) = \frac{{\partial {{U}_{{00}}}}}{{\partial t}}(x,0) = 0, \\ {{V}_{{00}}}(x,0) = 0,\quad \frac{{\partial {{V}_{{01}}}}}{{\partial t}}(x,0) = 0\quad {\text{для}}\;{\text{каждого}}\quad x \in {{\mathbb{R}}^{3}}. \\ \end{gathered} $Доказательство. Равенства (1.95) и (1.96) являются следствиями теоремы 2 и доказаны, например, в работе [3]. Равенства (1.97) являются следствиями леммы I.5.1.
Наконец, справедлива следующая
Теорема 4. Если ${{\rho }_{0}}(x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})),$ ${{\mu }_{0}}(x),{\kern 1pt} {{\mu }_{1}}(x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1),$ то
(1.99)
$\begin{gathered} {{\mathfrak{M}}_{{x,t}}}[{{V}_{{00}}}](x,t) = {{\mathfrak{M}}_{{x,t}}}[{{V}_{{01}}}](x,t) = 0\quad {\text{для}}\;{\text{всех}}\quad (x,t) \in {{\mathbb{R}}^{3}} \times [0,T], \\ {{\mathfrak{M}}_{{x,t}}}[w](x,t) = {{\Delta }_{x}}\frac{{{{\partial }^{2}}w(x,t)}}{{\partial {{t}^{2}}}} + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{{{\partial }^{2}}w(x,t)}}{{\partial x_{j}^{2}}}. \\ \end{gathered} $Доказательство. Пусть $\langle \langle \cdot , \cdot \rangle \rangle $ – скобки двойственности между пространством основных функций $\mathcal{D}({{\mathbb{R}}^{3}} \times (0,T))$ и пространством обобщенных функций $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{3}} \times (0,T))$, а $\langle \cdot , \cdot \rangle $ – скобки двойственности между пространством основных функций $\mathcal{D}({{\mathbb{R}}^{3}})$ и пространством обобщенных функций $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{3}})$. Тогда справедливы следующие равенства:
$\left\langle {\left\langle {{{U}_{0}}(x,t),\phi (x,t)} \right\rangle } \right\rangle \left\langle {\left\langle {\mathcal{E}(x,t) * {{\rho }_{0}}(x,t),\phi (x,t)} \right\rangle } \right\rangle ,\quad \left\langle {\left\langle {{{V}_{{00}}}(x,t),\phi (x,t)} \right\rangle } \right\rangle = \left\langle {\left\langle {\mathcal{E}(x,t) * \delta (t){{\mu }_{0}}(x),\phi (x,t)} \right\rangle } \right\rangle ,$
$\begin{gathered} \left\langle {\left\langle {{{V}_{{01}}}(x,t),\phi (x,t)} \right\rangle } \right\rangle = \left\langle {\left\langle {\mathcal{E}{\kern 1pt} '(x,t) * \delta (t){{\mu }_{1}}(x),\phi (x,t)} \right\rangle } \right\rangle = \\ \, = \left\langle {\left\langle {\mathcal{E}(x,t) * \delta {\kern 1pt} '(t){{\mu }_{1}}(x),\phi (x,t)} \right\rangle } \right\rangle \quad {\text{для}}\;{\text{любой}}\quad \phi (x,t) \in \mathcal{D}({{\mathbb{R}}^{3}} \times (0,T)). \\ \end{gathered} $
Используя известные результаты теории обобщенных функций, можно доказать следующие
равенства:
(1.100)
$\begin{gathered} \left\langle {\left\langle {{{\mathfrak{M}}_{{x,t}}}[{{U}_{0}}](x,t),\phi (x,t)} \right\rangle } \right\rangle \left\langle {\left\langle {{{\mathfrak{M}}_{{x,t}}}[\mathcal{E}](x,t) * {{\rho }_{0}}(x,t),\phi (x,t)} \right\rangle } \right\rangle = \\ \, = \left\langle {\left\langle {\delta (x,t) * {{\rho }_{0}}(x,t),\phi (x,t)} \right\rangle } \right\rangle \left\langle {\left\langle {{{\rho }_{0}}(x,t),\phi (x,t)} \right\rangle } \right\rangle , \\ \end{gathered} $
$\begin{gathered} \left\langle {\left\langle {{{\mathfrak{M}}_{{x,t}}}[{{V}_{{00}}}](x,t),\phi (x,t)} \right\rangle } \right\rangle = \left\langle {\left\langle {{{\mathfrak{M}}_{{x,t}}}[\mathcal{E}](x,t) * \delta (t){{\mu }_{0}}(x),\phi (x,t)} \right\rangle } \right\rangle = \\ = \left\langle {\left\langle {\delta (x,t) * \delta (t){{\mu }_{0}}(x),\phi (x,t)} \right\rangle } \right\rangle = \left\langle {\left\langle {\delta (t){{\mu }_{0}}(x),\phi (x,t)} \right\rangle } \right\rangle = \left\langle {{{\mu }_{0}}(x),\phi (x,0)} \right\rangle = 0, \\ \end{gathered} $
(1.101)
$\begin{gathered} \left\langle {\left\langle {{{\mathfrak{M}}_{{x,t}}}[{{V}_{{01}}}](x,t),\phi (x,t)} \right\rangle } \right\rangle = \left\langle {\left\langle {{{\mathfrak{M}}_{{x,t}}}[\mathcal{E}](x,t) * \delta {\kern 1pt} '(t){{\mu }_{1}}(x),\phi (x,t)} \right\rangle } \right\rangle = \\ = \left\langle {\left\langle {\delta (x,t) * \delta {\kern 1pt} '(t){{\mu }_{1}}(x),\phi (x,t)} \right\rangle } \right\rangle = \left\langle {\left\langle {\delta {\kern 1pt} '(t){{\mu }_{1}}(x),\phi (x,t)} \right\rangle } \right\rangle = - \left\langle {{{\mu }_{1}}(x),\phi {\kern 1pt} '(x,0)} \right\rangle = 0 \\ \end{gathered} $
$\int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \left[ {{{\mathfrak{M}}_{{x,t}}}[{{U}_{0}}](x,t) - {{\rho }_{0}}(x,t)} \right]\phi (x,t){\kern 1pt} dx{\kern 1pt} dt = 0,$
$\int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{\mathfrak{M}}_{{x,t}}}[{{V}_{{00}}}](x,t)\phi (x,t){\kern 1pt} dx{\kern 1pt} dt = 0,\quad \int\limits_0^T {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{\mathfrak{M}}_{{x,t}}}[{{V}_{{01}}}](x,t)\phi (x,t){\kern 1pt} dx{\kern 1pt} dt = 0$
для любых $\phi (x,t) \in \mathcal{D}({{\mathbb{R}}^{3}} \times (0,T))$. В силу основной леммы вариационного исчисления приходим к равенствам (1.98), (1.99).
Пусть
$L(x,t) = {{U}_{0}}[{{\rho }_{0}}](x,t) + {{V}_{{00}}}[{{\Delta }_{x}}{{u}_{1}}(x) - {{u}_{1}}(x)](x,t) + {{V}_{{01}}}[{{\Delta }_{x}}{{u}_{0}}(x) - {{u}_{0}}(x)](x,t).$
Справедлива следующая основная
Теорема 5. Если ${{\rho }_{0}}(x,t) \in \mathbb{C}([0,T];{{\mathbb{C}}^{\alpha }}((1 + \;{\text{|}}x{{{\text{|}}}^{2}}{{)}^{{\gamma /2}}};{{\mathbb{R}}^{3}})),$ при $\alpha \in (0,1)$ и
(1.102)
${{\Delta }_{x}}{{u}_{0}}(x) - {{u}_{0}}(x) \in {{\mathbb{C}}^{\alpha }}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}};{{\mathbb{R}}^{3}}),$(1.103)
${{\Delta }_{x}}{{u}_{1}}(x) - {{u}_{1}}(x) \in {{\mathbb{C}}^{\alpha }}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{3}}/2}}};{{\mathbb{R}}^{3}})$
$L(x,t) \in {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})) \cap \mathbb{C}_{b}^{{(2 + 2)}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}};{{\mathbb{R}}^{3}} \times [0,T]),$
${{\mathfrak{M}}_{{x,t}}}[L](x,t) = {{\rho }_{0}}(x,t)\quad для\;всех\quad (x,t) \in {{\mathbb{R}}^{3}} \times [0,T],$
$L(x,0) = {{u}_{0}}(x),\quad \frac{{\partial L(x,0)}}{{\partial t}} = {{u}_{1}}(x)\quad для\;всех\quad x \in {{\mathbb{R}}^{3}}.$
Доказательство. Доказательство основано на теоремах 2, 4 и лемме 1.2.
Замечание 1. Заметим, что мы имеем следующие достаточные условия на функции ${{u}_{0}}(x)$ и ${{u}_{1}}(x)$ такие, чтобы были выполнены соотношения (1.102), (1.103):
${{u}_{0}}(x) \in {{\mathbb{C}}^{{2 + \alpha }}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}};{{\mathbb{R}}^{3}}),\quad {{u}_{1}}(x) \in {{\mathbb{C}}^{{2 + \alpha }}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{3}}/2}}};{{\mathbb{R}}^{3}})$
при ${{\beta }_{2}}\; \geqslant \;0,$ ${{\beta }_{3}}\; \geqslant \;0$ и $\alpha \in (0,1)$. Действительно, пусть, например, ${{u}_{0}}(x) \in {{\mathbb{C}}^{{2 + \alpha }}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}};{{\mathbb{R}}^{3}})$. Тогда справедлива следующая цепочка равенств:
$\begin{gathered} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{2}}/2}}}\Delta {{u}_{0}}(x) = \Delta ((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}}{{u}_{0}}(x)) - {{u}_{0}}(x)\Delta {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{2}}/2}}} - \\ \, - 2\sum\limits_{j = 1}^3 \frac{{\partial {{u}_{0}}(x)}}{{\partial {{x}_{j}}}}\frac{{\partial {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{{\partial {{x}_{j}}}}\Delta ((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}}{{u}_{0}}(x)) - \\ \end{gathered} $
$\begin{gathered} - \;{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{2}}/2}}}{{u}_{0}}(x)\frac{{\Delta {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}} - 2\sum\limits_{j = 1}^3 \,{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{2}}/2}}}\frac{{\partial {{u}_{0}}(x)}}{{\partial {{x}_{j}}}}\frac{{\frac{{\partial {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{{\partial {{x}_{j}}}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}} = \\ \, = \Delta ((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}}{{u}_{0}}(x)) + {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{2}}/2}}}{{u}_{0}}(x)\frac{{\Delta {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}} - \\ \end{gathered} $
$ - \;2\sum\limits_{j = 1}^3 \frac{{\partial [(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}}{{u}_{0}}(x)]}}{{\partial {{x}_{j}}}}\frac{{\frac{{\partial {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{{\partial {{x}_{j}}}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}} + 2\sum\limits_{j = 1}^3 \,{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{2}}/2}}}{{u}_{0}}(x)\frac{{{{{\left( {\frac{{\partial {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{{\partial {{x}_{j}}}}} \right)}}^{2}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}}}}}} \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}).$
2. АПРИОРНАЯ ОЦЕНКА ТИПА ШАУДЕРА
Если $u(x,t) \in \mathbb{C}_{b}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T]),$ то справедлива следующая третья формула Грина (см. формулу (9.1) теоремы 3 статьи [1]):
(2.1)
$\begin{gathered} u(x,t) = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - \xi ,t - \tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau + \\ + \;\int\limits_{{{\mathbb{R}}^{3}}} \left[ {\mathcal{E}(x - \xi ,t)[{{\Delta }_{\xi }}{{u}_{1}}(\xi ) - {{u}_{1}}(\xi )] + \frac{{\partial{ \mathcal{E}}(x - \xi ,t)}}{{\partial t}}[{{\Delta }_{\xi }}{{u}_{0}}(\xi ) - {{u}_{0}}(\xi )]} \right]{\kern 1pt} d\xi . \\ \end{gathered} $
$\begin{gathered} \mathop {\sup }\limits_{t \in [0,T]} \left[ {{{{\left| {{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}u(x,t)} \right|}}_{{2 + \alpha }}} + {{{\left| {{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}u{\kern 1pt} '(x,t)} \right|}}_{{2 + \alpha }}}} \right. + \left. {{{{\left| {{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}u{\kern 1pt} '{\kern 1pt} '(x,t)} \right|}}_{{2 + \alpha }}}} \right]\;\leqslant \\ \leqslant \;a(T)\left[ {\mathop {\sup }\limits_{t \in [0,T]} {{{\left| {{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{\gamma /2}}}{{\mathfrak{M}}_{{x,t}}}[u](x,t)} \right|}}_{\alpha }}} \right. + \left. {{{{\left| {{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}[{{\Delta }_{x}}{{u}_{0}}(x) - {{u}_{0}}(x)]} \right|}}_{\alpha }} + {{{\left| {{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{{{\beta }_{3}}/2}}}[{{\Delta }_{x}}{{u}_{1}}(x) - {{u}_{1}}(x)]} \right|}}_{\alpha }}} \right]{\kern 1pt} , \\ \end{gathered} $
где $\alpha \in (0,1),$ $\min \{ \gamma ,{{\beta }_{2}},{{\beta }_{3}}\} \; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$.
3. ОЦЕНКИ ТИПА ШАУДЕРА ДЛЯ ПОТЕНЦИАЛОВ С ВЕСОМ
В этом разделе мы воспользуемся методами исследований из работы [2] (см. также работу [4]). Рассмотрим следующий потенциал с весом:
$u(x,t) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t)f(y){\kern 1pt} dy,$
$f(x) = \frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}},\quad \mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}),\quad {{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,\quad \alpha \in (0,1).$
Заметим, что справедливы следующие равенства:
$\frac{{{{\partial }^{2}}u(x,t)}}{{\partial {{x}_{j}}\partial {{x}_{i}}}} = \left[ {{{\beta }_{1}}{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 1}}}{{\delta }_{{ij}}} + {{\beta }_{1}}({{\beta }_{1}} - 2){{x}_{i}}{{x}_{j}}{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2 - 2}}}} \right]\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - y,t)f(y){\kern 1pt} dy + $
(3.1)
$ + \;{{\beta }_{1}}{{x}_{i}}{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{x}_{j}}}}f(y){\kern 1pt} dy + {{\beta }_{1}}{{x}_{j}}{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{x}_{i}}}}f(y){\kern 1pt} dy + $
$ + \;{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{i}}\partial {{x}_{j}}}}\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - y,t)f(y){\kern 1pt} dy = {{u}_{1}}(x,t) + {{u}_{2}}(x,t) + {{u}_{3}}(x,t) + {{u}_{4}}(x,t).$
Прежде всего нам нужно получить вспомогательные оценки. Справедливы равенства
(3.2)
$\begin{gathered} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}F({{x}_{1}} - y,t) - {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}F({{x}_{2}} - y,t) = \int\limits_0^1 \frac{\partial }{{\partial s}}\left[ {{{{(1 + \;{\text{|}}{{x}_{s}}{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}F({{x}_{s}} - y,t)} \right]{\kern 1pt} ds = \\ \, = \{ {{x}_{s}} = s{{x}_{1}} + (1 - s){{x}_{2}}\} = \int\limits_0^1 {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^3 \,{{\beta }_{1}}{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2 - 1}}}{{x}_{{sj}}}({{x}_{{1j}}} - {{x}_{{2j}}})F({{x}_{s}} - y,t){\kern 1pt} ds + \\ \, + \int\limits_0^1 \,{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\sum\limits_{j = 1}^3 \frac{{\partial F({{x}_{s}} - y,t)}}{{\partial {{x}_{{sj}}}}}({{x}_{{1j}}} - {{x}_{{2j}}}) = {{K}_{1}} + {{K}_{2}}. \\ \end{gathered} $(3.3)
${{(1 + \;{\text{|}}{{x}_{s}}{\kern 1pt} {{{\text{|}}}^{2}})}^{{1/2}}}\;\leqslant \;\sqrt 2 {{(1 + \;{\text{|}}{{x}_{s}} - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{1/2}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{1/2}}}.$(3.4)
${\text{|}}{{K}_{1}}{\text{|}}\;\leqslant \;3{{\beta }_{1}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \left| {F({{x}_{s}} - y,t){\kern 1pt} } \right|{\kern 1pt} ds,\quad {{\beta }_{1}} \in [0,1].$
$\begin{gathered} {\text{|}}{{K}_{1}}{\text{|}}\;\leqslant \;3{{\beta }_{1}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \,{{(1 + \;{\text{|}}{{x}_{s}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\text{|}}F({{x}_{s}} - y,t){\kern 1pt} {\text{|}}{\kern 1pt} ds\;\leqslant \;3{{\beta }_{1}}{{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}} \times \\ \, \times \int\limits_0^1 \,{{(1 + \;{\text{|}}{{x}_{s}} - y{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}\left| {F({{x}_{s}} - y,t)} \right|{\kern 1pt} ds,\quad {{\beta }_{1}} > 1. \\ \end{gathered} $
Для ${{K}_{2}}$ с учетом (3.3) справедлива следующая оценка:
(3.5)
${\text{|}}{{K}_{2}}{\text{|}}\;\leqslant \;{{2}^{{{{\beta }_{1}}/2}}}3(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \,{{(1 + \;{\text{|}}{{x}_{s}} - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\left| {{{D}_{x}}F({{x}_{s}} - y,t){\kern 1pt} } \right|{\kern 1pt} ds.$
$\left| {{{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}F({{x}_{1}} - y,t) - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}F({{x}_{2}} - y,t)} \right|\;\leqslant \;3{{\beta }_{1}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 {\kern 1pt} ds{\text{|}}F({{x}_{s}} - y,t){\kern 1pt} {\text{|}} \times $
(3.6)
$ \times \;\left\{ \begin{gathered} {{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}{{x}_{s}} - y{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}},\quad {\text{если}}\quad {{\beta }_{1}} > 1; \hfill \\ 1,\quad {\text{если}}\quad {{\beta }_{1}} \in [0,1]; \hfill \\ \end{gathered} \right. + $
$ + \;{{2}^{{{{\beta }_{1}}/2}}}3(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 {{(1 + \;{\text{|}}{{x}_{s}} - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\left| {{{D}_{x}}F({{x}_{s}} - y,t){\kern 1pt} } \right|{\kern 1pt} ds,$
где ${{x}_{s}} = s{{x}_{1}} + (1 - s){{x}_{2}},$ $s \in [0,1]$.
Заметим, что имеет место
Теорема 6. Если $\mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1),$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$, то
${\text{|}}{{u}_{4}}(x,t){\kern 1pt} {{{\text{|}}}_{\alpha }}\;\leqslant \;D(T){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}\quad для\;всех\quad t \in [0,T],$
где $D = D(T) > 0$ – монотонно неубывающая функция, ограниченная на компактах.
Доказательство.
Шаг 1: Пусть ${{x}_{1}},{{x}_{2}} \in {{\mathbb{R}}^{3}}$ такие точки, что
$\rho : = {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}} < 1,\quad {{x}_{0}}: = \frac{{{{x}_{1}} + {{x}_{2}}}}{2},\quad {{R}_{0}} > 1.$
Тогда очевидно, что
Заметим, что для потенциала
${{u}_{4}}(x,t) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}_{i}}\partial {{x}_{j}}}}\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - y,t)f(y){\kern 1pt} dy,$
$f(x) = \frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}},\quad {{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,\quad \mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}),\quad \alpha \in (0,1],$
в силу (4.11), в котором положим $z = {{x}_{0}}$ и $R = 2{{R}_{0}},$ справедливо следующее представление:
(3.7)
$\begin{gathered} {{u}_{4}}(x,t) = \int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}_{0}},2{{R}_{0}})} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}f(y){\kern 1pt} dy + \\ \, + \int\limits_{O({{x}_{0}},2{{R}_{0}})} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\left[ {f(y) - f(x)} \right]{\kern 1pt} dy + \\ + \;{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O({{x}_{0}},2{{R}_{0}})} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}},\quad x \in O({{x}_{0}},2{{R}_{0}}). \\ \end{gathered} $(3.8)
${{F}_{2}}(x,y,t): = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}.$(3.9)
${{u}_{4}}({{x}_{1}},t) - {{u}_{4}}({{x}_{2}},t) = {{I}_{0}} + {{I}_{1}} + {{I}_{2}} + {{I}_{3}} + {{I}_{4}} + {{I}_{5}} + {{I}_{6}},$(3.10)
${{I}_{0}}: = \int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}_{0}},2{{R}_{0}})} \left[ {{{F}_{2}}({{x}_{1}},y,t) - {{F}_{2}}({{x}_{2}},y,t)} \right]f(y){\kern 1pt} dy,$(3.11)
${{I}_{1}}: = (1 + \;{\text{|}}{{x}_{2}}{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}f({{x}_{2}})\int\limits_{\partial O({{x}_{0}},2{{R}_{0}})} \left[ {\frac{{\partial{ \mathcal{E}}({{x}_{1}} - y,t)}}{{\partial {{y}_{j}}}} - \frac{{\partial{ \mathcal{E}}({{x}_{2}} - y,t)}}{{\partial {{y}_{j}}}}} \right]\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}},$
${{I}_{2}}: = \left[ {{{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f({{x}_{1}}) - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f({{x}_{2}})} \right]\int\limits_{\partial O({{x}_{0}},2{{R}_{0}})} \frac{{\partial{ \mathcal{E}}({{x}_{1}} - y,t)}}{{\partial {{y}_{j}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}},$
(3.12)
${{I}_{3}}: = \int\limits_{O({{x}_{0}},\rho )} {{F}_{2}}({{x}_{2}},y,t)(f({{x}_{2}}) - f(y)){\kern 1pt} dy,$(3.13)
${{I}_{4}}: = \int\limits_{O({{x}_{0}},\rho )} {{F}_{2}}({{x}_{1}},y,t)(f(y) - f({{x}_{1}})){\kern 1pt} dy,$(3.14)
${{I}_{5}}: = (f({{x}_{2}}) - f({{x}_{1}}))\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} {{F}_{2}}({{x}_{2}},y,t){\kern 1pt} dy,$(3.15)
${{I}_{6}}: = \int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \left( {{{F}_{2}}({{x}_{2}},y,t) - {{F}_{2}}({{x}_{1}},y,t)} \right)(f({{x}_{1}}) - f(y)){\kern 1pt} dy.$Шаг 2: ${{I}_{0}}$. Заметим, что при ${\text{|}}y - {{x}_{0}}{\text{|}}\; \geqslant \;2{{R}_{0}}$ справедливы неравенства
(3.16)
${\text{|}}{{x}_{s}} - y{\text{|}}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}}\; - \;{\text{|}}{{x}_{s}} - {{x}_{0}}{\text{|}}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}} - \frac{1}{2}{\text{|}}y - {{x}_{0}}{\text{|}} = \frac{1}{2}{\text{|}}y - {{x}_{0}}{\text{|}}\; \geqslant \;{{R}_{0}} > 0,$(3.17)
${\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}}\;\leqslant \;{\text{|}}{{x}_{s}} - {{x}_{0}}{\text{|}}\; + \;{\text{|}}y - {{x}_{0}}{\text{|}}\;\leqslant \;\frac{1}{2}{\text{|}}y - {{x}_{0}}{\text{|}}\; + \;{\text{|}}y - {{x}_{0}}{\text{|}} = \frac{3}{2}{\text{|}}y - {{x}_{0}}{\text{|}}.$
$\begin{gathered} \left| {{{F}_{2}}({{x}_{1}},y,t) - {{F}_{2}}({{x}_{2}},y,t)} \right|\;\leqslant \;3{{\beta }_{1}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \left| {\frac{{{{\partial }^{2}}\mathcal{E}({{x}_{s}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}} \right|{\kern 1pt} ds + \\ + \;{{2}^{{{{\beta }_{1}}/2}}}3(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 {{\left( {1 + \;{\text{|}}{{x}_{s}} - y{\kern 1pt} {{{\text{|}}}^{2}}} \right)}^{{{{\beta }_{1}}/2}}}\left| {{{D}_{x}}\frac{{{{\partial }^{2}}\mathcal{E}({{x}_{s}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}} \right|{\kern 1pt} ds\;\leqslant \\ \end{gathered} $
(3.18)
$\begin{gathered} \leqslant \;{{D}_{1}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon )){\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}}}}{{{\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}}}}{\kern 1pt} ds + \\ + \;{{D}_{2}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\int\limits_0^1 \,{{(1 + \;{\text{|}}{{x}_{s}} - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon )){\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}}}}{{{\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}}}}{\kern 1pt} ds\;\leqslant \\ \end{gathered} $
$\begin{gathered} \leqslant \;{{D}_{3}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\frac{{\exp ( - (1 - \varepsilon ))(1{\text{/}}2){\kern 1pt} {\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}} + \\ + \;{{D}_{4}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}{{(1 + \;{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon )){\kern 1pt} {\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}, \\ \end{gathered} $
где ${{x}_{s}} = s{{x}_{1}} + (1 - s){{x}_{2}}$ и мы воспользовались оценками (6.11), (10.20) статьи [1]. Теперь получим оценку, аналогичную (3.18) в случае ${{\beta }_{1}} > 1.$ Из тех же соображений вытекает следующее неравенство:
(3.19)
$\begin{gathered} \left| {{{F}_{2}}({{x}_{1}},y,t) - {{F}_{2}}({{x}_{2}},y,t)} \right|\;\leqslant \;{{D}_{5}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}} \times \\ \times \;{{(1 + \;{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}\frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon )){\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}} + {{D}_{4}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}} \times \\ \, \times {{(1 + \;{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon )){\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}. \\ \end{gathered} $(3.20)
$\begin{gathered} {\text{|}}{{I}_{0}}{\text{|}}\;\leqslant \;{{D}_{3}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{||}}f(x){\kern 1pt} {{{\text{|}}}_{0}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}_{0}},2{{R}_{0}})} \frac{{\exp ( - (1 - \varepsilon ))(1{\text{/}}2){\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}{\kern 1pt} dy + \\ \, + {{D}_{4}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{\left| {f(x)(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}} \right|}_{0}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}_{0}},2{{R}_{0}})} {{(1 + \;{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}} \times \\ \times \;\frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon )){\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{6}}(T,{{R}_{0}},\varepsilon ){\text{|}}\mu {{{\text{|}}}_{0}}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} \in [0,1]. \\ \end{gathered} $
${\text{|}}{{I}_{0}}{\text{|}}\;\leqslant \;{{D}_{5}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{\left| {f(x)(1 + \;{\text{|}}x{{{\text{|}}}^{2}}{{)}^{{({{\beta }_{1}} - 1)/2}}}} \right|}_{0}} \times $
(3.21)
$\begin{gathered} \times \;\int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}_{0}},2{{R}_{0}})} {{(1 + \;{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}\frac{{\exp ( - (1 - \varepsilon ))(1{\text{/}}2){\kern 1pt} {\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}{\kern 1pt} dy + \\ \, + {{D}_{4}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{\left| {f(x)(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}} \right|}_{0}} \times \\ \end{gathered} $
$ \times \;\int\limits_{{{\mathbb{R}}^{3}}\backslash O({{x}_{0}},2{{R}_{0}})} {{(1 + \;{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon )){\text{|}}y - {{x}_{0}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{7}}(T,{{R}_{0}},\varepsilon ){\text{|}}\mu {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} > 1.$
Таким образом, из (3.20) и (3.21) вытекает единообразная оценка
(3.22)
${\text{|}}{{I}_{0}}{\text{|}}\;\leqslant \;{{D}_{8}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}.$Шаг 3: ${{I}_{1}}$. Справедливо следующее равенство:
$\frac{{\partial{ \mathcal{E}}({{x}_{1}} - y,t)}}{{\partial {{y}_{j}}}} - \frac{{\partial{ \mathcal{E}}({{x}_{2}} - y,t)}}{{\partial {{y}_{j}}}} = \int\limits_0^1 {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1}^3 \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{s}} - y,t)}}{{\partial {{x}_{{sk}}}\partial {{x}_{j}}}}[{{x}_{{1k}}} - {{x}_{{2k}}}]{\kern 1pt} ds,$
из которого при ${\text{|}}y - {{x}_{0}}{\text{|}} = 2{{R}_{0}}$ с учетом неравенств (3.16) и (3.17) вытекает цепочка неравенств
$\left| {\frac{{\partial{ \mathcal{E}}({{x}_{1}} - y,t)}}{{\partial {{y}_{j}}}} - \frac{{\partial{ \mathcal{E}}({{x}_{2}} - y,t)}}{{\partial {{y}_{j}}}}} \right|\;\leqslant \;3{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \left| {{{D}_{x}}\frac{{\partial{ \mathcal{E}}({{x}_{s}} - y,t)}}{{\partial {{y}_{j}}}}} \right|{\kern 1pt} ds\;\leqslant $
(3.23)
$\leqslant \;{{D}_{9}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon ){\kern 1pt} {\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}}}}{\kern 1pt} ds\;\leqslant $
$\leqslant \;{{D}_{{10}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon ){\kern 1pt} {\text{|}}y - {{x}_{0}}{\text{|}}{\kern 1pt} )}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}.$
С учетом (3.23) из (3.11) получаем искомую оценку
(3.24)
$\begin{gathered} {\text{|}}{{I}_{1}}{\text{|}}\;\leqslant \;{{\left| {{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(x)} \right|}_{0}}{{D}_{{10}}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}} \times \\ \, \times \int\limits_{\partial O({{x}_{0}},2{{R}_{0}})} \frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon ){\kern 1pt} {\text{|}}y - {{x}_{0}}{\text{|}})}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}{\kern 1pt} d{{S}_{y}}\;\leqslant \;{{D}_{{11}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}. \\ \end{gathered} $Шаг 4: ${{I}_{2}}.$ Справедлива следующая цепочка неравенств:
(3.25)
$\begin{gathered} {\text{|}}{{I}_{2}}{\text{|}}\;\leqslant \;{{D}_{{12}}}(T,{{R}_{0}},\varepsilon ){{\left[ {{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(x)} \right]}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}\int\limits_{\partial O({{x}_{0}},2{{R}_{0}})} \frac{{\exp ( - (1{\text{/}}2)(1 - \varepsilon ){\kern 1pt} {\text{|}}y - {{x}_{0}}{\text{|}}{\kern 1pt} )}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}{\kern 1pt} d{{S}_{y}}\;\leqslant \\ \leqslant \;{{D}_{{13}}}(T,{{R}_{0}},\varepsilon ){{\left[ {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}\;\leqslant \;{{D}_{{14}}}(T,{{R}_{0}},\varepsilon ){\text{|}}\mu {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}, \\ \end{gathered} $Шаг 5: ${{I}_{3}}$ и ${{I}_{4}}$. Получим оценку на интеграл ${{I}_{3}},$ поскольку оценка для интеграла ${{I}_{4}}$ получается заменой ${{x}_{2}} \leftrightarrow {{x}_{1}}.$ Выражение (3.12) для интеграла ${{I}_{3}}$ можно переписать в следующем виде:
$\begin{gathered} {{I}_{3}} = \int\limits_{O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\left[ {{{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f({{x}_{2}}) - {{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(y)} \right]{\kern 1pt} {\kern 1pt} dy + \\ + \;\int\limits_{O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}f(y)\left[ {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right]{\kern 1pt} {\kern 1pt} dy = :{{I}_{{31}}} + {{I}_{{32}}}. \\ \end{gathered} $
Заметим, что если ${\text{|}}y - {{x}_{0}}{\text{|}}\;\leqslant \;\rho $, то
(3.26)
${\text{|}}y - {{x}_{2}}{\text{|}}\;\leqslant \;{\text{|}}y - {{x}_{0}}{\text{|}}\; + \;{\text{|}}{{x}_{2}} - {{x}_{0}}{\text{|}}\;\leqslant \;\rho + \frac{\rho }{2} = \frac{{3\rho }}{2}.$(3.27)
${\text{|}}{{I}_{{31}}}{\text{|}}\;\leqslant \;{{D}_{{15}}}(T,{{R}_{0}},\varepsilon ){{\left[ {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]}_{\alpha }}\int\limits_{O({{x}_{2}},3\rho /2)} \frac{1}{{{\text{|}}y - {{x}_{2}}{{{\text{|}}}^{{3 - \alpha }}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{16}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}.$(3.28)
$\left| {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{\text{|}}y - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} \in [0,1],$(3.29)
$\begin{gathered} \left| {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\text{|}}y - {{x}_{2}}{\text{|}}{\kern 1pt} \int\limits_0^1 \,{{(1 + \;{\text{|}}{{x}_{s}} - y{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} ds\;\leqslant \\ \leqslant \;3{{\beta }_{1}}{{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}y - {{x}_{2}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} {\text{|}}y - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} > 1, \\ \end{gathered} $
${\text{|}}{{x}_{s}} - y{\kern 1pt} {\text{|}} = {\text{|}}sy + (1 - s){{x}_{2}} - y{\kern 1pt} {\text{|}} = (1 - s){\kern 1pt} {\text{|}}y - {{x}_{2}}{\text{|}}\;\leqslant \;{\text{|}}y - {{x}_{2}}{\text{|}},\quad s \in [0,1].$
Сначала получим оценку для ${{I}_{{32}}}$ при ${{\beta }_{1}} \in [0,1]$. Действительно, с учетом (3.26) и (3.28) справедливы следующие неравенства:
(3.30)
${\text{|}}{{I}_{{32}}}{\text{|}}\;\leqslant \;{{D}_{{17}}}(T,{{R}_{0}},\varepsilon ){\text{|}}f{{{\text{|}}}_{0}}\int\limits_{O({{x}_{2}},3\rho /2)} \frac{1}{{{\text{|}}y - {{x}_{2}}{\text{|}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{18}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{{0{\kern 1pt} }}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} \in [0,1].$(3.31)
$\begin{gathered} {\text{|}}{{I}_{{32}}}{\text{|}}\;\leqslant \;{{D}_{{19}}}(T,{{R}_{0}},\varepsilon ){{\left| {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{(1 + {{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right|}_{0}} \times \\ \times \;\int\limits_{O({{x}_{2}},3\rho /2)} \frac{{{{{(1 + \;{\text{|}}y - {{x}_{2}}{{{\text{|}}}^{2}})}}^{{({{\beta }_{1}} - 1)/2}}}}}{{{\text{|}}y - {{x}_{2}}{{{\text{|}}}^{2}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{20}}}(T,{{R}_{0}},\varepsilon ){\text{|}}\mu {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} > 1. \\ \end{gathered} $(3.32)
${\text{|}}{{I}_{3}}{\text{|}}\;\leqslant \;{{D}_{{21}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}.$(3.33)
${\text{|}}{{I}_{4}}{\text{|}}\;\leqslant \;{{D}_{{21}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}.$Шаг 6: ${{I}_{5}}.$ Выражение (3.14) можно переписать в следующем виде:
(3.34)
$\begin{gathered} {{I}_{5}} = \left[ {{{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f({{x}_{2}}) - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f({{x}_{1}})} \right]\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}{\kern 1pt} dy + \\ \, + \left[ {{{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right]f({{x}_{1}})\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}{\kern 1pt} dy:{{I}_{{51}}} + {{I}_{{52}}}. \\ \end{gathered} $
$J: = \int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}{\kern 1pt} dy.$
Для $J$ справедливо равенство
(3.35)
$J = \int\limits_{\partial O({{x}_{0}},2{{R}_{0}})} \frac{{\partial{ \mathcal{E}}({{x}_{2}} - y,t)}}{{\partial {{y}_{j}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} dy - \int\limits_{\partial O({{x}_{0}},\rho )} \frac{{\partial{ \mathcal{E}}({{x}_{2}} - y,t)}}{{\partial {{y}_{j}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} dy: = {{J}_{1}} + {{J}_{2}}.$(3.36)
${\text{|}}y - {{x}_{2}}{\text{|}}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}}\; - \;{\text{|}}{{x}_{2}} - {{x}_{0}}{\text{|}}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}} - \frac{\rho }{2}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}} - \frac{1}{4}{\text{|}}y - {{x}_{0}}{\text{|}} = \frac{3}{4}{\text{|}}y - {{x}_{0}}{\text{|}}.$(3.37)
${\text{|}}{{J}_{1}}{\text{|}}\;\leqslant \;{{D}_{{22}}}(T,{{R}_{0}},\varepsilon )\int\limits_{\partial O({{x}_{0}},2{{R}_{0}})} \frac{{\exp ( - (1 - \varepsilon )(3{\text{/}}4){\kern 1pt} {\text{|}}y - {{x}_{0}}{\text{|}}{\kern 1pt} )}}{{{\text{|}}y - {{x}_{0}}{\text{|}}}}{\kern 1pt} d{{S}_{y}}\;\leqslant \;{{D}_{{23}}}(T,{{R}_{0}},\varepsilon ) < + \infty .$(3.38)
${\text{|}}{{J}_{2}}{\text{|}}\;\leqslant \;{{D}_{{24}}}(T,{{R}_{0}},\varepsilon )\int\limits_{\partial O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{2}}{{{\text{|}}}^{2}}}}{\kern 1pt} d{{S}_{y}}\;\leqslant \;{{D}_{{25}}}(T,{{R}_{0}},\varepsilon )\int\limits_{\partial O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{2}}}}{\kern 1pt} d{{S}_{y}} = {{D}_{{26}}}(T,{{R}_{0}},\varepsilon ) < + \infty .$(3.39)
${\text{|}}J{\kern 1pt} {\text{|}}\;\leqslant \;{{D}_{{27}}}(T,{{R}_{0}},\varepsilon ) < + \infty .$(3.40)
${\text{|}}{{I}_{{51}}}{\text{|}}\;\leqslant \;{{D}_{{27}}}(T,{{R}_{0}},\varepsilon ){{\left[ {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}\;\leqslant \;{{D}_{{28}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}.$(3.41)
$\left| {{{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} \in [0,1],$(3.42)
$\begin{gathered} \left| {{{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} \int\limits_0^1 \,{{(1\; + \;{\text{|}}{{x}_{s}} - {{x}_{1}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} ds\;\leqslant \\ \leqslant \;3{{\beta }_{1}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}},\quad {{\beta }_{1}} > 1. \\ \end{gathered} $(3.43)
${\text{|}}{{I}_{{52}}}{\text{|}}\;\leqslant \;{{D}_{{29}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}f(x){{{\text{|}}}_{0}}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\;\leqslant \;{{D}_{{30}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu (x){\kern 1pt} {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} \in [0,1].$(3.44)
${\text{|}}{{I}_{{52}}}{\text{|}}\;\leqslant \;{{D}_{{31}}}(T,{{R}_{0}},\varepsilon ){{\left| {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{(1 + {{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right|}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\;\leqslant \;{{D}_{{32}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} > 1.$(3.45)
${\text{|}}{{I}_{5}}{\text{|}}\;\leqslant \;{{D}_{{33}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}.$Шаг 7: ${{I}_{6}}.$ Интеграл ${{I}_{6}},$ определенный равенством (3.15), можно представить в следующем виде:
${{I}_{{61}}}: = \left[ {{{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right]\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\left[ {f({{x}_{1}}) - f(y)} \right]{\kern 1pt} dy,$
(3.47)
${{I}_{{62}}}: = \int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \left[ {\frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}} - \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{1}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}} \right]\left[ {{{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f({{x}_{1}}) - {{{(1 + \;{\text{|}}y{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(y)} \right]{\kern 1pt} dy,$(3.48)
${{I}_{{63}}}: = \int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \left[ {\frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}} - \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{1}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}} \right]\left[ {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right]f(y){\kern 1pt} dy.$(3.49)
${\text{|}}{{x}_{1}} - y{\text{|}}\;\leqslant \;{\text{|}}y - {{x}_{0}}{\text{|}}\; + \;{\text{|}}{{x}_{1}} - {{x}_{0}}{\text{|}}\;\leqslant \;{\text{|}}y - {{x}_{0}}{\text{|}} + \frac{\rho }{2}\;\leqslant \;\frac{3}{2}{\text{|}}y - {{x}_{0}}{\text{|}},$(3.50)
${\text{|}}{{x}_{2}} - y{\text{|}}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}}\; - \;{\text{|}}{{x}_{2}} - {{x}_{0}}{\text{|}}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}} - \frac{\rho }{2}\; \geqslant \;\frac{1}{2}{\text{|}}y - {{x}_{0}}{\text{|}}.$(3.51)
$\begin{gathered} {\text{|}}{{I}_{{61}}}{\text{|}}\;\leqslant \;{{D}_{{34}}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{2}} - {{x}_{1}}{\text{|}}{\kern 1pt} {\kern 1pt} {{[f(x)]}_{\alpha }}\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{\text{|}}{{x}_{1}} - y{{{\text{|}}}^{\alpha }}}}{{{\text{|}}{{x}_{2}} - y{{{\text{|}}}^{3}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{35}}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{2}} - {{x}_{1}}{\text{|}}{\kern 1pt} {\kern 1pt} {{[f(x)]}_{\alpha }} \times \\ \, \times \int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{{3 - \alpha }}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{36}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu (x){\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}},\quad {{\beta }_{1}} \in [0,1]. \\ \end{gathered} $(3.52)
$\begin{gathered} {{I}_{{61}}}:\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\left[ {{{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right]f({{x}_{1}}){\kern 1pt} dy - \\ - \;\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\left[ {{{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right]f(y){\kern 1pt} dy: = {{I}_{{611}}} + {{I}_{{612}}}. \\ \end{gathered} $(3.53)
$\begin{gathered} \left| {{{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{{2}^{{({{\beta }_{1}} - 1)/2}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{\left( {1 + \;{\text{|}}{{x}_{2}} - {{x}_{1}}{{{\text{|}}}^{2}}} \right)}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}\;\leqslant \\ \leqslant \;3{{\beta }_{1}}{{2}^{{{{\beta }_{1}} - 1}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}. \\ \end{gathered} $(3.54)
$\begin{gathered} {\text{|}}{{I}_{{611}}}{\text{|}}\;\leqslant \;{{D}_{{37}}}(T,{{R}_{0}},\varepsilon ){{\left| {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{(1 + {{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right|}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}} \times \\ \times \;\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{3}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{37}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {\kern 1pt} \text{[}1 + \left| {\ln {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} } \right|{\kern 1pt} ]. \\ \end{gathered} $(3.55)
$\begin{gathered} \left| {{{{(1 + \;{\text{|}}{{x}_{2}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{{2}^{{({{\beta }_{1}} - 1)/2}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} \int\limits_0^1 \,{{(1 + \;{\text{|}}{{x}_{s}} - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} ds\;\leqslant \\ \leqslant \;3{{\beta }_{1}}{{2}^{{{{\beta }_{1}} - 1}}}{{(1 + {{(1{\text{/}}2 + 2{{R}_{0}})}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}. \\ \end{gathered} $(3.56)
$\begin{gathered} {\text{|}}{{I}_{{612}}}{\text{|}}\;\leqslant \;{{D}_{{38}}}(T,{{R}_{0}},\varepsilon ){{\left| {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{(1 + {{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right|}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{3}}}}{\kern 1pt} dy\;\leqslant \\ \leqslant \;{{D}_{{39}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {\kern 1pt} \text{[}1 + \left| {\ln {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}} \right|]. \\ \end{gathered} $(3.57)
${\text{|}}{{I}_{{61}}}{\text{|}}\;\leqslant \;{{D}_{{40}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\left\{ \begin{gathered} 1,\quad {\text{если}}\quad {{\beta }_{1}} \in [0,1]; \hfill \\ 1 + \left| {\ln {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} } \right|,\quad {\text{если}}\quad {{\beta }_{1}} > 1. \hfill \\ \end{gathered} \right.$
$\frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}} - \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{1}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}} = \int\limits_0^1 {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1}^3 \frac{{{{\partial }^{3}}\mathcal{E}({{x}_{s}} - y,t)}}{{\partial {{x}_{{sk}}}\partial {{y}_{i}}\partial {{y}_{j}}}}[{{x}_{{2k}}} - {{x}_{{1k}}}]{\kern 1pt} ds,$
из которого при $2{{R}_{0}}\; \geqslant \;{\text{|}}y - {{x}_{0}}{\text{|}}\; \geqslant \;\rho $ вытекает стандартным образом следующая оценка:
(3.58)
$\left| {\frac{{{{\partial }^{2}}\mathcal{E}({{x}_{2}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}} - \frac{{{{\partial }^{2}}\mathcal{E}({{x}_{1}} - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}} \right|\;\leqslant \;{{D}_{{41}}}(T,{{R}_{0}},\varepsilon )\frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{4}}}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}.$(3.59)
$\begin{gathered} {\text{|}}{{I}_{{62}}}{\text{|}}\;\leqslant \;{{D}_{{42}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{\left[ {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right]}_{\alpha }}\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{\text{|}}y - {{x}_{1}}{{{\text{|}}}^{\alpha }}}}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{4}}}}{\kern 1pt} dy\;\leqslant \\ \leqslant \;{{D}_{{43}}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{||}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{{4 - \alpha }}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{44}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}, \\ \end{gathered} $(3.60)
$\begin{gathered} {\text{|}}{{I}_{{63}}}{\text{|}}\;\leqslant \;{{D}_{{45}}}(T,{{R}_{0}},\varepsilon ){\text{|}}f{{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{{{\text{|}}y - {{x}_{1}}{\text{|}}}}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{4}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{46}}}(T,{{R}_{0}},\varepsilon ){\text{|}}f{{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}} \times \\ \, \times \int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{3}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{47}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\kern 1pt} {\kern 1pt} \text{[}1 + \left| {\ln {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} } \right|{\kern 1pt} ]. \\ \end{gathered} $
${\text{|}}{{x}_{1}} - y{\kern 1pt} {\text{|}}\;\leqslant \;{\text{|}}{{x}_{1}} - {{x}_{0}}{\text{|}}\; + \;{\text{|}}y - {{x}_{0}}{\text{|}}\;\leqslant \;\frac{1}{2} + 2{{R}_{0}},$
то справедлива оценка
(3.61)
$\left| {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}{{x}_{1}}{{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{{2}^{{({{\beta }_{1}} - 1)/1}}}{{\left( {1 + {{{(1{\text{/}}2 + 2{{R}_{0}})}}^{2}}} \right)}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\text{|}}{{x}_{1}} - y{\kern 1pt} {\text{|}}.$(3.62)
$\begin{gathered} {\text{|}}{{I}_{{63}}}{\text{|}}\;\leqslant \;{{D}_{{48}}}(T,{{R}_{0}},\varepsilon ){\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{{\left| {\frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{{{\text{|}}}^{2}})}}^{{(1 + {{\beta }_{2}} - {{\beta }_{1}})/2}}}}}} \right|}_{0}}\int\limits_{O({{x}_{0}},2{{R}_{0}})\backslash O({{x}_{0}},\rho )} \frac{1}{{{\text{|}}y - {{x}_{0}}{{{\text{|}}}^{3}}}}{\kern 1pt} dy\;\leqslant \\ \leqslant \;{{D}_{{49}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {\kern 1pt} \text{[}1 + \left| {\ln {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} } \right|{\kern 1pt} ]. \\ \end{gathered} $(3.63)
${\text{|}}{{I}_{6}}{\text{|}}\;\leqslant \;{{D}_{{50}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}\left( {{\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} {\kern 1pt} [1 + \left| {\ln {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}{\kern 1pt} } \right|{\kern 1pt} ]\; + \;{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}} \right).$(3.64)
$\left| {{{u}_{4}}({{x}_{1}},t) - {{u}_{4}}({{x}_{2}},t)} \right|\;\leqslant \;{{D}_{{51}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }},\quad \alpha \in (0,1),$Шаг 8: ${\text{|}}{{u}_{4}}{{{\text{|}}}_{0}}$. Теперь наша задача оценить – ${\text{|}}{{u}_{4}}{{{\text{|}}}_{0}}$. В силу равенства (4.8) справедливо следующее выражение для произвольного $\delta > 0$:
${{u}_{4}}(x,t) = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})f(y){\kern 1pt} dy + $
(3.65)
$\begin{gathered} \, + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,\delta )} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(y){\kern 1pt} dy + \\ + \;\int\limits_{O(x,\delta )} \frac{{{{\partial }^{2}}}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\mathcal{E}(x - y,t)\left[ {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(y) - {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(x)} \right]{\kern 1pt} dy + \\ \end{gathered} $
$ + \;{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O(x,\delta )} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}} = {{J}_{2}} + {{J}_{{11}}} + {{J}_{{12}}} + {{J}_{{13}}}.$
Оценим интеграл ${{J}_{2}}$. Сначала предположим, что ${{\beta }_{1}} \in [0,1]$. Тогда выполнено неравенство
(3.66)
$\left| {{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{\text{|}}x - y{\text{|}}.$(3.67)
$\left| {{\kern 1pt} {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}} \right|\;\leqslant \;3{{\beta }_{1}}{\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} {{2}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}.$(3.68)
$\begin{gathered} \left| {{{J}_{2}}} \right| = \left| {\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{j}}\partial {{y}_{i}}}}[(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}]f(y){\kern 1pt} dy} \right|\;\leqslant \;\int\limits_{O(x,{{R}_{0}})} \frac{{{{D}_{{52}}}(T,{{R}_{0}},\varepsilon )}}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}}}}{\text{|}}f(y){\kern 1pt} {\text{|}}{\kern 1pt} dy + \\ \, + {{D}_{{53}}}(T,{{R}_{0}},\varepsilon )\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{0}})} \exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )\,|\,{\text{|}}f(y){\text{|}}{\kern 1pt} dy\;\leqslant \;{{D}_{{54}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}},\quad {{\beta }_{1}} \in [0,1], \\ \end{gathered} $
$\left| {{{J}_{2}}} \right| = \left| {\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{j}}\partial {{y}_{i}}}}[(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}]f(y){\kern 1pt} dy} \right|\;\leqslant $
(3.69)
$\begin{gathered} \leqslant \;{{D}_{{55}}}(T,{{R}_{0}},\varepsilon )\int\limits_{O(x,{{R}_{0}})} \frac{{{{{(1\; + \;{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{1}} - 1)/2}}}}}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} {\text{|}}f(y){\kern 1pt} {\text{|}}{\kern 1pt} dy + \\ + \;{{D}_{{56}}}(T,{{R}_{0}},\varepsilon )\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{0}})} \exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}x - y{\text{|}}{\kern 1pt} )(1 + \;{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{({{\beta }_{1}} - 1)/2}}} \times \\ \end{gathered} $
$ \times \;{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{({{\beta }_{1}} - 1)/2}}}{\kern 1pt} {\text{|}}f(y){\kern 1pt} {\text{|}}{\kern 1pt} dy\;\leqslant \;{{D}_{{57}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}},\quad {{\beta }_{1}} > 1,$
поскольку по условию ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$.
Справедливы следующие оценки:
(3.70)
${\text{|}}{{J}_{{11}}}{\text{|}}\;\leqslant \;{{D}_{{58}}}(T,{{R}_{0}},\varepsilon ){\text{|}}\mu {{{\text{|}}}_{0}}\int\limits_{{{\mathbb{R}}^{3}}\backslash O(x,{{R}_{0}})} \frac{1}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{({{\beta }_{2}} - {{\beta }_{1}} + 1)/2}}}}}\frac{{\exp ( - (1 - \varepsilon ){\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{59}}}(T,{{R}_{0}},\varepsilon ){\text{|}}\mu {{{\text{|}}}_{0}},$(3.71)
${\text{|}}{{J}_{{12}}}{\text{|}}\;\leqslant \;{{D}_{{60}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}\int\limits_{O(x,{{R}_{0}})} \frac{1}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{{3 - \alpha }}}}}{\kern 1pt} dy\;\leqslant \;{{D}_{{61}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}},\quad {\text{|}}{{J}_{{13}}}{\text{|}}\;\leqslant \;{{D}_{{62}}}(T,{{R}_{0}},\varepsilon ){\text{|}}\mu {{{\text{|}}}_{0}}.$(3.72)
${\text{|}}{{J}_{1}}{\text{|}}\;\leqslant \;{{D}_{{63}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}.$(3.73)
${\text{|}}{{u}_{4}}{{{\text{|}}}_{0}}\;\leqslant \;{{D}_{{64}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }},\quad t \in [0,T].$Шаг 9: Заметим, что если $|{\kern 1pt} {{x}_{1}} - {{x}_{2}}{\kern 1pt} |\; \geqslant \;1,$ то в силу (3.73) справедливы неравенства
(3.74)
$\begin{gathered} {\text{|}}{{u}_{4}}({{x}_{1}},t) - {{u}_{4}}({{x}_{2}},t){\kern 1pt} {{{\text{|}}}_{0}}\;\leqslant \;2{\text{|}}{{u}_{4}}(x,t){{{\text{|}}}_{0}}\;\leqslant \;2{\text{|}}{{u}_{4}}(x,t){\kern 1pt} {{{\text{|}}}_{0}}{\kern 1pt} {\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}\;\leqslant \\ \leqslant \;{{D}_{{65}}}(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}{\text{|}}{{x}_{1}} - {{x}_{2}}{{{\text{|}}}^{\alpha }}\quad {\text{при}}\quad {\text{|}}{{x}_{1}} - {{x}_{2}}{\text{|}}\; \geqslant \;1. \\ \end{gathered} $
${\text{|}}{{u}_{4}}(x,t){\kern 1pt} {{{\text{|}}}_{\alpha }}\;\leqslant \;D(T,{{R}_{0}},\varepsilon ){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }},\quad \mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}),\quad t \in [0,T],\quad \alpha \in (0,1).$
Справедлива следующая
Лемма 3.1. Если $\mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,$ то справедливы следующие оценки:
${\text{|}}{{u}_{1}}(x,t){\kern 1pt} {{{\text{|}}}_{\alpha }}\;\leqslant \;a(T){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}}\quad для\;каждого\quad t \in [0,T],$
${\text{|}}{{u}_{2}}(x,t){\kern 1pt} {{{\text{|}}}_{\alpha }}\;\leqslant \;a(T){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}\quad для\;каждого\quad t \in [0,T],$
${\text{|}}{{u}_{3}}(x,t){\kern 1pt} {{{\text{|}}}_{\alpha }}\;\leqslant \;a(T){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }}\quad для\;каждого\quad t \in [0,T].$
Доказательство. Аналогичное утверждение доказано в [5].
Несложно доказывается следующая
Лемма 3.2. Пусть ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$ и $\mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1)$. Тогда справедливы следующие оценки:
${\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}_{0}}\;\leqslant \;{{d}_{1}}(T){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{0}},\quad {{\left| {\frac{{\partial u(x,t)}}{{\partial {{x}_{j}}}}} \right|}_{0}}\;\leqslant \;{{d}_{2}}(T){\kern 1pt} {\text{|}}\mu {\text{|}}{{{\kern 1pt} }_{0}},\quad j = 1,2,3,$
для всех $t \in [0,T],$ где
$u(x,t) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} \mathcal{E}(x - y,t)\frac{{\mu (y)}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy.$
Из результатов теоремы 6 и лемм 3.1, 3.2 вытекает следующая основная
Теорема 7. Для любой функции $\mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$ справедлива оценка типа Шаудера
(3.75)
$\begin{gathered} {\text{|}}u(x,t){\kern 1pt} {{{\text{|}}}_{{2 + \alpha }}}\;\leqslant \;d(T){\text{|}}\mu {{{\text{|}}}_{\alpha }},\quad t \in [0,T], \\ u(x,t) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t)\frac{{\mu (y)}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy, \\ \end{gathered} $Отметим, что в силу свойств гладкости фундаментального решения $\mathcal{E}(x,t),$ определенного равенством (5.6) [1], справедлива
Теорема 8. Для любой функции $\mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$ справедлива оценка типа Шаудера
(3.76)
$\begin{gathered} {\text{|}}{{u}_{k}}(x,t){\text{|}}{{{\kern 1pt} }_{{2 + \alpha }}}\;\leqslant \;{{d}_{k}}(T){\kern 1pt} {\text{|}}\mu {\kern 1pt} {{{\text{|}}}_{\alpha }},\quad t \in [0,T],\quad k \in \mathbb{N} \cup \{ 0\} , \\ {{u}_{k}}(x,t) = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{k}}\mathcal{E}(x - y,t)}}{{\partial {{t}^{k}}}}\frac{{\mu (y)}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}{\kern 1pt} dy, \\ \end{gathered} $Наконец, рассмотрим следующий потенциал с весом
$h(x) = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}}}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}}\frac{{\exp ( - {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\kern 1pt} {\text{|}})}}{{4\pi {\kern 1pt} {\text{|}}x - y{\kern 1pt} {\text{|}}}}\mu (y){\kern 1pt} dy.$
Для него справедлива следующая
Теорема 9. Для любой функции $\mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ при $\alpha \in (0,1)$ и ${{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0$ справедлива оценка типа Шаудера
4. ГЛАДКОСТЬ ВЕСОВОГО ПОТЕНЦИАЛА
В этом разделе мы воспользуемся методами исследований из работы [2].
Пусть $\eta (s) \in \mathbb{C}_{b}^{{(1)}}[0, + \infty )$ – функция следующего вида:
причем
$\eta (s) = \left\{ \begin{gathered} 0,\quad {\text{если}}\quad 0\;\leqslant \;s\;\leqslant \;1; \hfill \\ 1,\quad {\text{если}}\quad s\; \geqslant \;2, \hfill \\ \end{gathered} \right.\quad {{\eta }_{\varepsilon }}: = \eta \left( {\frac{{{\text{|}}x - y{\text{|}}}}{\varepsilon }} \right).$
Теперь определим следующие функции:
$u(x,t): = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})f(y){\kern 1pt} dy + $
(4.1)
$\begin{gathered} \, + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(z,R)} \frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(y){\kern 1pt} dy + \\ \, + \int\limits_{O(z,R)} \frac{{{{\partial }^{2}}}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\mathcal{E}(x - y,t)\left[ {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(y) - {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(x)} \right]{\kern 1pt} dy + \\ \end{gathered} $
$\, + {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O(z,R)} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}},\quad O(x,2\varepsilon ) \subset O(z,R){\kern 1pt} {\kern 1pt} ,$
(4.2)
$w(x,t): = \int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - y,t)f(y){\kern 1pt} dy,\quad {v}(x,t): = \frac{{\partial w(x,t)}}{{\partial {{x}_{j}}}} = - \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}f(y){\kern 1pt} dy,$(4.3)
$\begin{gathered} {{v}_{\varepsilon }}(x,t): = - \int\limits_{{{\mathbb{R}}^{3}}} {{\eta }_{\varepsilon }}\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}f(y){\kern 1pt} dy, \\ f(x) = \frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}},\quad {{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,\quad \mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}),\quad \alpha \in (0,1]. \\ \end{gathered} $
${{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{\partial {{v}_{\varepsilon }}(x,t)}}{{\partial {{x}_{i}}}} = {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{x}_{i}}}}\left( {{{\eta }_{\varepsilon }}\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{x}_{j}}}}} \right)f(y){\kern 1pt} dy = $
$ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{y}_{i}}}}\left( {{{\eta }_{\varepsilon }}\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right)[(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}]f(y){\kern 1pt} dy + $
$\, + \int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{y}_{i}}}}\left( {{{\eta }_{\varepsilon }}\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right){{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(y){\kern 1pt} dy = $
$ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{y}_{i}}}}\left( {{{\eta }_{\varepsilon }}\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right)[(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}]f(y){\kern 1pt} dy + $
$\, + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(z,R)} \frac{\partial }{{\partial {{y}_{i}}}}\left( {{{\eta }_{\varepsilon }}\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right){{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(y){\kern 1pt} dy + $
$\, + \int\limits_{O(z,R)} \frac{\partial }{{\partial {{y}_{i}}}}\left( {{{\eta }_{\varepsilon }}\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right)\left[ {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(y) - {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(x)} \right]{\kern 1pt} dy + $
$\, + {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O(z,R)} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}{{\eta }_{\varepsilon }}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} dy.$
Пусть $0 < 2\varepsilon < R$. Справедливо следующее равенство:
$u(x,t) - {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{\partial {{v}_{\varepsilon }}(x,t)}}{{\partial {{x}_{i}}}} = {{K}_{1}} + {{K}_{2}} + {{K}_{3}} + {{K}_{4}},$
${{K}_{1}}: = \int\limits_{{{\mathbb{R}}^{3}}} \frac{\partial }{{\partial {{y}_{i}}}}\left( {[1 - {{\eta }_{\varepsilon }}]\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right)[(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}]f(y){\kern 1pt} dy,$
(4.4)
${{K}_{2}}: = \int\limits_{{{\mathbb{R}}^{3}}\backslash O(z,R)} \frac{\partial }{{\partial {{y}_{i}}}}\left( {[1 - {{\eta }_{\varepsilon }}]\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right){{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(y){\kern 1pt} dy,$
${{K}_{3}}: = \int\limits_{O(z,R)} \frac{\partial }{{\partial {{y}_{i}}}}\left( {[1 - {{\eta }_{\varepsilon }}]\frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}} \right)\left[ {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(y) - {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(x)} \right]{\kern 1pt} dy,$
${{K}_{4}}: = (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O(z,R)} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}[1 - {{\eta }_{\varepsilon }}]\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} dy.$
Поскольку $2\varepsilon < R$, то сразу же имеем
Теперь нужно рассмотреть интегралы ${{K}_{1}}$ и ${{K}_{3}}$ отдельно при ${{\beta }_{1}} \in [0,1]$ и ${{\beta }_{1}} > 1$. Несложно доказать (см., например, [2] и [5]), что оба интеграла стремятся к нулю при $\varepsilon \to + 0$. Итак, из (4.4), (4.5) вытекает, что
(4.6)
$\mathop {\sup }\limits_{x \in \overline {O(0,R)} } \left| {u(x,t) - {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}\frac{{\partial {{v}_{\varepsilon }}(x,t)}}{{\partial {{x}_{i}}}}} \right| \to + 0\quad {\text{при}}\quad \varepsilon \to + 0$(4.7)
$\mathop {\sup }\limits_{x \in \overline {O(0,R)} } \left| {{{v}_{\varepsilon }}(x,t) - \frac{{\partial w(x,t)}}{{\partial {{x}_{j}}}}} \right| \to + 0\quad {\text{при}}\quad \varepsilon \to + 0$(4.8)
${{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}w(x,t)}}{{\partial {{x}_{i}}\partial {{x}_{j}}}} = u(x,t)\quad {\text{для}}\;{\text{всех}}\quad x \in {{\mathbb{R}}^{3}},\quad t \in [0,T],$(4.9)
${{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}{{w}_{k}}(x,t)}}{{\partial {{x}_{i}}\partial {{x}_{j}}}} = {{u}_{k}}(x,t)\quad {\text{для}}\;{\text{всех}}\quad x \in {{\mathbb{R}}^{3}},\quad t \in [0,T],$
${{w}_{k}}(x,t): = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{k}}\mathcal{E}(x - y,t)}}{{\partial {{t}^{k}}}}f(y){\kern 1pt} dy,\quad k \in \mathbb{N} \cup \{ 0\} ,$
${{u}_{k}}(x,t): = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{{{\partial }^{{2 + k}}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}\partial {{t}^{k}}}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}} - {{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}})f(y){\kern 1pt} dy + $
(4.10)
$\, + \int\limits_{{{\mathbb{R}}^{3}}\backslash O(z,R)} \frac{{{{\partial }^{{2 + k}}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}\partial {{t}^{k}}}}{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(y){\kern 1pt} dy + $
$\, + \int\limits_{O(z,R)} \frac{{{{\partial }^{{2 + k}}}}}{{\partial {{y}_{i}}\partial {{y}_{j}}\partial {{t}^{k}}}}\mathcal{E}(x - y,t)\left[ {{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(y) - {{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{1}}/2}}}f(x)} \right]{\kern 1pt} dy + $
$\, + {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O(z,R)} \frac{{{{\partial }^{{1 + k}}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{j}}\partial {{t}^{k}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}},$
$f(x) = \frac{{\mu (x)}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{{{\beta }_{2}}/2}}}}},\quad {{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,\quad \mu (x) \in {{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}}),\quad \alpha \in (0,1).$
Заметим, что представление (4.1) удобно переписать в следующем эквивалентном виде:
$u(x,t) = \int\limits_{{{\mathbb{R}}^{3}}\backslash O(z,R)} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}f(y){\kern 1pt} dy + $
(4.11)
$\, + \int\limits_{O(z,R)} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{2}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}}}\left[ {f(y) - f(x)} \right]{\kern 1pt} dy + $
$\, + {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O(z,R)} \frac{{\partial{ \mathcal{E}}(x - y,t)}}{{\partial {{y}_{j}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}},\quad x \in O(z,R),$
а представление (4.10) можно переписать в следующем виде:
${{u}_{k}}(x,t) = \int\limits_{{{\mathbb{R}}^{3}}\backslash O(z,R)} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{{2 + k}}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}\partial {{t}^{k}}}}f(y){\kern 1pt} dy + $
$\, + \int\limits_{O(z,R)} {{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}\frac{{{{\partial }^{{2 + k}}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{i}}\partial {{y}_{j}}\partial {{t}^{k}}}}\left[ {f(y) - f(x)} \right]{\kern 1pt} dy + $
$ + \;{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\beta }_{1}}/2}}}f(x)\int\limits_{\partial O(z,R)} \frac{{{{\partial }^{{1 + k}}}\mathcal{E}(x - y,t)}}{{\partial {{y}_{j}}\partial {{t}^{k}}}}\cos ({{n}_{y}},{{e}_{i}}){\kern 1pt} d{{S}_{y}},\quad x \in O(z,R),\quad k \in \mathbb{N} \cup \{ 0\} .$
Список литературы
Корпусов М.О., Овсянников Е.А. Локальная разрешимость, разрушение и гёльдеровская регулярность решений некоторых задач Коши для нелинейных уравнений теории волн в плазме. I. Формулы Грина // Ж. вычисл. матем. и матем. физ. 2022. Т. 62. № 10. С. 1639–1661.
Гилбарг Д., Трудингер М. Эллиптические дифференциальные уравнения с частными производными второго порядка. М.: Наука, 1989. С. 464.
Корпусов М.О., Яблочкин Д.К. Теория потенциала и оценка Шаудера в гёльдеровских пространствах для $3 + 1$–мерного уравнения Бенджамена–Бона–Махони–Бюргерса // Ж. вычисл. матем. и матем. физ. 2021. Т. 61. № 8. С. 1289–1314.
Ландис E.M. Уравнения второго порядка эллиптического и параболического типов. М.: Наука, 1971. С. 288.
Korpusov M.O., Matveeva A.K. On critical exponents for weak solutions to the Cauchy problem for one nonlinear equation with gradient nonlinearity // MMAS. 2022. V. 46. № 2. P. 1574–1630.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики
Пн.-пт.: 10.00-19.00