1. На главную
  2. Электронные версии
  3. Акустический журнал
  4. T. 66, № 1, 2020

Акустический журнал, 2020, T. 66, № 1, стр. 95-103

Передаточные матрицы четырехполюсников упругого пористого слоя

Л. Р. Яблоник *

Научно-производственное объединение по исследованию и проектированию энергетического оборудования им. И.И. Ползунова
191167 Санкт-Петербург, ул. Атаманская 3/6, Россия

* E-mail: yablonik@gmail.com

Поступила в редакцию 06.05.2019
После доработки 27.08.2019
Принята к публикации 05.09.2019

Полный текст (PDF)

Аннотация

Предложены соотношения для передаточных матриц линейных четырехполюсников, связывающих давления и нормальные компоненты скорости на свободных и/или непроницаемых границах плоского упругого пористого слоя. Зависимости получены в рамках безвихревой модели, предполагающей пренебрежимо малое влияние сдвиговых напряжений на передачу волновых возмущений поперек слоя. Показана возможность использования полученных результатов применительно к слоям нежестких пористых материалов в широком диапазоне углов падения звуковых волн.

Ключевые слова: упругий пористый слой, передаточная матрица, продольные и поперечные волны, безвихревая модель

ВВЕДЕНИЕ

Матричные методы традиционно используются при решении линейных задач акустики слоистых сред и многослойных систем [1–4]. При рассмотрении систем с упругими пористыми слоями, в частности, широко применяются [5–7] передаточные матрицы, определенным образом связывающие векторы динамических параметров на входной и выходной границах слоя. Ввиду возможности существования трех типов волн [6, 8] в упругой пористой среде, динамическое состояние на границах упругого пористого слоя принято в общем случае определять 6-мерным вектором, а передаточные свойства слоя – передаточной матрицей размера 6 × 6.

Существенно, что в дискретно-слоистой структуре границы слоя в терминах механики сплошной среды [9] представляют собой поверхности сильного разрыва, на которых скачкообразно разнятся физические свойства контактирующих сред. Форма динамических условий на внешних сторонах границ упругого пористого слоя, включая размерность вектора динамических параметров, зависит при этом от характеристик сред в примыкающих слоях либо полупространствах. В частности, внешние условия на обеих границах могут определяться стандартной парой динамических параметров – давлением p и нормальной компонентой скорости v, присущих однородным средам. В таком случае объединенная система “упругий пористый слой плюс границы” определяет линейную связь входного и выходного векторов с компонентами p, v, что позволяет рассматривать ее как линейный четырехполюсник вне зависимости от специфики волновых процессов, происходящих внутри слоя. Собственно передаточные свойства такого четырехполюсника при этом безусловно зависят как от особенностей волновых взаимодействий в слое, так и от вида условий, связывающих параметры на внешних и внутренних сторонах его границ.

В настоящей работе решается задача нахождения прямых выражений для передаточных матриц четырехполюсников, формируемых упругим пористым слоем со свободными и/или непроницаемыми границами. Предлагаемые зависимости получены для случаев, когда можно пренебречь влиянием сдвиговых напряжений (поперечных волн) на передачу волновых возмущений поперек слоя. Данное условие очевидно выполняется для волн, направленных по нормали к слою. Кроме того, как показано в [10], влияние поперечных волн незначительно в широком диапазоне углов падения для большинства волокнистых материалов ввиду относительно низкой скорости распространения структурных волн. Количественные соотношения для оценки роли $*$ поперечных волн рассматриваются в заключительной части статьи.

Статья ориентирована на акустические приложения, связанные с работой упругих пористых материалов в составе находящих все более широкое применение [4, 5, 11] многослойных структур. Задание передаточных свойств пористого слоя в такой структуре матрицей четырехполюсника способно существенно упростить прикладные акустические расчеты [10].

Используемая далее форма соотношений для передаточных матриц предполагает трактовку продольных волн первого и второго типа соответственно как воздушных (airborne) и структурных (frame-borne) волн. При этом никаких дополнительных ограничительных условий на характер волновых процессов в слое такая трактовка не требует.

Представляемые результаты – развитие и обобщение работы [10], в которой применен аналогичный подход при дополнительном условии частичного разделения (partial decoupling) воздушных и структурных волн.

ОСНОВНЫЕ ПАРАМЕТРЫ И СООТНОШЕНИЯ

Волновые свойства изотропной упругой пористой среды определяются зависящими от частоты комплексными значениями динамической плотности и динамического модуля объемного сжатия насыщающей жидкости, а также объемной плотности и модулей упругости пористого каркаса в вакууме и модуля объемного сжатия материала каркаса. Задание этих значений совместно с пористостью $\phi $, равной относительному объему пор, известным образом [6, 10] определяет три упругих ($P,~Q,~R$) и три массовых (${{\rho }_{{11}}},~{{\rho }_{{12}}},~{{\rho }_{{22}}}$) параметра, посредством которых представляются основные соотношения для волновых характеристик среды. К таковым, в частности, относятся волновые числа ${{\delta }_{1}},~{{\delta }_{2}}$ продольных волн (волн сжатия-расширения) первого и второго типа, а также соответствующие им отношения ${{{\mu }}_{1}},~{{{\mu }}_{2}}$ скорости движения насыщающей среды к скорости каркаса.

Волновые числа ${{\delta }_{1}},~{{\delta }_{2}}$ волн определяются по значениям корней квадратного уравнения

(1)
$\left| {{{\omega }^{2}}\left[ {\begin{array}{*{20}{c}} {{{\rho }_{{11}}}}&{{{\rho }_{{12}}}} \\ {{{\rho }_{{12}}}}&{{{\rho }_{{22}}}} \end{array}} \right] - {{\delta }^{2}}\left[ {\begin{array}{*{20}{c}} P&Q \\ Q&R \end{array}} \right]} \right| = 0.$

Параметры ${{\mu }_{1}}$ и ${{\mu }_{2}}$, как отмечено в [10], могут быть найдены из системы равенств

(2)
$P + Q\left( {{{\mu }_{1}} + {{\mu }_{2}}} \right) + R{{\mu }_{1}}{{\mu }_{2}} = 0,$
(3)
${{\rho }_{{11}}} + {{\rho }_{{12}}}\left( {{{\mu }_{1}} + {{\mu }_{2}}} \right) + {{\rho }_{{22}}}{{\mu }_{1}}{{\mu }_{2}} = 0.$

В рамках безвихревой волновой модели, предполагающей отсутствие поперечных волн и сдвиговых напряжений, связанные перемещения каркаса и насыщающей среды характеризуются соответственно потенциалами ${{{\varphi }}^{s}}$ и ${{{\varphi }}^{f}}$, при этом давления ${{\tilde {p}}^{s}}$ каркаса и ${{\tilde {p}}^{f}}$ насыщающей среды, а также нормальные к плоскости слоя компоненты их скоростей ${{\tilde {v}}^{s}},$ ${{\tilde {v}}^{f}}$ определяются соотношениями [10]

(4)
${{\tilde {p}}^{s}} = - P\frac{{{{\partial }^{2}}{{{\varphi }}^{s}}}}{{\partial {{{\xi }}^{2}}}} - Q\frac{{{{\partial }^{2}}{{{\varphi }}^{f}}}}{{\partial {{{\xi }}^{2}}}},$
(5)
${{\tilde {p}}^{f}} = - R\frac{{{{\partial }^{2}}{{{\varphi }}^{f}}}}{{\partial {{{\xi }}^{2}}}} - Q\frac{{{{\partial }^{2}}{{{\varphi }}^{s}}}}{{\partial {{{\xi }}^{2}}}},$
(6)
${{\tilde {v}}^{s}} = i{\omega }\frac{{\partial {{{\varphi }}^{s}}}}{{\partial x}},$
(7)
${{\tilde {v}}^{f}} = i{\omega }\frac{{\partial {{{\varphi }}^{f}}}}{{\partial x}},$
в которых ω – угловая частота, ξ – направление волны, x – направление нормали к слою.

Представление звукового поля в слое суперпозицией встречно направленных гармонических волн, потенциалы которых имеют амплитуды $A_{1}^{ + }$, $A_{1}^{ - }$ для волн первого типа и $A_{2}^{ + }$, $A_{2}^{ - }$ для волн второго типа приводит, ввиду (4)–(7), к зависимостям для амплитуд динамических параметров, которые представляются в матричной форме:

(8)
$\left[ {\begin{array}{*{20}{c}} {{{p}^{s}}} \\ {{{v}^{s}}} \\ {{{p}^{f}}} \\ {{{v}^{f}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{D}_{1}}\cos (\delta _{1}^{x}x)}&{ - i{{D}_{1}}\sin (\delta _{1}^{x}x)}&{{{D}_{2}}\cos (\delta _{2}^{x}x)}&{ - i{{D}_{2}}\sin (\delta _{2}^{x}x)} \\ { - i\omega \delta _{1}^{x}\sin (\delta _{1}^{x}x)}&{\omega \delta _{1}^{x}\cos (\delta _{1}^{x}x)}&{ - i\omega \delta _{2}^{x}\sin (\delta _{2}^{x}x)}&{\omega \delta _{2}^{x}\cos (\delta _{2}^{x}x)} \\ {{{E}_{1}}\cos (\delta _{1}^{x}x)}&{ - i{{E}_{1}}\sin (\delta _{1}^{x}x)}&{{{E}_{2}}\cos (\delta _{2}^{x}x)}&{ - i{{E}_{2}}\sin (\delta _{2}^{x}x)} \\ { - i\omega {{\mu }_{1}}\delta _{1}^{x}\sin (\delta _{1}^{x}x)}&{\omega {{\mu }_{1}}\delta _{1}^{x}\cos (\delta _{1}^{x}x)}&{ - i\omega {{\mu }_{2}}\delta _{2}^{x}\sin (\delta _{2}^{x}x)}&{\omega {{\mu }_{2}}\delta _{2}^{x}\cos (\delta _{2}^{x}x)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {A_{1}^{ + } + A_{1}^{ - }} \\ {A_{1}^{ + } - A_{1}^{ - }} \\ {A_{2}^{ + } + A_{2}^{ - }} \\ {A_{2}^{ + } - A_{2}^{ - }} \end{array}} \right].$

В последнем соотношении ${\delta }_{1}^{x},~{\delta }_{2}^{x}$ – проекции соответствующих волновых векторов на нормаль к плоскости слоя; параметры E1, D1, E2, D2 выражаются равенствами

(9)
${{D}_{n}} = \left( {P + Q{{{\mu }}_{n}}} \right){\delta }_{n}^{2}~\,\,~\left( {n = 1,~2} \right),$
(10)
${{E}_{n}} = \left( {R{{{\mu }}_{n}} + Q} \right){\delta }_{n}^{2}~~\left( {n = 1,~2} \right).$

Формула (8) отличается от соответствующей зависимости в [10], использующей гипотезу частичного разделения структурных и воздушных волн, наличием четырех ненулевых членов в правом нижнем углу $*$ квадратной матрицы. По сути, эта формула может рассматриваться как частный случай общих соотношений [6], относящийся к принятому условию несущественности поперечных волн и сдвиговых напряжений.

УНИВЕРСАЛЬНЫЕ ПЕРЕДАТОЧНЫЕ МАТРИЦЫ ВТОРОГО ПОРЯДКА

Соотношение (8) преобразуется к двум независимым системам, которые могут быть представлены в виде

(11)
$\left[ {\begin{array}{*{20}{c}} {{{p}^{f}} + \frac{1}{{{{{\mu }}_{1}}}}{{p}^{s}}} \\ {{{v}^{f}} - {{{\mu }}_{2}}{{v}^{s}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{E}_{1}}\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\text{cos}}\left( {{\delta }_{1}^{x}x} \right)}&{ - i{{E}_{1}}\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\text{sin}}\left( {{\delta }_{1}^{x}x} \right)} \\ { - i{\omega }{{{\mu }}_{1}}\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\delta }_{1}^{x}{\text{sin}}\left( {{\delta }_{1}^{x}x} \right)}&{{\omega }{{{\mu }}_{1}}\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\delta }_{1}^{x}{\text{cos}}\left( {{\delta }_{1}^{x}x} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{A}_{1}} + A_{1}^{'}} \\ {{{A}_{1}} - A_{1}^{'}} \end{array}} \right],$
(12)
$\left[ {\begin{array}{*{20}{c}} {{{p}^{s}} + {{{\mu }}_{2}}{{p}^{f}}} \\ {{{v}^{s}} - \frac{1}{{{{{\mu }}_{1}}}}{{v}^{f}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{D}_{2}}\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\text{cos}}\left( {{\delta }_{2}^{x}x} \right)}&{ - i{{D}_{2}}\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\text{sin}}\left( {{\delta }_{2}^{x}x} \right)} \\ { - i{\omega }\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\delta }_{2}^{x}{\text{sin}}\left( {{\delta }_{2}^{x}x} \right)}&{{\omega }\left( {1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}} \right){\delta }_{2}^{x}{\text{cos}}\left( {{\delta }_{2}^{x}x} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{A}_{2}} + A_{2}^{'}} \\ {{{A}_{2}} - A_{2}^{'}} \end{array}} \right].$

Представление (11), (12) использует равенства

$\frac{{{{D}_{1}}}}{{{{E}_{1}}}} = - {{{\mu }}_{2}};~\,\,\,\frac{{{{D}_{2}}}}{{{{E}_{2}}}} = - {{{\mu }}_{1}},$
следующие из формул (2), (9), (10).

Очевидно, что в силу равноправия волн первого и второго типа в исходных соотношениях индексы “1” и “2” в системах (11), (12) взаимозаменяемы, т.е. возможно тождественное представление этих равенств, в котором индексы “1” и “2” меняются местами. Представленный здесь выбор вносит определенность в трактовку физического смысла волн первого и второго типа в конкретных приложениях. Так, применительно к задачам распространения звука в слое заполненного воздухом пористого материала волны с индексом “1” в выбранном представлении трактуются как воздушные, а волны с индексом “2” – как структурные.

Используя формулы (11), (12) применительно ко входному (индекс “i”) и выходному (индекс “e”) сечениям слоя толщиной h и вводя смешанные динамические параметры

(13)
${{p}^{{fs}}} = {{p}^{f}} + \frac{1}{{{{{\mu }}_{1}}}}{{p}^{s}}~,\,\,\,\,{{v}^{{fs}}} = {{v}^{f}} - {{{\mu }}_{2}}{{v}^{s}},$
(14)
${{p}^{{sf}}} = {{p}^{s}} + {{{\mu }}_{2}}{{p}^{f}},\,\,\,\,{{v}^{{sf}}} = {{v}^{s}} - \frac{1}{{{{{\mu }}_{1}}}}{{v}^{f}},$
получаем из (11), (12) передаточные соотношения слоя в виде

(15)
$\left[ {\begin{array}{*{20}{c}} {p_{i}^{{fs}}} \\ {v_{i}^{{fs}}} \end{array}} \right] = \left[ {{{{\mathbf{T}}}^{{1u}}}} \right]\left[ {\begin{array}{*{20}{c}} {p_{e}^{{fs}}} \\ {v_{e}^{{fs}}} \end{array}} \right],$
(16)
$\left[ {\begin{array}{*{20}{c}} {p_{i}^{{sf}}} \\ {v_{i}^{{sf}}} \end{array}} \right] = \left[ {{{{\mathbf{T}}}^{{2u}}}} \right]\left[ {\begin{array}{*{20}{c}} {p_{e}^{{sf}}} \\ {v_{e}^{{sf}}} \end{array}} \right].$

Каждая из передаточных матриц второго порядка

(17)
$\left[ {{{{\mathbf{T}}}^{{1u}}}} \right] = \left[ {\begin{array}{*{20}{c}} {{\text{cos}}\left( {{\delta }_{1}^{x}h} \right)}&{i\frac{{{{E}_{1}}}}{{{\omega }{{{\mu }}_{1}}{\delta }_{1}^{x}}}{\text{sin}}\left( {{\delta }_{1}^{x}h} \right)} \\ {i\frac{{{\omega }{{{\mu }}_{1}}{\delta }_{1}^{x}}}{{{{E}_{1}}}}{\text{sin}}\left( {{\delta }_{1}^{x}h} \right)}&{{\text{cos}}\left( {{\delta }_{1}^{x}h} \right)} \end{array}} \right],$
(18)
$\left[ {{{{\mathbf{T}}}^{{2u}}}} \right] = \left[ {\begin{array}{*{20}{c}} {{\text{cos}}\left( {{\delta }_{2}^{x}h} \right)}&{i\frac{{{{D}_{2}}}}{{{\omega \delta }_{2}^{x}}}{\text{sin}}\left( {{\delta }_{2}^{x}h} \right)} \\ {i\frac{{{\omega \delta }_{2}^{x}}}{{{{D}_{2}}}}{\text{sin}}\left( {{\delta }_{2}^{x}h} \right)}&{{\text{cos}}\left( {{\delta }_{2}^{x}h} \right)} \end{array}} \right]$
определяется исключительно характеристиками соответствующего типа волн. При этом в предельном случае $\left| {{{{\mu }}_{1}}} \right| \to \infty ~\,\,{\text{и}}\,\,~\left| {{{{\mu }}_{2}}} \right| \to 0$ равенства (15)–(18) сводятся к представлению передаточных характеристик независимых колебаний насыщающей среды (индекс “1”) и каркаса (индекс “2”).

Соотношения (15), (16) характеризуют передачу смешанных динамических параметров (13), (14) по толщине слоя при безвихревом волновом движении посредством передаточных матриц второго порядка. Собственно передаточные матрицы (17), (18) не зависят от внешних условий на границах слоя, и в этом смысле являются универсальными. Линейные комбинации универсальных передаточных матриц позволяют по аналогии с [10] формировать в типовых схемах со свободными и/или непроницаемыми границами единую передаточную матрицу слоя, определяя тем самым параметры четырехполюсника, связывающего давления и нормальные компоненты скорости во входном и выходном сечениях.

ПОСТРОЕНИЕ ПЕРЕДАТОЧНЫХ МАТРИЦ ЧЕТЫРЕХПОЛЮСНИКОВ УПРУГОГО ПОРИСТОГО СЛОЯ

В дальнейшем будем полагать, что динамические условия на внешних сторонах границ упругого пористого слоя определяются давлением и нормальной компонентой скорости, обозначаемыми соответственно $p_{i}^{p},$ $v_{i}^{p}$ применительно ко входному сечению и $p_{e}^{p},$ $v_{e}^{p}$ применительно к выходному сечению.

Для определения свойств четырехполюсника, связывающего указанные пары параметров на входе и выходе, необходимо дополнить четыре универсальных передаточных соотношения (15), (16) внутри слоя шестью условиями, согласовывающими параметры по обе стороны его границ. Тогда получаемая система десяти равенств относительно двенадцати переменных ($p_{{i,e}}^{p},$ $v_{{i,e}}^{p},$ $~p_{{i,e}}^{f},$ $v_{{i,e}}^{f},$ $~p_{{i,e}}^{s},$ $v_{{i,e}}^{s}$) формально определяет при задании величин $p_{e}^{p},$ $v_{e}^{p}$ значения остальных параметров, в том числе входных параметров $p_{i}^{p}$, $v_{i}^{p}{\text{\;}}$ четырехполюсника.

Далее, основываясь на универсальных представлениях (15), (16) и учитывая граничные условия, установим выражения для передаточных матриц четырехполюсников плоских упругих пористых слоев с непроницаемыми и свободными границами. Рассмотрим все четыре варианта сочетания таких границ. При анализе помимо передаточных матриц $\left[ {\mathbf{T}} \right]$, определяемых общим равенством

$\left[ {\begin{array}{*{20}{c}} {{{p}_{i}}} \\ {{{v}_{i}}} \end{array}} \right] = \left[ {\mathbf{T}} \right]\left[ {\begin{array}{*{20}{c}} {{{p}_{e}}} \\ {{{v}_{e}}} \end{array}} \right],$
будем использовать также матрицы импедансов $\left[ {\mathbf{Z}} \right]$ и проводимостей [Y], а также перекрестные матрицы $\left[ {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}} \right]$ и $\left[ {{\mathbf{\bar {X}}}} \right]$, вводимые зависимостями

(19)
$\begin{gathered} \left[ {\begin{array}{*{20}{c}} {{{p}_{i}}} \\ {{{p}_{e}}} \end{array}} \right] = \left[ {\mathbf{Z}} \right]\left[ {\begin{array}{*{20}{c}} {{{v}_{i}}} \\ {{{v}_{e}}} \end{array}} \right],\,\,\,\,~\left[ {\begin{array}{*{20}{c}} {{{v}_{i}}} \\ {{{v}_{e}}} \end{array}} \right] = \left[ {\mathbf{Y}} \right]\left[ {\begin{array}{*{20}{c}} {{{p}_{i}}} \\ {{{p}_{e}}} \end{array}} \right], \\ ~\left[ {\begin{array}{*{20}{c}} {{{p}_{e}}} \\ {{{v}_{i}}} \end{array}} \right] = \left[ {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}} \right]\left[ {\begin{array}{*{20}{c}} {{{p}_{i}}} \\ {{{v}_{e}}} \end{array}} \right],\,\,\,\,~\left[ {\begin{array}{*{20}{c}} {{{p}_{i}}} \\ {{{v}_{e}}} \end{array}} \right] = \left[ {{\mathbf{\bar {X}}}} \right]\left[ {\begin{array}{*{20}{c}} {{{p}_{e}}} \\ {{{v}_{i}}} \end{array}} \right]. \\ \end{gathered} $

Задание любой из матриц (19) эквивалентно заданию передаточной матрицы [T], их компоненты связаны простыми соотношениями.

В качестве первого варианта рассмотрим случай двух непроницаемых границ слоя. Условия на границах слоя в таком сочетании имеют вид:

(20)
$v_{i}^{f} = v_{i}^{p},~\,\,\,\,v_{i}^{s} = v_{i}^{p},~\,\,\,\,v_{e}^{f} = v_{e}^{p},\,\,\,\,~v_{e}^{s} = v_{e}^{p},$
(21)
$p_{i}^{f} + p_{i}^{s} = p_{i}^{p},\,\,\,\,~p_{e}^{f} + p_{e}^{s} = p_{e}^{p}.$

В терминах матриц импедансов соотношения (15), (16) представляются в форме:

(22)
$\left[ {\begin{array}{*{20}{c}} {p_{i}^{f} + \frac{1}{{{{{\mu }}_{1}}}}p_{i}^{s}} \\ {p_{e}^{f} + \frac{1}{{{{{\mu }}_{1}}}}p_{e}^{s}} \end{array}} \right] = \left[ {{{{\mathbf{Z}}}^{{1u}}}} \right]\left[ {\begin{array}{*{20}{c}} {v_{i}^{f} - {{{\mu }}_{2}}v_{i}^{s}} \\ {v_{e}^{f} - {{{\mu }}_{2}}v_{e}^{s}} \end{array}} \right],$
(23)
$\left[ {\begin{array}{*{20}{c}} {p_{i}^{s} + {{{\mu }}_{2}}p_{i}^{f}} \\ {p_{e}^{s} + {{{\mu }}_{2}}p_{e}^{f}} \end{array}} \right] = \left[ {{{{\mathbf{Z}}}^{{2{\text{u}}}}}} \right]\left[ {\begin{array}{*{20}{c}} {v_{i}^{s} - \frac{1}{{{{{\mu }}_{1}}}}v_{i}^{f}} \\ {v_{e}^{s} - \frac{1}{{{{{\mu }}_{1}}}}v_{e}^{f}} \end{array}} \right].$

С учетом граничных условий (20), формулы (22), (23) приводятся к виду:

$\left[ {\begin{array}{*{20}{c}} {p_{i}^{f}} \\ {p_{e}^{f}} \end{array}} \right] + \frac{1}{{{{{\mu }}_{1}}}}\left[ {\begin{array}{*{20}{c}} {p_{i}^{s}} \\ {p_{e}^{s}} \end{array}} \right] = \left( {1 - {{{\mu }}_{2}}} \right)\left[ {{{{\mathbf{Z}}}^{{1u}}}} \right]\left[ {\begin{array}{*{20}{c}} {v_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right],$
${{{\mu }}_{2}}\left[ {\begin{array}{*{20}{c}} {p_{i}^{f}} \\ {p_{e}^{f}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {p_{i}^{s}} \\ {p_{e}^{s}} \end{array}} \right] = \left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right)\left[ {{{{\mathbf{Z}}}^{{2{\text{u}}}}}} \right]\left[ {\begin{array}{*{20}{c}} {v_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right].$

Отсюда следует, что

$\left[ {\begin{array}{*{20}{c}} {p_{i}^{f}} \\ {p_{e}^{f}} \end{array}} \right] = \frac{{\left( {1 - {{{\mu }}_{2}}} \right)\left[ {{{{\mathbf{Z}}}^{{1u}}}} \right] - \frac{1}{{{{{\mu }}_{1}}}}\left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right)\left[ {{{{\mathbf{Z}}}^{{2{\text{u}}}}}} \right]}}{{1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}}}\left[ {\begin{array}{*{20}{c}} {v_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right],$
$\left[ {\begin{array}{*{20}{c}} {p_{i}^{s}} \\ {p_{e}^{s}} \end{array}} \right] = \frac{{ - {{{\mu }}_{2}}\left( {1 - {{{\mu }}_{2}}} \right)\left[ {{{{\mathbf{Z}}}^{{1u}}}} \right] + \left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right)\left[ {{{{\mathbf{Z}}}^{{2{\text{u}}}}}} \right]}}{{1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}}}\left[ {\begin{array}{*{20}{c}} {v_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right].$

Суммируя последние равенства, получаем, ввиду (21), простое выражение

(24)
$\left[ {{{{\overline {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z} }}} }}^{p}}} \right] = \frac{{{{{\left( {1 - {{{\mu }}_{2}}} \right)}}^{2}}\left[ {{{{\mathbf{Z}}}^{{1u}}}} \right] + {{{\left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right)}}^{2}}\left[ {{{{\mathbf{Z}}}^{{2{\text{u}}}}}} \right]}}{{1 - \frac{{{{{\mu }}_{2}}}}{{{{{\mu }}_{1}}}}}}$
для матрицы импедансов $\left[ {{{{\overline {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z} }}} }}^{p}}} \right]$ упругого пористого слоя, заключенного между двумя непроницаемыми плоскими поверхностями. Равенство (24) однозначно определяет передаточные свойства слоя, которые в рассмотренной конфигурации зависят лишь от свойств универсальных передаточных матриц и параметров ${{{\mu }}_{1}}$и ${{{\mu }}_{2}}.$

В качестве второго варианта рассмотрим пористый слой с двумя свободными границами. Граничные условия в данном случае представляются в виде [6]:

(25)
$\begin{gathered} p_{i}^{f} = \phi p_{i}^{p},~\,\,\,\,~p_{i}^{s} = \left( {1 - \phi } \right)p_{i}^{p}, \\ p_{e}^{f} = \phi p_{e}^{p},\,\,\,\,~p_{e}^{s} = \left( {1 - \phi } \right)p_{e}^{p}, \\ \end{gathered} $
(26)
$\left( {1 - \phi } \right)v_{i}^{s} + \phi v_{i}^{f} = v_{i}^{p},\,\,\,\,\left( {1 - \phi } \right)v_{e}^{s} + \phi v_{e}^{f} = v_{e}^{p}.$

Здесь для построения передаточной матрицы пористого слоя используем матрицу проводимостей [Y]. При этом, в силу (15), (16),

$\left[ {\begin{array}{*{20}{c}} {v_{i}^{f} - {{{\mu }}_{2}}v_{i}^{s}} \\ {v_{e}^{f} - {{{\mu }}_{2}}v_{e}^{s}} \end{array}} \right] = \left[ {{{{\mathbf{Y}}}^{{1u}}}} \right]\left[ {\begin{array}{*{20}{c}} {p_{i}^{f} + \frac{1}{{{{{\mu }}_{1}}}}p_{i}^{s}} \\ {p_{e}^{f} + \frac{1}{{{{{\mu }}_{1}}}}p_{e}^{s}} \end{array}} \right],$
$\left[ {\begin{array}{*{20}{c}} {v_{i}^{s} - \frac{1}{{{{{\mu }}_{1}}}}v_{i}^{f}} \\ {v_{e}^{s} - \frac{1}{{{{{\mu }}_{1}}}}v_{e}^{f}} \end{array}} \right] = \left[ {{{{\mathbf{Y}}}^{{2u}}}} \right]\left[ {\begin{array}{*{20}{c}} {p_{i}^{s} + {{{\mu }}_{2}}p_{i}^{f}} \\ {p_{e}^{s} + {{{\mu }}_{2}}p_{e}^{f}} \end{array}} \right].$

Ввиду условий $(25)$ данные соотношения представляются в виде

$\left[ {\begin{array}{*{20}{c}} {v_{i}^{f}} \\ {v_{e}^{f}} \end{array}} \right] - {{{\mu }}_{2}}\left[ {\begin{array}{*{20}{c}} {v_{i}^{s}} \\ {v_{e}^{s}} \end{array}} \right] = \left[ {{{{\mathbf{Y}}}^{{1u}}}} \right]\left( {\phi + \frac{{1 - \phi }}{{{{{\mu }}_{1}}}}} \right)\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {p_{e}^{p}} \end{array}} \right],$
$ - \frac{1}{{{{{\mu }}_{1}}}}\left[ {\begin{array}{*{20}{c}} {v_{i}^{f}} \\ {v_{e}^{f}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {v_{i}^{s}} \\ {v_{e}^{s}} \end{array}} \right] = \left[ {{{{\mathbf{Y}}}^{{2u}}}} \right]\left( {1 - \phi + \phi {{\mu }_{2}}} \right)\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {p_{e}^{p}} \end{array}} \right].$

Из последних зависимостей следует, что

$\begin{gathered} \phi \left[ {\begin{array}{*{20}{c}} {v_{i}^{f}} \\ {v_{e}^{f}} \end{array}} \right] = \\ = \phi \frac{{\left[ {{{{\mathbf{Y}}}^{{1u}}}} \right]\left( {\phi + \frac{{1 - \phi }}{{{{\mu }_{1}}}}} \right) + {{\mu }_{2}}\left[ {{{{\mathbf{Y}}}^{{2u}}}} \right]\left( {1 - \phi + \phi {{\mu }_{2}}} \right)}}{{1 - \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}}}\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {p_{e}^{p}} \end{array}} \right], \\ \end{gathered} $
$\begin{gathered} \left( {1 - \phi } \right)\left[ {\begin{array}{*{20}{c}} {v_{i}^{s}} \\ {v_{e}^{s}} \end{array}} \right] = \left( {1 - \phi } \right) \times \\ \times \,\,\frac{{\frac{1}{{{{\mu }_{1}}}}\left[ {{{{\mathbf{Y}}}^{{1u}}}} \right]\left( {\phi + \frac{{1 - \phi }}{{{{\mu }_{1}}}}} \right) + \left[ {{{{\mathbf{Y}}}^{{2u}}}} \right]\left( {1 - \phi + \phi {{\mu }_{2}}} \right)}}{{1 - \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}}}\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {p_{e}^{p}} \end{array}} \right]. \\ \end{gathered} $

После суммирования последних равенств получаем, с учетом (26), выражение для матрицы проводимостей $\left[ {{{{\mathbf{Y}}}^{p}}} \right]$ упругого пористого слоя со свободными границами:

(27)
$\left[ {{{{\mathbf{Y}}}^{p}}} \right] = \frac{{{{{\left( {\phi + \frac{{1 - \phi }}{{{{{\mu }}_{1}}}}} \right)}}^{2}}\left[ {{{{\mathbf{Y}}}^{{1u}}}} \right] + {{{\left( {1 - \phi + \phi {{\mu }_{2}}} \right)}}^{2}}\left[ {{{{\mathbf{Y}}}^{{2u}}}} \right]}}{{1 - \frac{{{{\mu }_{2}}}}{{{{\mu }_{1}}}}}}.$

В данном случае, в отличие от формулы (24), в соотношение для передаточных характеристик слоя дополнительно входит пористость $\phi $ каркаса.

Третий вариант пористого слоя со свободной границей во входном сечении и с непроницаемой границей на выходе рассматривается похожим образом. Граничные условия в этом случае записываются в форме:

(28)
$v_{e}^{f} = v_{e}^{p},~\,\,\,\,~v_{e}^{s} = v_{e}^{p},~\,\,\,\,p_{i}^{f} = \phi p_{i}^{p},\,\,\,\,~p_{i}^{s} = \left( {1 - \phi } \right)p_{i}^{p},$
(29)
$\left( {1 - \phi } \right)v_{i}^{s} + \phi v_{i}^{f} = v_{i}^{p},\,\,\,\,~p_{e}^{f} + p_{e}^{s} = p_{e}^{p}.$

Соотношения (15), (16) в терминах перекрестной матрицы $\left[ {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}} \right]$ из (19) с учетом равенств (28) принимают вид:

$\left[ {\begin{array}{*{20}{c}} {p_{e}^{f} + \frac{1}{{{{\mu }_{1}}}}p_{e}^{s}} \\ {v_{i}^{f} - {{{\mu }}_{2}}v_{i}^{s}} \end{array}} \right] = \left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{1u}}}} \right]\left[ {\begin{array}{*{20}{c}} {\phi p_{i}^{p} + \frac{{1 - \phi }}{{{{{\mu }}_{1}}}}p_{i}^{p}} \\ {v_{e}^{p} - {{{\mu }}_{2}}v_{e}^{p}} \end{array}} \right],$
$\left[ {\begin{array}{*{20}{c}} {p_{e}^{s} + {{{\mu }}_{2}}p_{e}^{f}} \\ {v_{i}^{s} - \frac{1}{{{{{\mu }}_{1}}}}v_{i}^{f}} \end{array}} \right] = \left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{2u}}}} \right]\left[ {\begin{array}{*{20}{c}} {\left( {1 - \phi } \right)p_{i}^{p} + {{{\mu }}_{2}}\phi p_{i}^{p}} \\ {v_{e}^{p} - \frac{1}{{{{{\mu }}_{1}}}}v_{e}^{p}} \end{array}} \right].$

Элементарные преобразования приводят последние зависимости к равенствам

(30)
$\left[ {\begin{array}{*{20}{c}} {p_{e}^{f}} \\ {v_{i}^{f}} \end{array}} \right] = \left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{fp}}}} \right]\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right],$
(31)
$\left[ {\begin{array}{*{20}{c}} {p_{e}^{s}} \\ {v_{i}^{s}} \end{array}} \right] = \left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{sp}}}} \right]\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right],$
содержащим вспомогательные матрицы

(32)
$\left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{fp}}}} \right] = \frac{{\left[ {\begin{array}{*{20}{c}} {\left( {\phi + \frac{{1 - \phi }}{{{{{\mu }}_{1}}}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{1u}}}&{\left( {1 - {{{\mu }}_{2}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{1u}}} \\ {\left( {\phi + \frac{{1 - \phi }}{{{{{\mu }}_{1}}}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{1u}}}&{\left( {1 - {{{\mu }}_{2}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{1u}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{{{\mu }}_{1}}}}\left( {1 - \phi + {{{\mu }}_{2}}\phi } \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{2u}}}&{ - \frac{1}{{{{{\mu }}_{1}}}}\left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{2u}}} \\ {{{{\mu }}_{2}}\left( {1 - \phi + {{{\mu }}_{2}}\phi } \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{2u}}}&{{{{\mu }}_{2}}\left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{2u}}} \end{array}} \right]}}{{1 - {{{{{\mu }}_{2}}} \mathord{\left/ {\vphantom {{{{{\mu }}_{2}}} {{{{\mu }}_{1}}}}} \right. \kern-0em} {{{{\mu }}_{1}}}}}},$
(33)
$\left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{sp}}}} \right] = \frac{{\left[ {\begin{array}{*{20}{c}} {\left( {1 - \phi + \phi {{{\mu }}_{2}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{2u}}}&{\left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{2u}}} \\ {\left( {1 - \phi + \phi {{{\mu }}_{2}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{2u}}}&{\left( {1 - \frac{1}{{{{{\mu }}_{1}}}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{2u}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - {{{\mu }}_{2}}(\phi + \frac{{1 - \phi }}{{{{{\mu }}_{1}}}}){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{1u}}}&{ - {{{\mu }}_{2}}\left( {1 - {{{\mu }}_{2}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{1u}}} \\ {\frac{1}{{{{{\mu }}_{1}}}}\left( {\phi + \frac{{1 - \phi }}{{{{{\mu }}_{1}}}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{1u}}}&{\frac{1}{{{{\mu }_{1}}}}\left( {1 - {{{\mu }}_{2}}} \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{1u}}} \end{array}} \right]}}{{1 - {{{{{\mu }}_{2}}} \mathord{\left/ {\vphantom {{{{{\mu }}_{2}}} {{{{\mu }}_{1}}}}} \right. \kern-0em} {{{{\mu }}_{1}}}}}}.$

Из (30), (31) очевидно следуют соотношения

$\left[ {\begin{array}{*{20}{c}} {p_{e}^{f}} \\ {\phi v_{i}^{f}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{fp}}}&{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{fp}}} \\ {\phi {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{fp}}}&{\phi {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{fp}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right],$
$\left[ {\begin{array}{*{20}{c}} {p_{e}^{s}} \\ {\left( {1 - \phi } \right)v_{i}^{s}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{sp}}}&{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{sp}}} \\ {\left( {1 - \phi } \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{sp}}}&{\left( {1 - \phi } \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{sp}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {p_{i}^{p}} \\ {v_{e}^{p}} \end{array}} \right].$

Суммируя их, получаем с учетом (29) выражение

(34)
$\left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{p}}} \right]{\text{\;}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{fp}}}&{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{fp}}} \\ {\phi {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{fp}}}&{\phi {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{fp}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{11}}^{{sp}}}&{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{12}}^{{sp}}} \\ {\left( {1 - \phi } \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{21}}^{{sp}}}&{\left( {1 - \phi } \right){\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}_{{22}}^{{sp}}} \end{array}} \right],$

задающее перекрестную матрицу $\left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{p}}} \right]$ рассматриваемого пористого слоя c входной свободной и выходной непроницаемой границей.

В четвертом варианте с непроницаемой границей во входном сечении и со свободной границей на выходе определение передаточной матрицы пористого слоя производится практически по тем же соотношениям, что и в предыдущем случае. Разница состоит лишь в перемене местами индексов “i” и “e” во всех соотношениях, где они присутствуют, и замене перекрестных матриц $\left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{1u}}}} \right],~\left[ {{{{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}}^{{2u}}}} \right]~~$ на обратные матрицы $\left[ {{{{{\mathbf{\bar {X}}}}}^{{1u}}}} \right],~\left[ {{{{{\mathbf{\bar {X}}}}}^{{2u}}}} \right]~$ (19). На основании последних аналогично (32), (33) рассчитываются вспомогательные матрицы $\left[ {{{{{\mathbf{\bar {X}}}}}^{{fp}}}} \right]~$ и $\left[ {{{{{\mathbf{\bar {X}}}}}^{{sp}}}} \right]$ и, в соответствии с (34), перекрестная матрица слоя $\left[ {{{{{\mathbf{\bar {X}}}}}^{p}}} \right]$ представляется равенством:

(35)
${\text{\;}}\left[ {{{{{\mathbf{\bar {X}}}}}^{p}}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {X}}}_{{11}}^{{fp}}}&{{\mathbf{\bar {X}}}_{{12}}^{{fp}}} \\ {\phi {\mathbf{\bar {X}}}_{{21}}^{{fp}}}&{\phi {\mathbf{\bar {X}}}_{{22}}^{{fp}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathbf{\bar {X}}}_{{11}}^{{sp}}}&{{\mathbf{\bar {X}}}_{{12}}^{{sp}}} \\ {\left( {1 - \phi } \right){\mathbf{\bar {X}}}_{{21}}^{{sp}}}&{\left( {1 - \phi } \right){\mathbf{\bar {X}}}_{{22}}^{{sp}}} \end{array}} \right].$

Полученные соотношения (24), (27), (34), (35) определяют форму зависимостей для передаточных матриц четырехполюсников упругого пористого слоя с непроницаемыми и свободными границами в условиях безвихревой волновой модели.

ОЦЕНКИ ВЛИЯНИЯ ПОПЕРЕЧНЫХ ВОЛН

Как было показано в [10], допущение о слабом влиянии поперечных волн и связанных с ними сдвиговых напряжений на передаточные характеристики пористого упругого слоя оправдано при прохождении звука через слой волокнистого пористого материала, поскольку в этом случае скорость распространения структурных волн в слое как правило значительно ниже скорости звука во внешней воздушной среде. По той же причине используемое представление о несущественности поперечных волн применимо в широком диапазоне углов падения и для других относительно мягких пористых материалов достаточно высокой объемной плотности.

Практические оценки степени влияния вихревой компоненты на передаточные свойства слоя пористого материала при различных углах падения звуковых волн могут быть выполнены исходя из рассмотрения модели упругого пористого полупространства, на границе которого внешний звук формирует волновое возмущение.

Для получения конкретных соотношений рассмотрим схему заполняющей полупространство $x > 0$ пористой изотропной упругой среды, на границу которой извне падает наклонная плоская звуковая волна. От границы вглубь среды распространяются две продольные и одна поперечная волна. Потенциалы соответствующих волновых перемещений каркаса ${\tilde {\varphi }}_{1}^{s},~{\tilde {\varphi }}_{2}^{s},~{\tilde {\psi }}_{{z~}}^{s}$ этих волн представляются в форме:

(36)
${\tilde {\varphi }}_{{n~}}^{s} = ~A_{n}^{{s0}}\exp \left( { - i{\delta }_{n}^{x}x} \right)\exp \left( { - i{{k}_{y}}y} \right)~\,\,~\left( {n = 1,~2} \right),$
(37)
${\tilde {\psi }}_{{z~}}^{s} = A_{3}^{{s0}}\exp \left( { - i{\delta }_{3}^{x}x} \right)\exp \left( { - i{{k}_{y}}y} \right).$

Здесь ${{k}_{y}}$ – проекция волнового вектора падающей волны на плоскость раздела; ${\tilde {\psi }}_{{z~}}^{s}$ – проекция векторного потенциала ${{{\mathbf{\psi }}}^{s}}$ поперечных волн каркаса на ось z, перпендикулярную плоскости, образуемой осями x, y.

Компоненты $u_{x}^{s}$, $u_{y}^{s}$ перемещения каркаса определяются суперпозицией указанных трех волн, при этом

(38)
$u_{x}^{s} = \frac{{\partial {\tilde {\varphi }}_{{1~~~}}^{s}}}{{\partial x}} + \frac{{\partial {\tilde {\varphi }}_{{2~~~}}^{s}}}{{\partial x}} + \frac{{\partial {\tilde {\psi }}_{{z~}}^{s}}}{{\partial y}};~$
(39)
$u_{y}^{s} = \frac{{\partial {\tilde {\varphi }}_{{1~~~}}^{s}}}{{\partial y}} + \frac{{\partial {\tilde {\varphi }}_{{2~~~}}^{s}}}{{\partial y}} - \frac{{\partial {\tilde {\psi }}_{{z~}}^{s}}}{{\partial x}}.$

Далее основное внимание будет уделено варианту непроницаемой границы, на которой нормальная компонента $u_{x}^{f}$ перемещения насыщающей жидкости

$u_{x}^{f} = {{{\mu }}_{1}}\frac{{\partial {\tilde {\varphi }}_{{1~~~}}^{s}}}{{\partial x}} + {{{\mu }}_{2}}\frac{{\partial {\tilde {\varphi }}_{{2~~~}}^{s}}}{{\partial x}} + {{{\mu }}_{3}}\frac{{\partial {\tilde {\psi }}_{{z~}}^{s}}}{{\partial y}}$
равна $u_{x}^{s}$ , так что справедливо равенство

(40)
${{\left. {\left( {{{{\mu }}_{1}} - 1} \right)\frac{{\partial {\tilde {\varphi }}_{{1~~~}}^{s}}}{{\partial x}} + \left( {{{{\mu }}_{2}} - 1} \right)\frac{{\partial {\tilde {\varphi }}_{{2~~~}}^{s}}}{{\partial x}} + \left( {{{{\mu }}_{3}} - 1} \right)\frac{{\partial {\tilde {\psi }}_{{z~}}^{s}}}{{\partial y}}} \right|}_{{x = 0}}} = 0.$

Последнее, в силу (36), (37), может быть представлено в виде

(41)
$\left( {{{{\mu }}_{1}} - 1} \right)A_{1}^{s}{\delta }_{1}^{x} + \left( {{{{\mu }}_{2}} - 1} \right)A_{2}^{s}{\delta }_{2}^{x} + \left( {{{{\mu }}_{3}} - 1} \right)A_{3}^{s}{{k}_{y}} = 0.$

В случае отсутствия касательных напряжений, имеющем место как в случае свободной границы, так и при нефиксированном примыкании пористого материала к ограничивающему непроницаемому элементу (пластине, мембране, защитной пленке), сдвиговые деформации каркаса на граничной плоскости равны нулю. При этом, в силу (38), (39),

$2{{\left. {\frac{{{{\partial }^{2}}\left( {{\tilde {\varphi }}_{{1~}}^{s} + {\tilde {\varphi }}_{{2~}}^{s}} \right)}}{{\partial x~\partial y}} - \frac{{{{\partial }^{2}}{\tilde {\psi }}_{{z~}}^{s}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\tilde {\psi }}_{{z~}}^{s}}}{{\partial {{y}^{2}}}}} \right|}_{{x = 0}}} = 0.~$

Отсюда, ввиду равенств (36), (37), следует соотношение между амплитудами продольных и поперечных волн, распространяющихся по каркасу:

(42)
$A_{3}^{s} = \frac{{2{{k}_{y}}\left( {A_{1}^{s}{\delta }_{1}^{x} + A_{2}^{s}{\delta }_{2}^{x}} \right)}}{{{\delta }_{3}^{2} - 2k_{y}^{2}}}.$

Другому случаю фиксированного контакта пористого материала с относительно жестким граничным элементом соответствует модель нерастяжимой границы, в рамках которой выполняется условие

(43)
${{\left. {\frac{{{{\partial }^{2}}\left( {{\tilde {\varphi }}_{{1~}}^{s} + {\tilde {\varphi }}_{{2~}}^{s}} \right)}}{{\partial {{y}^{2}}}} - \frac{{{{\partial }^{2}}{\tilde {\psi }}_{{z~}}^{s}}}{{\partial x~\partial y}}} \right|}_{{x = 0}}} = 0,~$
приводящее к равенству

(44)
$A_{3}^{s} = \frac{{{{k}_{y}}\left( {A_{1}^{s} + A_{2}^{s}} \right)}}{{{\delta }_{3}^{x}}}.$

Пары соотношений (41), (42) и (41), (44) однозначно определяют относительные значения амплитуды $A_{3}^{{s0}}$ поперечной структурной волны на граничной плоскости применительно к рассматриваемым случаям граничных условий. Одновременно, в силу равенств (36)–(38), устанавливаются и соотношения между амплитудами нормальных компонент волновых перемещений $U_{1}^{{sx}},~\,U_{2}^{{sx}},~\,U_{3}^{{sx}}$ элементов каркаса, связанных с тремя рассматриваемыми волнами. При этом безразмерная величина

$\left| {\bar {U}_{3}^{{sx}}} \right| = \frac{{\left| {U_{3}^{{sx}}} \right|}}{{\left| {U_{1}^{{sx}} + U_{2}^{{sx}}} \right|}}$
характеризует относительную роль поперечных волн в передаче звука по каркасу. Применительно к границе без касательных напряжений этот параметр определяется лишь соотношением (42) и имеет вид
(45)
$\left| {\bar {U}_{3}^{{sx}}} \right| = \frac{{2k_{y}^{2}}}{{\left| {{\delta }_{3}^{2} - 2k_{y}^{2}} \right|}},$
справедливый как для свободной поверхности, так и для нефиксированного примыкания к непроницаемому граничному элементу. В данном случае значение $\bar {U}_{3}^{{sx}}$ зависит лишь от соотношения параметров ${{{\delta }}_{3}}$ и ${{k}_{y}}$.

Для фиксированного контакта, в силу (40), (43) выполняется равенство

(46)
$\left| {\bar {U}_{3}^{{sx}}} \right| = k_{y}^{2}\left| {\frac{{{\delta }_{2}^{x}\left( {{{{\mu }}_{2}} - 1} \right) - {\delta }_{1}^{x}\left( {{{{\mu }}_{1}} - 1} \right)}}{{k_{y}^{2}\left( {{{{\mu }}_{3}} - 1} \right)\left( {{\delta }_{1}^{x} - {\delta }_{2}^{x}} \right) - {\delta }_{1}^{x}{\delta }_{2}^{x}{\delta }_{3}^{x}\left( {{{{\mu }}_{1}} - {{{\mu }}_{2}}} \right)}}} \right|.$

Аналогичным образом находятся значения модулей относительных амплитуд $\bar {U}_{3}^{{fx}}$ нормальных перемещений насыщающей жидкости

$\left| {\bar {U}_{3}^{{fx}}} \right| = \frac{{\left| {{{{\mu }}_{3}}U_{3}^{{sx}}} \right|}}{{\left| {{{{\mu }}_{1}}U_{1}^{{sx}} + {{{\mu }}_{2}}U_{2}^{{sx}}} \right|}}$
для случая непроницаемой границы. Соответствующие выражения могут быть представлены в виде
(47)
$\left| {\bar {U}_{3}^{{fx}}} \right| = 2k_{y}^{2}\left| {\frac{{{{{\mu }}_{3}}}}{{{\delta }_{3}^{2} - 2{{{\mu }}_{3}}k_{y}^{2}}}} \right|$
для случая простого примыкания к граничному элементу и
(48)
$\begin{gathered} \left| {\bar {U}_{3}^{{fx}}} \right| = \\ = k_{y}^{2}\left| {{{{\mu }}_{3}}\frac{{{\delta }_{2}^{x}\left( {{{{\mu }}_{2}}\, - \,1} \right) - {\delta }_{1}^{x}\left( {{{{\mu }}_{1}}\, - \,1} \right)}}{{k_{y}^{2}\left( {{{{\mu }}_{3}}\, - \,1} \right)\left( {{\delta }_{1}^{x}{{{\mu }}_{1}}\, - \,{\delta }_{2}^{x}{{{\mu }}_{2}}} \right)\, - \,{\delta }_{1}^{x}{\delta }_{2}^{x}{\delta }_{3}^{x}\left( {{{{\mu }}_{1}}\, - \,{{{\mu }}_{2}}} \right)}}} \right| \\ \end{gathered} $
для фиксированного контакта.

В качестве примера на рис. 1 представлены результаты расчета относительных амплитуд $\left| {\bar {U}_{3}^{{sx}}} \right|$ и $\left| {\bar {U}_{3}^{{fx}}} \right|$ для эластичного пеноматериала, плотность которого равна 11.2 кг/м3, динамический модуль Юнга 2.93 × 105 × (1 + 0.06i) Па; коэффициент Пуассона 0.2; пористость ϕ = 0.98; сопротивление продуванию 6.6 × 104 Па с/м2; насыщающая среда – воздух в нормальных условиях. Для оценок по формулам (45)–(48) при расчете динамической плотности и динамического модуля объемного сжатия насыщающей жидкости (воздуха) аналогично [10] использовалась модифицированная модель Делани–Базли [12].

Рис. 1.

Относительные амплитуды нормальной компоненты перемещений каркаса и насыщающей среды в поперечной волне, формирующейся на непроницаемой границе эластичного пеноматериала. Углы падения звуковой волны: 1 – 30°; 2 – 45°; 3 – 75°. — – граница без трения; ---- – нерастяжимая граница.

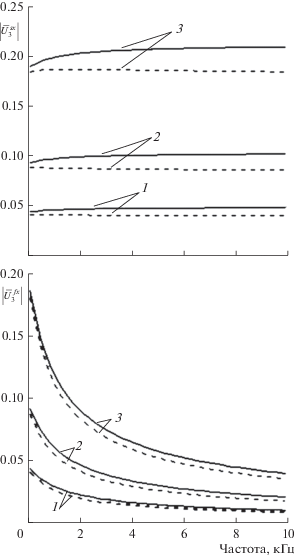
Априори допустимость пренебрежения вкладом поперечных волн в процессы прохождения звука в рассматриваемом примере не вполне очевидна, т.к. скорость распространения продольных волн по каркасу пеноматериала в вакууме (составляющая около 170 м/с) здесь, в отличие от рассмотренного в [10] случая волокнистых материалов, всего лишь вдвое ниже скорости звука в воздушной среде. Тем не менее, как свидетельствуют данные рис. 1, даже при больших углах падения звуковой волны относительные амплитуды, обусловленные поперечными волнами, довольно малы. Это позволяет, в частности, полагать, что передаточные характеристики слоев достаточно широкого класса нежестких пористых материалов могут быть с приемлемой точностью описаны матрицами четырехполюсников в пределах рассмотренной выше безвихревой модели.

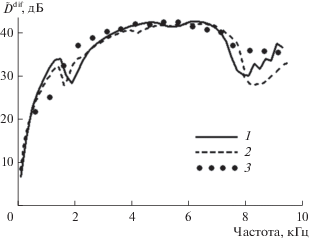
Последний вывод подтверждается представленными на рис. 2 результатами использования матрицы четырехполюсника при расчете звукоизоляции двуслойной системы, состоящей из алюминиевой пластины и слоя рассматриваемого пеноматериала, в диффузном поле падающих звуковых волн. Показатель звукоизоляции ${{\tilde {D}}^{{{\text{dif}}}}},$ дБ определяется здесь интегрированием по углам θ падения звуковой волны. Используется соотношение

${{\tilde {D}}^{{{\text{dif}}}}} = - 10{\text{lg}}\left\{ {2\int\limits_0^{{{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2} - 0} {{{{10}}^{{ - 0.1\widetilde {D(}{\theta })}}}} {\text{sin}}\left( {\theta } \right){\text{cos}}\left( {\theta } \right)d{\theta }} \right\},$
в котором значения звукоизоляции $\widetilde {D(}\theta )$ при каждом угле падения определяются в соответствии с [10] по компонентам передаточной матрицы, являющейся произведением передаточной матрицы пластины толщиной 1.6 мм и матрицы $\left[ {{{{\bar {T}}}^{p}}} \right]$ пористого слоя толщиной 25.4 мм.

Рис. 2.

Звукоизоляция двуслойной системы “пластина–пеноматериал” в диффузном поле. 1 – расчет по матрице четырехполюсника и модели [12]; 2 – полный расчет [6]; 3 – данные измерений [6].

На рисунке приведены также заимствованные из [6] (рис. 11.19 ) экспериментальные данные и результаты полного расчета той же системы, основанного на общей процедуре построения ее передаточной матрицы и использовании моделей [13, 14] с дополнительным заданием трех параметров пеноматериала – извилистости и двух характеристических длин.

Сопоставление данных рис. 2 показывает, что применение матрицы четырехполюсника приводит в данном случае к результатам, соответствие которых экспериментальным данным находится примерно на том же уровне, что и при использовании схемы полного расчета [6].

ЗАКЛЮЧЕНИЕ

Особенность упругого пористого слоя, ограниченного свободными и/или непроницаемыми границами, состоит в возможности определения его передаточных свойств линейным четырехполюсником, задающим связь граничных давлений и нормальных компонент скорости. В статье получены соотношения для передаточных матриц таких четырехполюсников в безвихревом приближении. Безвихревая модель основана на пренебрежении влиянием сдвиговых напряжений на передачу волновых возмущений поперек слоя, допустимом в общем случае при малых углах прохождения волны. Представленные в статье оценки показывают, что применительно к слоям нежестких пористых материалов полученные соотношения для передаточных матриц четырехполюсников могут использоваться в широком диапазоне углов падения звуковых волн.

Список литературы

  1. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука, 1989. 416 с.

  2. Бабич В.М., Краукдис П.В., Молотков Л.А. Динамические задачи геоакустики // Акуст. журн. 1984. Т. 30. № 5. С. 693–695.

  3. Молотков Л.А. Матричный метод в теории распространения волн в слоистых упругих и жидких средах. Л.: Наука, 1984. 201 с.

  4. Li B., Li M., Lu T. Interface waves in multilayered plates // J. Acoust. Soc. Am. 2018. V.143. P. 2541–2553.

  5. Tanneau O., Casimir J.B., Lamary P. Optimization of multilayered panels with poroelastic components for an acoustical transmission objective // J. Acoust. Soc. Am. 2006. V. 120. P. 1227–1238.

  6. Allard J.F., Atalla N. Propagation of sound in porous media: Modelling sound absorbing materials. 2nd ed. Wiley, 2009. 358 p.

  7. Verdière K., Panneton R., Elkoun S., Dupont T., Leclaire P. Transfer matrix method applied to the parallel assembly of sound absorbing materials // J. Acoust. Soc. Am. 2013. V. 134. P. 4648–4658.

  8. Biot M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low frequency range // J. Acoust. Soc. Am. 1956. V. 28. P. 168–178.

  9. Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1994. 528 с.

  10. Яблоник Л.Р. Упрощенный метод расчета многослойной звукоизоляции, включающей слои волокнистого пористого материала // Акуст. журн. 2018. Т. 64. № 5. С. 639–646.

  11. Зверев А.Я., Черных В.В. Экспериментальное определение акустических и виброакустических характеристик многослойных композитных панелей // Акуст. журн. 2018. Т. 64. № 6. С. 727–736.

  12. Miki Y. Acoustical properties of porous materials – Modifications of Delany-Bazley models // J. Acoust. Soc. Jpn. (E) 1990. V. 11. № 1. P. 19–24.

  13. Johnson D.L., Koplik J., Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media // J. Fluid Mech. 1987. V. 176. P. 379–402.

  14. Champoux Y., Allard J.F. Dynamic tortuosity and bulk modulus in air saturated porous media // J. Appl. Phys. 1991. V. 70. P. 1975–1979.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Акустический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал