Доклады Российской академии наук. Физика, технические науки, 2020, T. 490, № 1, стр. 43-47

Деформация кавитационных пузырьков при реализации их сверхсжатия в кластере

Академик РАН Р. И. Нигматулин^1, 2, А. А. Аганин¹, А. И. Давлетшин^1, *

¹ Институт механики и машиностроения Федерального исследовательского центра “Казанский научный центр Российской академии наук”
Казань, Россия

² Институт океанологии им. П.П. Ширшова Российской академии наук
Москва, Россия

^* E-mail: anas.davletshin@gmail.com

Поступила в редакцию 30.07.2019
После доработки 02.10.2019
Принята к публикации 28.11.2019

DOI: 10.31857/S2686740020010186

Полный текст (PDF)

Аннотация

Изучаются деформации кавитационных пузырьков в центральной области кластеров при их сверхсильном расширении и сжатии. Принимаются условия, близкие к используемым в известных экспериментах по акустической кавитации дейтерированного ацетона. Применяется простейшая модель кластера из семи изначально сферических одинаковых пузырьков с центрами на трех взаимно перпендикулярных прямых, пересекающихся в одной точке. Боковые пузырьки равноудалены от центрального, центр которого находится в точке пересечения указанных прямых. Для сравнения рассматривается также и простейшая модель стримера из трех пузырьков на одной прямой. Установлено, что в случае кластера максимальные деформации центрального пузырька оказываются на два порядка меньше, чем в случае стримера. При этом в кластере, как и стримере, центральный пузырек деформируется только в виде сферических гармоник с четными номерами, причем если в стримере максимальными оказываются деформации по вторым гармоникам, то в кластере – по четвертым.

Ключевые слова: кластер кавитационных пузырьков, деформация пузырьков, сильное сжатие пузырьков

В парогазовых пузырьках в жидкости при их сжатии (коллапсе) могут достигаться очень высокие давления, плотности и температуры [1]. В частности, экспериментально показано [2], что на режиме сонолюминесценции одиночного пузырька температура в его полости может превышать 16 000 K. В [3–5] выявлено, что на режиме акустической кавитации дейтерированного ацетона в кавитационных пузырьках, организованных в виде шаровых кластеров, можно достичь еще более высоких степеней сжатия их содержимого (с температурой до 10⁷ K и достижением термоядерных актов). К настоящему времени установилось представление [5], что сверхвысокие давления, плотности и температуры в пузырьке достигаются в результате фокусировки в его центральной области радиально-сходящихся ударных волн, возникающих в конце коллапса. При этом для осуществления сверхсильного сжатия содержимого пузырька необходимо, чтобы форма сходящихся ударных волн оставалась близкой к сферической, иначе степень фокусировки будет существенно снижена. Несферичность ударных волн при схождении может сильно возрастать. Следовательно, для реализации сверхсжатия ударные волны при возникновении должны мало отличаться от сферических. Геометрия возникающих в пузырьке ударных волн во многом определяется его формой в финальной стадии коллапса (несферичность пузырька при коллапсе также возрастает). Поэтому для достижения сверхвысокого сжатия среды в пузырьке необходимо, чтобы форма пузырька к концу его коллапса сохранялась достаточно близкой к сферической.

Оценке эволюции несферичности как одиночных, так и взаимодействующих пузырьков на режиме сонолюминесценции посвящено довольно много работ. На режиме сверхсжатия пузырьков при акустической кавитации дейтерированного ацетона такая оценка до настоящего времени проводилась, в основном, без учета наличия соседних пузырьков [6]. Однако взаимодействие между пузырьками может оказывать существенное влияние на их деформацию в ходе их сильного расширения и сжатия. Об этом свидетельствует ряд исследований, посвященных деформации пузырьков в стримерах [7], когда пузырьки находятся на одной прямой (подобные стримеры также возникали в экспериментах [3]). В настоящей работе анализируются особенности деформирования пузырьков в центральной области кластеров, состоящих из большого числа пузырьков, в условиях, близких к тем, что применялись в экспериментах [3].

ПОСТАНОВКА ЗАДАЧИ

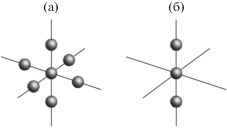
Изучаются особенности деформирования кавитационных пузырьков в центральной области пространственных кластеров, состоящих из большого числа пузырьков. Для этого используется простейшая модель, в которой считается, что кластер состоит из семи пузырьков с центрами на трех взаимно перпендикулярных прямых, пересекающихся в одной точке (рис. 1a). Изначально все пузырьки сферические, с одинаковым радиусом. Боковые пузырьки равноудалены от центрального, а центр последнего находится в точке пересечения трех указанных прямых. Для сравнения рассматривается также и простейшая модель стримеров, состоящих из большого числа кавитационных пузырьков, расположенных на одной прямой. В этой модели считается, что стример состоит из трех пузырьков, среди которых боковые равноудалены от центрального (рис. 1б). В данных простейших кластерах и стримерах динамика центрального и боковых пузырьков моделирует динамику пузырьков, расположенных соответственно в центральной области и на периферии кластеров и стримеров, состоящих из большого числа пузырьков.

Рис. 1.

Рассматриваемые модели кластера (а) и стримера (б).

Считается, что и кластер, и стример находятся в пучности ультразвуковой стоячей волны, где давление ${{p}_{\infty }}$ изменяется по гармоническому закону

(1)

${{p}_{\infty }} = {{p}_{0}} - {{p}_{a}}\cos \left( {\omega t} \right).$

Здесь p₀ – статическое давление, p_a, ω – амплитуда и частота колебаний, $t$ – время.

Входные данные принимаются близкими к тем, что применялись в экспериментах [3]. В частности полагается, что жидкостью является ацетон при температуре ${{T}_{0}} = 273.15$ K, давление жидкости в пучности волны ${{p}_{\infty }}$ изменяется с частотой ω = = $2\pi \times 19.3$ кГц и амплитудой ${{p}_{a}} = 15$ бар относительно статического давления p₀ ≈ 1 бар. Принимается, что при $t = 0$ радиус пузырьков равен 5 мкм, а пузырьки находятся в процессе расширения с радиальной скоростью 30 м/с. Начальное расстояние между центрами ближайших пузырьков равно 9 мм. В рассматриваемых условиях амплитуда ${{p}_{a}}$ значительно больше статического давления ${{p}_{0}}$, так что первоначально жидкость вокруг пузырьков испытывает большие растягивающие напряжения (p_∞ = –14 бар). В результате этого пузырьки сначала сильно расширяются, а затем в фазе положительного давления ${{p}_{\infty }}$ стремительно сжимаются. Анализируется первое расширение и последующее сжатие пузырьков, что для целей настоящей работы вполне достаточно. Отметим, что одно из существенных отличий динамики центральных пузырьков в больших кластерах и стримерах от динамики периферийных пузырьков, оказывающих влияние на их деформацию, состоит в их меньшей подвижности, что характерно и для центральных пузырьков в рассматриваемых простейших моделях кластера и стримера.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Уравнение поверхности k-го пузырька представляется в виде ряда

$\begin{gathered} {{F}_{k}}\left( {{{r}_{k}},{{\theta }_{k}},{{\varphi }_{k}},t} \right) = \\ = \;{{r}_{k}} - {{R}_{k}}\left( t \right) - \sum\limits_{n = 2}^N {{{{\mathbf{a}}}_{{n{\kern 1pt} k}}}} \left( t \right) \cdot {{{\mathbf{Y}}}_{n}}\left( {{{\theta }_{k}},{{\varphi }_{k}}} \right) = 0, \\ \end{gathered} $

где k = 1, 2, …, K, K – число пузырьков, r_k, θ_k, φ_k – сферическая система координат с началом отсчета в центре k-го пузырька; ${{{\mathbf{Y}}}_{n}}\left( {{{\theta }_{k}},{{\varphi }_{k}}} \right)$ = = $(Y_{{nk}}^{{ - n}},Y_{{nk}}^{{ - n + 1}}$, ..., $Y_{{nk}}^{{n - 1}},Y_{{nk}}^{n})$, $Y_{{nk}}^{m} = P_{n}^{{\left| m \right|}}(\cos {{\theta }_{k}}){{e}^{{im{{\varphi }_{k}}}}}$ – сферическая функция; $P_{n}^{{\left| m \right|}}$ – присоединенный полином Лежандра степени n порядка |m|; a_nk = = $\left( {\frac{{a_{{nk}}^{{ - n}} + ia_{{nk}}^{n}}}{2}} \right.$, …, $a_{{nk}}^{0}$, …, $\left. {\frac{{a_{{nk}}^{{ - n}} - ia_{{nk}}^{n}}}{2}} \right)$, $a_{{nk}}^{m}$ – амплитуда отклонения поверхности k-го пузырька от сферической r_k = R_k в виде поверхностной гармоники с номером n и порядком m; i – мнимая единица; N – максимальное значение номера сферических гармоник в представлении поверхности пузырьков. Отклонения от сферической формы пузырьков характеризуются величиной

(2)

$\left| {{{\varepsilon }_{n}}} \right| = \mathop {\max }\limits_{\theta ,\varphi } \left| {\sum\limits_{m = - n}^n {\varepsilon _{n}^{m}Y_{n}^{m}\left( {\theta ,\varphi } \right)} } \right|,$

где $\varepsilon _{{nk}}^{m} = \frac{{a_{{nk}}^{m}}}{{{{R}_{k}}}}$. Предполагается, что $\varepsilon _{n}^{2} \ll 1$.

Совместная динамика пузырьков описывается системой дифференциальных уравнений второго порядка [8] относительно радиусов пузырьков ${{R}_{k}}$, радиус-векторов их центров ${{{\mathbf{p}}}_{k}}$ и векторов ${{{\mathbf{a}}}_{{nk}}}$, определяющих несферичность пузырьков

$\begin{gathered} {{R}_{k}}{{{\ddot {R}}}_{k}} + \frac{{3\dot {R}_{k}^{2}}}{2} - \frac{{3{{{{\mathbf{\dot {p}}}}}_{k}}\left( {{{{{\mathbf{\dot {p}}}}}_{k}}{{{\mathbf{\beta }}}_{{110}}}} \right)}}{8} + \\ + \;\frac{{2\sigma }}{{{{\rho }_{0}}{{R}_{k}}}} - \frac{{{{p}_{k}} - {{p}_{\infty }}}}{{{{\rho }_{0}}}} + {{\psi }_{{0k}}} + {{\Delta }_{k}} = \\ = \;\sum\limits_{j = 1,j \ne k}^K {\left[ {\frac{{{{{\dot {B}}}_{{0j}}}}}{{{{d}_{{kj}}}}}} \right.} - \frac{{{{B}_{{0j}}}{{{\dot {d}}}_{{kj}}}}}{{d_{{kj}}^{2}}} - \frac{{(R_{j}^{3}{{{{\mathbf{\dot {p}}}}}_{j}}{{{\mathbf{C}}}_{{10kj}}}){\text{'}}}}{{2d_{{kj}}^{2}}} - \\ \end{gathered} $

(3)

$\begin{gathered} - \;\frac{{9{{B}_{{0j}}}{{{{\mathbf{\dot {p}}}}}_{k}}\left( {{{{\mathbf{C}}}_{{01kj}}}{{{\mathbf{\beta }}}_{{110}}}} \right)}}{{4d_{{kj}}^{2}}} + \frac{{(R_{j}^{3}{{B}_{{0s}}}{{{\mathbf{C}}}_{{01js}}}{{{\mathbf{C}}}_{{10kj}}}){\kern 1pt} '}}{{2d_{{kj}}^{2}d_{{js}}^{2}}} + \\ + \;\sum\limits_{s = 1,s \ne k}^K {\left. {\frac{{9{{B}_{{0j}}}{{B}_{{0s}}}{{{\mathbf{C}}}_{{01kj}}}\left( {{{{\mathbf{C}}}_{{01ks}}}{{{\mathbf{\beta }}}_{{110}}}} \right)}}{{8d_{{kj}}^{2}d_{{ks}}^{2}}}} \right]} , \\ \end{gathered} $

$\begin{gathered} {{R}_{k}}{{{{\mathbf{\ddot {p}}}}}_{k}} + 3{{{\dot {R}}}_{k}}{{{{\mathbf{\dot {p}}}}}_{k}} - 2{{{\dot {R}}}_{k}}{{{{\mathbf{\dot {p}}}}}_{k}}\left( {{{{\mathbf{\varepsilon }}}_{{2k}}}{{{\mathbf{\beta }}}_{{211}}}} \right) - \\ - \;\frac{{7{{{{\mathbf{\ddot {p}}}}}_{k}}\left( {{{{\mathbf{a}}}_{{2k}}}{{{\mathbf{\beta }}}_{{211}}}} \right)}}{6} - \frac{{3{{{{\mathbf{\dot {p}}}}}_{k}}\left( {{{{{\mathbf{\dot {a}}}}}_{{2k}}}{{{\mathbf{\beta }}}_{{211}}}} \right)}}{2} + {{\psi }_{{1k}}} = \\ \end{gathered} $

$\begin{gathered} = \;\sum\limits_{j = 1,j \ne k}^K {\left[ {\frac{{3({{R}_{k}}{{B}_{{0j}}}{{{\mathbf{C}}}_{{01kj}}}){\kern 1pt} '}}{{d_{{kj}}^{2}}}} \right.} - \\ - \;\frac{{3({{R}_{k}}R_{j}^{3}{{{{\mathbf{\dot {p}}}}}_{j}}{{{\mathbf{C}}}_{{11kj}}}){\kern 1pt} '}}{{2d_{{kj}}^{3}}} - \frac{{6{{R}_{k}}{{B}_{{0j}}}{{{\mathbf{C}}}_{{01kj}}}{{{\dot {d}}}_{{kj}}}}}{{d_{{kj}}^{3}}} - \\ \end{gathered} $

$\begin{gathered} - \;\frac{{5{{R}_{k}}{{B}_{{0j}}}{{{{\mathbf{\dot {p}}}}}_{k}}\left( {{{{\mathbf{C}}}_{{02kj}}}{{{\mathbf{\beta }}}_{{211}}}} \right)}}{{d_{{kj}}^{3}}} + \frac{{3({{B}_{{0j}}}{{{\mathbf{C}}}_{{01kj}}}({{{\mathbf{a}}}_{{2k}}}\Upsilon _{{211}}^{2}))'}}{{2d_{{kj}}^{2}}} - \\ - \;\left. {\frac{{{{B}_{{0j}}}({{{{\mathbf{\dot {a}}}}}_{{2k}}} + 2{{{\dot {R}}}_{k}}{{{\mathbf{\varepsilon }}}_{{2k}}})({{{\mathbf{C}}}_{{01kj}}}{{{\mathbf{\beta }}}_{{121}}})}}{{d_{{kj}}^{2}}}} \right], \\ \end{gathered} $

$\begin{gathered} {{R}_{k}}{{{{\mathbf{\ddot {a}}}}}_{{mk}}} + 3{{{\dot {R}}}_{k}}{{{{\mathbf{\dot {a}}}}}_{{mk}}} - (m - 1){{{\ddot {R}}}_{k}}{{{\mathbf{a}}}_{{mk}}} - \\ - \;{{\delta }_{{2m}}}\frac{{27{{{{\mathbf{\dot {p}}}}}_{k}}\left( {{{{{\mathbf{\dot {p}}}}}_{k}}{{{\mathbf{\beta }}}_{{112}}}} \right)}}{8} + \frac{3}{2}\sum\limits_{n = m - 1}^{n = m + 1} {\left[ {{{{{\mathbf{\dot {p}}}}}_{k}}({{{{\mathbf{\dot {a}}}}}_{{nk}}}\Upsilon _{{n1m}}^{2}){{ - }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}} \right.} \\ \end{gathered} $

$\begin{gathered} \left. { - \;\frac{{(m + 1)({{{{\mathbf{\dot {a}}}}}_{{nk}}} + 2{{{\dot {R}}}_{k}}{{{\mathbf{\varepsilon }}}_{{nk}}})\left( {{{{{\mathbf{\dot {p}}}}}_{k}}{{{\mathbf{\beta }}}_{{1nm}}}} \right)}}{{(n + 1)}} + {{{{\mathbf{\ddot {p}}}}}_{k}}({{{\mathbf{a}}}_{{nk}}}\Upsilon _{{n1m}}^{{2(2 - m)/3}})} \right] + \\ + \;\frac{{\sigma ({{m}^{2}} - 1)(m + 2){{{\mathbf{\varepsilon }}}_{{mk}}}}}{{{{\rho }_{0}}{{R}_{k}}}} + {{\psi }_{{mk}}} = \\ \end{gathered} $

$\begin{gathered} = \;\sum\limits_{j = 1,j \ne k}^K {\left[ { - \frac{{3(2m - 1)(m + 1)R_{k}^{{m - 2}}{{B}_{{0j}}}{{{{\mathbf{\dot {p}}}}}_{k}}({{{\mathbf{C}}}_{{0m - 1kj}}}{{{\mathbf{\beta }}}_{{m - 11m}}})}}{{2md_{{kj}}^{m}}}} \right.} + \\ + \;\frac{{(2m + 1)(R_{k}^{m}{{B}_{{0j}}}{{{\mathbf{C}}}_{{0mkj}}})'}}{{d_{{kj}}^{{m + 1}}}} + \\ \end{gathered} $

(5)

$\begin{gathered} + \;\sum\limits_{n = m - 1}^{m + 1} {\left( {\frac{{3{\text{(}}{{B}_{{0j}}}{{{\mathbf{a}}}_{{nk}}}({{{\mathbf{C}}}_{{01kj}}}\Upsilon _{{1nm}}^{2}){\text{)'}}}}{{2d_{{kj}}^{2}}}} \right.} - \\ - \;\left. {\left. {\frac{{3(m + 1){{B}_{{0j}}}({{{{\mathbf{\dot {a}}}}}_{{nk}}} + 2{{{\dot {R}}}_{k}}{{{\mathbf{\varepsilon }}}_{{nk}}})({{{\mathbf{C}}}_{{01kj}}}{{{\mathbf{\beta }}}_{{1nm}}})}}{{2(n + 1)d_{{kj}}^{2}}}} \right)} \right], \\ \end{gathered} $

где точка сверху и штрих означают производную по времени, ρ₀ – плотность жидкости, σ – коэффициент поверхностного натяжения, p_k – давление внутри k-го пузырька, ${{B}_{{0\,k}}} = - R_{k}^{2}{{\dot {R}}_{k}}$, ε_nk = $\frac{{{{{\mathbf{a}}}_{{nk}}}}}{{{{R}_{k}}}}$, d_kj = |p_k – p_j|, k, j = 1, 2, …, K, k ≠ j, m = 2, 3, …, N, ${{{\mathbf{C}}}_{{\gamma \varsigma kj}}}$, ${{{\mathbf{\beta }}}_{{\gamma \varsigma \varrho }}}$, $\Upsilon _{{\gamma \varsigma \varrho }}^{p}$ – матрицы чисел [8]. При выводе уравнений (3)–(5) полагается, что пузырьки расположены не очень близко друг к другу, а их несферичность и скорости пространственного смещения малы. Эффекты вязкости и сжимаемости жидкости считаются малыми, не зависящими от взаимодействия между пузырьками, и учитываются через поправки ψ_0k, ψ_1k, ψ_mk, Δ_k [8]. Принимается, что пар в пузырьках при их расширении и сжатии находится в состоянии насыщения при температуре жидкости T₀ с давлением p_s(T₀) ≈ 0.094 бар. Такое допущение существенно нарушается лишь в финальной высокоскоростной стадии коллапса, что на основные результаты и выводы настоящей работы не влияет. Возможность его использования при оценке деформаций пузырьков в стримере в рассматриваемых условиях показана в [7]. Предполагается, что сжатие пузырьков завершается при достижении их радиусом значения R_c = 22.5 мкм. Такая глубина коллапса получается при расчете расширения и коллапса одиночного сферически симметричного пузырька в аналогичных условиях в момент экстремального сжатия его содержимого с использованием модели работы [6], являющейся более адекватной в финальной стадии коллапса. Уравнения (3)–(5) решаются численно при соответствующих рассматриваемой задаче начальных значениях ${{R}_{k}}$, ${{{\mathbf{p}}}_{k}}$, ${{{\mathbf{a}}}_{{nk}}}$, ${{\dot {R}}_{k}}$, ${{{\mathbf{\dot {p}}}}_{k}}$ и ${{{\mathbf{\dot {a}}}}_{{nk}}}$. Среди этих параметров первые четыре определяются приведенными выше данными, а последние два равны нулю.

РАДИАЛЬНОЕ ДВИЖЕНИЕ ПУЗЫРЬКОВ

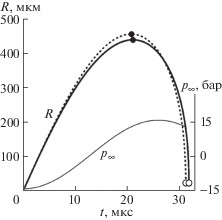
Рисунок 2 характеризует изменение радиусов центральных пузырьков в рассматриваемых простейших моделях кластера и стримера (рис. 1) в ходе первого расширения и последующего сжатия этих пузырьков под действием ультразвуковой волны (1). Видно, что первоначально пузырьки расширяются примерно до 450 мкм, что в 90 раз больше их начального радиуса. Далее они сильно сжимаются до уменьшения их радиусов примерно в 20 раз. В модели кластера центральный пузырек расширяется несколько меньше и коллапсирует немного позже, чем в модели стримера. Это обусловлено наличием большего числа соседних пузырьков (шесть в модели кластера против двух в модели стримера).

Рис. 2.

Изменение радиусов центральных пузырьков R в рассматриваемых моделях кластера (сплошная кривая) и стримера (пунктирная кривая) и давления жидкости p_∝. Точки – моменты максимального расширения пузырьков, кружки − конец коллапса.

ДЕФОРМАЦИЯ ПУЗЫРЬКОВ

Расчеты показывают, что в рассматриваемых простейших моделях кластера и стримера центральные пузырьки в процессе своего расширения и последующего сжатия остаются неподвижными. Это объясняется симметричным по отношению к ним расположением других пузырьков. В результате этого центральные пузырьки деформируются только в виде гармоник с четными номерами n. Примечательно, что у центрального пузырька в кластере деформаций в виде наиболее низкочастотных гармоник (с n = 2) вообще не возникает. С увеличением n величина деформаций центральных пузырьков в виде соответствующих гармоник как в кластере, так и в стримере уменьшается. В обеих конфигурациях боковые пузырьки в силу их подвижности деформируются намного больше центральных, причем в случае кластера возникают также и деформации в виде гармоник с n = 2.

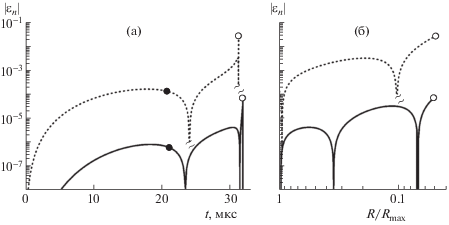
Рисунок 3 характеризует уровни и эволюцию максимальных по n несферичностей центральных пузырьков в кластере и стримере в виде отдельных сферических гармоник. В случае кластера максимум достигается при n = 4, а в случае стримера – при n = 2. Видно, что в случае кластера сферическая форма центрального пузырька как в ходе его расширения, так при последующем сжатии вплоть до его окончания искажается намного (примерно на 2 порядка) меньше, чем в случае стримера. При этом в большей части стадии расширения пузырьков (первоначально сферических) и в кластере, и в стримере величина их максимальных по n деформаций монотонно возрастает, что обусловлено гидродинамическим взаимодействием с соседними пузырьками (изначально сферический и неподвижный одиночный пузырек оставался бы таковым до конца сжатия). При последующем сжатии амплитуда деформаций возрастает в режиме колебаний относительно нулевого значения.

Рис. 3.

Изменение деформаций центральных пузырьков (рассчитаны по формуле (2)) в рассматриваемых простейших моделях кластера (в виде сферических гармоник с n = 4, сплошные кривые) и стримера (в виде сферических гармоник с n = 2, пунктирные кривые): a – в процессе расширения и последующего сжатия пузырьков, б – только на стадии их сжатия. Точками указаны моменты максимального расширения пузырьков, кружки соответствуют концу коллапса.

Таким образом, полученные результаты позволяют заключить, что пузырьки в центральной области кластеров деформируются намного (до 100 раз) меньше, чем в стримерах. Причина столь кардинальной разницы в том, что максимум их несферичности реализуется не в виде сферических гармоник с n = 2, как у пузырьков в стримере (или периферийных пузырьков в кластере), а в виде гармоник с n = 4. По-видимому, это является одной из причин того, что при образовании шаровых кластеров в экспериментах [3] фокусировка энергии с эмиссией нейтронов имела место, а при образовании стримеров – нет. С учетом этого можно предположить, что ограничения, накладываемые на сверхсжатие пузырьков в центральной области кластеров их гидродинамическим взаимодействием с соседними пузырьками, могут оказаться не более существенными, чем ограничения, накладываемые рядом других факторов (температурным эффектом, неустойчивостью кластера в целом и т.д.).

Список литературы

Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987. Т. 1, 2.
Flannigan D.J., Suslick K.S. // Nat. Phys. 2010. V. 6. P. 598–601.
Taleyarkhan R.P., West C.D., Cho J.S., et al. // Science. 2002. V. 295. P. 1868–1873.
Nigmatulin R.I, Akhatov I.Sh., Topolnikov A.S., et al. // Phys. Fluids. 2005. V. 17. № 10.107106.
Нигматулин Р.И., Лэхи Р.Т. (мл.), Талейархан Р.П. и др. // УФН. 2014. Т. 184. № 9. С. 947–960.
Нигматулин Р.И., Аганин А.А., Топорков Д.Ю. и др. // ДАН. 2014. Т. 458. № 3. С. 282–286.
Аганин А.А., Давлетшин А.И., Топорков Д.Ю. // Вычислительные технологии. 2014. Т. 19. № 1. С. 3–19.
Aganin A.A., Davletshin A.I. // Lobachevskii J. Mathematics. 2019. V. 40. № 6. P. 699–704.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал