Доклады Российской академии наук. Физика, технические науки, 2020, T. 491, № 1, стр. 37-43

ВВЕДЕНИЕ

Одним из направлений исследований в области механики многофазных сред является изучение законов течения сплошных сред сквозь стационарный зернистый слой при наличии заданных внешних границ разной геометрии [1]. Исследования в этой области особенно интенсивно проводились в период 1970–1990 гг. ([2–5] и др.). Однако полной ясности в отношении изучаемых законов в этой области до сих пор нет. Поэтому различные аспекты этой проблемы и в настоящее время находятся в фокусе внимания ученых [6–9].

В свое время в результате многочисленных экспериментов по течению газа сквозь стационарный зернистый слой [2] был обнаружен эффект аномально большой скорости газа на выходе из слоя в пристеночной области по сравнению с его скоростью в основной области потока. В качестве причин такой неравномерности в распределении скорости по сечению потока выдвигались две – неравномерность распределения гранул вблизи стенки и искривление границы зернистого слоя под действием набегающего потока. Для теоретического обоснования этих причин и выявления степени их влияния на итоговый профиль скорости газа использовались в основном различные феноменологические модели гидродинамического взаимодействия гранул слоя с внешним потоком газа с последующим численным интегрированием усредненных уравнений движения сплошной среды в тех или иных диапазонах определяющих гидродинамических критериев [2, 4–9]. В результате было показано, что упомянутые выше причины действительно приводят к возникновению неоднородности профиля скорости в пристеночной области потока.

В настоящей работе на основе достаточно строгой математической модели показано, что в приближении идеальной несжимаемой жидкости для несущей сплошной среды эффект пристеночной неоднородности профиля скорости имеет место даже тогда, когда нет неравномерности распределения гранул вблизи стенки и отсутствует искривление границ зернистого слоя. Задача определения усредненного профиля скорости жидкости решена в аналитическом виде в первом приближении по объемной доле гранул в слое как вне, так и внутри зернистого слоя. Решение получено на основе ранее разработанного метода самосогласованного поля [10, 11], который позволяет описывать эффекты коллективного гидродинамического взаимодействия любого числа сферических частиц в потенциальных потоках идеальной жидкости, в том числе при наличии внешних границ, и определять средние динамические характеристики таких потоков [12–14] в виде явных аналитических зависимостей от определяющих параметров.

КОНЕЧНАЯ СИСТЕМА НЕПОДВИЖНЫХ ЧАСТИЦ ВО ВНЕШНЕМ ПОТОКЕ ЖИДКОСТИ ПРИ НАЛИЧИИ ПЛОСКОЙ ГРАНИЦЫ

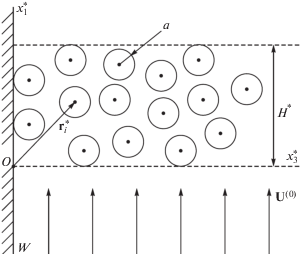
Рассмотрим систему из N сферических гранул радиуса a, погруженных в идеальную несжимаемую жидкость вблизи плоской бесконечной поверхности. Будем считать, что гранулы некоторым образом жестко связаны друг с другом и с заданной поверхностью и, таким образом, лишены возможности перемещаться относительно поверхности. Пронумеруем все сферы от 1 до N и обозначим безразмерные координаты центров сферических гранул в декартовой системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ как $x_{\gamma }^{{\left( i \right)}}$ (i = 1, 2, …, N, $\gamma = 1,2,3$). Рассмотрим задачу, когда в некоторый момент времени первоначально покоящаяся жидкость на бесконечности импульсно приводится в состояние движения с заданной постоянной скоростью $U_{\gamma }^{{\left( 0 \right)}}$, направленной вдоль плоской стенки W (рис. 1).

Классическая постановка этой задачи в предположении потенциальности течения жидкости, как известно, состоит в решении уравнения Лапласа для потенциала скорости φ и удовлетворении граничных условий непротекания на границе W и на поверхности всех гранул.

В рамках ранее разработанного метода самосогласованного поля [10, 11] граничные задачи динамики N сфер в идеальной (невязкой) несжимаемой жидкости в предположении потенциальности течения сведены к формальному решению системы уравнений для тензорных коэффициентов $C_{{{{\gamma }_{1}} \cdots {{\gamma }_{n}}}}^{{\left( i \right)}}$, входящих в полученное точное решение таких задач. Для сформулированной выше задачи при наличии плоской границы это решение для безразмерного потенциала скорости $\varphi $ имеет вид [10, 11]

где

а тензорные коэффициенты $C_{{{{\gamma }_{1}} \cdots {{\gamma }_{n}}}}^{{\left( i \right)}}~$удовлетворяют бесконечной ($1 \leqslant n < \infty $) системе алгебраических уравнений:

Здесь и далее приняты тензорные обозначения переменных с условием о суммировании по повторяющимся нижним координатным индексам, принимающим значения от 1 до 3. Это условие не распространяется только на переменные R_i и ${{\tilde {R}}_{i}}$. Верхние индексы относятся к гранулам, и чтобы отличать их от показателя степени, они заключены в круглые скобки. Соотношения (1) и (2) записаны в безразмерном виде. В качестве масштабов величин приняты характерное расстояние между центрами соседних гранул $L$ и заданная на бесконечности скорость потока U⁽⁰⁾.

Следует подчеркнуть, что решение (1) удовлетворяет граничным условиям непротекания на поверхности W и всех гранул в том случае, если тензорные коэффициенты $C_{{{{\gamma }_{1}} \cdots {{\gamma }_{n}}}}^{{\left( i \right)}}$ удовлетворяют системе уравнений (2).

Таким образом, задача определения потенциала скорости (1) сводится к нахождению коэффициентов $C_{{{{\gamma }_{1}} \cdots {{\gamma }_{n}}}}^{{\left( i \right)}}$ на основании системы уравнений (2). Для построения корректной математической процедуры решения этой системы примем предположение о малости параметра $\alpha \ll 1$. Отметим, что это не очень жесткое ограничение на параметр α, так как для всех зернистых сред, состоящих из сферических гранул, он всегда удовлетворяет условию $\alpha < \frac{1}{2}$. При условии $\alpha \ll 1~$ все неизвестные функции можно искать в виде рядов по степеням параметра α:

Подставляя разложения (3) в систему (2) и приравнивая члены при одинаковых степенях малого параметра, получим систему рекуррентных соотношений:

где δ_ji – символ Кронекера, квадратные скобки над знаком суммы обозначают целую часть числа.

Полученные рекуррентные соотношения (4) позволяют определить все тензорные коэффициенты $C_{{{{\gamma }_{1}} \cdots {{\gamma }_{m}}}}^{{\left( i \right)\left( k \right)}}$ в аналитическом виде в любом заданном приближении по малому параметру α. В настоящей работе они определены с точностью до O(α⁸). Подстановка полученных таким образом тензорных коэффициентов $C_{{{{\gamma }_{1}} \cdots {{\gamma }_{m}}}}^{{\left( i \right)\left( k \right)}}$ в выражение для потенциала скорости (1) с учетом соотношений (3) в итоге приводит к следующему выражению для продольной компоненты скорости жидкости:

Необходимо отметить, что при решении системы уравнений (4) в настоящей работе учтены члены, описывающие только непосредственный вклад каждой из частиц и соответствующий отклик от стенки в заданный поток. Члены, описывающие вклад частиц за счет парных взаимодействий и взаимодействий более высокого порядка, здесь опущены, так как они несущественны при последующем вычислении осредненных характеристик в рамках настоящей работы. При необходимости получить более точные выражения для тензорных коэффициентов $C_{{{{\gamma }_{1}} \cdots {{\gamma }_{m}}}}^{{\left( i \right)\left( k \right)}}$, а соответственно, и для скорости жидкости (5), включая члены, описывающие многочастичные взаимодействия заданного порядка, достаточно просто учесть все соответствующие функциональные члены при вычислениях по формулам (4).

ВЫЧИСЛЕНИЕ СРЕДНИХ ХАРАКТЕРИСТИК ПОТОКА

Формула (5) позволяет с высокой точностью определять скорость жидкости при наличии в ней любого конечного числа N сферических гранул при различных конфигурациях их взаимного расположения в пространстве. Однако для систем, состоящих из очень большого количества частиц, реализация такой процедуры вычислений становится затруднительной и вряд ли имеет смысл. В этом случае целесообразен переход к осредненному описанию динамики таких структур на основе хорошо известной процедуры осреднения [15] по различным возможным конфигурациям частиц в пространстве. В рамках такой процедуры суммирование известных функций в соотношении (5) фактически заменяется интегрированием по переменной $x_{\gamma }^{{\left( i \right)}}$ при условии, что частицы не пересекаются друг с другом, с точкой, в которой вычисляется средняя скорость, и с заданной поверхностью W.

Примем модель зернистого слоя как совокупность бесконечного числа идентичных сферических гранул радиуса α, центры которых статистически равномерно распределены в слое конечной толщины H = $\frac{{H{\text{*}}}}{L}$, расположенном перпендикулярно границе W (верхний индекс * обозначает соответствующую размерную величину). Это означает, что центры гранул расположены в области $\alpha \, \leqslant \,x_{1}^{{(i)}}\, \leqslant \,(H\, - \,\alpha )\, \cap \,x_{3}^{{(i)}}\, \geqslant \,\alpha $. В этом случае все гранулы находятся в слое толщиной H, не пересекая заданную поверхность W и плоскости x₁ = 0 и x₁ = H (см. рис. 1). При этих условиях весовой функцией в процедуре усреднения [15] будет числовая концентрация гранул в слое, которая в рамках принятых предположений – постоянная величина в объеме осреднения. Это упрощает выкладки и позволяет получить результаты в аналитическом виде. Если при вычислении средних величин ограничиться первым приближением по объемной доле гранул в слое ϕ, то в правой части равенства (5) необходимо учитывать лишь члены, которые описывают прямой вклад частиц и соответствующего отклика от стенки в заданный поток. Взаимодействия более высокого порядка вносят вклад только в коэффициенты при более высоких степенях параметра ϕ, поэтому в формулах (5) они заранее опущены.

Применение процедуры усреднения по ансамблю [15] к первому выражению в правой части равенства (5) при описанных выше условиях приводит к следующему результату для средней величины скорости жидкости внутри слоя в области $2\alpha \leqslant {{x}_{1}} \leqslant (H - 2\alpha )$ в зависимости от нормированных координат $~x = \frac{{{{x}_{1}}}}{\alpha } = \frac{{x_{1}^{*}}}{a}$ и $~z = \frac{{{{x}_{3}}}}{\alpha } = \frac{{x_{3}^{*}}}{a}$:

где $x_{1}^{*}$, $x_{3}^{*}$ и H* – соответствующие размерные переменные.

Вне слоя при $x \geqslant h \cup x \leqslant 0$ и любых значениях $z \geqslant 0$ выражение для усредненного профиля скорости также описывается формулой вида (6), в которой функция $k\left( {x,z} \right) = q\left( {x,z} \right)$.

На стенке (z = 0) усредненная скорость жидкости описывается формулой

Осреднение второго и третьего членов в правой части равенства (5) приводит к громоздким выражениям. При этом их суммарный вклад в итоговый результат для усредненного профиля скорости жидкости, как показывает сравнение всех полученных функций, не превышает величины 1%. В связи с этим выражения для этих функций опущены в итоговых результатах (6) и (7).

Следует отметить, что значения функций k₁(z), k₂(z) и их первых производных совпадают на границе области их определения в точке z = 2.

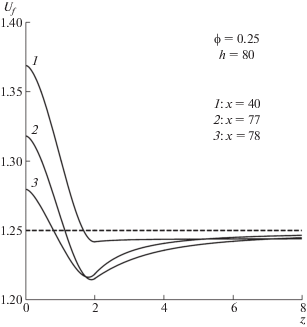
Для иллюстрации полученного результата (6) на рис. 2 приведены графики зависимости усредненной скорости жидкости ${{U}_{f}} = \left\langle {{{U}_{1}}{\text{/}}{{U}^{{\left( 0 \right)}}}} \right\rangle $ от координаты $z = x_{3}^{*}{\text{/}}a$ внутри зернистого слоя в разных его сечениях при заданном значении объемной доли гранул в слое ϕ = 0.25 и толщины слоя h = 80. Как видно из представленных графиков, максимальные значения скорости жидкости достигаются в пристеночной области. По мере удаления от стенки скорости достигают своего минимального значения и затем при $z \to \infty $ выходят на асимптотическое значение ${{U}_{f}} \to 1 + \phi $.

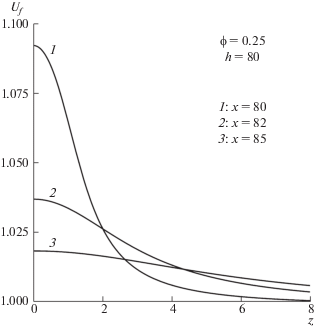
На рис. 3 приведены профили скорости в нескольких сечениях потока вне гранулированного слоя при тех же значениях объемной доли гранул ϕ = 0.25 и толщины слоя h = 80. Максимумы скорости в этом случае также достигаются на стенке. По мере удаления от слоя при $x \to \infty $, как и следовало ожидать, профиль скорости стремится к профилю заданного на бесконечности однородного потока.

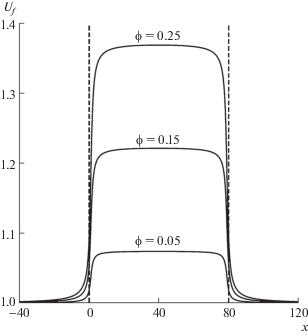
На рис. 4 приведены графики зависимости скорости жидкости на стенке (7) в зависимости от продольной координаты x при разных значениях объемной доли гранул ϕ и заданном значении толщины слоя h = 80. Максимальное значение скорости на стенке реализуется в центральном сечении слоя при x = $\frac{h}{2}$. При большой толщине слоя $h \gg 1$ скорость на стенке в области, близкой к центру слоя, как следует из формулы (7), примерно равна ${{U}_{f}} \approx 1 + \frac{{3\phi }}{2}$.

Следует отметить, что эффект проскальзывания жидкости в пристеночной области получен в предположении статистической равномерности распределения гранул в слое и при условии, что границы слоя образуют плоские (не искривленные) поверхности, перпендикулярные плоскости внешней границы W.

ЗАКЛЮЧЕНИЕ

В работе теоретически исследована задача о течении жидкости сквозь стационарный зернистый слой конечной толщины, расположенный перпендикулярно плоской твердой поверхности, с учетом эффектов коллективного гидродинамического взаимодействия гранул в заданном внешнем однородном потоке. Получено аналитическое решение для усредненного по ансамблю профиля скорости жидкости как вне, так и внутри зернистого слоя с учетом влияния внешней плоской границы. Задача решена в рамках модели идеальной (невязкой) несжимаемой жидкости для несущей сплошной среды в первом приближении по объемной доле гранул в слое при условии их статистически равномерного распределения в пространстве внутри слоя.

Полученный профиль скорости жидкости имеет характерную особенность – на стенке величина скорости жидкости как внутри слоя, так и на выходе из него превышает соответствующее значение скорости вдали от стенки. Следует подчеркнуть, что в отличие от предыдущих исследований эффект проскальзывания жидкости в пристеночной области получен без использования условий о неравномерности распределения гранул вблизи стенки и наличия искривления поверхности зернистого слоя. Это означает, что неоднородность профиля скорости в пристеночной области является, прежде всего, результатом гидродинамического взаимодействия большого количества гранул друг с другом и с внешней границей. А возможное наличие неравномерности распределения гранул в слое и искривление границы слоя способствуют усилению этого эффекта.

Следует отметить, что в записи решения (5) приведены только те функции, которые при осреднении дают вклад в коэффициент перед первой степенью объемной доли гранул в слое ϕ в формулах (6). Для получения решения вида (6) с точностью до более высоких степеней объемной доли ϕ необходимо при решении системы (4) просто учесть все функциональные члены, описывающие взаимодействия частиц соответствующего порядка, и затем применить к ним процедуру осреднения [15]. Это возможно в рамках метода [10, 11], что может быть предметом дальнейших исследований.