Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 13-20

ВВЕДЕНИЕ

Прямые и обратные задачи рассеяния акустических волн на неоднородностях малого волнового размера представляются, на первый взгляд, наиболее простыми. Вместе с тем, их рассмотрение позволяет выявить общие закономерности, частично остающиеся справедливыми и при увеличении размеров рассеивателей. Кроме того, задача рассеяния на малых одиночных неоднородностях имеет практическое значение при моделировании волновых процессов в метаматериалах – искусственных конструкциях, состоящих из элементов с размерами меньше длины волны используемого излучения.

Имеется прямая аналогия между процессом распространения электромагнитной или акустической волны через “классическую” среду, который сопровождается рассеянием этой волны на каждом отдельном атоме, и распространением волны в метаматериале, когда рассеяние происходит на каждом его элементе. Возможность искусственного изменения конструкции таких элементов позволяет управлять волновым процессом на “макроскопическом” уровне и влиять на эффективные упругие параметры метаматериала, значения которых могут существенно выходить за диапазон, характерный для “классических” сред. Среды с такими необычными значениями эффективных упругих параметров, особенности распространения в этих средах акустических волн и возможности использования обнаруженных эффектов на практике активно исследуются разными научными группами в России (например, [1, 2]) и за рубежом (например, одна из последних работ [3]). В представляемой работе использован подход, основанный на выявлении общих соотношений теории рассеяния на “микроскопическом” уровне, т.е. применительно к единственной неоднородности или единственному элементу метаматериала. Для перехода к “макроскопическому” описанию необходимо решение задачи рассеяния с учетом процессов многократного рассеяния между такими элементами. Ее решение с помощью матричного уравнения типа Липпмана–Швингера приведено в [1].

Распространение акустической волны в неоднородной среде можно представить как процесс многократного рассеяния падающей волны неоднородностями. Внутри неоднородностей возникают так называемые вторичные источники, которые порождают рассеянное поле. При этом каждый вторичный источник в каждой точке линейно пропорционален полному полю в данной точке; полное поле равно сумме падающего поля со всеми рассеянными полями, порождаемыми всеми вторичными источниками. Процессы многократного рассеяния имеют место даже внутри неоднородности малого размера. Это приводит к связи между амплитудой и фазой как для монопольной, так и для дипольной компонент рассеянного поля [4, 5]. В представляемой работе данный результат обобщается на случай более высоких порядков мультипольности, в том числе в присутствии поглощения внутри неоднородности. С этой целью применяется широко известный подход, основанный на мультипольном разложении полей [6, 7] и матрицах рассеяния [8].

СВЯЗЬ ПОТОКОВ МОЩНОСТИ ПАДАЮЩЕГО, РАССЕЯННОГО И ПОЛНОГО ПОЛЕЙ

Рассматривается прямая задача рассеяния акустической волны на элементе метаматериала в виде одиночной неоднородности, которая занимает в пространстве область $\Re $. Обсуждается двумерный случай, однако сделанные выводы могут быть обобщены и на трехмерную систему. Можно построить окружность $\Gamma $ с радиусом ${{\ell }_{0}}$ таким образом, чтобы область $\Re $ лежала полностью внутри нее. Начало координат выбирается в центре данной окружности.

Рассматривается монохроматический случай с временнóй зависимостью полей $\sim {\kern 1pt} {\text{exp}}( - i\omega t)$. Пространство вне $\Re $ заполнено фоновой жидкой однородной непоглощающей средой, которая характеризуется плотностью ρ₀ и волновым числом k₀. Первичные источники $\phi ({\mathbf{x}})$ акустического поля, падающего на неоднородность, расположены снаружи окружности Γ, т.е. $\left| {\mathbf{x}} \right| > {{\ell }_{0}}$ для всех x, где $\phi ({\mathbf{x}}) \ne 0$.

Относительно конструкции элемента метаматериала не делается никаких предположений за исключением того, что она не содержит внутренних источников энергии, и ее отклик линеен относительно падающего акустического поля, т.е. рассматриваются пассивные линейные метаматериалы. Физические процессы внутри $\Re $ могут быть, однако, произвольными, не ограничиваясь областью акустики. Например, метаматериал может содержать пьезоакустические преобразователи и подключенные к ним электрические схемы без источников энергии.

Элемент метаматериала можно условно классифицировать как непоглощающий или поглощающий. Для непоглощающего элемента суммарный поток акустической мощности полного поля через контур Γ равен нулю; здесь и далее поток рассматривается по направлению внешней нормали к Γ. При наличии в элементе поглощения данный поток становится отрицателен. Это обстоятельство учитывается ниже в связи с анализом соотношения (8). В силу закона сохранения энергии поток через $\Gamma $ может стать положительным, только если внутри $\Re $ находится активный первичный источник акустического поля, что в настоящей работе не рассматривается.

Первичные источники акустического поля $\phi ({\mathbf{x}})$ создают во всех точках пространства вне $\Re $ акустическое поле с потенциалом $\varphi _{{}}^{ + }({\mathbf{z}})$, который подчиняется уравнению Гельмгольца

Верхний индекс + здесь и далее означает, что рассматриваются те решения уравнения (1), которые удовлетворяют условию излучения Зоммерфельда на бесконечности. Если предположить отсутствие неоднородности, т.е. ситуацию, когда область $\Re $ заполнена той же однородной фоновой средой, то источники $\phi ({\mathbf{x}})$ будут создавать падающее акустическое поле. Это падающее поле будет описываться потенциалом $\varphi _{0}^{ + }({\mathbf{z}})$, который также удовлетворяет уравнению (1), но уже во всем пространстве. Разность $\varphi _{{}}^{ + }({\mathbf{z}})$ и $\varphi _{0}^{ + }({\mathbf{z}})$ определяет потенциал рассеянного поля $\varphi _{{{\text{sc}}}}^{ + }({\mathbf{z}}) = \varphi _{{}}^{ + }({\mathbf{z}}) - \varphi _{0}^{ + }({\mathbf{z}})$.

Поскольку внутри окружности Γ первичные источники отсутствуют, то падающее поле $\varphi _{0}^{ + }({\mathbf{z}})$ можно разложить по функциям Бесселя ${{J}_{n}}(\varsigma )$ n-го порядка в области $\left| {\mathbf{z}} \right| < {{x}_{{\min }}}$, где ${{x}_{{\min }}} = \mathop {\min }\limits_{\phi ({\mathbf{x}}) \ne 0} \left| {\mathbf{x}} \right|$ – минимальное расстояние от начала координат до первичных источников $\phi ({\mathbf{x}}) \ne 0$, причем ${{x}_{{\min }}} > {{\ell }_{0}}$ по построению окружности Γ:

Здесь введен угол $\theta $ полярной системы координат, в которой ${\mathbf{z}} = \left\{ {\left| {\mathbf{z}} \right|,\theta } \right\}$; $\Phi _{n}^{ + }$ – коэффициенты разложения, которые зависят от конфигурации падающего поля. Отдельные члены ряда (2) отвечают за наличие в структуре падающего поля мультипольных компонент, порядок которых задается величиной $\left| n \right|$. Например, член с n = 0 соответствует монопольной компоненте, члены с $n = \pm 1$ – дипольной, члены с $n = \pm 2$ – квадрупольной и т.д. Подход, основанный на мультипольном разложении, широко применяется в акустике [6, 8].

Рассеянное неоднородностью поле $\varphi _{{{\text{sc}}}}^{ + }$ также можно разложить в ряд по мультипольным компонентам. Вне области неоднородности $\Re $ (вторичные источники, создающие рассеянное поле, порождаются именно внутри $\Re $) это разложение можно записать в виде

Данное выражение отличается от (2) наличием функций Ханкеля $H_{n}^{{(\xi )}}(\varsigma )$ n-го порядка ξ-го рода вместо функций Бесселя. Коэффициенты разложения $B_{n}^{ + }$, как и $\Phi _{n}^{ + }$, зависят от конфигурации падающего поля.

Функция Бесселя в выражении (2) может быть представлена как линейная комбинация двух функций Ханкеля:

Это соответствует записи падающего поля в виде суммы двух составляющих:

Здесь

есть поле, “выходящее” из начала координат. Оно распространяется на бесконечность и удовлетворяет условию излучения Зоммерфельда. Наоборот, поле является “входящим”: оно распространяется из бесконечности к началу координат и не удовлетворяет условию излучения Зоммерфельда. Верхний индекс + во всех обозначениях сохранен; он имеет тот смысл, что исходное падающее поле удовлетворяет условию излучения Зоммерфельда.

Сравнивая теперь между собой выражения (3) и (4), можно отметить, что рассеянное поле является полностью “выходящим” из начала координат и, следовательно, из области, ограниченной окружностью $\Gamma $. По физическому смыслу это связано с тем, что вторичные источники находятся только в области $\Re $, которая, в свою очередь, окружена контуром $\Gamma $. Тем самым, поток мощности через $\Gamma $, обусловленный рассеянным полем, положителен. В то же время потоки мощности для составляющих падающего поля $\varphi _{{0 \to }}^{ + }({\mathbf{z}})$ и $\varphi _{{0 \leftarrow }}^{ + }({\mathbf{z}})$ равны по модулю и противоположны по знаку, поскольку в отсутствие неоднородности энергия не теряется.

Выражение для полного поля φ⁺(z) = $\varphi _{0}^{ + }({\mathbf{z}}) + \varphi _{{{\text{sc}}}}^{ + }({\mathbf{z}})$ можно получить, суммируя (3) и (4):

Поток мощности полного поля по направлению внешней нормали ${\mathbf{n}}({\mathbf{z}})$ к окружности $\Gamma $ вычисляется согласно выражению

где $p({\mathbf{z}}) = i\omega {{\rho }_{0}}{{\varphi }^{ + }}({\mathbf{z}})$ и ${\mathbf{v}}({\mathbf{z}}) = \nabla {{\varphi }^{ + }}({\mathbf{z}})$ – поля акустического давления и колебательной скорости; верхний символ * означает комплексное сопряжение. Поскольку Γ – окружность с центром в начале координат, то при вычислении $W_{\Gamma }^{ + }$ удобно учитывать, что ${\mathbf{v}}({\mathbf{z}}){\mathbf{n}}({\mathbf{z}}) = \frac{{\partial {{\varphi }^{ + }}({\mathbf{z}})}}{{\partial \left| {\mathbf{z}} \right|}}$, $\left| {\mathbf{z}} \right| = {{\ell }_{0}}$, $d\Gamma = {{\ell }_{0}}d\theta $, причем

Тогда с помощью (5) получается следующее выражение:

Аналогичное соотношение получается с помощью (4) для потока мощности $W_{{0,\,\Gamma }}^{ + }$ падающего поля $\varphi _{0}^{ + }({\mathbf{z}})$:

С целью упрощения записи вводятся составляющие потока мощности $W_{{0,n,\Gamma \to }}^{ + }$ для “выходящего” падающего поля и потока $W_{{0,n,\Gamma \leftarrow }}^{ + }$ для “входящего” падающего поля n-й мультипольности:

причем $W_{{0,n,\Gamma \to }}^{ + } = - W_{{0,n,\Gamma \leftarrow }}^{ + }$. Тогда из (7) следует, что а выражение (6) приобретает вид

Поток мощности $W_{\Gamma }^{ + }$ может быть либо равным нулю (случай непоглощающей неоднородности), либо меньше нуля (случай поглощающей неоднородности – тогда составляющая потока мощности, выходящая из области неоднородности $\Re $, становится по абсолютной величине меньше входящей составляющей). Таким образом, всегда $W_{\Gamma }^{ + } \leqslant 0$.

С помощью введенных обозначений $W_{{0,n,\Gamma \to }}^{ + }$ можно по аналогии записать поток мощности рассеянного поля

где ${{p}_{{{\text{sc}}}}}({\mathbf{z}}) = i\omega {{\rho }_{0}}\varphi _{{{\text{sc}}}}^{ + }({\mathbf{z}})$ и ${\mathbf{v}}_{{{\text{sc}}}}^{{}}({\mathbf{z}}) = \nabla \varphi _{{{\text{sc}}}}^{ + }({\mathbf{z}})$: где $W_{{{\text{sc}},n,\Gamma }}^{ + } = \frac{{{\text{|}}B_{n}^{ + }{{{\text{|}}}^{2}}}}{4}W_{{0,n,\Gamma \to }}^{ + }$.

Поскольку рассматривается задача, линейная относительно падающего поля, и значения $B_{n}^{ + }$ определяются падающим полем, то между ними и коэффициентами $\Phi _{n}^{ + }$ существует линейная связь: $B_{n}^{ + } = \sum\limits_{m = - \infty }^\infty {{{\chi }_{{mn}}}\Phi _{m}^{ + }} $, где χ_mn – коэффициенты связи, представляющие собой элементы некоторой матрицы $\hat {\chi }$. Такие матрицы были введены в [8]. В ряде случаев (например, слабоконтрастная неоднородность малого волнового размера или цилиндрически симметричная неоднородность) матрица $\hat {\chi }$ становится диагональной, и данная связь упрощается: $B_{n}^{ + } = \beta _{n}^{ + }\Phi _{n}^{ + }$. Величины $\beta _{n}^{ + } \equiv {{\chi }_{{nn}}}$ называются коэффициентами рассеяния [4, 5]. Тогда, с учетом того, что условие $W_{\Gamma }^{ + } \leqslant 0$ и соотношение (8) выполнены для любой конфигурации первичных источников, и, следовательно, для произвольного выбора коэффициентов $\Phi _{n}^{ + }$, данное условие $W_{\Gamma }^{ + } \leqslant 0$ сводится к набору условий $W_{{n,\Gamma }}^{ + } \leqslant 0$ при всех n. Это, в свою очередь, приводит, с учетом (8), к неравенству

откуда

Если поглощения в $\Re $ нет, но неравенства (10) переходят в равенства. Для чисто монопольной непоглощающей неоднородности малого волнового размера эти результаты были получены в [4], а для монопольно-дипольной – в [5].

Если представить каждый комплексный коэффициент рассеяния в виде $\beta _{n}^{ + } = \left| {\beta _{n}^{ + }} \right|\exp \left( {i{{\psi }_{n}}} \right)$, т.е. ввести его абсолютную величину $\left| {\beta _{n}^{ + }} \right|$ и фазу ${{\psi }_{n}}$, то (10) будет эквивалентно соотношению

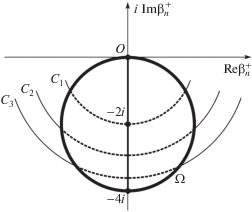
Множество допустимых значений $\beta _{n}^{ + }$, удовлетворяющих условию (11), образует на комплексной области круг с центром в точке –2i и радиусом 2 [9], а если поглощения нет – то его границу Ω (рис. 1). Такое представление позволяет классифицировать рассеиватели и наглядно отображать различные их свойства. Поскольку набор коэффициентов $\beta _{n}^{ + }$ определяет рассеянное поле, то знания этих коэффициентов достаточно, чтобы полностью охарактеризовать рассеиватель.

ОБРАТНАЯ ЗАДАЧА РАССЕЯНИЯ ДЛЯ РАССЕИВАТЕЛЕЙ МОНОПОЛЬНОГО ТИПА

Ниже будет рассмотрен наиболее простой случай, когда рассеянное поле является монопольным. Это характерно, например, для чисто рефракционных акустических неоднородностей (т.е. отличающихся от фоновой среды скоростью звука, но не плотностью) малого волнового размера. Тогда для описания рассеянного поля достаточно единственного коэффициента $\beta _{0}^{ + }$ (n = 0).

Согласно (9), при n = 0 и $B_{0}^{ + } = \beta _{0}^{ + }\Phi _{0}^{ + }$ значение $\left| {\beta _{0}^{ + }} \right|$ определяет величину потока мощности рассеянного поля. Коэффициенты рассеяния $\beta _{0}^{ + }$, которые соответствуют одинаковому фиксированному потоку мощности рассеянного поля (9), образуют на комплексной плоскости дугу окружности радиуса $\left| {\beta _{0}^{ + }} \right|$ с центром в начале координат (для примера на рис. 1 изображены дуги окружностей ${{C}_{1}}$, ${{C}_{2}}$ и ${{C}_{3}}$). Тем самым, поток мощности рассеянного поля является наиболее слабым при $\beta _{0}^{ + } \approx 0$ и достигает максимума при $\beta _{0}^{ + } = - 4i$.

С другой стороны, при решении прямых и обратных задач рассеяния существует понятие силы рассеивателя, т.е. рассеивающей неоднородности [10, 11]. Для слабых рассеивателей ${\text{|}}\varphi _{{{\text{sc}}}}^{ + }({\mathbf{z}}){\text{|}} \ll {\text{|}}\varphi _{{\text{0}}}^{ + }({\mathbf{z}}){\text{|}}$, $\forall {\mathbf{z}} \in \Re $; тогда полное поле $\varphi _{{}}^{ + }({\mathbf{z}}) \approx \varphi _{{\text{0}}}^{ + }({\mathbf{z}})$ при ${\mathbf{z}} \in \Re $, т.е. внутри неоднородности $\Re $. Этот факт позволяет не учитывать процессы многократного рассеяния, благодаря чему решение задач существенно облегчается. Для рассеивателей средней силы ${\text{|}}\varphi _{{{\text{sc}}}}^{ + }({\mathbf{z}}){\text{|}} \leqslant {\text{|}}\varphi _{{\text{0}}}^{ + }({\mathbf{z}}){\text{|}}$, $\forall {\mathbf{z}} \in \Re $; тогда можно ограничиться конечным числом актов многократного рассеяния и соответствующим числом членов ряда Борна–Неймана, в котором рассеянное поле выражается (интегральным образом) через падающее поле и функцию рассеивателя с помощью функции Грина фоновой среды. Для сильных рассеивателей (в том числе включающих резонансные элементы или элементы, фокусирующие поле) существуют точки ${\mathbf{z}} \in \Re $, в которых ${\text{|}}\varphi _{{{\text{sc}}}}^{ + }({\mathbf{z}}){\text{|}} > {\text{|}}\varphi _{{\text{0}}}^{ + }({\mathbf{z}}){\text{|}}$. Тогда решение обратной задачи рассеяния становится наиболее трудным с точки зрения обеспечения единственности и устойчивости решения [10, 11], и требуется привлечение специальных мер для обеспечения приемлемого результата.

Хотя значение ${\text{|}}\beta _{0}^{ + }{\text{|}}$ существенно влияет на силу рассеивателя, эта связь между ${\text{|}}\beta _{0}^{ + }{\text{|}}$ и силой рассеивателя не является однозначной. В [9] этот вопрос изучался применительно к непоглощающим рассеивателям, значения $\beta _{0}^{ + }$ которых принадлежат окружности $\Omega $ (рис. 1). Окружность $\Omega $ можно разбить на два семейства точек: семейству I соответствует правая ее часть ($\operatorname{Re} \beta _{0}^{ + } > 0$) и семейству II соответствует левая ее часть ($\operatorname{Re} \beta _{0}^{ + } < 0$). Таким образом, в отсутствие поглощения для каждого фиксированного значения ${\text{|}}\beta _{0}^{ + }{\text{|}}$ существует по одному рассеивателю из каждого семейства – например, на рис. 1 это точки пересечения каждой из окружностей ${{C}_{1}}$, ${{C}_{2}}$, ${{C}_{3}}$ с окружностью $\Omega $. Рассеиватели двух семейств при одинаковом $\left| {\beta _{0}^{ + }} \right|$ отличаются фазой ${{\psi }_{0}}$ коэффициента $\beta _{0}^{ + }$ за счет разных физических свойств этих рассеивателей. Так, если рассеиватели представлены некоторой средой, отличающейся от фоновой среды только скоростью звука, то для семейства I средняя скорость звука в рассеивателе оказывается больше фоновой, а для семейства II – меньше [9]. В итоге, в первом случае происходит дефокусировка, а во втором – фокусировка падающего акустического поля внутри рассеивателя. Как следствие, при фиксированном ${\text{|}}\beta _{0}^{ + }{\text{|}}$ сила рассеивателя семейства II больше, чем сила рассеивателя семейства I.

Задача восстановления рассеивателя (так называемая обратная задача) заключается в следующем. Пусть в каждой точке пространства z акустический потенциал $\varphi _{{}}^{ + }({\mathbf{z}})$ удовлетворяет уравнению Гельмгольца ${{\nabla }^{2}}\varphi _{{}}^{ + }({\mathbf{z}}) + k_{{}}^{2}({\mathbf{z}})\varphi _{{}}^{ + }({\mathbf{z}}) = \phi ({\mathbf{z}})$, где k(z) – волновое число, причем $k({\mathbf{z}}) \equiv k_{0}^{{}}$ при ${\mathbf{z}} \notin \Re $. Это уравнение можно преобразовать к виду ${{\nabla }^{2}}\varphi _{{}}^{ + }({\mathbf{z}}) + k_{0}^{2}\varphi _{{}}^{ + }({\mathbf{z}})$ = = ϕ(z) + ${v}({\mathbf{z}})\varphi _{{}}^{ + }({\mathbf{z}})$, где ${v}({\mathbf{z}}) = k_{0}^{2} - k_{{}}^{2}({\mathbf{z}})$ – функция рассеивателя. Именно функция рассеивателя ответственна за возникновение вторичных источников ${v}({\mathbf{z}})\varphi _{{}}^{ + }({\mathbf{z}})$ в ответ на полное поле $\varphi _{{}}^{ + }({\mathbf{z}})$. Целью обратной задачи является восстановление оценки ${\hat {v}}({\mathbf{z}})$ функции ${v}({\mathbf{z}})$ или восстановление пространственного спектра ${\hat {\tilde {v}}}({\mathbf{\xi }})\, \equiv \,\int\limits_\Re ^{} {{\hat {v}}({\mathbf{z}})\exp ( - i{\mathbf{\xi z}})} d{\mathbf{z}}$ этой оценки (где ξ – вектор пространственной частоты) на основе значений поля, измеренных в эксперименте или рассчитанных при численном моделировании на окружности ${\mathbf{z}} \in \Gamma $.

Для восстановления пространственного распределения оценки ${\hat {v}}({\mathbf{z}})$ двумерных рассеивателей с малым волновым размером и заданным монопольным коэффициентом рассеяния использовался монохроматический алгоритм Новикова [12–14]. Это один из лучших современных методов, позволяющий эффективно решать обратную задачу рассеяния без итераций. Оказалось, что начиная с некоторого минимального значения $\left| {\beta _{0}^{ + }} \right|$ и выше (это минимальное значение отличается для рассеивателей семейств I и II), процедура восстановления сопровождается заметным ростом ошибок в итоговой оценке ${\hat {v}}({\mathbf{z}})$. В частности, для семейства II это проявлялось в том, что пространственный спектр ${\hat {\tilde {v}}}({\mathbf{\xi }})$ восстановленного рассеивателя становился таким широким, что область его локализации существенно выходила за пределы круга $\left| {\mathbf{\xi }} \right| \leqslant 2{{k}_{0}}$.

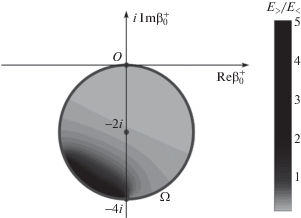
В общем случае, присутствие в пространственном спектре вторичных источников ${v}({\mathbf{z}})\varphi _{{}}^{ + }({\mathbf{z}})$ высокочастотных пространственно-спектральных компонент, соответствующих значениям ξ вне круга радиуса 2k₀, выступает в роли помехи при решении обратной задачи независимо от конкретного алгоритма ее решения [10]. С физической точки зрения это обстоятельство взаимосвязано с акустическим аналогом явления дифракционного предела – невозможностью устойчиво восстановить в пространственном спектре вторичных источников пространственные детали мельче четверти длины волны. Тем самым, если в результате восстановления в пространственном спектре получаемой оценки вторичных источников возникают упомянутые высокочастотные компоненты, то они заведомо являются ложными. Они обусловлены помехами разного типа и неустойчивостью процесса восстановления, которая проявляется тем сильнее, чем сильнее рассеиватель. С другой стороны, в алгоритме Новикова удобнее контролировать качество восстановления не вторичных источников, а оценки функции рассеивателя ${\hat {v}}({\mathbf{z}})$ и область локализации ее пространственного спектра ${\hat {\tilde {v}}}({\mathbf{\xi }})$. Процессы многократного рассеяния волн внутри области $\Re $ приводят к расширению области локализации пространственного спектра вторичных источников по сравнению с пространственным спектром рассеивателя [10, 15]. Поэтому не только пространственные компоненты с $\left| {\mathbf{\xi }} \right| > 2{{k}_{0}}$, присутствующие в ${\hat {\tilde {v}}}({\mathbf{\xi }})$, будут ложными, но и часть пространственных компонент с $\left| {\mathbf{\xi }} \right| \leqslant 2{{k}_{0}}$ могут оказаться ложными или восстановленными с заметной погрешностью.

Тем самым, расширение области локализации пространственного спектра ${\hat {\tilde {v}}}({\mathbf{\xi }})$ восстановленного рассеивателя ${\hat {v}}({\mathbf{z}})$ за пределы круга радиуса 2k₀ можно использовать в качестве нестрогого (“минимального”) критерия качества решения обратной задачи на практике. С этой целью можно вычислить энергию восстановленного пространственного спектра

и энергию

Значение ${{E}_{ > }} \ne 0$ свидетельствует о заведомо присутствующей ошибке восстановления, которую можно охарактеризовать численно отношением ${{{{E}_{ > }}} \mathord{\left/ {\vphantom {{{{E}_{ > }}} {{{E}_{ < }}}}} \right. \kern-0em} {{{E}_{ < }}}}$. Это отношение, рассчитанное по результатам восстановления ${\hat {v}}({\mathbf{z}})$ для всех значений истинного коэффициента рассеяния $\beta _{0}^{ + }$, изображено на рис. 2. Здесь четко видна несимметричность: наибольшие ошибки возникают в левой нижней части круга, соответствующей сильным рассеивателям семейства II, в то время как в области справа, симметричной относительно мнимой оси координат, ложное уширение пространственного спектра ${\hat {\tilde {v}}}({\mathbf{\xi }})$ незначительно.

ЗАКЛЮЧЕНИЕ

Таким образом, прямая и обратная задачи рассеяния на одиночной неоднородности обладают рядом особенностей. Вторичные источники, возникающие при падении исходного поля на неоднородность, создают рассеянное поле с компонентами разных порядков мультипольности. Эти компоненты связаны с мультипольными компонентами исходного падающего поля с помощью матрицы, у которой в ряде случаев являются ненулевыми только диагональные элементы – коэффициенты рассеяния. Закон сохранения энергии накладывает ограничения на значения этих коэффициентов. В случае неоднородности без поглощения они образуют на комплексной плоскости окружность $\Omega $, а в присутствии поглощения – ее внутреннюю часть. Физически этот эффект ограничения значений реализуется посредством процессов многократного рассеяния внутри неоднородности. Процессы многократного рассеяния необходимо учитывать даже в случае неоднородности малого волнового размера и в пределе – при рассмотрении δ-образной неоднородности [4].

С точки зрения решения обратной задачи рассеяния для монопольных неоднородностей с коэффициентами рассеяния, лежащими внутри Ω, можно выделить области значений $\beta _{0}^{ + }$, соответствующие различному качеству восстановления. При этом неоднородности с одинаковой амплитудой ${\text{|}}\beta _{0}^{ + }{\text{|}}$, но разной фазой коэффициента рассеяния могут обладать существенно разными свойствами. Это связано с тем, что левая половина области внутри Ω соответствует неоднородностям, которые характеризуются в среднем меньшей скоростью звука по сравнению с фоновым значением, а правая половина – большей скоростью звука. Поэтому для неоднородностей в левой половине области внутри Ω происходит фокусировка поля, что увеличивает их силу, затрудняет восстановление и вызывает ошибки.