Доклады Российской академии наук. Физика, технические науки, 2020, T. 494, № 1, стр. 69-74

ПЛОСКИЕ ДВИЖЕНИЯ ТЕЛА, УПРАВЛЯЕМОГО ПРИ ПОМОЩИ ПОДВИЖНОЙ МАССЫ

Академик РАН Ф. Л. Черноусько^1, *

¹ Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия

Поступила в редакцию 29.06.2020
После доработки 29.06.2020
Принята к публикации 01.07.2020

DOI: 10.31857/S2686740020050065

Аннотация

Рассматриваются плоские движения твердого тела, управляемого при помощи вспомогательной точечной подвижной массы. Между телом и горизонтальной плоскостью действуют силы сухого трения. Показано, что при определенных условиях тело может быть переведено в любое состояние на плоскости, так что система вполне управляема.

Ключевые слова: динамика твердого тела, сухое трение, управление, мобильные роботы

Проблемы динамики тела, несущего подвижные массы, актуальны в связи с созданием мобильных роботов, не имеющих внешних подвижных элементов [1–3]. Эти роботы, называемые капсульными, могут быть герметичными и способны перемещаться в агрессивных и ранимых средах, в трубах, внутри живых организмов и выполнять операции инспекции, мониторинга, диагностики и др. Ряд работ посвящен одномерным поступательным движениям этих систем при наличии сил внешнего сопротивления, построены оптимальные режимы движения [4, 5].

Двумерные плоские движения, важные для построения поворотов мобильных роботов, исследованы в работах [6, 7] при наличии сил сухого трения между телом и горизонтальной плоскостью. В этих работах предполагается, что внутренние подвижные массы имеют две степени свободы относительно несущего тела и состоят из ротора и материальной точки.

В данной работе, как в [8], рассматривается случай одной подвижной точки, управляющей плоским движением тела при наличии сил сухого трения между телом и плоскостью. Показано, что при довольно общих предположениях система вполне управляема. Она может быть переведена в любое состояние на плоскости даже в том случае, когда точка имеет лишь одну степень свободы и перемещается относительно тела по некоторой кривой.

МЕХАНИЧЕСКАЯ СИСТЕМА

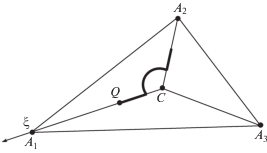
Система состоит из твердого тела Р массы M и материальной точки Q массы m (рис. 1). Обозначим через С центр масс тела Р и предположим, что одна из главных центральных осей инерции тела направлена вертикально. Тело скользит по неподвижной горизонтальной плоскости OXY в поле тяжести, опираясь на три точки A_i, $i = 1,2,3$. В случае трех опорных точек твердое тело является статически определимой системой, поэтому нормальные реакции N_i в точках А_i определяются однозначно. Силы сухого трения F_i, действующие на тело Р в точках А_i, подчиняются закону Кулона с коэффициентом трения f. Если ${{v}_{i}}$ – скорость точки опоры А_i, то силы трения определяются соотноше-ниями

(1)

$\begin{gathered} {{F}_{i}} = - \frac{{f{\text{ }}{{N}_{i}}{{v}_{i}}}}{{{{{v}}_{i}}}}{\text{,}}\quad {\text{если}}\quad {{{v}}_{i}} = \left| {{{v}_{i}}} \right| > 0, \\ \left| {{{F}_{i}}} \right| \leqslant f{{N}_{i}}{\text{,}}\quad {\text{если}}\quad {{{v}}_{i}} = 0,\quad i = 1,2,3. \\ \end{gathered} $

Рис. 1.

Механическая система.

Материальная точка Q снабжена актюатором и движется относительно тела Р по горизонтальной плоскости, параллельной плоскости OXY. Точка Q взаимодействует с телом Р и не взаимодействует с неподвижной плоскостью OXY. Таким образом, единственными внешними силами, действующими на систему $P + Q$, являются силы тяжести и силы реакции ${{N}_{i}}$ и ${{F}_{i}}$ в опорах A_i, $i = 1,2,3$.

Будем предполагать для упрощения, что расстояния от центра масс С и от горизонтальной плоскости, по которой движется точка Q, до неподвижной плоскости OXY малы по сравнению с горизонтальными линейными размерами тела Р. Предполагаем также, что проекции точек С и Q на плоскость OXY лежат внутри треугольника ${{A}_{1}}{{A}_{2}}{{A}_{3}}$. Эти предположения обеспечивают положительность нормальных реакций N_i и исключают “опрокидывание” тела Р. Поэтому будем считать, что центр масс С и точка Q движутся в плоскости OXY.

УРАВНЕНИЯ ДВИЖЕНИЯ

Обозначим через ${{v}_{с}}$ и ${{v}_{Q}}$ скорости точек C и Q относительно плоскости OXY, а через F силу, приложенную к точке Q со стороны актюатора. Тогда к телу Р в точке Q приложена сила (–F), и уравнение движения центра масс С тела Р имеет вид

(2)

$M{{\dot {v}}_{c}} = \sum\limits_{i = 1}^3 {{{F}_{i}} - F} ,$

где силы ${{F}_{i}}$ определены формулами (1). Точками обозначаются производные по времени t. Уравнение движения точки Q

$m{{\dot {v}}_{Q}} = F$

запишем в развернутом виде, представляя ее абсолютное ускорение в виде суммы переносного, кориолисова и относительного ускорений:

(3)

$m\left[ {{{{\dot {v}}}_{c}} + \dot {\omega } \times r + \omega \times (\omega \times r) + 2\omega \times v + w} \right] = F.$

Здесь $r = \overline {CQ} $ – радиус-вектор точки Q относительно центра масс С тела Р, v и w – относительные скорость и ускорение точки Q относительно тела Р, $\omega = \omega k$ – угловая скорость тела Р, k – единичный вектор, направленный вертикально вверх.

Составим еще уравнение моментов для тела Р вокруг вертикальной оси, проходящей через его центр С. Обозначая через J момент инерции тела P относительно этой оси, получим

(4)

$J\dot {\omega } = \left( {\sum\limits_{i = 1}^3 {\overline {C{{A}_{i}}} \times {{F}_{i}} - r \times F} } \right)k.$

На основе уравнений движения (2)–(4) рассмотрим некоторые типы возможных движений системы P + Q. Будем считать, что актюатор способен создать достаточно большое по величине и произвольное по направлению относительное ускорение w точки Q, которое играет роль управляющего воздействия.

МЕДЛЕННЫЕ И ОСТАТОЧНЫЕ ДВИЖЕНИЯ

Если точка Q движется относительно неподвижного тела Р с достаточно малым по величине относительным ускорением, то тело Р сохраняет состояние покоя из-за сил сухого трения, которые удерживают его в этом состоянии. Этими медленными движениями можно пользоваться для того, чтобы переместить точку Q из начального состояния покоя в произвольное терминальное состояние покоя относительно неподвижного тела Р.

Если точка Q неподвижна относительно тела Р, то система P + Q представляет собой твердое тело массы $M + m$, которое под действием сил сухого трения остановится за конечное время. Такие движения будем называть остаточными.

ПРЯМОЛИНЕЙНЫЕ ДВИЖЕНИЯ

Пусть в начальный момент времени t = 0 вся система P + Q покоится и точка Q находится на одной из прямых $C{{A}_{i}}$, $i = 1,\;2,\;3$, например, на прямой $C{{A}_{1}}$ (рис. 1). Покажем, что если точка Q движется прямолинейно вдоль прямой $C{{A}_{1}}$, то реализуется поступательное движение тела Р вдоль этой же прямой. Для этого достаточно убедиться, что все уравнения (2)–(4) удовлетворяются при таком движении.

При поступательном движении тела Р скорости ${{v}_{i}}$ всех его точек опоры равны ${{v}_{c}}$ и параллельны прямой $C{{A}_{1}}$. Согласно уравнениям (1), все силы трения F_i также параллельны прямой $C{{A}_{1}}$ и направлены против скорости ${{v}_{c}}$. Поэтому векторное уравнение (2) сводится к скалярному уравнению

(5)

$M{{{\dot {v}}}_{c}} = - f\sum\limits_{i = 1}^3 {{{N}_{i}}q({{{v}}_{с}})} - F,$

где введено следующее обозначение, отражающее закон Кулона (1):

(6)

$\begin{gathered} q({{{v}}_{c}}) = \operatorname{sgn} {{{v}}_{c}}\quad {\text{при}}\quad {{{v}}_{c}} \ne 0, \\ \left| {q({{{v}}_{c}})} \right| \leqslant 1\quad {\text{при}}\quad {{{v}}_{c}} = 0. \\ \end{gathered} $

Сумма всех нормальных реакций равна весу системы P + Q, т.е.

(7)

${{N}_{1}} + {{N}_{2}} + {{N}_{3}} = (M + m)g,$

где g – ускорение силы тяжести. Уравнение (5) с учетом равенства (7) примет вид

(8)

$M{{{\dot {v}}}_{c}} = - f(M + m)gq({{{v}}_{c}}) - F.$

Уравнение (3) для поступательного движения тела P, т.е. при ω = 0, приводится к скалярному уравнению

(9)

$m({{{\dot {v}}}_{c}} + w) = F.$

Исключая F из уравнений (8) и (9) и вводя обозначение

(10)

$\mu = \frac{m}{{M + m}},$

получим

(11)

${{{\dot {v}}}_{c}} = - \mu w - fgq({{{v}}_{c}}).$

Обратимся к уравнению (4) при ω = 0. Моменты относительно точки С сил ${{F}_{1}}$ и F, направленных по прямой $C{{A}_{1}}$, равны нулю, а моменты сил ${{F}_{2}}$ и ${{F}_{3}}$ уравновешивают друг друга, так как плечи этих сил, как и сил ${{N}_{2}}$ и ${{N}_{3}}$, обратно пропорциональны величинам сил.

Таким образом, все уравнения (2)–(4) удовлетворяются при прямолинейном движении точки Q по прямой $C{{A}_{1}}$ и поступательном движении тела Р вдоль этой прямой. Эти уравнения приводятся к одному динамическому уравнению (11). Имеют место также кинематические соотношения

(12)

$\dot {\xi } = {v},\quad {\dot {v}} = w,\quad \dot {x} = {{{v}}_{c}},$

где ξ – смещение точки Q по прямой $C{{A}_{1}}$ (рис. 1), отсчитываемое от начального положения этой точки, ${v}$ – ее скорость относительно тела Р, х – абсолютное смещение центра масс С тела Р вдоль направления $C{{A}_{1}}$. Начальные условия для уравнений (11) и (12) имеют вид

(13)

$\xi (0) = {v}(0) = x(0) = {{{v}}_{c}}(0) = 0.$

Зададим управление в виде кусочно-постоянного относительного ускорения

(14)

$\begin{gathered} w(t) = {{w}_{1}}\quad {\text{при}}\quad {\text{ }}t \in (0,{\text{ }}{{t}_{1}}), \\ w(t) = - {{w}_{2}}\quad {\text{при}}\quad {\text{ }}t \in ({{t}_{1}},{\text{ }}{{t}_{2}}),\quad 0 < {{t}_{1}} < {{t}_{2}}, \\ \end{gathered} $

где постоянные ${{w}_{1}}$ и ${{w}_{2}}$ удовлетворяют ограничениям

(15)

${{w}_{1}} > fg{{\mu }^{{ - 1}}},\quad 0 < {{w}_{2}} \leqslant fg{{\mu }^{{ - 1}}}.$

Интегрируя второе уравнение (12) при w(t), определяемом (14), при начальных условиях (13), получим

(16)

$\begin{gathered} {v}(t) = {{w}_{1}}t\quad {\text{при}}\quad t \in (0,{\text{ }}{{t}_{1}}), \\ {v}(t) = {{w}_{1}}{{t}_{1}} - {{w}_{2}}(t - {{t}_{1}})\quad {\text{при}}\quad t \in ({{t}_{1}},{\text{ }}{{t}_{2}}). \\ \end{gathered} $

Потребуем, чтобы относительная скорость ${v}$(t) обращалась в нуль при $t = {{t}_{2}}$. Получим

(17)

${{t}_{2}} = \frac{{({{w}_{1}} + {{w}_{2}}){{t}_{1}}}}{{{{w}_{2}}}}.$

Проинтегрируем первое уравнение (12) при ${v}$(t) из (16) и начальных условиях (13). В результате, используя также формулу (17), определим полное относительное смещение точки Q:

(18)

$\Delta \xi = \xi ({{t}_{2}}) = \frac{{{{w}_{1}}({{w}_{1}} + {{w}_{2}})t_{1}^{2}}}{{2{{\omega }_{2}}}}.$

Обращаясь к уравнению (11), будем исходить из того, что неравенство ${{{v}}_{c}} \leqslant 0$ имеет место при всех $t \in (0,{{t}_{2}})$. Интегрируя уравнение (11) при w(t), определяемом равенствами (14), и при начальных условиях (13), получим

(19)

$\begin{gathered} {{{v}}_{c}}(t) = - \,(\mu {{w}_{1}} - fg)t\quad {\text{при}}\quad t \in (0,{{t}_{1}}), \\ {{{v}}_{c}}(t) = - \,(\mu {{w}_{1}}\, - \,fg)t\, + \,(\mu {{w}_{2}}\, + \,fg)(t\, - \,{{t}_{1}})\,\,\,{\text{при}}\,\,\,t\, > \,{{t}_{1}}. \\ \end{gathered} $

Из последнего равенства (19) следует, что ${{{v}}_{c}}(t)$ обращается в нуль при $t = {{t}_{ * }}$, где

(20)

${{t}_{*}} = \mu ({{w}_{1}} + {{w}_{2}}){{t}_{1}}{{(\mu {{w}_{2}} + fg)}^{{ - 1}}}.$

Сравнивая равенства (17) и (20), можно убедиться в том, что ${{t}_{*}} \in ({{t}_{1}},{\text{ }}{{t}_{2}})$. При $t \in ({{t}_{ * }},{\text{ }}{{t}_{2}})$ в силу (15) имеем неравенство

(21)

$\left| {w(t)} \right| \leqslant fg{{\mu }^{{ - 1}}}.$

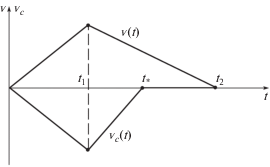
При условии (21) второе слагаемое в правой части уравнения (11) компенсирует, в силу свойства (6), первое слагаемое, так что имеем ${{{\dot {v}}}_{c}} = 0$ и, следовательно, ${{{v}}_{c}} \equiv 0$ при $t \in ({{t}_{*}},{\text{ }}{{t}_{2}})$. Зависимости ${v}$(t) и ${{{v}}_{c}}(t)$ на интервале $(0,\;{{t}_{2}})$ показаны на рис. 2. Определим еще полное перемещение тела Р, которое достигается при $t = {{t}_{*}}$. Используя уравнение (12) и начальные условия (13), получим

(22)

$\Delta x = \frac{{ - \mu ({{w}_{1}} + {{w}_{2}})(\mu {{w}_{1}} - fg){{{(\mu {{w}_{2}} + fg)}}^{{ - 1}}}t_{1}^{2}}}{2}.$

Рис. 2.

Функции ${v}$(t) и ${{{v}}_{c}}$(t).

Управление w(t), заданное соотношениями (14) и (15), обеспечивает относительное перемещение точки Q по прямой $C{{A}_{1}}$ на величину (18) и одновременно поступательное перемещение тела Р на величину (22). В начале и в конце движения вся система находится в состоянии покоя. Оба перемещения противоположны по знаку и пропорциональны $t_{1}^{2}$. Поэтому эти перемещения могут быть как угодно малыми. После окончания маневра перемещения, т.е. при $t > {{t}_{2}}$, точка Q может быть при помощи медленного движения с ускорением, удовлетворяющим условию (21), переведена в начальную точку ξ = 0 при неподвижном теле Р. Повторяя описанный маневр нужное число раз и подбирая каждый раз его параметры ${{w}_{1}}$, ${{w}_{2}}$ и ${{t}_{1}}$, можно осуществить перемещение тела P на произвольное расстояние вдоль направления $C{{A}_{1}}$ за конечное время. При этом точка Q может двигаться по любому конечному отрезку вдоль прямой $C{{A}_{1}}$. Вопросы оптимизации движений применительно к уравнению (11) рассмотрены в работах [4, 5, 8], где построены движения, имеющие максимальную среднюю скорость.

ВРАЩЕНИЕ

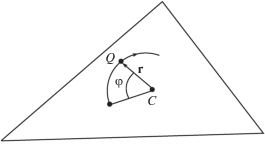
Рассмотрим движение точки Q по окружности S радиуса а вокруг точки C (рис. 3). Вектор ${{\dot {v}}_{c}}$ из уравнения (2) подставим в (3), найдем вектор F и подставим его в уравнение (4). После преобразований получим

(23)

$\begin{gathered} (J + \mu M{{r}^{2}})\dot {\omega } = \\ = \;\left\{ {\sum\limits_{i = 1}^3 {(\overline {C{{A}_{i}}} - \mu r) \times {{F}_{i}} - \mu M\left[ {2r\, \times \,(\omega \, \times \,v)\, + \,r\, \times \,w} \right]} } \right\}k, \\ \end{gathered} $

где μ введено соотношением (10). Обозначим через φ и $\Omega = \dot {\varphi }$ угловую координату и угловую скорость точки Q при ее движении по окружности S. Относительная скорость v точки Q направлена перпендикулярно r и равна по величине ${v} = a\Omega $, а ее относительное ускорение слагается из касательного ускорения ${\dot {v}} = a\dot {\Omega }$, направленного перпендикулярно вектору r, и нормального ускорения, равного ${{{v}}^{2}}{\text{/}}a$ и направленного против r. В результате упрощений уравнение (23) приводится к виду

(24)

$\dot {\omega } = - {{\mu }_{1}}z + R,$

где введены обозначения

(25)

$\begin{gathered} {{\mu }_{1}} = \mu M{{a}^{2}}{{(J + \mu M{{a}^{2}})}^{{ - 1}}}, \\ R = \left[ {\sum\limits_{i = 1}^3 {(\overline {C{{A}_{i}}} - \mu r) \times {{F}_{i}}} } \right]k{{(J + \mu M{{a}^{2}})}^{{ - 1}}}. \\ \end{gathered} $

Рис. 3.

Вращение.

Угловое ускорение $z = \dot {\Omega }$ играет роль управляющего воздействия. Обозначим через ψ угол поворота тела P относительно неподвижной плоскости OXY и запишем кинематические уравнения

(26)

$\dot {\varphi } = \Omega ,\quad \dot {\Omega } = z,\quad \dot {\psi } = \omega $

и начальные условия

(27)

$\varphi (0) = \Omega (0) = \psi (0) = \omega (0) = 0,$

подобные уравнениям (12) и условиям (13) для прямолинейных движений. Уравнение (24) также подобно уравнению (11), но выражение для R из (25) довольно громоздко, и поэтому здесь будут сделаны более сильные предположения. На основании соотношений (1) и (7) получим оценку

(28)

$\begin{gathered} \left| R \right| \leqslant {{R}_{o}} = (l + \mu a)fg(M + m){{(J + \mu M{{a}^{2}})}^{{ - 1}}}\, = \,{{T}^{{ - 2}}}, \\ l = \max C{{A}_{i}},\quad i = 1,\;2,\;3, \\ \end{gathered} $

где Т – характерная величина размерности времени.

Зададим управление z(t) в виде

(29)

$\begin{gathered} z(t) = Z\quad {\text{при}}\quad t \in (0,{\text{ }}\tau ), \\ z(t) = - Z\quad {\text{при}}\quad t \in (\tau ,{\text{ 2}}\tau ), \\ \end{gathered} $

где постоянные Z и τ таковы, что

(30)

${{{{\mu }_{1}}Z} \mathord{\left/ {\vphantom {{{{\mu }_{1}}Z} {{{R}_{o}}}}} \right. \kern-0em} {{{R}_{o}}}} \sim {{\varepsilon }^{{ - 2}}},\quad {\tau \mathord{\left/ {\vphantom {\tau {T \sim \varepsilon }}} \right. \kern-0em} {T \sim \varepsilon }},\quad \varepsilon \ll 1.$

Пренебрегая в уравнении (24) членами порядка ε² при ε → 0, имеем

$\dot {\omega } + {{\mu }_{1}}\dot {\Omega } = 0,$

откуда при начальных условиях (27) получим

(31)

$\begin{gathered} \omega (t) + {{\mu }_{1}}\Omega (t) = 0, \\ \psi (t) = - {{\mu }_{1}}\varphi (t)\quad {\text{при}}\quad t \in (0,2\tau ){\text{.}} \\ \end{gathered} $

Полные угловые перемещения точки Q и тела P за время 2τ определяются равенствами, вытекающими из (29), (26), (27) и (31):

(32)

$\Delta \varphi = \varphi (2\tau ) = Z{{\tau }^{2}},\quad \Delta \psi = \psi (2\tau ) = - {{\mu }_{1}}Z{{\tau }^{2}}.$

Из соотношений (30) и (32) следует, что угловые перемещения (32) конечны при ε → 0, пропорциональны друг другу и противоположны по знаку. За счет выбора τ они могут быть сделаны как угодно малыми. Выполняя описанный маневр нужное число раз и выбирая каждый раз параметр τ, можно осуществить поворот тела на заданный угол. Между этими маневрами точка Q может перемещаться по окружности S при помощи медленных движений. В результате можно повернуть тело P на заданный угол и переместить точку Q из начального положения в любое положение на окружности S. Центр масс С тела P может двигаться в течение описанного маневра. После его завершения вращение тела P и относительное движение точки Q прекращаются, но поступательное движение тела P может продолжаться. В этом остаточном движении система $P + Q$ придет в состояние покоя за конечное время.

УПРАВЛЯЕМОСТЬ

Покажем, что при помощи рассмотренных движений систему P + Q можно перевести из произвольного начального состояния покоя в заданное терминальное состояние покоя.

1. Сначала при помощи медленного движения переместим точку Q из начального положения в некоторую точку на окружности S. Тело P при этом не движется.

2. При помощи нескольких вращательных маневров осуществим поворот тела P так, чтобы его конечная ориентация совпала с заданной терминальной ориентацией. Между вращательными маневрами могут быть медленные и остаточные движения, описанные выше. В конце этого этапа система окажется в состоянии покоя, причем ориентация тела P будет совпадать с заданной.

3. При помощи прямолинейных движений по любым двум из трех возможных направлений $C{{A}_{i}}$, $i = 1,2,3$, переместим тело P в заданное конечное положение в плоскости. Маневры прямолинейных движений могут чередоваться с медленными движениями для перемещения точки Q вдоль прямых $C{{A}_{i}}$. Движение тела P при этом поступательное, его ориентация не меняется. В конце движения точка Q может быть переведена в заданное положение при помощи медленного движения.

Таким образом, установлено, что рассматриваемая система может быть переведена из произвольного начального в заданное конечное положение, если подвижная точка Q может двигаться относительно тела P с достаточно большим ускорением. При этом условии система вполне управляема.

Для реализации заданного перемещения достаточно, чтобы точка Q могла двигаться относительно тела P по некоторой (произвольной) дуге окружности S с центром в точке С и по двум произвольным отрезкам прямых $C{{A}_{i}}$, $i = 1,2,3$. Достаточно потребовать, например, чтобы точка Q могла двигаться относительно тела P по кривой, состоящей из отрезка прямой $C{{A}_{1}}$, дуги окружности S и отрезка прямой $C{{A}_{2}}$ (жирная кривая на рис. 1). Таким образом, точка Q может обладать лишь одной степенью свободы относительно тела P.

ЗАКЛЮЧЕНИЕ

Твердое тело, движущееся вдоль горизонтальной плоскости при наличии сил сухого трения и управляемое посредством подвижной массы, может быть переведено из произвольного начального состояния покоя в произвольное терминальное состояние покоя за конечное время. Управляемость системы имеет место, если подвижная масса может двигаться относительно тела по некоторой кривой с достаточно большим относительным ускорением.

Список литературы

Vartholomeos P., Papadopoulos E. Dynamics, design and simulation of a novel microrobotic platform employing vibration microactuators // Trans. ASME. J. Dyn. Syst. Meas. and Control. 2006. V. 128. № 1. P. 122–133.
Huda M.N., Yu H. Trajectory tracking control of an underactuated capsubot // Autonomous Robots. 2015. V. 39. № 2. P. 183–198.
Liu Y., Pavlovskaya E., Wiercigroch M. Experimental verification of the vibro-impact capsule model // Nonlinear Dynamics. 2016. V. 83. P. 1029–1041.
Черноусько Ф.Л. Анализ и оптимизация движения тела, управляемого посредством подвижной внутренней массы // ПММ. 2006. Т. 70. В. 6. С. 915–941.
Черноусько Ф.Л. Оптимальные периодические движения двухмассовой системы в сопротивляющейся среде // ПММ. 2008. Т. 72. В. 2. С. 202–215.
Черноусько Ф.Л. Движение тела по плоскости под влиянием подвижных внутренних масс // ДАН. 2016. Т. 470. № 4. С. 406–410.
Chernousko F.L. Two-dimensional motions of a body containing internal moving masses // Meccanica. 2016. V. 51. № 12. P. 3203–3209.
Chernousko F.L. Optimal motions of bodies controlled by internal moving masses // IFAC PapersOnLine. 2018. V. 51–32. P. 1–6.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал