Доклады Российской академии наук. Физика, технические науки, 2020, T. 495, № 1, стр. 39-45

ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, ПОДКРЕПЛЕННОЙ ПРОДОЛЬНЫМИ РЕБРАМИ КУСОЧНО-ПОСТОЯННОЙ ТОЛЩИНЫ, ПРИ ДЕЙСТВИИ ОСЕВОЙ НАГРУЗКИ

В. Н. Бакулин^1, *, А. Я. Недбай²

¹ Институт прикладной механики Российской академии наук
Москва, Россия

² АО Корпорация “Московский институт теплотехники”
Москва, Россия

^* E-mail: vbak@yandex.ru

Поступила в редакцию 23.09.2020
После доработки 30.09.2020
Принята к публикации 01.10.2020

DOI: 10.31857/S268674002006005X

Полный текст (PDF)

Аннотация

Предложена модель для исследования одновременных параметрических и продольных колебаний ортотропной цилиндрической оболочки, подкрепленной продольными ребрами кусочно-постоянной толщины, при действии осевой нагрузки, гармонически изменяющейся во времени. Учет дискретного расположения и изменения толщины ребер осуществляется с помощью обобщенных функций. Рассмотрены основные этапы решения задачи c помощью предложенной комбинации методов. На численном примере впервые построены зависимости главной области неустойчивости от геометрических параметров ребер и проведено сравнение с областями неустойчивости для ребер со среднеинтегральной толщиной. Разработанная модель позволяет значительно уточнить решения задач по расчету динамической устойчивости ортотропных цилиндрических оболочек с ребрами кусочно-постоянной толщины.

Ключевые слова: динамическая устойчивость, подкрепленная ортотропная цилиндрическая оболочка, продольные ребра кусочно-постоянной толщины, осевая нагрузка, гармонически изменяющаяся во времени, области неустойчивости

ВВЕДЕНИЕ

Создание современных летательных аппаратов (ЛА) требует решения ряда актуальных проблем, одной из которых является обеспечение динамической устойчивости цилиндрических оболочек, применяющихся, например, в конструкциях соединительных отсеков ракет и фюзеляжей самолетов. Для минимизации массы такие конструкции усиливаются продольными ребрами (стрингерами), которые, в свою очередь, могут быть переменной толщины. Изменение толщины ребер обусловлено конструктивными особенностями ЛА или различными технологическими причинами, включая аддитивные технологии.

В процессе полета на ЛА постоянно воздействуют осевые силы в виде тяги двигателей, лобового сопротивления воздуха и инерционных сил. Кроме того, на эти нагрузки накладываются пульсирующие силы, обусловленные вибрационным горением топлива, работой пневмо- и гидроагрегатов, а также турбулентностью или бафтингом воздушных потоков [1, 2]. При определенных значениях и сочетаниях этих нагрузок возможно возникновение параметрического резонанса и разрушение конструкции.

К настоящему времени по проблеме динамической и аэроупругой устойчивости оболочек опубликованы ряд монографий [3–7] и статей [8–14]. Однако поведение оболочек, подкрепленных продольными ребрами кусочно-постоянной толщины, остается практически не исследованным [9, 14].

В представленной работе впервые получены уравнения для решения задачи динамической устойчивости ортотропной цилиндрической оболочки, подкрепленной продольными ребрами кусочно-постоянной толщины, при действии осевой нагрузки, гармонически изменяющейся во времени, и внешнего давления. Учет дискретного расположения и изменения толщины ребер осуществляется с помощью обобщенных функций. Рассмотрены основные этапы решения задачи c помощью предложенной комбинации методов. Решение полученных уравнений ищется в виде двойных тригонометрических рядов по осевой и окружной координатам с применением процедуры Бубнова–Галёркина. В полученных неоднородных обыкновенных дифференциальных уравнениях типа Матье–Хилла удерживается один член временного тригонометрического ряда. В результате задача сводится к бесконечной системе алгебраических уравнений, редуцируя которую и приравнивая к нулю определитель полученной матрицы, приходим к характеристическому уравнению для нахождения критических частот.

Разработанная модель позволяет с необходимой точностью провести расчет динамической устойчивости ортотропных цилиндрических оболочек с продольными ребрами кусочно-постоянной толщины при указанной выше нагрузке.

Из полученных результатов расчетов динамической устойчивости ортотропной цилиндрической оболочки с продольными ребрами кусочно-постоянной толщины, при действии осевой нагрузки, гармонически изменяющейся во времени, и их анализа впервые установлен ряд важных для науки и практики зависимостей. Впервые получены и представлены зависимости, а также исследовано влияние на границы области неустойчивости внешнего давления, закона изменения высоты ребер, замены реального закона изменения высоты ребер на среднеинтегральную высоту, количества ребер при неизменной суммарной площади их сечения. Полученные результаты указывают на большие возможности весовой оптимизации рассмотренной конструкции за счет увеличения количества ребер и перераспределения материала между ребрами при неизменной суммарной площади их сечения, что говорит об актуальности решенной проблемы в свете весового совершенства летательных аппаратов. Построенные зависимости позволяют сделать вывод о величине погрешности определения площади области неустойчивости при использовании в расчетах среднеинтегральной толщины ребер. Погрешность может достигать больших значений, что также свидетельствует об актуальности решенной проблемы и необходимости применения рассмотренной модели при разработке и использовании аддитивной технологии для изготовления ребер, подкрепляющих оболочки.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

С помощью аппарата обобщенных функций, использование которого в настоящее время является перспективным направлением [15], предлагается модель одновременного учета влияния конструктивных особенностей и продольных колебаний ребер на динамическую устойчивость цилиндрической оболочки.

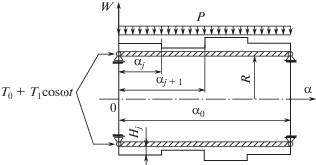
Рассмотрим ортотропную цилиндрическую оболочку, подкрепленную четным количеством равномерно расположенных продольных ребер. Торцы оболочки шарнирно оперты и нагружены осевыми сжимающими силами, включающими постоянную и гармонически изменяющуюся переменную составляющие. Ребра изготовлены из одного материала и имеют одинаковый закон изменения толщины. На внешнюю поверхность оболочки действует постоянное давление. Для упрощения толщина ребер на торцах принята одинаковой. Расчетная схема показана на рис. 1.

Рис. 1.

Расчетная схема.

Введем безразмерную систему цилиндрических координат, в которой линейные размеры отнесены к радиусу срединной поверхности оболочки. Тогда уравнение движения оболочки можно представить в виде [7]

$\begin{gathered} {{L}_{{11}}}U + {{L}_{{12}}}W = - {{l}_{{22}}}\sum\limits_{i = 1}^M {\left\{ {\sum\limits_{j = 1}^N {\left[ {a_{{10}}^{{(j)}}\frac{{{{\partial }^{2}}{{U}_{i}}}}{{\partial {{\alpha }^{2}}}}} \right.} } \right.} - \\ \, - a_{{13}}^{{(j)}}\frac{{{{\partial }^{2}}{{U}_{i}}}}{{\partial {{t}^{2}}}} + a_{{14}}^{{(j)}}\frac{{{{\partial }^{3}}{{W}_{i}}}}{{\partial {{\alpha }^{3}}}} + a_{{11}}^{{(j)}}({{T}_{0}} + {{T}_{1}}\cos \omega t)\left. {\frac{{\partial {{W}_{i}}}}{{\partial \alpha }}} \right] \times \\ \end{gathered} $

(1)

$\begin{gathered} \left. {\mathop {}\limits_{_{{_{{}}}}}^{^{{}}} \times \left[ {{{\sigma }_{0}}(\alpha - {{\alpha }_{{j - 1}}}) - {{\sigma }_{0}}(\alpha - {{\alpha }_{j}})} \right]} \right\}\delta (\beta - {{\beta }_{i}}); \\ {{L}_{{21}}}U + {{L}_{{22}}}W = - {{l}_{{22}}}\sum\limits_{i = 1}^M {\left\{ {\sum\limits_{j = 1}^N {\left[ {a_{{14}}^{{(j)}}\frac{{{{\partial }^{3}}{{U}_{i}}}}{{\partial {{\alpha }^{3}}}}} \right.} } \right.} + \\ \end{gathered} $

$\begin{gathered} \, + a_{{12}}^{{(j)}}\frac{{{{\partial }^{4}}{{W}_{i}}}}{{\partial {{\alpha }^{4}}}} + a_{{13}}^{{(j)}}\frac{{{{\partial }^{2}}{{W}_{i}}}}{{\partial {{t}^{2}}}} + a_{{11}}^{{(j)}}({{T}_{0}} + {{T}_{1}}\cos \omega t)\left. {\frac{{{{\partial }^{2}}{{W}_{i}}}}{{\partial {{\alpha }^{2}}}}} \right] \times \\ \left. {\mathop {}\limits_{_{{_{{}}}}}^{^{{}}} \times \left[ {{{\sigma }_{0}}(\alpha - {{\alpha }_{{j - 1}}}) - {{\sigma }_{0}}(\alpha - {{\alpha }_{j}})} \right]} \right\}\delta (\beta - {{\beta }_{i}}); \\ \end{gathered} $

где L_ks – дифференциальные операторы, имеющие вид

${{L}_{{11}}} = {{l}_{{11}}}{{l}_{{22}}} - l_{{12}}^{2};\quad {{L}_{{12}}} = {{l}_{{13}}}{{l}_{{22}}} - l_{{12}}^{{}}l_{{23}}^{{}};$

${{L}_{{21}}} = {{l}_{{31}}}{{l}_{{22}}} - l_{{32}}^{{}}l_{{21}}^{{}};\quad {{L}_{{22}}} = {{l}_{{22}}}{{l}_{{33}}} - l_{{23}}^{2};\;$

${{l}_{{11}}} = \frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}} + {{a}_{1}}\frac{{{{\partial }^{2}}}}{{\partial {{\beta }^{2}}}} - {{a}_{7}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}};\quad {{l}_{{12}}} = {{l}_{{21}}} = {{a}_{2}}\frac{{{{\partial }^{2}}}}{{\partial \alpha \partial \beta }};$

$\begin{gathered} {{l}_{{13}}} = {{\nu }_{\beta }}\frac{\partial }{{\partial \alpha }} + {{a}_{3}}\left( {{{a}_{1}}\frac{{{{\partial }^{3}}}}{{\partial \alpha \partial {{\beta }^{2}}}} - \frac{{{{\partial }^{3}}}}{{\partial {{\alpha }^{3}}}}} \right) + \\ \, + {{a}_{8}}\left( {{{T}_{0}} + {{T}_{1}}\cos \omega t} \right)\frac{\partial }{{\partial \alpha }}; \\ \end{gathered} $

${{l}_{{22}}} = {{a}_{1}}\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}}\; + {{a}_{4}}\frac{{{{\partial }^{2}}}}{{\partial {{\beta }^{2}}}};$

${{l}_{{31}}} = {{\nu }_{\beta }}\frac{{{{\partial }^{{}}}}}{{\partial \alpha }} + {{a}_{3}}\left( {{{a}_{1}}\frac{{{{\partial }^{3}}}}{{\partial \alpha \partial {{\beta }^{2}}}} - \frac{{{{\partial }^{3}}}}{{\partial {{\alpha }^{3}}}}} \right);$

${{l}_{{23}}} = {{l}_{{32}}} = {{a}_{4}}\frac{{{{\partial }^{{}}}}}{{\partial \beta }}\; - {{a}_{3}}{{a}_{5}}\frac{{{{\partial }^{3}}}}{{\partial {{\alpha }^{2}}\partial {{\beta }^{{}}}}};$

$\begin{gathered} {{l}_{{33}}} = {{a}_{4}} + {{a}_{3}}\left[ {\frac{{{{\partial }^{4}}}}{{\partial {{\alpha }^{4}}}} + 2{{a}_{6}}\frac{{{{\partial }^{4}}}}{{\partial {{\alpha }^{2}}\partial {{\beta }^{2}}}} + {{a}_{4}}{{{\left( {\frac{{{{\partial }^{2}}}}{{\partial {{\beta }^{2}}}} + 1} \right)}}^{2}}} \right] + \\ \, + {{a}_{7}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + {{a}_{8}}\left( {{{T}_{0}} + {{T}_{1}}\cos \omega t} \right)\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}} + {{a}_{9}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{\beta }^{2}}}} + 1} \right); \\ \end{gathered} $

${{a}_{1}} = \frac{{{{G}_{{\alpha \beta }}}\left( {1 - {{\nu }_{\alpha }}{{\nu }_{\beta }}} \right)}}{{{{E}_{\alpha }}}};\quad {{a}_{2}} = {{a}_{1}} + {{\nu }_{\beta }};\quad {{a}_{3}} = \frac{{{{h}^{2}}}}{{12{{R}^{2}}}};$

${{a}_{4}} = \frac{{{{E}_{\beta }}}}{{{{E}_{\alpha }}}};\quad {{a}_{5}} = 3{{a}_{1}} + {{\nu }_{\beta }};\quad {{a}_{6}} = 2{{a}_{1}} + {{\nu }_{\beta }};$

${{a}_{7}} = B{{\rho }_{0}}h;\quad {{a}_{8}} = \frac{{B{{E}_{\alpha }}h}}{{\left( {2\pi R{{E}_{\alpha }}h + ME{{F}_{0}}} \right){{R}^{2}}}};$

${{a}_{9}} = \frac{{BP}}{{{{R}^{{}}}}};\quad a_{{10}}^{{(j)}} = \frac{{BE{{F}_{j}}}}{{{{R}^{3}}}};$

${{F}_{j}} = b{{H}_{j}};\quad a_{{11}}^{{(j)}} = \frac{{BE{{F}_{j}}}}{{{{R}^{3}}\left( {2\pi R{{E}_{\alpha }}h + ME{{F}_{j}}} \right)}};$

$a_{{12}}^{{(j)}} = \frac{{BE{{I}_{j}}}}{{{{R}^{5}}}};\quad a_{{13}}^{{(j)}} = \frac{{B{{F}_{j}}\rho }}{R};$

$a_{{14}}^{{(j)}} = \frac{{BE{{F}_{j}}{{\zeta }_{j}}}}{{{{R}^{4}}}};\quad B = \frac{{{{R}^{2}}\left( {1 - {{\nu }_{\alpha }}{{\nu }_{\beta }}} \right)}}{{{{E}_{\alpha }}h}},$

где α, β – безразмерные координаты вдоль образующей и в окружном направлении; U, W – осевое и радиальное перемещения оболочки; $R,\;h$ – радиус и толщина оболочки; ${{E}_{\alpha }},\;{{E}_{\beta }},\;{{G}_{{\alpha \beta }}}$ – модуль упругости в осевом и окружном направлениях и модуль сдвига; ${{\nu }_{\alpha }},\;{{\nu }_{\beta }}$ – коэффициенты Пуассона; E – модуль упругости материала ребер; ${{F}_{j}},\;{{I}_{j}}$ – площадь и центральный момент инерции j-го участка ребра; ${{F}_{0}}$ – площадь торца ребра; $b,\;{{H}_{j}}$ – ширина и толщина (высота) j-го участка ребра; ${{\zeta }_{j}}$ – расстояние от осевой линии j-го участка ребра до срединной поверхности оболочки, принимаемое положительным при внутреннем расположении осевой линии ребра; ${{\rho }_{0}},\;\rho $ – плотность материала оболочки и ребер соответственно; ${{T}_{0}},\;{{T}_{1}}$ – постоянная составляющая и амплитуда переменной составляющей осевой силы; $P$ – внешнее давление; $\omega $ – частота пульсаций; $M$ – количество ребер; $N$ – количество участков на ребре; $\delta (\beta )$ – дельта-функция; ${{\sigma }_{0}}(\alpha )$ – единичная функция, равная единице при $\alpha $ > 0 и нулю при $\alpha $ < 0.

Решение уравнений (1) будем искать в виде

(2)

$\begin{gathered} U = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 0}^\infty {{{\varphi }_{{mn}}}(t)\cos {{\gamma }_{m}}\alpha \cos n\beta } } ; \\ W = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 0}^\infty {{{f}_{{mn}}}(t)\sin {{\gamma }_{m}}\alpha \cos n\beta } } ; \\ \end{gathered} $

где ${{\gamma }_{m}} = \frac{{m\pi }}{{{{\alpha }_{0}}}};$ ${{\alpha }_{0}} = \frac{L}{R}$; L – длина оболочки; $m$ – число полуволн по длине; $n$ – число волн в окружном направлении; ${{\varphi }_{{mn}}}(t),$ ${{f}_{{mn}}}(t)$ – неизвестные функции времени (в дальнейшем аргумент t опускается).

Разложим дельта-функцию в ряд Фурье:

$\delta (\beta - {{\beta }_{i}}) = \frac{1}{\pi }\left[ {\frac{1}{2} + \sum\limits_{n = 1}^\infty {\cos n(\beta - {{\beta }_{i}})} } \right]$

и подставим (2) в (1). Применяя процедуру Бубнова–Галёркина, получим систему обыкновенных неоднородных дифференциальных уравнений типа Матье–Хилла

$\begin{gathered} \left[ {b_{3}^{{(kn)}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}} + b_{1}^{{(kn)}}} \right]{{\varphi }_{{kn}}} - \\ \, - \left[ {b_{2}^{{(kn)}} + \frac{{b_{4}^{{(kn)}}}}{{{{\gamma }_{k}}}}({{T}_{0}} + {{T}_{1}}\cos \omega t)} \right]{{f}_{{kn}}} = \\ \end{gathered} $

(3)

$ = - \frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi }}\sum\limits_{i = 1}^M {\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {\left\{ {\left[ {a_{{10}}^{{(j)}}\gamma _{m}^{2} + a_{{13}}^{{(j)}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}}} \right]\,} \right.} } } {{U}_{{mi}}} + $

$\left. {\mathop {}\limits_{_{{}}}^{^{{}}} + \gamma _{m}^{{}}[a_{{14}}^{{(j)}}\gamma _{m}^{2}\, - \,a_{{11}}^{{(j)}}({{T}_{0}} + {{T}_{1}}{\text{cos}}\omega t)]{{W}_{{mi}}}} \right\}b_{0}^{{(mn)}}\psi _{{1j}}^{{(mk)}}{\text{cos}}n{{\beta }_{i}},$

$\begin{gathered} b_{2}^{{(kn)}}{{\varphi }_{{kn}}} - \left[ {b_{3}^{{(kn)}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}} - b_{4}^{{(kn)}}\left( {{{T}_{0}} + {{T}_{1}}\cos \omega t} \right) + b_{5}^{{(kn)}}} \right]{{f}_{{kn}}} = \\ \, = - \frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi }}\sum\limits_{i = 1}^M {\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {\left\{ {a_{{14}}^{{(j)}}\gamma _{m}^{3}{{U}_{{mi}}}\mathop + \limits_{}^{} } \right.} } } \\ \end{gathered} $

$\begin{gathered} \left. {\, + \left[ {a_{{13}}^{{(j)}}\frac{{{{d}^{2}}}}{{d{{t}^{2}}}} - a_{{11}}^{{(j)}}\gamma _{m}^{2}({{T}_{0}} + {{T}_{1}}\cos \omega t) + a_{{12}}^{{(j)}}\gamma _{m}^{4}} \right]{{W}_{{mi}}}} \right\} \times \\ \, \times b_{0}^{{(mn)}}\psi _{{2j}}^{{(mk)}}\cos n{{\beta }_{i}} \\ \end{gathered} $

($k = 1,2,3...$); где ${{\delta }_{{0n}}}$ – символ Кронекера,

$b_{0}^{{(kn)}} = {{a}_{1}}\gamma _{k}^{2} + {{a}_{4}}{{n}^{2}};\quad b_{1}^{{(kn)}} = b_{0}^{{(kn)}}(\gamma _{k}^{2} + {{a}_{1}}n_{{}}^{2}) - a_{2}^{2}\gamma _{k}^{2}{{n}^{2}};$

$b_{2}^{{(kn)}} = b_{0}^{{(kn)}}\gamma _{k}^{{}}[{{\nu }_{\beta }} + {{a}_{3}}(\gamma _{k}^{2} - {{a}_{1}}{{n}^{2}})] + a_{2}^{{}}\gamma _{k}^{{}}{{n}^{2}}({{a}_{4}} + {{a}_{3}}{{a}_{5}}\gamma _{k}^{2});$

$b_{3}^{{(kn)}} = {{a}_{7}}b_{0}^{{(kn)}}\gamma _{k}^{2};\quad b_{4}^{{(kn)}} = {{a}_{8}}b_{0}^{{(kn)}}\gamma _{k}^{2};$

$\begin{gathered} b_{5}^{{(kn)}} = b_{0}^{{(kn)}}\{ {{a}_{4}} + {{a}_{3}}[\gamma _{k}^{4} + 2{{a}_{6}}\gamma _{k}^{2}{{n}^{2}} + \\ \, + {{a}_{4}}{{({{n}^{2}} - 1)}^{2}}] + {{a}_{9}}(1 - {{n}^{2}})\} + {{({{a}_{4}} + {{a}_{3}}{{a}_{5}}\gamma _{k}^{2})}^{2}}{{n}^{2}}; \\ \end{gathered} $

$\psi _{{1j}}^{{(mk)}},\psi _{{2j}}^{{(mk)}} = \left\{ \begin{gathered} F_{k}^{{(j)}}\quad {\text{при}}\quad m = k, \hfill \\ F_{{mk}}^{{(j)}}\quad {\text{при}}\quad m \ne k, \hfill \\ \end{gathered} \right.$

$\begin{gathered} F_{k}^{{(j)}} = \frac{{{{\alpha }_{j}} - {{\alpha }_{{j - 1}}}}}{{{{\alpha }_{0}}}} \pm \\ \, \pm \frac{1}{{\pi k}}\cos \frac{{\pi k({{\alpha }_{j}} + {{\alpha }_{{j - 1}}})}}{{{{\alpha }_{0}}}}\sin \frac{{\pi k({{\alpha }_{j}} - {{\alpha }_{{j - 1}}})}}{{{{\alpha }_{0}}}}; \\ \end{gathered} $

$\begin{gathered} F_{{mk}}^{{(j)}} = \frac{2}{\pi }\left\{ {\frac{1}{{m - k}}} \right.\cos \frac{{\pi (m - k)\left( {{{\alpha }_{j}} + {{\alpha }_{{j - 1}}}} \right)}}{{2{{\alpha }_{0}}}} \times \\ \, \times \sin \frac{{\pi (m - k)\left( {{{\alpha }_{j}} - {{\alpha }_{{j - 1}}}} \right)}}{{2{{\alpha }_{0}}}} \pm \frac{1}{{m + k}} \times \\ \, \times \left. {\cos \frac{{\pi (m + k)\left( {{{\alpha }_{j}} + {{\alpha }_{{j - 1}}}} \right)}}{{2{{\alpha }_{0}}}}\sin \frac{{\pi (m + k)\left( {{{\alpha }_{j}} - {{\alpha }_{{j - 1}}}} \right)}}{{2{{\alpha }_{0}}}}} \right\}. \\ \end{gathered} $

Решение (3) будем искать в виде

(4)

$\begin{gathered} \left\{ {{{\varphi }_{{kn}}},{{f}_{{kn}}},{{U}_{{mi}}}{{W}_{{mi}}}} \right\} = \\ \, = \sum\limits_{r = 1,3...}^\infty {\left\{ {[A_{r}^{{(kn)}},A_{{r + 1}}^{{(kn)}},A_{{ri}}^{{(m)}},A_{{(r + 1)i}}^{{(m)}}]{{ \times }_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}} \right.} \\ \, \times \left. {\sin \frac{{r\omega t}}{2} + [B_{r}^{{(kn)}},B_{{r + 1}}^{{(kn)}},B_{{ri}}^{{(m)}},B_{{(r + 1)i}}^{{(m)}}]\cos \frac{{r\omega t}}{2}} \right\}. \\ \end{gathered} $

Подставим первую сумму из (4) в (3) и, приравнивая коэффициенты при одинаковых $\sin \frac{{r\omega t}}{2}$, получим систему неоднородных алгебраических уравнений. Ограничимся одним членом ряда, что, согласно [3], достаточно для практических расчетов. В результате получим

$C_{1}^{{(kn)}}A_{1}^{{(kn)}} + C_{2}^{{(kn)}}A_{2}^{{(kn)}} = \frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi }} \times $

(5)

$\begin{gathered} \, \times \sum\limits_{i = 1}^M {\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {[d_{{1j}}^{{(mk)}}A_{{1i}}^{{(m)}} + d_{{2j}}^{{(mk)}}A_{{2i}}^{{(m)}}]} } } \,b_{0}^{{(mn)}}\cos n{{\beta }_{i}}; \\ C_{3}^{{(kn)}}A_{1}^{{(kn)}} + C_{4}^{{(kn)}}A_{2}^{{(kn)}} = \frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi }} \times \\ \end{gathered} $

$\, \times \sum\limits_{i = 1}^M {\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {[d_{{3j}}^{{(mk)}}A_{{1i}}^{{(m)}} + d_{{4j}}^{{(mk)}}A_{{2i}}^{{(m)}}]} } } \,b_{0}^{{(mn)}}\cos n{{\beta }_{i}};$

где $C_{1}^{{(kn)}} = - b_{1}^{{(kn)}}\, + \,b_{3}^{{(kn)}}\frac{{{{\omega }^{2}}}}{4};$ $C_{2}^{{(kn)}}$ = $b_{2}^{{(kn)}}$ + $\frac{{b_{4}^{{(kn)}}}}{{{{\gamma }_{k}}}}\left( {{{T}_{0}}\, \mp \,\frac{{{{T}_{1}}}}{2}} \right);$ $C_{3}^{{(kn)}} = b_{2}^{{(kn)}};$

$C_{4}^{{(kn)}} = b_{3}^{{(kn)}}\frac{{{{\omega }^{2}}}}{4} - b_{5}^{{(kn)}} + b_{4}^{{(kn)}}\left( {{{T}_{0}} \mp \frac{{{{T}_{1}}}}{2}} \right);$

$d_{{1j}}^{{(mk)}} = \left[ {a_{{10}}^{{(j)}}\gamma _{m}^{2} - a_{{13}}^{{(j)}}\frac{{{{\omega }^{2}}}}{4}} \right]\psi _{{1j}}^{{(mk)}};$

$d_{{2j}}^{{(mk)}} = \gamma _{m}^{{}}\left[ {a_{{14}}^{{(j)}}\gamma _{m}^{2} - a_{{11}}^{{(j)}}\left( {{{T}_{0}} \mp \frac{{{{T}_{1}}}}{2}} \right)} \right]\psi _{{1j}}^{{(mk)}};$

$d_{{3j}}^{{(mk)}} = a_{{14}}^{{(j)}}\gamma _{m}^{3}\psi _{{2j}}^{{(mk)}};$

$d_{{4j}}^{{(mk)}} = \left[ { - a_{{13}}^{{(j)}}\frac{{{{\omega }^{2}}}}{4} + a_{{12}}^{{(j)}}\gamma _{m}^{4} - a_{{11}}^{{(j)}}\gamma _{m}^{2}\left( {{{T}_{0}} \mp \frac{{{{T}_{1}}}}{2}} \right)} \right]\psi _{{2j}}^{{(mk)}}.$

Решая систему (5) относительно $A_{1}^{{(kn)}},\,\,A_{2}^{{(kn)}}$, получим

$A_{1}^{{(kn)}} = \frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi {{\Delta }_{{kn}}}}} \times $

(6)

$\begin{gathered} \, \times \sum\limits_{i = 1}^M {\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {[D_{{1jn}}^{{(mk)}}A_{{1i}}^{{(m)}} + D_{{2jn}}^{{(mk)}}A_{{2i}}^{{(m)}}]} } } b_{0}^{{(mn)}}\cos {{\beta }_{i}}; \\ A_{2}^{{(kn)}} = \frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi {{\Delta }_{{kn}}}}} \times \\ \end{gathered} $

$\, \times \sum\limits_{i = 1}^M {\sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {\left[ {D_{{3jn}}^{{(mk)}}A_{{1i}}^{{(m)}} + D_{{4jn}}^{{(mk)}}A_{{2i}}^{{(m)}}} \right]} } } b_{0}^{{(mn)}}\cos {{\beta }_{i}};$

где ${{\Delta }_{{kn}}} = C_{1}^{{(kn)}}C_{4}^{{(kn)}} - C_{2}^{{(kn)}}C_{3}^{{(kn)}};$

$D_{{1jn}}^{{(mk)}} = C_{4}^{{(kn)}}d_{{1j}}^{{(mk)}} - C_{2}^{{(kn)}}d_{{3j}}^{{(mk)}};$

$D_{{2jn}}^{{(mk)}} = C_{4}^{{(kn)}}d_{{2j}}^{{(mk)}} - C_{2}^{{(kn)}}d_{{4j}}^{{(mk)}};$

$D_{{3jn}}^{{(mk)}} = C_{1}^{{(kn)}}d_{{3j}}^{{(mk)}} - C_{3}^{{(kn)}}d_{{1j}}^{{(mk)}};$

$D_{{4jn}}^{{(mk)}} = C_{1}^{{(kn)}}d_{{4j}}^{{(mk)}} - C_{3}^{{(kn)}}d_{{2j}}^{{(mk)}}.$

Так, в местах расположения ребер справедливо соотношение

$A_{{rl}}^{{(k)}} = \sum\limits_{n = 0}^\infty {A_{r}^{{(kn)}}\cos n{{\beta }_{l}}} ,$

подставив в него выражения (6), получим бесконечную систему алгебраических уравнений

$A_{{1l}}^{{(k)}} = \sum\limits_{i = 1}^M {\sum\limits_{n = 0}^\infty {\frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi {{\Delta }_{{kn}}}}}} } \sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {[D_{{1jn}}^{{(mk)}}A_{{1i}}^{{(m)}} + D_{{2jn}}^{{(mk)}}A_{{2i}}^{{(m)}}]} } \times $

(7)

$\begin{gathered} \, \times b_{0}^{{(mn)}}\cos n{{\beta }_{i}}\cos n{{\beta }_{l}}; \\ A_{{2l}}^{{(k)}} = \sum\limits_{i = 1}^M {\sum\limits_{n = 0}^\infty {\frac{{(2 - {{\delta }_{{0n}}})}}{{2\pi {{\Delta }_{{kn}}}}}} } \sum\limits_{m = 1}^\infty {\sum\limits_{j = 1}^N {[D_{{3jn}}^{{(mk)}}A_{{1i}}^{{(m)}} + D_{{4jn}}^{{(mk)}}A_{{2i}}^{{(m)}}]} } \times \\ \end{gathered} $

$\, \times b_{0}^{{(mn)}}\cos n{{\beta }_{i}}\cos n{{\beta }_{l}};\quad (l = 1,2,...,M;k = 1,2,\,\,...).$

Так как ребра одинаковые и расположены равномерно, решение системы (7) можно представить в виде

(8)

$A_{{rl}}^{{(k)}} = A_{r}^{{(k)}}\cos \frac{{2\pi ls}}{M},\quad 0 \leqslant s \leqslant \frac{M}{2};$

где s – целое число, характеризующее форму потери устойчивости.

Поставляя (8) в (7), получим

(9)

$\begin{gathered} \sum\limits_{m = 1}^\infty {\{ \theta _{1}^{{(mk)}}A_{1}^{{(m)}} + \theta _{2}^{{(mk)}}A_{2}^{{(m)}}\} } = 0; \\ \sum\limits_{m = 1}^\infty {\{ \theta _{3}^{{(mk)}}A_{1}^{{(m)}} + \theta _{4}^{{(mk)}}A_{2}^{{(m)}}\} } = 0 \\ (k = 1,2,3...), \\ \end{gathered} $

где

$\theta _{1}^{{(mk)}} = \frac{M}{{2\pi }}\sum\limits_{j = 1}^N {\sum\limits_n {\frac{{b_{0}^{{(mn)}}}}{{{{\Delta }_{{kn}}}}}D_{{1jn}}^{{(mk)}} - {{\delta }_{{mk}}}} } ;$

$\theta _{2}^{{(mk)}} = \frac{M}{{2\pi }}\sum\limits_{j = 1}^N {\sum\limits_n {\frac{{b_{0}^{{(mn)}}}}{{{{\Delta }_{{kn}}}}}D_{{2jn}}^{{(mk)}}} } ;$

$\theta _{3}^{{(mk)}} = \frac{M}{{2\pi }}\sum\limits_{j = 1}^N {\sum\limits_n {\frac{{b_{0}^{{(mn)}}}}{{{{\Delta }_{{kn}}}}}D_{{3jn}}^{{(mk)}}} } ;$

$\theta _{4}^{{(mk)}} = \frac{M}{{2\pi }}\sum\limits_{j = 1}^N {\sum\limits_n {\frac{{b_{0}^{{(mn)}}}}{{{{\Delta }_{{kn}}}}}D_{{4jn}}^{{(mk)}} - {{\delta }_{{mk}}}} } .$

Здесь суммирование производится по n, принимающему значения

$\begin{gathered} n = qM + s,\quad q = 0,1,2,... \\ n = qM - s,\quad q = 1,2,3,... \\ \end{gathered} $

Редуцируя систему (9) до количества членов m, удовлетворяющих заданной точности решения, и приравнивая к нулю определитель полученной матрицы, приходим к характеристическому уравнению для нахождения критических частот верхней границы области неустойчивости.

Подставляя вторую сумму из (4) в (3), получим аналогичное характеристическое уравнение, в котором неизвестные А₁, А₂ необходимо заменить на В₁, В₂, а в коэффициентах $C_{2}^{{(kn)}},\;C_{4}^{{(kn)}},\;d_{2}^{{(mk)}},\;d_{4}^{{(mk)}}$ поменять знак “–” на “+”. Придавая s различные целочисленные значения, определяем соответствующие величины критических частот нижней границы области неустойчивости.

ЧИСЛЕННЫЙ ПРИМЕР

В качестве примера рассмотрены две оболочки, подкрепленные равномерно расположенными ребрами. На первой оболочке высота ребер на концах в два раза больше, чем в середине. На второй оболочке высота ребер в середине в два раза больше, чем на концах. Базовые параметры оболочки и ребер были следующие:

$\frac{L}{R} = 6.0;\quad \frac{h}{R} = 0.008;\quad \frac{b}{R} = 0.06;\quad \frac{E}{{{{E}_{\alpha }}}} = 1.0;$

$\begin{gathered} \frac{{{{E}_{\beta }}}}{{{{E}_{\alpha }}}} = 1.5;\quad \frac{{{{G}_{{\alpha \beta }}}}}{{{{E}_{\alpha }}}} = 0.17;\quad {{\nu }_{\alpha }} = 0.15; \\ {{\nu }_{\beta }} = 0.23;\quad \frac{{H_{1}^{'}H_{3}^{'}H_{2}^{{''}}}}{R} = 0.08; \\ \end{gathered} $

$\begin{gathered} \frac{{H_{1}^{{''}}H_{3}^{{''}}H_{2}^{'}}}{R} = 0.04;\quad M = 4;\quad N = 3; \\ n = 40;\quad m = 20;\quad \frac{{{{T}_{0}}}}{{{{E}_{\alpha }}{{R}^{2}}}} = 1.5 \times {{10}^{{ - 4}}}; \\ \end{gathered} $

$\frac{P}{{{{E}_{\alpha }}}} = 2.2 \times {{10}^{{ - 6}}};\quad {{\alpha }_{1}} = 1.5;\quad {{\alpha }_{2}} = 4.5;$

${{H}_{1}},{{H}_{2}},{{H}_{3}}$ – высота ребра на соответствующем участке, верхние индексы (штрихи) соответствуют двум вариантам оболочки.

Во всех вариантах расчета оболочка нагружена осевой силой, постоянная составляющая которой равна половине критической силы гладкой оболочки. Сумма длин концевых участков равна длине среднего участка.

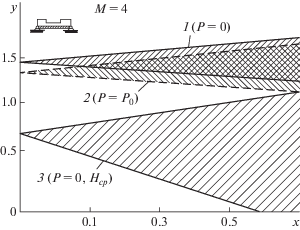
На рис. 2 показаны области неустойчивости (заштрихованная часть) первой оболочки, нагруженной внешним давлением и без него. Для сравнения приведены области неустойчивости для оболочки с ребрами, высота которых постоянна по всей длине и равна среднеинтегральному значению. По оси ординат отложены безразмерные значения критических частот ($y = \frac{\omega }{{{{\omega }_{0}}}}$, где ω₀ – собственная частота ненагруженной оболочки), а по оси абсцисс – безразмерная амплитуда переменной составляющей осевой силы $\left( {x = \frac{{{{T}_{1}}}}{{{{T}_{0}}}}} \right)$.

Рис. 2.

Области неустойчивости оболочек: 1 – с ребрами, усиленными на концах; 2 – нагруженных внешним давлением; 3 – с постоянной среднеинтегральной высотой ребер.

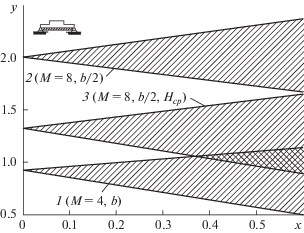
На рис. 3 изображены области неустойчивости для второй оболочки. Для сравнения показаны области неустойчивости двух оболочек с уменьшенной в два раза шириной ребер, но увеличенным их количеством. Общая площадь сечения восьми ребер равна площади сечения четырех ребер.

Рис. 3.

Области неустойчивости оболочек: 1 – с ребрами, усиленными в середине; 2 – с уменьшенной шириной ребер; 3 – с постоянной среднеинтегральной высотой ребер.

Из приведенного примера следует, что:

внешнее давление снижает границы области неустойчивости на 12%;

замена реального закона изменения высоты ребра на среднеинтегральную высоту снижает границы областей неустойчивости в 2 раза для первой оболочки и в 1.5 раза для второй, при этом расширяется (увеличивается) площадь областей неустойчивости;

увеличение количества ребер в 2 раза при неизменной суммарной площади их сечения повышает границы областей неустойчивости в 2.3 раза, что указывает на большие возможности весовой оптимизации только с помощью увеличения количества ребер и перераспределения материала между ребрами при неизменной суммарной площади их сечения;

увеличение высоты ребер на концевых участках повышает границы области в 1.7 раза по сравнению с увеличением высоты среднего участка (при этом сужается (уменьшается) площадь областей неустойчивости), что также говорит о необходимости применения данной методики при использовании аддитивной технологии для изготовления ребер, подкрепляющих оболочки.

ЗАКЛЮЧЕНИЕ

В представленном сообщении впервые получены уравнения для решения задачи динамической устойчивости ортотропной цилиндрической оболочки, подкрепленной продольными ребрами кусочно-постоянной толщины, при действии осевой нагрузки, гармонически изменяющейся во времени, и внешнего давления. Учет дискретного расположения и изменения толщины ребер осуществляется с помощью обобщенных функций. Рассмотрены основные этапы решения c помощью предложенной комбинации методов. Разработанная модель позволяет с необходимой точностью провести расчет динамической устойчивости ортотропных цилиндрических оболочек с продольными ребрами кусочно-постоянной толщины, при указанной выше нагрузке.

Полученные результаты указывают на возможности весовой оптимизации рассмотренной конструкции за счет увеличения количества ребер и перераспределения материала между ребрами при неизменной суммарной площади их сечения, что говорит об актуальности решенной проблемы в свете весового совершенства летательных аппаратов.

Список литературы

Вольмир А.С. Оболочки в потоке жидкости и газа. Задачи аэроупругости. М.: Физматлит, 1976. 416 с.
Липанов А.М., Карсканов С.А., Чернышев С.Л., Липатов И.И. Теоретическое исследование условий возникновения скоростного бафтинга // Вестн. Удмуртск. ун-та. Матем. Мех. Компьют. Науки. 2019. Т. 29. № 3. С. 382–395.
Болотин В.В. Динамическая устойчивость упругих систем. М.: ГИТТЛ, 1956. 600 с.
Бажанов В.Л., Гольденблат И.И., Копнов В.А., Поспелов А.Д., Сенюков А.М. Пластинки и оболочки из стеклопластиков. М.: Высшая школа, 1970. 408 с.
Огибалов П.М., Колтунов М.А. Оболочки и пластины. М.: ГИТТЛ, 1971. 696 с.
Майлыбаев А.А., Сейранян А.П. Многопараметрические задачи устойчивости. Теория и приложения в механике. М.: Физматлит, 2009. 400 с.
Соломонов Ю.С., Георгиевский В.П., Недбай А.Я., Андрюшин В.А. Прикладные задачи механики композитных цилиндрических оболочек. М.: Физматлит, 2014. 408 с.
Бакулин В.Н., Волков Е.Н., Недбай А.Я. Флаттер слоистой цилиндрической оболочки, подкрепленной кольцевыми ребрами и нагруженной осевыми силами // ДАН. 2015. Т. 463. № 4. С. 414–417.
Бакулин В.Н., Волков Е.Н., Недбай А.Я. Динамическая устойчивость цилиндрической оболочки, подкрепленной продольными ребрами и пустотелым цилиндром при действии осевых сил // Инж.-физ. журн. 2016. Т. 89. № 3. С. 742–747.
Бакулин В.Н., Волков Е.Н., Симонов А.И. Динамическая устойчивость цилиндрической оболочки при действии переменного по оси внешнего давления // Изв. вузов. Авиационная техника. 2017. № 4. С. 11–17.
Бакулин В.Н., Данилкин Е.В., Недбай А.Я. Динамическая устойчивость цилиндрической оболочки, подкрепленной цилиндром и продольными диафрагмами, при внешнем давлении // Инж.-физ. журн. 2018. Т. 91. № 2. С. 564–570.
Бакулин В.Н., Недбай А.Я., Шепелева И.О. Динамическая устойчивость ортотропной цилиндрической оболочки кусочно-постоянной толщины при действии внешнего пульсирующего давления // Изв. вузов. Авиационная техника. 2019. № 2. С. 19–25.
Соломонов Ю.С., Георгиевский В.П., Недбай А.Я., Волков Е.Н. Динамическая устойчивость слоистой цилиндрической оболочки, подкрепленной кольцевыми ребрами и цилиндром, при внешнем давлении // Механика композиционных материалов и конструкций. 2013. Т. 19. № 4. С. 614–623.
Бакулин В.Н., Конопельчев М.А., Недбай А.Я. Аэроупругая устойчивость композитной цилиндрической оболочки линейно-переменной толщины // ДАН. 2019. Т. 488. № 1. С. 595–601.
Соколов Е.В., Видюшенков С.А. Пластинки и оболочки вращения с разрывными грузовыми и жесткостными характеристиками. СПб: СПбГУ, 2010. 265 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал