Доклады Российской академии наук. Физика, технические науки, 2021, T. 500, № 1, стр. 48-52

Как известно [1, 2], релаксационный процесс характеризует стремление любой физической системы к равновесию. Такое стремление происходит далеко не с одинаковой скоростью для всех внутренних степеней свободы, описывающих динамику физической системы, и представляет собой многоступенчатый процессc множеством времен релаксаций, каждое из которых описывает его на различных масштабных уровнях. Для задач классической механики сплошной среды, в силу рассмотрения только коллективного движения частиц в элементарном объеме сплошной среды, процессы релаксации удовлетворяют известным уравнениям Эйлера и отличаются только в силу использования разных уравнений состояния сплошной среды.

Другая ситуация возникает, когда описание материала требует учета влияния на коллективное движение частиц новых степеней свободы, к примеру, их относительного движения или появления примесных частиц, дефектов. В этом случае обычно используется модель взаимопроникающих континуумов [3] или функционал свободной энергии с параметром концентрации примеси [4], которые позволяют получать новые уравнения состояния с эффективными параметрами, меняющимися согласно кинетическим и диффузионным уравнениям. В этом случае при динамическом воздействии на такую систему общий релаксационный процесс имеет два спектральных отклика. Первый из них определяется характерными временами динамического процесса, связанного с распространением волн в занимаемых областях сплошной среды. Кроме этого, на коллективную динамику частиц физической системы накладывается процесс, порождаемый движением дополнительных степеней свободы, которые обычно определяются диффузионными уравнениями с параметрами, зависящими от микроструктуры.

Таким образом, возникает самостоятельная проблема выделения из общего сигнала информации о содержании в материале дефектов различной природы, в частности включений и вакансий. Чтобы учесть их влияние, предлагается использовать двухкомпонентную модель материала [5], согласно которой его плотность равна суммарной плотности каждой из компонент. Тогда принимается, что связь между шаровой частью тензора напряжений $\sigma $ и изменением плотности материала $\Delta \rho $ имеет вид

где $\Delta {{\rho }_{f}}$– изменение плотности дефектов, ${{\rho }_{0}}$ – исходная плотность материала в недеформированном состоянии, K – модуль объемного расширения. Параметр $\Omega $ принимает значение 1 для включений и –1 в случае вакансий. При справедливости закона Фика плотность дефектов удовлетворяет диффузионному уравнению с источниковым членом $F({{\rho }_{f}},T)$, зависящим от температуры $T$ и определяющим скорость производства дефектов [4]. Если считать, что вся область с дефектами охвачена диффузионным процессом, то раскладывая функцию F в ряд Тейлора около равновесного состояния F(ρ_f0 + Δρ_f, ${{T}_{0}} + \vartheta )\, \approx \,F({{\rho }_{{f0}}},{{T}_{0}})\, + \,\frac{A}{{{{\tau }_{F}}}}\Delta {{\rho }_{f}}$ + Bϑ и вводя характерное время ${{\tau }_{f}} = \frac{{{{l}^{2}}}}{D}$, можно рассматривать релаксационную модель, описываемую линейным уравнением

Здесь введены следующие обозначения: ${{\rho }_{f}}_{0}$ – исходная плотность дефектов, ${{T}_{0}}$ – равновесная температура, $l$ – размер области, D – коэффициент диффузии, ${{\tau }_{r}} = \frac{{{{\tau }_{f}}{{\tau }_{F}}}}{{{{\tau }_{F}} - A{{\tau }_{f}}}}$ – эффективное время релаксации, τ_F – время образования дефекта. Константы A и B определяются физическим законом, управляющим источниковым членом, в качестве которого, к примеру, может быть взято соотношение Аррениуса [6]. В отсутствие собственной кинематики и источникового члена влияние дефектов сводится к изменению модуля объемного расширения, новое значение которого определяется выражением ${{K}_{{ef}}} = K\left( {1 + \Omega \frac{{{{\rho }_{{f0}}}}}{{{{\rho }_{0}}}}} \right)$. После интегрирования уравнения (2) и подстановки полученного результата в уравнение (1), при выполнении условий $\frac{{{{\rho }_{{{{f}_{0}}}}}}}{{{{\rho }_{0}}}} \ll 1{\text{ }}$ и ${{e}^{{ - \frac{t}{{{{t}_{r}}}}}}} \ll 1$, оно приобретает вид, соответствующий модели упруго-вязкого материала Кельвина–Фойгтаc дополнительным слагаемым, определяющим операторную зависимость от времени коэффициента линейного теплового расширения. При использовании преобразования Лапласа  f  ^L = $\int\limits_0^\infty {f(t){{e}^{{ - pt}}}dt} $ закон деформирования твердого тела может быть представлен в форме аналогичной закону Дюамеля–Неймана

однако модули $K(p)$ и $\alpha (p)$ не являются константами, а имеют динамический характер. При этом наиболее существенное влияние на термоакустический сигнал оказывает зависимость $\alpha (p)$ [7].

В качестве примера рассматривается модельная одномерная задача, где дефект в виде сосредоточенной массы расположен на торце полубесконечного стержня с модулем Юнга E и плотностью $\rho $. Будем полагать, что для него выполняются закон Фурье и соотношение Дюамеля–Неймана. Тогда динамические уравнения термоупругости [8] имеют вид

Здесь введены следующие обозначения: $u$ – смещение материальной точки, $k$ – коэффициент температуропроводности, ${{c}_{0}} = \sqrt {\frac{E}{\rho }} $ – скорость звука, $\alpha $ – коэффициент линейного теплового расширения. Описание динамики дефекта в виде сосредоточенного включения массой m требует введения дополнительной степени свободы ${{q}_{f}}(t)$, отвечающей его перемещению и удовлетворяющей уравнению $m{{\ddot {q}}_{f}} = F$, где через F обозначены силы, действующие на него со стороны стержня. Вид данной силы зависит от условий сопряжения. Здесь рассматривается простейший случай абсолютно жесткого контакта, когда перемещение дефекта на торце совпадает с перемещением стержня. Напряжения, возникающие в данной точке, уравновешиваются действием сил инерции от сосредоточенной массы. Действие теплового источника на границе задается в виде потока тепла, определяемого функцией $W(t)$. В этом случае граничные условия для системы уравнений (4)–(5) принимают вид

где h – это линейный размер дефекта, а через $\chi = \frac{{{{\rho }_{f}}}}{\rho }$ обозначено отношение плотности дефекта к плотности материала. Перейдя к безразмерным переменным ${{x}_{d}} = \frac{{{{c}_{0}}x}}{k}$, ${{t}_{d}} = \frac{{c_{0}^{2}t}}{k}$ и решив систему (4)–(7) с помощью преобразования Лапласа, нетрудно найти аналитическое представление для температуры $\vartheta $ и деформации $\varepsilon = \frac{{\partial u}}{{\partial x}}$ в изображениях где ${{\tau }_{d}} = \frac{{{{c}_{0}}\chi h}}{k}$ – безразмерное время релаксации, представляющее собой отношение произведения плотности дефекта на его линейный размер к акустическому сопротивлению среды. Данный параметр характеризует как свойства дефекта, так и самой среды, от которых зависит релаксационный процесс возвращения системы к исходному состоянию. При ${{\tau }_{d}} = 0$ выражение (9) переходит в хорошо известное решение, приведенное во многих работах [9, 10], которое мы обозначим через $\varepsilon _{c}^{L}$.

Используя его, выражение (9) можно представить в виде cуммы ${{\varepsilon }^{L}} = \varepsilon _{c}^{L} + \varepsilon _{D}^{L}$, где второе слагаемое

связанное с наличием инерционного включения, представляет собой акустическую волну, имеющую в районе фронта противоположный знак по отношению к классическому решению. Когда тепловой поток на границе W(t) имеет форму прямоугольного импульса высотой W₀ и длительностью ${{t}_{0}}$, т.е. $W(t) = {{W}_{0}}\left( {H(t) - H(t - {{t}_{0}})} \right)$, где H(t) – функция Хевисайда, то зависимость нормированной деформации ${{\varepsilon }_{d}} = \frac{{{{\varepsilon }_{D}}{{c}_{0}}}}{{\alpha {{W}_{0}}}}$ от времени, которая при числовых значениях параметров, близких к харак-теристикам алюминия (${{с}_{0}} = 6$ × 10³ м/с, $k = 1$ × × 10^–4 м²/с) и ${{t}_{{0d}}} = \frac{{c_{0}^{2}{{t}_{0}}}}{k} = 0.1$ соответствует пикосекундному воздействию, для ${{x}_{d}} = 0$ приведена на рис. 1.

Из представленного результата следует, что наибольшее влияние на амплитуду акустического сигнала имеет место, когда длительность импульса много меньше или сопоставима с временем релаксации ${{\tau }_{d}}$.

На границе области, где размещено инерционное включение, решение (9) с учетом выражения (8) можно записать в форме

аналогичной закону Дюамеля–Неймана при свободном расширении тела. Динамическая составляющая коэффициента линейного теплового расширения ${{\alpha }_{D}}(p)$, зависящая от вренени релаксации, определяется передаточной функцией

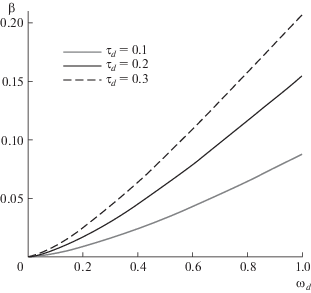
Зависимость эффективного коэффициента линейного теплового расширения от частоты на основе релаксационного уравнения (2) была введена в работе [11] c целью описания влияния точечных дефектов в алюминиевых мембранах на термоакустический сигнал при лазерном воздействии с частотой модуляции в несколько килогерц. На рис. 2 приведена спектральная характеристика данной функции для пикосекундного воздействия, где ${{\omega }_{d}}$ – безразмерная частота.

Из рис. 2 видно, что инерционное включение изменяет высокочастотную составляющую акустического сигнала, тогда как низкочастотная часть будет определяться эволюционным уравнением дефектной структуры.

Таким образом, наличие дефектов, занимающих поверхностную область в материале, может оказывать существенное влияние на спектральную характеристику коэффициента линейного теплового расширения, особенно при нестационарном воздействии. Показано, что при определенной длительности теплового воздействия оно приводит к уменьшению амплитуды волны деформаций, что важно с точки зрения как диагностики дефектной структуры, так и оценки напряженного состояния. В данной работе рассмотрен случай, когда она представляет собой сосредоточенное включение, характеризующееся линейным размером и расположенное на границе полубесконечной области, а время релаксации определяется временем пробега акустической волны по его длине. В общем случае, когда дефекты занимают поверхностный слой, определение данного параметра требует решения контактной задачи на границе между поверхностным слоем и чистым материалом.