Доклады Российской академии наук. Физика, технические науки, 2021, T. 500, № 1, стр. 34-38

О КОЛЕБАТЕЛЬНЫХ ДИССИПАТИВНЫХ СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ

А. Г. Петров^1, *

¹ Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия

Поступила в редакцию 07.04.2021
После доработки 16.08.2021
Принята к публикации 23.08.2021

DOI: 10.31857/S2686740021050072

Аннотация

Рассматриваются вынужденные линейные колебания диссипативных механических систем с двумя степенями свободы под действием периодических по времени сил. Уравнения в форме Лагранжа выражаются через три положительно определенные квадратичные формы: кинетическая энергия, диссипативная функция и потенциальная энергия. Показано, при условии равенства нулю определителя третьего порядка коэффициентов квадратичных форм все три квадратичные формы приводятся к сумме квадратов с некоторыми коэффициентами. В этом случае система уравнений четвертого порядка уравнения расщепляются на два независимых уравнения второго порядка для линейных осцилляторов, для которых решение системы находится в общем аналитическом виде. Эффективность метода демонстрируется на анализе вынужденных колебаний двойного маятника.

Ключевые слова: вынужденные линейные колебания, квадратичные формы, канонический вид, двойной маятник

ВВЕДЕНИЕ

Многие задачи интегрирования и качественного анализа дифференциальных уравнений значительно упрощаются после приведения исследуемых объектов к соответствующим нормальным формам. Необходимость в таком анализе возникает, например, для исследования малых колебаний механических систем [1, 2]. Консервативные механические системы характеризуются двумя квадратичными формами: кинетической и потенциальной энергией системы. Для них всегда существуют нормальные координаты, в которых обе квадратичные формы приводятся к сумме квадратов с некоторыми коэффициентами [3], а уравнения свободных и вынужденных колебаний расщепляются на независимые уравнения второго порядка (линейные осцилляторы). В диссипативных системах появляется третья квадратичная форма – функция Рэлея, определяющая линейные по скоростям обобщенные силы [1, 2].

Три квадратичные формы привести к сумме квадратов почти всегда невозможно, и поэтому система на независимые осцилляторы не расщепляется. Анализ таких систем сильно осложняется, даже в случае двух степеней свободы.

Наиболее общее условие приведения трех квадратичных форм с матрицами A, $B$ и $C$ к сумме квадратов получено Новиковым [4]:

$B{{A}^{{ - 1}}}C = C{{A}^{{ - 1}}}B.$

Для двух степеней свободы условие равносильно четырем равенствам нулю элементов соответствующей матрицы.

В данной работе вместо четырех условий получено одно простое необходимое и достаточное условие: равенство нулю определителя третьего порядка коэффициентов трех квадратичных форм. Вывод условия тоже упрощается и проводится, не опираясь на результат [4].

Дан пример применения полученного условия для анализа малых колебаний двойного маятника с учетом сил вязкого трения, линейных по скоростям [1, 2].

1. МАЛЫЕ КОЛЕБАНИЯ

Рассмотрим систему с двумя степенями свободы. Кинетическая $T$ и потенциальная $\Pi $ энергия, диссипативная функция Рэлея $R$ и мощность внешних сил $N$ имеют вид

(1)

$\begin{array}{*{20}{c}} \begin{gathered} T = \frac{1}{2}\left( {{{a}_{{11}}}\dot {x}_{1}^{2} + 2{{a}_{{12}}}{{{\dot {x}}}_{1}}{{{\dot {x}}}_{2}} + {{a}_{{22}}}\dot {x}_{2}^{2}} \right), \hfill \\ R = \frac{1}{2}\left( {{{b}_{{11}}}\dot {x}_{1}^{2} + 2{{b}_{{12}}}{{{\dot {x}}}_{1}}{{{\dot {x}}}_{2}} + {{b}_{{22}}}\dot {x}_{2}^{2}} \right), \hfill \\ \end{gathered} \\ \begin{gathered} \Pi = \frac{1}{2}\left( {{{c}_{{11}}}x_{1}^{2} + 2{{c}_{{12}}}{{x}_{1}}{{x}_{2}} + {{c}_{{22}}}x_{2}^{2}} \right), \\ N = ({{U}_{1}}{{{\dot {x}}}_{1}} + {{U}_{2}}{{{\dot {x}}}_{2}})sin\omega t. \\ \end{gathered} \end{array}$

Запишем уравнения движения механической системы, в которой $\Pi $, $R$ и $N$ определяют потенциальную, диссипативную и внешнюю силу, меняющуюся по гармоническому закону с амплитудами ${{U}_{1}}$, ${{U}_{2}}$:

(2)

$\frac{d}{{dt}}\frac{{\partial T}}{{\partial {{{\dot {x}}}_{i}}}} + \frac{{\partial R}}{{\partial {{{\dot {x}}}_{i}}}} + \frac{{\partial \Pi }}{{\partial {{x}_{i}}}} = \frac{{\partial N}}{{\partial {{{\dot {x}}}_{i}}}},\quad i = 1,2.$

В разделе 3 доказано, если определитель коэффициентов квадратичных форм равен нулю

(3)

$\Delta = \left| {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{22}}}} \\ {{{b}_{{11}}}}&{{{b}_{{12}}}}&{{{b}_{{22}}}} \\ {{{c}_{{11}}}}&{{{c}_{{12}}}}&{{{c}_{{22}}}} \end{array}} \right| = 0,$

то существует линейная замена

$Y = QX,\quad X = \left( {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \end{array}} \right),\quad Y = \left( {\begin{array}{*{20}{c}} {{{y}_{1}}} \\ {{{y}_{2}}} \end{array}} \right),\quad Q = \left( {\begin{array}{*{20}{c}} {{{q}_{{11}}}}&{{{q}_{{12}}}} \\ {{{q}_{{21}}}}&{{{q}_{{22}}}} \end{array}} \right),$

приводящая три квадратичные формы к сумме квадратов

$\begin{gathered} \frac{1}{2}\left( {a_{{11}}^{'}y_{1}^{2} + a_{{22}}^{'}y_{2}^{2}} \right), \\ \frac{1}{2}\left( {b_{{11}}^{'}y_{1}^{2} + b_{{22}}^{'}y_{2}^{2}} \right), \\ \frac{1}{2}\left( {c_{{11}}^{'}y_{1}^{2} + c_{{22}}^{'}y_{2}^{2}} \right), \\ \end{gathered} $

а уравнения (2) расщепляются на два независимых уравнения второго порядка для простейших ленейных осцилляторов

(4)

$\begin{array}{*{20}{c}} {\frac{{{{d}^{2}}y}}{{d{{t}^{2}}}} + {{A}_{i}}\frac{{dy}}{{dt}} + {{B}_{i}}y = {{E}_{i}}{\text{sin}}\omega t,\quad i = 1,2,} \\ {{{E}_{1}} = {{U}_{1}}{{q}_{{11}}} + {{U}_{2}}{{q}_{{21}}},\quad {{E}_{2}} = {{U}_{1}}{{q}_{{12}}} + {{U}_{2}}{{q}_{{22}}}.} \end{array}$

Анализ такой системы значительно упрощается. Решение для установившихся колебаний имеет вид

(5)

$\begin{array}{*{20}{c}} \begin{gathered} {{y}_{i}} = {{P}_{i}}sin\omega t - {{Q}_{i}}cos\omega t, \\ {{P}_{i}} = \frac{{{{E}_{i}}({{B}_{i}} - {{\omega }^{2}})}}{{{{{({{B}_{i}} - {{\omega }^{2}})}}^{2}} + A_{i}^{2}{{\omega }^{2}}}}, \\ {{Q}_{i}} = \frac{{{{E}_{i}}{{A}_{i}}\omega }}{{{{{({{B}_{i}} - {{\omega }^{2}})}}^{2}} + A_{i}^{2}{{\omega }^{2}}}}. \\ \end{gathered} \end{array}$

Амплитуды колебаний

(6)

$\begin{array}{*{20}{c}} {{{a}_{i}} = \sqrt {P_{i}^{2} + Q_{i}^{2}} = \frac{{{{E}_{i}}}}{{\sqrt {{{{({{B}_{i}} - {{\omega }^{2}})}}^{2}} + A_{i}^{2}{{\omega }^{2}}} }},\quad i = 1,2.} \end{array}$

Для описания переходного процесса, из состояния покоя до установления необходимо решить уравнение (4) с начальными условиями $y(0) = 0$, $\dot {y}(0) = 0$. Решение имеет вид

(7)

$\begin{array}{*{20}{c}} {{{y}_{i}}(t) = {{P}_{i}}{\text{sin}}\omega t - {{Q}_{i}}{\text{cos}}\omega t + {{J}_{i}}(t),\quad {{\omega }_{i}} = \sqrt {B_{i}^{2} - A_{i}^{2}{\text{/}}4} ,} \\ {{{J}_{i}}(t)\, = \,{{e}^{{ - At/2}}}\left( {\left( {\frac{{{{Q}_{i}} - 2{{P}_{i}}\omega }}{{2{{\omega }_{i}}}}} \right)sin({{\omega }_{i}}t) + {{Q}_{i}}cos({{\omega }_{i}}t)} \right).} \end{array}$

Полезность полученных формул ниже демонстрируется на исследовании малых вынужденных колебаний двойного плоского маятника с учетом сил трения.

2. ДВОЙНОЙ ПЛОСКИЙ МАЯТНИК

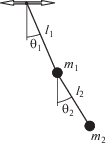
Рассмотрим малые колебания около положения равновесия двойного плоского маятника, у которого точка подвеса движется по горизонтали по гармоническому закону $x = asin\omega t$ (рис. 1).

Рис. 1.

Двойной маятник.

Стандартная методика [1, 2] сводит эту задачу к решению линейной системы четвертого порядка. Точное ее решение в силу большой громоздкости не выписывается и обычно ограничиваются качественным приближенным анализом. Если же подчинить параметры системы единственному условию (3), то система расщепится на два простейших линейных осциллятора, точное решение которых дается весьма простыми формулами (5), (7).

Запишем уравнения маятника в форме Лагранжа (1), (2) относительно углов ${{\theta }_{1}}$, ${{\theta }_{2}}$ [5]. В кинетической $T$ и потенциальной $\Pi $ энергиях и диссипативной функции $R$ учтем только квадратичные члены.

$\begin{array}{*{20}{c}} {T = \frac{1}{2}({{m}_{1}} + {{m}_{2}})l_{1}^{2}\dot {\theta }_{1}^{2} + \frac{{{{m}_{2}}}}{2}l_{2}^{2}\dot {\theta }_{2}^{2} + {{m}_{2}}{{l}_{1}}{{l}_{2}}{{{\dot {\theta }}}_{1}}{{{\dot {\theta }}}_{2}},} \\ {R = \frac{1}{2}{{r}_{1}}\dot {\theta }_{1}^{2} + \frac{1}{2}{{r}_{2}}{{{(\mathop {\dot {\theta }}\nolimits_2 - \mathop {\dot {\theta }}\nolimits_1 )}}^{2}},} \\ {\Pi = \frac{1}{2}({{m}_{1}} + {{m}_{2}})g{{l}_{1}}\theta _{1}^{2} + \frac{1}{2}{{m}_{2}}g{{l}_{2}}\theta _{2}^{2},} \\ {N = a{{\omega }^{2}}(({{m}_{1}} + {{m}_{2}}){{l}_{1}}\mathop {\dot {\theta }}\nolimits_1 + {{m}_{2}}{{l}_{2}}\mathop {\dot {\theta }}\nolimits_2 )sin\omega t,} \end{array}$

где предполагается линейный по относительной угловой скорости закон вязкого трения в шарнирах с коэффициентами ${{r}_{1}}$, ${{r}_{2}}$.

Из равенства нулю определителя коэффициентов квадратичных форм (3) вытекает: $\frac{{{{r}_{2}}}}{{{{r}_{1}}}} = \frac{{{{m}_{2}}}}{{{{m}_{1}}}}$, т.е. коэффициенты трения должны быть пропорциональны массам ${{r}_{1}} = r{{m}_{1}}$, ${{r}_{2}} = r{{m}_{2}}$. При этом условии все функции T, $R$, $\Pi $ приведутся к сумме квадратов. Чтобы найти такое преобразование, сначала делается замена переменных θ₁ = $\frac{{{{\xi }_{1}}}}{{\sqrt {g{{l}_{1}}({{m}_{1}} + {{m}_{2}})} }}$, ${{\theta }_{2}} = \frac{{{{\xi }_{2}}}}{{\sqrt {g{{l}_{2}}{{m}_{2}}} }}$, приводящая квадратичные формы к виду

$\begin{gathered} T = \frac{1}{2}(a_{{11}}^{'}\mathop {\dot {y}}\nolimits_1^2 + 2a_{{12}}^{'} + a_{{22}}^{'}\mathop {\dot {y}}\nolimits_2^2 ), \\ R = \frac{1}{2}(b_{{11}}^{'}\mathop {\dot {y}}\nolimits_1^2 + 2b_{{12}}^{'} + b_{{22}}^{'}\mathop {\dot {y}}\nolimits_2^2 ),\quad \Pi = \frac{1}{2}(y_{1}^{2} + y_{2}^{2}), \\ a_{{11}}^{'} = \frac{{{{l}_{1}}}}{g},\quad a_{{22}}^{'} = \frac{{{{l}_{2}}}}{g},\quad a_{{12}}^{'} = \sqrt {{{l}_{1}}{{l}_{2}}\mu } ,\quad \mu = \frac{{{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}, \\ b_{{11}}^{'} = \frac{r}{{({{l}_{1}}{{l}_{2}})a_{{22}}^{'}}},\quad b_{{22}}^{'} = \frac{r}{{({{l}_{1}}{{l}_{2}})a_{{11}}^{'}}},\quad b_{{12}}^{'} = - \frac{r}{{({{l}_{1}}{{l}_{2}})a_{{12}}^{'}}}. \\ \end{gathered} $

Построим, следуя [3], ортогональное преобразование, приводящее первую матрицу к диагональному виду. Для этого надо найти собственное число ${{\lambda }_{1}}$ и единичный собственный вектор ${{e}_{1}}$, ${{e}_{2}}$ из решения системы

$\left( {\begin{array}{*{20}{c}} {a_{{11}}^{'} - {{\lambda }_{1}}}&{a_{{11}}^{'}} \\ {a_{{12}}^{'}}&{a_{{22}}^{'} - {{\lambda }_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{e}_{1}}} \\ {{{e}_{2}}} \end{array}} \right) = 0.$

Второе собственное число ${{\lambda }_{2}}$ находится из аналогичного уравнения. Второй собственный вектор ортогонален первому. Они имеют вид

$\begin{array}{*{20}{c}} \begin{gathered} {{\lambda }_{1}} = \frac{1}{{2g}}({{l}_{1}} + {{l}_{2}} - ({{l}_{1}} - {{l}_{2}})\sqrt {1 + M} ), \\ {{\lambda }_{2}} = \frac{1}{{2g}}({{l}_{1}} + {{l}_{2}} + ({{l}_{1}} - {{l}_{2}})\sqrt {1 + M} ), \\ \end{gathered} \\ \begin{gathered} {{e}_{1}} = \sqrt {\frac{1}{2}\left( {1 - \frac{1}{{\sqrt {1 + M} }}} \right)} , \\ {{e}_{2}} = \sqrt {\frac{1}{2}\left( {1 + \frac{1}{{\sqrt {1 + M} }}} \right)} ,\quad M = \frac{{4{{l}_{1}}{{l}_{2}}\mu }}{{{{{({{l}_{1}} - {{l}_{2}})}}^{2}}}}. \\ \end{gathered} \end{array}$

Преобразование ${{\xi }_{1}} = {{e}_{1}}{{y}_{1}} + {{e}_{2}}{{y}_{2}}$, ${{\xi }_{2}} = - {{e}_{2}}{{y}_{1}} + {{e}_{1}}{{y}_{2}}$ приводит первую и вторую матрицы к диагональному виду. Собственные значения матрицы $R$ с точностью до множителя $r{\text{/}}({{l}_{1}}{{l}_{2}})$ совпадают с собственными значениями матрицы T, но меняются местами.

В преобразованных переменных функции T, $R$, $\Pi $ и $N$ примут вид

$\begin{array}{*{20}{c}} \begin{gathered} T = \frac{1}{2}\left( {{{\lambda }_{1}}\dot {y}_{1}^{2} + {{\lambda }_{2}}\dot {y}_{2}^{2}} \right),\quad R = \frac{r}{{2{{l}_{1}}{{l}_{2}}}}\left( {{{\lambda }_{2}}\dot {y}_{1}^{2} + {{\lambda }_{1}}\dot {y}_{2}^{2}} \right), \\ \Pi = \frac{1}{2}\left( {y_{1}^{2} + y_{2}^{2}} \right), \\ \end{gathered} \\ \begin{gathered} N = \frac{{a{{\omega }^{2}}}}{{\sqrt g }}\left( {\sqrt {{{m}_{2}}{{l}_{2}}} ( - {{e}_{2}}{{y}_{1}} + {{e}_{1}}{{y}_{2}})} \right. + \\ + \;\left. {\sqrt {({{m}_{1}} + {{m}_{2}}){{l}_{1}}} ({{e}_{1}}{{y}_{1}} + {{e}_{2}}{{y}_{2}})} \right), \\ \end{gathered} \end{array}$

а система уравнений приведется к виду (4), в которой

$\begin{array}{*{20}{c}} {{{A}_{1}} = \frac{r}{{{{l}_{1}}{{l}_{2}}}}\frac{{{{\lambda }_{2}}}}{{{{\lambda }_{1}}}},\quad {{A}_{2}} = \frac{r}{{{{l}_{1}}{{l}_{2}}}}\frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}}},\quad {{B}_{1}} = \frac{1}{{{{\lambda }_{1}}}},\quad {{B}_{2}} = \frac{1}{{{{\lambda }_{2}}}},} \\ {{{E}_{1}} = \frac{{a{{\omega }^{2}}}}{{{{\lambda }_{1}}\sqrt g }}( - {{e}_{2}}\sqrt {{{l}_{2}}{{m}_{2}}} + {{e}_{1}}\sqrt {{{l}_{1}}({{m}_{1}} + {{m}_{2}})} ),} \\ {{{E}_{2}} = \frac{{a{{\omega }^{2}}}}{{{{\lambda }_{2}}\sqrt g }}({{e}_{1}}\sqrt {{{l}_{2}}{{m}_{2}}} + {{e}_{2}}\sqrt {{{l}_{1}}({{m}_{1}} + {{m}_{2}})} ).} \end{array}$

Подставляя найденные коэффициенты ${{A}_{1}}$, ${{A}_{2}}$, ${{B}_{1}}$, ${{B}_{2}}$, ${{E}_{1}}$, ${{E}_{2}}$ в формулы (5), получим решение для установившихся колебаний маятника, а в формулы (7) – решение для переходного процесса. С помощью (6) находится амплитудная характеристика в переменных ${{y}_{1}}$, ${{y}_{2}}$. В исходных переменных решение выражается через функции ${{y}_{1}},{{y}_{2}}$:

(8)

${{\theta }_{1}} = \frac{{{{e}_{1}}{{y}_{1}} + {{e}_{2}}{{y}_{2}}}}{{\sqrt {g{{l}_{1}}({{m}_{1}} + {{m}_{2}})} }},\quad {{\theta }_{2}} = \frac{{ - {{e}_{2}}{{y}_{1}} + {{e}_{1}}{{y}_{2}}}}{{\sqrt {g{{l}_{2}}{{m}_{2}}} }}.$

В частном случае ${{l}_{1}} = {{l}_{2}} = l$ формулы упрощаются:

(9)

$\begin{array}{*{20}{c}} {{{\lambda }_{{1,2}}} = \frac{l}{g}(1 \mp \sqrt \mu ),\quad {{x}_{{1,2}}} = \frac{1}{{\sqrt 2 }}( - {{y}_{1}} \pm {{y}_{2}})),} \\ \begin{gathered} {{A}_{1}} = \frac{r}{{{{l}^{2}}}}\frac{{1 + \sqrt \mu }}{{1 - \sqrt \mu }},\quad {{A}_{2}} = \frac{r}{{{{l}^{2}}}}\frac{{1 - \sqrt \mu }}{{1 + \sqrt \mu }}, \hfill \\ {{B}_{1}} = \frac{g}{{l(1 - \sqrt \mu )}},\quad {{B}_{2}} = \frac{g}{{l(1 + \sqrt \mu )}}, \hfill \\ \end{gathered} \\ \begin{gathered} {{E}_{1}} = {{E}_{2}} = {{E}_{0}}{{\omega }^{2}},\quad {{E}_{0}} = a\sqrt {\frac{g}{{2l}}({{m}_{1}} + {{m}_{2}})} , \\ - {{e}_{1}} = {{e}_{2}} = \frac{1}{{\sqrt 2 }}. \\ \end{gathered} \end{array}$

Полное описание колебаний можно получить подстановкой найденных выражений ${{A}_{i}}$, ${{B}_{i}}$, ${{E}_{i}}$ в формулы (5), (7).

Подстановкой (9) в формулу (6) находятся амплитуды нормальных переменных ${{y}_{1}}$ и ${{y}_{2}}$ и их наибольшие значения:

$\begin{gathered} {{a}_{{yi}}} = \frac{{{{E}_{0}}{{\omega }^{2}}}}{{\sqrt {{{{({{B}_{i}} - {{\omega }^{2}})}}^{2}} + A_{i}^{2}{{\omega }^{2}}} }}, \\ {\text{max}}({{a}_{{yi}}}) = \frac{{2{{E}_{0}}{{B}_{i}}}}{{{{A}_{i}}\sqrt {4{{B}_{i}} - A_{i}^{2}} }},\quad i = 1,2, \\ \end{gathered} $

которые достигаются при ω = $\tfrac{{{{B}_{1}}}}{{\sqrt {{{B}_{1}} - A_{1}^{2}} }}$ и ω = = $\tfrac{{{{B}_{2}}}}{{\sqrt {{{B}_{2}} - A_{2}^{2}} }}$.

С помощью (9) находится отношение максимальных амплитуд

$\begin{gathered} \frac{{{\text{max}}({{a}_{{y2}}})}}{{{\text{max}}({{a}_{{y1}}})}} = \frac{{{{{(1 + \sqrt \mu )}}^{{3/2}}}\mathop {\left( {1 - {{\varepsilon }^{2}}\tfrac{{{{{(1 + \sqrt \mu )}}^{2}}}}{{4(1 - \sqrt \mu )}}} \right)}\nolimits^{1/2} }}{{{{{(1 - \sqrt \mu )}}^{{3/2}}}\mathop {\left( {1 - {{\varepsilon }^{2}}\tfrac{{{{{(1 - \sqrt \mu )}}^{2}}}}{{4(1 + \sqrt \mu )}}} \right)}\nolimits^{1/2} }}, \\ \varepsilon = \frac{r}{{\sqrt {g{{l}^{3}}} }}. \\ \end{gathered} $

В диапазоне параметров $\mu \in (1{\text{/}}2,\;1)$, $\varepsilon \in (0,\;1{\text{/}}2)$ значение ${\text{max}}({{a}_{{y2}}})$ превосходит ${\text{max}}({{a}_{{y1}}})$ более чем в 9 раз. Поэтому для амплитудных характеристик углов вместо формул (8) можно пользоваться упрощенными формулами

(10)

${{\theta }_{1}} \approx \mu {{\theta }_{2}},\quad {{\theta }_{2}} \approx \frac{{{{y}_{2}}}}{{\sqrt {2gl{{m}_{2}}} }}.$

Наибольшие значения амплитуд углов ${{\theta }_{1}}$ и ${{\theta }_{2}}$ достигаются при частоте $\omega = \tfrac{{{{B}_{2}}}}{{\sqrt {{{B}_{2}} - A_{2}^{2}{\text{/}}2} }}.$ Используя (9) и (10), находим

(11)

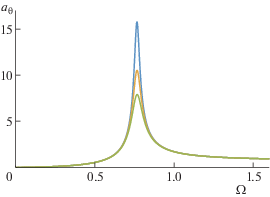
$\begin{array}{*{20}{c}} \begin{gathered} {\text{max}}({{\theta }_{1}}) \approx \frac{{{\text{max}}({{a}_{{y2}}})}}{{\sqrt {2gl({{m}_{1}} + {{m}_{2}})} }} = \\ = \;\frac{a}{{2l\varepsilon }}\frac{{\sqrt {1 + \sqrt \mu } }}{{(1 - \sqrt \mu )}}\mathop {\left( {1 - {{\varepsilon }^{2}}\frac{{{{{(1 - \sqrt \mu )}}^{2}}}}{{4(1 + \sqrt \mu )}}} \right)}\nolimits^{ - 1/2} , \\ \end{gathered} \\ {{\text{max}}({{\theta }_{2}}) \approx \frac{{{\text{max}}({{\theta }_{1}})}}{{\sqrt \mu }}.} \end{array}$

На рис. 2 изображены амплитудно-частотные характеристики для угла ${{\theta }_{2}}$ при $\varepsilon = 0.2,0.3$ и $0.4$ и ${{m}_{1}} = {{m}_{2}}$. По оси абсцисс откладывается безразмерная частота $\Omega = \frac{\omega }{{\sqrt {g{\text{/}}l} }}$, а по оси ординат – амплитуда угла, отнесенная к величине $\frac{a}{l}$. При увеличении диссипационного параметра $\varepsilon $ максимум амплитуды уменьшается по закону:

$\begin{gathered} {\text{max}}({{\theta }_{1}}) \approx 2.23\left( {\frac{a}{l}} \right){{({{\varepsilon }^{2}} - 0.012{{\varepsilon }^{4}})}^{{ - 1/2}}}, \\ {\text{max}}({{\theta }_{2}}) \approx 1.44{\text{max}}({{\theta }_{1}}). \\ \end{gathered} $

Рис. 2.

Амплитудно-частотная характеристика.

Приведенные графики приближенных формул (10) неотличимы от графиков, построенных по точным формулам.

На параметры задачи следует наложить условие ${\text{max}}({{\theta }_{2}}) \ll 1$, чтобы линейная теория колебаний была применима.

3. ТЕОРЕМА ОБ УСЛОВИИ ПРИВЕДЕНИЯ ТРЕХ НЕВЫРОЖДЕННЫХ МАТРИЦ К ДИАГОНАЛЬНОЙ ФОРМЕ

Пусть даны три квадратичные формы двух переменных:

$\begin{array}{*{20}{c}} \begin{gathered} {{f}_{1}} = \frac{1}{2}({{a}_{{11}}}x_{1}^{2} + 2{{a}_{{12}}}{{x}_{1}}{{x}_{2}} + {{a}_{{22}}}x_{2}^{2}), \hfill \\ {{f}_{2}} = \frac{1}{2}({{b}_{{11}}}x_{1}^{2} + 2{{b}_{{12}}}{{x}_{1}}{{x}_{2}} + {{b}_{{22}}}x_{2}^{2}), \hfill \\ \end{gathered} \\ {{{f}_{3}} = \frac{1}{2}({{c}_{{11}}}x_{1}^{2} + 2{{c}_{{12}}}{{x}_{1}}{{x}_{2}} + {{c}_{{22}}}x_{2}^{2}).} \end{array}$

Тогда для существования невырожденного преобразования, приводящего их к виду $\tfrac{1}{2}(a_{{11}}^{'}y_{1}^{2} + a_{{22}}^{'}y_{2}^{2})$, $\tfrac{1}{2}(b_{{11}}^{'}y_{1}^{2} + b_{{22}}^{'}y_{2}^{2})$, $\tfrac{1}{2}(c_{{11}}^{'}y_{1}^{2} + c_{{22}}^{'}y_{2}^{2})$, необходимо и достаточно выполнения условия (3), т.е. чтобы определитель $\Delta $, составленный из коэффициентов исходных квадратичных форм, обратился в ноль.

Доказательство. Квадратичные формы от двух переменных образуют векторное пространство размерности 3 из векторов ${\mathbf{a}}({{a}_{{11}}},{{a}_{{12}}},{{a}_{{22}}})$, ${\mathbf{b}}({{b}_{{11}}},{{b}_{{12}}},{{b}_{{22}}})$, ${\mathbf{c}}({{c}_{{11}}},{{c}_{{12}}},{{c}_{{22}}})$. Если квадратичные формы ${{f}_{1}}$, f₂, ${{f}_{3}}$ одновременно приводятся к каноническому виду, то линейная оболочка этих форм является подпространством размерности 2 или меньше, а следовательно, три формы линейно зависимы и определитель, составленный из координат векторов a, b, c, равен нулю $\Delta = 0$. Это и есть условие теоремы. Наоборот, если $\Delta = 0$, то ${{f}_{1}}$, f₂, ${{f}_{3}}$ линейно зависимы, и при этом ${{f}_{1}}$, ${{f}_{2}}$ линейно независимы, то ${{f}_{3}}$ линейно выражается через ${{f}_{1}}$, ${{f}_{2}}$, и тогда достаточно привести к каноническому виду две формы ${{f}_{1}}$, f₂. Если же ${{f}_{1}}$ пропорциональна f₂, то задача сводится к приведению двух форм f₂, ${{f}_{3}}$, что и требовалось доказать.

Второе доказательство. Теорема непосредственно вытекает из критерия Новикова [4] и тождества для матриц размерности 2:

$(A{{B}^{{ - 1}}}C - C{{B}^{{ - 1}}}A){\text{det}}(B) = \left( {\begin{array}{*{20}{c}} 0&\Delta \\ { - \Delta }&0 \end{array}} \right)$.

ЗАКЛЮЧЕНИЕ

Для вынужденных колебаний диссипативных механических систем с двумя степенями свободы получено простое условие расщепления системы уравнений 4-го порядка на две независимые системы 2-го порядка для линейных осцилляторов. Эта система значительно проще исходной и позволяет получать простое аналитическое решение системы в общем виде.

Список литературы

Журавлев В.Ф. Основы теоретической механики. М.: Наука, 2001.
Гантмахер Ф.Р. Лекции по аналитической механике. М.: Наука, 1966.
Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967.
Новиков М.А. // Известия вузов. Математика. 2014. № 12. С. 70–82.
Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 1965.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал