Доклады Российской академии наук. Физика, технические науки, 2022, T. 502, № 1, стр. 24-30

ПЕРИОДИЧНОСТЬ МЕХАНИЧЕСКИХ СВОЙСТВ ЛЬДА, ВОЗНИКАЮЩАЯ ПРИ ФОРМИРОВАНИИ ЛЕДЯНОГО ПОЛЯ В УСЛОВИЯХ СТЕСНЕНИЯ

В. П. Епифанов^1, *, С. А. Лычев¹

¹ Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия

Поступила в редакцию 01.10.2021
После доработки 01.10.2021
Принята к публикации 20.10.2021

EDN: TCLZXX
DOI: 10.31857/S2686740021060092

Аннотация

При формировании тонкой ледяной пластины на поверхности воды в условиях стесненного деформирования, которое обусловлено жесткими стенками бассейна, в ней возникают периодические изменения физических свойств, в частности сопротивления пенетрации. Экспериментальные результаты, подтверждающие этот факт, получены в Крыловском научном центре. Характерной особенностью этих результатов является возможность их представления как наложения двух периодических функций с различными периодами. В настоящей работе приводится модальный анализ экспериментальных данных, выделены длинноволновая и коротковолновая составляющие и предлагается теоретическая модель, объясняющая физические причины возникновения двойной периодичности.

Ключевые слова: вязкоупругий механизм образования коротковолновой двойной периодичности, модальный анализ, пенетрация, стесненное деформирование

Теоретические исследования физико-механических свойств ледяного покрова широко представлены в литературе, посвященной арктическим проблемам. В частности, деформирование и колебания тонкого слоя льда, плавающего на жидкости, исследовались в работах [1–3]. В большинстве исследований пластина льда рассматривалась как свободно плавающая [2, 3], либо как консольно закрепленная [4]. При таких краевых условиях усилия сжатия в пластине считались незначительными и слабо влияющими на ее изгибные деформации, в связи с чем моделирование изгиба пластины выполнялись с помощью линейных уравнений технической теории пластин [5]. Учет сжимающих усилий в плоскости упругой пластины, как правило, приводит к постановке задачи устойчивости [6], либо к нелинейной задаче для гибких пластин [7]. В настоящей работе рассмотрены докритические сжимающие усилия, которые влияют на эволюцию формы изгиба за счет релаксационных процессов, что проявляется в развитии периодического изгиба во времени. Подобный механизм реализуется, например, в аналоговом фильтре сигналов, который используется в электронных схемах. Именно свойство изгибаемой вязкоупругой пластины быть фильтром, выделяющим и накапливающим деформации с определенной пространственной структурой, является основой теоретического объяснения факта появления коротковолновой составляющей в экспериментальных данных [4, 8].

Феномен периодического изменения сопротивления пенетрации наблюдался в ледяном покрове прямоугольного бассейна с размерами $100 \times 10$ м². Длина большего периода соответствует ширине бассейна, длина второго периода – на порядок меньше. Экспериментально установлено, что периодичность второго (коротковолнового) типа слабо проявляется сразу после замораживания льда, однако уже через несколько часов ее вклад в сопротивляемость многократно увеличивается [9]. Вариации сопротивления пенетрации составляют $43 \pm 2\% $ в интервале от 26 до 60 кПа при ошибке измерений осевой силы пенетрации 5%.

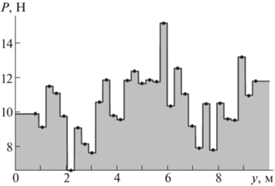
Измерения производились в четырех поперечных сечениях бассейна. Результаты измерений представлены кусочно-постоянными функциями f_n ($n$ – номер сечения). График одной из них показан на рис. 1. На рисунке точками указаны места и значения инструментальных измерений.

Рис. 1.

Зависимость осевой силы пенетрации от координаты точки измерений в поперечном профиле $x = 55$ м ледового бассейна.

Для выделения характерных периодов находилось наилучшее приближение экспериментальных данных следующими аппроксимирующими функциями:

${{\tilde {f}}_{n}}(x) = A_{n}^{0}\varphi _{n}^{0}(x) + A_{n}^{1}\varphi _{n}^{1}(x) + A_{n}^{2}\varphi _{n}^{2}(x),$

где $(\varphi _{n}^{0},\varphi _{n}^{1},\varphi _{n}^{2})$ – ортонормированные системы функций, таких, что первая представляет собой постоянную, вторая – длинноволновую квазипериодически изменяющуюся компоненту, а последняя – коротковолновую, причем волновые и фазовые параметры этих функций заранее не заданы, а подбираются из условия наилучшего совпадения с экспериментальными данными. Ортонормированность понимается в смысле следующего скалярного произведения:

(1)

$\left\langle {\varphi _{n}^{i},\varphi _{n}^{j}} \right\rangle = {{\delta }_{{ij}}},\quad \left\langle {u,{v}} \right\rangle : = \int\limits_0^L {u(x){v}(x)dx} .$

В качестве $\varphi _{n}^{k}$ использовались функции, получаемые в результате процесса ортогонализации Грама–Шмидта неортогональной системы:

(2)

$\begin{gathered} \psi _{n}^{0} = 1,\quad \psi _{n}^{1} = \sin ({{\Omega }_{n}}x + {{\epsilon }_{n}}), \\ \psi _{n}^{1} = \sin ({{\omega }_{n}}x + {{\varepsilon }_{n}}),\quad {{\omega }_{n}} > {{\Omega }_{n}}. \\ \end{gathered} $

Первая из них представляет постоянную составляющую данных, вторая – длинноволновую составляющую, третья – коротковолновую. В результате ортогонализации получен следующий набор ортонормированных функций:

(3)

$\begin{gathered} \varphi _{n}^{0} = \frac{1}{{\sqrt L }},\quad \varphi _{n}^{1}\frac{{{{\beta }_{n}} + \sin ({{\Omega }_{n}}x + {{\epsilon }_{n}})}}{{\sqrt {{{\nu }_{n}}} }}, \\ \varphi _{n}^{2} = \frac{{{{\delta }_{n}} + {{\sigma }_{n}}\sin ({{\Omega }_{n}}x + {{\epsilon }_{n}}) + \sin ({{\Omega }_{n}}x + {{\varepsilon }_{n}})}}{{\sqrt {{{\zeta }_{n}}} }}, \\ \end{gathered} $

где ${{\beta }_{n}}$, ${{\delta }_{n}}$, ${{\sigma }_{n}}$, ${{\nu }_{n}}$, ${{\zeta }_{n}}$ – числовые параметры, определяемые по произвольно принимаемым значениям для волновых ${{\Omega }_{n}}$, ${{\omega }_{n}}$ и фазовых ${{\epsilon }_{n}}$, ${{\varepsilon }_{n}}$ характеристик аппроксимирующей системы функций:

$\begin{gathered} {{\beta }_{n}} = \frac{{\cos ({{\Omega }_{n}}L + {{\epsilon }_{n}}) - \cos {{\epsilon }_{n}}}}{{L{{\Omega }_{n}}}}, \\ {{\delta }_{n}} = {{\sigma }_{n}}{{\beta }_{n}} + {{\xi }_{n}},\quad {{\sigma }_{n}} = \frac{{{{\xi }_{n}}{{\beta }_{n}}L - {{\mu }_{n}}}}{{{{\nu }_{n}}}}, \\ \end{gathered} $

${{\xi }_{n}} = \frac{{\cos ({{\omega }_{n}}L + {{\varepsilon }_{n}}) - \cos {{\varepsilon }_{n}}}}{{L{{\omega }_{n}}}},$

${{\nu }_{n}} = \frac{1}{{2\Omega _{n}^{2}}}({{L}^{2}}\Omega _{n}^{2} - 2 - \cos (2{{\epsilon }_{n}}) + 2\cos (L{{\Omega }_{n}}) - $

$ - \,\cos (2{{\epsilon }_{n}}\, + \,2L{{\Omega }_{n}})\, - \,\cos (2{{\epsilon }_{n}}\, + \,L{{\Omega }_{n}})(L{{\Omega }_{n}}{\text{sin}}(L{{\Omega }_{n}})\, - \,2)),$

${{\mu }_{n}} = \frac{{\sin ({{\epsilon }_{n}} - {{\varepsilon }_{n}}) - \sin ({{\epsilon }_{n}} - {{\varepsilon }_{n}} - L({{\omega }_{n}} - {{\Omega }_{n}}))}}{{2({{\omega }_{n}} - {{\Omega }_{n}})}} + $

$ + \;\frac{{\sin ({{\epsilon }_{n}} + {{\varepsilon }_{n}}) - \sin ({{\epsilon }_{n}} + {{\varepsilon }_{n}} + L({{\omega }_{n}} + {{\Omega }_{n}}))}}{{2({{\omega }_{n}} + {{\Omega }_{n}})}},$

$\begin{gathered} {{\zeta }_{n}} = \\ = \sigma _{n}^{2}\left( {\frac{{2L{{\Omega }_{n}}\, + \,{\text{sin}}(2{{\epsilon }_{n}})\, - \,{\text{sin}}(2{{\epsilon }_{n}}\, + \,2L{{\Omega }_{n}})}}{{4{{\Omega }_{n}}}}\, - \,2{{\nu }_{n}}\, - \,L\beta _{n}^{2}} \right) + \\ \end{gathered} $

$ + \;\frac{{2L{{\omega }_{n}} + \sin (2{{\varepsilon }_{n}}) - \sin (2{{\varepsilon }_{n}} + 2L{{\omega }_{n}})}}{{4{{\omega }_{n}}}} - L\xi _{n}^{2}.$

Отметим, что система функций (3), будучи ортонормированной, сохранила качественные свойства системы (2).

Для определения наилучших параметров ${{\Omega }_{n}}$, ${{\omega }_{n}}$, ${{\epsilon }_{n}}$, ${{\varepsilon }_{n}}$ для каждого сечения $n$ будем минимизировать невязку

(4)

${\text{||}}{{f}_{n}} - {{\tilde {f}}_{n}}{\text{||}} \to \min $

на множестве $({{\Omega }_{n}},{{\omega }_{n}},{{\epsilon }_{n}},{{\varepsilon }_{n}})\, \in \,(0,3)\, \times \,(3,10)\, \times \,(0,2\pi )$ × × (0, 2π), где норма ${\text{||}}\; \cdot \;{\text{||}}$ определяется скалярным произведением (1), а коэффициенты $A_{n}^{0},\; \ldots ,\;A_{n}^{2}$ вычисляются как проекции на элементы ортонормированной системы:

(5)

$A_{n}^{i} = \left\langle {{{f}_{n}},\varphi _{n}^{i}} \right\rangle ,\quad i = 0,\;1,\;2.$

Определение волновых и фазовых параметров, минимизирующих невязку, осуществлялась методом Монте–Карло с равномерным распределением пробных значений в области поиска. Для каждого сечения производилось 10⁶ вычислений. Результаты вычислений представлены в табл. 1 и проиллюстрированы на рис. 2.

Таблица 1.

Значения волновых и фазовых параметров

$n$	$A_{n}^{0}$	$A_{n}^{1}$	$A_{n}^{2}$	${{\Omega }_{n}}$	${{\omega }_{n}}$	${{\epsilon }_{n}}$	${{\varepsilon }_{n}}$
1	33.099	–3.160	–1.455	1.185	6.058	4.969	1.723
2	32.738	–2.152	–1.257	1.250	7.713	2.850	6.278
3	34.108	2.450	–1.373	1.247	7.010	0.855	1.715
4	33.479	1.851	–1.467	0.775	7.202	3.536	3.214

Примечание. Значения приведены для четырех серий измерений в поперечных сечениях бассейна с координатами точки измерений в поперечном профиле ледового бассейна: 1 – 55 м, 2 – 56 м, 3 – 57 м, 4 – 58 м.

Рис. 2.

Модальный анализ экспериментальных данных. Обозначения: 1 – постоянная, 2 – длинноволновая и 3 – коротковолновая составляющие; 4 – результаты измерений, 5 – аппроксимирующая комбинация.

Полученные результаты подтверждают двойную периодичность в сериях экспериментальных данных. Малый разброс волновых параметров ω_n и соответствующих коэффициентов $A_{n}^{2}$ коротковолновых составляющих характеризует коротковолновую компоненту как феномен, связанный с локальными свойствами ледовой пластины. Значительно больший разброс параметров длинноволновой компоненты так же имеет ясную физическую интерпретацию, связанную с деформированием всей ледовой пластины в целом. Действительно, оно определяется основной формой разложения, сечения которой для различных продольных координат различаются.

Идея, которую предлагается положить в основу теоретической интерпретации двойной периодичности, состоит в разделении изгиба на две составляющие. Первая соответствует изгибу на фундаментальной моде всей пластины в целом, а вторая характеризуется накоплением возмущений с пространственной периодичностью, отвечающей ее вязкоупругим свойствам.

Учитывая, что в рассматриваемом эксперименте ледовая пластина имеет длину, в 10 раз превышающую ширину, а вдоль длинных сторон пластина приморожена к жестким бортам, ее деформацию можно представить в рамках модели цилиндрического изгиба. Изгиб может быть вызван некоторой поперечной нагрузкой на пластину и изменением уровня воды в бассейне. Материал пластины предполагается однородным, изотропным, отклик которого определяется вязкоупругим законом Фойгта. С учетом этих предположений начально–краевая задача может быть сформулирована следующим образом:

$\left( {\tilde {E} + \tilde {R}\frac{\partial }{{\partial t}}} \right)\frac{{{{\partial }^{4}}w}}{{\partial {{y}^{4}}}} + P\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \rho gw = q,$

${{\left. w \right|}_{{y = 0}}} = {{\left. w \right|}_{{y = L}}} = {{\left. {\frac{{\partial w}}{{\partial y}}} \right|}_{{y = 0}}} = {{\left. {\frac{{\partial w}}{{\partial y}}} \right|}_{{y = L}}} = 0,\quad {{\left. w \right|}_{{t = 0}}} = {{w}_{0}}.$

Здесь $w$ – прогиб пластины, $\tilde {E}$ – цилиндрическая жесткость, $\tilde {R}$ – аналогичная характеристика, определяемая вязкой составляющей отклика:

$\tilde {E} = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}},\quad \tilde {R} = \frac{{R{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}},$

$E$ – модуль Юнга льда, $R$ – модуль вязкости, $h$ – толщина пластины, $\nu $ – коэффициент Пуассона льда, $P$ – погонное усилие сжатия, приложенное к длинным сторонам пластины, $\rho $ – плотность воды, $g$ – ускорение свободного падения, $q$ – поперечная нагрузка, ${{w}_{0}}$ – начальные отклонения от равновесного состояния.

Решение начально-краевой задачи предлагается отыскивать в виде суммы двух функций

$w(y,t) = {{w}_{e}}(y) + {{w}_{{v}}}(y,t).$

Первая функция, ${{w}_{e}}(y)$, зависит только от пространственной переменной и представляет постоянную во времени (или изменяемую по тому же закону, что и закон изменения поперечной нагрузки q) составляющую изгиба. Вторая, ${{w}_{{v}}}(y,t)$, определяет эволюцию изгиба, происходящую ввиду вязких свойств материала. Такое представление решения позволяет сформулировать две независимые краевые задачи относительно этих функций. Как будет показано далее, подобная декомпозиция позволяет выделить часть решения, которая соответствует длинноволновой составляющей прогибов, и часть, отвечающую коротковолновой составляющей.

Краевая задача относительно ${{w}_{e}}$ имеет вид

$\begin{gathered} \tilde {E}\frac{{{{d}^{4}}{{w}_{e}}}}{{d{{y}^{4}}}} + Pw_{e}^{{''}} + \rho g{{w}_{e}} = q, \\ {{\left. {{{w}_{e}}} \right|}_{{y = 0}}} = {{\left. {{{w}_{e}}} \right|}_{{y = L}}} = {{\left. {w_{e}^{'}} \right|}_{{x = 0}}} = {{\left. {w_{e}^{'}} \right|}_{{y = L}}} = 0. \\ \end{gathered} $

Начально-краевая задача для ${{w}_{{v}}}$ записывается следующим образом:

$\tilde {R}\frac{{{{\partial }^{5}}{{w}_{{v}}}}}{{\partial {{y}^{4}}\partial t}} + \tilde {E}\frac{{{{\partial }^{4}}{{w}_{{v}}}}}{{\partial {{y}^{4}}}} + P\frac{{{{\partial }^{2}}{{w}_{{v}}}}}{{\partial {{y}^{2}}}} + \rho g{{w}_{{v}}} = 0,$

$\begin{gathered} {{\left. {{{w}_{e}}} \right|}_{{y = 0}}} = {{\left. {{{w}_{e}}} \right|}_{{y = L}}} = {{\left. {\frac{{\partial {{w}_{e}}}}{{\partial y}}} \right|}_{{x = 0}}} = {{\left. {\frac{{\partial {{w}_{e}}}}{{\partial y}}} \right|}_{{y = L}}} = 0, \\ {{\left. {{{w}_{{v}}}} \right|}_{{t = 0}}} = {{w}_{0}}. \\ \end{gathered} $

Решения обеих задач может быть представлено в форме разложения по собственным функциям дифференциальных операторов, порождаемых каждой из них. Для ${{w}_{e}}$ имеем

(6)

${{w}_{e}} = \sum\limits_{n = 1}^\infty {{{W}_{n}}} \frac{{{{\alpha }_{n}}}}{{{{\lambda }_{n}}}},\quad {{\alpha }_{n}} = \int\limits_0^L q {{W}_{n}}dy,$

где W_n определяются из решений классической задачи Штурма–Лиувилля

$\tilde {E}\frac{{{{d}^{4}}}}{{d{{y}^{4}}}}{{W}_{n}} + PW_{n}^{{''}} + \rho g{{W}_{n}} = {{\lambda }_{n}}{{W}_{n}},\quad \left\| {{{W}_{n}}} \right\| = 1,$

${{\left. {{{W}_{n}}} \right|}_{{y = 0}}} = {{\left. {{{W}_{n}}} \right|}_{{y = L}}} = {{\left. {W_{n}^{'}} \right|}_{{x = 0}}} = {{\left. {W_{n}^{'}} \right|}_{{y = L}}} = 0.$

Решение второй задачи может быть представлено в аналогичной форме:

(7)

${{w}_{{v}}} = \sum\limits_{n = 1}^\infty {{{V}_{n}}} {{\beta }_{n}}{{e}^{{{{\xi }_{n}}t}}},\quad {{\beta }_{n}} = \int\limits_0^L {{{w}_{0}}} \frac{{{{d}^{4}}{{V}_{n}}}}{{d{{y}^{4}}}}dy.$

Здесь ${{V}_{n}}$ определяются из решений обобщенной задачи Штурма–Лиувилля

$(\tilde {E} + {{\xi }_{n}}\tilde {R})\frac{{{{d}^{4}}}}{{d{{y}^{4}}}}{{V}_{n}} + PV_{n}^{{''}} + \rho g{{V}_{n}} = 0,\quad \left\| {{{V}_{n}}} \right\| = 1,$

(8)

${{\left. {{{V}_{n}}} \right|}_{{y = 0}}} = {{\left. {{{V}_{n}}} \right|}_{{y = L}}} = {{\left. {V_{n}^{'}} \right|}_{{x = 0}}} = {{\left. {V_{n}^{'}} \right|}_{{y = L}}} = 0.$

В обеих постановках задачи допускают решения в элементарных функциях. Опуская очевидные детали их построения, приведем окончательный результат:

(9)

$\begin{gathered} {{W}_{n}} = \frac{A}{{\sqrt N }}\left( {{{\mu }_{1}}\sin \left( {{{\mu }_{2}}y} \right) - {{\mu }_{2}}\sin \left( {{{\mu }_{1}}y} \right)} \right) + \\ + \;\frac{B}{{\sqrt N }}\left( {\cos \left( {{{\mu }_{2}}y} \right) - \cos \left( {{{\mu }_{1}}y} \right)} \right), \\ \end{gathered} $

$\begin{gathered} {{\mu }_{1}} = \sqrt {\mathcal{P} + \sqrt {{{\lambda }_{n}}{\text{/}}\tilde {E} + {{\mathcal{P}}^{2}} - r} } , \\ {{\mu }_{2}} = \sqrt {\mathcal{P} - \sqrt {{{\lambda }_{n}}{\text{/}}\tilde {E} + {{\mathcal{P}}^{2}} - r} } , \\ \end{gathered} $

$\begin{gathered} {{c}_{1}} = \cos (L{{\mu }_{1}}),\quad {{c}_{2}} = \cos (L{{\mu }_{2}}), \\ {{s}_{1}} = \sin (L{{\mu }_{1}}),\quad {{s}_{2}} = \sin (L{{\mu }_{2}}), \\ \end{gathered} $

$\begin{gathered} \mathcal{P} = P{\text{/}}(2\tilde {E}),\quad r = \rho g{\text{/}}\tilde {E}, \\ A = {{c}_{1}} - {{c}_{2}},\quad B = {{\mu }_{1}}{{s}_{2}} - {{\mu }_{2}}{{s}_{1}}, \\ \end{gathered} $

$\begin{gathered} N = \frac{1}{{2{{\mu }_{1}}{{\mu }_{2}}(\mu _{1}^{2} - \mu _{2}^{2})}}\left\{ {{{A}^{2}}[\mu _{2}^{5}\left( {{{c}_{1}}{{s}_{1}} - {{\mu }_{1}}L} \right)} \right. - \\ - \;{{c}_{2}}\mu _{1}^{5}{{s}_{2}} + \left( {4{{c}_{1}} + {{c}_{2}}} \right)\mu _{2}^{2}\mu _{1}^{3}{{s}_{2}} - \\ \end{gathered} $

$\begin{gathered} - \;\left( {{{c}_{1}} + 4{{c}_{2}}} \right)\mu _{2}^{3}\mu _{1}^{2}{{s}_{1}} + {{\mu }_{2}}\mu _{1}^{5}L] + \\ + \;2AB(\mu _{1}^{2} - \mu _{2}^{2}){{\left( {{{\mu }_{1}}{{s}_{2}} - {{\mu }_{2}}{{s}_{1}}} \right)}^{2}} + \\ \end{gathered} $

$\begin{gathered} + \;{{B}^{2}}({{\mu }_{2}}\mu _{1}^{2}\left( {{{c}_{1}}{{s}_{1}} - 4{{c}_{2}}{{s}_{1}} + 2{{\mu }_{1}}L} \right) - \\ - \;\mu _{2}^{3}\left( {{{c}_{1}}{{s}_{1}} + 2{{\mu }_{1}}L} \right) + {{c}_{2}}\mu _{1}^{3}{{s}_{2}} + \left. {\left( {4{{c}_{1}} - {{c}_{2}}} \right)\mu _{2}^{2}{{\mu }_{1}}{{s}_{2}})} \right\}. \\ \end{gathered} $

Здесь ${{\lambda }_{n}}$ находятся как корни трансцендентного уравнения

$1 - {{c}_{1}}{{c}_{2}} - \mathcal{P}\frac{{{{s}_{1}}{{s}_{2}}}}{{{{\mu }_{1}}{{\mu }_{2}}}} = 0.$

Решение ${{V}_{n}}$ задачи (8) определяется по тем же формулам, если заменить приведенные выше выражения для ${{\mu }_{1}}$, ${{\mu }_{2}}$ на

$\begin{gathered} {{\mu }_{1}} = \sqrt {\frac{{\mathcal{P} + \sqrt {{{\mathcal{P}}^{2}} - r(1 + {{\xi }_{n}}\tilde {R}{\text{/}}\tilde {E})} }}{{1 + {{\xi }_{n}}\tilde {R}{\text{/}}\tilde {E}}}} , \\ {{\mu }_{2}} = \sqrt {\frac{{\mathcal{P} - \sqrt {{{\mathcal{P}}^{2}} - r(1 + {{\xi }_{n}}\tilde {R}{\text{/}}\tilde {E})} }}{{1 + {{\xi }_{n}}\tilde {R}{\text{/}}\tilde {E}}}} , \\ \end{gathered} $

а ${{\xi }_{n}}$ находить как корни уравнения

$1 - {{c}_{1}}{{c}_{2}} - \frac{{\mathcal{P}{{s}_{1}}{{s}_{2}}}}{{(1 + {{\xi }_{n}}\tilde {R}{\text{/}}\tilde {E}){{\mu }_{1}}{{\mu }_{2}}}} = 0.$

Пространственная периодичность построенного решения задачи (8) определяется значениями ${{\mu }_{1}}$ и ${{\mu }_{2}}$, которые, будучи корнями одного и того же алгебраического уравнения, удовлетворяют соотношению

${{\xi }_{n}} = \frac{{2\mathcal{P}{{\mu }^{2}} - r - {{\mu }^{4}}}}{{\tilde {R}{\text{/}}\tilde {E}{{\mu }^{4}}}}.$

Эта зависимость имеет максимум при

(10)

$\frac{{d{{\xi }_{n}}}}{{d\mu }} = \frac{{4(r - \mathcal{P}{{\mu }^{2}})}}{{\tilde {R}{\text{/}}\tilde {E}{{\mu }^{5}}}} = 0,\,\,{\text{т}}{\text{.е}}{\text{.}}\,\,\mu = \sqrt {\frac{r}{\mathcal{P}}} = \sqrt {\frac{{2\rho g}}{P}} .$

Учитывая форму решения (7), в котором каждый член умножается на ${{e}^{{{{\xi }_{n}}t}}}$, можно утверждать, что члены разложения c наибольшими значениями ${{\xi }_{n}}$ будут уменьшаться медленнее других и через некоторое время станут доминирующими. Именно этот эффект наблюдается в натурных испытаниях, когда после замораживания тонкого ледяного слоя в бассейне в нем через некоторое время возникает коротковолновая периодичность свойств.

В расчетах по приведенным выше формулам использовались следующие исходные данные: толщина пластины льда $h = 5 \times {{10}^{{ - 2}}}$ м, модуль Юнга E = 35 МПа, коэффициент Пуассона ν = 0.3, плотность воды $\rho = 1000$ кг/м³, модуль вязкости $R = 3$ МПа ⋅ с. Так как прямых измерений усилия сжатия пластины не производилось, их величина определялась косвенно. Поскольку объемное расширение воды при замораживании велико (около 9%), напряжения, которые при этом могли бы возникнуть в пластине льда, существенно превышают предел пластичности. В этой связи в качестве верхней оценки следует использовать значения усилий, развиваемых в ледяной пластине в предельном состоянии. Полагая, что предел пластичности льда 0.01 МПа, получим верхнюю оценку для погонной сжимающей силы $P < 500$ Н/м. В действительности, в виду наличия пор и дефектов структуры льда, это усилие меньше. Уточнение его значения может быть получено из условия наилучшей аппроксимации длинноволновой составляющей экспериментальных данных с помощью ${{w}_{e}}$ (6), либо из условий наилучшей аппроксимации коротковолновой составляющей посредством ${{w}_{{v}}}$ (7). Возможность построения двух оценок одной и той же величины позволяет показать их объективность, в случае, если найденные значения будут близки.

Отметим, что построенные выше теоретические решения определяют изгиб пластины, который непосредственно не определялся в эксперименте. Экспериментальные данные дают распределение усилий сквозной пенетрации пластины льда, и для того чтобы связать эксперимент и теорию, требуются дополнительные предположения. Они состоят в следующем: предполагается, что в областях, в которых развиваются максимальные напряжения, происходит упрочнение и, как следствие, повышенное сопротивление пенетрации. При этом распределение максимальных интенсивностей напряжений, вызванных изгибом по форме (9), в рамках кинематических гипотез технической теории пластин может быть определена следующим образом: $S \approx \alpha \left| {\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}}} \right|,$ где α – коэффициент, зависящий от физико-геометрических параметров пластины.

При идентификации длинноволновой составляющей решения (6) варьировались параметры α и $\mathcal{P}$ при фиксированных значении $L = 10$ м, $r = 24.525$. Находились величины, отвечающие наименьшим квадратичным отклонениям теоретических значений от экспериментальных. В результате анализа четырех сечений получены результаты: $\mathcal{P} = 0.25$, ${{\lambda }_{1}} = 24.511$. Им соответствует усилие обжатия $P = 200$ Н/м.

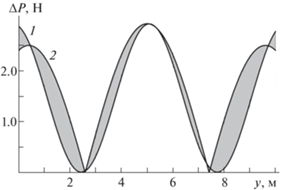
Наложение теоретических распределений на длинноволновые представления экспериментальных данных приведены на рис. 3. Заливкой показаны отличия распределений интенсивностей напряжений (нормированных соразмерно экспериментальным данным) и длинноволновой составляющей экспериментальных данных о пенетрации.

Рис. 3.

Нормированные максимальные интенсивности напряжений (кривая 1) и длинноволновая составляющая экспериментальных данных о силе пенетрации (кривая 2).

Идентификация усилия обжатия $P$ по коротковолновой составляющей производилась с помощью зависимости (10). Среднее значение коротковолнового параметра $\mu $ по четырем сечениям составило $\mu = 7.16$. Соответственно, $P = 382.5$ Н/м.

Поверхности, иллюстрирующие эволюцию прогибов, найденных по (7), приведены на рис. 4. Начальные изгибы соответствуют двум различным пространственным масштабам. Левая поверхность соответствует возмущению 70% ширины пластины, правая – 10$\% $. Видно, что изгибы, вызванные возмущением малой области, затухают во времени существенно медленнее изгибов, вызванных возмущением более широкой области. При этом протяженность малой области близка к периоду коротковолновой составляющей экспериментальных данных. Образно говоря, второй начальный изгиб оказывается в “резонансе” с собственными характеристиками пластины и след этого возмущения длительное время сохраняется. Выделяя подобные следы из случайных возмущений, вязкоупругая система проявляет свойства фильтра, создавая со временем упорядоченную структуру, которая и наблюдается в форме коротковолновых составляющих экспериментальных данных.

Рис. 4.

Эволюция прогибов при возмущениях на интервалах различной протяженности.

Верификация модели осуществлена путем сопоставления значения сжимающей силы, найденной из анализа длинноволнового распределения, со значением, которое определено по коротковолновой части. Несмотря на то, что они различаются почти в два раза, их значения одного порядка. Отличия могут быть объяснены недостаточной точностью моделирования условий адгезионного контакта на бортах. Cила сжатия, найденная по коротковолновой составляющей, оказалась близкой к теоретическому пределу (который был определен выше по пределу текучести льда), что позволяет в большей степени доверять именно этому значению.

Таким образом показано, что периодичность связана с экстремальным значением показателя экспоненциальных координатных функций, которое зависит от локальных физико-геометрических свойств ледяной пластины и слабо зависит от условий ее закрепления. В результате многократных случайных изгибов и последующих релаксационных процессов выделяется превалирующая составляющая, что и объясняет появление локальных зон упрочнения, пространственное распределение которых подобно коротковолновой составляющей экспериментальных данных об усилиях пенетрации.

Список литературы

Box F., Vella D., Style R.W., Neufeld J.A. Indentation of a floating elastic sheet: geometry versus applied tension // Proc. R. Soc. A. 2017. V. 473. P. 20170335. https://doi.org/10.1098/rspa.2017.0335
Meylan M.H. Time-Dependent Motion of a Floating Circular Elastic Plate // Fluids. 2021. V. 6. P. 29. https://doi.org/10.3390/ fluids6010029
Fox C., Squire V.A. On the Oblique Reflexion and Transmission of Ocean Waves at Shore Fast Sea Ice // Philosophical Transactions: Physical Sciences and Engineering. 1994. V. 347 (1682). P. 185–218. http://www.jstor.org/stable/54236
Staroszczyk R., Hedzielski B. Creep Buckling of a Wedge–Shaped Floating Ice Plate // Engineering Transactions. 2004. V. 52. P. 111–130.
Тимошенко С.П., Войновский–Кригер С. Пластинки и оболочки. М.: Наука, 1966. 636 с.
Вольмир А.С. Устойчивость упругих систем. М., 1963. 879 с.
Ciarlet P.G. Mathematical Elasticity. V. II. Theory of Plates. North–Holland. 1988. 262 p.
Stig–Göran Sjölind. Visco-elastic buckling analysis of floating ice sheets. Cold Regions Science and Technology. 1985. V. 11. Iss. 3. P. 241–246.
Епифанов В.П., Сазонов К.Е. Влияние стационарных периодических волновых структур на локальную прочность ледяного поля // Доклады РАН. Физика, технические науки. 2020. Т. 495. № 1. С. 18–25.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал