Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 490, № 1, стр. 59-62

Об асимптотических разложениях решений уравнения Риккати

В. С. Самовол^*

Национальный исследовательский университет “Высшая школа экономики”
Москва, Россия

Поступила в редакцию 26.11.2019
После доработки 27.11.2019
Принята к публикации 17.12.2019

DOI: 10.31857/S2686954320010191

Аннотация

Рассматриваются скалярные вещественные уравнения Риккати с коэффициентами, раскладывающимися в сходящиеся степенные ряды в окрестности бесконечности. Исследуются продолжаемые решения таких уравнений. Методами степенной геометрии получены условия асимптотических разложений этих решений.

Ключевые слова: уравнение Риккати, продолжаемое решение, степенная геометрия, многоугольник Ньютона, асимптотический ряд

Исследуется скалярное уравнение Риккати

(1)

$y{\text{'}} + \sum\limits_{i = 0}^2 {{{f}_{i}}(x)} {{y}^{i}} = 0,\quad y = y(x),\quad x,y \in \mathbb{R}.$

При этом считаем, что функции ${{f}_{i}}(x)$, $i \in {\text{\{ }}0$, 1, 2}, могут быть представлены в виде равномерно и абсолютно сходящихся в окрестности точки $x = + \infty $ вещественных степенных рядов

(2)

$\begin{gathered} {{f}_{i}}(x) = \sum\limits_{j = 1}^\infty {{{c}_{{ij}}}} {{x}^{{{{p}_{{ij}}}}}},\quad {{c}_{{ij}}},{{p}_{{ij}}} = {\text{const}} \in \mathbb{R}, \\ {{p}_{{ij + 1}}} < {{p}_{{ij}}},\quad \mathop {lim}\limits_{j \to \infty } {{p}_{{ij}}} = - \infty ,\quad i \in {\text{\{ }}0,1,2{\text{\} }}. \\ \end{gathered} $

Здесь и далее при упоминании степенных рядов, в отличие от традиционных степенных рядов, показатели степеней вещественные, но не обязательно целые числа. В данной работе изучаются произвольные решения уравнения (1), определенные в некоторой окрестности точки $x = + \infty $ (такие решения будем называть продолжаемыми).

Уравнение (1) считаем неоднородным, так как однородное уравнение является уравнением Бернулли и непосредственно интегрируется. Таким образом, везде ниже считаем, что в (2) ${{c}_{{01}}}{{c}_{{21}}} \ne 0$.

Риккати в [1] рассматривал уравнение вида (1)

(3)

$y{\text{'}} + a{{y}^{2}} + b{{x}^{p}} = 0,\quad a,b,p = {\text{const}}.$

Сначала исследовался вопрос об интегрировании уравнения (3) в квадратурах (см. [2]). После долгих подобных попыток Яков Бернулли открыл возможность разложения решений уравнения (3) в ряд (см. в [2] его переписку с Лейбницем). Позже выяснилось, что решения уравнения (3) могут быть разложены в сходящиеся ряды с использованием функций Бесселя (см., например, [3]). В последние годы разработаны методы степенной геометрии, позволяющие получать разложения решений дифференциальных уравнений в ряды [4].

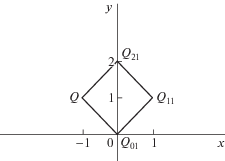
Далее мы будем пользоваться терминами, принятыми в степенной геометрии [4]. Многоугольник Ньютона $N$ уравнения (1) при условии (2) представляет собой замкнутую выпуклую оболочку точек $Q = ( - 1,1)$, ${{Q}_{{ij}}} = ({{p}_{{ij}}},i)$, $i \in {\text{\{ }}0,1,2{\text{\} }}$, $j \in {\text{\{ }}1,2$, ...}. При изучении асимптотических разложений решений уравнения (1) в окрестности точки $x = + \infty $ важную роль играет расположение точки Q относительно правой границы многоугольника N.

Случай, когда точка Q принадлежит правой границе многоугольника N, т.е. выполнено условие

(4)

$max({{p}_{{01}}} + {{p}_{{21}}},2{{p}_{{11}}}) \leqslant - 2,$

исследован в [5, 6], где показано, что продолжаемые решения уравнения (1) могут быть представлены в виде рядов, абсолютно и равномерно сходящихся в некоторой окрестности точки $x = + \infty $. Указанные ряды подробно описаны и указан алгоритм их вычисления.

В данной работе мы рассмотрим случай, когда нарушается условие (4), т.е. точка Q не принадлежит правой границе многоугольника N и выполняется неравенство

(5)

$max({{p}_{{01}}} + {{p}_{{21}}},2{{p}_{{11}}}) > - 2.$

Если при этом $2{{p}_{{11}}} > {{p}_{{01}}} + {{p}_{{21}}}$, то могут быть вычислены два формальных степенных ряда (формальные решения уравнения (1)), являющихся асимптотическими представлениями (разложениями) всех нетривиальных продолжаемых решений уравнения (1). Указанные ряды, вообще говоря, расходятся в окрестности точки $x = + \infty $.

Если $2{{p}_{{11}}} \leqslant {{p}_{{01}}} + {{p}_{{21}}}$, то дополнительно требуется анализ коэффициентов ${{c}_{{i1}}}$ первых приближений в разложениях функций ${{f}_{i}}(x)$. Если $\tilde {c}_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}}$ < 0, то уравнение (1) не имеет продолжаемых решений (здесь ${{\tilde {c}}_{{11}}} = {{c}_{{11}}}$, при 2p₁₁ = ${{p}_{{01}}} + {{p}_{{21}}}$ и ${{\tilde {c}}_{{11}}} = 0$ при 2p₁₁ < ${{p}_{{01}}} + {{p}_{{21}}}$). Если $\tilde {c}_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}}$ > 0, то продолжаемые решения есть и степенным преобразованием эта ситуация сводится к указанному выше основному случаю $2{{p}_{{11}}} > {{p}_{{01}}} + {{p}_{{21}}}$. При выполнении условия (5) и равенства $\tilde {c}_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}}$ = 0 уравнение (1) степенным преобразованием либо приводится к виду, где выполняется условие (4), либо к виду, где $\tilde {c}_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}} \ne 0$.

1. ФОРМУЛИРОВКА ОСНОВНЫХ РЕЗУЛЬТАТОВ

Замечание 1. Для формулировки результатов удобно использовать другую запись функции ${{f}_{1}}(x)$.

Если выполняется условие (5), то без ограничения общности будем считать, что в разложении в ряд функции ${{f}_{1}}(x) = \sum\limits_{j = 1}^\infty {{{c}_{{1j}}}} {{x}^{{{{p}_{{1j}}}}}}$ выполняется неравенство ${{p}_{{11}}} \geqslant 0.5({{p}_{{01}}} + {{p}_{{21}}})$ (при этом в случае ${{p}_{{11}}} = 0.5({{p}_{{01}}} + {{p}_{{21}}})$ коэффициент c₁₁ может быть равен нулю, если же ${{p}_{{11}}} > 0.5({{p}_{{01}}} + {{p}_{{21}}})$, то ${{c}_{{11}}} \ne 0$).

Напомним понятие асимптотического разложения (представления) функции.

Определение. Степенной ряд $\sum\limits_{i = 1}^\infty {{{c}_{i}}} {{x}^{{{{\alpha }_{i}}}}}$, ${{\alpha }_{{i + 1}}} < {{\alpha }_{i}}$, $\mathop {lim}\limits_{i \to \infty } {{\alpha }_{i}} = - \infty $, называется асимпто- тическим разложением (представлением) функции $f(x)$ при $x \to + \infty $, если при всех $m \geqslant 1$ будет

$\mathop {lim}\limits_{x \to + \infty } {{x}^{{ - {{\alpha }_{m}}}}}\left( {f(x) - \sum\limits_{i = 1}^m {{{c}_{i}}} {{x}^{{{{\alpha }_{i}}}}}} \right) = 0.$

Теорема 1. Если выполняются условия (2), (5) и одно из двух условий:

1) ${{p}_{{01}}} + {{p}_{{21}}} < 2{{p}_{{11}}}$,

2) ${{p}_{{01}}} + {{p}_{{21}}} = 2{{p}_{{11}}}$, $c_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}} > 0$,

то существуют два формальных ряда

(6)

$\begin{gathered} {{z}_{j}}(x) = \sum\limits_{i = 1}^\infty {{{a}_{{ji}}}} {{x}^{{{{s}_{{ji}}}}}},\quad j = 1,2, \\ {{s}_{{11}}} = {{p}_{{01}}} - {{p}_{{11}}},\quad {{s}_{{21}}} = {{p}_{{11}}} - {{p}_{{21}}},\quad {{s}_{{ji + 1}}} < {{s}_{{ji}}}, \\ \mathop {lim}\limits_{i \to \infty } {{s}_{{ji}}} = - \infty ,\quad {{a}_{{ji}}} = {\text{const}}, \\ \end{gathered} $

формально удовлетворяющих уравнению (1). При этом множество M продолжаемых решений уравнения (1) является объединением двух непустых множеств $M = {{M}_{1}} \cup {{M}_{2}}$, где элементами множеств M_j, $j = 1,2$, являются продолжаемые решения, асимптотическим разложением которых при $x \to + \infty $ является ряд ${{z}_{j}}(x)$. В (6) при выполнении условия 1)

${{a}_{{11}}} = - {{c}_{{01}}}{{({{c}_{{11}}})}^{{ - 1}}},\quad {{a}_{{21}}} = - {{c}_{{11}}}{{({{c}_{{21}}})}^{{ - 1}}},$

а при выполнении условия 2)

$\begin{gathered} {{a}_{{11}}} = {{(2{{c}_{{21}}})}^{{ - 1}}}( - {{c}_{{11}}} + b), \\ {{a}_{{21}}} = {{(2{{c}_{{21}}})}^{{ - 1}}}( - {{c}_{{11}}} - b),\quad b = \sqrt {c_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}}} . \\ \end{gathered} $

Смысл неравенства в условии 2) в теореме 1 раскрывается в теоремах 2 и 3.

Теорема 2. Если выполняются условия (2) и (5) и равенство ${{p}_{{01}}} + {{p}_{{21}}} = 2{{p}_{{11}}}$, то при $c_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}}$ < 0 уравнение (1) не имеет продолжаемых решений.

Замечание 2. Условие (2) в этой теореме является избыточным. Для справедливости теоремы достаточно, чтобы функции ${{f}_{i}}(x)$, $i \in {\text{\{ }}0,1,2{\text{\} }}$ обладали при $x \to + \infty $ степенной асимптотикой

$\begin{gathered} {{f}_{i}}(x) = {{c}_{{i1}}}{{x}^{{{{p}_{{i1}}}}}}(1 + o({{x}^{{ - \varepsilon }}})), \\ \varepsilon = {\text{const}} > 0,\quad i \in {\text{\{ }}0,1,2{\text{\} }}. \\ \end{gathered} $

Рассмотрим теперь случай, когда выполняются условия (2) и (5) и равенства ${{p}_{{01}}} + {{p}_{{21}}} = 2{{p}_{{11}}}$, $c_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}}$ = 0. Уравнение (1) в этом случае будем называть вырожденным, в обратном случае – невырожденным.

Теорема 3. Если уравнение (1) является вырожденным, то существует преобразование вида

(7)

$\begin{gathered} y = z + h(x), \\ h(x) = \sum\limits_{i = 1}^m {{{h}_{i}}} {{x}^{{{{r}_{i}}}}},\quad {{h}_{i}},{{r}_{i}} = {\text{const}}, \\ {{r}_{{i + 1}}} < {{r}_{i}},\quad {{r}_{1}} = {{p}_{{01}}} - {{p}_{{11}}},\quad {{h}_{1}} = - {{(2{{c}_{{21}}})}^{{ - 1}}}{{c}_{{11}}}, \\ \end{gathered} $

в результате которого уравнение (1) станет невырожденным.

Замечание 3. Если в результате преобразования (7) уравнение (1) примет вид

(8)

$\begin{gathered} z{\text{'}} + \sum\limits_{i = 0}^2 {{{g}_{i}}} (x){{z}^{i}} = 0, \\ {{g}_{i}}(x) = \sum\limits_{j = 1}^\infty {{{{\tilde {с}}}_{{ij}}}} {{x}^{{\mathop {\tilde {p}}\nolimits_{ij} }}},\quad {{{\tilde {p}}}_{{ij + 1}}} < \mathop {\tilde {p}}\nolimits_{ij} , \\ \end{gathered} $

где выполняется условие

(9)

$max(\mathop {\tilde {p}}\nolimits_{01} + \mathop {\tilde {p}}\nolimits_{21} ,2\mathop {\tilde {p}}\nolimits_{11} ) \leqslant - 2,$

то существующие продолжаемые решения уравнения (8) могут быть представлены в виде рядов, абсолютно и равномерно сходящихся в некоторой окрестности точки $x = + \infty $ (см. [5, 6]). Если же в невырожденном уравнении (8) условие (9) не выполняется, то эта ситуация описана выше в теоремах 1 и 2.

2. ПРИМЕРЫ

Пример 1. Рассмотрим уравнение

(10)

$y{\text{'}} + {{y}^{2}} - xy + 1 = 0,$

где выполняются условия теоремы 1. Покажем, что один из рядов (6) здесь является сходящимся, а второй – расходящимся. Для вычисления этих рядов будем рассматривать укороченные уравнения и соответствующие преобразования рассматриваемого уравнения (см. [4]). Многоугольник Ньютона N уравнения (10) представлен на рис. 1.

Рис. 1.

Функция ${{z}_{1}}(x) = {{u}_{1}}(x) = {{x}^{{ - 1}}}$, являющаяся решением укороченного уравнения $ - x{{u}_{1}} + 1 = 0$, соответствующего правому нижнему ребру многоугольника N, одновременно является и решением уравнения (10). Вычисление членов ряда z₂(x) = = $\sum\limits_{i = 1}^\infty {{{a}_{{2i}}}} {{x}^{{{{s}_{{2i}}}}}}$ приводит к следующим результатам. Первое слагаемое ${{{v}}_{1}} = {{a}_{{21}}}{{x}^{{{{s}_{{21}}}}}} = x$ является решением укороченного уравнения ${v}_{1}^{2} - x{{{v}}_{1}}$ = 0, соответствующего правому верхнему ребру многоугольника Ньютона уравнения (10). После замены $y = {{y}_{1}} + x$ уравнение (10) примет вид

(11)

$y_{1}^{'} + y_{1}^{2} + x{{y}_{1}} + 2 = 0.$

Следующее слагаемое ${{{v}}_{2}} = {{a}_{{22}}}{{x}^{{{{s}_{{22}}}}}} = - 2{{x}^{{ - 1}}}$ ряда ${{z}_{2}}(x)$ является решением укороченного уравнения $x{{{v}}_{2}} + 2$ = 0, соответствующего правому нижнему ребру многоугольника Ньютона уравнения (11). Делая замену ${{y}_{1}} = {{y}_{2}} - 2{{x}^{{ - 1}}}$, преобразуем уравнение (11), после чего опять рассматриваем укороченное уравнение, соответствующее правому нижнему ребру преобразованного уравнения. Продолжая этот процесс, вычисляем следующие члены формального ряда ${{z}_{2}}(x)$. В результате вычислений нетрудно видеть, что имеет место оценка ${{{v}}_{k}}(x) = {{a}_{{2k}}}{{x}^{{ - 2k + 3}}},\,\,\,\,{{a}_{{2k}}} \leqslant - k!,\,\,\,\,k \geqslant 2$, откуда следует, что ряд z₂(x) = $\sum\limits_{k = 1}^\infty {{{{v}}_{k}}} (x)$ расходится в любой окрестности точки $x = + \infty $.

Приведем теперь пример, иллюстрирующий теорему 3.

Пример 2. Рассмотрим следующее уравнение Риккати:

(12)

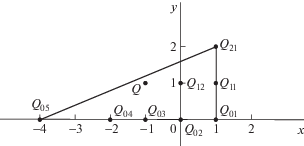
$y{\text{'}} + x{{y}^{2}} + (2x - 2)y\, + x - 2 + {{x}^{{ - 1}}} + {{x}^{{ - 2}}} + {{x}^{{ - 4}}} = 0.$

Данное уравнение является вырожденным, так как выполняются условия (2), (5) и равенства ${{p}_{{01}}} + {{p}_{{21}}} = 2{{p}_{{11}}}$, $c_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}}$ = 0. Многоугольник Ньютона N уравнения (12) представлен на рис. 2.

Рис. 2.

Функция ${{u}_{1}}(x) = - 1$ является решением укороченного уравнения $xu_{1}^{2} + 2{{u}_{1}}x + x = 0$, соответствующего правому вертикальному ребру многоугольника N. После замены $y = {{y}_{1}} - 1$ уравнение (12) примет вид

(13)

$y_{1}^{'} + xy_{1}^{2} - 2{{y}_{1}} + {{x}^{{ - 1}}} + {{x}^{{ - 2}}} + {{x}^{{ - 4}}} = 0.$

Здесь опять выполняются условие (5) и равенства ${{p}_{{01}}} + {{p}_{{21}}} = 2{{p}_{{11}}}$, $c_{{11}}^{2} - 4{{c}_{{01}}}{{c}_{{21}}} = 0$, т.е. уравнение (13) вырождено.

Функция ${{u}_{2}}(x) = {{x}^{{ - 1}}}$ является решением укороченного уравнения $xu_{2}^{2} - 2{{u}_{2}} + {{x}^{{ - 1}}} = 0$, соответствующего правому ребру многоугольника Ньютона уравнения (13). После замены ${{y}_{1}} = {{y}_{2}} + {{x}^{{ - 1}}}$ уравнение (13) примет вид

(14)

$y_{2}^{'} + xy_{2}^{2} + {{x}^{{ - 4}}} = 0.$

Полученное уравнение удовлетворяет условию (4) и, следовательно, является невырожденным. К этому уравнению применимы результаты работ [5, 6]. Функция ${{u}_{3}}(x) = \frac{1}{3}{{x}^{{ - 3}}}$ является решением укороченного уравнения $u_{3}^{'} + {{x}^{{ - 4}}} = 0$, соответствующего правому нижнему ребру многоугольника Ньютона уравнения (14). Продолжая вычисления, приходим к выводу, что уравнение (14) имеет решение в виде абсолютно и равномерно сходящегося в некоторой окрестности точки $x = + \infty $ степенного ряда ${{y}_{2}} = \frac{1}{3}{{x}^{{ - 3}}} + \; \ldots $. Уравнению (14) также соответствует укороченное уравнение ${v}{\text{'}} + x{{{v}}^{2}} = 0$, решением которого является функция ${v}(x) = 2{{x}^{{ - 2}}}$. Отсюда, продолжая вычисления согласно [5, 6], получаем решение уравнения (14), имеющее вид абсолютно и равномерно сходящегося в некоторой окрестности точки $x = + \infty $ ряда ${{y}_{2}} = 2{{x}^{{ - 2}}} - {{x}^{{ - 3}}} - {{x}^{{ - 4}}}({\text{ln}}x + a)$ + ..., слагаемыми которого являются произведения убывающих степеней переменной x на многочлены от lnx. В итоге получаем, что семейство продолжаемых решений уравнения (12) включает степенной ряд $y = - 1 + {{x}^{{ - 1}}} + \frac{1}{3}{{x}^{{ - 3}}} + \; \ldots $, а также семейство рядов

y = $ - 1 + {{x}^{{ - 1}}} + 2{{x}^{{ - 2}}} - {{x}^{{ - 3}}}$ – x^–4(lnx + a) + …,

где a – произвольная постоянная. Все ряды абсолютно и равномерно сходятся в некоторой окрестности точки $x = + \infty $. Можно показать, что других продолжаемых решений уравнение (12) не имеет.

Список литературы

Riccati J. // Acta eruditorum1724. Suppl. 8. P. 66–73.
Ватсон Г.Н. Теория бесселевых функций, Ч. 1. М.: Изд-во иностр. лит., 1949.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматлит, 1971.
Брюно А.Д. // УМН. 2004. Т. 59. В. 3. С. 31–80.
Самовол В.С. // ДАН. 2018. Т. 480. № 4. С. 401–404.
Самовол В.С. // Мат. заметки. 2019. Т. 105. В. 4. С. 603–615.
Samovol V.S. // Asymptotic Analysis. 2019. V. 115. P. 223–239.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал