Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 496, № 1, стр. 34-39
ПРИМЕНЕНИЕ ЧИСЛЕННО-АСИМПТОТИЧЕСКОГО ПОДХОДА В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ ПАРАМЕТРОВ ЛОКАЛЬНОГО СТАЦИОНАРНОГО ИСТОЧНИКА АНТРОПОГЕННОГО ЗАГРЯЗНЕНИЯ
М. А. Давыдова 1, *, член-корреспондент РАН Н. Ф. Еланский 2, **, С. А. Захарова 1, ***, О. В. Постыляков 2, ****
1 Московский государственный университет
имени М.В. Ломоносова
Москва, Россия
2 Институт физики атмосферы имени А.М. Обухова Российской академии наук
Москва, Россия
* E-mail: m.davydova@physics.msu.ru
** E-mail: n.f.elansky@mail.ru
*** E-mail: sa.zakharova@physics.msu.ru
**** E-mail: oleg.postylyakov@gmail.com
Поступила в редакцию 16.11.2020
После доработки 16.11.2020
Принята к публикации 14.12.2020
Аннотация
Рассматривается применение численно-асимптотического подхода к решению некоторых коэффициентных обратных задач диффузии примесей в атмосфере. Асимптотическое решение прямой задачи для эффективного прогностического уравнения в ближней зоне источника, полученное в результате строгого асимптотического анализа многомерной сингулярно возмущенной задачи реакция–диффузия–адвекция, используется в качестве априорной информации при построении численного алгоритма решения обратной задачи по восстановлению параметров источника антропогенного загрязнения. Реализация алгоритма основана на использовании данных зондирования состава атмосферы Земли с российского спутника Ресурс-П, полученных с рекордно высоким пространственным разрешением. Впервые с использованием высокоточного космического мониторинга и математических методов получена оценка выбросов загрязняющей атмосферу примеси (диоксида азота) изолированным промышленным предприятием.
В последнее время активно развивается новое направление в теории сингулярных возмущений, связанное с дальнейшим развитием и использованием методов асимптотического анализа [1, 2] при численном решении прямых [3] и обратных [4, 5] задач для нелинейных сингулярно возмущенных уравнений типа реакция–диффузия–адвекция. Среди приложений нового численно-асимптотического подхода можно выделить прямые и обратные задачи нелинейного теплообмена [6], задачи распространения нелинейных акустических волн [5] и др. Основу численно-асимптотического подхода составляет использование информации о свойствах решений прямых задач, полученной в результате строгого асимптотического анализа, с целью разработки метода генерации динамически адаптированных сеток для эффективных численных алгоритмов решения прямых задач или с целью восстановления параметров модели при решении обратных задач. В результате применения данного подхода удается свести исходную задачу к задаче с более простым численным решением и значительно сэкономить вычислительные ресурсы, сократить время счета, повысив стабильность работы вычислительного процесса по сравнению с альтернативными подходами.
В сообщении рассматривается применение численно-асимптотического подхода к решению некоторых коэффициентных обратных задач атмосферной диффузии примесей, связанных с восстановлением параметров стационарных источников антропогенного загрязнения, а также оценивание эмиссий загрязняющих веществ на основе разработанного метода. В отличие от традиционного описания миграций активных примесей в атмосферном пограничном слое (см., например, [7–9]), в настоящей работе изменение средней концентрации активной примеси в шлейфе источника антропогенного загрязнения описывается эффективным уравнением реакция–диффузия–адвекция, в котором цепь химических превращений примеси параметризуется путем введения эффективной скорости распада. Это позволяет свести нелинейную задачу о миграции активных примесей в шлейфе локального источника к серии линейных задач относительно эффективных прогностических уравнений. С использованием асимптотического решения сингулярно возмущенной задачи для эффективного прогностического уравнения в ближней зоне источника (решение прямой задачи) реализуется эффективный численный алгоритм решения обратной задачи по восстановлению параметров источника на конечнопараметрическом множестве [10]. При этом используются данные наблюдений распределения примеси в финальный момент времени, полученные с помощью высокоточной космической съемки шлейфа загрязненного воздуха от источника [11]. На основе этого подхода разрабатывается новый эффективный метод оценки мощности выброса примесей локальными источниками, точность которого определяется точностью модельного описания.
АСИМПТОТИЧЕСКОЕ ИССЛЕДОВАНИЕ СТАЦИОНАРНЫХ МОДЕЛЕЙ
Рассмотрим стационарную модель реакция–диффузия–адвекция:
(1)
$\begin{gathered} {{\varepsilon }^{2}}\nabla \left( {k\left( x \right)\nabla u} \right) - \varepsilon \left( {{\mathbf{A}}\left( x \right),\nabla u} \right) + f\left( {u,x} \right) = 0, \\ x \in G \subset {{R}^{2}}, \\ \end{gathered} $(2)
$ - \varepsilon k\left( x \right)\left( {\nabla u,{\mathbf{n}}} \right) = g\left( x \right),\quad x \in S,$Асимптотическое разложение по параметру ε решения задачи (1), (2) определяется в соответствии с алгоритмом А.Б. Васильевой [1]:
Подставляя разложение (3) в задачу (1), (2), получаем задачи для определения коэффициентов разложения (3). Для нахождения функций ${{\bar {u}}_{n}}(x),~\,n \geqslant 1,$ имеем конечные уравнения. Например, ${{\bar {u}}_{1}}(x)~$ = = $({\mathbf{A}}(x),\nabla \varphi (x))f_{{\mathbf{u}}}^{{ - 1}}~$(φ(x), x). Если граница S описывается явными уравнениями вида ${{y}_{1}} = R\left( \theta \right){\text{cos}}\theta ,~$ ${{y}_{2}} = R(\theta ){\text{sin}}\theta ,$ (y1, ${{y}_{2}}) \in S$, то функции ${{{\Pi }}_{n}}u\left( {\rho ,\theta } \right)$ при n ≥ 1 определяются задачами для уравнений второго порядка:
$~\frac{{\partial {{{\Pi }}_{n}}u\left( {0,\theta } \right)}}{{\partial \rho }} = {{q}_{n}}\left( \theta \right),$ ${{{\Pi }}_{n}}u( + \infty ,\theta )$ = 0.
Здесь ${{H}_{n}}\left( {\rho ,\theta } \right)$, ${{q}_{n}}\left( \theta \right)$ – известные функции, например, ${{H}_{1}}\left( {\rho ,\theta } \right) = 0~$, q1(θ) = $ - \bar {g}(0,\theta )~$ – $\frac{{\partial \varphi (0,\theta )}}{{\partial r}};~$ N(θ) := $ - {\text{\;}}{\kern 1pt} {{{\Psi }}^{{ - 1/2}}}(\theta )[(R{\kern 1pt} '(\theta ){\text{sin}}\theta $ + $R(\theta ){\text{cos}}\theta ){{A}_{1}}(0$, θ) – – $(R{\kern 1pt} '(\theta ){\text{cos}}\theta - R(\theta ){\text{sin}}\theta ){{A}_{2}}(0,\theta )]$, ${\Psi }(\theta ) = {{(R{\kern 1pt} '(\theta ))}^{2}} + $ $ + \,{{R}^{2}}(\theta ).$ Используя явный вид решений данных задач, который можно получить по аналогии с [12], легко установить справедливость экспоненциальных оценок:
Доказательство существования решения задачи (1), (2) с асимптотическим представлением (3) и оценка остаточного члена основаны на использовании принципа сравнения [13, 2 ]. Верхнее и нижнее решения задачи (1), (2) строятся в виде
Теорема 1. При достаточно малых ε > 0 существует классическое решение $u\left( {x,\varepsilon } \right)$ задачи (1), (2), имеющее асимптотическое представление (3) такое, что $\mathop {\max }\limits_{x \in G \cup S} \left| {u(x,\varepsilon ) - {{U}_{n}}(x,\varepsilon )} \right| = O({{\varepsilon }^{{n + 1}}}).$
Решение u(x, ε) задачи (1), (2) является устойчивым по Ляпунову стационарным решением параболической задачи [13]:
(4)
$\begin{gathered} {{{\bar {L}}}_{\varepsilon }}{v}: = {{\varepsilon }^{2}}(\nabla (k(x)\nabla {v}) - {{{v}}_{t}}) - \varepsilon ({\mathbf{A}}(x),\nabla {v}{\text{)}} + f({v},x) = 0, \\ x \in G \subset {{R}^{2}},\quad t > 0,~ \\ \end{gathered} $(5)
$\begin{gathered} - \varepsilon k(x)(\nabla {v},{\mathbf{n}}) = g(x),\quad x \in S,\quad t \geqslant 0, \\ {v}(x,0) = {{u}^{0}}(x),\quad ~x \in G \cup S~ \\ \end{gathered} $Теорема 2. При достаточно малых ε > 0 стационарное решение $u\left( {x,\varepsilon } \right)$ задачи (4), (5), имеющее асимптотическое представление (3), асимптотически устойчиво по Ляпунову с локальной областью притяжения: ${{u}^{0}}\left( x \right) \in \left[ {\alpha _{0}^{{\left( - \right)}}\left( {x,\varepsilon } \right),\alpha _{0}^{{\left( + \right)}}\left( {x,\varepsilon } \right)} \right]$.
При определенных ограничениях на функцию $f(u,x)$ имеет место
Теорема 3. Если ${{f}_{u}}\left( {u,x} \right) \leqslant 0,~~x \in G \cup S,$ то задача (1), (2) не может иметь более одного классического решения.
Для доказательства этой теоремы достаточно показать, что задача ${{L}_{\varepsilon }}w = 0$, $x \in G,$ $(\nabla w,{\mathbf{n}}) = 0$, $x \in S,$ относительно функции w(x) := u2(x, ε) – ‒ ${{u}_{1}}(x,\varepsilon ),$ где ${{L}_{\varepsilon }}: = {{\varepsilon }^{2}}\nabla \left( {k\left( x \right)\nabla } \right)~$ – $\varepsilon ({\mathbf{A}}(x),\nabla )~$ + + $\mathop \smallint \limits_0^1 {{f}_{u}}({{u}_{\xi }},x)d\xi ~$, $~{{u}_{\xi }}: = \xi {{u}_{2}} + \left( {1 - \xi } \right){{u}_{1}},~~$ ${{u}_{i}}\left( {x,\varepsilon } \right)$ – несовпадающие классические решения задачи (1), (2), имеет только тривиальное решение. Действительно, для любой функции ${v}(x) \in {{C}^{2}}(G) \cap {{C}^{1}}(G \cup S)$ справедливо равенство
Если положить ${v} \equiv w$ и учесть, что на границе поток обусловлен только диффузией, т.е. что $({\mathbf{A}}(x),n) = 0,x \in S,$ то получим $\begin{array}{*{20}{c}} {w \equiv 0,}&{x \in G \cup S.} \end{array}$
АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ЭФФЕКТИВНОГО УРАВНЕНИЯ
Поскольку на основе метода [11] устанавливается интегральное содержание NO2 в вертикальном столбе атмосферы высотой $H - {{H}_{0}}$, где H – средняя высота пограничного слоя, ${{H}_{0}} \approx {{10}^{4}}$ см (средняя высота дымовых труб), то с целью описания средней концентрации NO2 в шлейфе источника удобно использовать $({{x}_{1}},~{{x}_{2}})$ – приближение [9] эффективного прогностического уравнения:
(6)
$\begin{gathered} {{u}_{t}} = \left\langle k \right\rangle \Delta u - \nabla \left( {u{\mathbf{A}}\left( x \right)} \right) + {{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}\left( x \right) - \gamma \left( t \right)\left( {u - U} \right),~ \\ \nabla {\mathbf{A}}\left( x \right) = 0, \\ x \in G \in {{R}^{2}},\quad t \in \left( {{{t}_{0}},{{t}_{0}} + ~T} \right] \\ \end{gathered} $(7)
$\begin{gathered} - \left\langle k \right\rangle \left( {\nabla u,n} \right) = 0,\quad x \in S, \\ u\left( {x,{{t}_{0}}} \right) = {{u}^{0}}\left( x \right),\quad x \in G \cup S, \\ \end{gathered} $Определим круговую область G, центр которой совмещен с источником загрязнения, а радиус $L\sim {{10}^{5}}$ см (ближняя зона). В такой области мощность выброса диоксида азота в результате реакции окисления оксида азота по порядку величины равна мощности стока этой примеси при первичном фотолизе. Учитывая это и обозначая ε := := ${{({\text{P}}{{{\text{r}}}_{D}}{\text{Re}})}^{{ - 1}}}$ ~ 10–2, где PrD – турбулентное диффузионное число Прандтля, Re – число Рейнольдса, получаем задачу (6), (7) в ближней зоне в безразмерных переменных:
(8)
$\begin{gathered} {{\varepsilon }^{2}}\left( {\Delta u - {{u}_{t}}} \right) - \varepsilon ({\mathbf{A}}(x),\nabla u) + {{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}(x) - \gamma \left( t \right)\left( {u - 1} \right) = 0, \\ x \in {{K}^{1}},\quad t \in \left( {{{t}_{0}},{{t}_{0}} + 1} \right], \\ \end{gathered} $(9)
$\begin{gathered} \left( {\nabla u,n} \right) = 0,\quad x \in \partial {{K}^{1}}, \\ u\left( {x,{{t}_{0}}} \right) = {{u}^{0}}\left( x \right),\quad x \in {{K}^{1}} \cup \partial {{K}^{1}}. \\ \end{gathered} $Здесь $\partial {{K}^{1}}$ – граница круга K1 единичного радиуса. В задаче (8), (9) сохранены прежние обозначения для безразмерных переменных в целях удобства.
Если T ≈ 1 ч, то эффективную скорость распада можно считать постоянной величиной, и тогда в ближней зоне распределение безразмерной концентрации NO2 будет описывается задачей (8), (9) при замене γ(t) на константу γ ~ 1. Полученная таким образом задача относится к типу (4), (5). Поэтому существует единственное стационарное устойчивое состояние, описываемое безразмерным распределением типа (3):
(10)
$\begin{gathered} {{u}_{{st}}}\left( {x,\varepsilon } \right) = 1 + {{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}\left( x \right){{\gamma }^{{ - 1}}} - \varepsilon \left( {{\mathbf{A}}\left( x \right),\nabla {{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}\left( x \right)} \right){{\gamma }^{{ - 2}}} + \\ + {{\left. {\varepsilon \left( {{\mathbf{n}},\nabla {{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}\left( {\left( {1 - r} \right)\cos \theta ,\left( {1 - r} \right){\text{sin}}\theta } \right)} \right)} \right|}_{{r = 0}}} \times \\ \times \,{{(\gamma {\Upsilon }\left( \theta \right))}^{{ - 1}}}{{e}^{{ - {\Upsilon }\left( \theta \right)r{{\varepsilon }^{{ - 1}}}}}} + O({{\varepsilon }^{2}}), \\ \end{gathered} $Стабилизация решения задачи (8), (9) при $\gamma (t)$ = = γ к решению с асимптотикой (10) происходит за время ${{T}_{{st}}} \ll 1~$. Действительно, асимптотическое решение задачи (8), (9) при $\gamma \left( t \right) = \gamma $ можно построить на основе метода углового погранслоя [1]: u(x, t, ε) = = $1\, + \,{{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}(x){{\gamma }^{{ - 1}}}$ + (u0(x) – 1 – ${{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}(x){{\gamma }^{{ - 1}}}){{e}^{{ - \gamma t{{\varepsilon }^{{ - 2}}}}}}$ + O(ε) и обосновать построение на основе методов [13]. При $\left| {u\left( {x,{{T}_{{st}}},\varepsilon } \right) - {{u}_{{st}}}\left( {x,\varepsilon } \right)} \right| \leqslant O({{10}^{{ - 2}}}),$ ${{T}_{{st}}}\sim {{10}^{{ - 2}}}$, что соответствует размерному времени стабилизации около одной минуты. Эта оценка доказывает квазистационарный характер процесса (см. подробнее [9]) в ближней зоне и оправдывает использование асимптотики (10) с целью получения распределения интегрального содержания NO2 в столбе воздуха на временном интервале около часа.
В формуле (10) интенсивность источника задается следующим образом:
(11)
${{f}_{{{\text{N}}{{{\text{O}}}_{2}}}}}\left( x \right) = {{\alpha }_{{{\text{N}}{{{\text{O}}}_{2}}}}}\tilde {\gamma }{{u}_{{{\text{NO}}}}}\left( x \right){{u}_{{{{{\text{O}}}_{3}}}}}\left( x \right),~~$(12)
${{u}_{{{\text{N}}{{{\text{O}}}_{2}}}}}\left( x \right) = U \cdot \,~{{u}_{{st}}}\left( {x{\kern 1pt} ',\varepsilon } \right),$ВОССТАНОВЛЕНИЕ ПАРАМЕТРОВ ИСТОЧНИКА И ОЦЕНКА ЭМИССИЙ
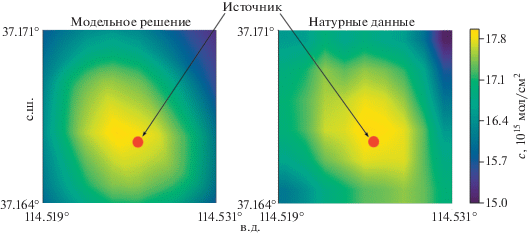
С целью восстановления параметров σ и l в распределении (11) применяется алгоритм решения коэффициентной обратной задачи [10], где в качестве решения прямой задачи в ближней зоне используется распределение (12). В итоге получены следующие значения: σ = 500 см и I = 2 × 104. На рис. 1 показано распределение интегрального содержания диоксида азота (NO2) в вертикальном столбе атмосферы в пределах ее пограничного слоя (0–2 км) в провинции Хэбэй КНР 29 сентября 2018 г. Распределение построено по данным наблюдений с российского спутника Ресурс-П, оборудованного гиперспектрометром изображения [11]. Впервые в мире распределение NO2 получено с высоким разрешением 2.4 км на сетке 120 м, которое позволяет выделять источники загрязнения атмосферы размером с отдельные промышленные предприятия. На фоне регионального загрязнения выделяется шлейф NO2 от химического предприятия по производству сажи и других продуктов, получаемых при переработке угля. Содержание NO2 в выбросе предприятием оксидов азота NOx (NOx = NO + NO2) составляет 10%, но в течение нескольких минут в результате взаимодействия NO с озоном доля NO2 в NOx увеличивается до 55% [14, 15]. На рис. 2 и 3 изображено распределение NO2 в ближней зоне источника, сформированное при ветре в момент наблюдений 1 м/с в результате выброса NOx из источника в течение одного часа, действия химической трансформации и турбулентной диффузии.
Рис. 1.
Распределение интегрального содержания диоксида азота в пограничном слое атмосферы в провинции Хэбэй 29.09.2018 г.
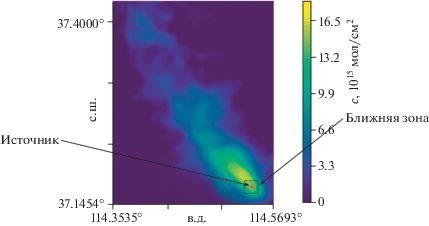
Рис. 3.
Сравнение аналитического решения (12) и натурного распределения интегрального содержания NO2 в ближней зоне в разрезе (учтен региональный фон, равный 2.7 × 1015 мол/см2).
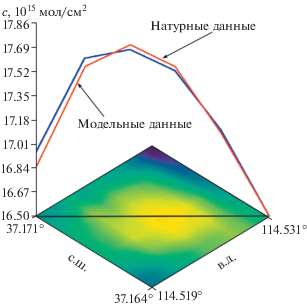
Используя представление (12) с восстановленными параметрами, получаем оценку среднего интегрального содержания NO2 за вычетом регионального фона в ближней зоне: 15 × 1015 мол/см2. Мощность выброса NO2 (эмиссии) определяется формулой
где V – характерная скорость переноса. Используя формулу (13) при V = 100 см/с, получаем оценку эмиссий NO2: 100 кг/ч. Данный пример демонстрирует возможность применения современных космических средств и математических методов для мониторинга качества воздуха в пределах городов и идентификации основных источников загрязнения атмосферы практически на всей территории планеты.ЗАКЛЮЧЕНИЕ
Дистанционное зондирование состава атмосферы с космических аппаратов активно используется для мониторинга его региональных и глобальных изменений. Совершенствование космических аппаратов и средств измерений делает возможным контролировать локальные особенности состава атмосферы и, следовательно, качество воздуха в городах, а также в окрестностях загрязняющих атмосферу предприятий. Первым примером реализации таких возможностей являются наблюдения со спутника Ресурс-П содержания в пограничном слое атмосферы важного химически активного соединения – диоксида азота. На основе метода [11] и алгоритма [10] с использованием распределения (11) получены оценки эмиссий NO2 (100 кг/ч). Разработанный эффективный алгоритм восстановления распределения концентрации примеси в ближней зоне источника загрязнения позволяет в короткое время выполнить оценку выбросов предприятиями загрязнений в атмосферу, что открывает широкие перспективы для оперативного мониторинга локальных особенностей загрязнения атмосферы в глобальном масштабе. Другим приложением результатов работы является прогнозирование поведения шлейфов загрязнений и образования экстремальных экологических ситуаций.
Список литературы
Васильева А.Б., Бутузов В.Ф. Асимптотические методы в теории сингулярных возмущений. М.: Высш. шк., 1990.
Васильева А.Б., Бутузов В.Ф., Нефедов Н.Н. Сингулярно возмущенные задачи с пограничными и внутренними слоями // Труды Мат. ин-та им. В.А. Стеклова РАН. 2010. № 268. С. 268.
Волков В.Т., Лукьяненко Д.В., Нефедов Н.Н. Аналитико-численный подход для описания периодических по времени движущихся фронтов в сингулярно возмущенных моделях реакция–диффузия–адвекция // ЖВМиМФ. 2019. Т. 59. № 1. С. 50–62.
Lukyanenko D.V., Shishlenin M.A., Volkov V.T. Asymptotic analysis of solving an inverse boundary value problem for a nonlinear singularly perturbed time-periodic reaction-diffusion-advection equation // J. of Inverse and Ill-Posed Problems. 2019. V. 27. № 5. P. 745–758.
Волков В.Т., Нефедов Н.Н. Асимптотическое решение коэффициентных обратных задач для уравнений типа Бюргерса // ЖВМиМФ. 2020. Т. 60. № 6. С. 975–984.
Давыдова М.А., Захарова С.А. Асимптотический анализ в задачах нелинейного теплообмена и его приложения. // Марчуковские научные чтения 2020: Тезисы Междунар. конф., посв. 95-летию со дня рождения акад. Г.И. Марчука, Новосибирск, 19–23 октябра 2020 г./ Ин-т вычислит. математики и матем. геофизики СО РАН. Новосибирск: ИПН НГУ, 2020. С. 10.
De More W.B. et al. Chemical Kinetics and Photochemical Data for Use in Stratospheric Modeling // NASA, California Institute of Technology. 1997.
Пономарев Н.А., Еланский Н.Ф., Кирсанов А.А., Постыляков О.В., Боровский А.Н., Веревкин Я.М. Применение химико-транспортных моделей атмосферы для валидации эмиссий загрязняющих примесей в Москве // Оптика атмосферы и океана. 2020. Т. 33. № 2. С. 119–126.
Марчук Г. И. Математическое моделирование в проблеме окружающей среды. М.: Наука, 1982.
Zakharova S.A., Davydova M.A., Lukyanenko D.V. Use of asymptotic analysis for solving the inverse problem of source parameters determination of nitrogen oxide emission in the atmosphere // Inverse Problems in Science and Engineering. 2020. https://doi.org/10.1080/17415977.2020.1785443
Postylyakov O.V., Borovski A.N., Makarenkov A.A. First experiment on retrieval of tropospheric NO2 over polluted areas with 2.4-km spatial resolution basing on satellite spectral measurements // Proc. of SPIE – The International Society for Optical Engineering. 2017. V. 10466. P.104662Y-8.
Давыдова М.А. Существование и устойчивость решений с пограничными слоями в многомерных сингулярно возмущенных задачах реакция-диффузия-адвекция // Матем. заметки. 2015. Т. 98. № 6. С. 853–864.
Wang J. Monotone method for diffusion equations with nonlinear diffusion coefficients // Nonlin. Anal. 1998. V. 12. № 1. P. 19–41.
Elansky N.F., Ponomarev N.A., Verevkin Ya.M. Air quality and pollutant emissions in the Moscow megacity in 2005–2014 // Atmospheric Environment. V. 175. February 2018. P. 54–64.
Elansky N.F., Shilkin A.V., Ponomarev N.A., Semutnikova E.G., Zakharova P.V. Weekly patterns and weekend effects of air pollution in the Moscow megacity. Atmospheric Environment. 2020. V. 224. 117303.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления