Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 505, № 1, стр. 42-45
О ПРИБЛИЖЕННОМ СУММИРОВАНИИ РЯДОВ ПУАНКАРЕ В МОДЕЛИ ШОТТКИ
С. Ю. Лямаев *
Институт вычислительной математики Российской академии наук им. Г.И. Марчука
Москва, Россия
* E-mail: sergei.lyamaev@gmail.com
Поступила в редакцию 09.01.2022
После доработки 16.04.2022
Принята к публикации 12.05.2022
- EDN: DZNTGA
- DOI: 10.31857/S2686954322040129
Аннотация
Предложены модификации алгоритмов Богатырёва и Шмиза для приближенного суммирования рядов Пуанкаре в модели Шоттки вещественных гиперэллиптических кривых, позволяющие сократить число суммируемых членов без потери точности.
Зафиксируем натуральное число g и разбиение $\left\{ {1,2, \ldots ,g} \right\} = {{\Sigma }^{ + }} \sqcup {{\Sigma }^{ - }}$. На g непересекающихся отрезках положительной полуоси как на диаметрах построим окружности
${{C}_{1}}, \ldots ,{{C}_{g}}$. Нумерация окружностей – слева направо. На всякой окружности Cj отметим пару точек: при $j \in {{\Sigma }^{ + }}$ отметим точки пересечения с вещественной осью ${{c}_{j}} \pm {{r}_{j}}$, при $j \in {{\Sigma }^{ - }}$ – произвольную пару комплексно сопряженных точек ${{c}_{j}} \pm i{{r}_{j}}$. Обозначим за ${{G}_{j}}$ дробно-линейную инволюцию, оставляющую на месте каждую из отмеченных на Cj точек. Отображение ${{G}_{j}}$ переводит внешность окружности Cj в ее внутренность, следовательно, гиперболическое преобразование ${{S}_{j}}u: = {{G}_{j}}( - u)$ переводит внешность окружности ${{C}_{{ - j}}}: = - {{C}_{j}}$ во внутренность Cj. Преобразования ${{S}_{1}}, \ldots ,{{S}_{g}}$ свободно порождают группу Шоттки, которую обозначим за $\mathfrak{S}$. Ее стандартная фундаментальная область $\mathcal{F}$ – это внешность $2g$ окружностей ${{C}_{{ \pm 1}}}, \ldots ,{{C}_{{ \pm g}}}$ в сфере Римана. Факторпространство  , где отношение эквивалентности склеивает пары окружностей ${{C}_{{ - j}}}$, Cj посредством преобразований ${{S}_{j}}$, $1 \leqslant j \leqslant g$, является вещественной гиперэллиптической кривой рода $g$ c $k$ вещественными и $k$ ковещественными овалами, где $k: = {\text{|}}{{\Sigma }^{ + }}{\text{|}} + 1$, – и всякая такая кривая может быть получена в результате проделанной геометрической
конструкции [2].
, где отношение эквивалентности склеивает пары окружностей ${{C}_{{ - j}}}$, Cj посредством преобразований ${{S}_{j}}$, $1 \leqslant j \leqslant g$, является вещественной гиперэллиптической кривой рода $g$ c $k$ вещественными и $k$ ковещественными овалами, где $k: = {\text{|}}{{\Sigma }^{ + }}{\text{|}} + 1$, – и всякая такая кривая может быть получена в результате проделанной геометрической
конструкции [2].
Эффективная теория функций на кривой в модели Шоттки строится на основе тета-рядов
Пуанкаре. Так, ключевой объект теории – нормированный абелев дифференциал третьего
рода ${{\eta }_{{zw}}}$ с полюсами в точках 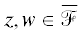 – получается усреднением по группе Шоттки рационального дифференциала на римановой
сфере:
– получается усреднением по группе Шоттки рационального дифференциала на римановой
сфере:
Этот линейный ряд Пуанкаре абсолютно сходится, поскольку фундаментальная область $\mathcal{F}$ удовлетворяет критерию Шоттки. Настоящее сообщение – о приближенном вычислении суммы такого ряда на компьютере. Вся техника прямо переносится и на другие бесконечные суммы и произведения, которыми записываются теоретико-функциональные объекты на кривой в модели Шоттки.
Введем обозначения ${{\sigma }_{j}}: = \pm 1$ при $j \in {{\Sigma }^{ \pm }}$ и ${{S}_{{ - j}}}\,{\text{: = }}\,S_{j}^{{ - 1}}$, ${\kern 1pt} {{c}_{{ - j}}}\,: = \, - {\kern 1pt} {{c}_{j}}$, ${\kern 1pt} {{r}_{{ - j}}}\,: = \,{{r}_{j}}$, ${\kern 1pt} {{\sigma }_{{ - j}}}\,: = \,{{\sigma }_{j}}$ при $1\, \leqslant \,j\, \leqslant \,g$. Справедлива формула
Группа Шоттки $\mathfrak{S}$ есть множество несократимых слов алфавита $\left\{ {{{S}_{j}}\,{\text{|}}\, j \in \Xi } \right\}$ с операцией конкатенации. Обозначим за ${\text{|}}S{\text{|}}$ количество букв в несократимой записи слова $S \in \mathfrak{S}$. Определим на $\mathfrak{S}$ отношение строгого частичного порядка: $S < T$, если $T = QS$, где $Q \ne id$ и ${\text{|}}T{\text{|}} = {\text{|}}Q\; + \;{\text{|}}S{\text{|}}$.
Граф Кэли группы Шоттки имеет вид бесконечного дерева, вершины которого взаимно-однозначно соответствуют элементам группы. Всякая вершина $S$ соединена ребрами с вершинами ${{S}_{j}}S, j \in \Xi $. Корень – вершина, отвечающая тождественному преобразованию id. Множество $\left\{ {S \in \mathfrak{S}:{\text{|}}S{\text{|}} = n} \right\}$ будем называть $n$-м уровнем дерева. Вершины, соединенные с S ребром и лежащие на следующем уровне по сравнению c S, – это дети вершины S. При $S \ne {\text{id}}$ имеется одна вершина, соединенная с S ребром и лежащая на предыдущем уровне, – будем называть ее родителем S. Назовем вершины братьями, если у них общий родитель. Если $T < S$, то вершину S будем называть потомком вершины $T$, а вершину $T$ – предком вершины S.
Для приближенного суммирования ряда Пуанкаре из бесконечного дерева Кэли нужно выделить конечное поддерево $\mathfrak{T} \subset \mathfrak{S}$, сумма по которому хорошо приближает точное значение. Скорость убывания членов ряда вдоль разных ветвей дерева Кэли значительно отличается, поэтому суммировать по нескольким первым уровням, взятым целиком, неэкономично. Для выделения конечного поддерева известны два эффективных подхода: алгоритм А.Б. Богатырёва [1, 2] и алгортим М. Шмиза [3].
Существуют также другие подходы к вычислению теоретико-функциональных объектов в модели Шоттки, не связанные с непосредственным суммированием рядов Пуанкаре: метод В. Митюшева, Н. Рылко [4, 5] и метод Д. Крауди, Дж. Маршалла, Н. Трефтена [6]. В рамках настоящей работы сравнение с этими методами не проводилось.
Пусть точки 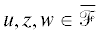 лежат в разных орбитах действия группы $\mathfrak{S}$. Можем оценить
лежат в разных орбитах действия группы $\mathfrak{S}$. Можем оценить
Для простоты потребуем, чтобы $\Phi (T)$ зависело только от первой слева буквы в несократимой записи слова T.
Алгоритм Богатырёва имеет апостериорную оценку точности. В каждый момент будем хранить в памяти путь от корня дерева Кэли до текущей вершины T вместе со значениями $Su$ и $S{\kern 1pt} 'u$ для всякой вершины $S$ на этом пути. При вычислении значений $Tu$ и $T{\kern 1pt} 'u$ для текущей вершины используем сохраненные в памяти значения для родительской вершины. Прибавим член ряда, отвечающий текущей вершине к приближенному значению суммы. Если число $\Omega (T): = \Phi (T){\text{|}}T{\kern 1pt} 'u{\text{|}}$ не меньше заранее выбранного малого параметра $\mu $, то продолжим движение по текущей ветви дерева Кэли – перейдем от вершины T к наибольшему в лексикографическом порядке ее ребенку. В противном случае исключим из счета все поддерево потомков вершины T и сместимся на соседнюю ветвь – перейдем к наибольшей в лексикографическом порядке вершине среди детей предков вершины T, меньших чем T в лексикографическом порядке. Если такой вершины нет, алгоритм останавливается – оценка погрешности равна сумме значений $\Omega (S)$ по всем листьям $S$ поддерева просуммированных вершин $\mathfrak{T}$. Стартует алгоритм с корня дерева Кэли.
Алгоритм Шмиза имеет априорную оценку точности и является жадным алгоритмом: на каждой итерации прибавляется вершина с наибольшей оценкой вклада в сумму. Реализовать эту идею можно, например, следующим образом. В каждый момент в памяти будем хранить все листья S поддерева просуммированных вершин, для них будем помнить значения Su, $S{\kern 1pt} 'u$, $\Omega (S)$ и первую слева букву в несократимой записи слова S. На каждой итерации из памяти удаляется вершина $T$ с максимальным значением $\Omega (T)$, вместо нее в память помещаются все ее дети и прибавляются к приближенному значению суммы. Текущая оценка погрешности равна сумме значений $\Omega (S)$ по всем сохраненным в памяти вершинам S – алгоритм останавливается, как только она становится меньше требуемого значения $\varepsilon $.
В обоих алгоритмах поддерево просуммированных вершин $\mathfrak{T}$ заранее неизвестно и формируется непосредственно в процессе счета. Если за $\mu $ в алгоритме Богатырёва положить минимальное значение $\Omega ( \cdot )$ среди всех нелистовых вершин поддерева, по которому просуммировал алгоритм Шмиза, то при условии, что в дереве Кэли есть только одна вершина с таким значением, алгоритм Богатырёва просуммирует ровно по тому же поддереву.
Заметим, что в обоих алгоритмах на основании значения $\Omega (T)$ принимается решение об учете в сумме сразу всех детей $T$. Это приводит к тому, что часть листьев поддерева просуммированных вершин $\mathfrak{T}$ вносит пренебрежимо малый вклад в сумму. При этом листовых вершин при $\mathfrak{T}\, \supset \,\{ S\, \in \,\mathfrak{S}\,:\,{\text{|}}S{\text{|}}\, < \,n\} $, $n \to \infty $ и $g > 1$ в $2g - 2$ раз больше, чем нелистовых. Особенно много неэффективной работы алгоритмы производят в ситуациях, когда какие-либо из граничных окружностей фундаментальной области очень близки друг к другу – в этом случае в поддереве просуммированных вершин будут присутствовать длинные ветви, у большинства вершин которых ровно один из $2g - 1$ детей вносит весомый вклад в сумму.
Предложим модификации алгоритмов на основе следующей идеи: решение об учете в сумме будем принимать по отдельности для каждого ребенка ${{S}_{j}}T$ вершины T с использованием оценки
Будем добавлять ребенка ${{S}_{j}}T$ вершины $T$ в поддерево $\mathfrak{T}$, если $\Theta ({{S}_{j}}T): = \Psi ({{S}_{j}}T){\text{|}}T{\kern 1pt} 'u{\text{|}} \geqslant \mu $, где $\mu $ – фиксированный малый параметр. Для братьев ${{T}_{1}}$ и ${{T}_{2}}$ введем старшинство: ${{T}_{1}}$ старше ${{T}_{2}}$, если $\Psi ({{T}_{2}}) < \Psi ({{T}_{1}})$. Обозначим за $\mathfrak{B}(S)$ множество, состоящее из самой вершины S и ее младших братьев. Для несократимых слов ${{T}_{1}}$ и ${{T}_{2}}$, у которых подслова из $n \geqslant 1$ первых справа букв являются братьями, определим старшинство так: ${{T}_{1}}$ старше ${{T}_{2}}$, если указанное подслово у ${{T}_{1}}$ старше, чем у ${{T}_{2}}$.
Алгоритм 1. (Модифицированный алгоритм Богатырёва). Зафиксируем $\mu > 0$. Присвоим $sum: = f({\text{id}})$ и err := 0. Будем хранить в памяти массив со следующей структурой: в момент перехода в вершину $T = {{S}_{{{{i}_{{|T|}}}}}} \ldots {{S}_{{{{i}_{2}}}}}{{S}_{{{{i}_{1}}}}}$ в n-й ячейке массива при $1 \leqslant n \leqslant {\text{|}}T{\text{|}} - 1$ записаны буква ${{S}_{{{{i}_{n}}}}}$ и вектор $h({{T}_{{[n]}}})$, где $h(S): = (Su,S{\kern 1pt} 'u,{\kern 1pt} {\text{|}}S{\kern 1pt} 'u{\text{|}})$, ${{T}_{{[n]}}}: = {{S}_{{{{i}_{n}}}}} \ldots {{S}_{{{{i}_{2}}}}}{{S}_{{{{i}_{1}}}}}$. Перейдем в самую старшую вершину первого уровня.
Итерация. Пусть T – вершина, в которую только что перешел алгоритм. Используя $({\text{|}}T{\text{|}} - 1)$-ю ячейку массива, вычислим вектор $h(T)$ и поместим его в |T|-ю ячейку вместе с буквой ${{S}_{{{{i}_{{|T|}}}}}}$. Присвоим $sum: = sum + f(T).$ Найдем следующую вершину рекурсивной процедурой поиска. Вначале за $\mathfrak{U}$ обозначим множество, состоящее из детей вершины $T$, а также из младших чем вершина $T$ детей ее предков. Пусть S – самая старшая вершина в $\mathfrak{U}$ среди лежащих на максимальном уровне в этом множестве. Если $\Theta (S) \geqslant \mu $, то поиск закончен – перейдем от $T$ к S. Иначе учтем вершину S и всех ее младших братьев вместе с поддеревьями потомков в оценке погрешности $err\,: = \,err\, + \,\sum\limits_{B \in \mathfrak{B}(S)}^{} {\Theta (B),} $ переобозначим $\mathfrak{U}\,: = \,\mathfrak{U}{{\backslash }}\mathfrak{B}(S)$ и повторим процедуру поиска с новым $\mathfrak{U}$. Если $\mathfrak{U} = \emptyset $, алгоритм останавливается и имеем $\left| {{{\eta }_{{zw}}}(u){\text{/}}du - sum} \right| \leqslant \Upsilon \cdot err.$
Алгоритм 2 (Модифицированный алгоритм Шмиза). Выберем целевую точность $\varepsilon > 0$. Присвоим $sum: = f(id)$, $err: = \sum\limits_{j \in \Xi }^{} {\Theta ({{S}_{j}})} $ и сохраним в памяти самую старшую вершину первого уровня. Для всякой сохраненной в памяти вершины S будем помнить вектор $h(Q)$, где Q – родитель S, а также $\Theta (S)$ и две первых слева буквы несократимого слова S.
Итерация. Удалить из памяти вершину $T$ с максимальным значением $\Theta (T)$, поместить в память ее старшего ребенка и, если $T$ не самый младший среди братьев, следующего по старшинству брата. Присвоить $sum: = sum + f(T)$ и err := := err – $\Theta (T) + \sum\limits_{j \in \Xi : {{S}_{j}}T > T}^{} {\Theta ({{S}_{j}}T).} $ Как только err < < $\varepsilon {\text{/}}\Upsilon $, алгоритм останавливается.
Перед стартом Алгоритма 1 необходимо вычислить и запомнить значения $\mu {\text{/}}\Psi ({{S}_{j}}T)$ и $\sum\limits_{B \in \mathfrak{B}({{S}_{j}}T)}^{} {\Psi (B)} $ для всех комбинаций первых двух слева букв слова ${{S}_{j}}T$, перед стартом Алгоритма 2 – значения $\Psi ({{S}_{j}}T)$ и $\sum\limits_{j \in \Xi }^{} {\Psi ({{S}_{j}}T)} $.
Если за $\mu $ в Алгоритме 1 положить минимальное значение $\Omega ( \cdot )$ по всем вершинам, просуммированным Алгоритмом 2, то при условии, что в дереве Кэли есть только одна вершина с таким значением, Алгоритм 1 просуммирует ровно по такому же поддереву.
Результаты сравнения алгоритмов на шести численных примерах – в табл. 1. В алгоритмах с апостериорной оценкой точности для малого параметра $\mu $, подаваемого на вход, подбиралось максимальное значение, с которым на выходе алгоритма достигается нужная точность ε. Во всех примерах алгоритмы Богатырёва и Шмиза суммировали одинаковое числов вершин ${{N}_{1}}$, поэтому их результаты объединены в одну колонку. По этой же причине в одну колонку объединены Алгоритмы 1 и 2, для них число просуммированных вершин обозначено за N2. В качестве $\Phi (T)$ использовалась оценка Бернсайда [3, 7] Φ(T) := := ${{\lambda }_{t}}{\text{/}}(1 - \lambda )$, применимая при условии $\lambda < 1$, где ${{\lambda }_{l}}: = \sum\limits_{j \in \Xi \backslash \{ - l\} }^{} {{{\Lambda }_{{jl}}}} $, $\lambda : = {{\max }_{{l \in \Xi }}}{{\lambda }_{l}},$ $t$ – индекс первой слева буквы в несократимой записи слова $T \ne id$. Во всех примерах использовались точки $u = - 1 + 2i$, $z = 3 + i$ и $w = - 2$.
Таблица 1.
Сравнение алгоритмов
| № | ${{N}_{1}}$ | ${{N}_{2}}$ | N1/N2 |
|---|---|---|---|
| 1 | 9617 | 7129 | 1.35 |
| 2 | 43 912 | 17 629 | 2.49 |
| 3 | 52 565 | 17 910 | 2.93 |
| 4 | 14 582 | 2899 | 5.03 |
| 5 | 23 922 | 2007 | 11.92 |
| 6 | 15 126 | 398 | 38.01 |
Массивы $c$ и $r$ имеют длину g – в них объединены значения для индексов $1, \ldots ,g$. За $\varepsilon $ обозначена требуемая оценка точности на выходе алгоритмов. Во всех примерах, кроме третьего, ${{\sigma }_{j}} = 1$, $1 \leqslant j \leqslant g$. Пример 1: $g = 3$, $c = (0.1$, $0.6$, $1)$, $r = 0.05 \cdot (1$, $1$, $1)$, $\varepsilon {{ = 10}^{{ - 10}}}$. Пример 2: $g = 3$, $c = (0.1$, $0.9$, $1)$, $r = (0.05$, $0.04$, $0.04)$, $\varepsilon {{ = 10}^{{ - 10}}}$. Пример 3: $g = 4$, $\sigma = (1, - 1, - 1,1)$, $c = (0.1$, $0.5$, $0.8$, $1)$, $r = 0.01 \cdot (1$, $1$, $6$, $8)$, $\varepsilon {{ = 10}^{{ - 10}}}$, окружность ${{C}_{2}}$ имеет центр $ \approx 0.5610$ и радиус $ \approx 0.06184$, окружность ${{C}_{3}}$ – центр $ \approx 0.8057$ и радиус $ \approx 0.06027$. Пример 4: $g = 8$, $c = (0.1$, 0.2, 0.5, 0.6, $0.7$, $0.75$, $0.9$, $1)$, $r = 0.01 \cdot (0.1$, $4$, $4$, $0.1$, $0.1$, 0.1, $4$, $4)$, $\varepsilon {{ = 10}^{{ - 7}}}$. Пример 5: g = 12, $c = (0.3$, $0.4$, $0.5$, $0.52$, $0.67$, $0.78$, $0.84$, $0.88$, $0.91$, $0.96$, $0.98$, $1)$, $r = 0.01 \cdot (2$, $4.5$, $1$, $0.8$, $3.6$, $0.9$, $1$, $2$, $0.5$, $0.5$, $0.5$, $1)$, $\varepsilon {{ = 10}^{{ - 4}}}$. Пример 6: $g = 100$, ${{c}_{j}} = j{\text{/}}100$, ${{r}_{j}}{{ = 10}^{{ - 4}}}$, $1 \leqslant j \leqslant 100$, ε = 10–10.
С изменением точности $\varepsilon $ при фиксированных остальных параметрах относительная разница между алгоритмами мало меняется. К примеру, в Примере 4 при $\varepsilon = {{10}^{{ - 5}}}$ имеем ${{N}_{1}}{\text{/}}{{N}_{2}} \approx 5.05$, при $\varepsilon = {{10}^{{ - 6}}}$ имеем ${{N}_{1}}{\text{/}}{{N}_{2}} \approx 4.85$, при $\varepsilon = {{10}^{{ - 8}}}$ – ${{N}_{1}}{\text{/}}{{N}_{2}} \approx 5.00$, при $\varepsilon = {{10}^{{ - 9}}}$ – ${{N}_{1}}{\text{/}}{{N}_{2}} \approx 4.99$.
Предложенные алгоритмы по сравнению с алгоритмами Богатырёва и Шмиза позволяют суммировать меньшее число членов ряда для достижения той же оценки точности на выходе: на десятки процентов в обычных ситуациях и в несколько раз в ситуациях медленной сходимости.
Список литературы
Богатырёв А.Б. Матем. сб. 1999. Т. 190. № 11. С. 15–50.
Богатырёв А.Б. Матем. сб. 2003. Т. 194. №‘4. С. 3–28.
Schmies M., Numerische Methoden für Riemannsche Flächen und Helikoide mit Henkeln. Ph.D. Thesis, Technische Universität Berlin, 2005.
Mityushev V., Rylko N. Mathematical and Computer Modelling. 2013. V. 57. P. 1350–1359.
Mityushev V. Analytic Number Theory, Approximation Theory, and Special Functions, Springer. 2014. P. 827–852.
Crowdy D.G., Marshall J.S. Comput. Methods Funct. Theory. 2010. V. 10. P. 501–517.
Burnside W. Proc. London Math. Soc. 1891. V. 23. P. 49–88.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


