1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 6, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 6, стр. 638-646

Статистические характеристики ансамбля солитонов внутренних волн

Е. Г. Диденкулова a, *, Е. Н. Пелиновский a, b, c, Т. Г. Талипова b, c

a Национальный исследовательский университет Высшая школа экономики
101000 Москва, ул. Мясницкая, 20, Россия

b Институт прикладной физики РАН
603155 Нижний Новгород, ул. Ульянова, 46, Россия

c Нижегородский государственный технический университет им. Р.Е. Алексеева
603155 Нижний Новгород, ул. Минина, 24, Россия

* E-mail: eshurgalina@mail.ru

Поступила в редакцию 19.03.2020
После доработки 29.07.2020
Принята к публикации 05.08.2020

Полный текст (PDF)

Аннотация

С помощью численного моделирования исследуются статистические характеристики ансамбля солитонов внутренних волн, распространяющихся в условиях, приближенных к условиям шельфа Австралии. Построено распределение амплитуды импульсов в зависимости от пройденного расстояния, а также такие статистические моменты, как асимметрия и эксцесс. Показано, что оба момента с расстоянием падают приблизительно на 20%.

Ключевые слова: внутренние волны, солитоны, солитонная турбулентность, уравнение Гарднера, численное моделирование, статистические моменты

ВВЕДЕНИЕ

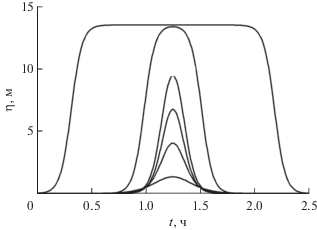
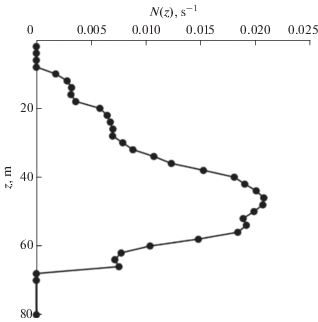
Внутренние волны на океанских шельфах присутствуют практически повсеместно, от крайнего севера и юга до экватора, от Атлантического океана до Тихого [1–11]. Отмечается, что внутренние волны на шельфах носят нелинейный характер и часто представлены в виде ансамбля солитоноподобных волн в основном первой, но также и второй, а иногда и более высоких мод [2, 6, 12–17]. Поверхностные солибры (ундулярные боры) также распространены повсеместно [18, 19]. Один из примеров записей солитоноподобных внутренних волн, взятый из статьи [2], приведен на рис. 1. Эта запись получена с двух буев на Северо-Западном шельфе Австралии в прибрежной зоне, глубина воды достигала 80 м, буи отстояли один от другого на расстояние около 2 км. Здесь имелась ярко выраженная плотностная стратификация, характерный вид частоты Вяйсяля–Брента (плавучести) представлен на рис. 2

Рис. 1.

Записи солитонных ансамблей внутренних волн в течение 24 ч на Северо-Западном шельфе Австралии в двух разных точках по трассе распространения волн. Волнограф “Shelf” отстоит от волнографа “Break” на расстояние менее 2 км.

Рис. 2.

Характерный вертикальный профиль частоты плавучести (Вяйсяля–Брента) на шельфе Австралии в области с глубиной 80 м.

Часто для описания нелинейных внутренних волн используются уравнения типа Кортевега–де Вриза [20–22]. При этом все расчеты выполняются в рамках динамической модели, когда один или несколько солитонов заданы в одном месте пространства, и определяются свойства волнового поля в другом месте [17, 23]. Между тем, число наблюдаемых солитонов в группах достаточно велико, так что для их описания необходимы статистические подходы. Большая база океанографических данных зарегистированных внутренних волн, естественно, подвергается статистической обработке. Обобщенный спектр внутренних волн в открытом океане был построен Гарретом и Манком еще в 1979 году [24]. Затем он адаптировался к различным прибрежным районам Мирового океана [25]. Также исследовалась частота повторяемости внутренних волн во многих регионах, в основном с применением пуассоновской статистики [26–31].

В последние годы много работ по статистическому анализу солитоноподобных волн и их ансамблей выполнено для Южно-Китайского моря ввиду эксплуатации месторождений углеводородов на его шельфе. Пожалуй, первая работа появилась в 2002 году [32], где построены гистограммы амплитуд внутренних волн, и дано их сравнение с гауссовым распределением. Записи получены в Желтом море; глубина, где стоял буй, составила 33 м. Здесь был хорошо перемешанный верхний слой толщиной около 10 м, а на оставшихся 23 м температура менялась от 26 до 16 градусов Цельсия по вертикали. Показано, что на такой мелкой воде распределение внутренних волн первой моды по амплитудам близко к распределению Гаусса, особенно на самой “теплой” – 25 градусов – и самой “холодной” – 17.5 градусов – изотермах. Действительно, на записях видна только первая мода, а характер внутренних волн близок к линейному.

В работе [33] построена гистограмма распределения числа солитонных ансамблей внутренних волн по широте от зоны генерации (Лузонский пролив) до западного (китайского) шельфа моря, а также приведена гистограмма частоты появления солитонных ансамблей по месяцам с максимумом в июне. В статье [12] солитоны внутренних волн изучались по записям с буев в течение года, рассредоточенных по всему западному шельфу Южно-Китайского моря. На основе данных построены гистограммы частоты появления солитонов первой и второй мод, а также волновых пакетов (ансамблей солитонов) по месяцам года. Здесь наибольшие значения частоты появления приходятся на июль. В работе [17] построены гистограммы амплитуд солитонов разных полярностей в зоне смены полярности солитонов на севере шельфа Южно-Китайского моря. Аналогичные обработки записей внутренних волн проведены для шельфа Нью-Джерси [34], где исследовались солитонные ансамбли и отдельные солитоны и строились гистограммы различных параметров внутренних волн. Статистический анализ сделан и для шельфа Калифорнии в работе [35], где определены среднестатистические характеристики солиборов и отдельных солитонов.

Динамика таких случайных последовательностей солитонов должна изучаться с использованием методов стохастического моделирования. В последнее время в физике сформировалось понятие солитонного газа, представляющего собой ансамбль солитонов со случайными амплитудами и фазами [36–42]. Взаимодействие даже двух солитонов представляет собой сложный процесс [43–47]. Однако к внутренним волнам в океане понятие солитонного газа практически не применялось. Целью настоящей работы является нахождение статистических характеристик ансамбля солитонов внутренних волн в идеализированных условиях, приближенным к условиям Северо-западного шельфа Австралии, а именно, из статьи [2] взята стратификация и глубина для моделируемого численного лотка.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Для описания динамики ансамбля солитонов внутренних волн выбрано уравнение Гарднера, которое отличается от известного уравнения Кортевега–де Вриза кубическим членом. Как уже упоминалось, это уравнение неоднократно применялось для описания трансформации внутреннего прилива на шельфе. Оно верифицировано как на модельных расчетах в численном лотке по уравнениям Эйлера [48], так и на данных натурных измерений [20]. Уравнение Гарднера имеет следующий вид

(1)
$\frac{{\partial \eta }}{{\partial t}} + (c + \alpha \eta + {{\alpha }_{1}}{{\eta }^{2}})\frac{{\partial \eta }}{{\partial x}} + \beta \frac{{{{\partial }^{3}}\eta }}{{\partial {{x}^{3}}}} = 0,$
где η есть вертикальное смещение пикноклина в максимуме модовой функции Ф(z), определяемой из граничной задачи

(2)
$\begin{gathered} \frac{{{{d}^{2}}\Phi }}{{d{{z}^{2}}}} + \frac{{{{N}^{2}}(z)}}{{{{с}^{2}}}}\Phi = 0,\,\,\,\Phi (0) = \Phi (H) = 0, \\ {{\Phi }_{{\max }}} = \Phi \left( {{{z}_{{\max }}}} \right) = 1, \\ \end{gathered} $

с – это собственное число, которое является линейной скоростью распространения длинных волн, а N2(z) – частота плавучести, определяемая по формуле

(3)
${{N}^{2}}(z) = - \frac{g}{{\rho (z)}}\frac{{d\rho (z)}}{{dz}}.$

Коэффициенты уравнения Гарднера, нелинейности, α и α1, и дисперсии, β, находятся в квадратурах от модовой функции, нелинейной поправки к ней и ее производных, см., например, [16, 20], и, в конечном счете, являются функциями вертикального профиля плотности воды, то есть зависят от ее стратификации. Мы не будем здесь приводить громоздких выражений для коэффициентов, а приведем сразу результаты расчета этих коэффициентов для стратификации, показанной на рис. 2:

$\begin{gathered} с\,\,~ = {\text{ }}0.32\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}},~\,\,\,\,\beta = 71.5\,\,{{{\text{м}}}^{3}}\,{{{\text{с}}}^{{ - 1}}},~\,\,\,\,\alpha = {\text{ }}0.00965{\text{ }}{{{\text{с}}}^{{ - 1}}};~ \\ ~{{\alpha }_{1}} = - {\text{ }}0.000715\,\,{\text{ }}{{{\text{м}}}^{{ - 1}}}{{{\text{с}}}^{{ - 1}}}. \\ \end{gathered} $

Наконец, уравнение (1) можно записать в системе отсчета, бегущей с линейной скоростью с, волны, введя время τ = x/с – t, и тогда уравнение Гарднера (1) будет иметь вид

(4)
$\frac{{\partial \eta }}{{\partial x}} + \left( {\frac{\alpha }{{{{c}^{2}}}}\eta + \frac{{{{\alpha }_{1}}}}{{{{c}^{2}}}}{{\eta }^{2}}} \right)\frac{{\partial \eta }}{{\partial \tau }} + \frac{\beta }{{{{c}^{4}}}}\frac{{{{\partial }^{3}}\eta }}{{\partial {{\tau }^{3}}}} = 0.$

Поскольку бароклинный прилив на широте Северо-Западного шельфа Австралии повторяется с инерционным периодом каждые 12.4 ч, то для численного моделирования логично ввести периодические граничные условия на временном интервале длительностью 12.4 ч. Уравнение (4) решается на этом выбранном временном интервале. В качестве “начальных” (х = 0) условий для уравнения (4) принимаются ансамбли солитонов вида (рис. 3)

(5)
$\begin{gathered} {{\eta }_{0}}(t) = \sum\limits_{i = 1}^{13} {\frac{{{{a}_{i}}\left( {2 - \frac{{{{a}_{i}}}}{{{{a}_{{\lim }}}}}} \right)}}{{1 + \left( {1 - \frac{{{{a}_{i}}}}{{{{a}_{{\lim }}}}}} \right)\cosh ({{\gamma }_{i}}{{V}_{i}}t + {{\varphi }_{i}})}}} , \\ {{\gamma }_{i}} = \sqrt {\frac{{\alpha {{a}_{i}}}}{{6\beta }}\left( {2 - \frac{{{{a}_{i}}}}{{{{a}_{{\lim }}}}}} \right)} ,\,\,\,\,{{V}_{i}} = \frac{{\alpha a}}{6}\left( {2 - \frac{{{{a}_{i}}}}{{{{a}_{{\lim }}}}}} \right), \\ \end{gathered} $
где ai есть амплитуда i-го солитона, alim есть амплитуда предельного или “толстого” солитона, в нашем случае:

(6)
${{a}_{{{\text{lim\;}}}}} = {{ - \alpha } \mathord{\left/ {\vphantom {{ - \alpha } {{{\alpha }_{1}}}}} \right. \kern-0em} {{{\alpha }_{1}}}} = 13.5{\text{ м}}.~$
Рис. 3.

Формы солитонов уравнения Гарднера для приведенных выше значений коэффициентов.

Оценка амплитуды толстой солитоноподобной волны на записях из рис. 1 также соответствует этой величине. Величина φi есть случайная фаза, определяющая положение солитона на выбранном временном интервале. Мы выбираем их так, чтобы солитоны не перекрывались. Один из примеров начального солитонного ансамбля приведен на рис. 4 для x = 0.

Рис. 4.

Эволюция одного из ансамблей солитоноподобных внутренних волн на разных расстояниях.

Для набора статистически достоверных результатов солитоны в ансамбле задавались с амплитудами, равномерно распределенными от 2.7 до 13.5 м (амплитуда предельного солитона). Всего для моделирования было подготовлено 50 таких ансамблей, каждый из которых служил начальным условием для уравнения (4). Динамика каждого ансамбля исследовалась на трассе длиной около 250 км. Интегрирование уравнения (4) велось по псевдо-спектральной схеме, описанной в [49].

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Трансформация волнового поля в одной из начальных реализаций на разных расстояниях показана на рис. 4.

Динамика такого поля довольно интересна. В начальной точке трассы мы видим все тринадцать солитонов, один из которых толстый, с длительностью 2.3 ч. Через 10 км число солитоноподобных импульсов уже двенадцать, солитон с самой маленькой амплитудой “спрятался” во взаимодействующих волнах. В точке 20 км и далее в точке 50 км трассы наблюдаются все так же отдельный толстый солитон и еще 8 изрезанных импульсов, которые образуют взаимодействующие солитоны. Через 100 км остается только 7 отдельных импульсов, и вступает во взаимодействие толстый солитон. Длительность этой волны с максимальной амплитудой выросла до 3 ч. Через 150 км отдельных импульсов опять девять, но толстый солитон вступил во взаимодействие уже с несколькими солитонами, и длительность результирующего импульса выросла до 3.3 ч. Наибольшей длительности 3.5 ч она достигает в точке 200 км. В конце трассы все остальные волны, кроме одной, “покинули” толстый солитон, и он возвращается к первоначальной ширине. Общее число волн также выросло до 11. Таким образом, длина этой трассы приблизительно совпадает с длиной квазирекурренции выбранного солитонного ансамбля. Аналогичное поведение происходит и в других реализациях волнового поля.

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ СОЛИТОННЫХ АНСАМБЛЕЙ

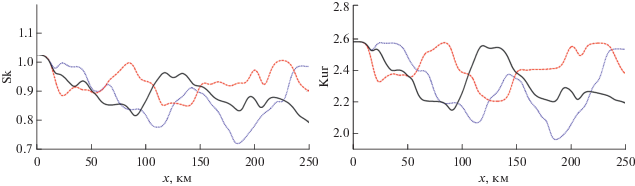
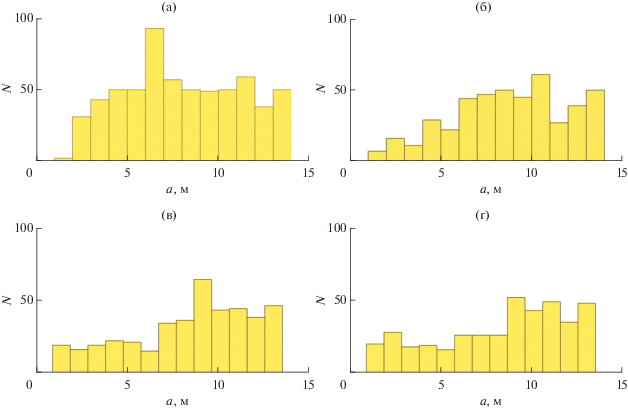
Гистограммы амплитуд всех ансамблей в точках x = 10, 50, 150, 250 км приведены на рис. 5. При x = 10 км, когда солитоны еще несильно “перемешались”, распределение амплитуд достаточно близко к равномерному как при x = 0, за исключением самых малых амплитуд, до 3 м, которые первыми взаимодействуют с солитонами больших амплитуд. Поэтому доля импульсов с амплитудами в районе 6–7 м значительно возросла, здесь присутствует пик с N ~ 90. В дальнейших точках наблюдения число волн с малыми амплитудами постепенно в среднем уменьшается, а с большими – увеличивается. Однако еще раз стоит отметить, что общее число импульсов падает при росте x, поэтому и общее число импульсов в гистограмме, соответствующей x = 250 км меньше, чем в гистограмме, соответствующей x = 10 км. Это связано со “слипанием” нескольких солитонов в один импульс на больших расстояниях.

Рис. 5.

Гистограммы амплитуд импульсов по уровню 1.5 м, усредненные по 50 реализациям в четырех локациях (а) x = = 10 км, (б) x = 50 км, (в) x = 150 км, (г) x = 250 км. N – количество импульсов.

Для дальнейшего анализа мы рассчитали эволюцию четырех статистических моментов волнового поля, проинтегрированных по приливному периоду.

Среднее значение поля:

(6)
$\left\langle {\eta \left( x \right)} \right\rangle ~ = \frac{1}{T}\int\limits_0^T {\eta \left( \tau \right)d\tau } ,$

Дисперсия поля (среднее квадратичное):

(7)
${{\sigma }^{2}}\left( x \right) = \frac{1}{T}\int\limits_0^T {[\eta {{{\left( {x,\tau } \right)}}^{2}}d\tau } - {{\left\langle {\eta \left( {x,\tau } \right)} \right\rangle }^{2}}]{\kern 1pt} {\kern 1pt} d\tau ,$

Асимметрия:

(8)
${\text{Sk}}\left( x \right) = \frac{1}{{T{{\sigma }^{3}}}}\int\limits_0^T {{{{\left[ {\eta \left( {x,\tau } \right) - \left\langle {\eta \left( {x,~\tau } \right)} \right\rangle } \right]}}^{3}}} d\tau ,$

Эксцесс:

(9)
${\text{Kur}}\left( x \right) = \frac{1}{{T{{\sigma }^{4}}}}\int\limits_0^T {{{{\left[ {\eta \left( {x,\tau } \right) - \left\langle {\eta \left( {x,\tau } \right)} \right\rangle } \right]}}^{4}}} d\tau .$

Сразу скажем, что первые два момента (среднее значение и дисперсия) являются инвариантами уравнения Гарднера и не меняются в пространстве. Поскольку начальные ансамбли состоят из одних и тех же солитонов (только случайным образом переставленных во времени), то эти моменты одинаковы для всех реализаций и равны 4 м и 21.87 м2 (среднеквадратичное отклонение – 4.68 м) соответственно.

Третий и четвертый моменты уже не являются инвариантами и будут меняться по мере распространения ансамбля. В начальной точке они, так же, как и первые два момента, одинаковы во всех реализациях и вычисляются аналитически. Они равны соответственно: асимметрия – Sk = 1.024 и эксцесс – Kur = 2.57.

Понятно, что поле солитонов не является гауссовым (для гауссова распределения Sk = 0 и Kur = 3), что, в сущности, видно из любой реализации (нет симметрии относительно обеих осей). Коэффициент асимметрии положительный, так что вклад в асимметрию дают больше горбы, чем впадины. Коэффициент эксцесса меньше трех (гауссово значение), что говорит об определенной узости плотности функции распределения.

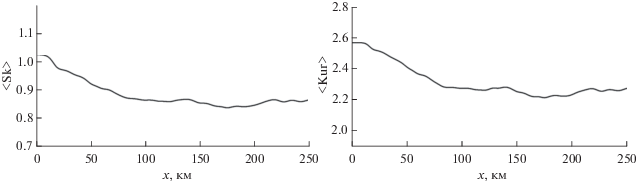
Изменение коэффициентов асимметрии (слева) и эксцесса (справа) со временем представлено на рис. 6 для произвольно выбранных трех реализаций. Как и ожидалось, в каждой реализации происходит достаточно сильное изменение величин моментов вследствие взаимодействия солитонов между собой, особенно с толстым солитоном, который несет на себе большую часть этих характеристик. В статье [50] было показано, что присутствие толстого солитона в волновой записи может менять высшие статистические моменты в разы. По отдельным реализациям видны квазирекуррентные возвращения третьего и четвертого моментов к начальным данным, но поскольку они происходят в разных точках трассы для разных реализаций, то при усреднении общая тенденция идет к уменьшению усредненных по 50 реализациям моментов примерно на 20% на расстоянии до 130 км (см. рис. 7). Далее они остаются фактически постоянными примерно на расстоянии в 100 км и могут рассматриваться как средние значения для ансамбля солитонов внутренних волн (солитонного газа).

Рис. 6.

Асимметрия (Sk) и эксцесс (Kur) вдоль трассы для трех реализаций волнового поля.

Рис. 7.

Усредненные по 50 реализациям значения асимметрии и эксцесса вдоль трассы.

ЗАКЛЮЧЕНИЕ

С помощью численного моделирования рассмотрена динамика ансамбля солитонов внутренних волн, распространяющихся в условиях, приближенных к условиям шельфа Австралии. Отмечается, что в процессе эволюции солитоны объединяются в импульсы сложной формы, в результате чего количество импульсов может заметно сокращаться вдоль трассы. Построены высшие статистические моменты (асимметрия и эксцесс) и их усредненные по 50 реализациям значения. Отмечено уменьшение усредненных моментов до 20% с расстоянием, в то время как моменты для одной реализации претерпевают сильное изменение, вплоть до возвращения к начальным значениям. Гистограммы амплитуд импульсов демонстрируют близкое к равномерному распределение амплитуд на малых расстояниях и значительное преобладание доли больших волн над маленькими с ростом расстояния, пройденного ансамблем.

Список литературы

  1. Small J., Sawyer T.C., Scott J.C. The evolution of an internal bore at the Malin shelf break // Ann. Geophysicae. 1999. V. 17. P. 547–565.

  2. Holloway P., Pelinovsky E., Talipova T., Barnes B. A Nonlinear Model of Internal Tide Transformation on the Australian North West Shelf // J. Physical Oceanography. 1997. V. 27. № 6. P. 871–896.

  3. Alford M.H., Lien R.-Ch., Simmons H., Klymak J., Ramp S., Yang Y.J., Tang D., Chang M.-H. Speed and Evolution of Nonlinear Internal Waves Transiting the South China Sea // J. Phys. Oceanogr. 2010. V. 40. P. 1338–1355.

  4. Bourgault D., Janes D.S., Galbraith P.S. Observations of a Large-Amplitude Internal Wave Train and Its Reflection off a Steep Slope // J. Phys. Oceanogr. 2010. V. 41. P. 586–600.

  5. Lamb K., Farmer D. Instabilities in an Internal Solitary-like Wave on the Oregon Shelf // J. Phys. Oceanogr. 2010. V. 41. P. 67–87.

  6. Vlasenko V., Stashchuk N. Internal tides near the Celtic Sea shelf break: A new look at a well known problem // Deep-Sea Research I. 2015. V. 103. P. 24–36.

  7. Ярощук И.О., Новотрясов В.В., Долгих Г.И., Пермяков М.С. Интенсивные волновые боры на осеннем пикноклине шельфовых вод залива Петра Великого Японского Моря // ДАН. 2018. Т. 479. № 2. С. 200–205.

  8. Морозов Е.Г., Пака В.Т. Внутренние волны в высокоширотном бассейне // Океанология. 2010. Т. 50. № 5. С. 709–715.

  9. Grimshaw R., da Silva J.C.B., Magalhaes J.M. Modelling and observations of oceanic nonlinear internal wave packets affected by the Earth’s rotation // Ocean Modelling. 2017. V. 116. P. 146–158.

  10. Kurkina O., Talipova T., Soomere T., Kurkin A., Rybin A. The impact of seasonal changes in stratification on the dynamics of internal waves in the Sea of Okhotsk // Estonian J. Earth Sciences. 2017. V. 66. № 4. P. 238–255.

  11. Zhang W., Didenkulova I., Kurkina O., Cui Y., Haberkern J., Aepfler R., Santos A.I., Zhang H., Hanebuth T.J.J. Internal solitary waves control offshore extension of mud depocenters on the NW Iberian shelf // Marine Geology. 2019. V. 409. P. 15–30.

  12. Chen L., Zheng Q., Xiong X., Yuan Y., Xie H., Guo Y., Long Y., Yun Sh. Dynamic and Statistical Features of Internal Solitary Waves on the Continental Slope in the Northern South China Sea Derived From Mooring Observations // J. Phys. Oceanogr. 2019. V. 124. № 6. P. 4078–4097.

  13. Шапиро Г.И., Шевченко В.П., Лисицын А.П., Серебряный А.Н., Политова Н.П., Акивис Т.М. Влияние внутренних волн на распределение взвешенного вещества в Печорском море // ДАН. 2000. Т. 373. № 1. С. 105–107.

  14. Sherwin T., Vlasenko V., Stashchuk N., Jeans D.G., Jones B. Along-slope generation as an explanation for some unusually large internal bores // Deep-Sea Res. 2002. V. 49. P. 1787–1799.

  15. Liang Ch., Zheng Q, Xiong X., Yuan Y., Xie H., Guo Y., Yu L., Yun Sh. Dynamic and Statistical Features of Internal Solitary Waves on the Continental Slope in the Northern South China Sea Derived From Mooring Observations // J. Geophys. Res. 2019. V. 124. № 6. P. 4078–4097.

  16. Talipova T., Pelinovsky E., Kurkina O., Kurkin A. Numerical modeling of the internal dispersive shock wave in the ocean // Shock and vibration. 2015. V. 2015. Article ID 875619.

  17. Zhang X., Huang X., Zhang Zh., Zhou Ch., Tian J., Zhao W. Polarity Variations of Internal Solitary Waves over the Continental Shelf of the Northern South China Sea: Impacts of Seasonal Stratification, Mesoscale Eddies, and Internal Tides // J. Phys. Oceanogr. 2018. V. 48. P. 1349–1364.

  18. Chanson H. Tidal Bores, Aegir, Eagre, Mascaret, Pororoca: Theory and Observations. Singapore: World Scientific, 2011. 220 p.

  19. Пелиновский Е.Н., Шургалина Е.Г., Родин А.А. О критериях перехода обрушающегося бора в волнообразный // Изв. РАН. Физика атмосферы и океана. 2015. Т. 51. № 5. С. 598–601.

  20. Талипова Т.Г., Пелиновский Е.Н., Куркин А.А., Куркина О.Е. Моделирование динамики длинных внутренних волн на шельфе // Изв. РАН. ФАО. 2014. Т. 50. № 6. С. 714–722.

  21. Tan D., Zhou J. Xu Wang X., Wang Zh. Combined effects of topography and bottom friction on shoaling internal solitary waves in the South China Sea // Applied Mathematics and Mechanics (English Edition). 2019. V. 40. № 4. P. 421–434.

  22. Grimshaw R., Pelinovsky E., Talipova T. The modified Korteweg–de Vries equation in the theory of the large–amplitude internal waves // Nonlinear Processes in Geophysics. 1997. V. 4. P. 237–250.

  23. Grimshaw R., Pelinovsky E., Talipova T. Modeling internal solitary waves in the coastal ocean // Survey in Geophysics. 2007. V. 28. № 2. P. 273–298.

  24. Garret C.J.R., Munk W.H. Internal waves in the ocean // Annual Rev. Fluid Mech. 1979. V. 11. P. 339–369.

  25. Морозов Е.Г., Фрей Д.И., Гладышев С.В., Клювиткин А.А., Новигатский А.Н. Внутренние приливные волны в Датском проливе // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 3. С. 78–84.

  26. Ivanov V.A., Pelinovsky E.N., Talipova T.G. The Long-Time Prediction of Intense Internal Wave Heights in the Tropical Region of the Atlantic // J. Physical Oceanography. 1993. V. 23. № 9. P. 2136–2142.

  27. Ivanov V.A., Pelinovsky E.N., Talipova T.G. Recurrence Frequency of Internal Wave Amplitudes in the Mediterranean // Oceanology. 1993. V. 33. № 2. P. 180–184.

  28. Pelinovsky E., Holloway P., Talipova T. A statistical analysis of extreme events in current variations due to internal waves from the Australian North West Shelf // J. Geophysical Research. 1995. V. 100 (C12). P. 24,831–24,839.

  29. Морозов Е.Г., Пелиновский Е.Н., Талипова Т.Г. Частота повторяемости внутренних волн на Мезополигоне-85 в Атлантике // Океанология. 1998. Т. 38. № 4. С. 521–527.

  30. Talipova T., Pelinovsky E., Kurkina O., Giniyatullin A., Kurkin A. Exceedance frequency of appearance of the extreme internal waves in the World Ocean // Nonlin. Processes Geophys. 2018. V. 25. P. 511–519.

  31. Зимин А.В., Свергун Е.И. Короткопериодные внутренние волны в шельфовых районах Белого, Баренцева и Охотского морей: оценка повторяемости экстремальных высот и динамических эффектов в придонном слое // Фундаментальная и прикладная гидрофизика. 2018. Т. 11. № 4. С. 66–72.

  32. Wang T., Gao T. Statisical properties of high – frequency internal waves in Quindao offshore area of the Yellow Sea // Chinese J. Oceanology and Limnology. 2002. V. 20. № 1. P. 16–21.

  33. Zheng Q., Susanto R.D., Ho Ch.-R., Y. Song T., Xu Q. Statistical and dynamical analyses of generation mechanisms of solitary internal waves in the northern South China Sea // Jour. Geophys. Res. 2007. V. 112. P. C03021.

  34. Badiey M., Wan L., Lynch J.F. Statistics of Nonlinear Internal Waves during the Shallow Water 2006 Experiment // J. Phys. Oceanogr. 2016. V. 33. P. 839–846.

  35. Colosi J.A., Kumar N., Suanda S.H., Freismuth T.M., MacMahan J.H. Statistics of Internal Tide Bores and Internal Solitary Waves Observed on the Inner Continental Shelf off Point Sal, California // J. Phys. Oceanogr. 2018. V. 48. P. 123–143.

  36. Agafontsev D.S., Zakharov V.E. Integrable turbulence generated from modulational instability of cnoidal waves // Nonlinearity. 2016. V. 29. P. 3551–3578.

  37. Shurgalina E.G., Pelinovsky E.N. Nonlinear dynamics of a soliton gas: Modified Korteweg-de Vries equation framework // Physics Letters A. 2016. V. 380. № 24. P. 2049–2053.

  38. El G.A. Critical density of a soliton gas // Chaos. 2016. V. 26. P. 023105.

  39. Gelash A.A., Agafontsev D.S. Strongly interacting soliton gas and formation of rogue waves // Phys. Rev. E. 2018. V. 98. P. 1–11.

  40. Pelinovsky E., Shurgalina E. KDV soliton gas: interactions and turbulence // Book: Challenges in Complexity: Dynamics, Patterns, Cognition (editors: I. Aronson, A. Pikovsky, N. Rulkov, L. Tsimring), Series: Nonlinear Systems and Complexit. Springer. 2017. V. 20. P. 295–306.

  41. Didenkulova (Shurgalina) E.G. Numerical modeling of soliton turbulence within the focusing Gardner equation: rogue wave emergence // Physica D. 2019. V. 399. P. 35–41.

  42. Пелиновский Е.Н., Шургалина Е.Г. Формирование волн-убийц в солитонном газе, описываемом модифицированным уравнением Кортевега-де Вриза // Докл. АН. 2016. Т. 470. № 1. С. 26–29.

  43. Pelinovsky E.N., Shurgalina E.G., Sergeeva A.V., Talipova T.G., El G.A., Grimshaw R.H.J. Two-soliton interaction as an elementary act of soliton turbulence in integrable systems // Physics Letters A. 2013. V. 377. № 3–4. P. 272–275.

  44. Пелиновский Е.Н., Шургалина Е.Г. Двухсолитонное взаимодействие в рамках модифицированного уравнения Кортевега–де Вриза // Изв. ВУЗов. Радиофизика. 2014. Т. 57. № 10. С. 825–833.

  45. Слюняев А.В. Динамика локализованных волн большой амплитуды в слабодиспергирующей среде с квадратичной и положительной кубической нелинейностью // Журн. экспер. теор. физ. 2001. Т. 19. С. 606–612.

  46. Шургалина Е.Г. Механизм образования волн-убийц в результате взаимодействия солитонов внутренних волн в стратифицированном водоеме // Изв. РАН. Механика жидкости и газа. 2018. Т. 1. С. 61–67.

  47. Шургалина Е.Г. Особенности двухсолитонного взаимодействия в рамках уравнения Гарднера // Изв. ВУЗов. Радиофизика. 2017. Т. 60. № 9. С. 787–792.

  48. Maderich V., Talipova T., Grimshaw R., Pelinovsky E., Choi B.H., Brovchenko I., Terletska K., Kim D.C. Internal solitary wave transformation at the bottom step in two-layer flow: the Gardner and Navier-Stokes frameworks // Nonlinear Processes in Geophysics. 2009. V. 16. P. 33–42.

  49. Fronberg B. A Practical Guide to Pseudospectral Methods. Cambrige: Cambrige University Press, 1998. 231 p.

  50. Диденкулова Е.Г., Пелиновский Е.Н. Роль “толстого” солитона в динамике солитонного газа в рамках уравнения Гарднера // Изв. ВУЗов. Радиофизика. 2018. Т. 61. № 8–9. С. 700–710.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал