Журнал физической химии, 2019, T. 93, № 6, стр. 930-937
Численный расчет концентрационной и температурной зависимостей коэффициента удельной электропроводности водных растворов электролитов
С. Одинаев a, *, Д. М. Акдодов b, Х. И. Идибегзода a
a Академия наук Республики Таджикистан, Физико-технический институт им. С.У. Умарова
Душанбе, Таджикистан
b Таджикский национальный университет
Душанбе, Таджикистан
* E-mail: odsb42@mail.ru
Поступила в редакцию 04.07.2018
После доработки 16.11.2018
Принята к публикации 19.11.2018
Аннотация
Методом кинетических уравнений получены аналитические выражения для динамического коэффициента удельной электропроводности $\sigma (\omega )$ и модуля электроупругости $ \in {\kern 1pt} (\omega )$, когда релаксирующие потоки затухают по экспоненциальному закону. Полученные коэффициенты в подынтегральных выражениях, наряду с молекулярными параметрами, содержат потенциальную энергию взаимодействия ${{\Phi }_{{ab}}}(\left| {\vec {r}} \right|)$ и радиальную функцию распределения ${{g}_{{ab}}}(\left| {\vec {r}} \right|)$. Для определенной модели раствора и явных выражений для ${{\Phi }_{{ab}}}(\left| {\vec {r}} \right|)$, ${{g}_{{ab}}}(\left| {\vec {r}} \right|)$, а также соответствующих значений концентраций С и температур Т проведен численный расчет изочастотного коэффициента удельной электропроводности $\sigma (\omega ,c,T)$ водных растворов электролитов LiCl, NaCl, KCl, CsCl. Результаты численных расчетов находятся в удовлетворительном согласии с экспериментом.
Широкое и оптимальное использование жидкостей и их растворов в промышленности, медицине и в качестве продуктов химической технологии требуют заранее знание следующих их физико-химических свойств, таких как транспортных, упругих, акустических, диэлектрических и электропроводящих свойств. Последние явления исследуются как теоретическими, так и экспериментальными физическими методами. Теоретические изучения этих свойств, которые являются следствием наличия необратимых процессов в жидкостях и их растворах являются сложными и по настоящее времени их исследования остаются открытыми.
Эта сложность при изучении электропроводящих свойств растворов электролитов, на основе строгой микроскопической теории, вызвана трудностями учета вкладов энергии взаимодействия между структурными единицами ионно-молекулярных систем в коэффициентах переноса и других физических параметров. Количественная теория электропроводящих свойств сильно разбавленных растворов электролитов дается теорией Дебая–Хюккеля [1–3]. При равновесии в растворах имеет место как ионная, так и дипольная атмосфера [1]. Согласно [3], приложенное внешнее электрическое поле или какое-либо другое атомное поле ионов, прежде всего, разрушает эти атмосферы, а значит и структуру растворителя, но одновременно связывает молекулы растворителя с упорядоченными ионами (сольватация или гидратация). Кроме того, в водных растворах электролитов на гидратацию, кроме фактора взаимодействия между постоянными дипольными моментами полярных молекул воды и ионами, влияет также поляризация (наведенный дипольный момент) молекул и дисперсионный эффект.
В [4–10] приводятся обзоры теоретических работ по исследованию коэффициентов удельной, молярной и эквивалентной электропроводностей растворов электролитов, а также их частотной дисперсии в условиях действия стационарных и переменных внешних электрических полей. В [11–13] развиты теории электропроводности электролитов на основе метода неравновесных многочастичных функций распределения. В [11] обобщается теория электропроводности растворов электролитов Онзагера, основанная на использовании строгих зацепляющихся интегро-дифференциальных уравнений для неравновесных частичных функций распределения при произвольном потенциале взаимодействия между ионами. Теория применяется для интерпретации электропроводности водных растворов щелочных галогенидов до концентрации ~4 моль/л. Объединение иерархии уравнений Эбелинга–Фалькенгагена с феноменологической теорией линейных необратимых процессов для бинарных растворов электролитов приводится в [12], где получены выражения для коэффициента электропроводности через равновесные бинарные функции распределения. В [13] на основе кинетических уравнений для s-частичных функций распределения разработана теория электропроводности растворов электролитов для слабых и сильных электрических полей и концентраций до ∼1 моль/л. Найдено стационарное решение уравнения для бинарной функции распределения в конфигурационном пространстве и использовано для определения коэффициента электропроводности.
Экспериментальному изучению коэффициентов электропроводности растворов электролитов также посвящено огромное количество работ. В последние годы в [14–17] исследуются коэффициенты удельной электропроводности как простых водных растворов хлоридов щелочных металлов, так и сложных концентрированных водных растворов. Температурная зависимость максимума удельной электропроводности в растворах сильных электролитов от концентрации изучена в [18–21] и установлено, что увеличение температуры приводит к смешению максимума в сторону более высокой концентрации. Для описания характера температурной зависимости электропроводности растворов электролитов, в [22–24] предложены различные уравнения, которые связывают коэффициент электропроводности со свойствами растворителя. Одним из первых вариантов является правило Вальдена, связывающее молярную (эквивалентную) электропроводность при бесконечном разведении λ0 и вязкости растворителя η, произведение которых должно быть постоянным. Установлено, что величина (λ0⋅η) изменяется не только при переходе от одного растворителя к другому, но также и при повышении температуры. Для слабых водных растворов электролитов при постоянной температуре исследованы зависимость коэффициента удельной электропроводности k от концентрации c и приведенного коэффициента электропроводности k/k∞=k* от приведенной концентрации с* = с/сm, соответственно, которая для всех водных растворов остается постоянной, то есть является аналогом выполнения закона соответственных состояний (ЗСС).
Представляет большой интерес теоретическое изучение электропроводящих свойств растворов электролитов с учетом вкладов взаимодействия структурных единиц раствора и внутренних релаксационных процессов в коэффициент удельной электропроводности и модуль электроупругости, а также их сравнение с существующими экспериментальными данными. С помощью результатов, полученных нами ранее методом кинетических уравнений, попытаемся установить аналитическое выражение для коэффициента удельной электропроводности, которое было бы удобно для проведения численных расчетов и сравнения результатов с экспериментом.
ОПРЕДЕЛЕНИЕ ИСХОДНЫХ ВЫРАЖЕНИЙ КОЭФФИЦИЕНТА УДЕЛЬНОЙ ЭЛЕКТРОПРОВОДНОСТИ И МОДУЛЯ ЭЛЕКТРОУПРУГОСТИ РАСТВОРОВ ЭЛЕКТРОЛИТОВ
Ранее, в [25, 26] на основе кинетического уравнения для одночастичной функции распределения ${{f}_{a}}({{\vec {q}}_{a}},{{\vec {p}}_{a}},t)$, с учетом определения импульсных моментов последнего, т.е. системы (4) работы [26], для Фурье-образа вектора плотности тока проводимости ${{j}^{\alpha }}({{\vec {q}}_{1}},t)$ было получено аналитическое выражение (3) работы [25], которое имеет следующий вид:
(1)
$\begin{gathered} {{j}^{\alpha }}(\omega ) = \sum\limits_a {j_{a}^{\alpha }(\omega ) = } \sum\limits_a {\tilde {\sigma }_{a}^{0}} (\omega ) \times \\ \times \;\left[ {{{E}^{\alpha }}(\omega ) + \frac{1}{{n_{a}^{0}{{e}_{a}}}}\sum\limits_b {d_{{ab}}^{3}\int {\frac{{\partial {{\Phi }_{{ab}}}(r)}}{{\partial {{r}^{\alpha }}}}{{n}_{{ab}}}(\omega ,{{{\vec {q}}}_{1}},\vec {r})d\vec {r}} } } \right], \\ \end{gathered} $(2)
${{n}_{{ab}}}({{\vec {q}}_{1}},{{\vec {q}}_{2}},t) = \int {{{f}_{{ab}}}({{{\vec {q}}}_{1}},{{{\vec {q}}}_{2}},{{{\vec {p}}}_{a}},{{{\vec {p}}}_{b}},t)} d{{\vec {p}}_{a}}d{{\vec {p}}_{b}}.$Для определения вектора плотности тока проводимости ${{j}^{\alpha }}(\omega )$ согласно (1) следует иметь уравнение для ${{n}_{{ab}}}({{\vec {q}}_{1}},{{\vec {q}}_{2}},t)$, которое на основе кинетического уравнения для двухчастичной функции распределения ${{f}_{{ab}}}({{\vec {q}}_{1}},{{\vec {q}}_{2}},{{\vec {p}}_{a}},{{\vec {p}}_{b}},t)$ в суперпозиционном приближении Кирквуда, в [25] получено уравнение имеющее следующий вид:
(3)
$\frac{{\partial {{n}_{{ab}}}}}{{\partial t}} + \frac{{kT}}{{d_{{ab}}^{2}}}\left( {\frac{1}{{{{\beta }_{a}}}} + \frac{1}{{{{\beta }_{b}}}}} \right)\hat {L}{{n}_{{ab}}} = {{F}_{{ab}}}({{\vec {q}}_{1}},\vec {r},t),$(4)
$\begin{gathered} {{F}_{{ab}}}({{{\vec {q}}}_{1}},\vec {r},t) = - {{\psi }_{{ab}}}(r)\operatorname{div} \vec {\vartheta } - \psi _{{ab}}^{{\alpha \beta }}(r) \times \\ \times \;\left\{ {\frac{{\partial {{\vartheta }^{\alpha }}}}{{\partial q_{1}^{\beta }}}} \right\} - \frac{{{{n}_{a}}{{n}_{b}}({{\beta }_{a}}{{e}_{b}} - {{\beta }_{b}}{{e}_{a}})}}{{{{\beta }_{a}}{{\beta }_{b}}{{d}_{{ab}}}}}\left( {\frac{{\partial g_{{ab}}^{0}(r)}}{{\partial {{r}^{\alpha }}}}} \right){{E}^{\alpha }}({{{\vec {q}}}_{1}},t). \\ \end{gathered} $Для случая независимых потоков, ограничившись учетом вклада третьего члена в выражении (4), решая уравнение (3) и совершая в нем Фурье-преобразование по времени, подставляя ${{n}_{{ab}}}(\omega )$ в (1) и сравнив полученные результаты с фурье-образом дифференциального закона Ома по времени, для комплексного коэффициента удельной электропроводности $\tilde {\sigma }(\omega )$ получим аналитическое выражение. После разделения в нем действительной и мнимой частей для модуля электроупругости $ \in {\kern 1pt} (\omega )$ и коэффициента удельной электропроводности $\sigma (\omega )$ получены выражения (10) и (11) работы [25], которые имеют следующий вид:
(5)
$\begin{gathered} \in {\kern 1pt} \left( \omega \right) = \sum\limits_a {\frac{{{{{(\omega {{\tau }_{a}})}}^{2}} \in _{a}^{0}}}{{1 + {{{\left( {\omega {{\tau }_{a}}} \right)}}^{2}}}}} \left[ {1 + \sum\limits_b {\frac{{\pi {{n}_{b}}d_{{ab}}^{3}}}{{12}}{{q}_{{ab}}}} } \right. \times \\ \times \;\int {d\vec {r}} \frac{{\partial {{{\mathop \Phi \limits^ * }}_{{ab}}}\left( r \right)}}{{\partial r}}\left. {\int {\left( {G_{{ab}}^{1}\left( \omega \right) - \frac{{G_{{ab}}^{2}\left( \omega \right)}}{{\omega {{\tau }_{a}}}}} \right)\frac{{\partial g_{{ab}}^{0}}}{{\partial {{r}_{1}}}}d{{{\vec {r}}}_{1}}} } \right], \\ \end{gathered} $(6)
$\begin{gathered} \sigma \left( \omega \right) = \sum\limits_a {\frac{{\sigma _{a}^{0}}}{{1 + {{{\left( {\omega {{\tau }_{a}}} \right)}}^{2}}}}} \left[ {1 + \sum\limits_b {\frac{{\pi {{n}_{b}}d_{{ab}}^{3}}}{{12}}{{q}_{{ab}}}} } \right. \times \\ \times \;\int {d\vec {r}\frac{{\partial {{{\mathop \Phi \limits^ * }}_{{ab}}}}}{{\partial r}}} \left. {\int {\left( {G_{{ab}}^{1}\left( \omega \right) + \omega {{\tau }_{a}}G_{{ab}}^{2}\left( \omega \right)} \right)\frac{{\partial g_{{ab}}^{0}}}{{\partial {{r}_{1}}}}d{{{\vec {r}}}_{1}}} } \right], \\ \end{gathered} $(7)
$\begin{gathered} G_{{1,2}}^{{ab}}(r,{{r}_{1}},\omega ) = \frac{{{{{(r{{r}_{1}})}}^{{ - 1}}}}}{{8{{\pi }^{2}}}}{{\left( {\frac{{\omega {{\tau }_{{ab}}}}}{2}} \right)}^{{ - 1/2}}} \times \\ \times \;\left[ {{{e}^{{ - {{\varphi }_{1}}}}}\left( {{\text{cos}}{{\varphi }_{1}} \mp {\text{sin}}{{\varphi }_{1}}} \right) - {{e}^{{ - {{\varphi }_{2}}}}}\left( {{\text{cos}}{{\varphi }_{2}} \mp {\text{sin}}{{\varphi }_{2}}} \right)} \right], \\ \end{gathered} $Уравнения (5) и (6) с учетом (7) описывают частотную дисперсию этих коэффициентов с учетом вкладов как трансляционных, так и структурных релаксационных процессов при наличии степенного закона затухания ${{t}^{{ - d/2}}}$ (d – размерность пространства). Однако эти коэффициенты в подынтегральных выражениях для потенциальных частей содержат сумму и разность $G_{1}^{{ab}}(\omega ) \pm G_{2}^{{ab}}(\omega )$ – фундаментальных решений уравнения Смолуховского (функций Грина), которые являются очень сложными и в таком виде трудно привести их к теоретическим расчетам, а также их сравнение с экспериментальными результатами. Поэтому переходим к рассмотрению электропроводящих свойств растворов электролитов, когда релаксационные процессы протекают по экспоненциальному закону.
В [28] для получения замкнутого уравнения для одночастичной функции распределения ${{f}_{a}}({{\vec {q}}_{1}},{{\vec {p}}_{a}},t)$ было решено уравнение для ${{f}_{{ab}}}({{\vec {q}}_{1}},{{\vec {q}}_{2}},{{\vec {p}}_{a}},{{\vec {p}}_{b}},t)$ методом Грэда и получена формула, которая определяется посредством импульсных моментов нулевого и первого порядка последнего, т.е. бинарной плотности ${{n}_{{ab}}}({{\vec {q}}_{1}},{{\vec {q}}_{2}},t)$ и бинарного потока $J_{{ab}}^{\alpha }({{\vec {q}}_{1}},{{\vec {q}}_{2}},t)$ частиц в конфигурационном пространстве. Ограничившись первым членом этого решения в определении (2), затем линеаризуя ее, для ${{n}_{{ab}}}({{\vec {q}}_{1}},\vec {r},t)$ получим
(8)
$\begin{gathered} {{n}_{{ab}}}({{{\vec {q}}}_{1}},\vec {r},t) = n_{{ab}}^{o}(r) + n_{a}^{'}({{{\vec {q}}}_{1}},t)n_{b}^{o}g_{{ab}}^{o}(r) + \\ + \;n_{a}^{o}n_{b}^{'}({{{\vec {q}}}_{2}},t)g_{{ab}}^{o}(r) + n_{a}^{o}n_{b}^{o}g_{{ab}}^{'}({{{\vec {q}}}_{1}},\vec {r},t), \\ \end{gathered} $Подставляя (8) в (3), заменяя оператор Смолуховского на релаксационный член вида
(9)
$\frac{{\partial g_{{ab}}^{'}({{{\vec {q}}}_{1}},\vec {r},t)}}{{\partial t}} + \frac{1}{{{{\tau }_{{ab}}}}}g_{{ab}}^{'}({{\vec {q}}_{1}},\vec {r},t) = F_{{ab}}^{'}({{\vec {q}}_{1}},\vec {r},t),$(10)
$\begin{gathered} {{j}^{\alpha }}({{{\vec {q}}}_{1}},\omega ) = \sum\limits_a {\frac{{\sigma _{a}^{0}}}{{1 - i\omega {{\tau }_{a}}}}} \times \\ \times \;\left\{ {1 + \sum\limits_b {\frac{{{{\pi }^{2}}}}{3}\frac{{d_{{ab}}^{3}n_{b}^{0}{{q}_{{ab}}}}}{{1 - i\omega {{\tau }_{{ab}}}}}\int {\frac{{\partial \Phi _{{ab}}^{*}(r)}}{{\partial r}}\frac{{\partial g_{{ab}}^{0}(r)}}{{\partial r}}{{r}^{2}}dr} } } \right\} \times \\ \times \;{{E}^{\alpha }}({{{\vec {q}}}_{1}},\omega ), \\ \end{gathered} $Сравнивая выражение (10) с Фурье-образом дифференциального закона Ома ${{j}^{\alpha }}({{\vec {q}}_{1}},\omega ) = $ $ = \;\tilde {\sigma }(\omega ){{E}^{\alpha }}({{\vec {q}}_{1}},\omega )$, для комплексного коэффициента удельной электропроводности $\tilde {\sigma }(\omega )$ получаем следующее аналитическое выражение:
(11)
$\tilde {\sigma }(\omega ) = \sum\limits_a {\frac{{\sigma _{a}^{0}}}{{1 - i\omega {{\tau }_{a}}}}} \left\{ {1 + \sum\limits_b {\frac{{G_{0}^{{ab}}(r)}}{{1 - i\omega {{\tau }_{{ab}}}}}} } \right\},$(12)
$G_{0}^{{ab}}(r) = 2\pi n_{b}^{*}{{q}_{{ab}}}\int {\frac{{\partial \Phi _{{ab}}^{*}(r)}}{{\partial r}}\frac{{\partial g_{{ab}}^{0}(r)}}{{\partial r}}{{r}^{2}}dr} .$(13)
$\tilde { \in }{\kern 1pt} (\omega ) = - i\omega \tilde {\sigma }(\omega ) = \; \in {\kern 1pt} (\omega ) - i\omega \sigma (\omega ),$Подставляя (11) в (13), разделяя реальную и мнимую части, для модуля электроупругости $ \in {\kern 1pt} (\omega )$ и коэффициента удельной электропроводности $\sigma (\omega )$ получим следующие выражения:
(14)
$\begin{gathered} \in {\kern 1pt} (\omega ) = \sum\limits_a {\frac{{{{{(\omega {{\tau }_{a}})}}^{2}} \in _{a}^{0}}}{{1 + {{{(\omega {{\tau }_{a}})}}^{2}}}}} \times \\ \times \;\left[ {1 + \sum\limits_b {\frac{{(1 + {{\tau }_{{ab}}}{\text{/}}{{\tau }_{a}})G_{0}^{{ab}}(r)}}{{1 + {{{(\omega {{\tau }_{a}})}}^{2}}{{{({{\tau }_{{ab}}}{\text{/}}{{\tau }_{a}})}}^{2}}}}} } \right], \\ \end{gathered} $(15)
$\begin{gathered} \sigma (\omega ) = \sum\limits_a {\frac{{\sigma _{a}^{0}}}{{1 + {{{(\omega {{\tau }_{a}})}}^{2}}}}} \times \\ \times \;\left[ {1 + \sum\limits_b {\frac{{1 - {{{(\omega {{\tau }_{a}})}}^{2}}({{\tau }_{{ab}}}{\text{/}}{{\tau }_{a}})}}{{1 + {{{(\omega {{\tau }_{a}})}}^{2}}{{{({{\tau }_{{ab}}}{\text{/}}{{\tau }_{a}})}}^{2}}}}G_{0}^{{ab}}(r)} } \right], \\ \end{gathered} $Согласно (14) и (15), динамический модуль электроупругости $ \in {\kern 1pt} (\omega )$ и коэффициент удельной электропроводности $\sigma (\omega )$ содержат вклады трансляционных ${{\tau }_{a}}$, ${{\tau }_{b}}$ и структурных ${{\tau }_{{ab}}}$ релаксационных процессов, где подынтегральное выражение функции $G_{0}^{{ab}}(r)$ непосредственно связаны со структурой раствора, определяемой посредством $\Phi _{{ab}}^{*}(r)$ и $g_{{ab}}^{0}(r)$.
Таким образом, полученные формулы (14) и (15) описывают электропроводящие свойства растворов электролитов, когда релаксирующие потоки затухают по экспоненциальному закону и при определенном выборе модели раствора позволяют вычисление $ \in (\omega )$ и $\sigma (\omega )$ в зависимости от концентрации с, плотности $\rho $ и температуры Т, в широком диапазоне изменения частот $\omega $.
ВЫБОР МОДЕЛИ РАСТВОРА И ПРОВЕДЕНИЕ ЧИСЛЕННЫХ РАСЧЕТОВ
Согласно аналитическим выражениям (14) и (15), модуль электроупругости $ \in {\kern 1pt} (\omega )$ и коэффициент удельной электропроводности $\sigma (\omega )$, наряду с межмолекулярным потенциалом взаимодействия ${{\Phi }_{{ab}}}\left( {\left| {\vec {r}} \right|} \right)$ и радиальной функцией распределения ${{g}_{{ab}}}\left( {\left| {\vec {r}} \right|} \right)$, еще содержат времена релаксации ${{\tau }_{a}}$, ${{\tau }_{b}}$ и ${{\tau }_{{ab}}}$, которые непосредственно определяются через коэффициенты трения ионов ${{\beta }_{a}}$ и ${{\beta }_{b}}$. Последние зависят как от структуры раствора, так и от термодинамических параметров состояния.
Согласно гидродинамической теории диффузии в [3], коэффициент трения растворов электролитов определяется посредством температуры и коэффициентом диффузии. Значение последнего берется из эксперимента. Однако теоретическое определение коэффициента диффузии является сложным. Определение коэффициента трения одноатомных жидкостей на основе микроскопической теории, согласно главе VI работы [31], выражаются посредством автокорреляционных функций скорости или силы и являются очень сложным. Там же, в сферико-симметричном случае, для коэффициента трения одноатомных жидкостей приведено аналитическое выражение, которое определяется посредством интегрирования потенциальной энергии взаимодействия и радиальной функции распределения, а в работе [32] это выражение обобщается для смеси жидкостей, которую в [33] мы пронимали в качестве исходной.
В ранее приведенных численных расчетах по вязкоупругим свойствам растворов электролитов [34] значения ${{\beta }_{a}}$ и ${{\beta }_{b}}$, а следовательно ${{\tau }_{a}}$, ${{\tau }_{b}}$ и ${{\tau }_{{ab}}}$, принимались постоянными. Чтобы улучшить согласие теоретически вычисленных значений $ \in {\kern 1pt} (\omega )$ и $\sigma (\omega )$ с экспериментальными результатами, следует учесть температурные, плотностные и концентрационные зависимости коэффициентов ${{\beta }_{a}}$ и ${{\beta }_{b}}$. Поэтому для решения этой задачи нами в [33] были использованы аналитические выражения для ${{\beta }_{a}}$ и ${{\beta }_{b}}$, в следующем виде:
(16)
$\begin{gathered} \beta _{a}^{2} = \sum\limits_a {\frac{{4\pi }}{3}} {{\rho }_{a}}kT\sum\limits_b {{{d}_{{ab}}}} \int\limits_0^\infty {{{\nabla }^{2}}} \Phi _{{ab}}^{*}(r)g_{{ab}}^{0}(r){{r}^{2}}dr, \\ \beta _{b}^{2} = \sum\limits_b {\frac{{4\pi }}{3}} {{\rho }_{b}}kT\sum\limits_a {{{d}_{{ab}}}} \int\limits_0^\infty {{{\nabla }^{2}}} \Phi _{{ab}}^{*}(r)g_{{ab}}^{0}(r){{r}^{2}}dr, \\ \end{gathered} $Аналитические выражения $ \in {\kern 1pt} (\omega )$, $\sigma (\omega )$, ${{\beta }_{a}}$ и ${{\beta }_{b}}$ согласно (14)–(16), определяются посредством потенциальной энергии межчастичного взаимодействия ${{\Phi }_{{ab}}}(r)$ и радиальной функции распределения $g_{{ab}}^{0}(r)$. Следовательно, для исследования электропроводящих свойств растворов электролитов и проведения численных расчетов потребуется знание явного вида функций ${{\Phi }_{{ab}}}\left( {\left| {\vec {r}} \right|} \right)$ и ${{g}_{{ab}}}\left( {\left| {\vec {r}} \right|} \right)$, которые соответствуют определенной модели раствора.
На основе подробного анализа количественных теорий для ионно-молекулярных систем, приведенных в [3, 4, 8], в приближении теории Мак-Миллана–Майера для ${{\Phi }_{{ab}}}(r)$ и $g_{{ab}}^{0}(r)$ в [33] были выбраны следующие модели. Для ${{\Phi }_{{ab}}}(r)$ принято выражение, состоящее из суммы потенциальной энергии Леннард-Джонса и обобщенного потенциала Дебая с учетом конфигурации размеров ионов, которое имеет вид
(17)
${{\Phi }_{{ab}}}(r) = \frac{{4{{\varepsilon }_{{ab}}}}}{{{{\varepsilon }_{{SS}}}}}({{r}^{{ - 12}}} - {{r}^{{ - 6}}}) + \frac{{{{R}_{{ab}}}}}{r}{{e}^{{ - \mathop {\chi r}\limits^ * }}},$Полуфеноменологическая модель в виде (17)–(19) позволяет провести численный расчет коэффициентов ${{\beta }_{a}}$, ${{\beta }_{b}}$, времена релаксации ${{\tau }_{a}}$, ${{\tau }_{b}}$, ${{\tau }_{{ab}}}$ и $ \in {\kern 1pt} (\omega )$, $\sigma (\omega )$ растворов электролитов в широком интервале изменения термодинамических параметров состояния и частот.
На основе (16), с учетом выражений (17)–(19), для соответствующих концентраций и температур были вычислены значения коэффициентов трения ${{\beta }_{a}}$ и ${{\beta }_{b}}$, времена релаксации ${{\tau }_{a}}$, ${{\tau }_{b}}$ и ${{\tau }_{{ab}}}$ водных растворов LiCl, NaCl, KCl и CsCl. Затем с учетом этих данных и выражения (15), а также выражений (17)–(19), были вычислены температурные и концентрационные зависимости изочастотных ω* = 10–6 ($\nu \sim {{10}^{7}}$ Гц) коэффициентов удельной электропроводности водных растворов LiCl, NaCl, KCl и CsCl, результаты которых приведены в табл. 1, а также на рис. 1–4.
Таблица 1.
Зависимость изочастотного коэффициента удельной электропроводности от концентрации и температуры для водных растворов NaCl и CsCl при ω* = 10–6 ($\nu \sim {{10}^{7}}$ Гц)
| c, моль/л [38] | ρ, кг/м3 | t, °C [38] | τ1 × 1013, с | τ2 × 1013, с |
τ11 × 1011, с | τ12 = τ21 × × 1011, с | τ22 × 1011, с | σ, См/м | ||
|---|---|---|---|---|---|---|---|---|---|---|
| [39] | [38] | Форм (15) | ||||||||
| NaCl | ||||||||||
| 0.490 | 1008.9 | 45 | 0.239 | 0.303 | 0.677 | 1.438 | 2.617 | 6.544 | 6.211 | 8.81 |
| 0.975 | 1031.9 | 35 | 0.169 | 0.208 | 0.990 | 2.130 | 3.940 | 10.07 | 9.697 | 11.73 |
| 1.916 | 1069.6 | 30 | 0.122 | 0.139 | 1.398 | 3.104 | 5.985 | 15.87 | 15.55 | 15.44 |
| 2.821 | 1105.5 | 25 | 0.102 | 0.106 | 1.696 | 3.912 | 7.958 | 18.90 | 18.72 | 17.50 |
| 4.521 | 1168.8 | 20 | 0.087 | 0.070 | 2.033 | 5.147 | 12.238 | 21.62 | 22.20 | 23.79 |
| CsCl | ||||||||||
| 1.82 | 1236.0 | 55 | 0.146 | 0.131 | 12.874 | 7.408 | 5.891 | 29.29 | 29.97 | 23.76 |
| 2.64 | 1353.0 | 35 | 0.117 | 0.102 | 17.137 | 10.013 | 7.999 | 31.46 | 33.18 | 25.46 |
| 3.40 | 1433.0 | 25 | 0.103 | 0.089 | 20.100 | 11.919 | 9.565 | 33.69 | 35.02 | 26.34 |
| 4.74 | 1585.5 | 20 | 0.084 | 0.068 | 24.910 | 15.473 | 12.603 | 39.50 | 39.59 | 28.44 |
| 5.87 | 1685.0 | 30 | 0.076 | 0.057 | 26.730 | 17.575 | 14.596 | 49.10 | 48.71 | 30.62 |
Рис. 1.
Зависимости коэффициента трения водного раствора NaCl от концентрации при различных температурах.
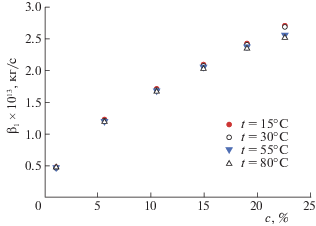
Рис. 2.
Концентрационные зависимости изотермического коэффициента трения водных растворов LiCl, NaCl, KCl и CsCl при t = 20°C.

Рис. 3.
Зависимости изочастотного динамического коэффициента удельной электропроводности водных растворов LiCl (а) и KCl (б) от концентрации, при ω* = 10–6 ($\nu \sim {{10}^{7}}$ Гц).
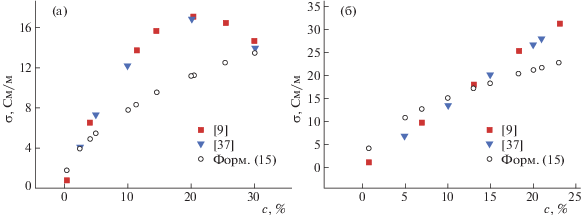
Рис. 4.
Зависимости изочастотного коэффициента удельной электропроводности водного раствора NaCl от температуры (а) и концентрации (б), при ω* = 10–6 ($\nu \sim {{10}^{7}}$ Гц), согласно табл. 1.
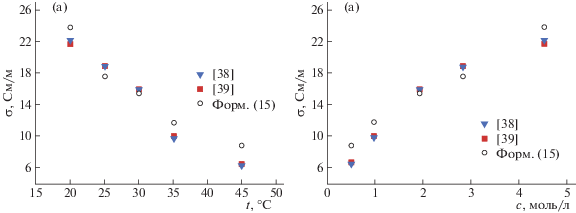
Полученные теоретические результаты находятся в удовлетворительном согласии с экспериментальными литературными данными. Ход температурной и концентрационной зависимостей вычисленных значений коэффициента удельной электропроводности $\sigma (\omega ,c,T)$ полностью соответствует экспериментальным результатам. Немного заниженные вычисленные значения $\sigma (\omega ,c,T)$ на основе (15), видимо, связаны с принятым приближением о неполном учете взаимодействия в ${{\Phi }_{{ab}}}(\vec {r})$ и ${{g}_{{ab}}}(\vec {r})$, т.е. наряду, с ион-ионным взаимодействием, следует еще учитывать ион-дипольное и диполь-дипольные (межмолекулярные) взаимодействия.
Список литературы
Семенченко В.К. Физическая теория растворов. М.–Л.: Госиздат технико-теоретической литературы, 1941. 382 с.
Харнед Г., Оуэн Б. Физическая химия растворов электролитов. М.: Изд. иностр. литер., 1952. 628 с.
Эрдей-Груз Т. Явления переноса в водных растворах. М.: Мир, 1976. 595 с.
Юхновский И.Р., Головко М.Ф. Статистическая теория классических равновесных систем. Киев: Наук. думка, 1980. 372 с.
Самойлов О.Я. Структура водных растворов электролитов и гидратация ионов. М.: Изд-во АН СССР, 1957. 182 с.
Робинсон Р., Стокс Р. Растворы электролитов. М.: Изд-во. иностр. литер., 1963. 646 с.
Шахпаронов М.И. Введение в современную теорию растворов. М.: Высш. школа, 1976. 296 с.
Смирнова Н.А. Молекулярные теории растворов. Л.: Химия, 1987. 336 с.
Максимова Н.И., Пак Ч.С., Правдин Н.Н. Свойства электролитов. М.: Металлургия, 1987. 128 с.
Пригожин И.Р. Молекулярная теория растворов. М.: Металлургия, 1990. 360 с.
Ebeling W., Feistel R., Kelbg G, Sanding R. // J. Non-Equilibr. Thermodyn. 1978. V. 3. № 1. P. 11.
Sanding R. // Z. Phys. Chem. (DDR). 1984. V. 265. № 4. P. 663.
Lessner G. // Physica. 1982. V. 116A. № 1–2. P. 272; 1983. 122A. № 3. P. 441.
Барон Н.М., Щерба М.У. // Журн. прикл. химии. 1971. Т. 44. № 9. С. 2118.
Darja Rudan-Tasic, Cveto Klofular, Marija Bester-Rogac // Acta Chim. Slov. 2006. V. 53. P. 324.
Демидов М.В., Понамарева Т.Н., Барботина Н.Н. // Успехи в химии и химической технологии. 2007. № 3 (71). С. 54.
Понамарева Т.Н., Барботина Н.Н. // Там же. 2008. № 3 (83). С. 108.
Wang P., Anderko A., Yung R.D. // Ind. Eng. Chem. Res. 2004. V. 43. P. 8083.
Wahab A., Mahiuddin S., Hefter G., Kunz W. // J. Chem. Ing. Data. 2006. V. 51. P. 1609.
Gilliam R.J., Graydon J.W., Kirk D.W., Thorpe S.J. // Int. J. Hydrogen Energy. 2007. V. 32. P. 359.
Bester-Rogac M. // J. Chem. Eng. Data. 2008. V. 53. P. 1355.
Щербаков В.В., Артемкина Ю.М. // Бюллетень Российского химического общества им. Д.И. Менделеева Химия в России. Май–август 2009. С. 7.
Shilajyav H.A. // Proceedings of the Yerevan State University: Chemistry and Biology. 2013. № 1. P. 3.
Maria Ashfag // European Journal of Chemistry. 2015. № 6 (1). P. 37.
Odinaev S., Ojimamadov I. // Modern Physics Letters B. 2001. V. 15. № 9–10. P. 285.
Odinaev S., Ojimamadov I. // Condensed Matter Physics. 2004. V. 7. № 4. P. 735.
Одинаев С. Обобщенная гидродинамика и вязкоупругие свойства ионных жидкостей. Препринт. Ин-т теоретической физики АН УССР, 91-13 Р (ИТФ, Киев). 16 с.
Одинаев С., Адхамов А.А. Молекулярная теория структурной релаксации и явлений переноса в жидкостях. Душанбе: Дониш, 1998. 230 с.
Одинаев С., Идибег Х. // Докл. Академии наук Республики Таджикистан. 2017. Т. 60. № 7–8. С. 320.
Nossal R. // Phys. Rev. 1968. V. 166. № 1. P. 81.
Физика простых жидкостей / Под ред. Темперли Г., Роулинсона Дж., Рашбрука Дж. М.: Мир, часть I, 1971. 308 с.
Musharaf A.Sk., Alok S., Swapan G.K. // J. Chem. Phys. 2001. V. 114. № 23. P. 10419.
Одинаев С., Акдодов Д.М. // Журн. физ. химии. 2013. Т. 87. № 7. С. 1154.
Одинаев С., Акдодов Д.М., Шарифов Н. и др. // Там же. 2010. Т. 84. № 6. С. 1063.
Richard J., Fries P.H., Krienke H. // J. Chem. Phys. 1998. V. 108. № 10. P. 4079.
Krienke H., Barthel J. // Equations of State for Fluids and Fluids Mixtures. Ch. 16: Jonic Fluids / Ed. by J.V. Sengers et al. Amsterdam: Elsevier, 2000. P. 751.
Добош Д. Электрохимические константы. Справочник для электрохимиков. М.: Мир. 1980. 365 с.
Кузнецов Н.М., Загоскин Ю.Д., Артемкина Ю.М., Щербаков В.В. // Успехи в химии и химической технологии. 2015. Т. 29. № 1. С. 55.
Lobo V.M.M., Quaresma J.L. Handbook of electrolyte solutions. Amsterdam: Elsevier, 1989. Pt. A. 1268 p., Pt. B. 1169 p.
Дополнительные материалы отсутствуют.
Инструменты
Журнал физической химии


