Физика металлов и металловедение, 2019, T. 120, № 12, стр. 1264-1270
Определение положения бинодали бинарного сплава на основе гипотезы слабой нелокальности
В. Л. Гапонцев a, *, А. В. Гапонцев b, В. В. Кондратьев c
a Уральский федеральный университет им. Б.Н. Ельцина
620002 Екатеринбург, ул. Мира, 19, Россия
b АО “СКБ ПН”, OOO “3Д-Технологии.Ру”
194044 Санкт-Петербург, Большой Сампсониевский пр., 60 лит. Щ, Россия
c Институт физики металлов им.М.Н. Михеева УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия
* E-mail: vlgap@mail.ru
Поступила в редакцию 24.04.2019
После доработки 11.06.2019
Принята к публикации 17.06.2019
Аннотация
Предложена методика расчета равновесных пределов растворимости в бинарных сплавах, альтернативная подходам, опирающимся на градиентные разложения. В ее основу положено описание сплавов в приближении слабой нелокальности, обобщающем классическую гипотезу локального равновесия. Это дало возможность развить теорию, которая позволяет получать явные концентрационные зависимости всех используемых параметров исключительно из знания концентрационной зависимости плотности свободной энергии, что невозможно в рамках существующих подходов.
ВВЕДЕНИЕ
Целью данной работы является развитие методов термодинамического описания неоднородных систем на примере бинарных твердых растворов. В настоящее время для такого описания используются градиентные разложения функционала свободной энергии [1, 2]. Они также нашли применение при изучении межфазной границы в системах пар-жидкость [2–4]. Наиболее широко градиентные разложения применяются при построении диаграмм равновесия двойных и тройных сплавов по методике CALPHAD. Было показано [5], что при нахождении бинодали методы, использующие термодинамическое описание на основе градиентных разложений, дают результаты, хорошо совпадающие с точным статистическим описанием. Однако при расчете положения спинодали результаты термодинамического и статистического описания существенно отличаются. Это различие связывается с тем, что на положение спинодали оказывают большое влияние корреляционные эффекты, которые не учитываются в модели неупорядоченных твердых растворов [5]. Тем не менее градиентные разложения в модели функционала Гинзбурга–Ландау применяли для анализа поведения сплавов с упругой анизотропией свойств при описании формирования в них модулированных структур [6]. По-видимому, в последнем случае этот вариант можно считать пригодным, поскольку задача вычисления точных количественных характеристик, как, например, в случае изучения спинодального распада [7], не ставилась. Аналогичная ситуация имеет место при анализе процесса распада межфазных границ при действии на них неравновесных потоков вакансий, возникающих при механосплавлении порошков чистых металлов, не смешиваемых в обычных условиях [8]. В этом случае также достаточно полуколичественного описания, поскольку ставится вопрос о принципиальной возможности эффекта распада межфазной границы и формирования на ее месте модуляций состава при интенсивной пластической деформации.
Особенностью подходов, использующих различные формы градиентного разложения, является феноменологический смысл этих разложений, не позволяющий определить концентрационные зависимости коэффициентов разложения в рамках термодинамического описания. Этого недостатка лишен подход, опирающийся на гипотезу слабой нелокальности, сформулированную в работе [8]. Гипотеза слабой нелокальности обобщает гипотезу локального равновесия, которая широко используется при анализе неравновесных процессов в гомогенных распределенных системах [9].
ГИПОТЕЗА СЛАБОЙ НЕЛОКАЛЬНОСТИ
Сформулируем гипотезу слабой нелокальности в следующем виде:
1. Неоднородную систему можно разбить на физически малые области, в пределах которых сохраняют вид все выражения равновесной термодинамики;
2. В каждой из этих областей состояние можно характеризовать интенсивными величинами, такими как плотности термодинамических потенциалов, параметры термодинамического состояния и параметры порядка;
3. Параметры состояния зависят от распределения локальных значений параметров порядка;
4. Степень влияния локальных состояний в двух областях друг на друга быстро убывает по мере увеличения пространственно-временного интервала между областями.
Химическое равновесие бинарного сплава можно определить условием
где ${{\mu }_{{A,B}}}$ – химические потенциалы компонентов сплава на один узел решетки. Условие (1) означает, что параметр состояния $\mu $ имеет в равновесии одно значение во всем объеме сплава. Этому параметру соответствует сопряженный ему параметр порядка, для бинарного сплава в нашем случае это числовая концентрация одного из его компонентов, а именно ${{C}_{A}}.$ Для нахождения равновесного распределения состава на основе уравнения (1) необходимо указать вид зависимостей химических потенциалов от концентрации. В случае гомогенного равновесного сплава концентрация в любой области сплава принимает одно и то же значение. Здесь, принимая в качестве аргумента параметра состояния $\mu $ величину самой концентрации, мы получаем на основе выражения (1) тривиальное уравнение $\mu ({{C}_{A}}) = {\text{const,}}$ из которого автоматически следует ${{C}_{A}} = {\text{const}}{\text{.}}$ Иная ситуация возникает в случае равновесия гетерогенного сплава, так как для него концентрация компонента имеет различные значения в каждой фазе. Теперь, опираясь на гипотезу слабой нелокальности, мы примем в качестве аргумента параметра состояния не локальное значение концентрации, а функционал концентрации ${{\Phi }_{{{{C}_{A}}}}}.$ В общем случае вид функционала от распределения параметра порядка приведен в работе [8]. Для одномерного бинарного сплава замещения запишем(2)
$\begin{gathered} {{\Phi }_{{{{C}_{A}}}}}(x) = \int\limits_{ - \infty }^{ + \infty } {{{C}_{A}}\left( {x{\kern 1pt} '} \right){{\delta }_{\Phi }}(\left| {x - x{\kern 1pt} '} \right|)dx{\kern 1pt} '} \cong \\ \cong {{C}_{A}}(x) + {{\Lambda }^{2}}\frac{{{{d}^{2}}{{C}_{A}}}}{{d{{x}^{2}}}}. \\ \end{gathered} $Правая часть выражения (2) получена разложением подынтегральной функции в ряд Тейлора по малому радиусу ядра интеграла $\Lambda \sim 3a,$ где $a$ – межатомное расстояние. Сомножитель три появляется на основе следующей оценки: при внедрении в трехмерную решетку атома другого сорта упругие искажения на расстоянии $3a$ уменьшаются на порядок по сравнению с их величиной на одном межатомном расстоянии. Кроме того, принято во внимание, что скорость переноса упругих деформаций (скорость звука) на много порядков превосходит скорость диффузионных процессов. Последнее означает, что временную часть записанного в [8] функционала можно не учитывать. В пренебрежении анизотропией кристаллической решетки и внешними полями, принята четная зависимость ядра интеграла от координат. При стремлении параметра $\Lambda $ к нулю из (2) получаем
Т.е. вдали от межфазной границы сплав можно описывать как однофазную систему. В более широком смысле, это означает, что все результаты, полученные методами термодинамики на основе гипотезы локального равновесия, сохраняются и в новом подходе как предельный случай.
РАВНОВЕСНОЕ РАСПРЕДЕЛЕНИЕ СОСТАВА ДВУХФАЗНОГО СПЛАВА
Химические потенциалы компонентов твердого раствора можно представить в виде [11]
где $\mu _{{A,B}}^{0}$ – не зависящие от состава слагаемые, $\gamma _{{A,B}}^{{}}$ – активности компонентов, учитывающие эффекты, связанные с неидеальностью. Согласно (1) для параметра состояния $\mu $ бинарного сплава можно записать(4)
${{\mu }^{{{\text{id}}}}} = \mu _{A}^{0} - \mu _{B}^{0} + kT\ln {{C}_{A}} - kT\ln (1 - {{C}_{A}}),$Здесь ${{\mu }^{{{\text{id}}}}}$ и ${{\mu }^{{XS}}}$ – параметр состояния идеального твердого раствора и избыточный параметр состояния, которые выражаются через соответствующие химические потенциалы компонентов твердого раствора. Следует учесть, что в идеальном твердом растворе отсутствуют фазы, и он представляет собой гомогенный по химическому составу сплав. Возникновение фаз связано с неидеальностью твердого раствора, которая учитывается активностями компонентов сплава, то есть избыточным значением параметра состояния. В рамках нашего подхода избыточный параметр состояния μXS должен учитывать и нелокальность. Поэтому примем для бинарного сплава $\mu = {{\mu }^{{{\text{id}}}}}\left( {{{C}_{A}}} \right) + {{\mu }^{{XS}}}\left( {{{\Phi }_{{{{C}_{A}}}}}(x)} \right).$ Теперь можно уточнить вид уравнения для определения равновесного распределения состава (1):
(6)
${{\mu }^{{{\text{id}}}}}\left( {{{C}_{A}}} \right) + {{\mu }^{{XS}}}\left( {{{\Phi }_{{{{C}_{A}}}}}(x)} \right) = {\text{const}}{\text{.}}$Обозначим постоянную в правой части выражения (6) символом ${{\mu }_{e}}.$ Ее величина определяет конкретный характер химического равновесия. Используя разложение функционала (2) и последующее разложение избыточного параметра состояния с точностью до ${{\Lambda }^{2}}$ (см. Приложение), получим
(7)
${{\Lambda }^{2}}\frac{{{{d}^{2}}{{f}_{{XS}}}({{C}_{A}})}}{{{{d}^{2}}C_{A}^{2}}}\frac{{{{d}^{2}}{{C}_{A}}}}{{d{{x}^{2}}}} + \frac{{df({{C}_{A}})}}{{d{{C}_{A}}}} - {{\mu }_{e}} = 0.$В уравнении (7) свободная энергия $f$ и избыточная свободная энергия ${{f}_{{XS}}}$ относятся к одному узлу решетки однородного твердого раствора.
Такой же вид уравнения для распределения состава двухфазного твердого раствора получается и на основе любой формы градиентного разложения, например, в [9]. Отличие заключается в том, что коэффициент формального градиентного разложения здесь выражен в виде произведения малого сомножителя, связанного с характерным размером атомной структуры сплава, и величины, имеющей ясный физический смысл. Действительно, вторая производная плотности избыточной свободной энергии становится известной функцией состава при выборе конкретной термодинамической модели сплава.
ТЕРМОДИНАМИЧЕСКИЕ МОДЕЛИ ТВЕРДЫХ РАСПЛАВОВ
Конкретный вид коэффициентов уравнения (7) определяется термодинамической моделью твердого раствора. Примем модель CALPHAD, использованную в работе [12]. Свободная энергия одного моля твердого раствора $F$ представлена в виде суммы свободной энергии идеального твердого раствора ${{F}_{{{\text{id}}}}}$ и избыточной свободной энергии ${{F}_{{XS}}},$ причем
(8)
$\begin{gathered} {{F}_{{{\text{id}}}}} = {{F}_{0}} + a_{A}^{f}{{C}_{A}} + a_{B}^{f}{{C}_{B}} + T\left[ {{{s}_{0}} + a_{A}^{s}{{C}_{A}} + a_{B}^{s}{{C}_{B}} + } \right. \\ + \,\,R\left. {\left( {{{C}_{A}}\ln {{C}_{A}} + {{C}_{B}}\ln {{C}_{B}}} \right)} \right], \\ \end{gathered} $(9)
${{F}_{{XS}}} = {{C}_{A}}{{C}_{B}}\left[ {\left( {b_{A}^{f}{{C}_{A}} + b_{B}^{f}{{C}_{B}}} \right) + T\left( {b_{A}^{s}{{C}_{A}} + b_{B}^{s}{{C}_{B}}} \right)} \right].$Размерные коэффициенты $a_{{A,B}}^{{f,s}}$ и $b_{{A,B}}^{{f,s}}$ характеризуют свойства конкретного сплава. Плотность свободной энергии одного моля твердого раствора связана со свободной энергией на один узел решетки, фигурирующей в уравнении (7), соотношением $F = {{N}_{{\text{A}}}}f,$ где ${{N}_{{\text{A}}}}$ – число Авогадро. И аналогично ${{F}_{{XS}}} = {{N}_{{\text{A}}}}{{f}_{{XS}}},$ ${{F}_{{{\text{id}}}}} = {{N}_{{\text{A}}}}{{f}_{{{\text{id}}}}}.$ Приведенный вид ${{F}_{{XS}}}$ удобен тем, что в случае регулярного твердого раствора энтропийная составляющая отсутствует, т.е. $b_{A}^{s} = b_{B}^{s} = 0,$ а в энергетическом слагаемом энергия смешения не зависит от состава, поскольку $b_{A}^{f} = b_{B}^{f} = {{b}_{{{\text{reg}}}}}$ и ${{C}_{A}} + {{C}_{B}} = 1.$ В этом случае имеем $f_{{XS}}^{{{\text{reg}}}} = {{b}_{{{\text{reg}}}}}{{C}_{A}}{{C}_{B}}.$ Модель регулярного твердого раствора особо выделена, поскольку она надежно обоснована методами статистической физики и является удобным предельным случаем, позволяющим тестировать более общие модели. В выражениях (8), (9) допускается зависимость коэффициентов от температуры, которая обычно принимается в виде ряда по степеням температуры. В результате удается описать реальные диаграммы фазового равновесия широкого класса бинарных металлических сплавов [12].
Теперь уравнение для расчета равновесного распределения состава можно представить в виде
(10)
${{\Lambda }^{2}}\gamma ({{C}_{A}})\frac{{{{d}^{2}}{{C}_{A}}}}{{d{{x}^{2}}}} - \frac{{df({{C}_{A}})}}{{d{{C}_{A}}}} + {{\mu }_{e}} = 0,$Рассмотрим равновесные распределения состава для некоторых моделей твердых растворов.
ИДЕАЛЬНЫЙ ТВЕРДЫЙ РАСТВОР
В этом случае: $b_{A}^{f} = b_{B}^{f} = b_{A}^{s} = b_{B}^{s} = 0.$ Равновесное распределение состава описывается уравнением
Его решение соответствует однородному сплаву с концентрацией ${{C}_{A}} = {\text{const,}}$ значение которой определяется постоянными ${{\mu }_{e}},\,\,a_{A}^{f},\,\,a_{B}^{f},\,\,a_{A}^{s},\,\,a_{B}^{s}$ и температурой.
РЕГУЛЯРНЫЙ ТВЕРДЫЙ РАСТВОР
Для него: $b_{A}^{f} = b_{B}^{f} = {{b}_{{{\text{reg}}}}},$ $b_{A}^{s} = b_{B}^{s} = 0.$ Уравнение для распределения состава имеет вид
Умножим его на $\frac{{d{{C}_{A}}}}{{dx}},$ и после интегрирования по координате получим
(14)
${{\Lambda }^{2}}{{b}_{{{\text{reg}}}}}{{\left( {\frac{{d{{C}_{A}}}}{{dx}}} \right)}^{2}} = {{f}_{{{\text{reg}}}}}({{C}_{A}}) - y({{C}_{A}}),$Линейные слагаемые плотности свободной энергии ${{f}_{0}} + a_{B}^{f} + {{s}_{0}}T + a_{B}^{s}T$ и $(a_{A}^{f} - a_{B}^{f}$ + $a_{A}^{s}T - a_{B}^{s}T){{C}_{A}}$ включены в постоянные интегрирования $E$ и μ. Постоянная ${{b}_{{{\text{reg}}}}}$ пропорциональна энергии смешения бинарного регулярного твердого раствора.
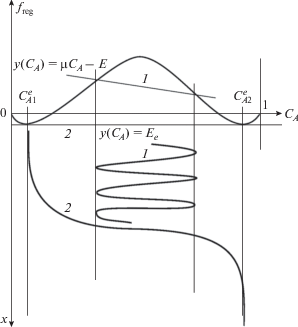
Уравнение (14) имеет вид уравнения нелинейных колебаний материальной точки. Вид его решений зависит от значений постоянных интегрирования. Он показан на рис. 1 для двух вариантов. В первом случае решение соответствует метастабильному состоянию, а второй вариант соответствует равновесному распределению состава образца, концы которого далеки от положения межфазной границы. Значения концентрации в точках кривой плотности свободной энергии, которых касается конода, удовлетворяют хорошо известному выражению для равновесных пределов растворимости регулярного раствора [13]:
КВАЗИРЕГУЛЯРНЫЙ ТВЕРДЫЙ РАСТВОР
Модель квазирегулярного твердого раствора мы получаем при замене в уравнении (10) коэффициента $\gamma ({{C}_{A}})$ некоторой постоянной $\bar {\gamma },$ равной усредненному значению этого коэффициента. При этом мы сохраняем зависимость плотности свободной энергии от концентрации в прежнем виде. Уравнение для распределения состава принимает вид
Этот вид уравнения с точностью до обозначений совпадает с уравнением для распределения состава, полученным Хачатуряном на основе метода функционала свободной энергии [6]. Интегрирование, как и в случае регулярного твердого раствора, приводит к уравнению той же формы, что и для классического нелинейного осцилятора:
(16)
$\frac{1}{2}{{\Lambda }^{2}}\bar {\gamma }{{\left( {\frac{{d{{C}_{A}}}}{{dx}}} \right)}^{2}} = f({{C}_{A}}) - y({{C}_{A}}).$Уравнение коноды в этом случае имеет прежний вид.
В правой части (14) первое слагаемое выражается через плотность свободной энергии регулярного твердого раствора, а соответствующее слагаемое в правой части уравнения (16), это плотность свободной энергии твердого раствора с произвольной зависимостью от состава.
Последнее обстоятельство позволяет аналитически обосновать предложенный Гиббсом метод построения равновесных пределов растворимости. В соответствии с правой частью уравнения (16) следует повторить рис. 1, изменив его в одном отношении. А именно, вместо симметричной кривой ${{f}_{{{\text{reg}}}}}({{C}_{A}})$ изобразить кривую $f({{C}_{A}}),$ минимумы которой лежат на различной высоте по вертикали и асимметричны относительно точки ${{C}_{A}} = 0.5$. В этом случае равновесному профилю распределения состава, как и прежде, будет соответствовать положение коноды $y({{C}_{A}}),$ при котором она будет касаться графика $f({{C}_{A}})$ в двух точках, которые в этом случае не будут точками минимума. Значения концентрации, соответствующие точкам касания – это и есть значения равновесных пределов растворимости. Это подтверждается нижней частью рис. 1, т.е. асимптотическим поведением графика ${{C}_{A}}(x) \to C_{{A1,2}}^{e}$ при $x \to \pm \infty .$ Наличие этих асимптот зависит не от конкретного вида концентрационной зависимости плотности свободной энергии, а только от общей формы графика $f({{C}_{A}}),$ допускающей наличие общей касательной для двух точек графика, так что сам график располагается выше касательной (коноды). Отметим, что верхняя часть измененного таким образом рис. 1 полностью повторяет классическое построение, предложенное Гиббсом для определения значений равновесных пределов растворимости [13–15]. Построение Гиббса основывалось на таких эвристических соображениях, как пренебрежение ролью межфазной границы из-за малого вклада в полную свободную энергию сплава. Но роль межфазной границы не сводится только к энергетическим эффектам. Она является потенциальным барьером, предопределяющим свойства фаз сплава. В нашем случае результат Гиббса возникает на основе формальных соображений, содержание которых можно проконтролировать количественно.
ТВЕРДЫЙ РАСТВОР В МОДЕЛИ CALPHAD БИНАРНОГО СПЛАВА (9)
Допустим, что коэффициент $\gamma ({{C}_{A}})$ в уравнении (10) не обращается в нуль во всем диапазоне составов. Поделим на него уравнение и затем проинтегрируем его по координате, предварительно умножив обе части на $\left( {\frac{{d{{C}_{A}}}}{{dx}}} \right).$ Получим
(17)
$\frac{1}{2}{{\Lambda }^{2}}{{\left( {\frac{{d{{C}_{A}}}}{{dx}}} \right)}^{2}} = U({{C}_{A}}) - y({{C}_{A}}).$Здесь введена “потенциальная” функция, связанная с плотностью свободной энергии соотношением
(18)
$U({{C}_{A}}) = \int {\frac{{\left( {df{{({{C}_{A}})} \mathord{\left/ {\vphantom {{({{C}_{A}})} {d{{C}_{A}}}}} \right. \kern-0em} {d{{C}_{A}}}}} \right) - {{\mu }_{e}}}}{{\gamma ({{C}_{A}})}}} d{{C}_{A}}.$Для единообразия подхода использовано уравнение коноды, которое в данном случае принимает вид
Как и прежние уравнения, выражение (17) имеет вид уравнения нелинейных колебаний материальной точки. Анализ возможных решений производится сходным образом и приводит к тем же трем типам возможных решений. Анализ их вида проведен в [6] для случая, который у нас соответствует квазирегулярному твердому раствору.
Общий случай отличается тем, что вместо плотности свободной энергии у нас фигурирует потенциальная функция, определенная выражением (18). Поэтому качественное поведение распределений состава такое же, как и в [6], но количественные характеристики другие.
Вновь возникают три возможных типа решений: 1-й реализуется при значениях параметров $E$ и μ, когда прямая $y({{C}_{A}}) = - E$ пересекает график кривой $U({{C}_{A}};\mu )$ в двух точках. Тогда формируются пространственные модуляции состава. 2-й возникает, когда прямая $y({{C}_{A}}) = - E$ и кривая $U({{C}_{A}};\mu )$ пересекаются в одной точке, при этом распределение состава имеет вид уединенного солитона. Эти два типа решений реализуют метастабильные состояния сплава [6]. Решения 3-его типа соответствуют равновесному состоянию, они возникают при условии, что прямая $y({{C}_{A}}) = E$ касается кривой $U({{C}_{A}};{{\mu }_{e}})$ в двух точках. Именно в этом случае асимптотическое поведение ${{C}_{A}}(x)$ при удалении в обе стороны от межфазной границы соответствует равновесному состоянию, когда градиенты концентрации стремятся к нулю.
Качественный вид решений 1-ого и 3-его типов приведен внизу рис. 1 в частном случае регулярного твердого раствора. Концентрации в точках касания обозначены $C_{{A1}}^{e}$ и $C_{{A2}}^{e}.$
В табл. 1 приведены полученные теоретически значения равновесных пределов растворимости для системы железо–медь. Коэффициенты концентрационной зависимости избыточной свободной энергии взяты из [12]. Для ГЦК-решетки эти значения равны $b_{{{\text{Fe}}}}^{f} = 54124.0,$ $b_{{{\text{Cu}}}}^{f} = 42288.0,$ $b_{{{\text{Fe}}}}^{s} = 13.4637$ и $b_{{{\text{Cu}}}}^{s} = 3.4292.$ Приведенные в табл. 1 пределы растворимости рассчитаны в соответствии с моделью квазирегулярного твердого раствора согласно уравнению (16) (столбец, обозначенный символом g), и согласно уравнению (17) (столбец, обозначенный символом U).
Таблица 1.
Температурные зависимости равновесных пределов растворимости и параметров спинодали в ГЦК-сплаве Fe–Cu. Расчет пределов растворимости проведен по модели Гиббса (g) и по модели, основанной на гипотезе слабой нелокальности (U). Параметры концентрационной зависимости плотности свободной энергии взяты из [14]
| T, K | $C_{{{\text{Fe}}}}^{{g - }},$ % | $C_{{{\text{Fe}}}}^{{U - }},$ % | $C_{{{\text{Cu}}}}^{{g + }},$ % | $C_{{{\text{Cu}}}}^{{U + }},$ % |
|---|---|---|---|---|
| 800 | 0.12 | 0.31 | 0.006 | 0.002 |
| 900 | 0.24 | 0.56 | 0.014 | 0.006 |
| 1000 | 0.42 | 0.90 | 0.029 | 0.014 |
| 1100 | 0.67 | 1.33 | 0.053 | 0.037 |
| 1200 | 1.00 | 1.85 | 0.088 | 0.048 |
| 1300 | 1.40 | 2.45 | 0.17 | 0.07 |
| 1400 | Liquid Cu | 0.19 | 0.12 | |
| 1500 | Liquid Cu, Fe | |||
Качественное поведение температурных зависимостей пределов растворимости, рассчитанных в рамках подхода Гиббса и на основе применения гипотезы слабой нелокальности одинаково. В рамках обоих подходов предел растворимости меди в железе на порядок меньше, чем предел растворимости железа в меди. Расчеты на основе гипотезы слабой нелокальности приводят к систематическому смещению положения бинодали в сторону увеличения содержания железа. Количественное различие результатов в том, что концентрация железа в меди больше на 36–158% в рамках предложенного нами подхода по сравнению со значением предела растворимости, полученного в рамках подхода Гиббса.
Необходимо отметить, что результаты расчетов, приведенные в табл. 1, основаны на концентрационной зависимости энтальпии смешения, взятой из работы [12]. Коэффициенты этой зависимости получены подгонкой к экспериментальным данным о положении бинодали в рамках методики CALPHAD, т.е. на основе градиентного разложения с постоянным значением коэффициента при старшей производной (в нашем случае это модель квазирегулярного твердого раствора, соответствующая построению Гиббса). Поэтому данные табл. 1 не следует рассматривать как результат независимых расчетов. Они характеризуют лишь разницу, возникающую при использовании двух различных моделей для описания одной и той же системы.
ЗАКЛЮЧЕНИЕ
Предложенный в настоящей работе подход позволяет определять в рамках термодинамики непрерывных систем параметры бинодалей бинарных сплавов. В основе подхода лежит использование гипотезы слабой нелокальности, которая является обобщением гипотезы локального равновесия. Знание зависимости плотности свободной энергии однородного сплава от его состава оказывается достаточным для определения положения ветвей бинодали. Область применимости гипотезы слабой нелокальности совпадает с областью применимости градиентных разложений свободной энергии в методе функционала Гинзбурга–Ландау. Это утверждение обосновывается тем, что формальный вид всех выражений, полученных в рамках обоих подходов, в случае сплавов совпадает. Однако при использовании гипотезы слабой нелокальности коэффициенты разложений принимают конкретный физический смысл, а их зависимость от состава прямо связана с выбором термодинамической модели сплава.
Физический смысл самой гипотезы слабой нелокальности заключается в косвенном учете коллективного взаимодействия, приводящего к появлению внутренних степеней свободы. Математический аппарат гипотезы строится на утверждении, что скорость изменения термодинамического состояния физически малой области зависит не только от значений его локальных параметров, но и от их распределения. При этом степень влияния одних локальных состояний на другие быстро уменьшается по мере увеличения интервала между областями.
Показано, что результаты применения гипотезы слабой нелокальности качественно совпадают с результатами, получаемыми как в рамках подхода Гиббса, так и в рамках приближения градиентных разложений, положенного в основу известной методики CALPHAD. Количественное отличие величин равновесных пределов растворимости лежит в диапазоне от 40 до 160% в зависимости от температуры.
Работа частично выполнена в рамках госзадания Минобрнауки РФ (тема “Давление” № AAAA-A18-118020190104-3).
Авторы выражают признательность участникам семинара лаборатории диффузии ИФМ УрО РАН и особенно заведующему лабораторией д.ф.-м.н., проф. В.В. Попову, д.ф.-м.н., проф. И.М. Куркину и д.ф.-м.н., проф. А.Е. Ермакову за обсуждение работы и полезные замечания.
Список литературы
Cahn J.W., Hillard J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy // J. Chem. Phys. 1958. V. 28. № 2. P. 1121–1124.
Hart E.W. Termodynamics of Inhomogeneous Systems // Phys. Rev. 1959. V. 113. № 2. P. 412–416.
Cahn J.W., Hillard J.E. Free Energy of a Nonuniform System. III. Nucleathion in a Two-Component Incompressible Fluid // J. Chem. Phys. 1959. V. 31. № 3. P. 688–699.
Cahn J.W. Free Energy of a Nonuniform System. II. Termodynamic Basis // J. Chem. Phys. 1959. V. 30. № 5. P. 258–267.
Вакс В.Г., Журавлев И.А., Хромов К.Ю. Расчеты бинодалей и спинодалей в многокомпонентных сплавах различными статистическими методами с применением к сплавам железо–медь–марганец // ЖЭТФ. 2010. Т. 138. Вып. 5(11). С. 902–920.
Хачатурян А.Г. Теория фазовых превращений и структура твердых растворов. М.: Наука, 1974. 384 с.
Cahn J.W. On spinodal decomposition. // Acta Metal. 1961. № 9. C. 795–801.
Гапонцев В.Л., Селезнев В.Д., Гапонцев А.В. Распад равновесной межфазной границы в сплавах замещения при механосплавлении // ФММ. 2017. Т. 118. № 7. С. 665–678.
Дьярмати И. Неравновесная термодинамика. Теория поля и вариационные принципы. М.: Мир, 1974. 304 с.
Румер Ю.Б., Рывкин М.Ш. Термодинамика. Статистическая физика и кинетика. М.: Наука, 1972. 400 с.
Боровский И.Б., Гуров К.П., Марчукова И.Д., Угасте Ю.Э. Процессы взаимной диффузии в сплавах. М.: Наука, 1973. 359 с.
Kaufman L, Nesor H. Coupled phase diagrams and termodchemmical data for transition metal binary systems. Ch. II // CALPHAD. 1978. V. 2. № 1. P. 81–108.
Кристиан Дж. Теория превращений в металлах и сплавах. М.: Мир, 1978. 806 с.
Гиббс Дж. В. Термодинамические работы / Пер. с англ. М., Л.: Гостехиздат, 1950. 492 с.
Лоренц Г.А. Лекции по термодинамике. Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001. 176 с.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение