1. На главную
  2. Электронные версии
  3. Физика металлов и металловедение
  4. T. 121, № 4, 2020

Физика металлов и металловедение, 2020, T. 121, № 4, стр. 346-351

Исследование фазовых переходов в антиферромагнитной модели Гейзенберга на объемно-центрированной кубической решетке методом Монте-Карло

А. К. Муртазаев a, *, Ф. А. Кассан-Оглы b, М. К. Рамазанов a, К. Ш. Муртазаев a

a Институт физики ДНЦ РАН
367003 Махачкала, ул. М. Ярагского, 94, Россия

b Институт физики металлов УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия

* E-mail: sheikh77@mail.ru

Поступила в редакцию 13.09.2019
После доработки 24.10.2019
Принята к публикации 15.11.2019

Полный текст (PDF)

Аннотация

На основе репличного алгоритма методом Монте-Карло выполнены исследования фазовых переходов антиферромагнитной модели Гейзенберга на объемно-центрированной кубической решетке с учетом взаимодействий между первыми и вторыми ближайшими соседями. Исследования проведены для отношения величины обменных взаимодействий между первыми и вторыми ближайшими соседями в интервале значений 0.0 ≤ r ≤ 1.0. Построена фазовая диаграмма зависимости критической температуры от величины взаимодействия вторых ближайших соседей. Впервые на диаграмме обнаружена область, где переход из антиферромагнитной фазы в парамагнитную является переходом первого рода.

ВВЕДЕНИЕ

Магнитные системы с конкурирующими антиферромагнитными обменными взаимодействиями между первыми и вторыми ближайшими соседями находятся в центре интенсивных исследований физики конденсированных сред уже более двух десятилетий [1–5]. Наличие конкурирующих обменных взаимодействий в магнитных материалах может привести к фрустрациям и большому разнообразию магнитных упорядоченных состояний и фазовых переходов (ФП) между ними. Кроме того, особенности ФП при разных значениях отношения обменных взаимодействий между первыми и вторыми ближайшими соседями известны лишь в общих чертах [4–6].

В настоящее время классическая двумерная модель Гейзенберга изучена достаточно хорошо и известны практически все ее свойства [7, 8]. Эта модель может быть использована для описания магнитных структур целого ряда реальных материалов.

В отличие от двумерного случая, трехмерная антиферромагнитная модель Гейзенберга на объемно-центрированной кубической (ОЦК) решетке с конкурирующими взаимодействиями до сих пор мало изучена.

Кроме того, учет взаимодействий вторых ближайших соседей может приводить к возникновению фрустраций, что усложняет решение этой модели.

Интерес к этой модели обусловлен еще и тем, что многие физические свойства фрустрированных систем сильно отличаются от соответствующих нефрустрированных систем.

При изучении спиновых систем с фрустрациями до сих пор основное внимание уделяли фрустрированным системам на квадратной, треугольной и гексагональной решетке [3, 9–11].

В настоящей работе на основе метода Монте-Карло (MК) проведены исследования ФП в классической антиферромагнитной модели Гейзенберга на ОЦК-решетке для различного отношения обменных взаимодействий между первыми и вторыми ближайшими соседями.

Из данных, полученных на сегодняшний день, нельзя однозначно определить характер ФП и закономерности изменения термодинамического поведения данной модели, и эти вопросы до сих пор остаются открытыми. Исследование антиферромагнитной модели Гейзенберга на ОЦК решетке с конкурирующими взаимодействиями между первыми и вторыми ближайшими соседями на основе современных методов и идей позволяет получить ответ на ряд вопросов, связанных с ФП, магнитными и термодинамическими свойствами фрустрированных спиновых систем.

МОДЕЛЬ И МЕТОД ИССЛЕДОВАНИЯ

Антиферромагнитная классическая модель Гейзенберга на ОЦК-решетке с учетом взаимодействий между первыми и вторыми ближайшими соседями описывается следующим гамильтонианом:

(1)
${\rm H} = - {{J}_{1}}\sum\limits_{\left\langle {i,j} \right\rangle } {({{S}_{i}} \cdot {{S}_{j}})} - {{J}_{2}}\sum\limits_{\left\langle {i,l} \right\rangle } {({{S}_{i}} \cdot {{S}_{l}})} ,$
где ${{S}_{i}}$ − трехкомпонентный единичный вектор ${{S}_{i}} = \left( {S_{i}^{x},S_{i}^{y},S_{i}^{z}} \right).$ Первый член в формуле (1) учитывает обменное взаимодействие между первыми ближайшими соседями (J1 < 0), а второй – между вторыми (J2 < 0). Известно, что для данной модели при J2 = 0 основным состоянием является обычное антиферромагнитное упорядочение. Ненулевое обменное взаимодействие J2 может нарушить данный порядок и привести к возникновению фрустраций. Достаточно большое значение J2 приводит к появлению страйповых структур.

В настоящее время ФП фрустрированных спиновых систем на основе микроскопических гамильтонианов довольно успешно изучаются методами МК [12–18]. Методы МК позволяют исследовать физические свойства спиновых систем практически любой сложности. На их основе, на сегодняшний день, изучены целые классы спиновых систем и рассчитаны критические индексы широкого спектра моделей. В данном исследовании мы использовали репличный обменный алгоритм метода МК [15, 17], который является наиболее мощным и эффективным для исследования фрустрированных спиновых систем. Более подробно этот алгоритм описан в работе [5].

Расчеты проведены для систем с периодическими граничными условиями и линейными размерами 2(L × L × L) = N, где L измеряется в размерах элементарной ячейки и изменяется в интервале 24–90. Отношение величины обменных взаимодействий между первыми и вторыми ближайшими соседями r = |J2/J1| меняется в интервале 0.0 ≤ r ≤ 1.0. Для вывода системы в состояние термодинамического равновесия отсекали неравновесный участок длиной τ0 = 4 × 105 шагов МК на спин, что в несколько раз больше длины неравновесного участка. Усреднение термодинамических параметров проводили вдоль марковской цепи длиной до τ = 500τ0 шагов МК на спин.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Для исследования температурной эволюции теплоемкости и восприимчивости использовали выражения [19]:

(2)
$C = (N{{K}^{2}})\left( {\left\langle {{{U}^{2}}} \right\rangle - {{{\left\langle U \right\rangle }}^{2}}} \right),$
(3)
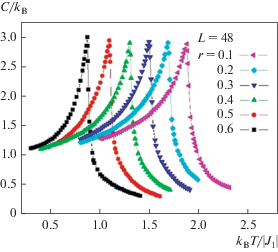
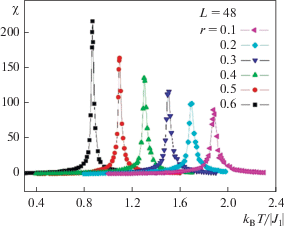
$\chi = \left\{ \begin{gathered} (NK)\left( {\left\langle {{{M}^{2}}} \right\rangle - {{{\left\langle {\left| M \right|} \right\rangle }}^{2}}} \right),\,\,\,\,T < {{T}_{N}} \hfill \\ \left( {NK} \right)\left\langle {{{M}^{2}}} \right\rangle ,\,\,\,\,T \geqslant {{T}_{N}} \hfill \\ \end{gathered} \right.,$
где $K = {{\left| {{{J}_{1}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{J}_{1}}} \right|} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}},$ N – число частиц, TN – критическая температура (здесь и далее температура и остальные термодинамические и магнитные величины измеряются, как это принято в теории низкоразмерных систем, в единицах |J1|/kB), U – внутренняя энергия, M – подрешеточная намагниченность.

На рис. 1 и 2 представлены температурные зависимости теплоемкости C и восприимчивости χ, полученные для L = 48 и различных значений r (здесь и далее статистическая погрешность не превышает размеров символов, использованных для построения зависимостей).

Рис. 1.

Зависимость теплоемкости C/kB от температуры kBT/|J1| для L = 48 и разных r.

Рис. 2.

Зависимость восприимчивости χ от температуры kBT/|J1| для L = 48 и разных r.

Из рисунков видно, что в зависимостях теплоемкости и восприимчивости от температуры для всех значений r вблизи критической температуры наблюдаются хорошо выраженные максимумы, которые с ростом r смещаются в сторону низких температур. Причем увеличение значения r приводит к росту абсолютных значений максимумов восприимчивости, что обусловлено усилением флуктуаций, вследствие увеличения конкуренции между первыми и вторыми ближайшими соседями.

Для определения критической температуры TN был использован метод кумулянтов Биндера UL четвертого порядка [20]:

(4)
${{V}_{L}} = 1 - \frac{{{{{\left\langle {{{U}^{4}}} \right\rangle }}_{L}}}}{{3\left\langle {{{U}^{2}}} \right\rangle _{L}^{2}}},$
(5)
${{U}_{L}} = 1 - \frac{{{{{\left\langle {{{M}^{4}}} \right\rangle }}_{L}}}}{{3{{{\left\langle {{{M}^{2}}} \right\rangle }}_{L}}^{2}}},$
где VL – кумулянт по энергии, UL – кумулянт по намагниченности.

Выражения (4) и (5) позволяют определить критическую температуру TN с большой точностью. Следует отметить, что применение кумулянтов Биндера дает также возможность хорошо тестировать тип ФП в системе. Известно, что в случае ФП второго рода кривые температурной зависимости кумулянтов Биндера UL имеют четко выраженную точку пересечения [20].

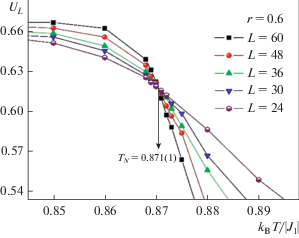
На рис. 3 представлена характерная зависимость UL от температуры для r = 0.6 при разных значениях L. Этот рисунок демонстрирует точность определения критической температуры. Видно, что в критической области наблюдается четко выраженная точка пересечения TN = 0.871(1), что свидетельствует о ФП второго рода. Аналогичным образом были определены критические температуры и для остальных значений r.

Рис. 3.

Зависимость кумулянта Биндера UL от температуры kBT/|J1| для r = 0.6 и разных L.

Для более подробного анализа характера ФП был также использован гистограммный анализ данных метода МК [18, 21]. Этот метод позволяет надежно определить род ФП. Методика определения рода ФП этим методом подробно описана в [11, 22].

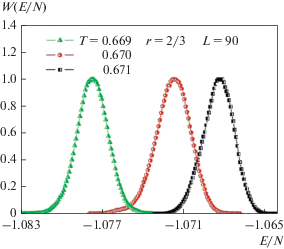
На рис. 4 представлены гистограммы распределения энергии для случая r = 2/3 с линейными размерами L = 90. Графики построены вблизи критической температуры TN = 0.670(1). Из рисунка видно, что в зависимости вероятности W от энергии E/N для всех значений температур наблюдается один хорошо выраженный максимум, который свидетельствует о ФП второго рода.

Рис. 4.

Гистограмма распределения энергии для r = = 2/3 и L = 90.

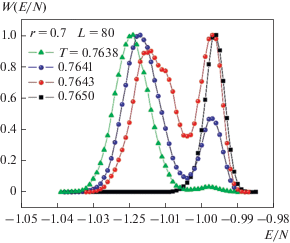
На рис. 5 представлены гистограммы распределения энергии для системы с линейными размерами L = 80 и r = 0.7. Как видно из рисунка, вблизи температуры ФП TN = 0.7643 в системе наблюдается бимодальное распределение энергии. Наличие двойного максимума в зависимости вероятности W от энергии E/N является характерным признаком ФП первого рода. Аналогичная картина наблюдается для всех значений взаимодействия вторых ближайших соседей в интервале 2/3 < r ≤ 0.75.

Рис. 5.

Гистограмма распределения энергии для r = = 0.7 и L = 80.

На рис. 6 приведена фазовая диаграмма зависимости критической температуры TN от величины взаимодействия вторых ближайших соседей r. Как видно из рисунка, по мере приближения к точке r = 2/3, где сосуществуют три фазы, температура ФП смещается в сторону низких температур. Для рассмотренной модели при r = 2/3 система имеет минимальную температуру ФП T = = 0.670(1). Из диаграммы видно, что в точке r = 2/3 пересекаются три различные фазы: антиферромагнитная AF1, парамагнитная PM и антиферромагнитная AF2 [22]. Наличие трех фаз было обнаружено на аналогичной фазовой диаграмме, полученной в [23] в модели Гейзенберга на гранецентрированной кубической решетке. Отличие фазовой диаграммы, представленной в [23], от полученной в данном исследовании, связано с тем, что в [23] рассматриваются взаимодействия первых, вторых и третьих ближайших соседей.

Рис. 6.

Фазовая диаграмма зависимости критической температуры от величины взаимодействия вторых ближайших соседей.

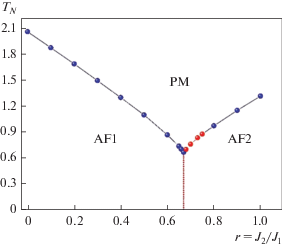
Переход AF1 → AF2 в классической модели Гейзенберга на ОЦК-решетке обусловлен изменением структуры основного состояния. В фазе AF1 могут реализоваться только две структуры основного состояния. В фазе AF2 реализуются четыре структуры основного состояния. Вдоль вертикальной линии, соответствующей значению r = 2/3, сосуществуют все шесть структур одновременно. Согласно данным, полученным на основе теории среднего поля, в модели Гейзенберга на ОЦК-решетке с взаимодействиями между первыми и вторыми ближайшими соседями значение r = 2/3 является классической точкой перехода, где происходит ФП AF1 → AF2. Этот переход в данной работе не рассматривается. Нами подробно изучены переходы AF1 → PM, а также ФП AF2 → PM.

Результаты, полученные в рамках данного исследования, показывают, что в интервалах 0.0 ≤ r ≤ ≤ 0.6 и 0.8 ≤ r ≤ 1.0 наблюдается ФП второго рода. Установлено, что в интервале 2/3 ≤ r ≤ 0.75 (на рис. 6 выделено красным цветом) переход из антиферромагнитной фазы в парамагнитную реализуется как ФП первого рода. Таким образом, в исследуемой модели учет взаимодействий вторых ближайших соседей приводит к смене рода ФП. Наличие ФП первого и второго рода в гейзенберговских антиферромагнетиках ранее обсуждали в [24, 25]. Согласно данным, полученным в [24], можно предположить, что наблюдаемый в настоящей работе ФП первого рода связан с бóльшим числом компонент параметра порядка для исследуемой модели. Численные исследования, проведенные в [26, 27], показывают, что в Гейзенберговских антиферромагнетиках на кубических решетках с учетом взаимодействия между первыми и вторыми ближайшими соседями реализуются ФП первого рода. Эти данные соответствуют нашим результатам, полученным для интервала 2/3 ≤ r ≤ 0.75. В [24] показано, что в антиферромагнитной модели Гейзенберга на кубических решетках наблюдается ФП второго рода, что подтверждает наши данные, полученные для интервалов 0.0 ≤ r ≤ 0.6 и 0.8 ≤ r ≤ 1.0.

Диаграмма, полученная в исследуемой классической модели Гейзенберга на ОЦК-решетке, качественно совпадает с диаграммой трехмерной модели Изинга на ОЦК-решетке [3, 12, 22].

Полученные в работе данные могут быть использованы для описания конкретных антиферромагнитных материалов, таких как FeCr, FeAl, FeCo и ряда других, имеющих ОЦК-решетку.

ЗАКЛЮЧЕНИЕ

Исследование фазовых переходов в антиферромагнитной модели Гейзенберга на объемно-центрированной кубической решетке с взаимодействиями между первыми и вторыми ближайшими соседями выполнено с использованием высокоэффективного репличного алгоритма метода Монте-Карло. На основе гистограммного метода и метода кумулянтов Биндера проведен анализ характера фазовых переходов для различной величины взаимодействия вторых ближайших соседей r. Построена фазовая диаграмма зависимости критической температуры от величины взаимодействия вторых ближайших соседей. Установлено, что в интервале значений 2/3 < r ≤ 0.75 в исследуемой модели переход из антиферромагнитной фазы в парамагнитную реализуется как фазовый переход первого рода.

Исследование выполнено в рамках госзадания МИНОБРНАУКИ России (тема Квант № АААА-А18-118020190095-4) при частичной финансовой поддержке РФФИ (проекты № 18-32-00391-мол-а, № 19-02-00153-а, 18-32-20098-мол-а-вед) и УрО РАН (проект № 18-2-2-11).

Список литературы

  1. Dotsenko V.S. Critical phenomena and quenched disorder // Phys. Usp. 1995. V. 38. P. 457–496.

  2. Korshunov S.E. Phase transitions in two-dimensional systems with continuous degeneracy // Phys. Usp. 2006. V. 49. P. 225–262.

  3. Ramazanov M.K., Murtazaev A.K. Phase transitions and critical characteristics in the layered antiferromagnetic Ising model with next-nearest-neighbor intralayer interactions // JETP Lett. 2015. V. 101. P. 714–718.

  4. Ramazanov M.K., Murtazaev A.K. Phase transitions in the antiferromagnetic layered Ising model on a cubic lattice // JETP Lett. 2016. V. 103. P. 460–464.

  5. Ramazanov M.K., Murtazaev A.K., Badiev M.K. Phase transitions and critical phenomena in the antiferromagnetic Ising model on a layered triangular lattice // Physica A. 2018. V. 507. P. 210–218.

  6. Murtazaev A.K., Ramazanov M.K., Kassan-Ogly F.A., Kurbanova D.R. Phase transitions in the antiferromagnetic Ising model on a body-centered cubic lattice with interactions between next-to-nearest neighbors // JETP. 2015. V. 120. P. 110–114.

  7. Dagotto E., Moreo A. Phase diagram of the frustrated spin-1/2 Heisenberg antiferromagnet in 2 dimensions // Phys. Rev. Lett. 1989. V. 63. P. 2148–2151.

  8. Manousakis E. The spin-1/2 Heisenberg antiferromagnet on a square lattice and its application to the cuprous oxides // Rev. Mod. Phys. 1991. V. 63. P. 1–62.

  9. Kassan-Ogly F.A., Murtazaev A.K., Zhuravlev A.K., Ramazanov M.K., Proshkin A.I. Ising model on a square lattice with second-neighbor and third-neighbor interactions // J. Magn. Magn. Mater. 2015. V. 384. P. 247–254.

  10. Kassan-Ogly F.A., Filippov B.N., Murtazaev A.K., Ramazanov M.K., Badiev M.K. Influence of field on frustrations in low-dimensional magnets // J. Magn. Magn. Mater. 2012. V. 324. P. 3418–3421.

  11. Ramazanov M.K., Murtazaev A.K., Magomedov M.A. Phase diagrams and ground-state structures of the Potts model on a triangular lattice // Physica A. 2019. V. 521. P. 543–550.

  12. Murtazaev A.K., Ramazanov M.K., Kurbanova D.R., Magomedov M.A., Murtazaev K.Sh. Phase diagrams and ground-state structures of the antiferromagnetic materials on a body-centered cubic lattice // Mater. Lett. 2019. V. 236. P. 669–671.

  13. Ramazanov M.K., Murtazaev A.K., Magomedov M.A., Badiev M.K. Phase transitions and thermodynamic properties of antiferromagnetic Ising model with next-nearest-neighbor interactions on the Kagomé lattice // Phase Trans. 2018. V. 91. P. 610–618.

  14. Ramazanov M.K., Murtazaev A.K., Investigation of critical phenomena of the frustrated Ising model on a cubic lattice with next-nearest-neighbor intralayer interactions by the Monte Carlo method // Phase Trans. 2018. V. 91. P. 83–91.

  15. Ramazanov M.K., Murtazaev A.K., Badiev M.K. Critical properties of the two-dimensional Ising model on a square lattice with competing interactions // Phys. B: Cond. Matt. 2015. V. 476. P. 1–5.

  16. Ramazanov M.K., Murtazaev A.K., Magomedov M.A. Thermodynamic, critical properties and phase transitions of the Ising model on a square lattice with competing interactions // Solid State Comm. 2016. V. 233. P. 35–40.

  17. Mitsutake A., Sugita Y., Okamoto Y. Generalized-ensemble algorithms for molecular simulations of biopolymers // Biopolymers (Peptide Science). 2001. V. 60. P. 96–123.

  18. Wang F., Landau D.P. Determining the density of states for classical statistical models: a random walk algorithm to produce a flat histogram // Phys. Rev. E. 2001. V. 64. P. 056101–1-056101–16.

  19. Binder K., Wang J.-Sh. Finite-size effects at critical points with anisotropic correlations: Phenomenological scaling theory and Monte Carlo simulations // J. Stat. Phys. 1989. V. 55. P. 87–126.

  20. Binder K., Heermann H.W. Monte Carlo Simulation in Statistical Physics. Springer-Verlag, 1988; M.: Nauka, 1995. 128 p.

  21. Wang F., Landau D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States // Phys. Rev. Lett. 2001. V. 86. P. 2050–2053.

  22. Murtazaev A.K., Magomedov M.A., Ramazanov M.K. Phase diagram and structure of the ground state of the antiferromagnetic Ising model on a body-centered cubic lattice // JETP Lett. 2018. V. 107. P. 259–263.

  23. Ignatenko A.N., Katanin A.A., Irkhin V.Yu. Strong fluctuations near the frustration point in cubic lattice ferromagnets with localized moments // JETP Lett. 2013. V. 97. P. 209–213.

  24. Brazovskii S.A., Dzyaloshinskii I.E., Kukharenko B.G. First-order magnetic phase transitions and fluctuations // JETP. 1976. V. 43. P. 1178–1183.

  25. Ignatenko A.N., Irkhin V.Yu. Frustrated Heisenberg Antiferromagnets on Cubic Lattices: Magnetic Structures, Exchange Gaps, and Non-Conventional Critical Behaviour // J. of Siberian Federal University. Mathematics & Physics. 2016. V. 9. P. 454–458.

  26. Diep H.T., Kawamura H. First-order phase transition in the fcc Heisenberg antiferromagnet // Phys. Rev. B. 1989. V. 40. P. 7019–7022.

  27. Alonso J.L., Tarancon A., Ballesteros H.G., Fernandez L.A., Martın-Mayor V., Munoz Sudupe A. Monte Carlo study of O(3) antiferromagnetic models in three dimensions // Phys. Rev. B. 1996. V. 53. P. 2537–2545.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал