Физика металлов и металловедение, 2021, T. 122, № 12, стр. 1296-1301
Краудион в деформируемом ГЦК-металле. Атомистическое моделирование
С. А. Стариков a, А. Р. Кузнецов a, *, В. В. Сагарадзе a
a Институт физики металлов УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия
* E-mail: a_kuznetsov@imp.uran.ru
Поступила в редакцию 19.05.2021
После доработки 04.08.2021
Принята к публикации 09.08.2021
Аннотация
Краудионы в металлах являются очень подвижными (обеспечивая массоперенос) по сравнению с другими точечными дефектами, что особенно важно при комнатной и более низких температурах. В данной работе теоретически исследовано поведение краудиона в ГЦК-металле (на примере никеля и меди), подвергаемом интенсивной деформации. Показано, что при определенной деформации краудионная конфигурация типа 〈110〉 собственного междоузельного атома становится предпочтительной по сравнению с гантельной в широком диапазоне температур. Поля атомных смещений краудиона описаны в модели Френкеля–Конторовой. Методом молекулярной динамики с использованием функций Грина найдена плотность состояний фононов. Найдена средняя скорость движения краудиона в зависимости от скорости деформации. Показано, что скорость движения краудиона существенно меньше скорости, соответствующей максимальной частоте в плотности состояний фононов, и снижается при снижении скорости деформации, что позволяет выявить характер движения краудиона.
ВВЕДЕНИЕ
Массоперенос точечными дефектами в кристаллических твердых телах, в частности, междоузельными атомами ответствен за многие физические процессы, происходящие во время пластической деформации [1–11] и облучения [12–18]. Роль междоузельных атомов значительно возрастает в неравновесных процессах. Расположенные в плотноупакованных атомных рядах междоузельные атомы называют краудионами. При экспериментальном изучении процесса низкотемпературного деформационно-индуцированного наноструктурирования (в том числе, при криогенных температурах до 77 К) при сдвиге под давлением была показана возможность аномального растворения частиц интерметаллида Ni3Al в матрице аустенитного сплава Fe–Ni–Al [19, 20]. Оценка подвижности различных дефектов, проведенная в данных работах и атомистическое моделирование деформационно-индуцированного растворения частицы [21] указывают на то, что важную роль в процессе растворения может играть краудионный механизм.
Краудионы в металлах изучали довольно интенсивно (см., напр., монографии и обзоры [2, 5, 11, 16, 22–24]) ввиду их важности, однако их поведение в условиях интенсивной деформации прямым атомистическим моделированием изучено недостаточно. Известно [23, 25], что неподвижный краудион нестабилен в ГЦК-металле при конечной температуре, существует временно, пока энергия междоузельного атома не понизится, например, энергия выбитого атома при облучении. Затем междоузельный атом переходит в гантельную конфигурацию или на стоки. По-видимому, учитывая это, а также условия образования краудионов при облучении, моделирование методом молекулярной динамики (МД) движения краудиона в ГЦК-металле при деформации авторы проводили, задавая сравнительно высокие начальные скорости краудиона, близкие к скорости звука или сверхзвуковые [5, 11]. Изучение движения краудиона в интенсивно деформируемом ГЦК-металле практически не проводили.
В данной работе изучается поведение краудиона в ГЦК-металле, в качестве которого взяты никель и медь, в процессе интенсивной деформации. Показано, что при интенсивной деформации краудионная конфигурация оказывается предпочтительной даже при неподвижном краудионе, а средняя скорость движения краудиона существенно ниже скорости звука. При наличии внешнего облучения оно должно способствовать образованию дополнительного количества междоузельных атомов и краудионов.
МЕТОД МОДЕЛИРОВАНИЯ
МД-моделирование проведено с использованием пакета LAMMPS [26] и программы визуализации OVITO [27]. Использованы межатомные потенциалы Ni из работы [28] и Cu [29], построенные в рамках многочастичного метода погруженного атома (embedded atom method, EAM) и доступные к использованию с указанным пакетом. Дополнительно, для расчета фононного спектра и фононной плотности состояний на основе МД-моделирования с использованием метода функций Грина (ФГМД) применена программа FixPhonon [30]. Данные потенциалы для Ni использованы ранее [21], показав свою адекватность для сходных условий моделирования, а потенциалы для Cu брали для расчета фононного спектра Cu методом ФГМД в [30] и хорошо описали экспериментальный фононный спектр. Некоторые расчеты проведены также с использованием других EAM-потенциалов: [31] – для Ni и [32] – для Cu. Результаты оказались близкими к результатам, полученным с помощью основных потенциалов.
Моделирование проводили при постоянной температуре (NVT ансамбль), использован термостат Нозе–Гувера [33, 34]. Для МД-моделирования брали кристаллит в виде куба (с гранями {100}) ~50 000 атомов, а для ФГМД-расчета фононного спектра Cu – триклинная ячейка, содержащая 8 × 8 × 8 примитивных ячеек (512 атомов). Шаг по времени составил 1 фс для МД-моделирования и 2 фс для ФГМД-расчета фононного спектра. В работе [30] показано, что для данного ФГМД-расчета этот шаг является оптимальным). В обоих случаях накладывали периодические граничные условия. Также в обоих случаях проводили предварительный отжиг для получения равновесной структуры.
При МД-моделировании, как и в [21], после предварительного релаксационного отжига кристаллит с частицей подвергали деформации сжатием на 20% (инженерная деформация) вдоль одной из осей (направление $\left\langle {100} \right\rangle $ в кристаллите) с сохранением объема. Использованы различные температуры (0–1200 K) и скорости деформации (2 × 107–8 × 108 с–1). Нижняя граница интервала скорости деформации обусловлена существенным увеличением времени моделирования и компьютерных ресурсов при дальнейшем понижении скорости деформации. Скорость краудиона определяли путем деления пройденного им некоторого расстояния (определяется как разность координат центра краудиона) в кристаллите на время прохождения. Среднюю скорость определяли усреднением скорости по возможно большему числу пройденных краудионом участков в кристаллите.
При МД-моделировании полей атомных смещений краудиона при конечных температурах проводили усреднение по параллельным расчетам деформируемого кристаллита до тех пор (до 12 параллельных расчетов), пока доверительные интервалы полей атомных смещений не переставали изменяться.
РЕЗУЛЬТАТЫ
В работах [15, 16, 22, 24, 35–37] изложены подходы к описанию краудионов (кинков) в кристаллах на основе использования модели Френкеля–Конторовой. Отмечается, что в металлах даже при отсутствии внешнего воздействия экспериментально наблюдается термически активируемое движение нанокластеров внедренных атомов, которые можно представить как ансамбли краудионов. Рассмотрим описание краудиона в модели Френкеля–Конторовой на основе указанных работ. Описывающие краудион уравнения движения можно записать в следующем виде:
(1)
$\begin{gathered} m\frac{{{{d}^{{\text{2}}}}{{u}_{n}}}}{{d{{t}^{2}}}} = \alpha \left( {{{u}_{{n + 1}}} + {{u}_{{n - 1}}} - 2{{u}_{n}}} \right) - \\ - \,\,\frac{{m\omega _{0}^{2}}}{{2\pi }}\sin \left( {\frac{{2\pi {{u}_{n}}}}{a}} \right), \\ \end{gathered} $(2)
$u\left[ {{{n - z(t)} \mathord{\left/ {\vphantom {{n - z(t)} a}} \right. \kern-0em} a}} \right] = \frac{{2a}}{\pi }{\text{arctg}}\left\{ {\exp \left[ {\frac{{na - z(t)}}{{Na}}} \right]} \right\},$Обычно неподвижный краудион нестабилен в ГЦК-металле при конечной температуре, временно существует только движущийся краудион, пока его энергия не понизится, и затем междоузельный атом переходит в гантельную конфигурацию или на стоки [23, 25]. В нашем МД-моделировании после введения междоузельного атома в краудионной конфигурации вдоль направления 〈110〉 цепочка атомов в краудионе релаксировала при конечной температуре, а затем междоузельный атом так же переходил в гантельную конфигурацию вдоль направления 〈100〉. Однако при деформации кристаллита вдоль 〈100〉 около 10% для исследованных скоростей деформации в диапазоне 2 × 107–8 × 108 с–1 и температур, начиная от криогенных до 900 К для меди и до 1200 K для никеля, междоузельный атом спонтанно переходил в краудионную конфигурацию вдоль направления 〈110〉, что говорит об энергетической выгодности краудионной конфигурации. Затем наблюдалось движение краудиона в направлении 〈110〉 в плоскости {100}, параллельной направлению деформирования.
По-видимому, такая величина деформации может достигаться при интенсивной деформации, в частности, наноматериалов, когда генерация дислокаций затруднена.
На рис. 1, 2 приведено сравнение полей атомных смещений краудиона, рассчитанных в МД для никеля и меди и описанных аналитическим решением (2). Показаны поля атомных смещений движущегося краудиона в процессе деформации при различных температурах. Видно, что получено удовлетворительное совпадение результатов МД-расчетов и аналитических кривых (2). На рис. 1 для примера приведена кристаллическая структура краудиона вдоль направления 〈110〉 в никеле при Т = 100 К.
Рис. 1.
Сравнение полей атомных смещений в движущемся краудионе, полученных в МД-моделировании и по формуле (2), при Т = 100 К в Ni (а) с кристаллической структурой краудиона в проекции на плоскость {100} (б) и в Cu (в) (скорость деформации 4 × × 107 с–1).
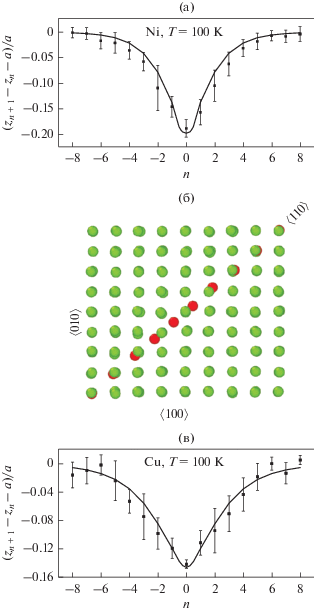
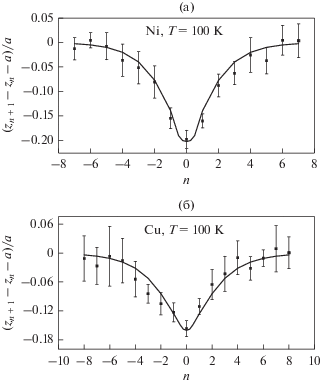
Рис. 2.
Сравнение полей атомных смещений в движущемся краудионе, полученных в МД-моделировании и по формуле (2), при Т = 300 К в Ni (а) и в Cu (б) (скорость деформации 4 × 107 с–1).
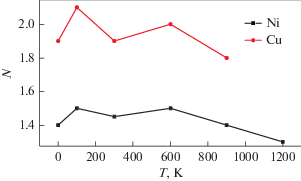
На рис. 3 приведена зависимость параметра N в уравнении (2) от температуры. Видно, что данный параметр остается приблизительно постоянным в широком диапазоне температур с тенденцией к понижению при сравнительно высоких температурах, что, возможно, связано с “размягчением” решетки при высоких температурах. Если принять за средние значения N при не очень высоких температурах величины 1.95 и 1.45 для Cu и Ni соответственно, то их отношение составит 1.35. Величины α и ${{m\omega _{0}^{2}} \mathord{\left/ {\vphantom {{m\omega _{0}^{2}} a}} \right. \kern-0em} a}$ можно рассматривать (следуя [39]) как имеющие смысл модуля нормальной упругости межатомной связи между атомами в данной цепочке и атомами данной цепочки и соседних цепочек соответственно, а величины α/$a$ и ${{m\omega _{0}^{2}} \mathord{\left/ {\vphantom {{m\omega _{0}^{2}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}$ – как пропорциональные модулю нормальной упругости вещества (модулю Юнга). Тогда отношение параметров N для отожженных Cu и Ni, рассчитанных с учетом скорости звука и модуля Юнга в данных металлах [40], составит 1.1, что качественно согласуется с величиной данного отношения 1.35, полученной из данных рис. 3. В данном случае не учитывали близкие m и a данных металлов; для Cu имеем пропорцианальность N $ \propto $ c/E1/2 = (3800 м/с)/(120 × 109 Па)1/2, для Ni N $ \propto $ (4800 м/с)/(210 × 109 Па)1/2. Представляет интерес проверить оценку для соотношения параметров N для других металлов.
Следует отметить, что во всех исследованных нами случаях минимальное расстояние между двумя атомами, нормированное на a, удовлетворяло условию самофокусировки ${{({{z}_{{n + 1}}} - {{z}_{n}})} \mathord{\left/ {\vphantom {{({{z}_{{n + 1}}} - {{z}_{n}})} a}} \right. \kern-0em} a} > {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ [8, 11]. В этом случае краудион может перемещаться на сравнительно большие расстояния.
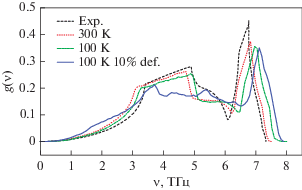
На рис. 4 приведены кривые плотности состояний фононов для недефомированной и деформированной на 10% меди при 300 и 100 К. Видно, что плотность состояний, как и максимальная частота ν, меняются незначительно. Средняя скорость движения краудиона составила около 400 м/с для Ni и Cu при скорости деформации 8 × 108 с–1 с ее понижением приблизительно на порядок при понижении скорости деформации до величины 2 × 107 с–1 (при Т = 100 К).
Оценим скорость краудиона vmax, соответствующую максимальному значению частоты фононов νmax = 8 ТГц (рис. 4) для деформированной меди с помощью соотношения ${{\nu }_{{\max }}} = a{{v}_{{\max }}},$ учитывая, что движение краудиона сопровождается периодическим “столкновением” (возмущением) атомов. Получается величина vmax ≈ 2000 м/с. По-видимому, и для никеля скорость краудиона v, соответствующая максимальному значению частоты νmax, близка к значению 2000 м/с. Исходя из этой оценки, можно сказать, что движение краудиона в условиях нашего моделирования (деформация до 20%, скорости деформации 2 × 107–8 × 108 с–1) для меди и никеля происходит при скоростях v < vmax, когда имеются радиационные потери при движении краудиона. Отметим, что, если частота атомных “столкновений” при движении краудиона превысит максимальную частоту фононного спектра, то излучение фонона движущимся краудионом будет минимально, и энергетические потери будут, в основном, из-за образования ударных волн [41]. МД-моделирование показало, что краудион обычно проходит расстояние порядка десяти a, а затем останавливается, по-видимому, в результате радиационных потерь. Такое движение краудиона повторяется.
Сходную картина движения краудионов (похожее на броуновское движение) наблюдали при конечных температурах в облученных металлах без деформации (см., напр., [16, 36, 37]), что объясняется взаимодействием краудионов с фононными возбуждениями. В [37] показано, что возникающая при движении краудиона сила торможения не зависит от температуры, т.к. колебания решетки в дискретном кристалле не являются независимыми от движения дефекта. Представляет интерес описать движение краудиона в рамках теории взаимодействия краудиона с фононными возбуждениями [37]. Возможность применения данной теории в случае деформируемого металла, по-видимому, потребует, по крайней мере, некоторой ее адаптации.
Теоретически исследовано поведение краудиона в деформируемом ГЦК-металле на примере никеля и меди. Показано, что при деформации около 10% в условиях моделирования краудионная конфигурация типа 〈110〉 собственного междоузельного атома становится предпочтительной по сравнению с гантельной в широком диапазоне температур. Поля атомных смещений краудиона описаны в модели Френкеля–Конторовой. Получена зависимость безразмерной ширины краудиона (параметра N модели) от температуры, относительное изменение параметра N для никеля и меди оценено, исходя из физических свойств металлов. Методом молекулярной динамики с использованием функций Грина найдена плотность состояний фононов в недеформированной и деформированной на 10% меди, показано, что максимальная частота меняется несущественно. Найдена средняя скорость движения краудиона в зависимости от скорости деформации в диапазоне 2 × 107–8 × 108 с–1. Показано, что скорость движения краудиона существенно меньше скорости, соответствующей максимальной частоте в плотности состояний фононов, и снижается при снижении скорости деформации, что позволяет выявить характер движения краудиона. Характер движения краудиона соответствует генерации излучения фононов. Найдено, что при движении краудиона в широком диапазоне температур удовлетворяется условие самофокусировки, что позволяет перемещаться краудиону на значительные по сравнению с параметром решетки расстояния. Таким образом повышается возможность массопереноса.
Работа выполнена в рамках государственного задания МИНОБРНАУКИ России (тема “Структура”, № АААА-А18-118020190116-6). Расчеты проведены с использованием суперкомпьютера “Уран” ИММ УрО РАН.
Список литературы
Инденбом В.Л. Межузельный (краудионный) механизм пластической деформации и разрушения // Письма в ЖЭТФ. 1970. Т. 12. Вып. 11. С. 526–528.
Головин Ю.И. Наноиндентирование и механические свойства твердых тел в субмикрообъемах, тонких приповерхностных слоях и пленках // ФТТ. 2008. Т. 50. Вып. 12. С. 2113–2142.
Нацик В.Д., Смирнов С.Н. Дислокации и краудионы в двумерных кристаллах. Часть III: Пластическая деформация кристалла как результат перемещения дефектов и их взаимодействие с полем упругих напряжений // ФНТ. 2016. Т. 42. № 3. С. 268–282.
Нацик В.Д., Смирнов С.Н., Белан В.И., Компьютерное моделирование и аналитическое описание дефектов структуры в двумерных кристаллах ограниченных размеров: свободная граница, дислокации, краудионы // ФНТ. 2018. Т. 44. № 7. С. 877–886.
Маркидонов А.В., Захаров П.В., Старостенков М.Д., Медведев Н.Н. Механизмы кооперативного поведения атомов в кристаллах. Новокузнецк: Филиал КузГТУ, 2016. 219 с.
Salehinia I., Bahr D.F. The impact of a variety of point defects on the inception of plastic deformation in dislocation-free metals // Scripta Mater. 2012. V. 66. P. 339–342.
Korbel A., Bochniak W. Stratified plastic flow in metals // International Journal of Mechanical Sciences. 2017. V. 128–129. P. 269–276.
Dmitriev S.V., Medvedev N.N., Chetverikov A.P., Zhou K., Velarde M.G. Highly Enhanced Transport by Supersonic N-Crowdions // Phys. Status Solidi RRL 2017, 1700298.
Дмитриев С.В., Корзникова Е.А., Четвериков А.П. Сверхзвуковые n-краудионы в двумерном кристалле морзе // ЖЭТФ. 2018. Т. 153. Вып. 3. С. 417–423.
Moradi Marjaneh A., Saadatmand D., Evazzade I., Babicheva R.I., Soboleva E.G., Srikanth N., Kun Zhou, Korznikova E.A., Dmitriev S.V. Mass transfer in the Frenkel–Kontorova chain initiated by molecule impact // Phys. Rev. E. 2018. V. 98. P. 023003.
Bayazitov A.M., Korznikova E.A., Shepelev I.A., Chetverikov A.P., Khadiullin S.Kh., Sharapov E.A., Zakha-rov P.V., Dmitriev S.V. Scenarios of mass transfer in fcc copper: the role of point defects // IOP Conf. Series: Mater. Sci. Eng. 2018. V. 447. 012040.
Арбузов В.Л., Гощицкий Б.Н., Сагарадзе В.В., Данилов С.Е., Карькин А.Е. Накопление и отжиг радиационных дефектов при электронном и нейтронном низкотемпературных облучениях в дуо-стали и сплавах Fe–Cr // ФММ. 2010. Т. 110. № 4. С. 384–395.
Арбузов В.Л., Гощицкий Б.Н., Сагарадзе В.В., Данилов С.Е., Зуев Ю.Н., Карькин А.Е., Пархоменко В.Д., Козлов А.В., Чернов В.М. Накопление и отжиг радиационных дефектов и влияние водорода на физко-механические свойства ванадиевых сплавов V4Ti4Cr и V10Ti5Cr при низкотемпературном (77 K) нейтронном облучении // ФММ. 2016. Т. 117. № 3. С. 311–317.
Данилов С.Е., Арбузов В.Л., Печеркина Н.Л., Сагарадзе В.В. Сепарация радиационных дефектов в деформированном никеле // ФММ. 2015. Т. 116. № 7. С. 750–756.
Dudarev S.L. Coherent motion of interstitial defects in a crystalline material // Phil. Mag. 2003. V. 83. Nos. 31–34. P. 3577–3597.
Derlet P. M., Nguyen-Manh D., Dudarev S.L. Multiscale modeling of crowdion and vacancy defects in body-centered-cubic transition metals // Phys. Rev. B. 2007. V. 76. P. 054107.
Swinburne T.D., Ma P.-W., Dudarev S.L. Low temperature diffusivity of self-interstitial defects in tungsten // New J. Phys. 2017. V. 19. P. 073024.
Toijer E., Messina L., Domain C., Vidal J., Becquart C.S., Olsson P. Solute-point defect interactions, coupled diffusion, and radiation-induced segregation in fcc nickel // Phys. Rev. Mater. 2021. V. 5. P. 013602.
Sagaradze V.V., Shabashov V.A., Kataeva N.V., Zavalishin V.A., Kozlov K.A., Kuznetsov A.R., Litvinov A.V., Pilyugin V.P. Deformation-induced dissolution of the intermetallics Ni3Ti and Ni3Al in austenitic steels at cryogenic temperatures // Phil. Mag. 2016. V. 96. № 17. P. 1724–1742.
Sagaradze V.V., Shabashov V.A., Kataeva N.V., Kozlov K.A., Kuznetsov A.R., Litvinov A.V. Anomalous diffusion processes “dissolution-precipitation” of γ' Phase Ni3Al in Fe–Ni–Al alloy during low temperature deformation // Mater. Lett. 2016. V. 172. P. 207–210.
Кузнецов А.Р., Стариков С.А., Сагарадзе В.В., Карькина Л.Е. Деформационно-индуцированное растворение частицы Ni3Al в никеле. атомистическое моделирование // ФММ. 2019. Т. 120. № 12. С. 1286–1291.
Браун О.М., Кившарь Ю.С. Модель Френкеля-Конторовой. Концепции, методы, приложения. М.: ФИЗМАТЛИТ, 2008. 536 с.
Кирсанов В. В., Орлов А. Н. Моделирование на ЭВМ атомных конфигураций дефектов в металлах // УФН. 1984. Т. 142. Вып. 2. С. 219–264.
Kosevich A.M. The crystal lattice: phonons, solitons, dislocations, superlattices. Berlin: Wiley-VCH, 2005. 345 p.
Was G.S. Fundamentals of Radiation Materials Science. Metals and Alloys. Berlin, Heidelberg, N.Y.: Springer, 2007. 827 p.
Plimpton S. Fast parallel algorithms for short-range molecular dynamics // J. Comp. Phys. 1995. V. 117. P. 1–19.
Stukowski A. Visualization and analysis of atomistic simulation data with OVITO – the Open Visualization Tool // Modelling Simul. Mater. Sci. Eng. 2010. V. 18. P. 015012.
Purja Pun G.P., Mishin Y. Development of an interatomic potential for the Ni–Al system // Phil. Mag. 2009. V. 89. № 34–36. P. 3245–3267.
Foiles S.M., Baskes M.I., Daw M.S. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys // Phys. Rev. B. 1986. V. 33. P. 7983.
Kong L.T. Phonon dispersion measured directly from molecular dynamics simulations // Computer Physics Communications. 2011. V.182. P. 2201–2207.
Baskes M.I., Shaz X., Angelox J.E., Moody N.R. Trapping of hydrogen to lattice defects in nickel // Modelling Simul. Mater. Sci. Eng. 1997. V. 5. P. 651–652.
Mishin Y., Mehl M.J., Papaconstantopoulos D.A., Voter A.F., Kress J.D. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations // Phys. Rev. B. 2001. V. 63. P. 224106.
Nosé S. A unified formulation of the constant temperature molecular-dynamics methods // J. Chem.l Phys. 1984. V. 81(1). P. 511–519.
Hoover W.G. Canonical dynamics: Equilibrium phase-space distributions // Phys. Rev. A. 1985. V. 31(3). P. 1695–1697.
Gornostyrev Yu.N., Katsnelson M.I., Kravtsov A.V., Trefilov A.V. Fluctuation-induced nucleation and dynamics of kinks on dislocation: Soliton and oscillation regimes in the two-dimensional Frenkel–Kontorova model // Phys. Rev. B. 1999. V. 60. P. 1013.
Dudarev S.L. The non-Arrhenius migration of interstitial defects in bcc transition metals // C. R. Physique. 2008. V. 9. P. 409–417.
Swinburne T.D., Dudarev S.L. Phonon drag force acting on a mobile crystal defect: Full treatment of discreteness and nonlinearity // Phys. Rev. B. 2015. V. 92. P. 134302.
Nicklow R.M., Gilat G., Smith H.G., Raubenheimer L.J., Wilkinson M.K. Phonon frequencies in copper at 49 and 298 K // Phys. Rev. 1967. V. 164. P. 922.
Орлов А.Н. Введение в теорию дефектов в кристаллах. М.: Высшая школа, 1983. 144 с.
Физические величины: Справочник, Под ред. И.С. Григорьева и Е.З. Мейлихова, М.: Энергоатомиздат, 1991. 1232 с.
Korznikova E.A., Sunagatova I.R., Bayazitov A.M., Semenov A.S., Dmitriev S.V. Effect of interatomic potentials on mass transfer by supersonic 2-crowdions // Letters on Mater. 2019. V. 9(4). P. 386–390.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение