Физика металлов и металловедение, 2021, T. 122, № 2, стр. 83-90
Влияние фокусировки фононов на термоэдс увлечения в монокристаллических нанопроводах калия при низких температурах
И. И. Кулеев a, *, И. Г. Кулеев a
a Институт физики металлов УрО РАН
620108 Екатеринбург, ул. С. Ковалевской, 18, Россия
* E-mail: kuleev@imp.uran.ru
Поступила в редакцию 21.08.2020
После доработки 30.09.2020
Принята к публикации 02.10.2020
Аннотация
Проанализирована роль сдвиговых волн и влияние фокусировки фононов на анизотропию термоэдс электрон-фононного увлечения в монокристаллических нанопроводах калия при низких температурах. Для продольных компонент упругих мод использована теория деформационного потенциала. Для сдвиговых компонент колебательных мод использована константа электрон-фононного взаимодействия, определенная ранее из сопоставления результатов расчета термоэдс с экспериментальными данными для объемных кристаллов калия. Показано, что сдвиговые волны вносят значительный вклад в термоэдс увлечения нанопроводов. В режиме кнудсеновского течения фононного газа для нанопроводов со стороной сечения D = 5 × 10–6 см вклад медленной поперечной моды t2 при учете только продольной компоненты в направлениях [111] оказался на 32% меньше, а при учете сдвиговой компоненты моды t2 он – на 12% больше, чем вклад продольных фононов. Определены направления, соответствующие максимальным и минимальным значениям термоэдс увлечения нанопроводов. Показано, что в условиях конкуренции граничного и объемных механизмов релаксации фононов с увеличением поперечного сечения нанопроводов анизотропия термоэдс увлечения изменяется немонотонным образом Она превышает 30%, не только в режиме кнудсеновского течения фононного газа, но и при толщине образцов на два порядка большей. Это делает анизотропию термоэдс доступной для экспериментальных исследований.
1.ВВЕДЕНИЕ
В работах [1–4] было проанализировано влияние фокусировки фононов на термоэдс увлечения и решеточную теплопроводность объемных кристаллов калия и наноструктур на его основе, а также определен спектр и вектора поляризации фононов. В этих работах при анализе термоэдс и решеточной теплопроводности предполагали, что квазипоперечные фононы в кристаллах калия могут взаимодействовать с электронами только благодаря их продольной компоненте, а константа деформационного потенциала E0λ одинакова для всех колебательных мод. Согласно [5–7], E0λ ≈ ≈ (n/N(εF)) = (2/3)εF ≈ 1.41 эВ, $n$ – концентрация электронов, N(εF) – плотность состояний на уровне Ферми. Было показано, что при низких температурах вклад медленных квазипоперечных мод в термоэдс увлечения в кристаллах калия, который ранее не учитывали (см. [8–12]), на порядок величины превышал вклад продольных фононов. Однако оказалось, что этого приближения недостаточно для объяснения экспериментальных данных [11]. Расчет термоэдс увлечения объемных кристаллов калия в работе [4] интервале Т = 1–3 К дал значения, почти в два раза меньшие данных работы [11].
В работе [13] впервые учтено влияние сдвиговых волн на электрон-фононную релаксацию и термоэдс увлечения в металлах при низких температурах. Из сопоставления результатов расчета термоэдс и решеточной теплопроводности в объемных кристаллах калия с экспериментальными данными [11] в работе [13] определена константа электрон-фононного взаимодействия для сдвиговых компонент колебательных мод E0t = 0.11 эВ. Она оказалась на порядок величины меньше, чем следует из теории деформационного потенциала для продольных компонент [5–7]: E0L ≈ (n/N(εF)) = = (2/3)εF ≈ 1.41 эВ, $n$ – концентрация электронов, N(εF) – плотность состояний на уровне Ферми. На необходимость учета влияния сдвиговых волн на электрон-фононную релаксацию в щелочных металлах указывал Займан в [5, 14]. Поскольку сфера Ферми в щелочных металлах подходит достаточно близко к границе зоны Бриллюэна, то должна деформироваться в соответствии с симметрией решетки. Благодаря анизотропии спектра фермиевские электроны получают возможность взаимодействовать со сдвиговыми деформациями, т.е. с поперечной компонентой колебательных мод (см. [5, 15]). Однако отклонение поверхности Ферми от сферической в кристаллах калия мало, оно составляет 7%. Поэтому полученное в [13] соотношение констант E0L и E0t не является удивительным. Оно существенно отличается от полупроводниковых кристаллов, где благодаря значительно большей анизотропии спектра носителей тока константа E0t на два порядка больше, и, как правило, превышает значение E0L для продольных фононов мод (см., напр., [15, 16]).
Основной целью настоящей работы является анализ влияния сдвиговых волн на анизотропию термоэдс увлечения в монокристаллических нанопроводах калия при низких температурах. Полученные в работе результаты открывают новые перспективы для экспериментальных исследований электрон-фононной релаксации в щелочных и благородных металлах, а также влияния фокусировки фононов на термоэдс увлечения в нано-структурах на их основе.
2. ЭЛЕКТРОН-ФОНОННАЯ РЕЛАКСАЦИЯ В УПРУГО-АНИЗОТРОПНЫХ КРИСТАЛЛАХ
Ранее при исследовании электрон-фононного увлечения в металлах для фононов использовали модель изотропной среды (см., напр., [8–12, 17–19]). В этой модели электроны могут взаимодействовать только с продольными фононами. В упруго-анизотропных кристаллах распространяются квазипродольные и квазипоперечные колебания, которые не являются ни чисто продольными, ни чисто поперечными: их вектора поляризации ${{{\mathbf{e}}}^{\lambda }}({\mathbf{q}})$ не совпадают ни с направлением волнового вектора q, ни с нормалью к нему [20–22]. Индекс поляризации L соответствует продольным фононам, t1 и t2 – соответственно “быстрой” и “медленной” поперечным модам. Значения модулей упругости второго порядка при T = 4.2 K взяты из работы [21]. В упруго-анизотропных металлах квазипоперечные фононы могут взаимодействовать с электронами и вносить вклад в термоэдс увлечения за счет продольной компоненты, которая определяется скалярным произведением $\left( {{{{\mathbf{e}}}^{{\lambda }}}{\mathbf{n}}} \right),$ n = (q/q) – единичный волновой вектор фонона. В работе [13] сформулирован феноменологический метод, который позволяет учесть влияние сдвиговых волн на электрон-фононную релаксацию и термоэдс увлечения в металлах. Он основан на том, что поле смещений в упругой среде u = A eλ(q)exp(i(ωt – qr)) можно представить в виде суммы двух слагаемых: первое из них характеризует потенциальное поле, обусловленное деформациями сжатия и растяжения, – поле смещений для продольных волн, а второе– вихревое поле, обусловленное сдвиговыми деформациями, для поперечных волн (см. подробнее [21], раздел 3):
(1)
${\mathbf{u}} = \nabla \psi + {\text{ }}[\nabla \times \chi ] \Rightarrow {\mathbf{n}}({{{\mathbf{e}}}^{\lambda }}{\mathbf{n}}){\text{ }} + {\text{ }}[{{{\mathbf{e}}}^{\lambda }}{\mathbf{n}}].$Поэтому согласно [13] фурье-образ матричного элемента электрон-фононного взаимодействия при выделении продольных и поперечных компонент векторов поляризации колебательных мод можно представить в виде:
(2)
$\begin{gathered} {{\left. {\left| {C_{q}^{{\lambda }}(\theta ,\varphi )} \right.} \right|}^{2}} = {{\left( {C_{0}^{{\lambda }}(\theta ,\varphi )} \right)}^{2}}q,\,\,\,\,{{\left( {C_{0}^{{\lambda }}(\theta ,\varphi )} \right)}^{2}} \cong \\ \cong {{{{{\left( {E_{{{\text{eff}}}}^{{\lambda }}} \right)}}^{2}}\hbar } \mathord{\left/ {\vphantom {{{{{\left( {E_{{{\text{eff}}}}^{{\lambda }}} \right)}}^{2}}\hbar } {{{S}^{{\lambda }}}(\theta ,\varphi )\rho }}} \right. \kern-0em} {{{S}^{{\lambda }}}(\theta ,\varphi )\rho }},\,\,\,\, \\ {{\left( {E_{{{\text{eff}}}}^{{\lambda }}} \right)}^{2}} = \left( {E_{{0L}}^{2}{{{\left( {{{{\mathbf{e}}}^{{\lambda }}}{\mathbf{n}}{\text{ }}} \right)}}^{2}} + E_{{0t}}^{2}\left( {{{{\left[ {{{{\mathbf{e}}}^{{\lambda }}}{\mathbf{n}}} \right]}}^{2}}} \right)} \right). \\ \end{gathered} $Фазовые скорости фононов ${{S}^{{\lambda }}}(\theta ,\varphi )$ определены в работах [1–3].
Отметим, что в отличие от модели изотропной среды, эффективная константа связи ${{\left( {E_{{{\text{eff}}}}^{{\lambda }}(\theta ,\varphi )} \right)}^{2}}$ является функцией углов θ и φ, которые определяются квадратами продольных и поперечных компонент векторов поляризаций (см. табл. 1). Для продольных фононов отклонение от изотропного распределения малы, они не превышает 10% (см. [13], рис. 1). Однако для медленной поперечной моды величина ${{\left( {E_{{{\text{eff}}}}^{{t2}}(\theta ,\varphi )} \right)}^{2}}$ меняется достаточно резко за счет вклада продольной компоненты, тогда как вклад сдвиговой компоненты остается практически изотропным (см. [13], рис. 1, кривая 3).
Таблица 1.
Средние значения продольных и поперечных компонент колебательных мод, а также их безразмерных скоростей релаксации на электронах, согласно формуле (6)
| Переменная | L | T1 | T2 |
|---|---|---|---|
| $\left\langle {{{{\left( {{{{\mathbf{e}}}^{{\lambda }}}{\mathbf{n}}} \right)}}^{2}}} \right\rangle $ | 0.9649 | 0.0028 | 0.0323 |
| $\left\langle {{{{\left[ {{{{\mathbf{e}}}^{{\lambda }}}{\mathbf{n}}} \right]}}^{2}}} \right\rangle $ | 0.0351 | 0.9972 | 0.9677 |
| $\left\langle {\left| {\left[ {{{{\mathbf{e}}}^{{\lambda }}}{\mathbf{n}}} \right]} \right|({{{\mathbf{e}}}^{{\lambda }}}{\mathbf{n}})} \right\rangle $ | 2.8591 × 10–6 | 6.91 × 10–9 | 1.18 × 10–8 |
| $\left\langle {\nu _{{pe\_L}}^{{ * {\lambda }}}(\theta ,\varphi )} \right\rangle $ | 9.969 × 104 | 287 | 3.33 × 103 |
| $\left\langle {\nu _{{pe\_T}}^{{ * {\lambda }}}(\theta ,\varphi )} \right\rangle $ | 627 | 608 | |
| $\left\langle {\nu _{{pe}}^{{ * {\lambda }}}(\theta ,\varphi )} \right\rangle $ | 9.969 × 104 | 914 | 3.94 × 103 |
Рис. 1.
Угловые зависимости средних длин пробега $\Lambda _{{[I({\psi })]}}^{{\{ J\} }}$ (кривые 4), а также длин пробега продольных (кривые 3), быстрых (кривые 2) и медленных квазипоперечных фононов (кривые 1), рассчитанных в режиме граничного рассеяния, для образцов калия с квадратным сечением D = 5 × 10–6 см и длиной L = 50 D в случаях, когда градиент температуры вращается в плоскости грани куба (а), в диагональной плоскости (б).

3. РОЛЬ СДВИГОВЫХ ВОЛН В ТЕРМОЭДС УВЛЕЧЕНИЯ НАНОПРОВОДОВ ИЗ КРИСТАЛЛОВ КАЛИЯ
Детали расчета термоэдс увлечения приведены в работах [2–4], поэтому их здесь мы не воспроизводим, а ограничимся конечными выражениями:
(3)
$\begin{gathered} {{\alpha }_{{{\text{drag}}}}} = \frac{{{{k}_{{\text{B}}}}}}{e}\sum\limits_{\lambda } 3 \left\langle {\int\limits_0^\infty {{{{\left( {Z_{q}^{{\lambda }}} \right)}}^{3}}{\text{th}}\left( {{{Z_{q}^{{\lambda }}} \mathord{\left/ {\vphantom {{Z_{q}^{{\lambda }}} 2}} \right. \kern-0em} 2}} \right)dZ_{q}^{{\lambda }}} } \right. \times \\ \left. { \times \,\,\left( {\frac{{\nu _{{eph0}}^{{\lambda }}\left( {{{k}_{{\text{F}}}},q_{T}^{{\lambda }}} \right)}}{{\nu _{{ph}}^{{\lambda }}(q)}}} \right)\left( {\frac{{T_{{\delta }}^{{\lambda }}}}{T}} \right)\left\{ {\tilde {V}_{{g3}}^{{\lambda }}{{n}_{{q3}}}} \right\}} \right\rangle , \\ T_{{\delta }}^{{\lambda }} = {{2{{m}_{F}}{{{\left( {{{S}^{{\lambda }}}(\theta ,\varphi )} \right)}}^{2}}} \mathord{\left/ {\vphantom {{2{{m}_{F}}{{{\left( {{{S}^{{\lambda }}}(\theta ,\varphi )} \right)}}^{2}}} {{{k}_{{\text{B}}}}}}} \right. \kern-0em} {{{k}_{{\text{B}}}}}},\,\,\,\,q_{T}^{{\lambda }} = \frac{{{{k}_{{\text{B}}}}T}}{{\hbar {{S}^{{\lambda }}}(\theta ,\varphi )}}, \\ \left\langle {A(\theta ,\varphi )} \right\rangle = \frac{1}{{4\pi }}\int {d{{\Omega }_{q}}A(\theta ,\varphi )} ,\,\,\,\,Z_{q}^{{\lambda }} = \frac{{\hbar \omega _{q}^{{\lambda }}}}{{{{k}_{{\text{B}}}}T}}. \\ \end{gathered} $Здесь kB – постоянная Больцмана, Т – температура, $\tilde {V}_{{g3}}^{{\lambda }}$ и ${{n}_{{q3}}}$ – проекции групповой скорости и единичного волнового вектора фонона на направление градиента температур.
(4)
$\nu _{{eph0}}^{{\lambda }}\left( {{{k}_{{\text{F}}}},q_{{\text{T}}}^{{\lambda }}} \right) = \frac{{m({{\varepsilon }_{{\text{F}}}}){{{\left( {C_{0}^{{\lambda }}} \right)}}^{2}}}}{{2\pi {{\hbar }^{3}}k_{{\text{F}}}^{3}}}{{\left( {q_{{\text{T}}}^{{\lambda }}} \right)}^{5}}N_{{q{\lambda }}}^{0}\left( {N_{{q{\lambda }}}^{0} + 1} \right).$Здесь $N_{{q{\lambda }}}^{0}$ – функция Планка, фурье-компонента ${{\left( {C_{0}^{{\lambda }}(\theta ,\varphi )} \right)}^{2}}$ определена выражением (2). В работах [8–11] исследования термоэдс и решеточной теплопроводности проводили на кристаллах калия с концентрацией электронов ne = 1.4 × 1022 см–3, kF = 0.75 × 108 см–1, эффективной массой mF = = 1.1m0 (m0 – масса свободного электрона), εF ≈ ≈ 2.12 эВ, ρ ≈ 0.91 × 108 г см–3. Для актуальных механизмов рассеяния скорость релаксации фононов может быть представлена в виде [1–4]:
(5)
$\begin{gathered} \nu _{{ph}}^{{\lambda }}(q,\theta ,\varphi ) = \nu _{{{\text{phB}}}}^{{\lambda }}(\theta ,\varphi ) + \frac{{{{k}_{{\text{B}}}}T}}{\hbar }Z_{q}^{{\lambda }}\left[ {\nu _{{pde}}^{{ * {\lambda }}}(\theta ,\varphi } \right] + \\ + \,\,\nu _{{phi}}^{{\lambda }}(q,\theta ,\varphi ),\,\,\,\,\nu _{{pde}}^{{ \bullet {\lambda }}} = \left[ {\nu _{{pd}}^{{ * {\lambda }}}(\theta ,\varphi ) + \nu _{{pe}}^{{ * {\lambda }}}(\theta ,\varphi )} \right]. \\ \end{gathered} $Здесь $\nu _{{pB}}^{{\lambda }}(\theta ,\varphi )$ и $\nu _{{pi}}^{{\lambda }}(q,\theta ,\varphi )$ – скорости релаксации фононов на границах и изотопическом беспорядке (см. [1–4]). Согласно оценкам [1, 2, 11], вклад изотопического рассеяния в теплосопротивление кристаллов калия при Т = 2 К мал, составляет менее 1.5%. Параметры $\nu _{{pe}}^{{ * {\lambda }}}(\theta ,\varphi )$ и $\nu _{{pd}}^{{ * {\lambda }}}(\theta ,\varphi )$ являются безразмерными скоростями релаксации фононов на электронах и дислокациях [1, 4]. Согласно [1, 2], $\nu _{{pd}}^{{ * {\lambda }}}(\theta ,\varphi )$ ≅ $2.03 \times {{10}^{{ - 4}}}{{\tilde {N}}_{d}},$ ${{N}_{d}} = {{10}^{{11}}}\,\,{\text{с}}{{{\text{м}}}^{{ - 2}}} \times {{\tilde {N}}_{d}}$ – концентрация дислокаций, параметр ${{\tilde {N}}_{d}}$ для образцов с различной степенью деформации определен в [13] (см. табл. 1). Скорость релаксации фононов с поляризацией λ на электронах можно представить в виде:
(6)
$\nu _{{pe}}^{{ * {\lambda }}}(\theta ,\varphi ) = m_{{\text{F}}}^{2}{{{{{\left( {C_{0}^{{\lambda }}(\theta ,\varphi )} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {C_{0}^{{\lambda }}(\theta ,\varphi )} \right)}}^{2}}} {2\pi {{\hbar }^{4}}}}} \right. \kern-0em} {2\pi {{\hbar }^{4}}}}.$Как видно из табл. 2 , скорость релаксации продольных фононов на электронах в 25 раз больше, чем для моды t2. Из (5) видно, при понижении температуры роль рассеяния на дислокациях и электронах уменьшается.
Рассмотрим влияние фокусировки фононов на анизотропию термоэдс увлечения в нанопроводах с квадратным сечением D = 5 × 10–6 см и длиной L = 50 D в режиме граничного рассеяния. В этом случае размерное квантование электронного спектра можно не учитывать, поскольку поперечные размеры нанопровода D гораздо больше длины волны электрона:энергия Ферми εF ≅ 2.12 эВ, длина волны фермиевского электрона ~(10–8–10–7) см, что гораздо меньше поперечного размера нанопровода. Анализ, проведенный в работе [23] (см. также [24]) показал, что для нанопроводов с диаметрами большими 50 нм в интервале температур от 20 до 50 К теплопроводность следовала зависимости $\kappa (T)\sim {{T}^{3}},$ как и теплоемкость объемных образцов в теории Дебая. Поэтому при указанных ограничениях влиянием пространственного конфаймента на спектр акустических мод можно пренебречь и использовать модель анизотропного континуума для анализа фононного транспорта в нанопроводах.
В этом случае термоэдс увлечения нанопроводов может быть представлена в виде:
(7)
$\begin{gathered} {{\alpha }_{{{\text{drag}}}}} = {{J}_{4}}\frac{{{{k}_{{\text{B}}}}}}{e}\sum\limits_{\lambda } {\left( {\frac{{{{{\left( {{{m}_{{\text{F}}}}} \right)}}^{2}}{{{\left( {{{k}_{{\text{B}}}}T} \right)}}^{4}}}}{{n_{e}^{3}{{\hbar }^{8}}}}} \right)\left( {\frac{1}{{4\pi }}} \right)\int {d{{\Omega }_{q}}} } \times \\ \times \,\,\left( {\frac{{{{{\left( {C_{0}^{{\lambda }}(\theta ,\varphi )} \right)}}^{2}}\tilde {V}_{{g3}}^{{\lambda }}{{n}_{{q3}}}}}{{\nu _{{phB}}^{{\lambda }}(q){{{\left( {{{S}^{{\lambda }}}(\theta ,\varphi )} \right)}}^{3}}}}} \right),\,\,\,\,{{J}_{4}} = \left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right) \times \\ \times \,\,\int\limits_0^\infty {{{{{{\left( {Z_{q}^{{\lambda }}} \right)}}^{4}}{\text{th}}\left( {{{Z_{q}^{{\lambda }}} \mathord{\left/ {\vphantom {{Z_{q}^{{\lambda }}} 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{{{{\left( {Z_{q}^{{\lambda }}} \right)}}^{4}}{\text{th}}\left( {{{Z_{q}^{{\lambda }}} \mathord{\left/ {\vphantom {{Z_{q}^{{\lambda }}} 2}} \right. \kern-0em} 2}} \right)} {{{{\left( {{\text{sh}}({{{{Z}_{q}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}} 2}} \right. \kern-0em} 2})} \right)}}^{2}}dZ_{q}^{{\lambda }}}}} \right. \kern-0em} {{{{\left( {{\text{sh}}({{{{Z}_{q}}} \mathord{\left/ {\vphantom {{{{Z}_{q}}} 2}} \right. \kern-0em} 2})} \right)}}^{2}}dZ_{q}^{{\lambda }}}}} \equiv 24.1. \\ \end{gathered} $В этом пределе термоэдс увлечения в нанопроводах будет анизотропной и следовать зависимости ${{\alpha }_{{{\text{drag}}}}} \approx {{В}_{2}}{{T}^{4}}$ ([2, 3]). Однако при доминирующей роли объемных механизмов релаксации фононов на электронах и дислокациях термоэдс увлечения в калии будет изотропной и следовать асимптотики ${{\alpha }_{{{\text{drag}}}}}(Т) \approx А{{T}^{3}}$ [4–13]. Скорости релаксации фононов на границах определяются кусочно-гладкими функциями для различных интервалов углов, определяемых соотношениями между компонентами групповой скорости и геометрическим параметром ${{k}_{0}} = {L \mathord{\left/ {\vphantom {L {2D}}} \right. \kern-0em} {2D}}$ [2, 24]. При выполнении неравенств $\left| {V_{{g1}}^{{\lambda }}} \right| > \left| {V_{{g2}}^{{\lambda }}} \right|$ и $\left| {{{V_{{g3}}^{{\lambda }}} \mathord{\left/ {\vphantom {{V_{{g3}}^{{\lambda }}} {V_{{g1}}^{{\lambda }}}}} \right. \kern-0em} {V_{{g1}}^{{\lambda }}}}} \right| \geqslant {{k}_{0}}{\kern 1pt} :$ или $\left| {V_{{g1}}^{{\lambda }}} \right| < \left| {V_{{g2}}^{{\lambda }}} \right|$ и $\left| {{{V_{{g3}}^{{\lambda }}} \mathord{\left/ {\vphantom {{V_{{g3}}^{{\lambda }}} {V_{{g2}}^{{\lambda }}}}} \right. \kern-0em} {V_{{g2}}^{{\lambda }}}}} \right| \geqslant {{k}_{0}}$:
(8)
$\begin{gathered} \nu _{{B[I({\psi })]}}^{{{\lambda }\{ J\} }}(\theta ,\varphi ) = \\ = \frac{{\left| {V_{{g3}}^{{\lambda }}} \right|}}{{{{k}_{0}}D}}{{\left\{ {1 - \frac{{{{k}_{0}}}}{2}\frac{{\left( {\left| {V_{{g2}}^{{\lambda }}} \right| + \left| {V_{{g1}}^{{\lambda }}} \right|} \right)}}{{\left| {V_{{g3}}^{{\lambda }}} \right|}} + \frac{{{{{\left( {{{k}_{0}}} \right)}}^{2}}}}{3}\frac{{\left| {V_{{g1}}^{{\lambda }}} \right|\left| {V_{{g2}}^{{\lambda }}} \right|}}{{{{{\left( {V_{{g3}}^{{\lambda }}} \right)}}^{2}}}}} \right\}}^{{ - 1}}}. \\ \end{gathered} $При выполнении противоположных неравенств они имеют вид:
(9)
$\nu _{{B[I]}}^{{{\lambda }\{ J\} }}(\theta ,\varphi ) = \left\{ \begin{gathered} \frac{6}{D}\frac{{{{{\left( {V_{{g1}}^{{\lambda }}} \right)}}^{2}}}}{{\left( {3\left| {V_{{g1}}^{{\lambda }}} \right| - \left| {V_{{g2}}^{{\lambda }}} \right|} \right)}},\,\,\,{\text{если}}\,\,\,\left| {{{V}_{{g2}}}} \right| < \left| {{{V}_{{g1}}}} \right|\,\,\,{\text{и}}\,\,\,\left| {{{V_{{g3}}^{{\lambda }}} \mathord{\left/ {\vphantom {{V_{{g3}}^{{\lambda }}} {V_{{g1}}^{{\lambda }}}}} \right. \kern-0em} {V_{{g1}}^{{\lambda }}}}} \right| < {{k}_{0}}; \hfill \\ \frac{6}{D}\frac{{{{{\left( {V_{{g2}}^{{\lambda }}} \right)}}^{2}}}}{{\left( {3\left| {V_{{g2}}^{{\lambda }}} \right| - \left| {V_{{g1}}^{{\lambda }}} \right|} \right)}},\,\,\,{\text{если}}\,\,\,\left| {{{V}_{{g2}}}} \right| > \left| {{{V}_{{g1}}}} \right|\,\,\,{\text{и}}\,\,\,\left| {{{V_{{g3}}^{{\lambda }}} \mathord{\left/ {\vphantom {{V_{{g3}}^{{\lambda }}} {V_{{g2}}^{{\lambda }}}}} \right. \kern-0em} {V_{{g2}}^{{\lambda }}}}} \right| < {{k}_{0}}. \hfill \\ \end{gathered} \right.$Как видно из формул (8) и (9), с уменьшением D скорости релаксации на границах возрастают. Поэтому для реализации кнудсеновского течения фононного газа в кристаллах калия необходимо уменьшить поперечные размеры нанопроводов до D < 10–5 см, чтобы диффузное рассеяние фононов на границах образца было более эффективно, чем в объемных механизмах релаксации.
Мы зафиксировали температуру 2 К и рассчитали угловые зависимости термоэдс увлечения и вклады в нее от различных ветвей фононного спектра при вращении градиента температуры в плоскостях {100} и {110} (см. рис. 1). Из сравнения рис. 1 и 2 видно, что для всех мод угловые зависимости термоэдс увлечения качественно согласуются с зависимостями длин свободного пробега. Длины свободного пробега достигают максимальных и минимальных значений в направлениях фокусировки и дефокусировки фононов: для медленной квазипоперечной моды – это направления ${{\theta }_{{\max }}} = 0.58 \pm ({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2})n,$ соответствующих групповым скоростям в точках нулевой кривизны на изоэнергетических поверхностях и направлениях дефокусировки – [111], соответственно (см. работы [1–3]). Для продольных фононов – наоборот: направления фокусировки – [111], а минимумы – в направлениях дефокусировки – [001]. Из рис. 2 следует, что величины термоэдс колебательных мод также достигают максимальных и минимальных значений в направлениях фокусировки и дефокусировки фононов. Это неудивительно, так как, чем больше длина свободного пробега относительно рассеяния фононов на границах образца, тем больше вероятность электрона столкнуться с неравновесным фононом и получить дополнительный импульс от градиента температуры.
Рис. 2.
Угловые зависимости термоэдс ${{\alpha }_{{{\text{drag}}}}}$ (мкВ/К) (кривые 4), вкладов продольных $\alpha _{{{\text{drag}}}}^{L}$ (кривые 3), квазипоперечных фононов $\alpha _{{{\text{drag}}}}^{{t2}}$ (кривые 2) и $\alpha _{{{\text{drag}}}}^{{t1}}$ (кривые 1), а также вкладов от продольной (кривые 2a) и сдвиговой (кривые 2b) компоненты моды t2, рассчитанные в режиме кнудсеновского течения фононного газа, для нанопроводов калия с квадратным сечением D = 5 × 10–6 см и длиной L = 50D в случаях, когда градиент температуры вращается в плоскости грани куба (а), в диагональной плоскости (б). Штриховая кривая 4c – полная термоэдс с учетом объемных механизмов релаксации для образца К5 с ε ≈ 0.053.

Как видно из рис. 2, преобладающий вклад в термоэдс увлечения нанопроводов вносят медленные квазипоперечные фононы: их вклады в симметричных направлениях [001], [011] и [111] составляют 78, 65 и 57% соответственно (см. рис. 1). Это связано с аномально большим вкладом моды t2 в решеточную теплоемкость, которая в дебаевском приближении в 21 раз больше, чем для продольных фононов [4]:
Анизотропия вкладов в термоэдс для моды t2 достаточно велика – отношения вкладов имеет вид: $\alpha _{{{{{\theta }}_{{\max }}}}}^{{{{t}_{2}}\{ 100\} }}:\alpha _{{[100]}}^{{{{t}_{2}}\{ 100\} }}:\alpha _{{[110]}}^{{{{t}_{2}}\{ 110\} }}:\alpha _{{[111]}}^{{{{t}_{2}}\{ 110\} }}$ = $2:1.5:1.4:1.$ Вклады продольных фононов в термоэдс увлечения также являются сильно анизотропными, они достигают максимумов в направлениях фокусировки – [111], а минимумов – в направлениях дефокусировки [001]: $\alpha _{{[111]}}^{{L\{ 110\} }}:\alpha _{{[110]}}^{{L\{ 100\} }}$ : $\alpha _{{[100]}}^{{L\{ 100\} }}$ = = $2.5:1.9:1.$ Поскольку направления дефокусировки и минимумы вклада моды t2 соответствуют направлениям фокусировки и максимумам вклада продольных фононов, то в значительной степени они компенсируют друг друга. Поэтому анизотропия полной термоэдс значительно уменьшается: $\alpha _{{{{{\theta }}_{{\max }}}}}^{{\{ 100\} }}:\alpha _{{[110]}}^{{\{ 110\} }}$ : $\alpha _{{[100]}}^{{\{ 100\} }}:\alpha _{{[111]}}^{{\{ 110\} }}$ = $1.32:1.1:1.01:1.$ Заметим, что при измерении термоэдс в симметричных направлениях ее анизотропия будет значительно меньше: $\alpha _{{[110]}}^{{\{ 110\} }}:\alpha _{{[100]}}^{{\{ 100\} }}$ : $\alpha _{{[111]}}^{{\{ 110\} }}$ = $1.1:1.01:1.$ Вклад сдвиговой компоненты моды t2 в термоэдс увлечения по порядку величины совпадает с вкладом продольных фононов (см. рис. 2, кривая 2b). Сдвиговые волны оказывают значительное влияние на соотношение вкладов моды t2 и продольных фононов, а также на анизотропию термоэдс увлечения. В направлениях фокусировки продольных фононов [111] вклад моды t2$\alpha _{{[111]}}^{{{{t}_{2}}\{ 110\} }}$ без учета сдвиговой компоненты оказался на 32% меньше, чем вклад $\alpha _{{[111]}}^{{L\{ 110\} }}.$ Однако при учете сдвиговой компоненты моды t2 вклад $\alpha _{{[111]}}^{{{{t}_{2}}\{ 110\} }}$ стал на 12% больше, чем вклад $\alpha _{{[111]}}^{{L\{ 110\} }}.$ Для нанопроводов с D = 5 × 10–6 см граничное рассеяние вносит доминирующий вклад в релаксацию фононов. Роль объемных механизмов мала: они обеспечивают уменьшение термоэдс увлечения от 1.5 до 5% для нанопроводов калия с ε = 0, и от 2 до 7% для нанопроводов на основе К5 с ε ≈ 0.053.
4. АНИЗОТРОПИИ ТЕРМОЭДС УВЛЕЧЕНИЯ В УСЛОВИЯХ КОНКУРЕНЦИИ ГРАНИЧНОГО И ОБЪЕМНЫХ МЕХАНИЗМОВ РЕЛАКСАЦИИ ФОНОНОВ
Рассмотрим изменение анизотропии термоэдс увлечения в условиях конкуренции граничного и объемных механизмов релаксации фононов. С увеличением поперечного сечения нанопроводов скорость релаксации фононов на границах ослабляется, а роль объемных механизмов возрастает. В результате этого анизотропия вкладов продольной и квазипоперечных мод в термоэдс увлечения монотонно уменьшается (см. рис. 3). Из рис. 3 видно, что кривые 3 и 3а соответствуют зависимостям максимальных и минимальных величин термоэдс увлечения для образца К4 с ε ≈ 0.1 от D. При $D \geqslant 0.1 \times {{10}^{{ - 2}}}\,\,{\text{cм}}$ они выходят на насыщение и сливаются в одну линию. В этом пределе доминируют объемные механизмы релаксации, и значения термоэдс слабо зависят от геометрических параметров образцов. Поэтому для образцов с различной концентрацией дислокаций при $D = 0.1\,\,{\text{cм}}$ рассчитанные значения термоэдс увлечения совпадают с полученными в [11] для образцов с прямоугольным сечением $D \times W$ = ${\text{0}}{\text{.15}} \times {\text{0}}{\text{.5}}\,\,{\text{с}}{{{\text{м}}}^{{\text{2}}}}{\text{.}}$ Как видно из рис. 3, во всем исследованном интервале D вклад сдвиговой компоненты значительно превышает вклад быстрой поперечной моды. При D = 5 × 10–6 см он на 32% больше минимального значения вклада $\alpha _{{{\text{drag}}}}^{L}$ (см. рис. 1а), а при D > > 4 × 10–5 см он становится больше максимального значения вклада $\alpha _{{{\text{drag}}}}^{L}$ (см. рис. 3 кривая 4). При переходе к объемным образцам ($D \geqslant 1 \times {{10}^{{ - 1}}}\,\,{\text{cм}}$) вклад сдвиговой компоненты для образца К4 с ε ≈ 0.1 превышает $\alpha _{{{\text{drag}}}}^{L}$ в 4 раза (см. рис. 3 кривые 2b и 3).
Рис. 3.
Зависимости максимальных значений полной термоэдс увлечения от толщины D нанопроводов калия c концентрацией дислокаций: ε = 0, ε ≈ 0.053 (К5) и ε ≈ 0.1 (К4) кривые 1, 2 и 3 соответственно. Кривая 3a дает зависимость минимальных значений полной термоэдс увлечения $\alpha _{{{\text{drag}}}}^{{[111]}};$ кривые (4, 4a), (5, 5а) и (6, 6a) – зависимости максимальных и минимальных значений вкладов продольных $\alpha _{{{\text{drag}}}}^{L},$ медленных и быстрых квазипоперечных фононов, соответственно; кривая 5b – вклад сдвиговых волн калия К4 c концентрацией дислокаций с ε ≈ 0.1.

В области малых значений D поперечного сечения $D \leqslant {{10}^{{ - 4}}}\,\,{\text{cм}}$ доминирует граничное рассеяние, и кривые, соответствующие различным концентрациям дислокаций, для каждого направления теплового потока сливаются в одну (см. рис. 3 кривые 1, 2, 3). А для больших значений поперечного сечения $D \geqslant 1 \times {{10}^{{ - 3}}}\,\,{\text{cм}}$ кривые, соответствующие образцам с различными концентрациями дислокаций, расходятся, и при $D \geqslant 1 \times {{10}^{{ - 1}}}\,\,{\text{cм}}$ они выходят на насыщение, соответствующее значениям для объемных образцов (см. рис. 3).
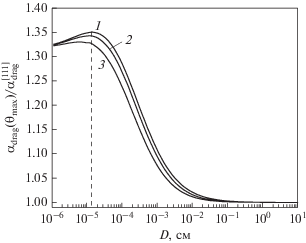
Следует отметить, что с увеличением поперечного сечения нанопроводов максимальная анизотропия термоэдс увлечения, пропорциональная отношению ${{{{\alpha }_{{{\text{drag}}}}}({{\theta }_{{\max }}})} \mathord{\left/ {\vphantom {{{{\alpha }_{{{\text{drag}}}}}({{\theta }_{{\max }}})} {\alpha _{{{\text{drag}}}}^{{[111]}}}}} \right. \kern-0em} {\alpha _{{{\text{drag}}}}^{{[111]}}}},$ изменяется немонотонным образом (см. рис. 4). При переходе от режима кнудсеновского течения фононного газа ($D < {{10}^{{ - 5}}}\,\,{\text{cм}}$) к режиму объемных механизмов релаксации ($D \geqslant 0.1\,\,{\text{cм}}$) она сначала возрастает от 32% при D ≈ 10–6 см, достигая максимума 36% при D ≈ 3 × 10–5 см, затем уменьшается и при D ≥ 0.1 см исчезает (см. рис. 4). Этот эффект обусловлен тем, что продольные фононы значительно сильнее рассеиваются на электронах, чем медленные поперечные и их относительный вклад уменьшается и изотропизируется значительно быстрее, чем $\alpha _{{{\text{drag}}}}^{{t2}}.$ Поэтому минимум термоэдс, в который значительный вклад вносят L-фононы, убывает быстрее, чем максимум термоэдс, определяемый главным образом вкладом t2-моды (см. рис. 2 и 3). В результате анизотропия термоэдс увлечения изменяется немонотонным образом. Причем чем меньше концентрация дислокаций, тем анизотропия – больше (см. рис. 4). Такие величины анизотропии термоэдс вполне доступны экспериментальному определению. Из рис. 4 следует, что анизотропия термоэдс в 30% достигается не только в режиме кнудсеновского течения фононного газа D < 10–5 см, но и при толщинах образцов, на два порядка больших: D ≈ (0.4–2) × × 10–3 см. Отметим, что эта особенность анизотропии термоэдс существенно упрощает проблему экспериментальной проверки рассчитанных в настоящей работе эффектов.
Рис. 4.
Зависимости отношения термоэдс ${{{{\alpha }_{{{\text{drag}}}}}({{\theta }_{{\max }}})} \mathord{\left/ {\vphantom {{{{\alpha }_{{{\text{drag}}}}}({{\theta }_{{\max }}})} {\alpha _{{{\text{drag}}}}^{{[111]}}}}} \right. \kern-0em} {\alpha _{{{\text{drag}}}}^{{[111]}}}}$ в образцах с квадратным сечением от толщины D, рассчитанные для кристаллов калия: ε = 0 (кривая 1), К5 для ε ≈ 0.053 (кривая 2), для ε ≈ 0.1 (кривая 3).
ЗАКЛЮЧЕНИЕ
Проанализирована роль сдвиговых волн в термоэдс увлечения нанопроводов калия при низких температурах. Основные результаты работы можно сформулировать следующим образом.
1. Анализ термоэдс увлечения показал, что сдвиговые волны вносят значительный вклад в термоэдс увлечения нанопроводов. По порядку величины он совпадает с вкладом продольных фононов, а в некоторых направлениях превосходит его. Вклад моды t2 при учете только продольной компоненты в направлениях [111] оказался на 32% меньше, а при учете сдвиговой компоненты моды t2 он – на 12% больше, чем вклад продольных фононов.
2. Определены направления, соответствующие максимальным и минимальным значениям термоэдс увлечения нанопроводов. Установлено, что вклады колебательных мод в термоэдс достигают максимальных и минимальных значений в направлениях фокусировки и дефокусировки фононов.
3. Показано, что в условиях конкуренции граничного и объемных механизмов релаксации фононов с увеличением поперечного сечения нанопроводов анизотропии термоэдс увлечения изменяется немонотонным образом. Этот эффект обусловлен конкуренцией вкладов t2-моды и L‑фононов в термоэдс увлечения в направлениях [111] и существенно более сильной релаксацией L-фононов на электронах при увеличении поперечных размеров нанопроводов. Причем величины анизотропии термоэдс, достаточные для экспериментальной проверки, достигаются не только в режиме кнудсеновского течения фононного газа, но и при толщинах образцов на два порядка больших.
Работа выполнена в рамках государственного задания МИНОБРНАУКИ России (тема “Функция”, № AAAA-A19-119012990095-0).
Список литературы
Кулеев И.И., Кулеев И.Г. Фокусировка фононов и анизотропия решеточной теплопроводности кристаллов калия при низких температурах // ФММ. 2018. Т. 119. С. 1203–1209.
Кулеев И.И., Кулеев И.Г. Роль квазипродольных и квазипоперечных фононов в термоэдс увлечения кристаллов калия при низких температурах // ЖЭТФ. 2019. Т. 156. С. 56–70.
Kuleyev I.I., Kuleyev I.G. Drag thermopower in nanowires and bulk potassium crystals under the conditions of competition between the boundary and bulk mechanisms of phonon relaxation // J. Phys.: Cond. Matt. 2019. V. 31. 375701(13 pp).
Кулеев И.И., Кулеев И.Г. Влияние анизотропии упругой энергии на электрон-фононное увлечение и температурные зависимости термоэдс в кристаллах калия при низких температура // ФММ. 2019. Т. 120. С. 1129–1135.
Займан Дж. Электроны и фононы. М.: ИИЛ, 1962. 488 с.
Блатт Ф. Физика электронной проводимости в твердых телах. М.: ИИЛ, 1971. 470 с.
Anselm A.I. Introduction to Semiconductor Theory, Prentice-Hall, New Jersey (1981).
MacDonald D.K.C., Pearson W.B. and Templeton I.M. Thermo-Electricity at Low Temperatures. VIII. Thermo-Electricity of the Alkali Metals Below 2 K // Proc. R. Soc. Lond. A 1960. V. 256. P. 334–358.
Guenault A.M., MacDonald D.K.C. Electron and phonon scattering thermoelectricity in potassium and alloys at very low temperatures // Proc. R. Soc. Lond. A 1961. V. 264. P. 41–59.
Stinson M.R., Fletcher R., Leavens C.R. Thermomagnetic and thermoelectric properties of potassium // Phys. Rev. B. 1979. V. 20. P. 3970–3990.
Fletcher R. Scattering of phonons by dislocations in potassium // Phys. Rev. B. 1987. V. 36. P. 3042–3051.
Blatt F.J., Schroeder P.A., Foiles C.L., Greig D. Thermoelectric power of metals. New York and London: Plenum press, 1976.
Кулеев И.И., Кулеев И.Г. Влияние анизотропии упругой энергии на электрон-фононное увлечение и температурные зависимости термоэдс в кристаллах калия при низких температура // ФММ. 2020. Т. 121. № 10. С. 1–8.
Zyman J.M. The thermoelectric power of the alkali metals at low temperatures // Phil. Mag. 1959. V. 4. P. 371–379.
Herring C., Vogt E. Transport and Deformation-Potential Theory for Many-Valley Semiconductors with Anisotropic Scattering // Phys. Rev. 1956. V. 101. P. 944–961.
Кардона П.Ю.М. Основы физики полупроводников, М.: Физматлит, 2002. 560 с.
Гуревич Л.Э. Термоэлектрические свойства проводников. I // ЖЭТФ. 1946. Т.16. С.193.
Kuleyev I.G., Kuleyev I.I., Taldenkov A.N., Inyushkin A.V., Ozhogin V.I., Itoh K.M., Haller E.E. Normal processes of phonon-phonon scattering and the drag thermal EMF in germanium crystals with isotopic disorder // JETP. 2003. V. 96. P. 1078.
Mahan G.D., Lindsay L., Broido D.A. The Seebeck coefficient and phonon drag in silicon // J. Appl. Phys. 2014. V. 116. P. 245102.
Федоров Ф.И. Теория упругих волн в кристаллах. М.: Наука, 1965. 386 с.
Truel B., Elbaum C., Chick B.B. Ultrasonic methods in solid state physics. Academic Press, N.Y.−London. 1969. 307 c.
Кулеев И.Г., Кулеев И.И. Упругие волны в кубических кристаллах с положительной и отрицательной анизотропией модулей упругости второго порядка // ФТТ. 2007. Т. 49. № 3. С. 422–429.
Li D., Wu Y., Kim P., Shi L., Yang P., Majumdar A. Thermal conductivity of individual silicon nanowires // Applied Physics Letters. 2003. V. 83. P. 2934–2936.
Кулеев И.Г., Кулеев И.И., Бахарев С.М., Устинов В.В. Фокусировка фононов и фононный транспорт в монокристаллических наноструктурах. Екатеринбург: Изд-во УМЦ УПИ, 2018. 256 с.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение


