Физика металлов и металловедение, 2021, T. 122, № 3, стр. 248-254

Диэлектрическая функция сферической металлической наночастицы

А. А. Коваль^a, А. В. Коротун^a, *

^a Национальный университет “Запорожская политехника”
69063 Запорожье, ул. Жуковского, 64, Украина

Поступила в редакцию 28.08.2020
После доработки 11.10.2020
Принята к публикации 17.11.2020

DOI: 10.31857/S0015323021030104

Аннотация

Исследовано взаимодействие электромагнитных волн со сферической металлической наночастицей. В рамках модели сферической потенциальной ямы бесконечной глубины с учетом размерной зависимости энергии Ферми получена формула для диэлектрического тензора и рассчитаны его диагональные компоненты. Результаты расчетов демонстрируют сильную размерную и частотную зависимость действительной и мнимой частей диэлектрической функции. Вычисления проведены для частиц Ag, Cu и Al.

Ключевые слова: металлическая наночастица, диэлектрический тензор, размерное квантование, энергия Ферми

ВВЕДЕНИЕ

Оптические свойства металлических наночастиц достаточно давно изучаются как теоретически, так и экспериментально [1–9]. Это обусловлено широким спектром их применения, в частности, при создании метаматериалов [10], в устройствах сберхбыстрой оптоэлектроники [11] и суперлинзах [12], а также для терапии рака [13].

Разработаны усовершенствованные методы получения и созданы методики исследования оптических свойств ансамблей малых металлических частиц [14, 15]. При этом получение идентичных по своим параметрам частиц все еще остается нерешенной задачей [16]. Однако исследование единичных структур спектроскопическими методами позволяет избежать усреднения и, как следствие, потери физической информации.

Известно, что свойства малых частиц и их ансамблей отличаются от свойств массивных тел. Так, при приближении размера частицы к фермиевской длине волны становится существенным квантование электронного спектра. Новые закономерности также наблюдаются в поглощении света малыми металлическими частицами. Исследования указывают на тот факт, что оптические свойства малых металлических частиц в значительной степени определяются их составом, структурой, размером и формой [1, 2, 5, 17, 18].

Диэлектрическая функция является важной физической величиной для изучения спектра оптического поглощения малых металлических частиц [2, 7, 19]. Расчет диэлектрической функции с использованием теории линейного отклика представлен в работе [18]. Сравнение различных квантово-механических подходов [18, 20, 21], а также их применение к вычислению диэлектрической функции для систем пониженной размерности различной геометрии дано в [1].

Среди сравнительно недавних работ следует отметить [9], в которой были выполнены численные расчеты диэлектрической функции с использованием различных наборов собственных значений энергий для наночастиц серебра различных размеров и трех видов ограничивающего потенциала. Влияние размерного квантования на диэлектрическую проницаемость наночастиц металлов с использованием модели потенциальной ямы рассматривается в [22].

Целью настоящей работы является вычисление компонент диэлектрического тензора сферической металлической наночастицы. Для этого используется подход [2], адаптированный для ультратонких пленок и нитей в работе [23].

ЭНЕРГИЯ ФЕРМИ

Решение уравнения Шредингера для сферически симметричной прямоугольной потенциальной ямы бесконечной глубины

$U\left( r \right) = \left\{ {\begin{array}{*{20}{c}} {\infty ,\,\,\,\,r > {{r}_{0}}} \\ {0,\,\,\,\,r \leqslant {{r}_{0}}} \end{array}} \right.$

имеет следующий вид:

(1)

${{\psi }_{{nlm}}}\left( {r,\theta ,\varphi } \right) = {{R}_{{nl}}}\left( r \right){{Y}_{{lm}}}\left( {\theta ,\varphi } \right).$

Радиальная зависимость волновой функции описывается сферическими функциями Бесселя целого порядка:

(2)

${{R}_{{nl}}}\left( r \right) = {{C}_{{nl}}}{{j}_{l}}\left( {{{k}_{{nl}}}r} \right),$

(3)

${{C}_{{nl}}} = {{\left\{ {\int\limits_0^{{{r}_{0}}} {j_{l}^{2}\left( {{{k}_{{nl}}}r} \right){{r}^{2}}dr} } \right\}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$

${{k}_{{nl}}} = {{{{\chi }_{{nl}}}} \mathord{\left/ {\vphantom {{{{\chi }_{{nl}}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}},$ где ${{\chi }_{{nl}}}$ – положительные нули сферической функции Бесселя l-го порядка, числа $n = 1,2, \ldots $ нумеруют корни функции Бесселя порядка l.

Шаровая функция описывается выражением

(4)

${{Y}_{{lm}}}\left( {{\theta },{\varphi }} \right) = \sqrt {\frac{{2l + 1}}{{4{\pi }}}\frac{{\left( {l - m} \right)!}}{{\left( {l + m} \right)!}}} P_{l}^{m}\left( {\cos {\theta }} \right){{\operatorname{e} }^{{{\text{i}}m{\varphi }}}},$

где $m = 0, \pm 1, \pm 2 \ldots \pm l,$ $P_{l}^{m}\left( {\cos {\theta }} \right)$ – присоединенная функция Лежандра.

Приравнивая число заполненных состояний к числу электронов проводимости N, получим:

(5)

$N = \int\limits_0^{{{{\varepsilon }}_{{\text{F}}}}} {g\left( \varepsilon \right)} d\varepsilon = 2\int\limits_0^{{{{\varepsilon }}_{{\text{F}}}}} {\sum\limits_{n,l} {{\delta }\left( {\varepsilon - {{\varepsilon }_{{nl}}}} \right)} } d\varepsilon ,$

где $g\left( {\varepsilon } \right) = 2\sum\nolimits_{n,l} {\delta \left( {\varepsilon - {{\varepsilon }_{{nl}}}} \right)} $ – энергетическая плотность состояний 0D-системы, а уровни энергии определяются соотношением:

(6)

${{{\varepsilon }}_{{nl}}} = \frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}}}k_{{nl}}^{2}.$

Для вычисления интеграла в (5) воспользуемся разложением $\delta $-функции в ряд Фурье по синусам на конечном интервале $\varepsilon \in \left( {0,{{\varepsilon }_{F}}} \right)$ [24]:

(7)

$\delta \left( {\varepsilon - {{\varepsilon }_{{nl}}}} \right) = \frac{2}{{{{\varepsilon }_{{\text{F}}}}}}\sum\limits_{\kappa = 1}^\infty {\sin \frac{{\pi \kappa \varepsilon }}{{{{\varepsilon }_{{\text{F}}}}}}\sin \frac{{\pi \kappa {{\varepsilon }_{{nl}}}}}{{{{\varepsilon }_{{\text{F}}}}}}} .$

Подставляя (7) в (5), учитывая, что

(8)

$N = \bar {n}\Omega ,$

где $\bar {n}$ – концентрация электронов проводимости, $\Omega = {{4\pi r_{0}^{3}} \mathord{\left/ {\vphantom {{4\pi r_{0}^{3}} 3}} \right. \kern-0em} 3}$ – объем частицы, получаем трансцендентное уравнение для определения энергии Ферми ${{{\varepsilon }}_{{\text{F}}}}{\text{:}}$

(9)

$\bar {n}\Omega = \sum\limits_{\kappa = 1}^\infty {\frac{4}{{{\pi }\kappa }}\left( {1 - \cos {\pi }\kappa } \right)\sum\limits_{n,l} {\sin \frac{{{\pi }\kappa {{{\varepsilon }}_{{nl}}}}}{{{{{\varepsilon }}_{{\text{F}}}}}}} } .$

Предполагается, что концентрация электронов проводимости в наночастице такая же, что и в бесконечном металле. Суммирование выполняется по всем значениям $n$ и $l$, для которых

(10)

${{{\varepsilon }}_{{nl}}} = \frac{{{{\hbar }^{2}}}}{{2{{m}_{e}}r_{0}^{2}}}{\chi }_{{nl}}^{2} \leqslant {{{\varepsilon }}_{{\text{F}}}}.$

ДИЭЛЕКТРИЧЕСКИЙ ТЕНЗОР

Связь между компонентами индукции ${{D}_{{\mu }}}$ и напряженности ${{E}_{{\nu }}}$ электрического поля для анизотропных систем имеет вид

(11)

${{D}_{{\mu }}} = \sum\limits_{\nu } {{{\epsilon }_{{{\mu \nu }}}}\left( {q,\omega } \right){{E}_{{\nu }}}} ,$

где ${{\epsilon }_{{{\mu \nu }}}}$ – диэлектрический тензор.

Используя выражение

(12)

${{\epsilon }_{{\mu \nu }}} = {{\delta }_{{\mu \nu }}} + \operatorname{i} \frac{{4\pi }}{\omega }{{\sigma }_{{\mu \nu }}},$

а также результаты [23], диэлектрический тензор можно представить как

(13)

$\begin{gathered} {{\epsilon }_{{{\mu \nu }}}} = {{{\delta }}_{{{\mu \nu }}}} - \frac{{4{\pi }{{e}^{2}}}}{{m_{e}^{2}{{{\omega }}^{2}}\Omega }}\sum\limits_{i,j} {\frac{{{{f}_{i}} - {{f}_{j}}}}{{{{{\varepsilon }}_{{ij}}} - \hbar {\omega }}}\left\{ {\left\langle {\left. j \right|{{\operatorname{e} }^{{ - \operatorname{i} q \cdot r}}}{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle - } \right.} \\ \left. { - \,\,\frac{1}{2}\hbar {{q}_{{\mu }}}\left\langle {\left. j \right|{{\operatorname{e} }^{{ - \operatorname{i} q \cdot r}}}\left| i \right.} \right\rangle } \right\}\left\{ {\left\langle {\left. i \right|{{\operatorname{e} }^{{\operatorname{i} q \cdot r}}}{{{\hat {p}}}_{{\nu }}}\left| j \right.} \right\rangle + \frac{1}{2}\hbar {{q}_{{\nu }}}\left\langle {\left. j \right|{{\operatorname{e} }^{{\operatorname{i} q \cdot r}}}\left| i \right.} \right\rangle } \right\}. \\ \end{gathered} $

Здесь ${\text{i}} = \sqrt { - 1} ;$ ${{m}_{e}}$ – масса электрона; ${{f}_{i}} = {{\left[ {\exp \left( {{{\left( {{{\varepsilon }_{i}} - {{\varepsilon }_{{\text{F}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\varepsilon }_{i}} - {{\varepsilon }_{{\text{F}}}}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}} \right) + 1} \right]}^{{ - 1}}}$ – коэффициент заполнения состояния с энергией ${{\varepsilon }_{i}};$ $\left| i \right\rangle \equiv \left| {n,l,m} \right\rangle ,$ $\left\langle j \right| \equiv \left\langle {n{\kern 1pt} ',l{\kern 1pt} ',m{\kern 1pt} '} \right|$ – векторы начального и конечного состояния; ${{\varepsilon }_{{ij}}} = {{\varepsilon }_{i}} - {{\varepsilon }_{j}};$ Т – температура. В дальнейшем будем считать $T = 0.$

Считаем, что волновой вектор лежит в плоскости zx, т.е. ${{q}_{y}} = 0.$ Направив ось z вдоль направления распространения волны, получим ${{q}_{x}} = 0,$ $q \cdot r = {{q}_{z}}z \simeq {{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} \lambda }} \right. \kern-0em} \lambda } \ll 1$ и

${{\operatorname{e} }^{{ \pm \operatorname{i} q \cdot r}}} \approx 1 \pm {\text{i}}{{q}_{z}}z.$

В нулевом приближении по малому параметру ${{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {\lambda }}} \right. \kern-0em} {\lambda }}$ выражение для диэлектрической функции принимает вид:

(14)

${{\epsilon }_{{{\mu \nu }}}} = {{\delta }_{{{\mu \nu }}}} - \frac{{4\pi {{e}^{2}}}}{{m_{e}^{2}{{\omega }^{2}}\Omega }}\sum\limits_{i,j} {\frac{{{{f}_{i}} - {{f}_{j}}}}{{{{\varepsilon }_{{ij}}} - \hbar \omega }}\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle \left\langle {\left. i \right|{{{\hat {p}}}_{{\nu }}}\left| j \right.} \right\rangle } .$

Преобразовывая (14) путем почленного деления на ${{\varepsilon }_{{ij}}} - \hbar \omega $ под знаком суммы и последующей перестановки индексов начального и конечного состояний во втором слагаемом, получаем

(15)

$\begin{gathered} {{\epsilon }_{{{\mu \nu }}}} = {{\delta }_{{{\mu \nu }}}} - \frac{{4\pi {{e}^{2}}}}{{m_{e}^{2}{{\omega }^{2}}\Omega }} \times \\ \times \,\,\sum\limits_{i,j} {{{f}_{i}}\left\{ {\frac{{\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle \left\langle {\left. i \right|{{{\hat {p}}}_{{\nu }}}\left| j \right.} \right\rangle }}{{{{\varepsilon }_{{ij}}} - \hbar \omega }} + \frac{{\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle {\text{*}}\left\langle {\left. i \right|{{{\hat {p}}}_{{\nu }}}\left| j \right.} \right\rangle {\text{*}}}}{{{{\varepsilon }_{{ij}}} + \hbar \omega }}} \right\}} . \\ \end{gathered} $

Матричные элементы различных проекций оператора импульса можно представить следующим образом

(16)

$\begin{gathered} \left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle = \\ = \left\{ {\begin{array}{*{20}{c}} { - {\text{i}}\hbar {{{\delta }}_{{mm{\kern 1pt} '}}}\left\{ {{{\mathcal{G}}_{{\left( - \right)}}}{{\mathcal{L}}_{{\left( 1 \right)}}}{{{\delta }}_{{l - 1,l{\kern 1pt} '}}} - {{\mathcal{G}}_{{\left( + \right)}}}{{\mathcal{L}}_{{\left( 2 \right)}}}{{{\delta }}_{{l + 1,l{\kern 1pt} '}}}} \right\},\,\,\,\,{\mu } = z;} \\ { - \operatorname{i} \frac{\hbar }{2}\left\{ {{{\mathcal{G}}_{{\left( - \right)}}}{{\mathcal{M}}_{{\left( - \right)}}}{{{\delta }}_{{l - 1,l{\kern 1pt} '}}} + {{\mathcal{G}}_{{\left( + \right)}}}{{\mathcal{N}}_{{\left( - \right)}}}{{{\delta }}_{{l + 1,l{\kern 1pt} '}}}} \right\},\,\,\,\,{\mu } = x;} \\ { - \frac{\hbar }{2}\left\{ {{{\mathcal{G}}_{{\left( - \right)}}}{{\mathcal{M}}_{{\left( + \right)}}}{{{\delta }}_{{l - 1,l{\kern 1pt} '}}} + {{\mathcal{G}}_{{\left( + \right)}}}{{\mathcal{N}}_{{\left( + \right)}}}{{{\delta }}_{{l + 1,l{\kern 1pt} '}}}} \right\},\,\,\,\,{\mu } = y,} \end{array}} \right. \\ \end{gathered} $

где ${{\mathcal{G}}_{{\left( \mp \right)}}} = {{k}_{{nl}}}{{C}_{{nl}}}{{C}_{{n{\kern 1pt} ',l \mp 1}}}$$\int_0^{{{r}_{0}}} {{{j}_{{l \mp 1}}}\left( {{{k}_{{n{\kern 1pt} ',l \mp 1}}}r} \right){{j}_{{l \mp 1}}}\left( {{{k}_{{nl}}}r} \right){{r}^{2}}dr} ,$

$\begin{gathered} {{\mathcal{L}}_{{\left( 1 \right)}}} = \sqrt {\frac{{\left( {l - m} \right)\left( {l + m} \right)}}{{\left( {2l - 1} \right)\left( {2l + 1} \right)}}} , \\ {{\mathcal{L}}_{{\left( 2 \right)}}} = \sqrt {\frac{{\left( {l - m + 1} \right)\left( {l + m + 1} \right)}}{{\left( {2l + 1} \right)\left( {2l + 3} \right)}}} , \\ {{\mathcal{M}}_{{\left( \mp \right)}}} = \mathcal{J}_{{\left( - \right)}}^{{\left( 1 \right)}}{{{\delta }}_{{m + 1,m{\kern 1pt} '}}} \mp \mathcal{J}_{{\left( + \right)}}^{{\left( 1 \right)}}{{{\delta }}_{{m - 1,m{\kern 1pt} '}}}, \\ {{\mathcal{N}}_{{\left( \mp \right)}}} = \mathcal{J}_{{\left( + \right)}}^{{\left( 2 \right)}}{{{\delta }}_{{m + 1,m{\kern 1pt} '}}} \mp \mathcal{J}_{{\left( - \right)}}^{{\left( 2 \right)}}{{{\delta }}_{{m - 1,m{\kern 1pt} '}}}, \\ \mathcal{J}_{{\left( \mp \right)}}^{{\left( 1 \right)}} = \sqrt {\frac{{\left( {l \mp m - 1} \right)\left( {l \mp m} \right)}}{{\left( {2l - 1} \right)\left( {2l + 1} \right)}}} , \\ \mathcal{J}_{{\left( \mp \right)}}^{{\left( 2 \right)}} = \sqrt {\frac{{\left( {l \mp m + 1} \right)\left( {l \mp m + 2} \right)}}{{\left( {2l + 1} \right)\left( {2l + 3} \right)}}} \\ \end{gathered} $

и ${{\delta }_{{{\mu \nu }}}}$ – символ Кронекера.

Правила отбора для проекции оператора импульса на ось z имеют вид:

$\Delta m = m - m{\kern 1pt} ' = 0,\,\,\,\,\Delta l = l - l{\kern 1pt} ' = \pm 1;$

для проекции оператора импульса на оси x и y

$\Delta m = m - m{\kern 1pt} ' = \pm 1,\,\,\,\,\Delta l = l - l{\kern 1pt} ' = \pm 1.$

Вследствие специфического вида матричного элемента $\left\langle {\left. j \right|{{{\hat {p}}}_{z}}\left| i \right.} \right\rangle $ сумма в выражении (14) обращается в нуль, если $\mu = z$ или $\nu = z.$ Поэтому

(17)

${{\epsilon }_{{xz}}} = {{\epsilon }_{{zx}}} = {{\epsilon }_{{yz}}} = {{\epsilon }_{{zy}}} = 0.$

Диагональные компоненты диэлектрического тензора:

(18)

${{\epsilon }_{{{\mu \mu }}}} = 1 - \frac{{8\pi {{e}^{2}}{{\hbar }^{2}}}}{{m_{e}^{2}\Omega }}\sum\limits_{i,j} {\frac{{{{f}_{i}}}}{{{{\varepsilon }_{{ij}}}\left( {\varepsilon _{{ij}}^{2} - {{\hbar }^{2}}{{\omega }^{2}}} \right)}}{{{\left| {\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle } \right|}}^{2}}} ,$

где индекс $\mu = x,y,z.$ Поглощение учитывается посредством замены $\omega \to \omega + {{\text{i}} \mathord{\left/ {\vphantom {{\text{i}} \tau }} \right. \kern-0em} \tau }$ в выражении для диэлектрической функции (18), где $\tau $ – время релаксации. Это приводит к локальному несохранению числа электронов. Во избежание этого используют комплексную диэлектрическую функцию $\bar {\epsilon }\left( {\omega ,\tau } \right)$ [2], действительная и мнимая части которой определяются как:

(19)

$\operatorname{Re} \bar {\epsilon }\left( {\omega ,\tau } \right) = \operatorname{Re} \epsilon \left( {\omega + {{\text{i}} \mathord{\left/ {\vphantom {{\text{i}} \tau }} \right. \kern-0em} \tau }} \right) - \frac{1}{{\omega \tau }}\operatorname{Im} \epsilon \left( {\omega + {{\text{i}} \mathord{\left/ {\vphantom {{\text{i}} \tau }} \right. \kern-0em} \tau }} \right),$

(20)

$\begin{gathered} \operatorname{Im} \bar {\epsilon }\left( {\omega ,\tau } \right) = \operatorname{Im} \epsilon \left( {\omega + {{\text{i}} \mathord{\left/ {\vphantom {{\text{i}} \tau }} \right. \kern-0em} \tau }} \right) + \\ + \,\,\frac{1}{{\omega \tau }}\left[ {\operatorname{Re} \epsilon \left( {\omega + {{\text{i}} \mathord{\left/ {\vphantom {{\text{i}} \tau }} \right. \kern-0em} \tau }} \right) - 1} \right]. \\ \end{gathered} $

В результате подстановки (18) в (19) и (20) получаем:

(21)

$\begin{gathered} \operatorname{Re} {{{\bar {\epsilon }}}_{{{\mu \mu }}}}\left( {{{k}_{{\omega }}},{{k}_{{\tau }}}} \right) = 1 - \frac{{4k_{p}^{4}}}{{{{\hbar }^{2}}N}}{{\Phi }_{{\left( - \right)}}}, \\ \operatorname{Im} {{{\bar {\epsilon }}}_{{{\mu \mu }}}}\left( {{{k}_{{\omega }}},\,\,{{k}_{{\tau }}}} \right) = - \frac{{4k_{p}^{4}}}{{{{\hbar }^{2}}N}}\frac{{k_{{\tau }}^{2}}}{{k_{{\omega }}^{2}}}{{\Phi }_{{\left( + \right)}}}, \\ \end{gathered} $

(22)

$\begin{gathered} {{\Phi }_{{\left( \mp \right)}}} = \sum\limits_{n,l,m,n{\kern 1pt} '} {\frac{{{{f}_{{nlm}}}{{{\left| {\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle } \right|}}^{2}}}}{{k_{{nl}}^{2} - k_{{n{\kern 1pt} 'l{\kern 1pt} '}}^{2}}}} \times \\ \times \,\,\frac{{{{{\left( {k_{{nl}}^{2} - k_{{n{\kern 1pt} 'l{\kern 1pt} '}}^{2}} \right)}}^{2}} \mp k_{{\omega }}^{4} \mp k_{{\tau }}^{4}}}{{{{{\left[ {{{{\left( {k_{{nl}}^{2} - k_{{n{\kern 1pt} 'l{\kern 1pt} '}}^{2}} \right)}}^{2}} - k_{{\omega }}^{4} + k_{{\tau }}^{4}} \right]}}^{2}} + 4k_{{\omega }}^{4}k_{{\tau }}^{4}}}, \\ \end{gathered} $

где $k_{p}^{2} = {{2{{m}_{e}}{{\omega }_{p}}} \mathord{\left/ {\vphantom {{2{{m}_{e}}{{\omega }_{p}}} \hbar }} \right. \kern-0em} \hbar },$ $k_{{\omega }}^{2} = {{2{{m}_{e}}\omega } \mathord{\left/ {\vphantom {{2{{m}_{e}}\omega } \hbar }} \right. \kern-0em} \hbar },$ $k_{{\tau }}^{2} = {{2{{m}_{e}}} \mathord{\left/ {\vphantom {{2{{m}_{e}}} {\hbar \tau }}} \right. \kern-0em} {\hbar \tau }},$ $\omega _{p}^{2} = {{4\pi {{e}^{2}}\bar {n}} \mathord{\left/ {\vphantom {{4\pi {{e}^{2}}\bar {n}} {{{m}_{e}}}}} \right. \kern-0em} {{{m}_{e}}}}$ и в качестве аппроксимации коэффициента заполнения использована ступенчатая функция ${{f}_{{nlm}}} = \Theta \left( {{{{\varepsilon }}_{{\text{F}}}} - {{{\varepsilon }}_{{nlm}}}} \right).$

Несложно заметить, что при фиксированном направлении поляризации суммирование в (22) по всем m (и $m{\kern 1pt} '$) не зависит от направления. Согласно этому:

$\begin{gathered} \sum\limits_m {{{{\left| {z_{{nlm}}^{{n{\kern 1pt} ',l - 1,m}}} \right|}}^{2}}} = \mathcal{G}_{{\left( - \right)}}^{2}\sum\limits_{m = - l}^l {\frac{{\left( {l - m} \right)\left( {l + m} \right)}}{{\left( {2l - 1} \right)\left( {2l + 1} \right)}}} = \frac{l}{3}\mathcal{G}_{{\left( - \right)}}^{2}; \\ \sum\limits_m {{{{\left| {z_{{nlm}}^{{n{\kern 1pt} ',l + 1,m}}} \right|}}^{2}}} = \mathcal{G}_{{\left( + \right)}}^{2}\sum\limits_{m = - l}^l {\frac{{\left( {l - m + 1} \right)\left( {l + m + 1} \right)}}{{\left( {2l + 1} \right)\left( {2l + 3} \right)}}} = \\ = \frac{{l + 1}}{3}\mathcal{G}_{{\left( + \right)}}^{2};\,\,\,\,\sum\limits_m {{{{\left| {x_{{nlm}}^{{n{\kern 1pt} ',l - 1,m + 1}}} \right|}}^{2}} + {{{\left| {x_{{nlm}}^{{n{\kern 1pt} ',l - 1,m - 1}}} \right|}}^{2}}} = \mathcal{G}_{{\left( - \right)}}^{2} \times \\ \times \,\,\sum\limits_{m = - l}^l {\frac{1}{2}\left( {\frac{{\left( {l - m - 1} \right)\left( {l - m} \right)}}{{\left( {2l - 1} \right)\left( {2l + 1} \right)}} + \frac{{\left( {l + m - 1} \right)\left( {l + m} \right)}}{{\left( {2l - 1} \right)\left( {2l + 1} \right)}}} \right)} = \\ = \frac{l}{3}\mathcal{G}_{{\left( - \right)}}^{2};\,\,\,\,\sum\limits_m {{{{\left| {x_{{nlm}}^{{n{\kern 1pt} ',l + 1,m + 1}}} \right|}}^{2}} + {{{\left| {x_{{nlm}}^{{n{\kern 1pt} ',l + 1,m - 1}}} \right|}}^{2}}} = \mathcal{G}_{{\left( + \right)}}^{2} \times \\ \times \,\,\sum\limits_{m = - l}^l {\frac{1}{2}\left( {\frac{{\left( {l + m + 1} \right)\left( {l + m + 2} \right)}}{{\left( {2l + 1} \right)\left( {2l + 3} \right)}} + } \right.} \\ \left. { + \,\,\frac{{\left( {l - m + 1} \right)\left( {l - m + 2} \right)}}{{\left( {2l + 1} \right)\left( {2l - 3} \right)}}} \right) = \frac{{l + 1}}{3}\mathcal{G}_{{\left( + \right)}}^{2}. \\ \end{gathered} $

Тогда квадрат матричного элемента проекции оператора импульса (16) также не зависит от направления и имеет вид:

(23)

${{\left| {\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle } \right|}^{2}} = \frac{{{{\hbar }^{2}}}}{3}\left\{ {l\mathcal{G}_{{\left( - \right)}}^{2}{{\delta }_{{l - 1,l{\kern 1pt} '}}} + \left( {l + 1} \right)\mathcal{G}_{{\left( + \right)}}^{2}{{\delta }_{{l + 1,l{\kern 1pt} '}}}} \right\}.$

Выражение для недиагональных компонент ${{\epsilon }_{{xy}}}$ и ${{\epsilon }_{{yx}}}$ следует из (15):

(24)

$\begin{gathered} {{\epsilon }_{{{\mu \nu }}}} = {{\delta }_{{{\mu \nu }}}} - \frac{{4\pi {{e}^{2}}}}{{m_{e}^{2}{{\omega }^{2}}\Omega }} \times \\ \times \,\,\sum\limits_{i,j} {{{f}_{i}}\left\{ {\frac{{\left\langle {\left. j \right|{{{\hat {p}}}_{x}}\left| i \right.} \right\rangle \left\langle {\left. i \right|{{{\hat {p}}}_{y}}\left| j \right.} \right\rangle }}{{{{\varepsilon }_{{ij}}} \mp \hbar \omega }} + \frac{{\left\langle {\left. j \right|{{{\hat {p}}}_{x}}\left| i \right.} \right\rangle {\kern 1pt} {\text{*}}\left\langle {\left. i \right|{{{\hat {p}}}_{y}}\left| j \right.} \right\rangle {\kern 1pt} {\text{*}}}}{{{{\varepsilon }_{{ij}}} \pm \hbar \omega }}} \right\}} . \\ \end{gathered} $

Верхний знак соответствует $\mu = x,$ $\nu = y,$ нижний знак – $\mu = y,$ $\nu = x.$

Анализ (24) показывает, что для каждого орбитального числа l происходит суммирование как по положительным, так и по отрицательным значениям m (и $m{\kern 1pt} '$). Вследствие этого произведение матричных элементов обращается в нуль и

(25)

${{\epsilon }_{{xy}}}\, = \,{{\epsilon }_{{yx}}}\, = 0.$

Таким образом, все недиагональные компоненты диэлектрического тензора в нулевом порядке разложения по параметру ${{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {\lambda }}} \right. \kern-0em} {\lambda }}$ равны нулю, а сам диэлектрический тензор вырождается в скаляр.

В дальнейшем для расчета диагональной компоненты диэлектрического тензора используются формулы (21), (22) с учетом выражения (23) для квадрата матричного элемента проекции оператора импульса.

РЕЗУЛЬТАТЫ РАСЧЕТОВ И ОБСУЖДЕНИЕ

Вычисления проведены для наночастиц Ag, Cu и Al со значениями электронных концентраций $\bar {n} = {{\left( {{{4\pi r_{s}^{3}} \mathord{\left/ {\vphantom {{4\pi r_{s}^{3}} 3}} \right. \kern-0em} 3}} \right)}^{{ - 1}}},$ где ${{r}_{s}}$ – среднее расстояние между электронами. Значения ${{r}_{s}}$ и τ для различных металлов приведены в табл. 1.

Таблица 1.

Параметры металлов [25]

Металл	${{{{r}_{s}}} \mathord{\left/ {\vphantom {{{{r}_{s}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$	$\tau ,\,\,{{10}^{{ - 14}}}$ c	${\hbar \mathord{\left/ {\vphantom {\hbar \tau }} \right. \kern-0em} \tau }$, эВ
Ag	3.02	4.0	0.016
Cu	2.67	2.7	0.024
Al	2.07	0.8	0.082

На рис. 1 представлены частотные зависимости $\operatorname{Re} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ и $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ для наночастиц Cu различных радиусов. Пики соответствуют переходам между уровнями размерного квантования. В наночастицах с малым радиусом число подзон, заполненных электронами полностью или частично, невелико. Как следствие, количество пиков также невелико. С увеличением радиуса все пики смещаются в область меньших частот, расстояния между ними уменьшаются, и пики начинают сливаться друг с другом. Это обусловлено тем, что с увеличением радиуса влияние квантовых эффектов нивелируется, а размерные осцилляции исчезают.

Рис. 1.

Частотные зависимости действительной (a) и мнимой (б) частей диагональной компоненты ${{\epsilon }_{{{\mu \mu }}}}$ диэлектрического тензора наночастицы Cu с различными значениями радиуса: 1 – ${{r}_{0}} = 1$ нм; 2 – ${{r}_{0}} = 1.5$ нм; 3 – ${{r}_{0}} = 2$ нм.

Определим для наночастицы Cu положение пика $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ имеющего наибольшую высоту. Высота пиков пропорциональна квадрату матричного элемента оператора ${{\hat {p}}_{{\mu }}},$ а сам матричный элемент имеет максимальную величину при $n{\kern 1pt} ' = n,$ так как соответствующий интеграл в (22) при этом условии принимает максимальное значение. Таким образом, максимальное значение $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ достигается при $l = 0$ и $n{\kern 1pt} ' = n = {{n}_{{\text{F}}}}.$ Считая ${{k}_{{\text{F}}}} \approx {{k}_{{{{{\text{F}}}_{0}}}}} = {{\left( {3{{{\pi }}^{2}}\bar {n}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ получаем, что для ${{r}_{0}} = 1$ нм число ${{n}_{{\text{F}}}} \approx {{{{k}_{{{{{\text{F}}}_{0}}}}}{{r}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{{{{{\text{F}}}_{0}}}}}{{r}_{0}}} {\pi }}} \right. \kern-0em} {\pi }} = 4.$ В результате имеем

$\hbar {{{\omega }}_{{\max }}}\, = \frac{{{{\hbar }^{2}}\left( {k_{{4,1}}^{2} - k_{{4,0}}^{2}} \right)}}{{2{{m}_{e}}}} = \frac{{{{\hbar }^{2}}\left( {{\chi }_{{4,1}}^{2} - {\chi }_{{4,0}}^{2}} \right)}}{{2{{m}_{e}}r_{0}^{2}}}\, = 1.49\,\,{\text{эВ}}{\text{.}}$

Ошибка примерно в 10% связана с предположением о равномерности распределения уровней.

Оценим теперь величину $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ при $\hbar {{{\omega }}_{{\max }}}$ = = 1.49 эВ. Принимая во внимание, что

(26)

${{\left| {\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle } \right|}^{2}} \cong \frac{{{{\hbar }^{2}}k_{{{{{\text{F}}}_{0}}}}^{2}}}{3}\left( {2l + 1} \right),$

используя выражения (21), (22) с учетом того, что $k_{{nl}}^{2} - k_{{n{\kern 1pt} 'l{\kern 1pt} '}}^{2} \cong k_{{\omega }}^{2},$ ${{k}_{\tau }} \ll {{k}_{\omega }},$ получаем

(27)

$\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}} \cong \,\,\,\frac{{2k_{p}^{4}}}{{{{\hbar }^{2}}Nk_{{\omega }}^{4}k_{{\tau }}^{2}}}\sum\limits_{i,j} {{{f}_{i}}{{{\left| {\left\langle {\left. j \right|{{{\hat {p}}}_{{\mu }}}\left| i \right.} \right\rangle } \right|}}^{2}}} .$

Подставим (26) в (27):

$\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}} \cong \,\,\,\frac{{8{{m}_{e}}{{e}^{2}}}}{{{{\hbar }^{2}}r_{0}^{3}}}\frac{{k_{{{{{\text{F}}}_{0}}}}^{2}}}{{k_{{\omega }}^{4}k_{{\tau }}^{2}}}\sum\limits_l {\left( {2l + 1} \right)} \approx 450.$

Указанная величина хорошо согласуется с данными вычислений, приведенными на рис. 1 (первый максимум на кривой 1).

Рисунок 1 демонстрирует важный факт неотрицательности $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ во всем исследуемом частотном диапазоне, в то время как $\operatorname{Re} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ является знакопеременной функцией частоты.

На рис. 2 приведено сравнение результатов расчетов $\operatorname{Re} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ и $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ с результатами работы [9], в которой использован подход, предложенный в [21].

Рис. 2.

Частотные зависимости действительной (a) и мнимой (б, в) частей диагональной компоненты ${{\epsilon }_{{{\mu \mu }}}}$ наночастицы Ag рассчитанные по формулам (21), (22) (сплошные линии); пунктирные линии – результаты, взятые из работы [9]. Кривые 1, 2 соответствуют ${{r}_{0}} = 1$ нм; 3, 4 – ${{r}_{0}} = 2$ нм.

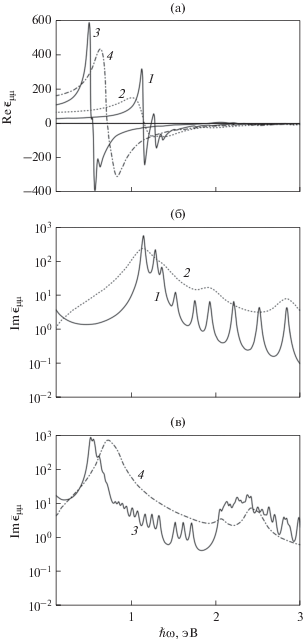
Следует отметить, что полученные результаты качественно подобны, с тем отличием, что количество экстремумов, рассчитанных по формулам (21), (22), больше, чем в работе [9]. Это связано с тем, что в работе [9] используется вместо ${\tau } = {{{\tau }}_{{{\text{bulk}}}}}$ эффективное время релаксации ${\tau }_{{{\text{eff}}}}^{{ - 1}} = {\tau }_{{{\text{bulk}}}}^{{ - 1}} + {\tau }_{s}^{{ - 1}},$ где величина ${\tau }_{s}^{{ - 1}} = {{\mathcal{A}{{{v}}_{{\text{F}}}}} \mathord{\left/ {\vphantom {{\mathcal{A}{{{v}}_{{\text{F}}}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$ определяется эффектами поверхностного рассеяния. Однако поверхностное рассеяние учтено при решении квантово-механической задачи о движении электрона в сферически симметричной потенциальной яме. Как показали авторы работы [2], уже само наложение граничных условий на волновые функции электрона приводит к классическому выражению ${{\mathcal{A}{{{v}}_{{\text{F}}}}} \mathord{\left/ {\vphantom {{\mathcal{A}{{{v}}_{{\text{F}}}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}.$ Поэтому введение поверхностного рассеяния, определяющего собственные состояния частицы, является нецелесообразным.

Положение пика для наночастицы Ag может быть найдено таким же способом, как ранее было определено для наночастицы Cu, с тем отличием, что теперь ${{n}_{{\text{F}}}} = 3.$ Тогда при ${{r}_{0}} = 1$ нм

$\hbar {{{\omega }}_{{\max }}} = \frac{{{{\hbar }^{2}}\left( {{\chi }_{{3,1}}^{2} - {\chi }_{{3,0}}^{2}} \right)}}{{2{{m}_{e}}r_{0}^{2}}} = 1.15\,\,{\text{эВ}},$

что с хорошей точностью соответствует результатам расчетов, приведенным на рис. 2б.

Сравним результаты расчетов диэлектрической функции металлических наночастиц с аналогичными результатами для тонких металлических нитей [23]. Для нити радиусом ${{{\rho }}_{{\text{0}}}}$ при $\alpha = x,y$ квадрат матричного элемента проекции оператора импульса имеет вид

$\begin{gathered} {{\left| {\left\langle {\left. j \right|{{{\hat {p}}}_{{\alpha }}}\left| i \right.} \right\rangle } \right|}^{2}} = \frac{{{{\hbar }^{2}}}}{4}{{\delta }_{{pp{\kern 1pt} '}}}\left\{ {\mathcal{F}_{{\left( - \right)}}^{2}{{\delta }_{{m - 1,m'}}} + \mathcal{F}_{{\left( + \right)}}^{2}{{\delta }_{{m + 1,m{\kern 1pt} '}}}} \right\}, \\ {{\mathcal{F}}_{{\left( \mp \right)}}} = {{k}_{{mn}}}{{C}_{{mn}}}{{C}_{{m \mp 1,n{\kern 1pt} '}}}\int\limits_0^{{{{\rho }}_{{\text{0}}}}} {{{I}_{{m \mp 1}}}\left( {{{k}_{{m \mp 1,n{\kern 1pt} '}}}\rho } \right){{I}_{{m \mp 1}}}\left( {{{k}_{{mn}}}\rho } \right)\rho d\rho } , \\ \end{gathered} $

где ${{C}_{{mn}}} = \frac{{\sqrt 2 }}{{{{\rho }_{0}}\left| {I_{m}^{'}\left( {{{k}_{{mn}}}{{\rho }_{0}}} \right)} \right|}},$ ${{k}_{{mn}}} = {{{{a}_{{mn}}}} \mathord{\left/ {\vphantom {{{{a}_{{mn}}}} {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}},$ ${{a}_{{mn}}}$ – положительные нули цилиндрической функции Бесселя m-го порядка ${{I}_{m}}\left( \xi \right),$ $n = 1,2 \ldots .$

На рис. 3 представлены результаты расчета частотных зависимостей $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ для наночастицы и нити Cu. Отличия в положении и величине пиков объясняется разными энергетическими спектрами 0D и 1D-систем. После пересчета в 0D-системе остается суммирование по квантовым числам n и l, а в случае 1D-системы это n и m. Считая, что $\sum\nolimits_p 1 \cong \frac{{2L}}{\pi }{{k}_{{{{{\text{F}}}_{0}}}}}$ и ${{\left| {\left\langle {\left. {m{\kern 1pt} 'n{\kern 1pt} '} \right|{{{\hat {p}}}_{{\alpha }}}\left| {mn} \right.} \right\rangle } \right|}^{2}}$ ≅ $\frac{1}{4}{{\hbar }^{2}}k_{{{{{\text{F}}}_{0}}}}^{2},$ получим

$\frac{{\operatorname{Im} \bar {\epsilon }_{{{\mu \mu }}}^{{sphere}}}}{{\operatorname{Im} \bar {\epsilon }_{{{\alpha \alpha }}}^{{wire}}}} \cong \frac{{\Omega _{{0{\text{D}}}}^{{ - 1}}\sum\limits_{i,j} {{{{\left| {\left\langle {\left. {n{\kern 1pt} 'l{\kern 1pt} '} \right|{{{\hat {p}}}_{{\mu }}}\left| {nl} \right.} \right\rangle } \right|}}^{2}}} }}{{\Omega _{{1{\text{D}}}}^{{ - 1}}\sum\limits_{i,j} {{{{\left| {\left\langle {\left. {m{\kern 1pt} 'n{\kern 1pt} '} \right|{{{\hat {p}}}_{{\alpha }}}\left| {mn} \right.} \right\rangle } \right|}}^{2}}} \sum\limits_p 1 }} = \frac{{\pi \sum\limits_l {\left( {2l + 1} \right)} }}{{2{{r}_{0}}{{k}_{{{{{\text{F}}}_{0}}}}}}}.$

Рис. 3.

Частотные зависимости мнимой части диагональной компоненты ${{\epsilon }_{{{\mu \mu }}}}$ наночастицы (сплошная линия) и нанонити (пунктирная линия) Cu радиусом ${{r}_{0}} = {{\rho }_{0}} = 1.5$ нм.

Для Cu при ${{r}_{0}} = {{\rho }_{0}} = 1.5$ нм и ${{k}_{{{{{\text{F}}}_{0}}}}} \cong 1.36 \times {{10}^{{10}}}$ м^–1 (${{n}_{{\text{F}}}} = 6;$ $l = 0 \ldots {{n}_{{\text{F}}}} - 1$) имеем

${{\operatorname{Im} \bar {\epsilon }_{{{\mu \mu }}}^{{{\text{sphere}}}}} \mathord{\left/ {\vphantom {{\operatorname{Im} \bar {\epsilon }_{{{\mu \mu }}}^{{{\text{sphere}}}}} {\operatorname{Im} \bar {\epsilon }_{{{\alpha \alpha }}}^{{{\text{wire}}}}}}} \right. \kern-0em} {\operatorname{Im} \bar {\epsilon }_{{{\alpha \alpha }}}^{{{\text{wire}}}}}} \cong 2.8,$

что с достаточной точностью соответствует результатам расчетов.

Частотные зависимости мнимой части диэлектрической функции для различных металлов при фиксированном значении радиуса частицы (${{r}_{0}} = 1.5$ нм) приведены на рис. 4. Полученные результаты имеют качественно и количественно разный характер для частиц Ag, Cu и Al. Так, в случае наночастиц Ag и Cu, в отличие от Al, имеют место сильные осцилляции $\operatorname{Im} {{\bar {\epsilon }}_{{{\mu \mu }}}}$ практически во всем рассматриваемом частотном диапазоне. Такой характер зависимости объясняется отличиями во времени релаксации электронов различных металлов. Для Al время релаксации наименьшее, поэтому и ширина пиков – наибольшая.

Рис. 4.

Зависимость мнимой части диагональной компоненты ${{\epsilon }_{{{\mu \mu }}}}$ диэлектрического тензора для наночастиц различных металлов: 1 – Ag; 2 – Cu; 3 – Al.

ЗАКЛЮЧЕНИЕ

Введен диэлектрический тензор для сферических металлических наночастиц и вычислены его диагональные компоненты с использованием разложения по степеням ${{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {\lambda }}} \right. \kern-0em} {\lambda }}.$ Проанализирована эволюция частотных зависимостей действительной и мнимой частей диэлектрической функции при вариации радиуса. Показано, что действительные части являются знакопеременными функциями частоты, в то время как мнимые части неотрицательны во всем исследуемом диапазоне частот. Установлено, что с увеличением радиуса наночастицы максимумы действительной и мнимой частей компонент диэлектрического тензора смещаются в область меньших частот, а сами максимумы сливаются друг с другом, что связано с увеличением количества уровней размерного квантования, а следовательно, и числа возможных переходов между ними.

Расчеты компонент диэлектрического тензора выполнены для частиц Ag, Cu и Al. Отличия в характере частотных зависимостей наночастиц различных металлов обусловлены отличиями в значениях времени релаксации электронов проводимости.

Список литературы

Ruppin R., Yatom H. Size and shape effects on the broadening of the plasma resonance absorption in metals // Phys. Stat. Sol. B. 1976. V. 74. P. 647–654.
Wood D.M., Ashcroft N.W. Quantum size effects in the optical properties of small metallic particles // Phys. Rev. B. 1982. V. 25. P. 6255–6274.
Kreibig U., Genzel L. Optical absorption of small metallic particles // Surf. Sci. 1985. V. 156. P. 678–700.
Klar T., Perner M., Grosse S., von Plessen G., Spirkl W., Feldmann J. Surface-plasmon resonances in single metallic nanoparticles // Phys. Rev. Lett. 1988. V. 80. P. 4249–4252.
Томчук П.М., Томчук Б.П. Оптическое поглощение малых металлических частиц // ЖЭТФ. 1997. Т. 112. №2. С. 661–678.
Serota R.A., Goodman B. Quantum absorption in small metal particles // Mod. Phys. Lett. B. 1999. V. 13. P. 969–976.
Ivanyuk F.A. Dielectric function of metal clusters: Finite-size effects and the macroscopic limit // Phys. Rev. B. 2008. V. 77. id. 155425.
Govyadinov A.A., Panasyuk G.Y., Schotland J.C., Markel V.A. Theoretical and numerical investigation of the size dependent optical effects in metal nanoparticles // Phys. Rev. B. 2011. V. 84. id.155461.
Zapata-Herrera M., Camacho A.S., Ramírez H.Y. Influence of the confinement potential on the size-dependent optical response of metallic nanometric particles // Comput. Phys. Comm. 2018. V. 227. P. 1–8.
Shalaev V.M. Optical negative-index metamaterials // Nat. Photonics. 2007. V. 1. P. 41–48.
MacDonald K.F., Sámson Z.L., Stockman M.I., Zheludev N.I. Ultrafast active plasmonics // Nat. Photonics. 2009. V. 3. P. 55–58.
Nielsen R.B., Thoreson M.D., Chen W., Kristensen A., Hvam J.M., Shalaev V.M., Boltasseva A. Toward superlensing with metal–dielectric composites and multilayer // Appl. Phys. B. 2010. V. 100. P. 93–100.
Huang X., Jain P.K., El-Sayed I.H., El-Sayed M.A. Gold nanoparticles: interesting optical properties and recent applications in cancer diagnostics and therapy // Nanomedicine. 2007. V. 2. P. 681–693.
Freeman R.G., Grabar K.C., Allison K.J., Bright R.M., Davis J.A., Guthrie A.P., Hommer M.B., Jackson M.A., Smith P.C., Walter D.G., Natan M.J. Self-assembled metal colloid monolayers: an approach to SERS substrates // Science. 1995. V. 267. P. 1629–1632.
Andres R.P., Bielefeld J.D., Henderson J.I., Janes D.B., Kolagunta V.R., Kubiak C.P., Mahoney W.J., Osifchin R.G. Self-assembly of a two-dimensional superlattice of molecularly linked metal clusters // Science. 1996. V. 273. P. 1690–1693.
Балыкин В.И., Мелентьев П.Н. Оптика и спектроскопия единичной плазмонной наноструктуры // УФН. 2018. Т. 188. №2. С. 143–168.
Коротун А.В., Коваль А.А. Диэлектрический тензор металлической нанопроволочки с эллиптическим сечением // ФММ. 2019. Т. 120. №7. С. 675–680.
Kawabata A., Kubo R. Electronic properties of fine metallic particles. II. Plasma resonance absorption// J. Phys. Soc. Japan. 1966. V. 21. P. 1765–1772.
Huang W.C., Lue J.T. Quantum size effect on the optical properties of small metallic particles // Phys. Rev. B. 1994. V. 49. P. 17279–17285.
Sander L. Quantum theory of perpendicular electrical conductivity in a thin metallic film // J. Phys. Chem. Solids. 1968. V. 29. P. 291–294.
Cini M., Ascarelli P. Quantum size effects in metal particles and thin films by an extended RPA // J. Phys. F. 1974. V. 4. P. 1998–2008.
Blackman G.N. Genov D.A. Bounds on quantum confinement effects in metal nanoparticles // Phys. Rev. B. 2018. V. 97. id. 115440.
Kurbatsky V.P., Pogosov V.V. Optical conductivity of metal nanofilms and nanowires: The rectangular-box model // Phys. Rev. B. 2010. V. 81. id. 155404.
Korotun A.V. Size dependence of the Fermi energy of spherical metal nanocluster // J. Nano- Electron. Phys. 2015. V. 7. № 3. id. 03028.
Ашкрофт Н., Мермин Н. Физика твердого тела. М.: Мир, 1979. Т. 1. 400 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика металлов и металловедение

Архивы выпусков Информация о журнале Отправить рукопись в журнал