Физика металлов и металловедение, 2021, T. 122, № 4, стр. 339-346
Энергетический спектр и оптические свойства фуллерена C26 в модели Хаббарда
А. В. Силантьев *
Марийский государственный университет
424000 Йошкар-Ола, пл. Ленина, 1, Россия
* E-mail: kvvant@rambler.ru
Поступила в редакцию 14.11.2020
После доработки 01.12.2020
Принята к публикации 01.12.2020
Аннотация
В рамках модели Хаббарда в приближении среднего поля получены в аналитическом виде антикоммутаторные функции Грина и энергетические спектры фуллерена С26 и эндоэдрального фуллерена U@C26 с группой симметрии D3h. Используя методы теории групп, проведена классификация энергетических состояний, а также определены разрешенные переходы в энергетических спектрах молекул С26 и U@C26 с группой симметрии D3h.
ВВЕДЕНИЕ
После открытия в 1985 г. фуллерена С60 [1] началось интенсивное исследование углеродных кластеров. Эти исследования привели к открытию целого ряда фуллеренов Cn с n > 60, эндоэдральных фуллеренов A@Cn, а также нанотрубок. Исследования также проводили по поиску малых фуллеренов Cn с n < 60. В настоящее время большое число исследований посвящено изучению свойств малых фуллеренов: С20 [2, 3], С24 [4, 5], С28 [6, 7], С36 [8, 9]. Одним из малых является фуллерен С26, существование которого было экспериментально подтверждено в ряде работ [10, 11]. Исследованию физических и химических свойств фуллерена С26 посвящено довольно много работ [12–15].
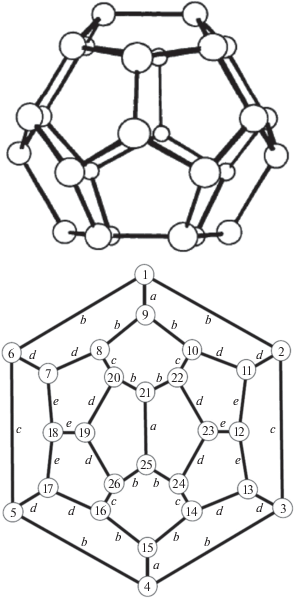
Фуллерен С26 c группой симметрии D3h состоит из 12 пентагонов и 3 гексагонов, как показано на диаграмме Шлегеля, рис. 1. Из диаграммы видно, что фуллерен С26 с группой симметрии D3h содержит пять неэквивалентных связей и четыре группы неэквивалентных атомов углерода: G1 = = {1, 4, 9, 15, 21, 25}, G2 = {2, 3, 5, 6, 8, 10, 14, 16, 20, 22, 24, 26}, G3 = {7, 11, 13, 17, 19, 23}, G4 = {12, 18}. Множеству G1 принадлежат атомы, которые находятся в вершинах сочленения одного гексагона и двух пентагонов, общая граница которых связывает два гексагона. Множеству G2 принадлежат атомы, которые находятся в вершинах сочленения одного гексагона и двух пентагонов, общая граница которых связывает гексагон и пентагон. Множеству G3 принадлежат атомы, которые находятся в вершинах сочленения трех пентагонов, общая граница которых связывает пентагон и гексагон. Множеству G4 принадлежат атомы, которые находятся в вершинах сочленения трех пентагонов, общая граница которых связывает два пентагона.
Рис. 1.
Фуллерен С26 с группой симметрии D3h и его диаграмма Шлегеля с указанием положения атомов углерода и связей между атомами углерода.
Для описания электронных свойств углеродных наносистем широко используется модель Хаббарда [16]. В рамках этой модели были изучены электронные и оптические свойства различных наносистем [17–25]. Так, например, в рамках модели Хаббарда в приближении среднего поля были получены энергетические спектры и спектры оптического поглощения фуллерена С60 [18], фуллерена С70 [19], фуллерена С36 с группой симметрии D6h [20], фуллерена С28 с группой симметрии Td [21], фуллерена С24 с группами симметрии Oh, D6 и D6d [22] и фуллерена С20 с группами симметрии Ih, D5d и D3d [23], в работе [24] были исследованы электронные свойства углеродных нанотрубок. Полученные в работах [18, 19] результаты достаточно хорошо согласуются с экспериментальными данными.
Целью данной работы является исследование энергетического спектра фуллерена С26 с группой симметрии D3h в рамках модели Хаббарда в приближении среднего поля.
ЭНЕРГЕТИЧЕСКИЙ СПЕКТР ФУЛЛЕРЕНА С26
Для описания π-электронной системы фуллерена С26 воспользуемся моделью Хаббарда [16]:
(1)
$H = \sum\limits_{\sigma ,i} {{{\varepsilon }_{i}}{{n}_{{i\sigma }}}} + \sum\limits_{\sigma ,i \ne j} {{{t}_{{ij}}}c_{{i\sigma }}^{ + }{{c}_{{j\sigma }}}} + \frac{1}{2}\sum\limits_{\sigma ,i} {{{U}_{i}}{{n}_{{i\sigma }}}{{n}_{{i\bar {\sigma }}}}} ,$Найдем энергетический спектр фуллерена С26 в приближении среднего поля. Для этого в гамильтониане (1) сделаем следующую замену:
(2)
${{n}_{{i\sigma }}}{{n}_{{i\bar {\sigma }}}} \to {{n}_{{i\sigma }}}\left\langle {{{n}_{{i\bar {\sigma }}}}} \right\rangle + {{n}_{{i\bar {\sigma }}}}\left\langle {{{n}_{{i\sigma }}}} \right\rangle ,$Подставляя соотношение (2) в гамильтониан (1), получим гамильтониан модели Хаббарда в приближении среднего поля:
(3)
$H = \sum\limits_{\sigma ,i} {\varepsilon _{{i\sigma }}^{'}{{n}_{{i\sigma }}}} + \sum\limits_{\sigma ,i \ne j} {{{t}_{{ij}}}c_{{i\sigma }}^{ + }{{c}_{{j\sigma }}}} ,$(4)
$\varepsilon _{{i\sigma }}^{'} = {{\varepsilon }_{i}} + U\left\langle {{{n}_{{\bar {\sigma }}}}} \right\rangle .$Поскольку в фуллерене С26 имеется четыре типа неэквивалентных связей, то, как видно из диаграммы Шлегеля, в рамках модели Хаббарда этим связям соответствуют четыре интеграла переноса:
Используя гамильтониан (3) и данные рис. 1, запишем уравнения движения для всех операторов рождения $c_{{f\sigma }}^{ + }(\tau ),$ заданных в представлении Гейзенберга:
(5)
$\left\{ \begin{gathered} \frac{{dc_{{1\sigma }}^{ + }}}{{d\tau }} = \varepsilon _{\sigma }^{'}c_{{{\text{1}}\sigma }}^{ + } + {{t}_{b}}\left( {c_{{2\sigma }}^{ + } + c_{{6\sigma }}^{ + }} \right) + {{t}_{a}}c_{{9\sigma }}^{ + } \hfill \\ ...................................................... \hfill \\ \frac{{dc_{{{\text{26}}\sigma }}^{ + }}}{{d\tau }} = \varepsilon _{\sigma }^{'}c_{{{\text{26}}\sigma }}^{ + } + {{t}_{b}}c_{{{\text{25}}\sigma }}^{ + } + {{t}_{c}}c_{{{\text{16}}\sigma }}^{ + } + {{t}_{d}}c_{{{\text{19}}\sigma }}^{ + } \hfill \\ \end{gathered} \right.\,\,.$Система уравнений (5) имеет точное аналитическое решение. Используя это решение, можно найти фурье-образы антикоммутаторных функций Грина:
(6)
$\left\langle {\left\langle {{c_{{j\sigma }}^{ + }}} \mathrel{\left | {\vphantom {{c_{{j\sigma }}^{ + }} {{{c}_{{j\sigma }}}}}} \right. \kern-0em} {{{{c}_{{j\sigma }}}}} \right\rangle } \right\rangle = \frac{i}{{2\pi }}\sum\limits_{m = 1}^{18} {\frac{{{{Q}_{{j,m}}}}}{{E - {{E}_{m}} + ih}}} ,\,\,\,\,{{E}_{m}} = \varepsilon {\kern 1pt} '\,\, + {{e}_{m}},$где
(7)
$\begin{gathered} {{Q}_{{s,k}}} = \frac{1}{2}\left( {e_{k}^{3} - e_{k}^{2}({{t}_{a}} + {{t}_{c}}) + {{e}_{k}}\left( {{{t}_{a}}{{t}_{c}} - 2t_{b}^{2} - 2t_{d}^{2}} \right) + } \right. \\ \left. { + \,\,2{{t}_{a}}t_{d}^{2}} \right):\left( {4e_{k}^{3} - 3e_{k}^{2}({{t}_{a}} + {{t}_{c}}) + } \right. \\ \left. { + \,\,2\left( {{{t}_{c}}{{t}_{a}} - 3t_{e}^{2} - 2t_{b}^{2} - 2t_{d}^{2}} \right){{e}_{k}} + \,\,3t_{e}^{2}({{t}_{a}} + {{t}_{c}}) + 2t_{d}^{2}{{t}_{a}}} \right), \\ k = 10,\,\,11,\,\,12,\,\,13;\,\,\,\,x \in {{G}_{1}},\,\,\,\,y \in {{G}_{2}},\,\,\,\,p \in {{G}_{3}},\,\,\,\,s \in {{G}_{4}}; \\ \end{gathered} $(8)
$\begin{gathered} {{\varphi }_{2}} = \arccos \left( {\frac{{{{t}_{c}}\left( {t_{c}^{2} + 9t_{d}^{2} - 27t_{e}^{2}} \right)}}{{{{{\left( {t_{c}^{2} + 6t_{d}^{2} + 9t_{e}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right), \\ {{\varphi }_{3}} = \arccos \left( {\frac{{{{3}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}t_{d}^{2}{{t}_{c}}}}{{2{{{(t_{c}^{2} + 2t_{d}^{2})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right), \\ \end{gathered} $(9)
$\begin{gathered} {{x}^{5}} - \left( {t_{a}^{2} + 4t_{b}^{2} + t_{c}^{2} + 2t_{d}^{2}} \right){{x}^{3}} + t_{d}^{2}{{t}_{c}}{{x}^{2}} - 4t_{d}^{2}t_{b}^{2}{{t}_{a}} - \\ - \,\,t_{a}^{2}t_{d}^{2}{{t}_{c}} + \left( {4t_{d}^{2}t_{b}^{2} + 4t_{b}^{4} + t_{a}^{2}t_{c}^{2} + 2t_{a}^{2}t_{d}^{2} + 2t_{b}^{2}{{t}_{c}}{{t}_{a}}} \right)x = 0. \\ \end{gathered} $Зная фурье-образ антикоммутаторной функции Грина, можно найти энергетический спектр квантовой системы, который определяется полюсами функции Грина [26]. Следовательно, энергетический спектр фуллерена С26 с группой симметрии D3h определяется величинами Em, которые входят в функцию Грина (6). Отметим, что величины ${{e}_{m}},$ которые определяются соотношениями (7), характеризуют энергетический спектр фуллерена С26 относительно энергии $\varepsilon {\kern 1pt} '.$
Энергетические состояния фуллерена С26 с группой симметрии D3h можно классифицировать в соответствии с неприводимыми представлениями группы D3h. Как известно, группа D3h имеет четыре одномерных неприводимых представлений $a_{1}^{'},$ $a_{1}^{{''}},$ $a_{2}^{'},$ $a_{2}^{{''}}$ и два двумерных неприводимых представлений $e{\kern 1pt} ',$ $e{\kern 1pt} ''$ [27]. Можно показать, что энергетические состояния фуллерена С26, определяемые полюсами функции Грина (6), связаны следующим образом с неприводимыми представлениями группы D3h: ${{E}_{1}}(a_{1}^{{''}}),$ ${{E}_{2}}(a_{2}^{'}),$ ${{E}_{3}}(a_{2}^{'}),$ ${{E}_{4}}(e{\kern 1pt} ''),$ ${{E}_{5}}(e{\kern 1pt} ''),$ ${{E}_{6}}(e{\kern 1pt} ''),$ ${{E}_{7}}(a_{2}^{{''}}),$ ${{E}_{8}}(a_{2}^{{''}}),$ ${{E}_{9}}(a_{2}^{{''}}),$ ${{E}_{{10}}}(a_{1}^{'}),$ ${{E}_{{11}}}(a_{1}^{'}),$ ${{E}_{{12}}}(a_{1}^{'}),$ ${{E}_{{13}}}(a_{1}^{'}),$ ${{E}_{{14}}}(e{\kern 1pt} '),$ ${{E}_{{15}}}(e{\kern 1pt} '),$ ${{E}_{{16}}}(e{\kern 1pt} '),$ ${{E}_{{17}}}(e{\kern 1pt} '),$ ${{E}_{{18}}}(e{\kern 1pt} ').$
Важной физической характеристикой каждого энергетического уровня квантовой системы является степень его вырождения. Для того чтобы найти степень вырождения энергетических уровней фуллерена C26, воспользуемся следующим соотношением [18, 19]:
где N – число узлов в наносистеме.Подставляя величины Qj,i, которые определяются соотношениями (7), в формулу (10), получим для степеней вырождения энергетических уровней фуллерена C26 следующие значения:
(11)
$\begin{gathered} {{g}_{1}} = {{g}_{2}} = {{g}_{3}} = {{g}_{7}} = {{g}_{8}} = \\ = {{g}_{9}} = {{g}_{{10}}} = {{g}_{{11}}} = {{g}_{{12}}} = {{g}_{{13}}} = 1, \\ {{g}_{4}} = {{g}_{5}} = {{g}_{6}} = {{g}_{{14}}} = {{g}_{{15}}} = {{g}_{{16}}} = {{g}_{{17}}} = {{g}_{{18}}} = 2. \\ \end{gathered} $Таким образом, соотношения (8) и (11) описывают энергетические спектры фуллерена С26 с группой симметрии D3h в модели Хаббарда в приближении среднего поля.
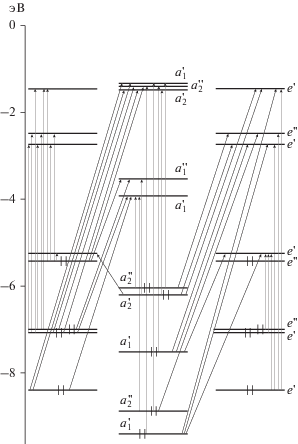
Результаты данных вычислений приведены в табл. 1, а также на рис. 2, и из них следует, что энергетический спектр фуллерена С26 с группой симметрии D3h состоит из 18 энергетических состояний, из которых 10 состояний не вырождены, а 8 состояний являются двукратно вырожденными.
Таблица 1.
Энергетический спектр фуллерена С26 с группой симметрии D3h: значения энергии уровней, кратность их вырождения и неприводимые представления группы D3h, к которым они относятся
| № | ej, eV | Ej, eV | gj | E (Гj) |
|---|---|---|---|---|
| 1 | –4.444 | –9.423 | 1 | ${{E}_{{13}}}(a_{1}^{'})$ |
| 2 | –3.904 | –8.883 | 1 | ${{E}_{9}}(a_{2}^{{''}})$ |
| 3 | –3.426 | –8.405 | 2 | ${{E}_{{18}}}(e{\kern 1pt} ')$ |
| 4 | –2.535 | –7.514 | 1 | ${{E}_{{12}}}(a_{1}^{'})$ |
| 6 | –2.086 | –7.065 | 2 | ${{E}_{{17}}}(e{\kern 1pt} ')$ |
| 5 | –2.036 | –7.016 | 2 | ${{E}_{6}}(e{\kern 1pt} '')$ |
| 8 | –1.212 | –6.192 | 1 | ${{E}_{3}}(a_{2}^{'})$ |
| 7 | –1.071 | –6.051 | 1 | ${{E}_{8}}(a_{2}^{{''}})$ |
| 9 | –0.454 | –5.433 | 2 | ${{E}_{5}}(e{\kern 1pt} '')$ |
| 10 | –0.286 | –5.265 | 2 | ${{E}_{{16}}}(e{\kern 1pt} ')$ |
| 11 | 1.058 | –3.922 | 1 | ${{E}_{{11}}}(a_{1}^{'})$ |
| 12 | 1.448 | –3.531 | 1 | ${{E}_{1}}(a_{1}^{{''}})$ |
| 13 | 2.242 | –2.738 | 2 | ${{E}_{{14}}}(e{\kern 1pt} ')$ |
| 14 | 2.490 | –2.489 | 2 | ${{E}_{4}}(e{\kern 1pt} '')$ |
| 16 | 3.503 | –1.477 | 1 | ${{E}_{2}}(a_{2}^{'})$ |
| 15 | 3.556 | –1.424 | 2 | ${{E}_{{15}}}(e{\kern 1pt} ')$ |
| 17 | 3.527 | –1.453 | 1 | ${{E}_{7}}(a_{2}^{{''}})$ |
| 18 | 3.630 | –1.349 | 1 | ${{E}_{{10}}}(a_{1}^{'})$ |
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Исследования, выполненные в работе [15], показали, что расстояния между атомами углерода в фуллерене С26 с группой симметрии D3h имеют следующие значения:
(12)
$\begin{gathered} {{x}_{a}} = 1.540\,\,{\text{{\AA}}},\,\,\,{{x}_{b}} = 1.428\,\,{\text{{\AA}}},\,\,\,{{x}_{c}} = 1.450\,\,{\text{{\AA}}},\,\,\, \\ {{x}_{d}} = 1.473\,\,{\text{{\AA}}},\,\,\,{{x}_{e}} = 1.410\,\,{\text{{\AA}}}{\text{.}} \\ \end{gathered} $Для того чтобы найти численные значения интегралов переноса, которые соответствуют фуллерену С26, воспользуемся следующим соотношением [19, 22]:
Подставляя (12) в соотношение (13), получим численные значения интегралов переноса для фуллерена С26 с группой симметрии D3h:
(14)
$\begin{gathered} {{t}_{a}} = - 0.84231\,\,{\text{эВ}},\,\,\,\,{{t}_{b}} = - 1.65319\,\,{\text{эВ}}, \\ {{t}_{c}} = - 1.44809\,\,{\text{эВ}},\,\,\,\,{{t}_{d}} = - 1.26083\,\,{\text{эВ}}, \\ {{t}_{e}} = - 1.84241\,\,{\text{эВ}}. \\ \end{gathered} $Подставляя численные значения интегралов переноса (14) в соотношение (8), получим для фуллерена С26 численные значения для величин ${{e}_{k}},$ которые приведены в табл. 1.
Теперь, как это следует из (6), для того чтобы получить энергетический спектр фуллерена С26, следует воспользоваться следующей формулой:
Подставляя численные значения для ${{e}_{k}}$ из табл. 1, а также ε' = –4.979 эВ [19] в соотношение (15), получим энергетический спектр фуллерена С26 с группой симметрии D3h. Результаты вычислений приведены в табл. 1, а также на рис. 2.
Рассмотрим структуру энергетического спектра фуллерена С26. Как видно из соотношения (15) и рис. 2, в энергетической зоне фуллерена С26 энергетические уровни сосредоточены вблизи энергии
(16)
$\varepsilon {\kern 1pt} ' = \varepsilon + U\left\langle {{{n}_{{\bar {\sigma }}}}} \right\rangle .$Из соотношений (15), (8), (11), рис. 2 и табл. 1 следует, что в основном состоянии у фуллерена С26 с группой симметрии D3h на энергетическом уровне, который соответствует энергии ${{E}_{{16}}}(e{\kern 1pt} '),$ расположены две связывающие орбитали, на которых отсутствуют электроны. Поэтому фуллерен С26 с группой симметрии D3h должен обладать довольно высокой химической активностью. Стабилизацию фуллерена С26 можно осуществить при помощи образования эндофуллеренов M@С26 с элементами, которые помещаются внутрь фуллерена и способны принимать электронные конфигурации M4+. В качестве таких элементов могут выступать, например, Ti, U. При образовании эндоэдральных фуллеренов M@С26, четыре валентных электрона атома металла переходят в оболочку фуллерена С26. Считается, что внедрение атома металла внутрь фуллерена не приводит к существенному изменению его энергетических уровней. Поэтому в первом приближении можно считать, что влияние внедренного атома приводит лишь к добавлению лишних электронов в остов фуллерена [28]. Четыре электрона, перешедшие с атома металла на фуллерен С26, займут энергетический уровень ${{E}_{{16}}}(e{\kern 1pt} ').$ Проведенные исследования показали [15], что эндоэдральный фуллерен U@С26, как и фуллерен С26, обладает группой симметрии D3h. Исследования эндоэдрального фуллерена U@С26 также показали [15], что расстояния между атомами углерода в этой молекуле имеют следующие значения:
(17)
$\begin{gathered} {{x}_{a}} = 1.531\,\,{\text{{\AA}}},\,\,\,{{x}_{b}} = 1.480\,\,{\text{{\AA}}},\,\,\,{{x}_{c}} = 1.486\,\,{\text{{\AA}}},\,\,\, \\ {{x}_{d}} = 1.514\,\,{\text{{\AA}}},\,\,\,{{x}_{e}} = 1.433\,\,{\text{{\AA}}}{\text{.}} \\ \end{gathered} $Подставляя (17) в соотношение (13), получим численные значения интегралов переноса у молекулы U@С26:
(18)
$\begin{gathered} {{t}_{a}} = - 0.88921\,\,{\text{эВ}},\,\,\,\,{{t}_{b}} = - 1.20880\,\,{\text{эВ}}, \\ {{t}_{c}} = - 1.16591\,\,{\text{эВ}},\,\,\,\,{{t}_{d}} = - 0.98504\,\,{\text{эВ}}, \\ {{t}_{e}} = - 1.60416\,\,{\text{эВ}}. \\ \end{gathered} $Подставляя численные значения интегралов переноса (18) в соотношение (8), получим для эндоэдрального фуллерена U@С26 численные значения величин ${{e}_{k}},$ которые приведены в табл. 2.
Таблица 2.
Энергетический спектр эндофуллерена U@С26 с группой симметрии D3h: значения энергии уровней, кратность их вырождения и неприводимые представления группы D3h, к которым они относятся
| № | ej,eV | Ej,eV | gj | E(Гj) |
|---|---|---|---|---|
| 1 | –3.592 | –7.700 | 1 | ${{E}_{{13}}}(a_{1}^{'})$ |
| 2 | –3.276 | –7.384 | 1 | ${{E}_{9}}(a_{2}^{{''}})$ |
| 3 | –2.644 | –6.752 | 2 | ${{E}_{{18}}}(e{\kern 1pt} ')$ |
| 4 | –2.148 | –6.256 | 1 | ${{E}_{{12}}}(a_{1}^{'})$ |
| 5 | –1.612 | –5.720 | 2 | ${{E}_{6}}(e{\kern 1pt} '')$ |
| 6 | –1.524 | –5.632 | 2 | ${{E}_{{17}}}(e{\kern 1pt} ')$ |
| 7 | –0.910 | –5.018 | 1 | ${{E}_{8}}(a_{2}^{{''}})$ |
| 8 | –0.688 | –4.796 | 1 | ${{E}_{3}}(a_{2}^{'})$ |
| 9 | –0.357 | –4.465 | 2 | ${{E}_{5}}(e{\kern 1pt} '')$ |
| 10 | –0.308 | –4.416 | 2 | ${{E}_{{16}}}(e{\kern 1pt} ')$ |
| 11 | 0.615 | –3.493 | 1 | ${{E}_{{11}}}(a_{1}^{'})$ |
| 12 | 1.166 | –2.942 | 1 | ${{E}_{1}}(a_{1}^{{''}})$ |
| 13 | 1.763 | –2.345 | 2 | ${{E}_{{14}}}(e{\kern 1pt} ')$ |
| 14 | 1.968 | –2.140 | 2 | ${{E}_{4}}(e{\kern 1pt} '')$ |
| 15 | 2.712 | –1.396 | 2 | ${{E}_{{15}}}(e{\kern 1pt} ')$ |
| 16 | 2.743 | –1.365 | 1 | ${{E}_{2}}(a_{2}^{'})$ |
| 17 | 3.020 | –1.088 | 1 | ${{E}_{7}}(a_{2}^{{''}})$ |
| 18 | 3.070 | –1.038 | 1 | ${{E}_{{10}}}(a_{1}^{'})$ |
Из соотношения (16) следует, что при помещении атома металла внутрь фуллерена происходит смещение энергии $\varepsilon {\kern 1pt} '{\text{:}}$
(19)
$\varepsilon {\kern 1pt} ' = \left\{ \begin{gathered} \varepsilon _{{{{{\text{C}}}_{n}}}}^{'},\,\,\,\,{\text{для}}\,\,\,\,{{{\text{C}}}_{n}} \hfill \\ \varepsilon _{{{{{\text{C}}}_{n}}}}^{'} + {{qU} \mathord{\left/ {\vphantom {{qU} n}} \right. \kern-0em} n},\,\,\,\,{\text{для}}\,\,\,\,{{{\text{M}}}^{{ + q}}}{\text{@C}}_{n}^{{ - q}} \hfill \\ \end{gathered} \right.,$Из соотношения (19) следует, что при помещении атома урана внутрь фуллерена С26 параметр $\varepsilon {\kern 1pt} '$ смещается на десятые доли электрон-вольта:
(20)
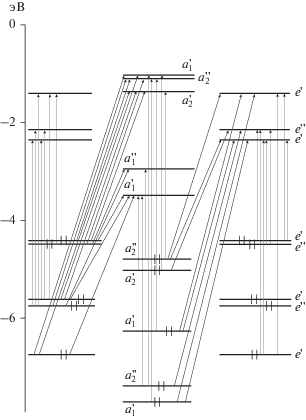
$\begin{gathered} \varepsilon _{{{\text{U@}}{{{\text{C}}}_{{26}}}}}^{'} = \varepsilon _{{{{{\text{C}}}_{{26}}}}}^{'} + \frac{{qU}}{n} = - 4.979 + \\ + \,\,\frac{{4 \times 5.662}}{{26}} = - 4.108\,\,{\text{эВ}}, \\ \end{gathered} $Из рис. 2, 3, табл. 1 и 2 видно, что энергетические спектры молекул С26 и U@С26 отличаются друг от друга относительным расположением энергетических состояний ${{E}_{{17}}}(e{\kern 1pt} '),$ ${{E}_{6}}(e{\kern 1pt} ''),$ ${{E}_{3}}(a_{2}^{'}),$ ${{E}_{8}}(a_{2}^{{''}}),$ ${{E}_{2}}(a_{2}^{'}),$ ${{E}_{{15}}}(e{\kern 1pt} ').$
Рис. 3.
Энергетический спектр U@С26 с группой симметрии D3h. Вертикальными стрелками показаны разрешенные переходы.
Одной из важнейших характеристик квантовой системы является спектр оптического поглощения. Используя полученные выше энергетические спектры молекул С26 и U@С26 с группой симметрии D3h, можно найти переходы, которые обуславливают оптические спектры этих молекул. С помощью теории групп [29] найдем, какие переходы в молекулах С26 и U@С26 разрешены, а какие запрещены с точки зрения симметрии.
Можно показать, что в энергетическом спектре молекулы с группой симметрии D3h разрешены следующие переходы:
(21)
$\begin{gathered} a_{1}^{'} \leftrightarrow e{\kern 1pt} ',\,\,\,\,a_{2}^{'} \leftrightarrow e{\kern 1pt} ',\,\,\,\,e{\kern 1pt} ' \leftrightarrow e{\kern 1pt} ',\,\,\,\,a_{1}^{{''}} \leftrightarrow e{\kern 1pt} '', \\ a_{2}^{{''}} \leftrightarrow e{\kern 1pt} '',\,\,\,\,e{\kern 1pt} '' \leftrightarrow e{\kern 1pt} '',\,\,\,\,a_{1}^{'} \leftrightarrow a_{2}^{{''}},\,\,\,\,a_{2}^{'} \leftrightarrow a_{1}^{{''}},\,\,\,\,e{\kern 1pt} ' \leftrightarrow e{\kern 1pt} ''. \\ \end{gathered} $Из анализа энергетических спектров (8), (11), (15) и (21) следует, что фуллерен С26 имеет 45 разрешенных переходов, молекула U@С26 имеет 44 разрешенных перехода. Разрешенные переходы в молекулах С26 и U@С26 показаны вертикальными стрелками на рис. 2 и 3 соответственно. Из рисунков видно, в результате внедрения атома урана в фуллерен С26 семь разрешенных переходов исчезают с двух связывающих орбиталей с энергией ${{E}_{{16}}}(e{\kern 1pt} '),$ так как четыре электрона, перешедших с атома урана на фуллерен С26, заполняют четыре свободных энергетических состояния на двух связывающих орбиталях с энергией ${{E}_{{16}}}(e{\kern 1pt} ').$ При этом появляются шесть новых переходов со связывающих орбиталей с энергией ${{E}_{{16}}}(e{\kern 1pt} ').$
ЗАКЛЮЧЕНИЕ
Исследование фуллерена С26 с группой симметрии D3h в рамках модели Хаббарда в приближении среднего поля показало, что в основном состоянии в этом фуллерене энергетический уровень ${{E}_{{16}}}(e{\kern 1pt} ')$ дважды вырожден и на этом уровне находятся две связывающие орбитали, при этом электроны на них отсутствуют. Это приводит к тому, что фуллерен С26 с группой симметрии D3h является неустойчивой молекулой. Образование эндофуллерена U@С26 приводит к образованию устойчивой молекулы за счет перехода четырех электронов от атома урана на фуллерен С26. Кроме того, данные исследования показали, что в формировании оптических спектров поглощения молекул С26 и U@С26 участвуют 45 и 44 разрешенных переходов соответственно.
Отметим также, что исследования оптических свойств фуллеренов C60 и С70, выполненные в рамках модели Хаббарда [18, 19], показали хорошее соответствие между экспериментальными данными и теоретическими результатами. Это позволяет считать, что модель Хаббарда в приближении среднего поля достаточно хорошо описывает электронные свойства углеродных наносистем.
Список литературы
Kroto H.W., Heath J.R., O’Brien S.C., Curl R.F., Smalley R.E. C60: Buckminsterfullerene // Nature 1985. V. 318. P. 162–163.
Yi-Peng An, Chuan-Lu Yang, Mei-Shan Wang, Xiao-Guang Ma, De-Hua Wang. First-principles study of structure and quantum transport properties of C20 fullerene // J. Chem. Phys. 2009. V. 131. P. 024 311.
Katin K.P., Maslov M.M. Stone-Wales defects in nitrogen-doped C20 fullerenes: Insight from ab initio calculations // Physica E. 2018. V. 96. P. 6–10.
Lin W.-H., Tu Ch.-Ch., Lee S.-L. Theoretical studies of growth mechanism of small fullerene cage C24(D6d)+// Inter. J. Quantum Chem. 2005. V. 103 P. 355–368.
Zhang Y., Cheng X. Hydrogen storage property of alkali and alkaline-earth metal atoms decorated C24 fullerene: A DFT study // Chem. Phys. 2018. V. 505. P. 26–33.
Dognon J.-P., Clavaguera C., Pyykko P. A Predicted Organometallic Series Following a 32-Electron Principle: An@C28 (An = Th, Pa+, U2+, Pu4+) // J. Am. Chem. Soc. 2009. V. 131. P. 238–243.
Enyashin A.N., Ivanovskii A.L. Structural, electronic and elastic properties of ultra-light diamond-like crystalline allotropes of carbon-functionalized fullerenes C28 // Chem. Phys. Letters. 2009. V. 473. P. 108–110.
Naderi1 F., Rostamian S., Naderi B. A study on the electronic and structural properties of fullerene C36 and its interaction with amino acid // Inter. J. Phys. Sci. 2012. V. 7. 2006–2009.
Grishakov K.S., Katin K.P., Maslov M.M. Strain-induced semiconductor-to-metal transitions in C36-based carbon peapods: Ab initio study// Diamond & Related Materials. 2018. V. 84. P. 112–118.
Hallett R.P., McKay K.G., Balm S.P., Allaf A.W., Kroto H.W., Stace A.J. Reaction studies of carbon clusters// Z. Phys. D. 1995. V. 34. P. 65–70.
Wang Z.X., Wang W.M., Zhu F.Y., Li X.P., Ruan M.L., Chen H., Huang R.B., Zheng L.S. Synthesis of C26 crystallite polyethylene by ${\text{C}}_{{\text{2}}}^{ + }$ ion bombardment // High Energy Phys. Nucl. Phys. 2001. V. 25. P. 69–73.
Kent R.C., Towler M.D., Needs R.J., Rajagopal G. Carbon clusters near the crossover to fullerene stability// Phys. Rev. B. 2000. V. 62. P. 15 394.
Maruyama M., Okada S. Two-Dimensional Metallic Molecular Sheet of Fused C26 Fullerene // J. Phys. Soc. Jpn. 2013. V. 82. P. 043 708.
Hong B., Chang Y., Jalbout A.F., Su Z., Wang R. On the chlorides of C26 fullerene. A theoretical study // Molecular Physics. 2007. V. 105. P. 95–99.
Manna D., Ghanty T.K. Prediction of a New Series of Thermodynamically Stable Actinide Encapsulated Fullerene Systems Fulfilling the 32-Electron Principle // J. Phys. Chem. C. 2012. V. 116. P. 25 630–25 641.
Hubbard J. Electron correlations in narrow energy bands // Proc. Roy. Soc. London A. 1963. V. 276. P. 238–257.
Силантьев А.В. Исследование наносистем в модели Хаббарда в приближении среднего поля // Известия Вузов. Поволжский регион. Физ.-мат. науки. 2016. № 1. С. 101–112.
Силантьев А.В. Энергетический спектр и оптические свойства фуллерена C60 в модели Хаббарда // ФММ. 2017. Т. 118. № 1 С. 3–11.
Силантьев А.В. Энергетический спектр и оптические свойства фуллерена C70 в модели Хаббарда // Оптика и спектроскопия. 2018. Т. 124. № 2. С. 159–166.
Силантьев А.В. Энергетический спектр и оптические свойства фуллерена C36 в модели Хаббарда // Оптика и спектроскопия. 2019. Т. 127. № 2. С. 191–199.
Силантьев А.В. Энергетический спектр и оптические свойства фуллерена C28 в модели Хаббарда // ФММ. 2020. Т. 121. № 6. С. 557–563.
Силантьев А.В. Энергетический спектр и оптические свойства фуллерена C24 в модели Хаббарда // ФММ. 2020. Т. 121. № 3. С. 227–234.
Силантьев А.В. Влияние деформации на энергетический спектр и оптические свойства фуллерена C20 в модели Хаббарда // ФММ. 2018. Т. 119. № 6. С. 541–549.
Иванченко Г.С., Лебедев Н.Г. Проводимость двухслойных углеродных нанотрубок в рамках модели Хаббарда // ФТТ. 2007. Т. 49. С. 183–189.
Силантьев А.В. Энергетический спектр и спектр оптического поглощения фуллерена С60 в модели Хаббарда // ЖЭТФ. 2015. Т. 148. № 4. С. 749–757.
Тябликов С.В. Методы квантовой теории магнетизма. М.: Наука, 1975. 527 с.
Каплан И.Г. Симметрия многоэлектронных систем. М. Наука, 1969. 427 с.
Елецкий А.В. Эндоэдральные структуры // УФН. 2000. Т. 170. № 2. С. 113–142.
Вигнер Е.П. Теория групп и ее приложения к квантовомеханической теории спектров. М.: ИИЛ, 1961. 564 с.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение