Физика металлов и металловедение, 2021, T. 122, № 4, стр. 347-369
Электрические и магнитные свойства “модели смешения бинарных гетерогенных систем”
С. Н. Старостенко a, *, К. Н. Розанов a, А. Н. Лагарьков a
a Институт теоретической и прикладной электродинамики РАН
125412 Москва, ул. Ижорская, 13, Россия
* E-mail: snstar@itae.ru
Поступила в редакцию 17.08.2020
После доработки 12.11.2020
Принята к публикации 17.11.2020
Аннотация
Приведен сравнительный анализ моделей смешения, используемых в радиофизике для описания эффективных свойств композитных материалов, сформулированы ограничения применимости моделей смешения и критерии проверки их корректности. Выбраны две наиболее общие модели, учитывающие трансформацию структуры композита при изменении его состава. Рассмотрена проблема соответствия выбранной модели результатам эксперимента. Показано влияние структуры композита на частоту максимума и форму линии его диэлектрического поглощения. Из проведенного анализа следует, что усложнение моделей по сравнению с уже известными и увеличение числа определяемых из эксперимента параметров нецелесообразно при имеющейся погрешности измерений состава, материальных параметров (диэлектрической и магнитной проницаемостей) композита, а также существенном вкладе размерных и поверхностных эффектов, не учитываемом в квазистатических моделей смешения.
ВВЕДЕНИЕ
Большая часть используемых в технике и встречающихся в природе материалов является гетерогенными системами. Модели смешения (физически обоснованные формулы, связывающие свойства смеси со свойствами и концентрацией ее компонентов) используют для расчета широкого круга явлений переноса в гетерогенных средах, а также состава и структуры этих сред: в медицине для оценки пористости костной ткани по измерениям ее импеданса [1], в химии для оценки коэффициентов диффузии [2], в геологии для оценки влагопроницаемости почв (ламинарное течение жидкости по порам) [3, 4] в теплофизике для оценки теплопроводности композитов [5, 6], в механике для расчета модуля упругости и скорости звука [7, 8] и т.д. Классические бинарные (двухкомонентные) модели (формулы Максвелла Гарнетта [9], Брюггемана [10], Ландау–Лифшица–Лоенги [11, 12]) выведены из первых принципов и являются строгими, но описывают идеализированные структуры, редко встречающиеся на практике. Дальнейшее развитие теории шло по пути использования коэффициентов, определяемых из эксперимента. Обзорные работы по связи свойств композита и его компонентов известны с 50-х гг. [13, 14], но подобные работы продолжают появляться до настоящего времени [15–17], что свидетельствует об отсутствии удовлетворительного решения и, соответственно, об актуальности этой проблемы.
Наиболее высокие требования к формулам смешения предъявляет радиофизика, в рамках которой и проводится представленный ниже анализ известных моделей смешения. В радиофизике обычно требуется описание динамических материальных параметров композитов, а именно зависящих от частоты комплексных диэлектрической и магнитной проницаемостей, тогда как известные модели смешения выведены в статическом приближении. В них не рассматривается масштаб неоднородности в композите по отношению к длине волны и игнорируется тот факт, что динамические параметры композита могут быть обусловлены не только свойствами составляющие его компонентов, но и, например, гранулометрией, формой и чистотой поверхности электропроводящих частиц. Частично эти проблемы решаются введением эффективных свойств частиц наполнителя. Эффективные свойства частицы, в отличие от свойств составляющего ее вещества, могут зависеть от ее формы, размера, чистоты поверхности и т.д.
При анализе композита (гетерогенной системы) с требуемыми свойствами (упругостью, проводимостью, диэлектрической или магнитной проницаемостью и т.д.) необходимо усреднить эти свойства по объему системы путем введения эффективных (соответствующих гомогенной системе) параметров, корректно учитывающих структуру композита. С практической точки зрения при этом возникают две задачи: (1) вычисление восприимчивости смеси по составу и восприимчивости ее компонентов (прямая задача смешения) и (2) определение восприимчивости одного из компонентов смеси по измеренной восприимчивости смеси и ее составу (обратная задача смешения). Решению этих задач препятствует неопределенность в выборе модели смешения из множества известных (табл. 1–4) даже в бинарных системах.
Таблица 1.
Строго выведенные модели, не имеющие эмпирических параметров
| Матричные структуры | Симметричные структуры | Малый контраст свойств компонентов |
|---|---|---|
| ${{\chi }_{{32}}} = \frac{{3{{\chi }_{{12}}}p}}{{{{\chi }_{{12}}}\left( {1 - p} \right) + 3}}$ прямая формула Клаузиус–Мосотти, 1850; Лорентц–Лоренц, 1880; Максвелл–Гарнетт, 1904; Вагнер, 1914 |
$\frac{{p\left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right)}}{{3 + {{\chi }_{{12}}} + 2{{\chi }_{{32}}}}} = \frac{{{{\chi }_{{32}}}(1 - p)}}{{3 + 2{{\chi }_{{32}}}}}$ симметричная формула Брюггеман, 1936 |
${{\left( {{{\chi }_{{32}}} + 1} \right)}^{{1/3}}} - 1 = p\left[ {{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{{1/3}}} - 1} \right]$ Ландау–Лифшиц–Лоенга, 1938, 1965 ${\text{lg}}\left( {{{\chi }_{{32}}} + 1} \right) = p{\kern 1pt} {\text{lg}}\left( {{{\chi }_{{12}}} + 1} \right)$ Лихтенекер, 1926, ${{\chi }_{{12}}}\left( {1 - p} \right) = \left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right){{\left( {{{\chi }_{{32}}} + 1} \right)}^{{ - 1/3}}}$ асимметричная формула Брюггемана, низкое наполнение 1935, формула Ханая (обобщение на динамические свойства), 1968 |
Таблица 2.
Модели с эмпирическим форм-фактором N компонента 1 (включений)
| Матричные структуры | Гибридные структуры | Симметричные структуры | Малый контраст свойств компонентов, дифференциальные формулы |
|---|---|---|---|
| ${{\chi }_{{32}}} = \frac{p}{{\left( {1 - p} \right)N + \frac{1}{{{{\chi }_{{12}}}}}}}$ обобщенная прямая формула Максвелла Гарнетта, Оллендорф, 1931, Оделевский, 1947 $\begin{gathered} {{\chi }_{{32\_{\text{inv}}}}} = p{{\chi }_{{12}}} \times \\ \times \,\,\frac{{1 + {{\chi }_{{12}}} - N{{\chi }_{{12}}}}}{{1 + {{\chi }_{{12}}} - Np{{\chi }_{{12}}}}} \\ \end{gathered} $ обобщенная инверсная формула Максвелл Гарнетта |
${{\chi }_{a}} = \frac{{3{{\chi }_{{12}}}p}}{{{{\chi }_{{12}}}\left( {1 - p} \right) + 3}}$ ${{\chi }_{b}} = p{{\chi }_{{12}}}\frac{{3 + 3{{\chi }_{{12}}} - {{\chi }_{{12}}}}}{{3 + 3{{\chi }_{{12}}} - p{{\chi }_{{12}}}}}$${{\chi }_{{\frac{{{\text{mix}}}}{b}}}} = \frac{{3{{P}_{{{\text{fit}}}}}{{\chi }_{{a/b}}}}}{{{{\chi }_{{a/b}}} + 3 - {{P}_{{{\text{fit}}}}}{{\chi }_{{a/b}}}}}$ Мусал–Хан–Буш, 1988 |
$\begin{gathered} \frac{{p\left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right)}}{{1 + N{{\chi }_{{12}}} + {{\chi }_{{32}}}\left( {1 - N} \right)}} = \hfill \\ = \frac{{(1 - p){{\chi }_{{32}}}}}{{1 + {{\chi }_{{32}}}\left( {1 - N} \right)}} \hfill \\ \end{gathered} $ обобщенная симметричная формула Брюггемана $\frac{{p\left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right)}}{{1 + N{{\chi }_{{12}}} + {{\chi }_{{32}}}}} = \frac{{(1 - p){{\chi }_{{32}}}}}{{1 + {{\chi }_{{32}}}}}$ когерентный потенциал 1968 |
$\begin{gathered} {{\left( {{{\chi }_{{32}}} + 1} \right)}^{{1/\left( {1 - 2N} \right)}}} - 1 = \hfill \\ = \,\,p\left[ {{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{{1/\left( {1 - 2N} \right)}}} - 1} \right] \hfill \\ \end{gathered} $ Лоенга–Бойль, 1985, $\begin{gathered} {\text{lg}}\left( {{{\chi }_{{32}}} + 1} \right) = \hfill \\ = p\left( {1 - N} \right){\text{lg}}\left( {{{\chi }_{{12}}} + 1} \right) \hfill \\ \end{gathered} $ Лихтенеккер–Ротер, 1931 ${{\chi }_{{12}}}\left( {1 - p} \right) = \left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right){{\left( {{{\chi }_{{32}}} + 1} \right)}^{{ - N}}}$ асимметричная формула Ханай–Брюггеман для низкого наполнения, Буссиан, Бонед–Пейреласс, 1983 $p{{\chi }_{{12}}}{{\left( {{{\chi }_{{32}}} + 1} \right)}^{N}} = {{\chi }_{{32}}}{{\left( {{{\chi }_{{12}}} + 1} \right)}^{N}}$ асимметричная формула Брюггемана для высокого наполнения, Семенов, 2018 |
Таблица 3.
Модели с двумя эмпирическими параметрами
| Матричные смеси | Симметричные смеси |
|---|---|
| ${{\chi }_{{32}}} = \frac{p}{{\left( {1 - \frac{p}{{{{p}_{c}}}}} \right)N + \frac{1}{{{{\chi }_{{12}}}}}}}$ Оделевский, 1947 $\frac{{\left( {1 - p} \right){{\chi }_{{12}}}}}{{D\left( {{{\chi }_{{12}}} - p{{\chi }_{{32}}}} \right)}} = N\left( {1 - \frac{p}{{{{p}_{c}}}}} \right) - \frac{p}{{{{\chi }_{{32}}}}}$ Розанов–Колединцева–Древняк, 2012 |
$\frac{{{{\chi }_{{32}}}}}{{{{\chi }_{{12}}}}} = p\frac{{\mathop \Sigma \limits_{k = 1}^3 \frac{{1 + a{{\chi }_{{32}}}}}{{1 + a{{\chi }_{{32}}} + {{N}_{k}}{{\chi }_{{12}}}}}}}{{3 - p{{\chi }_{{12}}}\mathop \Sigma \limits_{k = 1}^3 \frac{{{{N}_{k}}}}{{1 + a{{\chi }_{{32}}} + {{N}_{k}}{{\chi }_{{12}}}}}}}$ Сихвола, 1999 |
Таблица 4.
Модели с тремя эмпирическими параметрами
| Матричные смеси | Симметричные смеси |
|---|---|
| ${{\chi }_{{32}}} = \frac{{{{\chi }_{{12}}}p\left[ {1 + \left( {1 - N} \right)\left( {\frac{N}{{{{p}_{c}}}}\frac{{1 - {{p}_{c}}}}{{1 - N}}} \right)p{{\chi }_{{12}}}^{{w\left( p \right)}}} \right]}}{{N{{\chi }_{{12}}}\left( {1 - p} \right) + \left[ {1 + \left( {1 - N} \right)\left( {\frac{N}{{{{p}_{c}}}}\frac{{1 - {{p}_{c}}}}{{1 - N}}} \right)p{{\chi }_{{12}}}^{{w\left( p \right)}}} \right]}}$ Старостенко–Розанов, 2020 |
$\begin{gathered} p\frac{{{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{\Omega }} - {{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Omega }}}}{{{{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Omega }} + N\left[ {{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{\Omega }} - {{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Omega }}} \right]}} = \hfill \\ = \,\,\frac{{(1 - p)\left[ {{{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Psi }} - 1} \right]}}{{{{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Psi }} - N\left[ {{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{\Psi }} - 1} \right]}} \hfill \\ \end{gathered} $ МакЛахлан, 1992 |
Цель настоящей работы – анализ и сравнение моделей смешения применительно к оценке высокочастотной магнитной проницаемости металла, прямое измерение которой невозможно из-за влияния скин-эффекта, а также высокочастотной диэлектрической проницаемости композитов с электропроводящими включениями. Детали вывода конкретных моделей смешения можно найти в обзорных статьях, цитируемых выше.
Для анализа и сравнения моделей смешения, как правило, исследуют концентрационные серии композитных образцов. Обычно используется жидкое полимерное связующее, наполненное частицами исследуемого металла известных размеров и формы. Для измерений проницаемости необходимы образцы заданных размеров и формы, поэтому после перемешивания частиц наполнителя и связующего смесь отверждается (за счет полимеризации, охлаждения и т.д.). Измеряют комплексные материальные параметры серии образцов, содержание частиц металла в которых меняется от единиц объемных процентов до величины, ограниченной доступной технологией приготовления композита.
Обзор имеет следующую структуру. В разд. 2 рассмотрена связь уравнений диффузионного переноса с характеристической функцией Бергмана–Милтона и формулами смешения и определены понятия обобщенной проводимости и нормированной восприимчивости. В разд. 3 рассмотрены способы учета динамических эффектов за счет введения эффективных свойств частиц наполнителя. В разд. 4 сформулированы принципы отбора и систематизации формул смешения и рассмотрен учет анизотропии смеси. В разд. 5 формулы систематизированы по группам, оценены их области применимости и ограничения. В разд. 6 проведено сравнение концентрационных и частотных зависимостей диэлектрической проницаемости, описываемых моделями смешения для композитов с электропроводящими частицами. В разд. 7 рассмотрены спектральные геометрические функции основных моделей смешения. В разд. 8 рассмотрены проблемы экспериментальной верификации моделей смешения.
2. УРАВНЕНИЯ ДИФФУЗИОННОГО ПЕРЕНОСА, СВЯЗЬ С МОДЕЛЯМИ СМЕШЕНИЯ
В твердом теле (здесь рассматриваются только твердые композиты), где какие-либо механические, например, конвективные, потоки невозможны, актуальным является лишь механизм диффузионного переноса (массы, заряда, температуры, и т.д.), когда движущей силой потока $\vec {A}$ является исключительно градиент скалярного поля (потенциала $\varphi $).
Рассматриваемые композиты не имеют внутренних источников, поэтому в любой точке такой гетерогенной системы дивергенция потока равна нулю ${\text{div}}\vec {A} = 0.$ В пределах каждого однофазного участка системы ${\text{div}}\left[ { - {\text{grad}}\left( \varphi \right)} \right] = \nabla \varphi = 0,$ или
(1)
${\text{div}}\vec {A} = \frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} = 0.$Решение интегрального уравнения переноса в такой системе сводится к закону переноса, связывающего поток с градиентом потенциала через скалярный множитель, являющийся обобщенной проводимостью $\Lambda .$ Частными случаями закона переноса являются закон Фика в случае переноса массы, где $\Lambda $ является коэффициентом диффузии, $\varphi $ является концентрацией; закон Фурье для переноса тепла, где $\Lambda $ является теплопроводностью, $\varphi $ – температурой; закон Ома для статического переноса заряда, где $\Lambda $ является электропроводностью, $\varphi $ – электрическим потенциалом; закон Хагена–Пуазейля для ламинарного переноса жидкости, где $\Lambda $ является функцией вязкости и параметров канала (поры), $\varphi $ является градиентом давления, и т.д.
Для однозначного решения уравнения переноса в случае гетерогенной системы достаточно знать геометрическую конфигурацию этой системы, обобщенную проводимость каждого компонента системы и потенциал на граничных поверхностях. В общем случае для получения интегрального уравнения переноса требуется решение системы дифференциальных уравнений в частных производных для локальных полей на границах раздела фаз [19, 20].
Необходимо отметить, что в таком чисто структурном подходе отсутствует концентрация компонентов в явном виде, и он не учитывает особенности переноса на границе раздела фаз гетерогенной системы, например, контактные явления при расчете электропроводности [21, 22]. Пренебрежение явлениями на границе раздела фаз является недостатком всех известных моделей смешения (см. разд. 3).
Результатом решения уравнения переноса является характеристическая геометрическая функция Бергмана–Милтона, связывающая отношение обобщенной проводимости смеси к соответствующей проводимости включений (частиц наполнителя) $m = {{{{\Lambda }_{{{\text{mix}}}}}} \mathord{\left/ {\vphantom {{{{\Lambda }_{{{\text{mix}}}}}} {{{\Lambda }_{{{\text{incl}}}}}}}} \right. \kern-0em} {{{\Lambda }_{{{\text{incl}}}}}}}$ (или обратную ей величину) со структурой (с геометрической конфигурацией) системы [19, 20]. Существенным для практических задач недостатком такого подхода является отсутствие однозначной связи обобщенной проводимости Λ с концентрацией p компонентов гетерогенной системы.
При выводе моделей смешения обычно исходят из какой-либо умозрительной структуры смеси, а модель лишь описывает изменение этой структуры, обусловленное изменением концентрации компонентов смеси. В этом случае характеристическая геометрическая функция уже включает в себя в качестве параметров и объемную концентрацию p, и форму включений (форм-фактор N, разд. 4). Таким образом, она становится функциональной зависимостью $m\left( p \right) = {{{{\Lambda }_{{{\text{mix}}}}}\left( p \right)} \mathord{\left/ {\vphantom {{{{\Lambda }_{{{\text{mix}}}}}\left( p \right)} {{{\Lambda }_{{{\text{incl}}}}}}}} \right. \kern-0em} {{{\Lambda }_{{{\text{incl}}}}}}},$ специфичной для конкретной модели смешения.
При анализе модели смешения удобнее пользоваться не характеристической, а спектральной геометрической функцией, а именно зависимостью плотности распределения форм-факторов кластеров включений (спектром эффективных форм-факторов) от концентрации включений $b\left( {n,p} \right)$ (разд. 7) [24]. В литературе анализ спектральных геометрических функций предлагаемых моделей смешения встречается редко [26, 27, 30], хотя вид частотной дисперсии материальных параметров смеси определяется как свойствами компонентов, так и спектральной геометрической функцией (разд. 6, 7).
Для облегчения сравнения моделей, используемых в различных дисциплинах, все приведенные ниже формулы записаны в терминах обобщенной восприимчивости, т.е. обобщенной проводимости, нормированной на соответствующую проводимость компонента, являющегося непрерывной средой или матрицей. Переход от диэлектрической ε или магнитной µ проницаемости к соответствующей восприимчивости χ упрощает сравнение и адаптацию рассматриваемых моделей для расчета любой обобщенной проводимости [13, 21], описывающей процесс диффузионного переноса в бинарной смеси: заряда (электропроводность σ), электрической и магнитной поляризации (диэлектрическая ε и магнитная μ проницаемости), массы (коэффициент диффузии), тепла (коэффициент теплопроводности), механического напряжения (модуль Юнга), и т.д. Так, например, нормированная диэлектрическая восприимчивость частиц и смеси записывается как ${{\chi }_{{12}}} = {{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}} - 1$ и ${{\chi }_{{32}}} = {{{{\varepsilon }_{3}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{3}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}} - 1,$ где ε – диэлектрическая проницаемость. Индекс 1 относится к частицам наполнителя (металла в рассматриваемом случае), индекс 2 – к полимерной матрице, индекс 3 – к смеси. Заметим, что при немагнитной матрице (${{\mu }_{2}} = 1$) нормированная восприимчивость совпадает с общепринятым определением магнитной восприимчивости: для частиц металла ${{\chi }_{{12}}} = {{\mu }_{1}} - 1,$ а для смеси ${{\chi }_{{32}}} = {{\mu }_{3}} - 1,$ где ${{\mu }_{1}}$ – магнитная проницаемость частицы, ${{\mu }_{3}}$– магнитная проницаемость смеси.
Приведенные выше обозначения используются далее для единообразия записи и удобства сравнения моделей смешения.
3. ЭФФЕКТИВНЫЕ СВОЙСТВА ЧАСТИЦ, УЧЕТ ДИНАМИЧЕСКИХ ЭФФЕКТОВ
В известных моделях смешения принимается, что свойства компонентов постоянны и не зависят от концентрации компонентов и условий измерения. Эти модели описывают только статические параметры и не учитывают особенности переноса на границе частиц (контактные явления, например). Частично это ограничение снимается учетом эффективных свойств компонентов. Так, наличие оксидной оболочки на частицах металла учитывается введением конформной диэлектрической “скорлупы” с соответствующей коррекцией объемной доли частиц наполнителя и их эффективных свойств [13, 29, 35]. При расчете электропроводности смеси делаются оценки площади контакта частиц, зависящей от морфологии смеси, и вводится контактная проводимость, отличная от проводимости массивного компонента смеси [21, 22].
Расчет динамических свойств смеси осложняется тем, что частотная дисперсия диэлектрической и магнитной проницаемостей частицы зависит не только от свойств составляющего ее металла, но и от ее размеров и формы [30–33]. Так, на частоте f эффективные (с учетом скин-эффекта) свойства частиц с диэлектрической проницаемостью ε1 и магнитной проницаемостью µ1 в виде сфер диаметром d определяются их оптической толщиной $\theta = 2\pi fd\sqrt {{{\varepsilon }_{0}}{{\varepsilon }_{{\text{1}}}}{{\mu }_{0}}{{\mu }_{{\text{1}}}}} .$ В этом выражении ε1 и µ1 – внутренние проницаемости материала частицы, ${{\varepsilon }_{0}} = 8.85 \times {{10}^{{ - 12}}}\,\,{{\text{Ф}} \mathord{\left/ {\vphantom {{\text{Ф}} {\text{м}}}} \right. \kern-0em} {\text{м}}},$ ${{\mu }_{0}} = 1.257 \times {{10}^{{ - 6}}}\,\,{{{\text{Гн}}} \mathord{\left/ {\vphantom {{{\text{Гн}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}.$
Для частиц металлов диэлектрическая проницаемость определяется электропроводностью σ и частотой f: $\varepsilon = {{1 + i\sigma } \mathord{\left/ {\vphantom {{1 + i\sigma } {\left( {2\pi f{{\varepsilon }_{0}}} \right)}}} \right. \kern-0em} {\left( {2\pi f{{\varepsilon }_{0}}} \right)}}.$ Эффективная восприимчивость сферических частиц определяется как ${{\chi }_{{{\text{12eff}}}}}$ = ${{\chi }_{{12}}}\frac{{2\left( {{\text{tg}}{\kern 1pt} \theta - \theta } \right)}}{{\left( {{{\theta }^{2}} - 1} \right){\text{tg}}{\kern 1pt} \theta + \theta }}$ [11, 34], тонких пленок (дисков или чешуек толщиной d) – как ${{\chi }_{{{\text{12eff}}}}}$ = ${{\chi }_{{12}}}\frac{{{\text{tg}}{\kern 1pt} {\kern 1pt} \theta }}{\theta }$ [30], сильно вытянутых эллипсоидов (иголок, волокон, нитей) – как ${{\chi }_{{{\text{12eff}}}}}$ = = ${{\chi }_{{12}}}\frac{{{{J}_{1}}\left( \theta \right)}}{{\theta \times {{J}_{0}}\left( \theta \right) - {{J}_{1}}\left( \theta \right)}}.$ Здесь J0 и J1 – функции Бесселя, µ1 – магнитная проницаемость, d – диаметр нити [35].
Приведенные оценки вклада скин-эффекта являются грубыми по двум причинам. Во-первых, оптическая толщина θ точно определена только для сфер, бесконечных пленок и бесконечных нитей. Во-вторых, эти оценки не учитывают распределение частиц наполнителя по размерам и форме.
Необходимо отметить, что динамические эффекты не сводятся только к скин-эффекту. Когда длина l вытянутой частицы ($l \gg d$) сопоставима с длиной волны λ, следует учитывать полную комплексную проводимость частицы. При $d \ll l \leqslant 0.5\lambda $ проводимость имеет индуктивный характер. Индуктивность L нити приближенно определяется как $L = l\frac{{{{\mu }_{0}}}}{{{{\pi }^{2}}}}\ln \left( {{l \mathord{\left/ {\vphantom {l d}} \right. \kern-0em} d}} \right)$ [11]. Тогда эффективная восприимчивость проводящей нити ${{\chi }_{{{\text{12eff}}}}}$ обусловлена не только восприимчивостью материала нити, но также ее размерами l, d и частотой f [35]:
(2)
${{\chi }_{{{\text{12eff}}}}} = \frac{{{{\chi }_{{12}}}}}{{1 - {{\chi }_{{12}}}\pi {{d}^{2}}\ln \left( {\frac{l}{d}} \right){{{\left( {f\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} } \right)}}^{2}}}} - 1.$При неупорядоченном расположении отрезков высокопроводящих нитей в композите помимо омических потерь появляются потери на излучение, обусловленные излучением нитей как полуволновых диполей [35].
Другой размерный эффект проявляется в магнитной восприимчивости композита. Он обусловлен тем, что частота ферромагнитного резонанса частиц с минимальным размером d, близким или меньшим размера домена, определяется не только материалом частицы, но и ее формой [30–32]. Поэтому динамическая магнитная проницаемость, в отличие от статической, является эффективным свойством, характеризующим скорее конкретную частицу, чем составляющее ее вещество.
Из-за этих эффектов в моделях смешения для расчета высокочастотных свойств композитов вместо восприимчивости материала включения ${{\chi }_{{12}}}$ приходится использовать эффективную восприимчивость ${{\chi }_{{{\text{12eff}}}}},$ зависящую еще от формы и размеров включения.
4. ПРИНЦИПЫ ОТБОРА, СРАВНЕНИЯ И ВЕРИФИКАЦИИ МОДЕЛЕЙ СМЕШЕНИЯ
Общее число опубликованных формул смешения сложно подсчитать точно, многие из них дублируют друг друга, являются эмпирическими или применимыми для каких-либо частных случаев, поэтому при анализе формул смешения необходимо, прежде всего, сформулировать принципы их выбора и сравнения.
Выбранные формулы группируются ниже по типу структуры смеси и по числу параметров, которые определяются из экспериментальных данных.
Выбранные формулы должны физически корректно описывать частотную дисперсию комплексных материальных параметров смеси, в которой контраст проводимостей ${{{{\Lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\Lambda }_{1}}} {{{\Lambda }_{2}}}}} \right. \kern-0em} {{{\Lambda }_{2}}}}$ компонентов может меняться от нуля до бесконечности. Формулы должны учитывать форму включений, обычно характеризуемую коэффициентом деполяризации N, и порог перколяции pc (концентрацию включений, выше которой они образуют бесконечные кластеры).
Необходимо заметить, что величину pc формально определяют как переход от изолятора к проводнику, то есть при ${{\chi }_{{12}}} = \infty $ на пороге перколяции наблюдается разрыв производной восприимчивости по концентрации включений ${{\partial {{\chi }_{{32}}}} \mathord{\left/ {\vphantom {{\partial {{\chi }_{{32}}}} {\partial p}}} \right. \kern-0em} {\partial p}} = \infty .$ Заметим, что при таком определении величина pc зависит от отношения размеров образца (или в динамике длины волны λ) к радиусу перколяции, который, в свою очередь, зависит от размеров включений. При конечных размерах образца, включений, конечной восприимчивости включений ${{\chi }_{{12}}} < \infty $ и неизбежных флуктуациях концентрации включений p, эффект перколяции удобнее рассматривать как фазовый переход второго рода, где величине pc соответствует точка перегиба на концентрационной зависимости восприимчивости. В реальных композитах именно наличие максимума ${{\partial {{\chi }_{{32}}}} \mathord{\left/ {\vphantom {{\partial {{\chi }_{{32}}}} {\partial p}}} \right. \kern-0em} {\partial p}},$ положение которого на оси концентрации не зависит от величины ${{\chi }_{{12}}},$ является проявлением эффекта перколяции (фазовый переход является перестройкой структуры, которая не зависит от величины обобщенной проводимости Λ1 или восприимчивости χ12 включений, то есть ${{p}_{c}} \ne f\left( {{{\chi }_{{12}}}} \right)$). Величина максимума ${{\partial {{\chi }_{{32}}}} \mathord{\left/ {\vphantom {{\partial {{\chi }_{{32}}}} {\partial p}}} \right. \kern-0em} {\partial p}}$ и ширина переходной зоны $\Delta {{p}_{c}}$ обусловлены флуктуациями концентрации компонентов по объему образца.
Для учета эффектов, не описываемых в рамках первых принципов, в формулы могут вводиться параметры, подбираемые из обработки экспериментальных данных. Число этих параметров должно быть минимальным, а сами параметры должны иметь ясный физический смысл.
В известных моделях смешения частицы аппроксимируются эллипсоидами вращения, форма которых описывается двумя осями. В зависимости от объемной концентрации один или оба компонента бинарной смеси рассматриваются как сильно вытянутые или сплюснутые эллипсоиды; при этом отношение длины осей эллипсоида (удлинение или эксцентриситет) может быть близко к нулю для чешуек, к бесконечности для нитей, или к единице для сфер. Ограничения на отличие формы частиц от сферической обусловлено в настоящем обзоре приближенным учетом анизотропии смеси, заключающемся в учете не действительной, а эффективной концентрации частиц. При этом учитываются лишь частицы, большая ось которых параллельна возбуждающему электрическому или магнитному полю. Этот подход справедлив только для частиц с коэффициентами деполяризации N ≈ 1/3 (сферы), N → 0 (нити и диски). Таким образом, приводимые ниже формулы описывают изотропные композиты со сферическими частицами, анизотропные одномерные композиты с волокнами и плоско-анизотропные композиты с чешуйками или дисками. Для изотропных композитов с волокнами эффективная концентрация составляет 1/3 от реальной концентрации волокон; для изотропных композитов с чешуйками эффективная концентрация составляет 1/2 от реальной концентрации чешуек. Этот метод широко используется для оценки свойств изотропного композита с частицами, сильно отличающимися от сфер [32]. При незначительных отличиях формы частиц от сферической зависимостью поляризуемости частицы от направления обычно пренебрегают.
Известно много публикаций, посвященных анализу и классификации моделей смешения [14–16]. Модели обычно сравнивают на основе физических предположений, на которых они построены, при этом различие в числе параметров, подбираемых из экспериментальных данных, из сравнения выпадает. Эти параметры обычно связаны с эффектами, которые не учитывают в моделях, выведенных из первых принципов. Таким образом, оценки области применимости той или иной модели строго в литературе не рассматривали.
Применимость выбранной модели смешения к исследуемым композитам обычно оценивается по величине среднеквадратичного расхождения (невязке) между экспериментальной и расчетной восприимчивостью серии образцов композитов с различной концентрацией частиц наполнителя. Предполагается, что чем меньше невязка исследуемой восприимчивости, тем точнее выбранная модель описывает исследуемый композит. Такой общепринятый подход имеет низкую селективность к тестируемым формулам и часто не позволяет выбрать наиболее подходящую формулу из нескольких, удовлетворительно описывающих свойства концентрационной серии образцов, даже при известных свойствах компонентов смеси.
Оценка применимости выбранной модели смешения к композитам заданного качественного состава (т.е. из заданных компонентов) является существенно более сложной, чем простое сравнение расчета по выбранной модели с измеренной зависимостью материального параметра смеси от концентрации ее компонентов. Несоответствующая структуре смеси модель может быть с успехом использована для интерполяции измеренной зависимости материального параметра от концентрации, являясь в то же время лишь эмпирической формулой с какими-то формальными параметрами, как, например, в работе [30]. При этом экстраполяция по ошибочно выбранной модели в сторону больших концентраций частиц наполнителя будет давать неизвестную погрешность. Попытка применить явно ошибочную модель смешения для расчета другого материального параметра той же смеси с иным контрастом в свойствах компонентов ведет к высокой невязке с измеренными данными [31].
Использование эмпирических формул ограничивается тем, что они неприменимы для описания широкого круга свойств компонентов смеси, а их область применимости неизвестна.
Восстановление микроволновой магнитной проницаемости металлических включений из измерений соответствующей проницаемости композита осложняется тем, что высокочастотная проницаемость (и, следовательно, контраст свойств компонентов смеси) изменяется из-за частотной дисперсии от единицы до нескольких сотен или выше в зависимости от используемого ферромагнитного сплава. Определяемые аппроксимацией экспериментальных данных параметры ошибочно выбранной формулы смешения (восприимчивость наполнителя ${{\chi }_{{12}}}$ является не параметром, а исходной, или наоборот, искомой величиной) меняются с частотой аналогично контрасту проницаемостей ${{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}}$ или ${{{{\mu }_{1}}} \mathord{\left/ {\vphantom {{{{\mu }_{1}}} {{{\mu }_{2}}}}} \right. \kern-0em} {{{\mu }_{2}}}},$ тогда как параметры верной формулы смешения не должны зависеть от частоты. В реальных измерениях динамической восприимчивости подобранные параметры зависят от частоты для любой модели из-за ошибок измерения, а также потому, что все модели справедливы лишь для идеализированных упрощенных структур смеси. Поэтому выбор модели смешения формально является задачей математической статистики (чем сильнее зависимость параметров модели от контраста восприимчивостей при одном и том же числе подбираемых параметров, тем менее достоверна тестируемая модель). К сожалению, подобные вероятностные оценки применимости той или иной модели смешения мало актуальны для практических задач.
Более близкий к практике метод верификации выбранной модели смешения предложен в работах [30, 31]. Он основан на том, что в исследуемой серии различающихся по составу образцов измеряют как минимум две различные по физической природе обобщенные проводимости, имеющие для одних и тех же компонентов смеси разный контраст свойств, но одинаково зависящие от структуры смеси.
Таким методом восстанавливается магнитная проницаемость металлических частиц [30, 31], которая меняется в широких пределах в зависимости от частоты. В качестве второй обобщенной проводимости выбрана диэлектрическая проницаемость смеси. Для одних и тех же образов композитов измеряются высокочастотные диэлектрическая и магнитная проницаемости. Объемное содержание частиц в образцах варьируется от нуля до максимума. Максимальное наполнение ограничивается хрупкостью образцов и используемой технологией их изготовления.
Чем меньше влияет концентрация металлических частиц в композите на восстановленную частотную зависимость магнитной проницаемости частиц, тем точнее выбранная модель смешения описывает исследуемые композиты. Соответственно, тем ближе полученная частотная зависимость магнитной проницаемости к реальным свойствам частиц металла.
Для упрощения выбора и верификации моделей смешения необходимо систематизировать и критически сравнить известные модели. Это позволит оценить области применимости и ограничения рассматриваемых моделей и исключить из процедуры верификации модели, явно неподходящие для описания свойств исследуемых композитов.
Из литературы известно более пятидесяти моделей смешения. Число оригинальных формул много меньше, так как одни и те же формулы выводятся несколько раз и называются по именам новых авторов. Так формула Максвелла Гарнета, записанная для эллипсоидальных включений, называется формулой Оллендорфа [37], формула Брюггемана [10] имеет названия формул Полдера–Ван Сантена, Дас–Дас Гупта или Рао [38–40].
Дополнительным осложнением является то, что при цитировании формулы редактируют или видоизменяют для описания конкретных образцов; видоизмененная формула часто имеет мало общего с оригинальной. Например, формула Винера обычно записывается в виде ${{\varepsilon }_{3}} = {{\varepsilon }_{1}}{{p}_{1}} + {{\varepsilon }_{2}}{{p}_{2}},$ или в терминах нормированной восприимчивости:
где ${{\chi }_{{12}}} = {{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}} - 1$ и ${{\chi }_{{32}}} = {{{{\varepsilon }_{3}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{3}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}} - 1.$На самом деле выражение (3) является лишь упрощением формулы Винера [41] для анизотропного композита, в котором оба компонента образуют взаимопроникающую анизотропную слоистую или нитевидную структуру. В этой структуре слои или нити ориентированы параллельно внешнему полю. Оригинальная формула Винера сложнее и включает, как дополнительный параметр, величину локальной восприимчивости ${{\chi }_{{{\text{local2}}}}}$ вблизи частицы наполнителя
Модели, рассматриваемые в данном обзоре, отобраны по следующим принципам. Эти модели должны описывать комплексные материальные параметры и их частотную дисперсию (комплексные диэлектрическую ε(f) и магнитную µ(f) проницаемости) композита при восприимчивости включений (см. разд. 2) от нуля до бесконечности. Модели должны учитывать форму включений (коэффициент деполяризации N) и порог перколяции. Формулы смешения должны включать в себя минимальное число подбираемых из эксперимента параметров, а эти параметры должны иметь ясный физический смысл.
Из рассмотрения исключаются численные алгоритмы (их обзор представлен в работе [17]) и модели, применимые лишь к каким-либо частным структурам смеси, формам включений [42], ограниченному контрасту свойств компонентов [43], диапазону концентраций и т.д.
В частности, оригинальная формула Винера [41] не рассматривается, так как используемая в ней величина локальной восприимчивости в общем случае не определена, и формула не дает явной функциональной связи между составом смеси, ее проводимостью и проводимостью компонентов.
В зависимости от объемной доли p один или оба компонента можно рассматривать как вытянутые или сплюснутые эллипсоиды [44]. Отношение длины поперечного размера эллипсоида d к длине оси вращения D (эксцентриситет или удлинение) может быть близким к нулю (диски или хлопья), к бесконечности (нити или волокна), или к единице (сферы). Коэффициент деполяризации, или форм-фактор N, входящий в большинство формул смешения как определяемый из эксперимента параметр, является функцией эксцентриситета ${d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D}$ [25, 30, 31, 44–46]. Для нитей (вытянутых эллипсоидов при d/D > 1) минимальный коэффициент деполяризации (вдоль оси вращения) вычисляется как:
(4)
${{N}_{{{\text{needle}}}}} = \frac{1}{{{{{\left( {{d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D}} \right)}}^{2}} - 1}} \times \left[ {\left( {\frac{d}{D}} \right)\frac{{{\text{arсh}}\left( {{d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D}} \right)}}{{\sqrt {{{{\left( {{d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D}} \right)}}^{2}} - 1} }} - 1} \right].$Для дисков (при ${d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D} < 1$) коэффициент деполяризации минимален (вносит основной вклад в поляризуемость) в плоскости диска:
(5)
$\begin{gathered} {{N}_{{{\text{disk}}}}} = \frac{1}{2}\left\{ {1 - \frac{1}{{1 - {{{\left( {{d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D}} \right)}}^{2}}}} \times _{{}}^{{^{{^{{^{{^{{}}}}}}}}}}} \right. \hfill \\ \left. { \times \,\,\left[ {1 - \left( {\frac{d}{D}} \right)\frac{{{\text{arсh}}\left( {{d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D}} \right)}}{{\sqrt {1 - {{{\left( {{d \mathord{\left/ {\vphantom {d D}} \right. \kern-0em} D}} \right)}}^{2}}} }}} \right]} \right\}. \hfill \\ \end{gathered} $Ограничение на отклонение от сферичности, неявно присутствующее в большинстве моделей, накладывается приближенным учетом анизотропии смеси с помощью эффективной концентрации (доли частиц, взаимодействующих с однородным внешним полем). Этот учет точен для сферических частиц (N = 1/3) и для частиц с форм-фактором, близким к нулю (волокна ${{N}_{1}} \approx 0,$ ${{N}_{2}} = {{N}_{3}} \approx 0.5$ и диски ${{N}_{2}} = {{N}_{3}} \approx 0,$ ${{N}_{1}} \approx 1$).
Рассматриваемые ниже модели описывают изотропную смесь в случае сферических частиц, одномерную одноосно анизотропную смесь в случае волокон, двумерную плоско анизотропную смесь в случае дисков. Очевидно, что учет анизотропии методом эффективной концентрации (разд. 3) является приближенным [25], но более точный учет, общий для всех моделей смешения, неизвестен.
В обзоре приведены оригинальные выражения из первоисточников, однако ради удобства сравнения эти выражения переписаны в терминах нормированной восприимчивости (нормированной обобщенной проводимости, см. раздел 2). Из удобства классификации и сравнения, представленные формулы разделены по группам (таблицам) с одинаковым числом подбираемых из эксперимента параметров.
Внутри каждой таблицы в столбцах формулы сгруппированы по типу структуры, принципу вывода или области применимости.
5. КЛАССИФИКАЦИЯ МОДЕЛЕЙ СМЕШЕНИЯ
Модели смешения, отобранные в соответствии с изложенными выше принципами, представлены в табл. 1–4. В правой колонке таблиц представлены формулы, полученные дифференцированием по концентрации формул, описывающих смеси с симметричной структурой [28], а также полученные для случая малого контраста проницаемостей компонентов [11].
Эти формулы выделены в отдельную группу из-за малой чувствительности к структуре смеси.
В табл. 1 приведены классические формулы, выведенные для смесей, содержащих сферические включения. Эти формулы не имеют эмпирических параметров и не допускают отклонения от идеализированных гипотетических структур, для которых они были выведены.
Формула Максвелла–Гарнетта (известная также как формула Клаузиуса–Моссотти и Лоренц–Лорентца) и формула Брюггемана (первая и вторая колонки) имеют ограниченную применимость и низкую точность, так как даже идеально сферические частицы агрегируются в кластеры с эффективной формой, отличающейся от сферической. Вывод этих формул основан на том, что суммарная поляризуемость включений, помещенных в среду, являющуюся либо матрицей (компонент 2), либо самой смесью (компонент 3) обусловливает проницаемость однородной эффективной среды.
В настоящее время эти формулы представляют скорее исторический интерес, тем не менее их выводили и публиковали повторно [48–51] с незначительными вариациями, претендующими на увеличение точности. В современной практике эти формулы обычно используют без должных процедур верификации (разд. 4), оказываясь при этом лишь популярными эмпирическими формулами для интерполяции экспериментальных данных.
Экспоненциальные [12, 28, 52] и логарифмические [53, 54] формулы, полученные дифференцированием по концентрации формул для симметричной [28] или матричной [52] смеси, широко используются в геологии для оценки влагопроницаемости почв, несмотря на ограничение по контрасту свойств компонентов. Для согласования с экспериментальными данными в оригинальные формулы включаются эмпирические коэффициенты, полученные выражения известны как формулы Арчи и Топпа [3, 4, 55, 56].
Исключением из ограничения по контрасту свойств компонентов является асимметричная формула Брюггемана, примененная Ханаем для расчета динамических свойств [52]. Эта формула известна в двух вариантах, для низкой и для высокой концентраций компонента 1 (табл. 2) [28].
В табл. 2 представлены формулы, в которых учитывается форма включений как выбираемый из эксперимента эмпирический параметр. Исключением является формула Мусала–Хана–Буша [57], полученная применением формул для прямой и инверсной матричной смесей и рассмотрением новых квазикомпонентов (${{\chi }_{a}}$ и ${{\chi }_{b}}$) в качестве наполнителя и матрицы. В ней эмпирический параметр ${{P}_{{{\text{fit}}}}},$ предназначенный для достижения согласия между теорией и экспериментом, не имеет физического обоснования. Последовательное применение нескольких моделей смешения встречается и в более новых публикациях [57, 58]. Однако анализ частотной дисперсии динамической восприимчивости, а также геометрической спектральной функции показывает, что последовательное применение формул, описывающих различные структуры смеси, приводит к физически некорректным результатам (к появлению ложных максимумов спектральной геометрической функции и соответствующих им пиков поглощения).
Заметим, что в формулах табл. 2 форма включений аппроксимируется эллипсоидом вращения с коэффициентом деполяризации, или форм-фактором N. При этом формулы табл. 2 и далее описывают восприимчивость анизотропных смесей с эллипсоидами, параллельными внешнему (электрическому для проводимости или диэлектрической проницаемости, магнитному для магнитной проницаемости) полю, тогда как формулы табл. 1 описывают свойства изотропных смесей со сферическими частицами.
Именно отличная от сферической форма включений и их ориентация определяют анизотропию всего композита. Наиболее интересными для практики являются композиты, наполненные либо сильно вытянутыми эллипсоидами (иголки или волокна), либо, напротив, сильно сплюснутыми эллипсоидами (диски, чешуйки, хлопья). Такое отличие формы частиц от сферической и оправдывает применение метода эффективных концентраций для учета хаотической ориентации несферических включений в изотропных композитах. Учет является приближенным, так как в нем не учитывают поляризуемость эллипсоидов, ориентированных перпендикулярно внешнему полю (вкладом больших коэффициентов деполяризации). При этом метод эффективных концентраций неприменим к включениям с формой, близкой к сферической (N ~ 0.3).
Приведенные в табл. 2 формулы широко применяются в расчетах в настоящее время, поэтому рассмотрим их подробнее.
Из них наиболее известны обобщенные для эллипсоидов вращения формулы Максвелла Гарнетта [13, 37] и симметричная формула Брюггемана. Формула Максвелла Гарнетта может быть записана в двух вариантах. Обычно используется формула для прямой матричной смеси (6):
(6)
${{\chi }_{{32}}} = \frac{p}{{\left( {1 - p} \right)N + {1 \mathord{\left/ {\vphantom {1 {{{\chi }_{{12}}}}}} \right. \kern-0em} {{{\chi }_{{12}}}}}}}.$Инверсная формула Максвелла–Гарнетта (7) описывает смесь, в которой роли матрицы (компонент 2) и включений (компонент 1) инвертированы [28] и форм фактор N относится к компоненту 2:
(7)
${{\chi }_{{32}}} = {{\chi }_{{12}}}p\frac{{{{\chi }_{{12}}}\left( {1 - N} \right) + 1}}{{{{\chi }_{{12}}}\left( {1 - pN} \right) + 1}}.$Для анизотропной смеси прямая и инверсная (при ${{N}_{2}} = {{N}_{1}}$) формулы Максвелла–Гарнетта (6), (7) совпадают с границами Хашина–Штрикмана [18], включающими физически допустимые величины обобщенной проводимости для изотропного композита.
Отличительной чертой моделей симметричного типа является учет появления сквозной проводимости по кластерам включений при концентрации включений, равной порогу перколяции ${{p}_{c}}.$ В моделях матричного типа (6), (7) такая проводимость появляется при ${{p}_{1}} = 1,$ либо при ${{p}_{1}} = 0.$ В модели Брюггемана для сферических частиц (табл. 1) ${{p}_{c}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}.$
Широко используемое обобщение симметричной формулы Брюггемана на несферические частицы (8) является физически противоречивым (компоненты симметричной бинарной смеси могут иметь одинаковую форму только в случае сфер, иначе появляется третий компонент – поры) [28, 61] и некорректным (например, расхождение с формулой (7) при ${{p}_{1}} \to 1$ [62]). Помимо этого, симметричная модель Брюггемана пренебрегает важными физико-химическими эффектами, определяющими агрегацию частиц в гетерогенной системе (смачивание, технология перемешивания, и т.д.).
В результате в этой модели порог перколяции определяется исключительно формой частиц наполнителя и равен их форм-фактору ${{p}_{c}} \equiv N{\text{:}}$
(8)
$\frac{{p\left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right)}}{{1 + N{{\chi }_{{12}}} + {{\chi }_{{32}}}\left( {1 - N} \right)}} = \frac{{(1 - p){{\chi }_{{32}}}}}{{1 + {{\chi }_{{32}}}\left( {1 - N} \right)}}.$Более новая и малоизвестная модель когерентного потенциала [60] дает зависимость восприимчивости смеси от наполнения, близкую к обобщенной симметричной модели Брюггемана, и имеет все ее недостатки. Отличие формулы когерентного потенциала (9) от формулы Брюггемана (8) лишь в том, что порог перколяции оказывается несколько меньше коэффициента деполяризации:
(9)
$\frac{{p\left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right)}}{{1 + N{{\chi }_{{12}}} + {{\chi }_{{32}}}}} = \frac{{(1 - p){{\chi }_{{32}}}}}{{1 + {{\chi }_{{32}}}}}.$Отличительно чертой моделей симметричного типа, осложняющей решение задач смешения, является наличие двух корней.
Обобщенные на несферические включения степенная [38]:
(10)
${{\left( {{{\chi }_{{32}}} + 1} \right)}^{{1/\left( {1 - 2N} \right)}}} - 1 = p\left[ {{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{{1/\left( {1 - 2N} \right)}}} - 1} \right]$(11)
${\text{lg}}\left( {{{\chi }_{{32}}} + 1} \right) = p\left( {1 - N} \right){\text{lg}}\left( {{{\chi }_{{12}}} + 1} \right)$Более гибкой является асимметричная модель Брюггемана, обобщенная Буссианом [63] и Ханаем [52] для эллипсоидальных включений. По аналогии с прямой и инверсной формулами Максвелла Гарнетта получены две асимметричных формулы Брюггемана–Буссиана [10, 63]. Первая (12) получена дифференцированием (8) для смеси с низкой концентрацией компонента 1, вторая (13) – для смеси с высокой концентрацией компонента 1 [10, 28, 52]. При этом модель (12) оказывается близка к прямой (6), а (13) – к инверсной (7) моделям Максвелла Гарнетта.
Модель Брюггемана–Буссиана–Ханая описывает S-образную зависимость $\chi _{{32}}^{{''}}\left( p \right)$ с точкой перегиба, похожую на зависимость, свойственную перколяционным моделям. Но положение точки перегиба $\chi _{{32}}^{{''}}\left( p \right)$ в формулах (12), (13) зависит от восприимчивости включений χ12, поэтому модели Брюггемана–Буссиана–Ханая не описывают эффект перколяции:
(12)
$1 - p = \frac{{{{\chi }_{{12}}} - {{\chi }_{{32}}}}}{{{{\chi }_{{12}}}}}{{\left( {\frac{1}{{{{\chi }_{{32}}} + 1}}} \right)}^{N}};$(13)
$p = \frac{{{{\chi }_{{32}}}}}{{{{\chi }_{{12}}}}}{{\left( {\frac{{{{\chi }_{{12}}} + 1}}{{{{\chi }_{{32}}} + 1}}} \right)}^{N}}.$Недостатки обоих асимметричных формул Брюггемана–Буссиана–Ханая те же, что и в исходной обобщенной симметричной формуле Брюггемана (8). Эти модели “игнорируют имеющуюся структуру смеси, при расчете эффекта от добавления малого количества одного из компонентов” [28].
Общий недостаток моделей (табл. 2), которые учитывают форму включений и описывают эффект перколяции, заключается в пренебрежении эффектами, определяющими агрегацию включений, и, соответственно, оказывающими не менее сильное влияние на величину порога перколяции pc (критическое наполнение, или пороговую объемную концентрацию включений), чем форма этих включений.
В табл. 3 приведены формулы смешения с двумя эмпирическими параметрами. Первым, как и в более простых моделях предыдущей группы, является форм-фактор включений N. Вторым – порог перколяции ${{p}_{c}},$ который зависит не только от формы включений, но и от ряда других факторов, которые сложно определить и перечислить.
Простейшая из этих моделей, предложенная Оделевским [13], является, по сути, формулой Максвелла Гарнетта для анизотропной смеси с регулярно расположенными эллиптическими включениями (6). Отличие заключается в перенормировке концентрации включений на порог перколяции (на диапазон наполнений, в пределах которого смесь сохраняет матричную структуру):
(14)
${{\chi }_{{32}}} = \frac{p}{{\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{c}}}}} \right. \kern-0em} {{{p}_{c}}}}} \right)N + {1 \mathord{\left/ {\vphantom {1 {{{\chi }_{{12}}}}}} \right. \kern-0em} {{{\chi }_{{12}}}}}}}\mathop \approx \limits_{{{\chi }_{{12}}} \to \infty } \frac{p}{{\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{c}}}}} \right. \kern-0em} {{{p}_{c}}}}} \right)N}}.$Очевидными недостатками модели Оделевского (14) являются ограниченный диапазон концентраций ($0 < p < {{p}_{c}},$ тогда как корректные модели должны быть применимы в диапазоне $0 < p < 1$) и расхождение аппроксимации низкого контраста проницаемостей со строгой формулой Ландау–Лифшица–Лоенги [11, 12] вблизи ${{p}_{c}}.$
За порогом перколяции предполагается, что концентрационная зависимость проницаемости смеси близка к популярной версии формулы Винера (3), в которой одним из компонентов является смесь с критическим наполнением, а вторым – компонент 1, из которого состоят включения.
Подход, предложенный Оделевским, является кусочной сшивкой прямой матричной и симметричной моделей на пороге перколяции. Очевидно, что вблизи критического наполнения ${{p}_{c}}$ точность такой модели низка, потому что эти структуры сильно различаются и перестройка структуры смеси в реальности происходит постепенно в каком-то переходном диапазоне концентраций. Более корректна модель Сихволы [15, 39, 57], также имеющая два эмпирических параметра:
(15)
$\frac{{{{\chi }_{{32}}}}}{{{{\chi }_{{12}}}}} = p\frac{{\sum\limits_{k = 1}^3 {\frac{{1 + a{{\chi }_{{32}}}}}{{1 + a{{\chi }_{{32}}} + {{N}_{k}}{{\chi }_{{12}}}}}} }}{{3 - p{{\chi }_{{12}}}\sum\limits_{k = 1}^3 {\frac{{{{N}_{k}}}}{{1 + a{{\chi }_{{32}}} + {{N}_{k}}{{\chi }_{{12}}}}}} }}.$Первым является, как и в модели Оделевского, форм-фактор включений N, второй параметр a Сихвола определяется как некий формальный структурный параметр. Заметим, что оригинальная модель Сихволы (15) предполагает точное описание изотропной смеси с несферическими частицами с тремя разными размерами (различающимися форм-факторами ${{N}_{1}} \ne {{N}_{2}} \ne {{N}_{3}}$).
Для удобства сравнения формула (13) переписана для случая анизотропного композита с регулярно ориентированными несферическими частицами (14), а восприимчивость изотропной смеси учитывается методом эффективной концентрации (см. разд. 2). При такой записи легко показать [30], что формальный параметр a функционально связан с порогом перколяции $a = N\left( {p_{c}^{{ - 1}} - 1} \right),$ а параметры формулы Сихволы оказываются теми же параметрами, что и в формуле Оделевского, с ясным физическим смыслом:
(16)
$\frac{{p\left( {{{\chi }_{{12}}} - {{\chi }_{{32}}}} \right)}}{{1 + N{{\chi }_{{12}}} + N\left( {p_{c}^{{ - 1}} - 1} \right){{\chi }_{{32}}}}} = \frac{{(1 - p){{\chi }_{{32}}}}}{{1 + N\left( {p_{c}^{{ - 1}} - 1} \right){{\chi }_{{32}}}}}.$Модель Сихволы весьма универсальна, формула (16) может быть превращена в формулу Максвелла Гарнетта (6), Брюггемана (8), когерентного потенциала (9), за счет выбора соответствующего значения порога перколяции (${{p}_{c}} = 1,$ ${{p}_{c}} = N,$ ${{p}_{c}} = {N \mathord{\left/ {\vphantom {N {\left( {1 + N} \right)}}} \right. \kern-0em} {\left( {1 + N} \right)}}$) [30]. Формула Оделевского (14) при $p < {{p}_{c}}$ также является частным случаем (16), но лишь при бесконечном контрасте ${{\chi }_{{12}}} \to \infty .$
В отличие от (14), формула Сихволы (16) справедлива при $0 < p < 1$ и учитывает неоднородное взаимодействие включений за счет распределения эффективных форм-факторов, не учитываемое в моделях матричного типа (разд. 7).
Легко показать, что симметричная формула Брюггемана (8) приводит к ${{p}_{c}} = N$ (заметим, что модель (8) предполагает, что оба компонента смеси имеют одинаковую форму). Совместное решение (7) и (16) показывает, что при $p < {{p}_{c}}$ компонент 2, являющийся средой или матрицей, можно описать форм-фактором ${{N}_{2}} = {{p}_{c}}.$ Таким образом, модель Сихволы является моделью симметричной смеси с корректным учетом формы эллипсоидальных включений.
Следующую модель (формулу Розанова–Колединцевой–Древняка [65]) можно поместить и в табл. 2, и в табл.3 потому, что третьим параметром является мерность гетерогенной системы D (15). При выводе принимается, что мерность может принимать лишь фиксированные целочисленные значения (D = 1, 2, 3). Для анизотропных композитов D = 1, 2, для изотропных – D = 3, поэтому отнести мерность к эмпирическим параметрам можно весьма условно. Анизотропия задается технологией изготовления композита и не является идеально линейной или плоской. В этой модели остается неясным описание композитов, не относящихся к идеальным линейным, плоским или объемным структурам (с мерностью $1 \leqslant D \leqslant 3$):
(17)
$\frac{{\left( {1 - p} \right){{\chi }_{{12}}}}}{{D\left( {{{\chi }_{{12}}} - p{{\chi }_{{32}}}} \right)}} = N\left( {1 - \frac{p}{{{{p}_{c}}}}} \right) - \frac{p}{{{{\chi }_{{32}}}}}.$Оставшиеся два параметра (коэффициент деполяризации N и критическое наполнение ${{p}_{c}}$), входящие в формулу (17), идентичны параметрам формул Оделевского (14) и Сихволы (16). Необходимо отметить, что геометрическая спектральная функция выбрана в формуле (15) с одним максимумом, поэтому форм фактор включений и мерность смеси не связаны друг с другом, и применение метода эффективных концентраций к модели (17) некорректно. По этой же причине модель (17) применима лишь к включениям с формой, близкой к сферической $N \approx {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}.$
В табл. 4 представлены формулы, имеющие три параметра, определяемые из массива экспериментальных данных. Модель МакЛахлана [66] – модель эффективной среды (описывает смесь с симметричной структурой). Первым эмпирическим параметром является форм-фактор включений, который входит во все модели, имеющие подгоночные параметры. Оставшиеся в формуле (18) два свободных параметра – показатели экспонент Ψ и Ω – формальные критические индексы, т.е. эмпирические параметры, физический смысл которых не определен:
(18)
$\begin{gathered} p\frac{{{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{\Omega }} - {{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Omega }}}}{{{{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Omega }} + N\left[ {{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{\Omega }} - {{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Omega }}} \right]}} = \\ = \frac{{(1 - p)\left[ {{{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Psi }} - 1} \right]}}{{{{{\left( {{{\chi }_{{32}}} + 1} \right)}}^{\Psi }} - N\left[ {{{{\left( {{{\chi }_{{12}}} + 1} \right)}}^{\Psi }} - 1} \right]}}. \\ \end{gathered} $Выражение (18) получено без строгого вывода эвристически, и даже спустя 30 лет после публикации [66] остаются сомнения в экспериментальном подтверждении и в физической корректности этой модели. В частности, формула (18) не описывает частотную дисперсию диэлектрической проницаемости электропроводящих композитов (${{\chi }_{{32}}}\sim {{\left( {2\pi \rho f} \right)}^{{ - 1}}},$ где $\rho $ – удельное сопротивление, f – частота).
Недостатком наиболее пригодных по точности для прикладных расчетов моделей Максвелла Гарнетта, Оделевского, Брюггемана и Сихволы является то, что каждая из этих моделей применима лишь к одной структуре смесей из трех возможных (прямая матричная, симметричная, обратная матричная). Сходство между матричной и симметричной структурами при низкой концентрации компонента 1 (разд. 6, рис. 2, 3) является кажущимся. Попытка описать в рамках одной модели диэлектрическую и магнитную проницаемости (с различным контрастом свойств компонентов) одного и того же образца проявляет различие моделей [5, 30, 31].
Рис. 1.
Зависимость весового множителя w от концентрации включений для $\delta = 0.05$ (точки), $\delta = 0.5$ (сплошная линия), $\delta = 4$ (пунктир) и ${{p}_{c}} = 0.33.$ Серым тоном залита область структурного перехода $\Delta {{p}_{c}}$ для $\delta = 0.5.$ Черные линии соответствуют распределению (20), серая – аппроксимирующей формуле (21) для $\delta = 4.$ При $\delta < 1$ кривые, рассчитанные по формулам (20) и (21), совпадают с графической точностью.
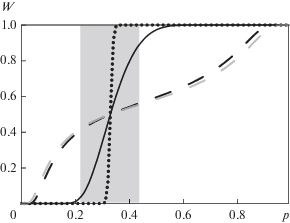
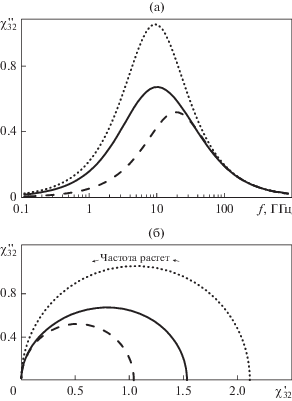
Рис. 2.
Зависимость а) действительной, б) мнимой частей (залита область Хашина–Штрикмана) восприимчивости смеси от концентрации p; в) годограф комплексной восприимчивости смеси при ${{\chi }_{{12}}} = 0 + i100,$ ${{p}_{c}} = 0.33,$ $N = 0.24.$ Черные сплошная, пунктирная и точечная линии соответствуют модели с инверсией матрицы (19) при $\delta = 0.5,4,0.05.$ Серые линии соответствуют модели Сихволы (16), сплошная ${{p}_{c}} = 0.33,$ пунктир ${{p}_{c}} = 0.7.$ Точками на годографе отмечено положение ${{p}_{c}}.$ Чем меньше величина флуктуаций δ, тем ближе порог перколяции (серая точка) к точке инверсии матричной структуры (черная точка).
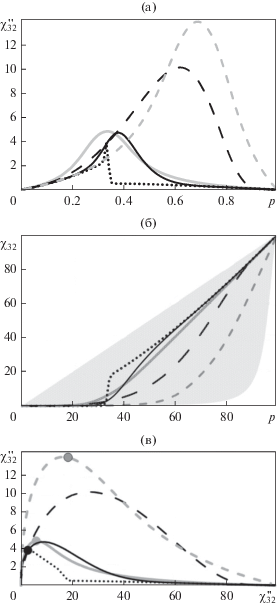
Рис. 3.
Зависимость а) действительной, б) мнимой частей (залита область Хашина–Штрикмана) восприимчивости смеси от концентрации; в) годограф комплексной восприимчивости смеси при ${{\chi }_{{12}}} = 0 + i100,$ ${{p}_{c}} = 0.33,$ $N = 0.24.$ Сплошные линии соответствуют асимметричной модели Брюггемана–Ханая (12), пунктирные – модели Оделевского (14), точечные – модели Максвелла–Гарнетта (6).
Более общей представляется модель [44], учитывающая возможность инверсии матричной структуры, при этом структура, подобная симметричной, рассматривается как переходная область $\Delta {{p}_{c}}$ в окрестности точки инверсии, которая обозначена аналогично порогу перколяции ${{p}_{c}}.$
Одинаковые обозначения выбраны потому, что величины критической концентрации и концентрации инверсии матричной структуры близки при малой ширине переходной области, хотя и имеют разный физический смысл:
(19)
${{\chi }_{{32}}} = \frac{{{{\chi }_{{12}}}p\left[ {1 + \left( {1 - N} \right)\left( {\frac{N}{{{{p}_{c}}}}\frac{{1 - {{p}_{c}}}}{{1 - N}}} \right)p\chi _{{12}}^{{w\left( p \right)}}} \right]}}{{N{{\chi }_{{12}}}\left( {1 - p} \right) + \left[ {1 + \left( {1 - N} \right)\left( {\frac{N}{{{{p}_{c}}}}\frac{{1 - {{p}_{c}}}}{{1 - N}}} \right)p\chi _{{12}}^{{w\left( p \right)}}} \right]}}.$Вывод формулы (19) основан на предположении о том [44], что локальная в окрестности включения восприимчивость ${{\chi }_{{{\text{local2}}}}}$ (восприимчивость среды, в которой по модели Винера [41] находится включение) является средним между восприимчивостями прямой ${{\chi }_{{12}}}$ и обратной ${{\chi }_{{22}}}$ матричных смесей. В моделях, описывающих смеси с симметричной структурой, среда имеет восприимчивость смеси ${{\chi }_{{32}}},$ в моделях с матричной структурой, среда – один из компонентов смеси. В инверсно-матричной модели (19) восприимчивость ${{\chi }_{{{\text{local2}}}}}$ определяется как взвешенное среднее между восприимчивостями прямой $p \times {{\chi }_{{12}}}$ и обратной $\left( {1 - p} \right){{\chi }_{{22}}} \equiv 0$ матричных смесей (только такое усреднение описывает эффект перколяции [44]):
Локальная концентрация включений флуктуируют относительно средней по объему образца величины p, характеризующей композит. Предполагается, что разброс локальных концентраций относительно средней по образцу концентрации p описывается нормальным (гауссовым) распределением. При этом весовой множитель w, входящий в формулу (17) является кумулятивным (интегральным) гауссовым распределением локальной концентрации, нормированной на отклонение от точки инверсии ${{p}_{c}}$:
(20)
$w\left( p \right) = \frac{1}{2}\left( {1 - \frac{2}{\pi }\int\limits_0^{ - \frac{1}{{\sqrt 2 {\delta }}}\frac{{{{p}_{c}} - p}}{{p\left( {1 - p} \right)}}} {{{e}^{{ - {{t}^{2}}}}}dt} } \right).$Величина флуктуации δ в этом распределении является стандартным отклонением и определяется технологией изготовления композита. Это стандартное отклонение δ является третьим (помимо N и ${{p}_{c}}$) параметром, определяемым из эксперимента. Оно определяет диапазон переходных концентраций $\Delta {{p}_{c}},$ в котором локальное наполнение $p$ отличается от ${{p}_{c}}$ на величину, не превышающую $\delta $ с вероятностью 95%: $\Delta {{p}_{c}} \approx 2\delta \left( {1 - {{p}_{c}}} \right){{p}_{c}}.$ Внутри переходной области образуется структура, близкая по свойствам к симметричной, за пределами $\Delta {{p}_{c}}$ флуктуации концентрации не влияют на структуру композита (смесь остается либо прямой, либо инверсной матричной).
При выводе формулы (17) закон распределения Гаусса (18) выбран как наиболее вероятный, но было показано (рис. 1), что закон распределения можно заменить на простое аппроксимирующее выражение практически без потери точности [44]:
(21)
$w\left( p \right) = \frac{1}{2}\left\{ {1 + {\text{th}}\left[ {\frac{{p - {{p}_{c}}}}{{p\left( {1 - p} \right)\delta }}} \right]} \right\}.$Несмотря на кажущуюся сложность инверсно-матричной модели (17), решение прямой и обратной задач смешения для этой модели проще, чем для моделей симметричного типа (14), так как формула (17) имеет единственное решение, не требующее выбора физически значимого корня.
Из приведенной выше классификации для дальнейшего анализа имеет смысл выбрать наиболее универсальные модели, представляющие интерес для практических расчетов. Очевидно, что модели без эмпирических параметров описывают лишь идеализированные гипотетические структуры, не встречающиеся в реальности. Также нецелесообразно анализировать модели с ограничением по контрасту обобщенных проводимостей компонентов, так как эти модели являются асимптотикой более общих моделей и не учитывают влияние формы включений. Выбор сужается еще больше, если учесть, что обобщенные модели Максвелла–Гарнетта, Брюггемана и когерентного потенциала, имеющие один эмпирическиий параметр, являются частным случаем модели Сихволы с двумя параметрами. Обобщенные модели Максвелла–Гарнетта являются частным случаем и модели Сихволы, и инверсно-матричной модели.
Таким образом, интерес представляет анализ наиболее общих, но полученных из разных подходов моделей, а именно, модели Оделевского (14) как обобщение модели (6), асимметричной модели Брюггемана–Ханая (12), модели Сихволы (16) и модели с инверсией матричной структуры (19).
6. КОНЦЕНТРАЦИОННЫЕ И ЧАСТОТНЫЕ ДИСПЕРСИИ ВОСПРИИМЧИВОСТИ В РАЗЛИЧНЫХ МОДЕЛЯХ СМЕШЕНИЯ
Сравнение выбранных моделей смешения проведено методом компьютерного моделирования. Из приведенного выше многообразия моделей для расчетов выбраны наиболее общие из тех, которые не имеют ограничений на контраст свойств компонентов и описывают эффект перколяции. Так как все модели симметричного типа являются частными случаями модели Сихволы (16), то рассматриваются результаты расчета комплексной восприимчивости по формулам (16), (19), (12).
Расчеты по формулам Максвелла Гарнетта и частному случаю формулы Винера (3) приведены как ограничение области допустимых для анизотропной смеси значений восприимчивости (границы Хашина–Штрикмана [18]).
Форма включений и порог перколяции выбраны близкими к величинам, встречающимся на практике для композитов, наполненных сферическими частицами:${{p}_{c}} = 0.33,$ $N = 0.24$ [30, 31]. Включения считаются электропроводящими с удельной проводимостью σ1 = 55.62 Ом–1 м–1. На постоянной частоте f мнимая часть восприимчивости смеси $\chi _{{32}}^{{''}}$ связана с проводимостью σ: $\chi _{{32}}^{{''}}{{\varepsilon }_{2}}{{\varepsilon }_{0}} = 2\pi f\sigma $ (${{\varepsilon }_{0}} = 8.82 \times {{10}^{{ - 12}}}\,\,{{\text{Ф}} \mathord{\left/ {\vphantom {{\text{Ф}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$). Таким образом, контраст диэлектрических проницаемостей компонентов смеси ${{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}}$ является комплексной величиной, зависящей от частоты. В расчетах моделируется измерение диэлектрической проницаемости на частоте $f = 10\,\,{\text{ГГц}},$ обеспечивающей контраст в два порядка в проницаемости компонентов смеси: ${{\chi }_{{12}}} = {{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}} - 1 = 0 + i100.$ Величины проводимости и частоты выбраны для отчетливого проявления эффекта перколяции и для того, чтобы пики диэлектрического поглощения, описываемые различными моделями смешения, для удобства совмещения кривых на одном графике находились при средних наполнениях в диапазоне частот 3–30 ГГц.
На рис. 2 представлены результаты расчетов по наиболее общим моделям (16), (19). На рис. 3 представлены результаты расчетов по модели Брюггемана–Ханая (12), описывающей эффект перколяции (12), а также по модели Максвелла–Гарнетта (6). Заливкой на рис. 2б, 3б выделена область допустимых значений $\chi _{{32}}^{{''}}$ в границах [18].
Инверсно-матричная модель с тремя свободными параметрами (19) является наиболее гибкой, изменением ширины области инверсии можно получить концентрационные зависимости восприимчивости ${{\chi }_{{32}}}\left( p \right)$ (рис. 2), подобные зависимостям для симметричных моделей (16) и кусочно-матричной модели Оделевского (14) (рис. 3). Для смесей симметричного типа модель Сихволы (16) является более строгой и общей, поэтому в переходной $\Delta {{p}_{c}}$ области формула (19) может иметь большую погрешность, чем (16).
Вид годографа концентрационной зависимости восприимчивости смеси ${{\chi }_{{32}}}\left( p \right)$ специфичен для каждой модели смешения. Так, в моделях с кусочной сшивкой прямой матричной с симметричной (14), или инвертированной матричной структурой при отсутствии флуктуаций наполнения $\delta \to 0$ (19) эта сшивка проявляется в виде изломов. По виду этого годографа часто можно определить модель, соответствующую исследуемому композиту, аналогично тому, как по виду годографа частотной дисперсии восприимчивости можно определить тип (форму) линии поглощения (сравним рис. 2а, 2в, 3а, 3в и рис. 4а, 4б, 5а, 5б).
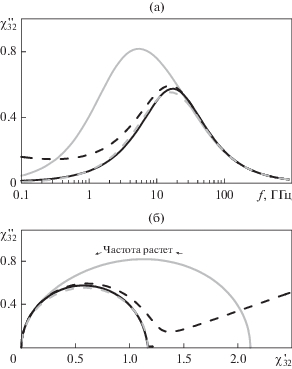
Рис. 4.
Частотная зависимость мнимой части восприимчивости (спектр поглощения) – а; б – годограф (частота растет против часовой стрелки) комплексной восприимчивости композита с 20 об. % частиц с проводимостью (σ1 = 55.62 Ом–1 м–1) при $N = 0.24.$ Инверсно-матричная модель (19) представлена черными линиями, сплошной – $\delta = 0.5$, пунктиром – $\delta = 0.8$. Серыми линиями представлена модель Сихволы (16), сплошной – ${{p}_{c}} = 0.7,$ пунктиром – ${{p}_{c}} = 0.33.$
Проблема в том, что построение по экспериментальным данным концентрационного годографа восприимчивости смеси возможно лишь в отдельных случаях, так как получение двухфазных композитов с закритическим ($p > {{p}_{c}}$) наполнением твердыми частицами представляет большие технологические проблемы (растет хрупкость, появляется неконтролируемая пористость и композит становится трехфазным, что выходит за границы применимости бинарных моделей).
При концентрации включений меньше критической ($p < 0.75{{p}_{c}}$) сравнение с экспериментальными концентрационными зависимостями диэлектрической восприимчивости позволяет отсеять модели, лишь явно не соответствующие исследуемому композиту. Выбор между моделями с одинаковым числом свободных параметров, например, (14), (16), только по концентрационным зависимостям восприимчивости проблематичен [5, 31, 44].
В противоположность концентрационным годографам, построение годографов частотной дисперсии восприимчивости (рис. 4б, 5б) по результатам измерений комплексной восприимчивости проблем не представляет.
Очевидно, что структура композита определяет форму спектра диэлектрического поглощения наравне с проводимостью, размерами и формой частиц наполнителя. Впервые эта связь была выведена в работе [34] для композита, наполненного сферическими электропроводящими частицами и описываемого моделью Максвелла Гарнетта (6). Сравнение частотных (рис. 4б, 5б) и концентрационных (рис. 2в, 3в) годографов показывает, что в композитах с матричной структурой и электропроводящими включениями диэлектрическое поглощение является релаксационным с единственным временем релаксации (линия Дебая) (22)
(22)
$\chi \left( f \right) = {{\chi \left( 0 \right)} \mathord{\left/ {\vphantom {{\chi \left( 0 \right)} {\left( {1 + i{f \mathord{\left/ {\vphantom {f {{{F}_{{{\text{rel}}}}}}}} \right. \kern-0em} {{{F}_{{{\text{rel}}}}}}}} \right)}}} \right. \kern-0em} {\left( {1 + i{f \mathord{\left/ {\vphantom {f {{{F}_{{{\text{rel}}}}}}}} \right. \kern-0em} {{{F}_{{{\text{rel}}}}}}}} \right)}}.$Для удобства сравнения с графиками частотных зависимостей восприимчивости (рис. 4, 5) выражения, описывающие спектр поглощения, записаны в терминах текущей частоты $f,$ частоты релаксации ${{F}_{{{\text{rel}}}}}$ и статической восприимчивости $\chi \left( 0 \right).$ В этом случае, с точки зрения радиофизики композит можно рассматривать как набор идентичных RC-цепочек. Совместное решение (14), (22) (для оценок выбрана модель (14), как более общая по сравнению с (6)) позволяет определить и частоту ${{F}_{{rel}}}$ максимума потерь, и их величину $\chi _{{32\max }}^{{''}}{\text{:}}$
(23)
${{F}_{{{\text{rel}}}}} = \frac{{\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{c}}}}} \right. \kern-0em} {{{p}_{c}}}}} \right)}}{{\left[ {N\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{c}}}}} \right. \kern-0em} {{{p}_{c}}}}} \right) + 1} \right]}} \times \frac{{N\sigma }}{{2\pi {{\varepsilon }_{0}}{{\varepsilon }_{2}}}};$(24)
$\chi _{{32\max }}^{{''}} = \frac{{p\left[ {N\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{c}}}}} \right. \kern-0em} {{{p}_{c}}}}} \right) - 1} \right]}}{{2N\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{c}}}}} \right. \kern-0em} {{{p}_{c}}}}} \right){{{\left[ {N\left( {1 - {p \mathord{\left/ {\vphantom {p {{{p}_{c}}}}} \right. \kern-0em} {{{p}_{c}}}}} \right) - 1} \right]}}^{2}}}}.$Рис. 5.
Частотная зависимость мнимой части восприимчивости (спектр поглощения) – а; б – годограф (частота растет против часовой стрелки) комплексной восприимчивости композита с 20 об. % частиц с проводимостью (σ1 = 55.62 Ом–1 м–1) при $N = 0.24.$ Сплошной линий представлена асимметричная модель Брюггемана–Буссиана–Ханая (12), пунктиром – модель Максвелл Гарнетта (6), точками – модель Оделевского (14) с ${{p}_{c}} = 0.33.$
Величина максимальных потерь $\chi _{{32\max }}^{{''}}$ определяется исключительно концентрацией и формой включений, частота максимума потерь ${{F}_{{{\text{rel}}}}}$ определяется также проводимостью включений и диэлектрической проницаемостью матрицы ${{\varepsilon }_{2}}.$
В композитах с тем же наполнителем и симметричной или инверсно-матричной структурой линия поглощения близка при докритическом наполнении к линии Гавриляка–Негами [67], в которой имеется асимметричное распределение времен релаксации:
(25)
$\chi \left( f \right) = \frac{{\chi \left( 0 \right)}}{{{{{\left[ {1 + i{{{\left( {{f \mathord{\left/ {\vphantom {f {{{F}_{{{\text{rel}}}}}}}} \right. \kern-0em} {{{F}_{{{\text{rel}}}}}}}} \right)}}^{\beta }}} \right]}}^{\alpha }}}}.$В этом выражении параметр $\beta $ характеризует ширину распределения времен релаксации, $\alpha $ – его асимметрию.
Заметим, что пренебрежение абсолютным максимальным размером (учет только скин-эффекта) не позволяет получить наблюдаемую в экспериментах с высокопроводящими волокнами [35] резонансную дисперсию диэлектрической проницаемости, с лоренцевой формой (26) линии поглощения:
(26)
$\chi \left( f \right) = \frac{{\chi \left( 0 \right)}}{{1 - {{{\left( {\frac{f}{{{{F}_{{{\text{rez}}}}}}}} \right)}}^{2}} + i\left( {\frac{f}{{\Gamma {{F}_{{{\text{rez}}}}}}}} \right)}}.$В этом выражении $f$ – текущая частота, ${{F}_{{{\text{rez}}}}}$ – резонансная частота, $\Gamma $ – коэффициент затухания, $\chi \left( 0 \right)$ – статическая восприимчивость.
Резонансное поглощение описывается моделями смешения только в том случае, когда учитывается размер включения, нормированный на длину волны (когда учитывается его индуктивность L).
При этом композит можно рассматривать как набор идентичных резонансных RCL-цепочек [35], а годограф частотной дисперсии восприимчивости трансформируется при уменьшении коэффициента затухания, из полуокружности в окружность при $\Gamma \to 0$ (при $\Gamma \to \infty $ и ${{F}_{{{\text{rel}}}}} = \Gamma {{F}_{{{\text{rez}}}}}$ выражение (26) трансформируется в (22)).
Характерным отличием инверсно-матричной (19) от модели Сихволы (16) является одновременное (при $p = {\text{const}}$) наличие в модели (19) двух механизмов поглощения: за счет статической проводимости и за счет релаксационной дисперсии восприимчивости. В модели (16) в зависимости от концентрации включений наблюдается лишь один из этих механизмов поглощения. Так, на годографе (рис. 4б, черный пунктир) появляется линейный участок, а на частотной зависимости мнимой части диэлектрической восприимчивости $\chi _{{32}}^{{''}}\left( {f \to 0} \right)$ появляется подъем (рис. 4а), обусловленный статической проводимостью.
В противоположность этому, в моделях с симметричной структурой смеси линия поглощения при приближении к порогу перколяции уширяется, смещается в низкочастотную сторону, но смесь остается изолятором. За порогом перколяции статическая проводимость растет с увеличением концентрации включений, а действительная часть восприимчивости падает. Именно это различие может позволить разделить модели смешения, описывающие близкие концентрационные зависимости диэлектрической восприимчивости (рис. 2).
Для иллюстрации различий в спектрах поглощения, описываемых различными моделями смешения для одинакового состава смеси, на рис. 6 представлены трехмерные зависимости мнимой части восприимчивости $\chi _{{32}}^{{''}}$ от частоты f и концентрации p включений для моделей Максвелла Гарнетта (6), Брюггемана–Ханая (12), Оделевского (14), Сихволы (17) и инверсно-матричной модели (19).
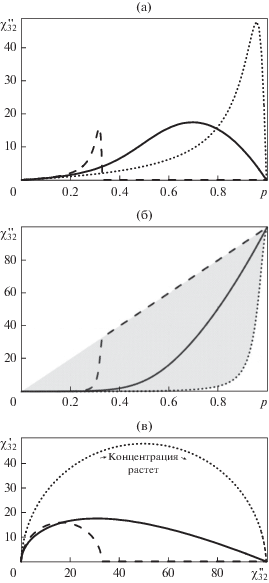
Рис. 6.
Зависимость мнимой части диэлектрической восприимчивости смеси $\chi _{{32}}^{{''}}$от объемной концентрации p проводящих включений (σ1 = 55.62 Ом–1 м–1, $N = 0.24$) и частоты f [Гц]: а – для модели Максвелла Гарнетта (6); б – для асимметричной модели Брюггемана–Буссиана–Ханая (12); в – для модели Оделевского (14) при ${{p}_{c}} = 0.33;$ г – для модели Сихволы (16) при ${{p}_{c}} = 0.33;$ д – для инверсно-матричной модели смешения (19) при ${{p}_{c}} = 0.33$ и $\delta = 0.5.$
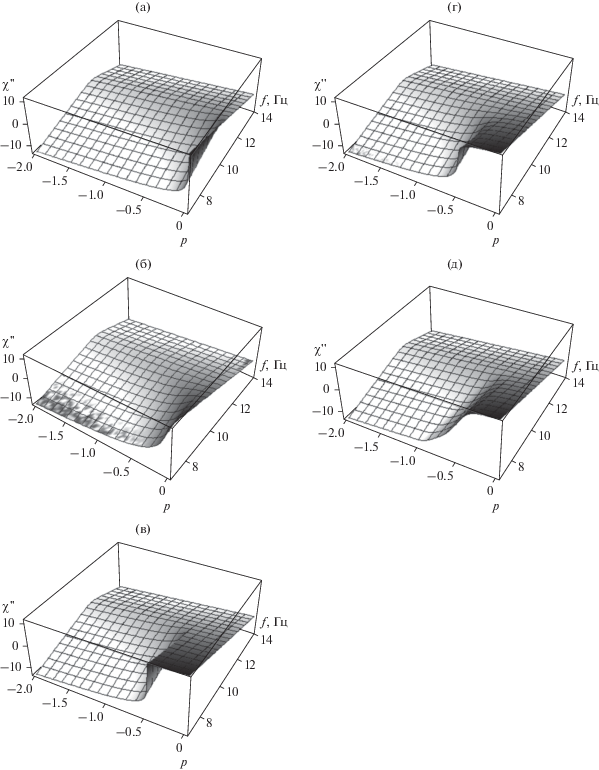
Проводимость и форма включений соответствуют выбранным для графиков на рис. 2–4 (σ1 = = 55.62 Ом–1 м–1, $N = 0.24$). В связи с широким диапазоном изменения восприимчивости (10–10 ≤ $ \leqslant \chi _{{32}}^{{''}}$ ≤ 1010), частоты (100 МГц ≤ f ≤ 100 ТГц), а также с необходимостью представления спектра поглощения и при малых, и при близких к единице концентрациях включений ($0.01 \leqslant p \leqslant 1$), по осям концентрации p и восприимчивости χ'' (рис. 6) выбрана логарифмическая система координат. На всех графиках при малых концентрациях включений ($p < {{10}^{{ - 1}}}$) видна линия поглощения в области 10–12 ГГц. Приближение к порогу перколяции (${{p}_{c}} = 0.33$) вызывает изменение механизма поглощения с релаксационного на поглощение за счет проводимости всего композита.
Понижение частоты вызывает увеличение контраста проницаемостей компонентов смеси $\left| {{{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}}} \right|$ и соответствующее увеличение скачка восприимчивости $\chi _{{32}}^{{''}}$ на пороге перколяции ${{p}_{c}}.$ В модели Максвелла Гарнетта (6) порог перколяции соответствует материалу включений ${{p}_{c}} \equiv 1,$ а перегиб, наблюдающийся на зависимости $\chi _{{32}}^{{''}}\left( p \right)$ в модели (12) при высокой концентрации включений, не является перколяционным переходом. В асимметричной модели Брюггемана–Ханая концентрация p, соответствующая точке перегиба, зависит от частоты (от контраста $\left| {{{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}}} \right|$). В моделях перколяционного типа (14), (16), (19) концентрация, соответствующая точке перегиба, от частоты не зависит.
Совместное решение формул смешения (12), (16), (19) с наиболее общей формулой, описывающей спектр поглощения (25), аналогичное совместному решению формул (23), (24) для матричной смеси, невозможно. Проблема в том, что более сложные модели смешения (12), (16, (19) описывают спектры поглощения, для которых формула Гавриляка–Негами (25) является лишь грубым приближением. Тем не менее соответствие эффективного (вероятнейшего) коэффициента деполяризации и частоты максимума потерь (23) сохраняются.
Распределение времен релаксации определяет форму спектра поглощения. Оно обусловлено распределением форм-факторов кластеров включений. При этом вид частотной дисперсии диэлектрической восприимчивости смесей с проводящими включениями связан со спектральной геометрической функцией, описывающей плотность распределения форм-факторов кластеров при заданной концентрации и форме включений [24].
7. СПЕКТРАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ МОДЕЛЕЙ СМЕШЕНИЯ
Вывод моделей смешения основан на гипотезе о конкретной структуре композита, поэтому топология спектральной геометрической функции специфична для каждой модели смешения, а данные по частотной зависимости одного материального параметра образца композита из компонентов с известными свойствами могут использоваться для восстановления любой обобщенной проводимости этого образца [30, 31, 44, 64].
Известно несколько методов определения плотности распределения эффективных форм-факторов (спектральной геометрической функции Бергмана–Милтона) $b\left( n \right)$ из зависимости восприимчивости смеси ${{\chi }_{{32}}}\left( p \right)$ от объемной концентрацией включений p, характеризуемых форм-фактором N [19, 20, 61]. Проще всего спектральная геометрическая функция выбранной формулы смешения определяется методом Гоша–Фукса [24]:
(27)
$b\left( n \right) = \frac{1}{{\pi p}}\mathop {{\text{lim}}}\limits_{s \to 0} \left[ {{{\chi }_{{32}}}\left( {p,N,{{\chi }_{{12}}}} \right)} \right].$Расчет (27) основан на том, что эффективная восприимчивость идеально проводящего кластера включений определяется его текущим форм-фактором n: ${{\chi }_{{12}}} = - {{\left( {n + is} \right)}^{{ - 1}}}.$ Формальный параметр $s \to 0$ – величина, пропорциональная удельному сопротивлению кластера включений, а текущий форм-фактор n – аргумент геометрической спектральной функции.
Заметим, что текущий эффективный форм-фактор n характеризует кластер включений и отличается от исходного форм-фактора N одиночной частицы ($n = N$ лишь при $p \to 0$).
Спектральные геометрические функции экспоненциальных и логарифмических формул смешения рассмотрены в работах [27, 69]. Ниже рассматриваются спектральные функции наиболее общих моделей смешения (см. разд. 6).
В моделях матричного типа (6), (14) форма включений одинакова и увеличение концентрации ведет к одинаковому удлинению всех кластеров, поэтому для этих моделей плотность распределения форм-факторов является дельта-функций, смещающейся с ростом концентрации p к $n = 0$ при $p = 1$ (6), или при $p = {{p}_{c}}$ (14).
На рис. 7–9 приведены зависимости плотности распределения форм-факторов кластеров от концентрации p и исходной формы N включений, рассчитанные для моделей (12), (16), (19). Под трехмерными картами спектральных геометрических функций $b\left( {n,N,p} \right)$ приведено их сечение при концентрации включений ниже порога перколяции $p \ll {{p}_{c}},$ близкой к порогу перколяции $p \approx {{p}_{c}}$ и превышающей порог перколяции $p > {{p}_{c}}.$
Рис. 7.
Зависимость плотности распределения эффективных форм-факторов $b\left( n \right)$ от форм-фактора кластеров для низконаполненной асимметричной модели Брюггемана–Буссиана–Ханая (12) при форм-факторе исходных включений $N = 0.24$ – а; сечение $b\left( n \right)$ при концентрации включений p = 0.01, 0.33, 0.68 более темная и толстая линия соответствует большей концентрации – б.
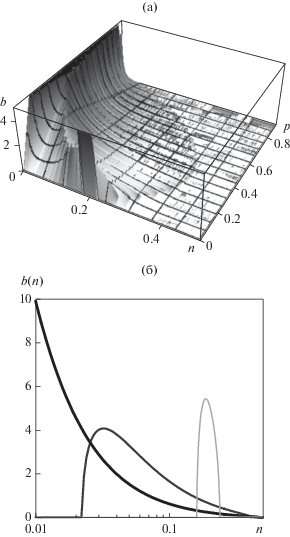
Рис. 8.
Плотность распределения эффективных форм-факторов для модели Сихволы (16). Трехмерный график вверху представляет зависимость b(n) от объемной концентрации $p$ и форм-фактора кластеров при $N = 0.24$ исходных включений. Затемнение поверхности соответствует увеличению $b\left( n \right)$ – а; сечение поверхности $b\left( {n,p} \right)$ для концентрации включений p = 0.02, 0.33, 0.6; более темная линия соответствует большей концентрации – б.
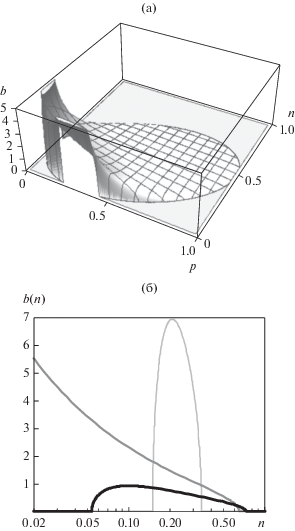
Рис. 9.
Плотность распределения эффективных форм-факторов для инверсно-матричной (19) при $\delta = 0.5.$ Трехмерный график вверху представляет зависимость $b\left( n \right)$ от объемной концентрации $p$ и форм-фактора кластеров при $N = 0.24$ исходных включений. Затемнение поверхности соответствует увеличению b(n) – а; б – сечение поверхности $b\left( {n,p} \right)$ для концентрации включений p = 0.2, 0.33, 0.6; более темная линия соответствует большей концентрации.
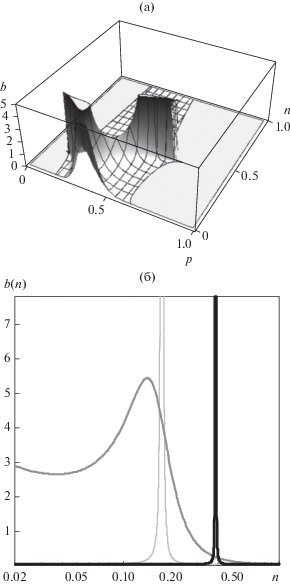
Сравнение трехмерных карт геометрической спектральной функции (рис. 7–9) показывает, что при увеличении концентрации включений до порога перколяции все модели описывают формирование кластеров, образующих удлиненные цепочки из исходных включений. Коренное отличие анализируемых моделей от моделей с матричной структурой (6), (14) в том, что в последних длина всех цепочек идентична и зависит только от концентрации и исходной формы включений.
Плотность распределения эффективных (описывающих форму кластеров частиц) форм факторов моделей (6), (14) представляет собой δ-функцию. Увеличение концентрации включений ведет к уменьшению эффективного форм-фактора. Бесконечный (с ${{N}_{{{\text{eff}}}}} = 0$) кластер образуется для модели Оделевского (14) при $p = {{p}_{c}},$ а для модели Максвелла–Гарнетта (6) при $p = 1.$
Модели (12), (16), (19) также описывают уменьшение эффективного форм-фактора по сравнению с форм-фактором отдельного включения $N,$ но одновременно с увеличением концентрации включений растет и разброс форм факторов $n$ относительно наивероятнейшей величины ${{N}_{{{\text{eff}}}}}.$ Закон распределения эффективных форм-факторов как функция концентрации и исходной формы включений определяется выбранной моделью смешения.
Наиболее простой закон распределения (рис. 6), описывающий монотонное уплощение кривой плотности распределения и сдвиг максимума с увеличением концентрации включений к ${{N}_{{{\text{eff}}}}} = 0$ при p = pc, задается асимметричной моделью Брюггемана–Буссиана–Ханая (10).
В модели Сихволы (16) закон распределения (рис. 7) сложнее. Увеличение концентрации включений выше порога перколяции $p > {{p}_{c}}$ ведет к одновременному образованию бесконечно длинных кластеров с ${{N}_{{{\text{eff}}}}} = 0$ (плотность распределения близка к δ-функции) и коротких фрагментов с широким распределением по длинам в модели Сихволы (16).
В инверсно-матричной модели (19) приближение к точке инверсии ведет к образованию двух раздельных пиков плотности распределения эффективных форм-факторов (рис. 8). Пик с ${{N}_{{{\text{eff}}}}} \to 0$ тоже соответствует формированию длинных кластеров, но в отличие от модели (16) здесь наблюдается широкое распределение кластеров по длинам при незначительной доле бесконечных кластеров с ${{N}_{{{\text{eff}}}}} = 0.$ Положение второго пика обусловлено и исходной формой отдельного включения, и концентрацией. Как и в модели (16), он обусловлен ориентацией близких по форме кластеров перпендикулярно внешнему полю, но в инверсно-матричной модели этот пик плотности распределения форм-факторов близок по форме к Δ-функции. При $p \to 1$ $b\left( n \right)$ представляет собой сумму двух Δ‑функций, первая соответствует бесконечным кластерам, ориентированным вдоль поля, вторая – перпендикулярно полю.
Знание спектральной геометрической функции необходимо для правильного выбора модели по форме спектра поглощения. Измерение частотной зависимости диэлектрического поглощения $\chi _{{32}}^{{''}}\left( f \right)$ композитов с электропроводящими включениями (${{\varepsilon }_{1}} = {{2\pi f{{\sigma }_{1}}} \mathord{\left/ {\vphantom {{2\pi f{{\sigma }_{1}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}$) может быть дополнительным (помимо концентрационной зависимости восприимчивости ${{\chi }_{{32}}}(p)$) условием, позволяющим выбрать модель смешения, наиболее соответствующую структуре исследуемого композита.
Спектры диэлектрического поглощения (рис. 4, 5) и спектры плотности распределения эффективных форм-факторов (рис. 7б–9б) функционально связаны. Казалось бы, достаточно измерить зависимость $\chi _{{32}}^{{''}}\left( f \right)$ образца композита с известным содержанием ($p = {\text{const}}$) электропроводящих включений, чтобы определить его геометрическую спектральную функцию $b\left( n \right).$ Знание этой функции позволяет решать прямую и обратную задачу смешения для любой обобщенной проводимости ${{\Lambda }_{{{\text{mix}}}}}$ исследуемого образца, так как характеристическая геометрическая функция $m = {{{{\Lambda }_{{{\text{mix}}}}}} \mathord{\left/ {\vphantom {{{{\Lambda }_{{{\text{mix}}}}}} {{{\Lambda }_{{{\text{incl}}}}}}}} \right. \kern-0em} {{{\Lambda }_{{{\text{incl}}}}}}}$ = = ${{\left( {{{\chi }_{{32}}} + 1} \right)} \mathord{\left/ {\vphantom {{\left( {{{\chi }_{{32}}} + 1} \right)} {\left( {{{\chi }_{{12}}} + 1} \right)}}} \right. \kern-0em} {\left( {{{\chi }_{{12}}} + 1} \right)}}$ определяется лишь структурой этого образца.
В более общем случае по измеренным зависимостям диэлектрического поглощения серии композитов от концентрации частиц и частоты $\chi _{{32}}^{{''}}\left( {f,p} \right)$ (рис. 6) и спектрам плотности распределения эффективных форм-факторов $b\left( {n,p} \right)$ (рис. 7а–9а) можно выбрать модель смешения, наиболее корректно описывающую исследуемые образцы.
Описанные выше подходы на практике не реализованы из-за ряда проблем.
Во-первых, восстановление спектральной геометрической функции из дисперсионной зависимости комплексной восприимчивости композита является некорректной задачей [68], а возможное решение [70] осложняется тем, что частицы реальных порошков неоднородны по форме.
Во-вторых, в случае композитов с частицами металлов, максимум поглощения оказывается в области жесткого ультрафиолета (оценка частоты релаксации по формуле (23) для сфер железа дает при $p \ll {{p}_{c}}$ ${{F}_{{{\text{rel}}}}} \approx {{10}^{{16}}}\,\,{\text{Гц}}$). В этом диапазоне и размер частиц металла, и расстояние между ними намного превышают длину волны ${{\Lambda }_{{{\text{rel}}}}} \approx 0.01$ мкм. К тому же учет скин-эффекта является приближенным для несферических частиц, в нем не учитывается гранулометрическое распределение частиц, а поверхностная проводимость дисперсных порошков может существенно отличатся от удельной проводимости металла.
В-третьих, наблюдаемые в микроволновой области широкие полосы диэлектрического поглощения композитов с высоким содержанием металлических включений [30–32, 71] имеют низкую интенсивность и плохую воспроизводимость тонкой структуры. Это обусловлено, по-видимому, поверхностными и контактными явлениями, выходящими за рамки бинарных моделей смешения.
Поэтому для верификации модели при восстановлении магнитной проницаемости частиц металла обычно используют не спектры диэлектрического поглощения, а данные по концентрационной зависимости статической или низкочастотной диэлектрической проницаемости [30, 44].
8. ВЫВОДЫ
Анализ моделей смешения показывает, что для интерполяции измеренных концентрационных зависимостей обобщенной восприимчивости смеси можно использовать практически любую из описанных формул. Но формула, выбранная без проверки соответствия модели структуре композита, является лишь эмпирическим уравнением. Так модели, не имеющие определяемых из эксперимента параметров (табл. 1), верны лишь для идеализированных структур, редко встречающихся в реальности. Ошибка в выборе модели проявляется при экстраполяции экспериментальных данных в область более высоких концентраций включений и, в радиофизике, в описании частной дисперсии восприимчивости композита. Наиболее жесткие требования к корректности выбора модели смешения проявляются при попытке экстраполировать концентрационную зависимость комплексной восприимчивости смеси на неизвестную восприимчивость материала включений. Расчеты показывают, что расхождение между величинами ${{\chi }_{{12}}},$ предсказываемыми моделями (12), (14), (16), (19), являющимися наиболее общими из рассмотренных (табл. 2–4), может составлять несколько порядков.
Для выбора корректной модели смешения необходимо проводить исследования концентрационной зависимости нескольких различных по физической природе и контрасту величин обобщенной восприимчивости (в радиофизике такими величинами могут являться, например, магнитная и диэлектрическая восприимчивости). Чем ближе структура композита к структуре в основе выбранной модели, тем меньше невязка с измеренными данными в описании всех восприимчивостей при выбранных параметрах модели (разд. 4). При этом в практических расчетах, по мнению авторов, целесообразно использовать наиболее общие модели смешения (16), (19), так как остальные модели являются, по сути, их частными случаями, получающимися при искусственном введении связи между порогом протекания и формой частиц, при ограничении контраста в проницаемостях компонентов смеси, и т.д.
Необходимо отметить, что погрешность методов измерения и состава, и восприимчивости смеси растет с увеличением концентрации включений. Известные методы [24, 56, 72] измерения микроволновой диэлектрической и магнитной проницаемостей имеют относительную погрешность порядка 10% (точную величину погрешности привести невозможно, эта величина зависит от многих факторов: частоты, тангенса потерь, величин восприимчивости, методики измерений, и т.д.), пикнометрическая погрешность измерения концентрации включений имеет тот же порядок.
Здесь же следует упомянуть эффекты, влияющие на восприимчивость смеси, но не рассматриваемые бинарными моделями смешения. Это, прежде всего, гранулометрическое распределение включений, влияющее на микроструктуру смеси. Во-вторых, это поверхностные эффекты, из-за которых свойства вещества на поверхности и в объеме включения различаются. Например, проводимость контактов между включениями может быть существенно ниже объемной проводимости включений. Это может сказаться как на проводимости смеси за порогом перколяции, так и на вкладе скин-эффекта в динамическую восприимчивость включения. Попытка учета свойств поверхностного слоя приводит к тому, что смесь престает быть бинарной.
Кроме того, квазистатические модели смешения имеют дополнительные погрешности, растущие с увеличением частоты. Так, при линейном размере (длине нити) высокопроводящего включения, близком к длине волны, частотная дисперсия диэлектрической восприимчивости становится резонансной, а линия Дебая (22) превращается в линию Лоренца (26). Высокочастотная магнитная восприимчивость оказывается также зависимой от абсолютного размера (толщины) включений. В результате модели смешения связывают высокочастотную восприимчивость композита со свойствами конкретных частиц, а не вещества. Пересчет восприимчивости частицы на удельные свойства вещества является грубо приближенным, использует дополнительные параметры, определяемые экспериментально, и, строго говоря, выходит за рамки моделей смешения.
При погрешностях измерений концентрации компонентов p и восприимчивости смеси χ32 порядка 10%, а также при пренебрежении контактными явлениями и грубом учете размерных эффектов (гранулометрическое распределение частиц обычно заменяют монодисперными частицами с наивероятнейшим размером и формой), статистически достоверное разделение моделей (16) и (19) проблематично. Поэтому, по мнению авторов, усложнение квазистатической модели смешения, например, за счет учета мультипольного взаимодействия включений, и увеличение числа определяемых из эксперимента параметров выше трех нецелесообразно.
Работа выполнена при частичной поддержке РФФИ (грант 20-52-53020).
Список литературы
Bonifasi-Lista C., Cherkaev E. Electrical impedance spectroscopy as a potential tool for recovering bone porosity // Phys. Med. Biol. 2009. V. 54. P. 3063–3082.
Carrique F., Arroyo F.J., Jimenez M.L., Delgado A.V. Dielectric response of concentrated colloidal suspensions // J. Chem. Physics. 2003. V. 118. № 4. P. 1945–1956.
Glover P.W.J. Archie’s law – a reappraisal // Solid Earth. 2016. V. 7. P. 1157–1169.
Cosenza P., Ghorbani A., Camerlynck C., Rejibal F., Guérin1 R., Tabbagh A. Effective medium theories for modeling the relationships between electromagnetic properties and hydrological variables in geomaterials: a review // Near Surface Geophysics. 2009. P. 563–578.
Дульнев Г.Н., Заричняк Ю.П. Теплопроводность смесей и композиционных материалов // Ленинград, Энергия, 1974. 264 с.
Логинов В.И., Кучеров В.Г. Теплопроводность гомогенных смесей // Прикладная механика и техническая физика. 1991. Т. 32. № 4(188). С. 120–125.
Berryman J.G. Effective medium theory for elastic composites, in Elastic wave scattering and propagation. Ed. V.K. Varadan, V.V. Varadan, Ann Arbor, 1982.
Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook, Cambridge University Press, 2009.
Maxwell Garnett J.C. Colours in metal glasses and in metallic films, Philosophical Transactions of the Royal Society. 1904. V. 203. P. 359–371.
Bruggeman D.A.G. Berechnung verschiedener physikalischer konstanten von heterogenen substanzen, i. dielektrizitätskonstanten und leitfähigkeiten der mischkörper aus isotropen substanzen, Ann. Phys. 1935. P. 636–664.
Ландау Л., Лифшиц Е. Электродинамика сплошных сред. М.: Наука, 1982.
Looyenga H. Dielectric constants of mixtures, Physica. 1965. V. 31. P. 401–406.
Оделевский В.И. Обобщенная проводимость гетерогенных систем. Дис. ... канд. техн. наук, 1947.
Reynolds J.A., Hough J.M. Formulae for Dielectric Constant of Mixtures // Proc. Phys. Soc. 1957. B 70. P. 769–780.
Sihvola A.H. Electromagnetic Mixing Formulas and Applications. London: The institution of Electrical Engineers, 1999, 296 p.
Scheller M., Jansen C., Koch M. Applications of Effective Medium Theories in the Terahertz Regime, in Recent Optical and Photonic Technologies, ed. Ki Young Kim, InTech. 2010. P. 231–250.
Brosseau C. Modelling and Simulation of Dielectric Heterostructures: A Physical Survey from an Historical Perspective // J. Physics D, Applied Physics, 2006. V. 39. № 7. P. 1277–1290.
Hashin Z., Shtrikman S. A variational approach to the theory of the effective magnetic permeability of multiphase materials // J. Appl. Phys. 1962. V. 33. № 10. P. 3125–3131.
Bergman D.J. Dielectric constant of a two-component granular composite: A practical scheme for calculating the pole spectrum // Phys. Rev. 1979. V. 19. № 4. P. 2359–2368.
Bergman D.J. Bounds for the complex dielectric constant of a two component material, Phys. Rev. B. 1981. V. 23. P. 3058–3065
Pal R. Electromagnetic, Mechanical, and Transport Properties of Composite Materials, 2015, CRC press, Taylor&Frances.
Sancaktar E., Lan Bai. Electrically Conductive Epoxy Adhesives // Polymers. 2011. V. 3. P. 427.
Mamunya Ye.P., Davydenko V.V., Pissis P., Lebedev E.V. Electrical and thermal conductivity of polymers filled with metal powders // European Polymer J. 2002. V. 38. P. 1887–1897.
Ghosh K., Fuchs R. Spectral theory for two-component porous media // Phys Rev. B. 1988. V. 38. № 8. P. 5222–5236.
Старостенко C.Н. Розанов К.Н., Простой метод калибровки для измерений магнитной проницаемости в короткозамкнутой полосковой ячейке // Радиотехника и электроника, 2013. Т. 58. № 10. С. 1–9.
Tuncer E. Geometrical Description in Binary Composites and Spectral Density Representation // Materials. 2010. V. 3. P. 585–613.
Goncharenko A.V., Lozovski V.Z., Venger E.F. Lichtenecker’s equation: applicability and limitations // Optics Communic. 2000. V. 174. P. 19–32.
Semenov A.K. On applicability of differential mixing rules for statistically homogeneous and isotropic dispersions // J. Phys. Commun. 2018. V. 2. P. 035 045.
Maklakov S.S., Lagarkov A.N., Maklakov S.A., Adamovich Y.A., Petrov D.A., Rozanov K.N., Ryzhikov I.A., Zarubina A.Yu., Pokholok K.V., Filimonov D.S. Corrosion-resistive magnetic powder Fe@SiO2 for microwave applications // J. Alloys & Compounds. 2017. V. 706. P. 267–273.
Starostenko S.N., Rozanov K.N., Shiryaev A.O., Lagarkov A.N. A technique to retrieve high-frequency permeability of metals from constitutive parameters of composites with metal inclusions of arbitrary shape, estimate of the microwave permeability of nickel // PIER M. 2018. V. 76. P. 143–155.
Starostenko S.N., Rozanov K.N., Shiryaev A.O., Lagarkov A.N., Shalygin A.N. Determination of sendust intrinsic permeability from microwave constitutive parameters of composites with sendust spheres and flakes // J. Appl. Phys. 2017. V. 121. P. 245107.
Розанов К.Н., Петров Д.А., Маратканова А.Н., Чулкина А.А., Ломаева C.Ф. // ФММ. 2018. Т. 115. № 7. С. 682–690.
Кузнецов П.А., Старицын М.В., Самоделкин Е.А., Климов В.Н. Исследование радиотехнических параметров порошков аморфного магнитомягкого сплава AMAG-200 // ФММ. 2018. Т. 119. С. 459–464.
Meyer E., Scmitt H., Severin H-Y. Dielektrizitatskonstante und Permeabilitat kunstlicher Dielectrica bei 3 cm Wellenlange // Zeitscrift fur angewandte Physik, 1956. Bd. 8. S. 257–263.
Starostenko S.N., Rozanov K.N., Microwave screen with magnetically controlled attenuation, Progress In Electromagnetics Research // PIER 2009. V. 99. P. 405–426.
Lagarkov A.N., Rozanov K.N. High-frequency behavior of magnetic composites // J. Mag. Magnet. Mater. 2009. V. 321. № 14. P. 2082–2092.
Ollendorff F. Magnetostatik der Massekerne // Arch. f. Eledtrotechnik., 1931. Bd. 25. S. 436–447.
Polder D., van Santen J.H. The effective permeability of mixtures of solids // Physica. 1946. V. 12. № 5. P. 257–270.
Das C.J., Das-Gupta D.K. Inorganic ceramic/polymer ferroelectric composite electrets // IEEE Transactions on Dielectrics and Electrical Insulation. 1996. V. 3. № 5. P. 706–734.
Rao Y., Qu J., Marinis T., Wong C.P. A precise numerical prediction of effective dielectric constant for polymer-ceramic composite based on effective-medium theory // IEEE Transactions on Components and Packaging Technologies, 2000. V. 23. P. 680.
O. Wiener, Der Abhandlungen der Mathematisch-Physischen Klasse der Konigl // Sachsischen Gesellschaft der Wissenschaften. 1912. Bd. 32. S. 509.
Moore R. Development of a volume fraction scaling function for demagnetization factors in effective media theories of magnetic composites // AIP Advances. 2019. V. 9. P. 015 115-14.
Doyle W.T., Jacobs I.S. Effective cluster model of dielectric enhancement in metal-insulator composites // J. Appl. Phys. 1992. V. 71. № 8. P. 3927.
StarostenkoS.N., Rozanov K.N., Bovtun V., Shiryaev A.O. A mixing formula accounting for inversion of matrix structure // AIP Advances. 2020. V. 10. P. 015 115.
Boyle M.H. The electrical properties of heterogeneous mixtures containing an oriented spheroidal dispersed phase // Colloid and Polymer Science. 1985. V. 263. P. 51–57.
Sihvola A. Dielectric Polarization and Particle Shape Effects // J. Nanomater. 2007. Article ID 45090. https://doi.org/10.1155/2007/45090
Moroz A. Depolarization field of spheroidal particles // J. Opt. Soc. Am. B. 2009.V. 26. P. 517–527.
Tinga W.R., Voss W.A.G., Blossey F. Generalized Approach to Multiphase Dielectric Mixture Theory // J. Applied Physics. 1973. V. 44. № 9. P. 3897–3902.
Sillars R.W. The properties of a dielectric containing semiconducting particles of various shapes // J. Institution of Electrical Engineers. 1937. V. 80. Iss. 484. P. 378–394.
Bottcher C.J.F. Theory of electric polarization, 1973. Elsevier, Amsterdam. P. 377.
Kerner E.H. The Elastic and Thermoelastic Properties of Composite Media // Proceedings of the Physical Society Section B. 1956. V. 69. P. 808–813.
Hanai T. Dielectric theory on the interfacial polarization for two phase mixtures // Bull. Inst. Chem. Res. 1961. V. 39. P. 341–367.
Lichtenecker K., Rother K. Die herleitung des logarithmischen mischungsgesetzes aus allgemeinen prinzipien der stationären strömung // Phys. Zeitschr. 1931. Bd. 32. S. 255–260.
Rother M. Über das Konkurrenzverhalten von Dielektrika bei der Mikrowellenerwärmung, KIT scientific publishing, 2010. P. 196.
Hunt A., Ewing R. Percolation Theory for Flow in Porous Media, 2005, Springer, Switzerland.
Topp G.C., Davis J.L., Annan A.P. Electromagnetic determination of soil water content: Measurement in coaxial transmission lines // Water Resour. Res. 1980. V. 16. P. 574–582.
Musal H.M., Hahn J.H.T., Bush G.G. Validation of mixture equations for dielectric-magnetic composites // J. Appl. Phys. 1988. V. 63. № 8. P. 3768–3770.
Yuan L., Wang B., Xu Y., Wu Q. Calculating the effective permittivity and permeability of composites based on the dilution process model // Advanced Composites Letters. 2017. V. 25. Iss. 6. P. 189–193.
Boned C., Peyrelasse J. Some comments on the complex permittivity of ellipsoids dispersed in continuum media // J. Phys. D: Appl. Phys. 1983. V. 16. P. 1777–1784.
Garner A.L., Parker G.J., Simone D.L. Predicting effective permittivity of composites containing conductive inclusions at microwave frequencies // AIP Advances. 2012. V. 2. P. 032109-6.
Markel V.A., Introduction to the Maxwell Garnett approximation: tutorial // J. Optical Society of America A. 2016. V. 33. № 7. P. 2237–2255.
Jamaian S.S., Mackay T.G., On limitations of the Bruggeman formalism for inverse homogenization // J. Nanophotonics, April 2010. https://doi.org/10.1117/1.3460908
Bussian A.E. Electrical conductance in a porous media // Geophysics. 1983. V. 48. P. 1258–1268.
Sihvola A. Homogenization principles and effect of mixing on dielectric behavior // Photonics and Nanostructures – Fundamentals and Applications. 2013. V. 11. Iss. 4. P. 364–373.
Rozanov K.N., Koledintseva M.Y., Drewniak J. A mixing rule for predicting frequency dependence of material parameters in magnetic composites // J. Magn. Magn. Mater. 2012. V. 324. P. 1063–1066.
McLachlan D.S., Priou A., Chenerie I., Isaac E., Henry F. Modeling of the permittivity of composite materials with a general effective medium equation // Waves&Appl. 1992. V. 6. P. 1099–1131.
Causley M.F., Petropoulos P.G. On the Time-domain Response of Havriliak-Negami Dielectrics // IEEE Trans. on Ant.&Prop. 2013. V. 61. Iss. 6. P. 3182–3189.
Cherkaev E., Zhang Dali. Coupling of the effective properties of a random mixture through the reconstructed spectral representation // Physica B. 2003. V. 338. P. 16–23.
Simpkin R. Derivation of Lichtenecker’s Logarithmic Mixture Formula From Maxwell’s Equations // IEEE Trans. on MTT. 2010. V. 58. № 3. P. 545–550.
Cherkaev E., Yvonne Ou M-J. Dehomogenization: reconstruction of moments of the spectral measure of the composite // Inverse Problems. 2008. V. 24. P. 065 008–06 5017.
Ломаева С.Ф., Маратканова А.Н., Сюгаев А.В., Розанов К.Н., Петров Д.А. Структурнофазовый состав, строение поверхности, магнитостатические и СВЧ свойства порошков, полученных измельчением Fe в полистироле с добавками поверхностно активных веществ // ФММ. 2015. Т. 116. № 8. С. 803–810.
Heuermann H., Schiek B. Procedures for the Determination of the Scattering Parameters for Network Analyzer Calibration // IEEE Trans. Inst&Meas. 1993. V. 42. № 2. P. 528–531.
Дополнительные материалы отсутствуют.
Инструменты
Физика металлов и металловедение


