Физика плазмы, 2020, T. 46, № 4, стр. 368-379
Спектральные характеристики малоразмерных кластерных систем (цепочечные структуры)
a Объединенный институт высоких температур РАН
Москва, Россия
b Московский физико-технический институт (государственный университет)
Московская обл., Долгопрудный, Россия
* E-mail: olga.vaulina@bk.ru
Поступила в редакцию 06.11.2019
После доработки 19.11.2019
Принята к публикации 21.11.2019
Аннотация
Представлены результаты исследования спектральных характеристик стохастического движения заряженных частиц, взаимодействующих с произвольным попарным потенциалом, для малоразмерных цепочечных структур в анизотропном электрическом поле ловушки. Рассмотрены характерные частоты частиц и способ их аналитического вычисления. Приведены соотношения для спектральной плотности смещений в системах, состоящих из нескольких частиц.
1. ВВЕДЕНИЕ
Стохастическое (тепловое) движение в системах взаимодействующих частиц широко распространено в природе и наблюдается, например, в биологических и полимерных коллоидных растворах, в плазме продуктов сгорания, в атмосфере Земли и т.д. [1–6]. Исследование такого движения представляет интерес в различных областях науки и техники.
Комплексная (пылевая) плазма представляет собой ионизованный газ, содержащий заряженные частицы вещества микронных размеров (пыль). Экспериментальный, теоретический и численный анализ теплового движения взаимодействующих пылевых частиц в протяженных и ограниченных ансамблях, формирующихся в газоразрядной плазме, дан в работах [7–13]. Отметим, что в обычных тлеющих разрядах в центре газоразрядных камер наблюдается некоторое превышение концентрации ионов плазмы над концентрацией ее электронной компоненты [14]. Данное обстоятельство приводит к формированию эффективных ловушек для отрицательно заряженных частиц пыли [1, 2]. Лабораторные эксперименты с небольшим количеством пылевых частиц (от двух до ~10) позволяют: определять характер межчастичного взаимодействия; проводить исследования спектров собственных и вынужденных колебаний частиц; изучать влияние различных внешних воздействий; разрабатывать новые методы диагностики и т.д. [15–22].
Для анализа особенностей теплового движения взаимодействующих частиц можно воспользоваться спектральной плотностью их смещений. В общем случае спектральная плотность определяется как преобразование Фурье от корреляционной функции для некоторой физической характеристики анализируемого процесса, а для случайного процесса является косинус-преобразованием Фурье для соответствующей корреляционной функции [23–25]. В отличие от других характеристик системы (параметра неидеальности, коэффициентов тепло- и массопереноса и т.д.) информация о спектральной плотности тепловых смещений частиц позволяет анализировать спектр частот их собственных колебаний в исследуемых системах. Это, в свою очередь, дает возможность оценить реакцию системы на кратковременные или периодические внешние возмущения, а также позволяет определить характер и тип потенциала взаимодействия между частицами среды [7–9, 26, 27].
Несмотря на большое количество работ по изучению теплового движения заряженных частиц во внешнем электрическом поле, вопрос о спектральной плотности смещений для отдельных частиц до конца не выяснен, за исключением случаев одной и/или двух заряженных частиц [28]. В настоящей работе представлены результаты исследования спектральных характеристик для частиц, взаимодействующих с произвольным попарным потенциалом, в малоразмерных цепочечных структурах, включающих до шести заряженных частиц.
2. ОСНОВНЫЕ СООТНОШЕНИЯ
2.1. Общий случай
Рассмотрим равновесную систему, состоящую из N частиц массой M и зарядами Qi, взаимодействующих с произвольной формой потенциала в линейном электрическом поле E(r, z) цилиндрической ловушки с радиальной составляющей Er = = βrr и вертикальной составляющей ${{E}_{z}} = E_{z}^{{^{ \circ }}} + {{\beta }^{z}}z$. Здесь r ≡ (x2 + y2)1/2 – радиальная координата, z – вертикальная координата по оси z в направлении силы тяжести, βr и βz – величины градиентов электрического поля, а значение $E_{z}^{{^{ \circ }}}$ определяется балансом сил, действующих в системе.
В предположении, что смещение ξi частиц (где i = 1,2, …, N) от их положения равновесия под действием некоторой случайной силы Fbi ограничено малыми отклонениями, систему линеаризованных уравнений движения в выбранном направлении для каждой из степеней свободы можно записать в общем виде
(1)
$\begin{gathered} \frac{{d{{V}_{i}}}}{{dt}} = - \nu {{V}_{i}} - {{Q}_{i}}{{\beta }^{{r(z)}}}{{\xi }_{i}}{\text{/}}M + \\ \, + \sum\limits_{j = 1,j \ne i}^N {({{b}_{{ji}}}{{\xi }_{i}} - {{b}_{{ij}}}{{\xi }_{j}})} + {{F}_{{bi}}}{\text{/}}M, \\ \end{gathered} $Основные гармоники для системы (1) (ее характерные частоты) можно найти путем решения характеристического уравнения f(λ) = anλn + + an ‒ 1λn– 1 + … + a1λ + a0, где n определяется числом N взаимодействующих частиц; если корни этого уравнения имеют положительную действительную часть – решение системы (1) является неустойчивым. Корни характеристического уравнения (а, соответственно, значения характерных частот, ωn) могут быть получены численно на основе существующих программных пакетов, которые используют различные методики для их вычисления, а также путем аналитического решения задачи способом, описанным в последующих разделах.
Задача об устойчивой конфигурации двух идентичных частиц, взаимодействующих с различными типами потенциалов, в линейном электрическом поле рассматривалась в работах [20, 21, 29–31], где было показано, что устойчивость вертикальной (цепочечной) конфигурации имеет место при βr > βz, в обратном случае (βr < βz) формируется горизонтальная конфигурация частиц. Критерии устойчивости малоразмерных кластерных систем, включающих до шести заряженных частиц, взаимодействующих с произвольным попарным потенциалом, подробно рассмотрены в работе [31].
2.2. Случай двух частиц
Рассмотрим систему линеаризованных уравнений движения, описывающих отклонения двух заряженных частиц равной массы и размера с зарядами Q1(2) от их положения равновесия, ξ1(2), для выбранной степени свободы в линейном электрическом поле ловушки под действием случайной силы Fb1(2)
(2a)
$\frac{{{{d}^{2}}{{\xi }_{1}}}}{{d{{t}^{2}}}} = - v\frac{{d{{\xi }_{1}}}}{{dt}} - {{a}_{1}}{{\xi }_{1}} + b{{\xi }_{2}} + F_{{b1}}^{{}}{\text{/}}M,$(2б)
$\frac{{{{d}^{2}}{{\xi }_{2}}}}{{d{{t}^{2}}}} = - v\frac{{d{{\xi }_{2}}}}{{dt}} - {{a}_{2}}{{\xi }_{2}} + b{{\xi }_{1}} + F_{{b2}}^{{}}{\text{/}}M.$Остановимся на случае вертикальной конфигурации частиц, рис. 1а, когда
что при Q1 = Q2 сводится к известному соотношению βr > βz [29, 30]. (Все решения для горизонтальной конфигурации частиц, βr < 2βzQ1(2)/(Q1 + + Q2), будут аналогичными, см. рис. 1б.) Тогда для вертикальных смещений частиц, ξ1(2) = z1(2), коэффициент a1(2) = (Q1(2)βz – F')/M и b = –F'/M, где F' – производная силы F взаимодействия между двумя частицами в направлении оси z. Для радиальных смещений частиц, ξ1(2)= r1(2) , величина a1(2) = (Q1(2)βr – F/l) /M, а b = F/lM, где l – расстояние между частицами. Уравнение баланса сил для двух частиц, движение которых описывается уравнениями (2а), (2б), дает βzl = F(Q1 + + Q2)/Q1Q2. Для кулоновского взаимодействия F = Q1Q2/l2; F' = –2Q1Q2/l3.Рис. 1.
Вертикальная (а) и горизонтальная (б) конфигурации двух взаимодействующих частиц в электрическом поле ловушки E = E(z, r) с цилиндрической симметрией.
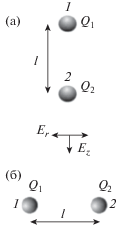
Добавим, что случай a1 ≠ a2 может реализоваться для пылевых частиц в лабораторной плазме не только за счет разницы в зарядах частиц (Q1 ≠ Q2), но и за счет отличия градиентов внешнего поля (β1 ≠ β2) в точке равновесного положения частиц. Оба фактора могут быть связаны с возможным пространственным изменением параметров окружающей плазмы (концентраций и температур ионов/электронов).
Для поиска корреляторов скоростей и смещений частиц в системе, заданной уравнениями (2а), (2б), отметим, что корреляторы случайной силы Fb1(2) подчиняются уравнениям 〈Fb1〉 = 〈Fb2〉 ≡ 0, 〈Fb1Fb2〉 = 0, 〈Fb1V2〉 = 〈Fb2V1〉 ≡ 0, 〈Fb1ξ2〉 = 〈Fb2ξ1〉 ≡ 0, 〈Fb1ξ1〉 = 〈Fb2ξ2〉 ≡ 0, 〈Fb1V2〉 = 〈Fb2V1〉 ≡ 0. Здесь и далее угловые скобки 〈 〉 обозначают усреднение по времени при t→ ∞.
При движении частиц по ограниченным траекториям величины 〈ξ1V1〉 = 〈ξ2V2〉 ≡ 0 и 〈V1(2)Fb1(2)〉 = = νT, где T ≡ T1(2) = M〈$V_{{1\left( 2 \right)}}^{2}$〉 – кинетическая температура частиц (удвоенная кинетическая энергия их стохастического движения). Тогда уравнения для корреляторов скоростей и смещений частиц можно представить в виде [32, 33]
(3а)
$ - {{a}_{{1(2)}}}\left\langle {{{{(\xi _{{1(2)}}^{{}})}}^{2}}} \right\rangle + b\left\langle {\xi _{1}^{{}}\xi _{2}^{{}}} \right\rangle + T{\text{/}}M = 0,$(3б)
$\begin{gathered} - \nu \left\langle {V_{{1(2)}}^{{}}\xi _{{2(1)}}^{{}}} \right\rangle - {{a}_{{1(2)}}}\left\langle {\xi _{1}^{{}}\xi _{2}^{{}}} \right\rangle + \\ + \;b\left\langle {{{{(\xi _{{2(1)}}^{{}})}}^{2}}} \right\rangle + \left\langle {V_{1}^{{}}V_{2}^{{}}} \right\rangle = 0, \\ \end{gathered} $(3в)
$ - 2\nu \left\langle {V_{1}^{{}}V_{2}^{{}}} \right\rangle - {{a}_{1}}\left\langle {\xi _{1}^{{}}V_{2}^{{}}} \right\rangle - {{a}_{2}}\left\langle {\xi _{2}^{{}}V_{1}^{{}}} \right\rangle = 0.$Решение системы уравнений (3а), (3б) дает соотношения для корреляторов скоростей и смещений частиц: 〈V1V2〉 = 0, 〈ξ2V1〉 = –〈ξ1V2〉 ≡ 0 и
(4)
$\left\langle {\xi _{{1(2)}}^{2}} \right\rangle = \frac{{{{a}_{{2(1)}}}T}}{{({{a}_{1}}a{}_{2} - {{b}^{2}})M}}.$Перейдем к определению спектральных характеристик рассматриваемой системы. При вычислениях спектральной плотности обычно используют преобразование Фурье для среднеквадратичного отклонения частиц от их начального положения 〈(ξ1(2)(t) – ξ1(2)(0))2〉t, где угловые скобки 〈…〉t описывают усреднение по всем отрезкам времени, равным t [23–25].
Корни характеристического уравнения для задачи (2а), (2б) можно записать в виде
(5а)
${{\lambda }_{{1,2}}} = ~--\nu {\text{/}}2 \pm {{({{\nu }^{2}}{\text{/}}4 - \omega _{1}^{2})}^{{1/2}}},$(5б)
${{\lambda }_{{3,4}}} = --\nu {\text{/}}2 \pm {{({{\nu }^{2}}{\text{/}}4 - \omega _{2}^{2})}^{{1/2}}},$Тогда любое решение F(t) для задачи (2а), (2б) можно представить в виде суперпозиции
где коэффициенты С0 и Сi определяются граничными условиями (что включает начальные условия при t = 0 и условия при t → ∞). Коэффициенты С0 и Сi даны в Приложении. Фурье-преобразование для этого случая дает для спектральной плотности смещений частиц, G1(2) = G1(2)(ω), соотношение(7)
${{G}_{{1\left( 2 \right)}}} = \frac{{2\nu T{\text{/}}M\{ {{{({{\omega }^{2}} + {{a}_{{2(1)}}})}}^{2}} + {{\nu }^{2}}{{\omega }^{2}} + {{b}^{2}}\} }}{{\{ {{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{1}^{2}){{\omega }^{2}} + \omega _{1}^{4}\} \{ {{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{2}^{2}){{\omega }^{2}} + \omega _{2}^{4}\} }}.$Решение (7) может быть представлено в виде суперпозиции спектральных плотностей для двух классических осцилляторов Si = Si(ω, ωi, ν)
(8)
$\begin{gathered} {{G}_{{1\left( 2 \right)}}} = {{A}_{{1(2)}}}\frac{{2\nu T{\text{/}}M}}{{\{ {{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{1}^{2}){{\omega }^{2}} + \omega _{1}^{4}\} }} + \\ \, + {{A}_{{2(1)}}}\frac{{2\nu T{\text{/}}M}}{{\{ {{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{2}^{2}){{\omega }^{2}} + \omega _{2}^{4}\} }} \equiv \\ \, \equiv {{A}_{{1(2)}}}{{S}_{1}} + {{A}_{{2(1)}}}{{S}_{2}}, \\ \end{gathered} $(9)
$G(\omega ) = \sum\limits_{i = 1}^2 {\frac{{\nu T{\text{/}}M}}{{\{ {{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{i}^{2}){{\omega }^{2}} + \omega _{i}^{4}\} }}} \equiv \sum\limits_{i = 1}^2 {\frac{1}{2}} {{S}_{i}}.$В случае одной частицы (N = 1) в ловушке получим формулу для простого классического осциллятора с
(10)
${{G}_{1}}(\omega ) = \frac{{2\nu T{\text{/}}M}}{{\{ {{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{1}^{2}){{\omega }^{2}} + \omega _{1}^{4}\} }},$В общем случае процедуру вычисления спектральной плотности каждой из частиц в ограниченной цепочке Gj(ω) (j = 1, 2, … N) можно свести к определению суперпозиции спектральных плотностей Sk = Sk(ω, ωi, ν) для отдельных гармоник системы ωk
(11)
$\begin{gathered} {{G}_{j}}(\omega ) = \sum\limits_{k = 1}^N {{{A}_{i}}} \frac{{2\nu T{\text{/}}M}}{{\{ {{\omega }^{4}} + ({{\nu }^{2}} - 2\omega _{k}^{2}){{\omega }^{2}} + \omega _{k}^{4}\} }} \equiv \\ \equiv \sum\limits_{k = 1}^N {{{A}_{k}}} {{S}_{k}}, \\ \end{gathered} $Нормированные спектральные плотности G*(ω) = G(ω)/B, $S_{1}^{*}(\omega )$ = S1(ω)/B и $S_{2}^{*}(\omega )$ = S2(ω)/B смещений в вертикальном и в радиальном направлениях для двух идентичных частиц с кулоновским взаимодействием показаны на рис. 2а, 2б при βr/βz = 4 и ν = 5 с–1, когда $\omega _{t}^{z}{\text{/}}\nu $ = 2, а $\omega _{t}^{r}{\text{/}}\nu $ = 4. Здесь B = 2Т/($\omega _{t}^{2}\nu М$), а ωt =$\omega _{t}^{{z(r)}}$ ≡ (Qβz(r)/M)1/2 – частота ловушки. Следует отметить, что при (ωi/ν)2 ≫ 1 максимум спектральных функций G(ω), S1(ω), S2(ω) хорошо соответствует аналитическим значениям ωi/ν. С уменьшением отношения ωi/ν (например, с ростом коэффициента трения ν) максимум упомянутых функций смещается в сторону более низких частот [23, 28], см. рис. 3а, 3б.
Рис. 2.
Функции G*(ω), $S_{1}^{*}$(ω) и $S_{2}^{*}$(ω) для вертикального (а) и радиального (б) направлений смещения частиц при βr/βz = 4, ν = 5 с–1 , $\omega _{t}^{z}{\text{/}}\nu $ = 2 и $\omega _{t}^{r}{\text{/}}\nu $ = 4.
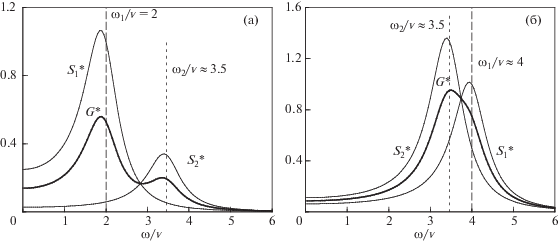
Рис. 3.
Функции G*(ω) для вертикального (а) и радиального (б) направлений смещения частиц при βr/βz = 4, $\omega _{t}^{z}$ = 10 с–1 и $\omega _{t}^{r}$ = 20 с–1 и коэффициентах трения ν: 1 – 10 с–1 ; 2 – 5 с–1 ; 3 – 2 с–1 .
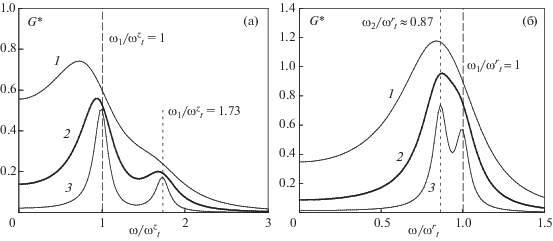
Далее мы рассмотрим спектральные характеристики для случая трех (N = 3), четырех (N = 4) и пяти (N = 5) идентичных частиц (Q i = Q), взаимодействующих с произвольной силой Fij = F(lij) в линейном электрическом поле E(r, z) ловушки с цилиндрической симметрией (см. рис. 4); здесь i = 1, 2, … N, j = 1, 2, … N и i ≠ j. В силу симметрии задачи относительно центра ловушки для систем идентичных частиц функции Gj(ω) и Gi(ω) для частиц j и i, находящихся на одинаковом расстоянии от центра структуры (рис. 4), равны.
Рис. 4.
Вертикальная конфигурация трех (a), четырех (б) и пяти (в) взаимодействующих частиц в электрическом поле ловушки E = E(z, r) с цилиндрической симметрией.
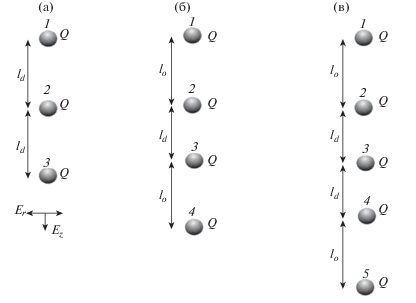
Выбор параметров для иллюстрации расчетов опирался на демонстрацию зависимости результатов от коэффициента трения частиц и величины радиального градиента, ограничивающего их движение в цепочечной структуре.
2.3. Три частицы
Обратимся к случаю трех идентичных частиц (N = 3), рис. 4а. В состоянии равновесия средние расстояния между двумя ближайшими частицами равны l12 = l23 ≡ ld, а уравнение баланса сил дает Qβz ld = F12+ F13, где F12 = F23 ≡ F. Исследование динамики таких частиц в цепочечной структуре сводится к анализу системы уравнений движения (1) для i = 1, 2, 3.
Для поиска спектральных характеристик выполним замену переменных: η1 = ξ1 + ξ2 + ξ3; η2 = = ξ1 – ξ3; η3 = 2ξ2 – (ξ1 + ξ3). (Здесь для вертикальных смещений частиц в цепочке – ξi = zi, а для их радиальных смещений –ξi = ri.) С учетом указанной замены переменных преобразуем систему уравнений движения (1) к виду
(12а)
${{d}^{2}}{{\eta }_{1}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{1}}{\text{/}}dt--(Q\beta {\text{/}}M){{\eta }_{1}},$(12б)
${{d}^{2}}{{\eta }_{2}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{2}}{\text{/}}dt--(Q\beta {\text{/}}M--{{b}_{{12}}}--2{{b}_{{13}}}){{\eta }_{2}},$(12в)
${{d}^{2}}{{\eta }_{3}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{3}}{\text{/}}dt--(Q\beta {\text{/}}M--3{{b}_{{12}}}){{\eta }_{3}}.$Рассматриваемая система имеет по три характерных частоты движений в вертикальном и радиальном направлениях, соответственно: $\omega _{1}^{2}$ = = (Qβ/M); $\omega _{2}^{2}$ = (Qβ/M – b12 – 2b13); $\omega _{3}^{2}$ = (Qβ/M – 3b12). При этом в случае вертикальных смещений частиц от их положения равновесия имеем β = βz, b12= $F_{{12}}^{'}$ ≡ $F_{{23}}^{'}$ = F', b13= $F_{{13}}^{'}$, где F' – первая производная силы взаимодействия F в точке ld и $F_{{13}}^{'}$ – первая производная силы взаимодействия F13 в точке l13 ≡ 2ld. Для радиальных смещений частиц будет β = βr, b12= F/ld, b13= F13/2ld. (Для систем с кулоновским взаимодействием F = ${{Q}^{2}}{\text{/}}l_{d}^{2}$, F13 = = ${{Q}^{2}}{\text{/}}4l_{d}^{2}$, F' = $ - 2{{Q}^{2}}{\text{/}}l_{d}^{3}$, $F_{{13}}^{'} = - {{Q}^{2}}{\text{/}}4l_{d}^{3}$.)
Решение системы (12а)–(12в) для 〈$\eta _{k}^{2}$〉 (k = 1, 2, 3) с учетом 〈ξiξj〉 = 0 при i ≠ j дает для спектральной плотности смещений частиц
(13б)
${{G}_{1}}(\omega ) \equiv {{G}_{3}}(\omega ) = (2{{G}_{2}}(\omega )--{{S}_{3}} + {{S}_{2}}){\text{/}}2,$Отметим, что спектральная плотность для смещений ηk является фурье-преобразованием функций 〈$\eta _{k}^{2}$〉t и соответствует Sηk = Dk Sk, здесь угловые скобки 〈…〉t описывают усреднение по всем отрезкам времени равным t, а коэффициент Dk определяется суммарной температурой частиц, входящих в данный коррелятор. Так, для η1 величина D1 = 3, для η2 будет D2 = 2, а для η3 – D3 = 6.
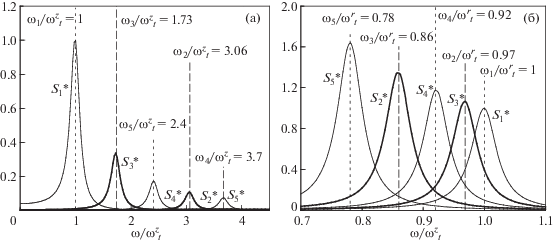
Для системы из трех идентичных частиц с кулоновским взаимодействием нормированные спектральные плотности $G_{i}^{*}(\omega )$ = Gi(ω)/B и $S_{i}^{*}(\omega )$ = Si(ω)/B смещений в вертикальном и в радиальном направлениях представлены на рис. 5а, 5б и рис. 6а, 6б, соответственно, при ν = 2 с–1 и βr/βz = 4. Здесь B = 2Т/($\omega _{t}^{2}\nu М$), а ωt = $\omega _{t}^{{z(r)}}$ ≡ ≡ (Qβz(r)/M)1/2 – частота ловушки.
Рис. 5.
Функции $S_{i}^{*}$(ω) (рисунок а) и $G_{i}^{*}$(ω) (б) для вертикальных смещений частиц при βr/βz = 4, $\omega _{t}^{z}$ = 10 с–1 и ν = 2 с–1.
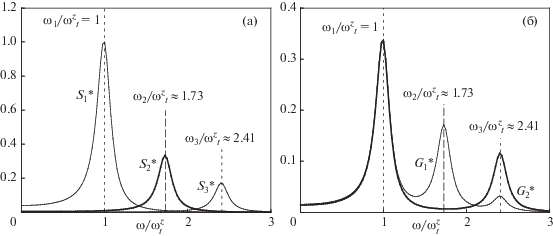
Рис. 6.
Функции $S_{i}^{*}$(ω) (а) и $G_{i}^{*}$(ω) (б) для радиальных смещений частиц при βr/βz = 4, $\omega _{t}^{r}$ = 20 с–1 и ν = 2 с–1 .
Отметим, что рассматриваемая вертикальная конфигурация из трех частиц может терять устойчивость только при их радиальных смещениях от положения равновесия, см. (12а)–(12в). Условия устойчивости для такой системы можно записать как [31]
2.4. Четыре частицы
Уравнения баланса сил для вертикальной конфигурации четырех частиц (N = 4), рис. 4б, можно записать в виде системы двух уравнений
где ld – среднее расстояние между двумя центральными частицами, а lo – среднее расстояние между двумя частицами на периферии. Здесь Fs1 ≡ ≡ F23 + F24 – F12 ≡ F23 + F13 – F34, Fs2 ≡ F13 + F14 + F12 ≡ ≡ F34 + F14 + F24, поскольку цепочка симметрична относительно центра системы. Совместное решение уравнений (15а), (15б) позволяет найти отношение lo/ld и величину равновесного градиента βz электрического поля ловушки. Для систем с кулоновским взаимодействием: F14 = $\frac{{{{Q}^{2}}}}{{{{{({{l}_{{d{\text{ }}}}} + 2{{l}_{{\text{о}}}})}}^{2}}}}$; F23 = $\frac{{{{Q}^{2}}}}{{{{l}_{{d{\text{ }}}}}^{2}}}$; F24 = F13 = $\frac{{{{Q}^{2}}}}{{{{{({{l}_{{d{\text{ }}}}} + {{l}_{{\text{о}}}})}}^{2}}}}$; F12 = F34 = $\frac{{{{Q}^{2}}}}{{{{l}_{{\text{о}}}}^{2}}}$. Критерий устойчивости такой системы приведен в работе [31].Исследование динамики четырех частиц в цепочечной структуре сводится к анализу системы уравнений (1) для i = 1, 2, 3, 4. Для отыскания спектральных характеристик выполним замену переменных: η1 = ξ1 + ξ2 + ξ3 + ξ4; η2 = (ξ1 + ξ4) – (ξ2 + ξ3); η3 = ξ1 – ξ4; η4 = ξ2 – ξ3. (Для вертикальных смещений частиц в цепочке – ξi = zi, а для их радиальных смещений – ξi = ri.) С учетом указанной замены преобразуем систему уравнений движения (1) к виду
(16а)
${{d}^{2}}{{\eta }_{1}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{1}}{\text{/}}dt--Q\beta {\text{/}}M{{\eta }_{1}},$(16б)
$\begin{gathered} {{d}^{2}}{{\eta }_{2}}{\text{/}}d{{t}^{2}} = \\ = --\nu d{{\eta }_{2}}{\text{/}}dt--(Q\beta {\text{/}}M~--{\text{ }}2({{b}_{{12}}} + {{b}_{{13}}})){{\eta }_{2}}. \\ \end{gathered} $(16в)
$\begin{gathered} {{d}^{2}}{{\eta }_{3}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{3}}{\text{/}}dt-- \\ - \;(Q\beta {\text{/}}M--2{{b}_{{14}}}--{{b}_{{12}}} - {{b}_{{13}}}){{\eta }_{3}} + {\text{ }}({{b}_{{13}}}--{{b}_{{12}}}){{\eta }_{4}}, \\ \end{gathered} $(16г)
$\begin{gathered} {{d}^{2}}{{\eta }_{4}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{4}}{\text{/}}dt-- \\ - \;(Q\beta {\text{/}}M - 2{{b}_{{23}}} - {{b}_{{12}}} - {{b}_{{13}}}){{\eta }_{4}} + ({{b}_{{13}}}--{{b}_{{12}}}){{\eta }_{3}}. \\ \end{gathered} $Рассматриваемая система имеет по четыре характерных частоты смещений в вертикальном и радиальном направлениях, соответственно: $\omega _{1}^{2}$ = = (Qβ/M); $\omega _{2}^{2}$ = (Qβ/M – 2(b12+ b13)); $\omega _{3}^{2}$ = = (Qβ/M – b14– b23 – b12 – b13) – d; $\omega _{4}^{2}$ = (Qβ/M – – b14– b23b12 – b13) + d, где d = {(b14– b23)2 + (b13– – b12)2}1/2. При этом в случае вертикальных смещений частиц от их положения равновесия: β = = βz, b12= $F_{{12}}^{'}$, b13= $F_{{13}}^{'}$, b14 = $F_{{14}}^{'}$, b23 = $F_{{23}}^{'}$, где F ' – первая производная соответствующей силы взаимодействия; а в случае радиальных смещений частиц: β = βr, b12 = F12/lо, b13 = F13/(ld + lо), b14 = = F14/(ld + 2lо), b23 = F23/ld.
Решение системы (16а)–(16г) дает для спектральной плотности смещений частиц выражения
(17а)
${{G}_{1}}(\omega ) \equiv {{G}_{4}}(\omega ) = (({{S}_{1}} + {{S}_{2}}){\text{/}}2{\text{ }} + {{A}_{1}}{{S}_{3}} + {{A}_{2}}{{S}_{4}}){\text{/}}2,$(17б)
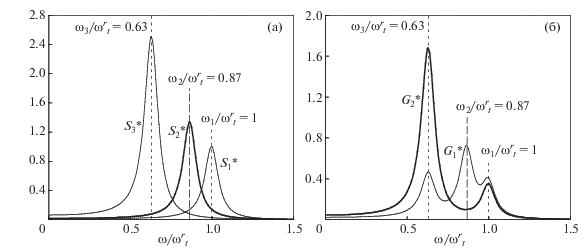
${{G}_{2}}(\omega ) \equiv {{G}_{3}}(\omega ) = (({{S}_{1}} + {{S}_{2}}){\text{/}}2{\text{ }} + {{A}_{2}}{{S}_{3}} + {{A}_{1}}{{S}_{4}}){\text{/}}2,$Для системы из четырех идентичных частиц с кулоновским взаимодействием нормированные спектральные плотности $G_{i}^{*}(\omega )$ = Gi(ω)/B и $S_{i}^{*}(\omega )$ = Si(ω)/B смещений в вертикальном и в радиальном направлениях представлены на рис. 7а, 7б и рис. 8а, 8б, соответственно, при ν = 5 с–1 и βr/βz = 9. Здесь B = 2Т/($\omega _{t}^{2}\nu М$), а ωt = $\omega _{t}^{{z(r)}}$ ≡ ≡ (Qβz(r)/M)1/2 – частота ловушки.
Рис. 7.
Функции $S_{i}^{*}$(ω) (а) и $G_{i}^{*}$(ω) (б) для вертикальных смещений частиц при βr/βz = 9, $\omega _{t}^{z}$ = 10 с–1 и ν = 5 с–1 .
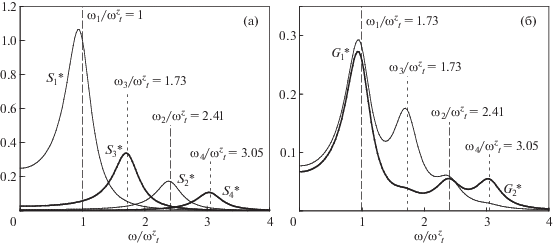
Рис. 8.
Функции $S_{i}^{*}$(ω) (а) и $G_{i}^{*}$(ω) (б) для радиальных смещений частиц при βr/βz = 9, $\omega _{t}^{r}$ = 30 с–1 и ν = 5 с–1 .
Отметим, что с ростом коэффициента трения, ν, или радиальной частоты ловушки, $\omega _{t}^{r}$, экспериментальный анализ спектра частот для отдельных частиц с целью определения основных характеристик системы (ωk, ν) становится затруднительным, см. рис. 3, 7б, 8б. Тем не менее, измерение характерных смещений ηk в системе частиц позволяет без особого труда определить и коэффициент трения частиц ν, и основные гармоники системы ωk, величина которых непосредственно связана с потенциалом взаимодействия частиц. Спектральные плотности Sηk(ω) для рассматриваемых смещений ηk (k = 1–4) связаны с функцией Sk(ω) соотношениями Sηk = 4Sk для k = 1, 2; а сумма спектральных плотностей Sη3 + Sη4 ≡ S3 + S4, см. рис. 9.
Рис. 9.
Нормированные функции $S_{{\eta k}}^{*}$(ω) = Sηk(ω)/B для вертикальных (а) и радиальных (б) смещений частиц: 1 – $S_{{\eta 1}}^{*}$/4 = $S_{1}^{*}$; 2 – $S_{{\eta 2}}^{*}$/4 = $S_{2}^{*}$; 3 – $S_{{\eta 3}}^{*}$ + $S_{{\eta 4}}^{*}$ ≡ $S_{3}^{*}$ + $S_{4}^{*}$. Здесь B = 2Т/($\omega _{t}^{2}\nu М$), где ωt = $\omega _{t}^{{z(r)}}$ ≡ (Qβz(r)/M)1/2.
2.5. Пять частиц
Уравнения баланса сил для вертикальной конфигурации пяти частиц (N = 5), рис. 4в, можно записать как систему двух уравнений
где ld = l23 ≡ l34 – среднее расстояние между центральными частицами системы, а lo = l12 ≡ l45 – среднее расстояние между двумя частицами на периферии. Здесь Fs1 ≡ F23 + F24 + F25 – F12, Fs2 ≡ ≡ F12 + F13 + F14 + F15. Совместное решение уравнений (18а), (18б) позволяет найти и отношение lo/ld , и величину равновесного градиента βz электрического поля ловушки. Для систем с кулоновским взаимодействием между частицами величина ${{F}_{{12}}} = \frac{{{{Q}^{2}}}}{{l_{o}^{2}}}$; ${{F}_{{13}}} = \frac{{{{Q}^{2}}}}{{{{{({{l}_{d}} + {{l}_{о}})}}^{2}}}}$; ${{F}_{{14}}} \equiv {{F}_{{25}}} = \frac{{{{Q}^{2}}}}{{{{{(2{{l}_{{d{\text{ }}}}} + {{l}_{о}})}}^{2}}}}$; ${{F}_{{15}}} = \frac{{{{Q}^{2}}}}{{{{{(2{{l}_{{d{\text{ }}}}} + 2{{l}_{о}})}}^{2}}}}$; ${{F}_{{23}}} = \frac{{{{Q}^{2}}}}{{l_{d}^{2}}}$; ${{F}_{{24}}} = \frac{{{{Q}^{2}}}}{{4l_{d}^{2}}}$. (Критерий устойчивости такой системы см. в работе [31].)Исследование динамики пяти частиц в цепочечной структуре сводится к анализу системы уравнений (1) с i = 1, 2, 3, 4, 5. Для нахождения спектральных характеристик выполним замену переменных: η1 = ξ1 + ξ2 + ξ3 + ξ4 + ξ5; η2 = ξ1 – ξ5; η3 = ξ2 – ξ4; η4 = 2ξ3 – (ξ1 + ξ5); η5 = 2ξ3 – (ξ2 + ξ4). (Для вертикальных смещений частиц в цепочке – ξi = zi, а для радиальных смещений – ξi = ri.) С учетом указанной замены преобразуем систему уравнений движения (1) к
(19а)
${{d}^{2}}{{\eta }_{1}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{1}}{\text{/}}dt--Q\beta {\text{/}}M{{\eta }_{1}},$(19б)
$\begin{gathered} {{d}^{2}}{{\eta }_{2}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{2}}{\text{/}}dt-- \\ - \;(Q\beta {\text{/}}M--2{{b}_{{15}}}--{{b}_{{12}}} - {{b}_{{13}}} - {{b}_{{14}}}){{\eta }_{2}} + \\ + \;({{b}_{{14}}}--{{b}_{{12}}}){{\eta }_{3}}, \\ \end{gathered} $(19в)
$\begin{gathered} {{d}^{2}}{{\eta }_{3}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{3}}{\text{/}}dt-- \\ - \;(Q\beta {\text{/}}M - 2{{b}_{{24}}} - {{b}_{{12}}} - {{b}_{{13}}} - {{b}_{{14}}}){{\eta }_{3}} + \\ + \;({{b}_{{14}}}--{{b}_{{12}}}){{\eta }_{2}}. \\ \end{gathered} $(19г)
$\begin{gathered} {{d}^{2}}{{\eta }_{4}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{4}}{\text{/}}dt-- \\ - \;(Q\beta {\text{/}}M--3{{b}_{{13}}}--{{b}_{{12}}} - {{b}_{{14}}}){{\eta }_{4}} + \\ + \;\left( {2{{b}_{{23}}}--{\text{ }}{{b}_{{12}}} - {\text{ }}{{b}_{{14}}}} \right){{\eta }_{5}}, \\ \end{gathered} $(19д)
$\begin{gathered} {{d}^{2}}{{\eta }_{5}}{\text{/}}d{{t}^{2}} = --\nu d{{\eta }_{5}}{\text{/}}dt-- \\ - \;(Q\beta {\text{/}}M - 3{{b}_{{23}}} - {{b}_{{12}}} - {\text{ }}{{b}_{{14}}}){{\eta }_{5}} + \\ + \;\left( {2{{b}_{{13}}}--{{b}_{{12}}} - {{b}_{{14}}}} \right){{\eta }_{4}}. \\ \end{gathered} $Рассматриваемая система имеет по пять характерных частот движений в вертикальном и радиальном направлениях, соответственно: $\omega _{1}^{2}$ = = (Qβ/M); $\omega _{2}^{2}$ = с1 + d1; $\omega _{3}^{2}$ = с1 – d1; $\omega _{4}^{2}$ = с2 – d2; $\omega _{5}^{2}$ = с2 + d2. Здесь с1 = Qβ/M – b14– b15 – b24 – b12 – – (b13+ b23)/2, с2 = Qβ/M – b12– b14 – 3(b13+ b23)/2, d1 = {(b13 + 2b13 – b23 – 2b24)2/4 + (b14– b12)2}1/2, d2 = = {9(b13– b23)2/4 + (2b23– b12– b14) (2b13– b12– ‒ b14)}1/2. В случае вертикальных смещений частиц от их положения равновесия: β = βz, b12= $F_{{12}}^{'}$, b13= $F_{{13}}^{'}$, b14 = $F_{{14}}^{'}$, b15 = $F_{{15}}^{'}$, b23 = $F_{{23}}^{'}$, b24 = $F_{{24}}^{'}$, где F ' – первая производная соответствующей силы взаимодействия. А для радиальных смещений частиц: β = βr, b12 = F12/lо, b13 = F13/(ld + lо), b14 = = F14/(2ld + lо), b15 = F15/(2ld + 2lо), b23 = F23/ld, b24 = = F24/4ld.
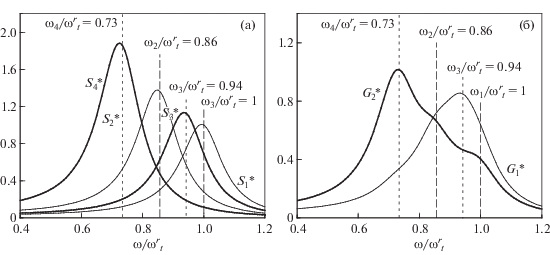
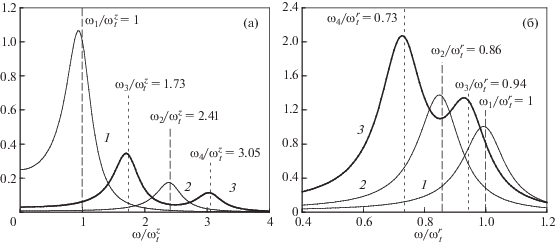
Нормированные спектральные плотности $S_{i}^{*}(\omega )$ = Si(ω)/B для системы из пяти идентичных частиц с кулоновским взаимодействием в вертикальном и в радиальном направлениях показаны на рис. 10а и рис. 10б, соответственно, при ν = 2 с–1 и βr/βz = 16. Здесь B = 2Т/($\omega _{t}^{2}\nu М$), а ωt = $\omega _{t}^{{z(r)}}$ ≡ ≡ (Qβz(r)/M)1/2 – частота ловушки. Еще раз подчеркнем, что измерение смещений ηk в ходе реальных экспериментов с последующим вычислением их спектральных плотностей, Sηk(ω), позволяет определить и коэффициент трения частиц, ν, и основные гармоники системы, ωk.
Рис. 10.
Функции $S_{i}^{*}$(ω) для вертикальных (а) и радиальных (б) смещений частиц при βr/βz = 16, $\omega _{t}^{z}$ = 10 с–1, $\omega _{t}^{r}$ = 40 с–1 и ν = 2 с–1 .
Для систем идентичных частиц с кулоновским взаимодействием в цепочечных структурах, состоящих из N ≤ 5 частиц, квадрат характерных частот частиц, $\omega _{k}^{2}$, для их вертикальных смещений при $\omega _{t}^{z}$ = 10 с–1 представлен в табл. 1, а для радиальных смещений частиц при $\omega _{t}^{r}$ = 30 с–1 – в табл. 2. Легко увидеть, что значения характерных частот, ωk, наблюдаемых в рассматриваемых системах, близки по величине. (Данные о характерных частотах для заряженных частиц в бесконечной цепочке и для случая бесконечного пылевого кристалла приведены в [20, 34].)
Таблица 1.
Квадрат характерных частот, $\omega _{k}^{2}$, по мере их возрастания, в цепочечных структурах, состоящих из N частиц, для вертикальных смещений частиц при $\omega _{t}^{z}$ = 10 с–1
| Число частиц, N | Квадрат характерных частот частиц, $\omega _{k}^{2}$ (c–2), по мере их возрастания | ||||
|---|---|---|---|---|---|
| 1 | 100 | ||||
| 2 | 100 | 300 | |||
| 3 | 100 | 300 | 580 | ||
| 4 | 100 | 301.24 | 580.99 | 930.96 | |
| 5 | 100 | 298.5 | 581.77 | 934.71 | 1347.48 |
Таблица 2.
Квадрат характерных частот, $\omega _{k}^{2}$, по мере их убывания, в цепочечных структурах, состоящих из N частиц, для радиальных смещений частиц при $\omega _{t}^{r}$ = = 30 с–1
| Число частиц, N | Квадрат характерных частот частиц, $\omega _{k}^{2}$ (c–2), по мере их убывания | ||||
|---|---|---|---|---|---|
| 1 | 900 | ||||
| 2 | 900 | 800 | |||
| 3 | 900 | 800 | 660 | ||
| 4 | 900 | 799.38 | 659.5 | 484.52 | |
| 5 | 900 | 800.75 | 659.12 | 482.64 | 276.26 |
3. ЗАКЛЮЧЕНИЕ
Представлены результаты исследования спектральных характеристик стохастического движения для малоразмерных цепочечных структур (состоящих из нескольких частиц, взаимодействующих с произвольным попарным потенциалом) в анизотропном электрическом поле ловушки. Приведены соотношения для спектральной плотности смещений частиц в таких системах. Рассмотрены характерные частоты частиц и способ их аналитического вычисления.
Отметим, что значение характерных частот, ωk, в системе из любого количества N взаимодействующих частиц равной массы и размеров можно получить численно путем определения корней характеристического уравнения для системы линейных дифференциальных уравнений (1). При этом как коэффициент трения частиц, ν, так и частоту ловушки ωt = $\omega _{t}^{{z(r)}}$ ≡ (Qβz(r)/M)1/2 (а, соответственно, и величину градиентов внешнего поля, βz и βr) в реальном эксперименте легко определить из измерений спектральной плотности для суммарных смещений частиц, η1 = ξ1 + ξ2 + …+ + ξN, которые пропорциональны смещению центра масс анализируемой системы. Для определения других гармоник системы, ωk ≠ ωt , можно использовать как измерения спектральных плотностей для отдельных частиц Gi(ω), так и измерения спектральных плотностей для их взаимных смещений (ξi – ξj); здесь i = 1, 2, … N, j = 1, 2, … N и i ≠ j. Последняя процедура является предпочтительней, поскольку с ростом коэффициента трения частиц, ν, или радиальной частоты ловушки, $\omega _{t}^{r}$, экспериментальный анализ спектра частот для отдельных частиц, Gi(ω), становится затруднительным. Добавим также, что измерение вертикальных и радиальных смещений в цепочке заряженных частиц дает информацию о силах межчастичного взаимодействия Fij = F(lij) и их производных $F_{{ij}}^{'}$, что, в свою очередь, позволяет определить характер и тип потенциала взаимодействия между частицами системы.
Результаты настоящей работы применимы для систем при любом типе попарных взаимодействий, а также могут быть адаптированы к случаю непопарных (невзаимных) потенциалов. Полученные результаты могут быть полезны для разработки новых методов диагностики физических свойств пылевой плазмы.
Работа была частично поддержана Российским фондом фундаментальных исследований (грант № 18-38-20175), а также Программой президиума РАН.
Список литературы
Ваулина О.С., Петров О.Ф., Фортов В.Е., Хра-пак А.Г., Храпак С.А. Пылевая плазма (эксперимент и теория). М.: Физматлит, 2009.
Complex and Dusty Plasmas / Ed. by V.E. Fortov and G.E. Morfill. CRC Press, 2010.
Ivlev A., Morfill G., Lowen H., Royall C.P. Complex Plasmas and Colloidal Dispersions: Particle-Resolved Studies of Classical Liquids and Solids. Singapore: World Scientific, 2012.
Photon Correlation and Light Beating Spectroscopy / Ed. by H.Z. Cummins and E.R. Pike. New York: Plenum, 1974.
Pullman B. Intermolecular Interactions: From Diatomics to Biopolymers. Chichester: Wiley Interscience, 1978.
Овчинников А.А., Тимашев С.Ф., Белый А.А. Кинетика диффузионно-контролируемых химических процессов. М.: Химия, 1986.
Ваулина О.С., Адамович К.Г. // ЖЭТФ. 2008. Т. 133. С. 1091.
Ваулина О.С., Адамович К.Г., Петров О.Ф., Фортов В.Е. // ЖЭТФ. 2008. Т. 134. С. 367.
Lisin E.A., Timirkhanov R.A., Vaulina O.S., Petrov O.F., Fortov V.E. // New J. Physics. 2013. V. 15. 053004.
Vaulina O.S., Lisin E.A. // Phys. Plasmas. 2009. V. 16. 113702.
Фортов В.Е., Петров О.Ф., Ваулина О.С., Косс К.Г. // Письма в ЖЭТФ. 2013. Т. 97. С. 366.
Hebner G.A., Riley M.E., Greenberg K.E. // Phys. Rev. E. 2002. V. 66. 046407.
Vaulina O.S., Drangevski I.E. // Phys. Scripta. 2006. V. 73. P. 577.
Райзер Ю.П. Физика газового разряда. М.: Наука, 1987.
Juan W.-T., Huang Z.-H., Hsu J.-W., Lai Y.-J., I L. // Phys. Rev. E. 1998. V. 58. P. 6947.
Ishihara O., Kamimura T., Hirose K.I., Sato N. // Phys. Rev. E. 2002. V. 66. 046406.
Klindworth M., Melzer A., Piel A., Schweigert V.A. // Phys. Rev. B. 2000. V. 61. P. 8404.
Melzer A., Klindworth M., Piel A. // Phys. Rev. Lett. 2001. V. 87. 115002.
Ivlev A.V., Bartnick J., Heinen M., Du C.R., Nosenko V., Löwen H. // Phys. Rev. X. 2015. V. 5. 011035.
Ваулина О.С., Лисина И.И., Косс К.Г. // Физика плазмы. 2013. Т. 39. С. 455.
Lisina I.I., Vaulina O.S. // EPL. 2003. V. 103. 55002.
Mukhopadhyay A.K., Goree J. // Phys. Rev. E. 2014. V. 90. 013102.
Ваулина О.С., Саметов Э. А. // ЖЭТФ. 2018. Т. 154. С. 407.
Климонтович Ю.Л. Статистическая физика. М.: Наука, 1982.
Воронов А.А. Теория автоматического управления. Часть 2. М.: Высшая школа, 1986.
Лисин Е.А., Ваулина О.С. // ЖЭТФ. 2012. Т. 142. С. 1077.
Лисин Е.А., Ваулина О.С., Петров О.Ф. // ЖЭТФ. 2017. Т. 151. С. 791.
Саметов Э.А., Лисин Е.А., Ваулина О.С. // ЖЭТФ. 2020.
Ваулина О.С., Адамович К.Г., Дранжевский И.Е. // Физика плазмы. 2005. Т. 31. С. 562.
Vaulina O.S., Adamovich X.G., Vladimirov S.V. // Phys. Scripta. 2009. V. 79. 035501.
Ваулина О.С., Лисина И.И., Лисин Е.А. // Физика плазмы. 2018. Т. 44. С. 229.
Vaulina O.S. // Phys. Plasmas. 2017. V. 24. 023705.
Ваулина О.С. // ЖЭТФ. 2017. Т. 151. С. 982.
Игнатов А.М. // Физика плазмы. 2017. Т. 43. С. 560.
Дополнительные материалы отсутствуют.


