Физика плазмы, 2023, T. 49, № 4, стр. 342-347

Аналитическое описание циклотронных плазменных резонансов в монослойном графене

А. М. Ишханян^a, b, В. П. Крайнов^c, *

^a Российско-армянский университет
Ереван, Армения

^b Институт физических исследований НАН Армении
Аштарак, Армения

^c Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Россия

^* E-mail: vpkrainov@mail.ru

Поступила в редакцию 21.09.2022
После доработки 17.11.2022
Принята к публикации 26.12.2022

EDN: FKKADS
DOI: 10.31857/S0367292122601163

Полный текст (PDF)

Аннотация

На основе кинетического уравнения Больцмана аналитически рассмотрено распространение продольных гармонических плазменных колебаний в монослойном графене в присутствии внешнего магнитного поля. Представлены простые аналитические формулы для положений циклотронных резонансов в спектре магнето-плазменных колебаний.

Ключевые слова: кинетическое уравнение Больцмана, монослой, графен, продольные плазменные волны, циклотронные резонансы, спектр магнето-плазменных колебаний

1. ВВЕДЕНИЕ

Поверхностные магнето-плазмоны в двумерном графене представляют большой интерес для инфракрасной плазмоники [1–12]. Во внешнем магнитном поле спектр плазмонов имеет аномальное поведение, связанное с циклотронными резонансами (резонансами Бернштейна) [2, 3, 13].

Монослойный графен – это двумерный монослой атомов углерода, помещенных в структуру типа “пчелиные соты” с регулярной гексагональной решеткой. Три из четырех валентных электронов атома углерода образуют локализованные σ-связи с соседними атомами углерода. Четвертый электрон образует делокализованную π-связь и может двигаться свободно. Именно этот электрон и обеспечивает уникальные оптоэлектрические и фотоэлектрические свойства графена. Экспериментальный энергетический спектр этого электрона в зоне Бриллюэна является сплошным и с хорошей точностью представляется двумя верхними гранями равнобедренного треугольника с горизонтальным основанием и с максимумом в центре зоны Бриллюэна. Высота треугольника в энергетических единицах составляет около 15 эВ. Аналитически их можно приближенно описать простой формулой $\varepsilon = \pm v\left| {\mathbf{p}} \right|$. Величина $v$ имеет размерность скорости. Она мала по сравнению со скоростью света, так что название “дираковский спектр” носит условный характер, отражая только линейную зависимость энергии электрона от его импульса. Щель между валентной зоной, которая приближенно имеет вид параболы, и зоной проводимости равна нулю, так что с этой точки зрения графен можно назвать полуметаллом. Для описания длинноволновых плазменных колебаний в графене применимо классическое уравнение Больцмана, хотя характерная длина волны для магнето-плазмонов в графене много меньше, чем в обычных металлах.

Де-бройлевская длина волны электрона проводимости порядка межатомного расстояния как в обычном металле, так и в графене, что гораздо меньше всех характерных длин в поставленной задаче. Эта де-бройлевская длина электрона в данном случае есть длина волны плазмона, и обратно пропорциональная волновому числу. Обычно в металлах при расчетах кинетических коэффициентов всегда используется классическое кинетическое уравнение Больцмана, где предполагается, что де-бройлевская длина волны электрона проводимости мала по сравнению с длиной пробега. Учет конечности длины волны электрона, и учет того, что электрон-квантовая частица, имеющая волновые свойства, ведет к увеличению электрического сопротивления. Таким образом, здесь предполагается высокая плотность электронов и, соответственно, малая де-бройлевская длина волны электрона. Кинетическое уравнение Больцмана пишется для функции распределения электронов по импульсам, а какая эта функция − больцмановская, фермиевская или бозевская − вообще становится неважным в бесстолкновительном случае, так как вид функции обычно учитывается только в записи столкновительного члена уравнения. Если температура достаточно низкая, что имеет место в случае графена (масштаб зоны проводимости составляет несколько электрон-вольт), то электроны проводимости образуют вырожденное “ферми-море”, и можно определить поверхность Ферми (в двумерном случае – это линия). Соответственно определяется импульс Ферми. В двумерном случае импульс Ферми p_F определяется через двумерную концентрацию электронов проводимости n_s соотношением ${{p}_{F}} = \hbar \sqrt {\pi {{n}_{s}}} .$ Соответственно энергия Ферми равна ${{\varepsilon }_{F}} = v{{p}_{F}}.$ В соответствии с экспериментальными данными о плотности электронов в графене заполняется лишь небольшая часть зоны проводимости [4].

В этой работе мы аналитически решаем кинетическое уравнение Больцмана для описания распространения магнето-плазмонов в графене в окрестности циклотронных резонансов. Классическое кинетическое уравнение может описывать вырожденный электронный газ при рассмотрении длинноволновых плазмонных эффектов.

2. КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА

Рассмотрим графен как двухмерный монослой электронной плазмы в отсутствие магнитного поля. Кинетическое бесстолкновительное уравнение Больцмана для функции распределения $n\left( {{\mathbf{r}},{\mathbf{p}},t} \right)$имеет известный вид

(1)

$\frac{{\partial n}}{{\partial t}} + \frac{{d\varepsilon }}{{d{\mathbf{p}}}}\frac{{\partial n}}{{\partial {\mathbf{r}}}} + {\mathbf{F}}\frac{{\partial n}}{{\partial {\mathbf{p}}}} = 0.$

Здесь введена сила Лоренца для электронов проводимости

(2)

${\mathbf{F}} = - e\left( {{\mathbf{E}} + \frac{1}{c}\left[ {\frac{{d\varepsilon }}{{d{\mathbf{p}}}},{\mathbf{Н}}} \right]} \right).$

Внешнее постоянное магнитное поле Н направлено перпендикулярно поверхности слоя графена (в этом разделе будем считать Н = 0, а случай Н ≠ 0 будет рассмотрен в следующем разделе). ${\mathbf{E}} = {\mathbf{E}}\left( {{\mathbf{r}},t} \right)$ – напряженность электрического поля плазменных колебаний в плоскости слоя графена. Здесь $\varepsilon = \pm v\left| {\mathbf{p}} \right|$ – линейный спектр энергий электрона в монослойном графене. Скорость нерелятивистского электрона $v = {\text{const}}$, ${\mathbf{v}} \equiv {\mathbf{p}}v{\text{/}}p$. Из эксперимента следует, что $v = 1.0 \times {{10}^{6}}$ м/с, что много меньше, чем скорость света.

Малое отклонение функции распределение $\delta n\left( {{\mathbf{r,p}},t} \right)$, производимое этой силой Лоренца, удовлетворяет уравнению, следующему из (1):

(3)

$\begin{gathered} \frac{{\partial \delta n}}{{\partial t}} + v\frac{{\mathbf{p}}}{p}\frac{{\partial \delta n}}{{\partial {\mathbf{r}}}} - \frac{{ev}}{{pc}}\left[ {{\mathbf{p,H}}} \right]\frac{{\partial \delta n}}{{\partial {\mathbf{p}}}} = \\ \, = e{\mathbf{E}}\frac{{\partial {{n}_{0}}}}{{\partial {\mathbf{p}}}} = \frac{{ev}}{p}\left( {{\mathbf{pE}}} \right)\frac{{\partial {{n}_{0}}}}{{\partial \varepsilon }}. \\ \end{gathered} $

Здесь ${{n}_{0}}\left( р \right) = - \delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right)$ – равновесная функция распределения Ферми при нулевой температуре, что является хорошим приближением для графена.

Считаем электрическое поле гармоническим: ${\mathbf{E}}\left( {{\mathbf{r}},t} \right) = {\mathbf{E}}\exp \left( {i{\mathbf{kr}} - i\omega t} \right).$ Для продольных колебаний волновой вектор k направлен вдоль вектора Е. Уравнение (3) – линейное, поэтому и $\delta n\left( {{\mathbf{r}},{\mathbf{v}},t} \right)$ = $\delta n\left( {{\mathbf{k}},\omega ,{\mathbf{v}}} \right)\exp \left( {i{\mathbf{kr}} - i\omega t} \right)$. При Н = 0, подставляя ${\mathbf{E}}\left( {{\mathbf{r}},t} \right) = {\mathbf{E}}\exp \left( {i{\mathbf{kr}} - i\omega t} \right)$ в (3), находим малое отклонение функции распределения от равновесной функции распределения Ферми

(4)

$\begin{gathered} \delta n\left( {{\mathbf{k}},\omega ,{\mathbf{v}}} \right) = \frac{{ie\left( {{\mathbf{vE}}} \right)}}{{\omega - \left( {{\mathbf{kv}}} \right)}}\frac{{\partial {{n}_{0}}}}{{\partial \varepsilon }} = \\ \, = - \frac{{ievE\cos \theta }}{{\omega - kv\cos \theta }}\delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right) \\ \end{gathered} $

Здесь θ – полярный угол между импульсом электрона р и вектором напряженности электрического поля Е.

Вычисляем двумерную плотность поляризационных зарядов с учетом двукратного вырождения по спину электрона и двух энергетических зон в спектре графена

(5)

$\begin{gathered} \rho \left( {{\mathbf{k}},\omega } \right) = - e\int {\delta n\left( {{\mathbf{k}},\omega ,{\mathbf{v}}} \right)\frac{{4{{d}^{2}}{\mathbf{p}}}}{{{{{\left( {2\pi \hbar } \right)}}^{2}}}}} = \\ \, = 4i{{e}^{2}}{v}E\int {\frac{{\cos \theta }}{{\omega - kv\cos \theta }}\delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right)} \frac{{pdpd\theta }}{{{{{\left( {2\pi \hbar } \right)}}^{2}}}}. \\ \end{gathered} $

Множитель 2 возникает из-за вырождения спектра по спину электрона. Второй фактор 2 возникает из-за двух подзон графена, $\varepsilon = \pm vp$. При переходе от интегрирования по импульсам к интегрированию по энергиям в (5) возникает энергетическая плотность состояний (учитывается одна из двух дельта-функций)

(6)

$g\left( \varepsilon \right) = \int\limits_0^\infty {pdp\left\{ {\delta \left( {\varepsilon - vp} \right) + \delta \left( {\varepsilon + vp} \right)} \right\}} = \frac{{\left| \varepsilon \right|}}{{{{v}^{2}}}}.$

Тогда из (5) находим

(7)

$\rho \left( {{\mathbf{k}},\omega } \right) = \frac{{i{{e}^{2}}{{\varepsilon }_{F}}E}}{{v{{\pi }^{2}}{{\hbar }^{2}}}}\int\limits_0^{2\pi } {\frac{{\cos \theta d\theta }}{{\omega - kv\cos \theta }}} .$

Вычисляем интеграл по полярному углу между импульсом электрона р и напряженностью электрического поля Е:

(8)

$\frac{1}{{2\pi }}\int\limits_0^{2\pi } {\frac{{\cos \theta d\theta }}{{s - \cos \theta }} = - 1 + \frac{s}{{\sqrt {{{s}^{2}} - 1} }}} ;\quad s = \frac{\omega }{{kv}} > 1.$

Подставляя (8) в (7), находим

(9)

$\rho \left( {{\mathbf{k}},\omega } \right) = \frac{{2i{{e}^{2}}{{\varepsilon }_{F}}E}}{{k{{v}^{2}}\pi {{\hbar }^{2}}}}\left( { - 1 + \frac{s}{{\sqrt {{{s}^{2}} - 1} }}} \right).$

Зная координатную двумерную плотность зарядов $\rho \left( r \right)$, вычисляем соответствующий поляризационный потенциал по закону Кулона

$\varphi \left( {\mathbf{r}} \right) = \int {\frac{{\rho \left( {{\mathbf{r}}{\kern 1pt} '} \right)}}{{\left| {{\mathbf{r}} - {\mathbf{r}}{\kern 1pt} '} \right|}}{{d}^{2}}{\mathbf{r}}{\kern 1pt} '} = \rho \left( {k,\omega } \right)\int {\frac{{\exp \left( {i{\mathbf{kr}}{\kern 1pt} '} \right)}}{{\left| {{\mathbf{r}} - {\mathbf{r}}{\kern 1pt} '} \right|}}{{d}^{2}}{\mathbf{r}}{\kern 1pt} '} = $

(10)

$\begin{gathered} \, = \rho \left( {k,\omega } \right)\exp \left( {i{\mathbf{kr}}} \right)\int\limits_0^\infty {dr} \int\limits_0^{2\pi } {\exp \left( {ikr\cos \psi } \right)} d\psi = \\ \, = 2\pi \rho \left( {k,\omega } \right)\exp \left( {i{\mathbf{kr}}} \right)\int\limits_0^\infty {dr} {{J}_{0}}\left( {kr} \right) = \\ \end{gathered} $

$\, = \frac{1}{k}2\pi \rho \left( {k,\omega } \right)\exp \left( {i{\mathbf{kr}}} \right).$

Таким образом,

(11)

$\varphi \left( {k,\omega } \right) = \frac{{2\pi }}{k}\rho \left( {k,\omega } \right)$

Двумерная плотность зарядов отлична от нуля только в монослое графена, вне его она равна нулю. Согласно уравнению (11) над и под слоем равны нулю потенциал и напряженность электрического поля волны. Напряженность электрического поля волны может быть направлена как вдоль волнового вектора, так и поперек. Здесь рассматриваются только продольные волны ${\mathbf{k}}\,{\text{||}}\,{\mathbf{E}}({\mathbf{r}},t)$.

Вычисляем компоненту индуцированной напряженности электрического поля, параллельной электронному слою

(12)

${{{\mathbf{E}}}_{0}}\left( {\mathbf{r}} \right) = - \frac{{\partial \varphi \left( {\mathbf{r}} \right)}}{{\partial {\mathbf{r}}}};\quad {{{\mathbf{E}}}_{0}}\left( {{\mathbf{k}},\omega } \right) = i{\mathbf{k}}\varphi \left( {k,\omega } \right).$

Подставляя (11) в (12), находим

(13)

${{{\mathbf{E}}}_{0}}\left( {{\mathbf{k}},\omega } \right) = \frac{{2\pi i}}{k}{\mathbf{k}}\rho \left( {{\mathbf{k}},\omega } \right).$

Подставляя (9) в (13), получим окончательное выражение для напряженности индуцированного поля и, следовательно, для вектора электрической поляризации ${\mathbf{P}} = {{{\mathbf{E}}}_{0}}{\text{/}}4\pi $

(14)

${\mathbf{P}}\left( {{\mathbf{k}},\omega } \right) = \frac{i}{{2k}}{\mathbf{k}}\rho \left( {{\mathbf{k}},\omega } \right) = - \frac{{{{e}^{2}}{{\varepsilon }_{F}}E}}{{k{{v}^{2}}\pi {{\hbar }^{2}}}}\left( {\frac{s}{{\sqrt {{{s}^{2}} - 1} }} - 1} \right)\frac{{\mathbf{k}}}{k}$

Отсюда находим продольную диэлектрическую проницаемость тонкого плазменного слоя:

(15)

${{\varepsilon }_{l}}\left( {k,\omega } \right) = 1 - \frac{{4{{e}^{2}}{{\varepsilon }_{F}}}}{{k{{v}^{2}}{{\hbar }^{2}}}}\left( {\frac{s}{{\sqrt {{{s}^{2}} - 1} }} - 1} \right).$

Приравнивая диэлектрическую проницаемость нулю, получаем уравнение для спектра продольных плазмонов в графене

(16)

$1 = \frac{{2\kappa }}{{k{{v}^{2}}}}\left( {\frac{s}{{\sqrt {{{s}^{2}} - 1} }} - 1} \right);\quad \kappa = \frac{{2{{e}^{2}}{{\varepsilon }_{F}}}}{{{{\hbar }^{2}}}}$

Из (16) находим спектр продольных плазмонов [14]

(17)

${{\omega }^{2}} = \frac{{\kappa k}}{{1 + {{v}^{2}}k{\text{/}}4\kappa }} + {{v}^{2}}{{k}^{2}}.$

Он упрощается в наиболее интересной длинноволновой области $k \ll \kappa {\text{/}}{{{v}}^{2}}$

(18)

$\omega = \sqrt {\kappa k} \gg k{v};\quad s \gg 1,$

и в менее интересной коротковолновой области $k \gg \kappa {\text{/}}{{{v}}^{2}}$ (здесь нет дисперсии)

(19)

$\omega = k{v}$

Отличие от плазменных колебаний в обычной плазме небольшое: это другая зависимость энергии электрона от импульса. В обычной нерелятивистской плазме это было бы $\varepsilon = {{p}^{2}}{\text{/}}2m$. В рассмотренном случае ситуация более похожа на ультрарелятивистскую плазму, где $\varepsilon = cp$ и с – скорость света. Но и здесь нет полного совпадения, так как есть ветвь спектра $\varepsilon = - cp$. И, конечно, в графене величина с только по размерности совпадает с размерностью скорости. В действительности это – феноменологическое описание реального спектра. Как это не удивительно, но в двухслойном графене спектр является параболическим, как и в обычной нерелятивистской плазме, но с некоторой эффективной массой. Возбуждение ионно-звуковых колебаний в монослойном графене не реализуется, в отличие от обычной плазмы.

3. КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА В МАГНИТНОМ ПОЛЕ

Теперь включим постоянное поперечное магнитное поле Н. В отличие от обычного трехмерного металла, здесь картина более простая – внешнее магнитное поле перпендикулярно поверхности графена. Возбуждаемая волна является продольной, как и в случае без магнитного поля. А для образования поляритонов нужно несколько слоев графена.

Из (3) находим

(20)

$\begin{gathered} \frac{{\partial \delta n}}{{\partial t}} + {v}\frac{{\mathbf{p}}}{p}\frac{{\partial \delta n}}{{\partial {\mathbf{r}}}} - \frac{{e{v}}}{{pc}}\left[ {{\mathbf{p,H}}} \right]\frac{{\partial \delta n}}{{\partial {\mathbf{p}}}} = \\ \, = - \frac{{e{v}}}{p}\left( {{\mathbf{pE}}} \right)\delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right). \\ \end{gathered} $

Снова полагаем

(21)

$\delta n\left( {{\mathbf{r}},{\mathbf{p}},t} \right) = \delta n\left( {{\mathbf{k}},\omega ,{\mathbf{p}}} \right)\exp \left( {i{\mathbf{kr}} - i\omega t} \right).$

Определим циклотронную частоту

(22)

${{\omega }_{C}} = \frac{{e{v}H}}{{c{{p}_{F}}}}$

Здесь определено ${{p}_{F}} = {{\varepsilon }_{F}}{\text{/}}{v}$. Тогда из (20) получим дифференциальное уравнение для фурье-компоненты отклонения функции распределения $\delta n\left( {k,\omega ,{\mathbf{p}}} \right)$

(23)

$\begin{gathered} \frac{{\partial \delta n\left( {k,\omega ,\theta } \right)}}{{\partial \theta }} + i\left( {\alpha + \beta \cos \theta } \right)\delta n\left( {k,\omega ,\theta } \right) = \\ \, = - \frac{{e{v}E\cos \theta }}{{{{\omega }_{C}}}}\delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right); \\ \alpha = - \frac{\omega }{{{{\omega }_{C}}}};\quad \beta = \frac{{k{v}}}{{{{\omega }_{C}}}}. \\ \end{gathered} $

Здесь, как и выше, θ – полярный угол между импульсом электрона р и напряженностью электрического поля Е. Производя замену δn = $ = \exp \left( { - i\beta \sin \theta } \right)g\left( {k,\omega ,\theta } \right)$, из (23) получим уравнение

(24)

$\frac{{\partial g}}{{\partial \theta }} + i\alpha g = \exp \left( {i\beta \sin \theta } \right)\frac{{e{v}E\cos \theta }}{{{{\omega }_{C}}}}\delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right).$

Решение этого дифференциального уравнения ищем в виде ряда Фурье:

(25)

$g\left( \theta \right) = \sum\limits_{N = - \infty }^\infty {\exp \left( {iN\theta } \right){{g}_{N}}} $

Подставляя (25) в (24), находим коэффициенты разложения:

(26)

${{g}_{N}} = - \frac{{i{{Q}_{N}}}}{{\alpha + N}}.$

Здесь

(27)

$\begin{gathered} {{Q}_{N}} = \\ = \;\frac{{e{v}E}}{{\pi {{\omega }_{C}}}}\delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right)\int\limits_0^\pi {\cos \left( { - N\tau + \beta \sin \tau } \right)\cos \tau d\tau } . \\ \end{gathered} $

Вычисляя интеграл, находим функцию распределения

(28)

$\begin{gathered} \delta n\left( {k,\omega ,\theta } \right) = - \frac{{ieE}}{k}\delta \left( {\varepsilon - {{\varepsilon }_{F}}} \right) \times \\ \, \times \sum\limits_{N = - \infty }^\infty {\frac{N}{{\left( {\alpha + N} \right)}}{{J}_{N}}\left( \beta \right)\exp \left( {iN\theta - i\beta \sin \theta } \right)} . \\ \end{gathered} $

Здесь ${{J}_{N}}\left( \beta \right)$ – функция Бесселя. В соответствии с (5) находим электрическую поляризацию

(29)

$\begin{gathered} Р\left( {k,\omega } \right) = - \frac{{ie}}{2}\int {\delta n\left( {{\mathbf{k}},\omega ,{\mathbf{v}}} \right)\frac{{4{{d}^{2}}{\mathbf{p}}}}{{{{{\left( {2\pi \hbar } \right)}}^{2}}}}} = \\ \, = - \frac{{E\kappa }}{{2k\pi {{\nu }^{2}}}}\sum\limits_{N = - \infty }^\infty {\frac{N}{{\left( {\alpha + N} \right)}}J_{N}^{2}\left( \beta \right)} ;\quad \kappa = \frac{{2{{e}^{2}}{{\varepsilon }_{F}}}}{{{{\hbar }^{2}}}}. \\ \end{gathered} $

Дисперсионный спектр магнето-плазмонов, содержащий много ветвей, имеет вид

(30)

$1 = \frac{C}{\beta }\sum\limits_{N = 1}^\infty {\frac{{{{N}^{2}}}}{{{{\alpha }^{2}} - {{N}^{2}}}}J_{N}^{2}\left( \beta \right)} .$

Здесь обозначено $C = \frac{{4\kappa }}{{{v}{{\omega }_{C}}}}$. Для обычного двумерного металла это уравнение было получено в работе [15]. Например, в окрестности первого циклотронного резонанса N = 1 из (30) имеем

(31)

${{\omega }^{2}} = \omega _{C}^{2} + \frac{{4\kappa \omega _{C}^{2}}}{{k{{\nu }^{2}}}}J_{1}^{2}\left( {\frac{{k{v}}}{{{{\omega }_{C}}}}} \right).$

В частности, в длинноволновой области $k{v} \ll {{\omega }_{C}}$ из (31) получим простой закон дисперсии

(32)

${{\omega }^{2}} = \omega _{C}^{2} + \kappa k.$

В отсутствие магнитного поля из (32), как и должно быть, получаем длинноволновую часть спектра (18). Аналогичное выражение было получено ранее [16, 17] для двумерного слоя металла с обычным нерелятивистским законом дисперсии $\varepsilon = {{p}^{2}}{\text{/}}2m$

(33)

${{\omega }^{2}} = \omega _{C}^{2} + \frac{{2\pi {{e}^{2}}\rho d}}{m}k$

Здесь ρ – плотность электронов, а d – толщина двумерного слоя металла. Переход от обычного двумерного металла к графену меняет только численный коэффициент в законе дисперсии [16, 17]

(34)

$\frac{{2\pi {{e}^{2}}\rho d}}{m} \to \frac{{2{{e}^{2}}{{\varepsilon }_{F}}}}{{{{\hbar }^{2}}}}$

Две ветви спектра (30) учитывающие два первых резонанса, имеют вид

(35)

$\alpha _{ \pm }^{2} = \frac{1}{2}\left( {5 + \frac{C}{\beta }J_{1}^{2}\left( \beta \right) + \frac{{4C}}{\beta }J_{2}^{2}\left( \beta \right)} \right) \pm \sqrt {\frac{1}{4}{{{\left( {5 + \frac{C}{\beta }J_{1}^{2}\left( \beta \right) + \frac{{4C}}{\beta }J_{2}^{2}\left( \beta \right)} \right)}}^{2}} - 4 - \frac{{4C}}{\beta }\left( {J_{1}^{2}\left( \beta \right) + J_{2}^{2}\left( \beta \right)} \right)} ,$

где параметр $\beta = kv{\text{/}}{{\omega }_{C}}.$ Ветвь спектра при знаке “минус” показана на рис. 1 при С =1. Она отражает первый циклотронный резонанс (при учете второго). Ветвь спектра при знаке “плюс” показана на рис. 2. Она отражает второй резонанс (при учете первого). Ветви не пересекаются друг с другом. Ветвь спектра на рис. 1 слабо отличается от ветви, в которой второй резонанс не учитывается. При $\beta < 1$ это объясняется тем, что вклад функций Бесселя быстро убывает с увеличением их индекса. А при $\beta > 1$ частота плазмона для каждого номера резонанса становится близкой к соответствующей циклотронной частоте. Отметим существенно разный масштаб по оси ординат на рис. 1 и 2 .

Рис. 1.

Зависимость отношения квадратов частот ${{\left( {{{\omega }_{ - }}{\text{/}}{{\omega }_{С}}} \right)}^{2}}$ от параметра $\beta = k{v}{\text{/}}{{\omega }_{C}}$ согласно (35).

Рис. 2.

Зависимость отношения квадратов частот ${{\left( {{{\omega }_{ + }}{\text{/}}{{\omega }_{С}}} \right)}^{2}}$ от параметра $\beta = k{v}{\text{/}}{{\omega }_{C}}$ согласно (35).

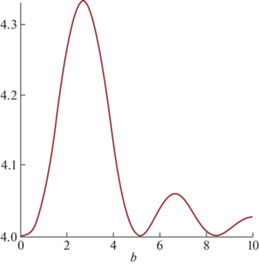
Начальная часть этой кривой при малых волновых числах была получена для идеального газа вырожденных электронов в обычном металле в работе [18]

(36)

$\omega _{ - }^{2} = \omega _{C}^{2} + \frac{{2\pi {{e}^{2}}\rho d}}{m}k - \gamma {{k}^{3}}.$

Здесь величина γ отражает влияние второго циклотронного резонанса. Отметим, что уравнения (16)–(17) (в отсутствие магнитного поля) не являются новыми. Результаты в уравнениях (30)–(31), (35) (в присутствии магнитного поля) являются новыми. Формулы (32)–(34), (36) также не являются новыми.

4. ЗАКЛЮЧЕНИЕ

Из спектра (31) следует, что роль магнитного поля уменьшается при высоких частотах, и спектр описывается зависимостью $\omega = \sqrt {\kappa k} \gg k{v}$; $s \gg 1$ (18). Магнитное поле существенно изменяет плазмонный спектр при низких частотах. Мы пренебрегли в кинетическом уравнении электрон-электронными столкновениями и другими столкновительными эффектами [11]. Роль электрон-электронных столкновений существенна как в пределе слабой связи, когда электронно-дырочные возбуждения определяются коллективными модами, так и в пределе сильной связи для частично заполненных релятивистских уровней Ландау [12]. В последнем случае экзотические ферромагнитные фазы и несжимаемые квантовые жидкости могут быть причиной возникновения квантового эффекта Холла. В сильном магнитном поле плазмонный спектр может изменяться из-за электрон-фононной связи.

Сегодня электроника, основанная на кремнии, достигла предела в миниатюризации, составляющего 50 нм для электронного канала. Полоска монослойного графена в 2–3 нм может быть использована как транзистор, − основной компонент электроники нового поколения. В присутствии магнитного поля в графене перспективно исследование роли квантового эффекта Холла в электронике. Толщина двумерных металлических пленок обычно больше постоянной кристаллической решетки. Полученные результаты относятся к монослою графена, дираковский спектр электронов проводимости которого существенно отличается от спектра электронов в тонких металлических пленках. Даже в двухслойном графене электронный спектр совершенно другой – он ближе к спектру электронов в металлических пленках.

Вследствие линейности электронного спектра графен представляет собой идеальный кандидат для проверки теоретических моделей квантовых полей, развиваемых в физике высоких энергий. Электроны в графене можно рассматривать как безмассовые заряженные фермионы, существующие в двухмерном пространстве. Действительно, все известные безмассовые частицы (фотоны, нейтрино) электрически нейтральны. Поэтому графен представляет собой мостик между физикой твердого тела и физикой высоких энергий. Плотность носителей в графене удобно контролировать, в отличие от обычного металла, прикладывая электрическое напряжение к концам образца.

Работа поддержана РФФИ (проект № 20-52-05012), комитетом Армении по науке (проекты № 20RF-171 и 21AG-1C064), а также Министерством науки и высшего образования РФ (проект № FSMG-2021-0005).

Список литературы

Hu B. Plasmonics / Ed. by Tatjana Gric, New York: I-ntech-Open, 2018. P. 213.
Hu B., Tao J., Zhang Y., Wang Q. // Optics Express. 2014. V. 22. 21727.
Heydari M.B., Samiei M.H.V. // arXiv.org/abs/2103.08557. 2021.
Wallbank J.R. Electronic properties of graphene heterostructures with hexagonal crystals. Berlin: Springer, 2014.
Guo J., Dai X., Xiang Y., Tang D. // J. Appl. Phys. 2019. V. 125. 013102.
Kapralov K., Svintsov D. // arXiv: 2203.04479v2 [cond-mat.mes-hall] 7 Jul 2022.
Bandurin D.A., Mönch E., Kapralov K. et al. // Nature Physics. 2022. V. 18. P. 462.https://doi.org/10.1038/s41567-021-01494-8
Cui L., Wang J., Sun M. // Reviews in Physics. 2021. V. 6. 100054.
Goerbig M.O. // Rev. Mod. Phys. 2011. V. 83. P. 1193.
Castro Neto A.H., Guinea H., Peres N.M.R., Novose-lov K.S., Geim A.K. // Rev. Mod. Phys. 2009. V. 81. P. 109.
Levitov L.S., Shtyk A.V., and Feigelman M.V. // a-rXiv:1302.5036v2. 2013.
Emani N., Kildishev A.V., Shalaev V.M., Boltasseva A. // Nanophotonics 2015. V. 4. P. 214–223. https://doi.org/10.1515/nanoph-2015-0014
Volkov V.A., Zabolotnykh A.A. // Phys. Rev. 2014. B 89. 121410(R).
Бурмистров С.Н. Задачи по физической кинетике. Долгопрудный: изд-во “Интеллект”. 2014. Задача 28.
Chaplik A.V., Heitmann D. // J. Phys. C: Solid State Phys. 1985 V. 18. P. 3357. Eq. (7).
Horing N.M., Yildiz M. // Physics Letters A. 1973. V. 44. P. 386.
Horing N.M., Yildiz M. // Annals of Physics. 1976. V. 97. P. 216. Eq. (72).
Ando T., Fowler A., Stern F. // Rev. Mod. Phys. 1982. V. 54. P. 437.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Физика плазмы

Архивы выпусков Информация о журнале Отправить рукопись в журнал