Геомагнетизм и аэрономия, 2020, T. 60, № 4, стр. 502-507

Характеристики инкремента нарастания дрейфово-диссипативной неустойчивости на фронтах экваториальных плазменных пузырей

Н. М. Кащенко^1, *, М. А. Никитин^1, **

¹ Балтийский федеральный университет им. Иммануила Канта
г. Калининград, Россия

^* E-mail: kaschtschenko@mail.ru
^** E-mail: manikitin@mail.ru

Поступила в редакцию 08.07.2019
После доработки 07.08.2019
Принята к публикации 23.01.2020

DOI: 10.31857/S0016794020030074

Аннотация

Данные наземных и спутниковых измерений, а также результаты численного моделирования пространственной структуры экваториальных ионосферных пузырей показывают, что долготные градиенты логарифма электронной концентрации на вертикальных границах пузырей могут достигать значений 10^–3 м^–1. При таких градиентах электронной концентрации возможно развитие дрейфово-диссипативной неустойчивости, которая может генерировать неоднородности ионосферной плазмы с пространственно-временны́ми масштабами, характерными для экваториального F-рассеяния. В данной статье представлены результаты расчетов инкремента нарастания градиентно-дрейфовой неустойчивости на боковых стенках ионосферных пузырей, полученные на основе численного моделирования структуры экваториальных плазменных пузырей и дисперсионного уравнения дрейфово-диссипативной неустойчивости. Моделирование экваториальных плазменных пузырей осуществлялось на основе двумерной численной модели неустойчивости Рэлея-Тейлора в экваториальной ионосфере Земли, пригодной для моделирования сильно вытянутых вдоль силовых линий магнитного поля неоднородностей рэлей-тейлоровского и градиентного типов. Результаты численных экспериментов подтверждают возможность генерации дрейфово-диссипативной неустойчивости ионосферной плазмы за счет значительных долготных градиентов плазмы на фронтах развитого экваториального плазменного пузыря.

1. ВВЕДЕНИЕ

Плазменные пузыри в экваториальной F-области являются сильно неоднородными и нестационарными образованиями. Они характеризуются достаточно широким спектром пространственных масштабов, включающим как среднемасштабные, так и мелкомасштабные неоднородности [Farley et al., 1970; Rottger, 1973, 1976; Woodman, 2009; Reinisch et al., 2004; Saito et al., 2008]. К среднемасштабным неоднородностям можно отнести высотную и долготную структуру развитого пузыря, к мелкомасштабным – эффекты F-рассеяния. Происхождение среднемасштабных ионосферных пузырей связано с развитием неустойчивости Рэлея-Тейлора (НРТ) в ионосферной плазме [Ossakow and Chaturvedi, 1978; Кащенко и др., 1989; Huba et al., 2008], мелкомасштабных – с развитием градиентных неустойчивостей плазмы, в частности, дрейфово-диссипативной неустойчивости [Costa and Kelley, 1978].

В данной работе на основе численной модели ионосферных пузырей рассмотрен вопрос о возможности развития дрейфово-диссипативной неустойчивости на фронтах экваториальных плазменных пузырей (ЭПП). Основанием для подобного сценария являются большие долготные градиенты логарифма концентрации плазмы на фронтах развитых пузырей, которые могут достигать значении 10^–3 м^–1 и более. Из-за сложностей одновременного учета развития рэлей-тейлоровской и дрейфово-диссипативной неустойчивостей инкремент нарастания дрейфово-диссипативной неустойчивости рассчитывается в линейном приближении на основе характеристик ионосферного пузыря, смоделированного на двумерной модели в предположении сильной вытянутости плазменного пузыря вдоль силовых линий геомагнитного поля [Кащенко и др., 1989, 2018].

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НЕУСТОЙЧИВОСТИ РЭЛЕЯ-ТЕЙЛОРА

Математическую основу численной модели составляют уравнения плазменной гидродинамики, содержащие следующие уравнения:

– уравнения непрерывности ионов (концентрация электронов выражается через концентрацию ионов в предположении квазинейтральности ионосферной плазмы):

(1)

$\frac{{\partial {{n}_{j}}}}{{\partial t}} + \nabla \left( {{{n}_{j}}{{{\mathbf{V}}}_{j}}} \right) = {{Q}_{j}} - {{L}_{j}}$

– уравнения движения ионов и электронов в диффузионном приближении:

(2)

$\begin{gathered} - \frac{{\nabla {{p}_{j}}}}{{{{n}_{j}}{{m}_{j}}}} + \frac{{{{e}_{j}}}}{{{{m}_{j}}}}\left( {{\mathbf{E}} + {{{\mathbf{V}}}_{j}} \times {\mathbf{B}}} \right) - {{{v}}_{{jn}}}\left( {{{{\mathbf{V}}}_{j}} - {{{\mathbf{V}}}_{n}}} \right) - \\ - \,\,\sum\limits_{l \ne j} {{{{v}}_{{jl}}}\left( {{{{\mathbf{V}}}_{j}} - {{{\mathbf{V}}}_{l}}} \right) + {\mathbf{g}}} = 0 \\ \end{gathered} $

– уравнения теплопроводности ионов и электронов:

(3)

$\frac{3}{2}{{n}_{j}}k\left( {\frac{{\partial {{T}_{j}}}}{{\partial t}} + \left( {{{{\mathbf{V}}}_{j}}\nabla } \right){{T}_{j}}} \right) + {{p}_{j}}\nabla {{{\mathbf{V}}}_{j}} + \nabla {{{\mathbf{q}}}_{j}} = {{G}_{j}} - {{P}_{j}}$

– уравнения потенциальности электрического поля:

(4)

$\nabla \times {\mathbf{E}} = 0$

– уравнения непрерывности электрического тока:

(5)

$\nabla {\mathbf{J}} \equiv \nabla \sum {{{e}_{j}}{{n}_{j}}{{{\mathbf{V}}}_{j}}} = 0,$

где j – сорт заряженных частиц: ионов O⁺ и NO⁺ и электронов; V_j – скорости заряженных частиц; Q_j, L_j – скорости образования и потерь ионов; n_j – концентрация заряженных частиц; m_j – масса заряженных частиц; e_j – заряд частиц; p_j – давление газа заряженных частиц; ν_jn – частоты соударений заряженных частиц с нейтралами; ν_jl – частоты столкновений между заряженными частицами; T_j – температура заряженных частиц; q_j – плотность теплового потока; G_j, P_j – скорости нагрева и скорость охлаждения заряженных частиц; индексы указывает на типы частиц; k – постоянная Больцмана; E – напряженность электрического поля; J – плотность электрического тока.

Далее будем считать, что вследствие замагниченности ионосферной плазмы F-области процессы переноса вдоль магнитного поля будут определяться столкновениями, а поперек поля – дрейфовым движением плазмы. Из-за сильной анизотропии, обусловленной магнитным полем Земли, процессы диффузионного переноса и теплопроводности в области F экваториальной ионосферы происходят в основном вдоль силовых линий геомагнитного поля, а благодаря условию электростатики (4) электрическое поле потенциально:

(6)

${\mathbf{E}} = - \nabla \Phi ,$

где Ф – потенциал электрического поля.

Магнитное поле Земли будем считать постоянным по времени и дипольным, поэтому размерность уравнения для потенциала (5) может быть понижена до двух интегрированием вдоль силовых линий магнитного поля уравнения непрерывности электрического тока:

(7)

${{\nabla }_{ \bot }}\left( {\hat {\sigma }{{\nabla }_{ \bot }}{\Phi }} \right) = {{\nabla }_{ \bot }}{\mathbf{A}},$

где $\hat {\sigma }$ – тензор интегральных проводимостей поперек магнитного поля.

Для вычисления параметров нейтральных частиц использовалась глобальная термосферная модель MSIS [Hedin, 1977a; Hedin, 1977b]. Начальные значения вычисляемых переменных для численных экспериментов задавались путем решения низкоширотной модели ионосферы до получения периодического по суткам решения.

В данной работе численное моделирование системы уравнений (1–7) проводится в предположении достаточно развитых ЭПП, вытянутых вдоль магнитного поля Земли [Кащенко и др., 1989, 2018]. Это позволяет существенно упростить математическую модель экваториальных пузырей, используя двухмерную запись уравнений модели в экваториальной плоскости, перпендикулярной магнитным силовым линиям. В результате двумерное приближение модели (1–7) включает в себя двумерные уравнения непрерывности ионов, двумерные уравнения движения ионов и электронов в диффузионном приближении, двумерные уравнения теплопроводности ионов и электронов и уравнения (6, 7).

Для численного решения полученной модели и используется прямоугольная система координат, через x обозначена координата, направленная вдоль геомагнитного поля Земли, через y обозначена горизонтальная координата, направленная на восток, через z – вертикальная координата, направленная вверх.

3. МОДЕЛЬ ДРЕЙФОВО-ДИССИПАТИВНОЙ НЕУСТОЙЧИВОСТИ

В условиях развитого плазменного пузыря формируются значительные градиенты концентрации плазмы в горизонтальном направлении поперек геомагнитного поля (вдоль координаты y). Эти градиенты способны породить поперечную дрейфовую волну, распространяющуюся со скоростью дрейфового движения электронов в плоскости х–z. Возмущения концентрации электронов n¹ в такой волне имеют вид:

(8)

${{n}^{1}} = A(y){\text{exp}}(--i\omega t + i{{k}_{x}}x + i{{k}_{z}}z).$

Характерные соотношения волновых чисел k_x и k_z в выражении (8) могут быть определены на основании следующих соображений. В развитом плазменном пузыре пространственные характеристики имеют следующие масштабы: L_x ≈ 100 км (за счет сильной вытянутости вдоль геомагнитного поля), L_y ≈ 1 км в области “ножки”, L_z – десятки км в области “шляпки” пузыря. С учетом этих величин, а также данных по характерным размерам неоднородностей F-рассеяния [Farley et al., 1970; Rottger, 1973, 1976; Saito et al., 2008] и условиям существования дрейфово-диссипативных волн [Чен, 1987]:

$\begin{gathered} {{k}_{x}} \ll {{k}_{z}},\,\,\,\,V\left( {{\text{тепл}}{\text{.,}}\,\,{\text{ион}}{\text{.}}} \right) \ll {{{{\omega }_{d}}} \mathord{\left/ {\vphantom {{{{\omega }_{d}}} {{{k}_{x}}}}} \right. \kern-0em} {{{k}_{x}}}} \ll \\ \ll V\left( {{\text{тепл}}{\text{.,}}\,\,{\text{электр}}{\text{.}}} \right), \\ \end{gathered} $

получаем следующие ограничения на волновые числа:

${{k}_{x}} < {\text{1}}{{0}^{{ - {\text{2}}}}}\,\,{{{\text{м}}}^{{ - {\text{1}}}}},\,\,\,\,{\text{1}}{{0}^{{ - {\text{3}}}}}\,\,{{{\text{м}}}^{{ - {\text{1}}}}} \ll {{k}_{z}} < {\text{1}}{{0}^{{ - {\text{1}}}}}\,\,{{{\text{м}}}^{{ - {\text{1}}}}}.$

Для нахождения инкремента нарастания дрейфово-диссипативной неустойчивости воспользуемся дисперсионного соотношением, представленным в книге [Рожанский, 2012]. Оно имеет вид:

(9)

${{\omega }^{2}} + i\omega {{\omega }_{s}}--i{{\omega }_{d}}{{\omega }_{s}} = 0,$

здесь ${{\omega }_{s}} = \frac{{k_{x}^{2}}}{{k_{z}^{2}}}\frac{{{{\omega }_{{ce}}}{{\omega }_{{ci}}}}}{{0.51{{{v}}_{{ei}}}}};$ ${{\omega }_{d}} = - {{k}_{z}}\frac{{k{{T}_{e}}}}{{eB}}\frac{{\partial \left( {\ln {{n}_{0}}} \right)}}{{\partial y}};$ ω_ce и ω_ci – гирочастоты электронов и ионов соответственно; T_e – температура электронов; ${{\nu }_{{ei}}}$ – частота столкновений электронов с ионами.

Разрешая уравнение (9) относительно ω, найдем его мнимую часть – инкремент нарастания дрейфово-диссипативной неустойчивости:

(10)

${{\gamma }_{d}} = - \frac{{{{\omega }_{s}}}}{2} + \sqrt {\frac{{\omega _{s}^{2}}}{8} + \frac{{{{\omega }_{s}}}}{8}\sqrt {\omega _{s}^{2} + 16\omega _{d}^{2}} } .$

Выражение (10) использовано далее для расчета инкремента нарастания дрейфовой волны.

4. ЧИСЛЕННАЯ МОДЕЛЬ

4.1. Условия численного моделирования

Численное моделирование проводилось в области, ограниченной снизу высотой 100 км, сверху высотой 1700 км, по горизонтали протяженность области интегрирования равна 400 км.

Три уравнения вышеприведенной двумерной модели решались численно конечноразностными методами на квазиравномерных сетках, сгущающихся к центру области решения. Сетка выбрана так, что в центральной области шаги равны 0.8 км по координатам y и z.

Условия расчетов соответствовали среднему уровню солнечной активности с F10.7 = 150 и уровню геомагнитной активности kp = 3.

Для потенциала граничные условия заданы через фоновое электрическое поле. Восточная компонента фонового электрического поля задавалась модельно положительным значением (в представленных расчетах 10^–3 В/м).

Для концентраций и температур на нижней границе заданы соответственно условия химического равновесия и равенства нейтральной температуре, вверху и на боковых границах задано условие равенства нулю потоков.

Начальные неоднородности электронной концентрации плазмы, в дальнейшем развивающиеся в результате НРТ в ЭПП, в данной работе задавались модельно круглой формы по формуле:

$\begin{gathered} {{n}_{i}} = {{n}_{{i0}}}\left( {1 + \left( {{{a}_{n}} - 1} \right)} \right. \times \\ \left. { \times \,\,{\text{exp}}\left( { - {{{\left( {{{\left( {y - {{y}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {y - {{y}_{0}}} \right)} {{{r}_{y}}}}} \right. \kern-0em} {{{r}_{y}}}}} \right)}}^{2}} - {{{\left( {{{\left( {z - {{z}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {z - {{z}_{0}}} \right)} {{{r}_{z}}}}} \right. \kern-0em} {{{r}_{z}}}}} \right)}}^{2}}} \right)} \right), \\ \end{gathered} $

где n_i0 – фоновая концентрация ионов; a_n – отношение концентрации в центре неоднородности к фоновому значению концентрации на этой высоте, в представленных расчетах используется значение 1/2; (y₀, z₀) – координаты центра начальной неоднородности; ${{r}_{y}},$ ${{r}_{z}}$ – полурадиусы области начальной неоднородности по координатам y и z соответственно, в представленных расчетах оба полурадиуса равны 5 км.

4.2. Используемые численные методы

Уравнения двумерной модели являются уравнениями переноса поперек магнитного поля, особенностью которых является слабая сжимаемость ионосферной плазмы, поскольку для ионосферной плазмы выполнено условие:

${{\nabla }_{ \bot }}({\mathbf{V}}) \approx 0.$

Уравнение движения двумерной модели алгебраическое по отношению к дрейфовой скорости заряженных частиц. Уравнение потенциала двумерной модели – эллиптическое с несамосопряженным оператором, сильно зависящим от концентраций заряженных частиц.

Для решения уравнений модели использованы конечно-разностные методы второго порядка точности. Применение двумерного приближения математико-численной модели позволяет использовать достаточно подробные вычислительные сетки, что важно по причине малых поперечных размеров основания плазменных пузырей.

Разностные схемы, предназначенные для решения уравнений переноса в задачах моделирования НРТ, должны обладать достаточной точностью при моделировании на сравнительно грубых сетках. Основная проблема для рассматриваемых задач – усиление неоднородностей механизмом НРТ в режиме с обострением. При этом могут усиливаться и погрешности аппроксимации, что приводит к нефизическим результатам. Поэтому выбор метода решения уравнений переноса в задачах моделирования НРТ является ключевой проблемой.

Двумерные уравнения переноса решаются по схеме расщепления, симметрированной для получения второго порядка точности. Для решения одномерных уравнений переноса выбран монотонный метод с нелинейной коррекцией потоков и выбором ограничителя minmod [Ладонкина и др., 2009; Сафронов, 2010].

Для решения уравнения потенциала электрического поля применен геометрический многосеточный метод.

5. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Численная модель НРТ (1–5) была использована для нахождения долготно-высотных профилей и соответственно долготных и высотных градиентов ионосферной плазмы в экваториальном пузыре, определяющих величину инкремента нарастания дрейфово-диссипативной неустойчивости. На рисунке 1 представлены используемые в расчетах профили, рассчитанные для области размером 100 км по долготе и в диапазоне от 150 км до 950 км по вертикали в разные моменты времени от начала инициализации плазменного пузыря. Черная точка соответствует положению максимального значения инкремента нарастания дрейфово-диссипативной неустойчивости (9). Как показывают данные рис. 1, зона максимального значения инкремента нарастания дрейфово-диссипативной неустойчивости находится вблизи максимума F-области.

Рис. 1.

Распределение электронной концентрации в разные моменты времени от начала инициализации в плоскости магнитного экватора. Метки на границах зон – десятичный логарифм от электронной концентрации.

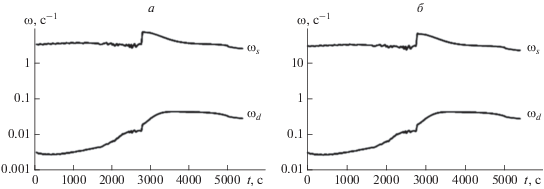
На рисунке 2 приведены рассчитанные зависимости максимального значения инкремента нарастания γ_d (с^–1) дрейфово-диссипативной неустойчивости (а), характерного времени 1/γ_d (с) (б) и высоты максимального значения инкремента нарастания γ_d (км) (в) для k_x = 10^–5 м^–1, k_z = 10^–2 м^–1.

Рис. 2.

Зависимости инкремента нарастания дрейфово-диссипативной неустойчивости (а), времени нарастания (б) и высоты максимума инкремента (в) от времени с начала инициализации плазменного пузыря для значений волновых чисел k_x = 10^–5 м^–1, k_z = 10^–2 м^–1.

На рисунке 3 приведены рассчитанные зависимости значения инкремента нарастания ${{\gamma }_{d}}$ (с^–1) дрейфово-диссипативной неустойчивости от высоты z для моментов времени с начала инициализации плазменного пузыря 2520 с, 2820 с, 3120 с, 3420 с и 3720 с для указанных выше значений волновых чисел.

Рис. 3.

Зависимости инкремента нарастания дрейфово-диссипативной неустойчивости γ_d от высоты z для моментов времени с начала инициализации плазменного пузыря 2520 с (1), 2820 с (2), 3120 с (3), 3420 с (4) и 3720 с (5) и для значений волновых чисел k_x = 10^–5 м^–1, k_z = 10^–2 м^–1.

Во втором численном эксперименте были заданы следующие параметры волны: k_x = 3 × 10^–4 м^–1, k_z = 10^–1 м^–1, что также соответствует указанным выше ограничениям. Результаты расчетов представлены на рис. 4 и 5 .

Рис. 4.

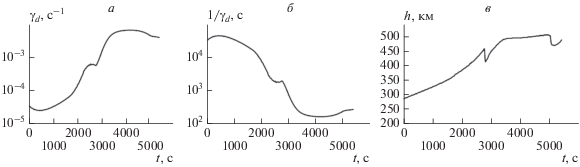
Рис. 5.

Зависимости от времени с начала инициализации плазменного пузыря важных для оценок инкремента нарастания дрейфово-диссипативной неустойчивости параметров ω_d и ω_s в точке максимума инкремента приведены на рис. 6. Слева – для первого численного эксперимента, справа – для второго численного эксперимента.

Рис. 6.

Зависимости ω_d и ω_s от времени развития ионосферного пузыря.

На рисунках 2–6 в кривых временны́х и высотных зависимостей имеется характерные изломы. Эти изломы появляются в результате “перескока” области максимального инкремента нарастания дрейфово-диссипативной неустойчивости с области шляпки грибовидного плазменного пузыря в область его ножки за счет динамики самого пузыря.

6. ЗАКЛЮЧЕНИЕ

Представленные выше результаты численных экспериментов позволяют сделать следующие выводы.

1. Долготные градиенты электронной концентрации на боковых фронтах развитого ионосферного пузыря могут быть эффективным механизмом развития дрейфово-диссипативной неустойчивости.

2. Инкремент нарастания дрейфово-диссипативной неустойчивости сильно зависит от соотношения волновых чисел продольного по магнитному полю k_x и высотного k_z.

3. Максимальные инкременты нарастания имеют место для мелкомасштабных по высоте неоднородностей с характерным масштабом порядка десятков метров, что совпадает с данными наблюдений экваториального F-рассеяния.

Список литературы

– Кащенко Н.М., Ишанов С.А., Мациевский С.В. Развитие неустойчивости Рэлея – Тейлора в экваториальной ионосфере и геометрия начальной неоднородности // Математическое моделирование. Т. 30(9). С. 21–32. 2018.
– Кащенко Н.М., Мациевский С.В., Никитин М.А. Ионосферные пузыри: ионный состав, скорости движения плазмы и структура // Изв. вузов. Радиофизика. Т. 32(11). С. 1320–1326. 1989.
– Ладонкина М.Е., Неклюдова О.А., Тишкин В.Ф., Чеванин В.С. Об одном варианте существенно неосциллирующих разностных схем высокого порядка точности для систем законов сохранения // Математическое моделирование. Т. 21(11). С. 19–32. 2009.
– Рожанский В.А. Теория плазмы. СПб.: Изд-во “Лань”. 320 с. 2012.
– Сафронов А.В. Оценка точности и сравнительный анализ разностных схем сквозного счета повышенного порядка // Вычислительные методы и программирование. Т. 11(1). С. 137–143. 2010.
– Чен Ф. Введение в физику плазмы. М.: Мир. 398 с. 1987.
– Costa E., Kelley M.C. Linear theory for collision less drift waves with wavelengths near the ion gyroradius // J. Geophys. Res. V. 83. P. 4365–4368. 1978.
– Farley D.T., Balsley B.B., Woodman R.F., McClure J.P. Equatorial spread F: Implications of VHF radar observations // J. Geophys. Res. V. 75. P. 7199–7216. 1970.
– Hedin A.E., Reber C.A., Newton G.P. et al. A global thermospheric model based on mass spectrometer and incoherent scatter data MSIS 2. Composition // Ibid. V. 82(A1). P. 2148–2156. 1977a.
– Hedin A.E., Salah J.E., Evans J.E. et al. A global thermospheric model based on mass spectrometer and incoherent scatter data MSIS 1. N2 density and temperature // J. Geophys. Res. V. 82(A1). P. 2139–2147. 1977b.
– Huba J.D., Joyce G., Krall J. Three-dimensional equatorial spread F modeling // Geophys. Res. Lett. V. 35. P. L10102. 2008.
– Ossakow S.L., Chaturvedi P.K. Morphological studies of rising equatorial spread F bubbles // J. Geophys. Res. V. 83. P. 2085–2090. 1978.
– Reinisch B.W., Abdu M., Batista I., Sales G.S., Khmyrov G., Bullett T.A., Chau J., Rios V. Multistation digisonde observations of equatorial spread in South America // Ann. Geophysicae. V. 22. P. 3145–3153. 2004.
– Rottger J. The macro-scale structure of equatorial spread-F irregularities // J. Atmos. Terr. Phys. V. 38. P. 97–101. 1976.
– Rottger J. Wave-like structures of large-scale equatorial spread-F irregularities// J. Atmos. Terr. Phys. V. 35. P. 1195–1206. 1973.
– Saito S., Maruyama T., Ishii M., Kubota M., Ma G., Chen Y., Li J., Duyen C.H., Truong T.L. Observations of small- to large-scale ionospheric irregularities associated with plasma bubbles with a transequatorial HF propagation experiment and spaced GPS receivers // J. Geophys. Res. V. 113(A1). P. 2313. 2008.
– Woodman R.F. Spread-F – an old equatorial aeronomy problem finally resolved? // Ann. Geophysicae. V. 27. № 5. P. 1915–1934. 2009.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геомагнетизм и аэрономия

Архивы выпусков Информация о журнале Отправить рукопись в журнал