1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 83, № 1, 2019

Известия РАН. Серия физическая, 2019, T. 83, № 1, стр. 37-40

Моделирование нелинейнных оптических процессов в РДС-кристалле
А. В. Белинский, Р. Сингх

А. В. Белинский 1, *, Р. Сингх 1, **

1 Федеральное государственное бюджетное образовательное учреждение высшего образования Московский государственный университет имени М.В. Ломоносова, физический факультет
Москва, Россия

* E-mail: belinsky@inbox.ru
** E-mail: ranjit.singh@mail.ru

Полный текст (PDF)

Аннотация

Рассмотрены три невырожденных процесса – параметрический и одновременная генерация суммарных частот в кристаллах с регулярной доменной структурой (РДС). С помощью численного метода изучены поведение среднего числа фотонов взаимодействующих мод и их взаимные корреляции 3, 4 и 5-го порядков. Обнаружен новый эффект инверсии взаимной корреляции мод генерируемого излучения при превышении определенной длины взаимодействия.

ВВЕДЕНИЕ

РДС-кристаллы с квадратичной нелинейностью или, как их иногда называют, фотонные кристаллы вызывают пристальный интерес исследователей в связи с тем, что изучение квантовых статистических характеристик формируемого в них излучения важно не только в чисто теоретических, но и в прикладных задачах квантовой информатики (см., например, [1–3]). В частности, корреляционные характеристики генерируемых световых пучков используются для формирования и компьютерной обработки фантомных изображений [2, 3]. При решении подобных задач обычно применяют приближение заданного поля для линеаризации нелинейных классических и операторных уравнений [1–3]. Такой метод дает возможность получить решения в аналитической форме, что в свою очередь, позволяет проводить анализ взаимодействующих мод в тонких РДС-кристаллах при слабом энергообмене. Однако при усилении энергообмена и заметном истощении накачки точность метода теряется. Лучшее приближение дает теория возмущений [4, 5], что, однако, достигается усложнением расчета за счет увеличения числа слагаемых высших порядков. Более точное квантовое решение можно получить численным алгоритмом диагонализации гамильтониана взаимодействия и нахождения собственных векторов и собственных значений квантовых состояний [6, 7]. Следует также отметить, что существует еще один метод решения задач квантовой нелинейной оптики, который основан на полиномиальной алгебре [8]. Впервые в работе [7] была решена задача квантового описания взаимодействия плоских монохроматических мод в РДС-кристалле с помощью метода диагонализации при полном учете квантовомеханического взаимодействия всех 5 плоских монохроматических мод и истощения накачки. В [7] изучено поведение среднего числа фотонов взаимодействующих мод и их взаимных корреляций 2-го порядка.

В настоящей работе исследованы корреляций 3, 4 и 5-го порядков. Полученные результаты отличаются от приближенного метода заданного поля [1] в случае сильного энергообмена, когда происходит заметное истощение накачки. Показана динамика эволюции среднего числа фотонов в модах и их взаимная корреляция, что особенно важно для компьютерной обработки информации в условиях зашумления, поскольку известные корреляционные зависимости позволяют эффективно выделять полезные сигналы на фоне шума, например, при работе с квантовыми фантомными изображениями, их мультиплицирования и компьютерной обработки с целью повышения соотношения сигнал/шум [2, 3].

НЕВЫРОЖДЕННЫЕ ПРОЦЕССЫ И УСЛОВИЯ ИХ КВАЗИСИНХРОНИЗМА

Пусть 5 плоских монохроматических мод необыкновенных поляризаций, характеризуемых операторами уничтожения фотона ${{\hat {a}}_{1}},$ ${{\hat {a}}_{2}},$ ${{\hat {a}}_{3}},$ ${{\hat {a}}_{4}},$ и ${{\hat {a}}_{5}}$ на оптических частотах ω1, ω2, ω3, ω4 и ω5, коллинеарно распространяются внутри РДС-кристалла с квадратичной нелинейностью. Происходят 3 процесса: параметрическая генерация субгармоник и преобразование частоты вверх:

(1а)
$\begin{gathered} {{\omega }_{3}} = {{\omega }_{1}} + {{\omega }_{2}}, \\ \delta {{k}_{3}} = {{k}_{3}} - {{k}_{1}} - {{k}_{2}} + {{m}_{3}}{{G}_{3}} = \Delta {{k}_{3}} + {{m}_{3}}{{G}_{3}}, \\ \end{gathered} $
(1б)
$\begin{gathered} {{\omega }_{1}} + {{\omega }_{3}} = {{\omega }_{4}}, \\ \delta {{k}_{4}} = {{k}_{4}} - {{k}_{1}} - {{k}_{3}} + {{m}_{4}}{{G}_{4}} = \Delta {{k}_{4}} + {{m}_{4}}{{G}_{4}}, \\ \end{gathered} $
(1в)
$\begin{gathered} {{\omega }_{2}} + {{\omega }_{4}} = {{\omega }_{5}}, \\ \delta {{k}_{5}} = {{k}_{5}} - {{k}_{2}} - {{k}_{3}} + {{m}_{5}}{{G}_{5}} = \Delta {{k}_{5}} + {{m}_{5}}{{G}_{5}}. \\ \end{gathered} $
Здесь kj – абсолютные значения волновых векторов соответствующих мод с частотами ωj; j = 1, 2, 3, 4, 5; Δkq – волновые расстройки соответствующего процесса для однородного кристалла; q = 3, 4, 5; mq = ±1, ±3, ±5, … – порядки квазисинхронизма; Gq = 2π/Λq – волновое число (модуль “псевдовектора” решетки доменной структуры с периодом Λq). Условие выполнения квазисинхронизма процессов (1a–1в) были найдены в работе [7] для кристалла LiNbO3.

Гамильтониан взаимодействия рассматриваемых процессов представляется в следующем виде [1]:

(2)
${{\hat {H}}_{I}} = h(\beta {{\hat {a}}_{1}}{{\hat {a}}_{2}}\hat {a}_{3}^{ + } + {{\gamma }_{1}}{{\hat {a}}_{1}}{{\hat {a}}_{3}}\hat {a}_{4}^{ + } + {{\gamma }_{2}}{{\hat {a}}_{2}}{{\hat {a}}_{3}}\hat {a}_{5}^{ + }) + H.c.,$
где h – постоянная Планка, β и γ1, 2 – коэффициенты нелинейного взаимодействия, Н.с. – эрмитово сопряжение.

Операторные уравнения движения по длине взаимодействия z внутри РДС-кристалла в представлении Гейзенберга описываются уравнением

(3)
$\frac{{d{{{\hat {a}}}_{j}}}}{{dz}} = - \frac{i}{h}\left[ {{{{\hat {a}}}_{j}},{{{\hat {H}}}_{I}}} \right].$

Квантовую задачу с помощью метода диагонализации можно решить следующим образом. Запишем матричные элементы оператора уничтожения в энергетическом представлении:

(4)
${{\hat {a}}_{{{{j}_{{n',n}}}}}} = \left\langle {n'\left| {{{{\hat {a}}}_{j}}} \right|n} \right\rangle = {{\delta }_{{n',n - 1}}}\sqrt n .$

Аналогичным образом выражаются матричные элементы оператора рождения $\hat {a}_{j}^{ + }.$ Введем безразмерные нелинейные коэффициенты связи ${{\xi }_{{1,2}}} = \frac{{{{\gamma }_{{1,2}}}}}{\beta }.$ Тогда гамильтониан взаимодействия (2) принимает следующий вид:

(2.а)
$\hat {H}_{I}^{'} = h(\hat {a}_{1}^{'}\hat {a}_{2}^{'}\hat {a}_{3}^{{' + }} + {{\xi }_{1}}\hat {a}_{1}^{'}\hat {a}_{3}^{'}\hat {a}_{4}^{{' + }} + {{\xi }_{2}}\hat {a}_{2}^{'}\hat {a}_{3}^{'}\hat {a}_{5}^{{' + }}) + H.c.,$
где
$\begin{gathered} \hat {a}_{1}^{'} = \left( {{{{\hat {a}}}_{{{{1}_{{n_{1}^{'},{{n}_{1}}}}}}}}} \right) \otimes {{{\hat {E}}}_{2}} \otimes {{{\hat {E}}}_{3}} \otimes {{{\hat {E}}}_{4}} \otimes {{{\hat {E}}}_{5}}, \\ \hat {a}_{2}^{'} = {{{\hat {E}}}_{1}} \otimes \left( {{{{\hat {a}}}_{{{{2}_{{n_{2}^{'},{{n}_{2}}}}}}}}} \right) \otimes {{{\hat {E}}}_{3}} \otimes {{{\hat {E}}}_{4}} \otimes {{{\hat {E}}}_{5}}, \\ \hat {a}_{3}^{'} = {{{\hat {E}}}_{1}} \otimes {{{\hat {E}}}_{2}} \otimes \left( {{{{\hat {a}}}_{{{{3}_{{n_{3}^{'},{{n}_{3}}}}}}}}} \right) \otimes {{{\hat {E}}}_{4}} \otimes {{{\hat {E}}}_{5}}, \\ \hat {a}_{4}^{'} = {{{\hat {E}}}_{1}} \otimes {{{\hat {E}}}_{2}} \otimes {{{\hat {E}}}_{3}} \otimes \left( {{{{\hat {a}}}_{{{{4}_{{n_{4}^{'},{{n}_{4}}}}}}}}} \right) \otimes {{{\hat {E}}}_{5}}, \\ \hat {a}_{5}^{'} = {{{\hat {E}}}_{1}} \otimes {{{\hat {E}}}_{2}} \otimes {{{\hat {E}}}_{3}} \otimes {{{\hat {E}}}_{4}} \otimes \left( {{{{\hat {a}}}_{{{{5}_{{n_{5}^{'},{{n}_{5}}}}}}}}} \right), \\ \end{gathered} $
${{\hat {E}}_{j}}$ – единичные матрицы соответствующих мод, матрица $\left( {{{{\hat {a}}}_{{{{j}_{{n{\text{',}}n}}}}}}} \right)$ состоит из матричных элементов ${{\hat {a}}_{{{{j}_{{n{\text{',}}n}}}}}},$ $ \otimes $ обозначает тензорное произведение и $j = \overline {1,5} .$

Диагонализируем гамильтониан взаимодействия (2.а) и найдем его собственные векторы и собственные значения. Оператор эволюции в матричном представлении вычисляется как

(5)
$\hat {U}(\zeta ) = \sum\limits_{m = 0}^M {{{e}^{{ - i{{\lambda }_{m}}\zeta }}}} \left| m \right\rangle \left\langle m \right|,$
где ζ = βz – приведенная длина взаимодействия; M = (n1 + 1)(n2 + 1)(n3 + 1)(n4 + 1)(n5 + 1); nj – числа фотонов в модах; $\left| m \right\rangle $ – собственный вектор с числом фотонов m при собственном значении λm гамильтониана взаимодействия (2.a) $\hat {H}_{I}^{'}\left| m \right\rangle = {{\lambda }_{m}}\left| m \right\rangle .$

Матрица плотности вычисляется как

(6)
$\hat {\rho }(\zeta ) = \hat {U}(\zeta )\hat {\rho }(0){{\hat {U}}^{ + }}(\zeta ).$
Здесь $\hat {\rho }(0) = \left| {{{\psi }_{0}}} \right\rangle \left\langle {{{\psi }_{0}}} \right|$ – матрица плотности начального состояния для всех пяти мод на входе РДС-кристалла. В тензорном представлении эта матрица плотности принимает следующий вид:

(7)
$\hat {\rho }(0) = {{\hat {\rho }}_{1}}(0) \otimes {{\hat {\rho }}_{2}}(0) \otimes {{\hat {\rho }}_{3}}(0) \otimes {{\hat {\rho }}_{4}}(0) \otimes {{\hat {\rho }}_{5}}(0).$

КВАНТОВЫЕ СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ

Вычислим средние значения чисел фотонов и коэффициентов корреляции 3, 4 и 5-го порядков или фактора g(3,4,5) в модах по формулам:

(8)
${{N}_{j}}(\zeta ) = \left\langle {\hat {a}_{j}^{{' + }}(\zeta )\hat {a}_{j}^{'}(\zeta )} \right\rangle ,$
(9)
$\left( {\begin{array}{*{20}{c}} {g_{{jkl}}^{{(3)}}(\zeta )} \\ {g_{{jklm}}^{{(4)}}(\zeta )} \\ {g_{{12345}}^{{(5)}}(\zeta )} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\frac{{\left\langle {\hat {a}_{j}^{{' + }}(\zeta )\hat {a}_{j}^{'}(\zeta )\hat {a}_{k}^{{' + }}(\zeta )\hat {a}_{k}^{'}(\zeta )\hat {a}_{l}^{{' + }}(\zeta )\hat {a}_{l}^{'}(\zeta )} \right\rangle }}{{{{N}_{j}}(\zeta ){{N}_{k}}(\zeta ){{N}_{l}}(\zeta )}}} \\ {\frac{{\left\langle {\hat {a}_{j}^{{' + }}(\zeta )\hat {a}_{j}^{'}(\zeta )\hat {a}_{k}^{{' + }}(\zeta )\hat {a}_{k}^{'}(\zeta )\hat {a}_{l}^{{' + }}(\zeta )\hat {a}_{l}^{'}(\zeta )\hat {a}_{m}^{{' + }}(\zeta )\hat {a}_{m}^{'}(\zeta )} \right\rangle }}{{{{N}_{j}}(\zeta ){{N}_{k}}(\zeta ){{N}_{l}}(\zeta ){{N}_{m}}(\zeta )}}} \\ {\frac{{\left\langle {\hat {a}_{1}^{{' + }}(\zeta )\hat {a}_{1}^{'}(\zeta )\hat {a}_{2}^{{' + }}(\zeta )\hat {a}_{2}^{'}(\zeta )\hat {a}_{3}^{{' + }}(\zeta )\hat {a}_{3}^{'}(\zeta )\hat {a}_{4}^{{' + }}(\zeta )\hat {a}_{4}^{'}(\zeta )\hat {a}_{5}^{{' + }}(\zeta )\hat {a}_{5}^{'}(\zeta )} \right\rangle }}{{{{N}_{1}}(\zeta ){{N}_{2}}(\zeta ){{N}_{3}}(\zeta ){{N}_{4}}(\zeta ){{N}_{5}}(\zeta )}}} \end{array}} \right).$
Здесь нижние индексы при g(3,4,5) обозначают номера мод, между которыми вычисляется коэффициент корреляции, и $j,k,l,m = \overline {1,5} .$

Нами проводились расчеты для случая ${{\xi }_{1}} = 0.6,$ ${{\xi }_{2}} = 0.4,$ когда моды находились в состоянии $\left| {{{\psi }_{0}}} \right\rangle = \left| {{{n}_{{10}}}} \right\rangle \left| {{{n}_{{20}}}} \right\rangle \left| {{{\alpha }_{{30}}}} \right\rangle \left| {{{n}_{{40}}}} \right\rangle \left| {{{n}_{{50}}}} \right\rangle $ на входе $\zeta = 0$ РДС-кристалла, причем моды 1, 2, 4, 5 полагались в вакуумном состоянии $\left| 0 \right\rangle ,$ а накачка – в когерентном состоянии со средним числом фотонов ${{\left| {{{\alpha }_{{30}}}} \right|}^{2}} = 3$ фазой ${{\varphi }_{{30}}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3}.$ Постоянная начальная фаза накачки влияет на результаты расчета, потому что ею определяются условия вхождения излучения в нелинейный кристалл. Правильность вычислений проверялась контролем коммутационных соотношений $\left[ {\hat {a}{{{_{j}^{'}}}_{{}}}\left( \zeta \right),\hat {a}_{j}^{{' + }}\left( \zeta \right)} \right] = 1.$

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

На рис. 1 кривые ${{N}_{1}},$ ${{N}_{2}},$ ${{N}_{3}},$ ${{N}_{4}},$ ${{N}_{5}}$ демонстрирует почти периодические осцилляции среднего числа фотонов. На начальном этапе взаимодействия идет невырожденный параметрический процесс распада фотона моды 3 на два фотона мод 1 и 2 ${{\omega }_{3}} \to {{\omega }_{1}} + {{\omega }_{2}}$ и затем генерации суммарной частоты c ${{\omega }_{1}} + {{\omega }_{3}} \to {{\omega }_{4}},$ ${{\omega }_{2}} + {{\omega }_{3}} \to {{\omega }_{5}}.$

Рис. 1.

Эволюция среднего числа фотонов в модах.

В дальнейшем идет обратный процесс, причем они конкурируют между собой, что хорошо видно из осциллирующего характера кривых ${{N}_{1}},$ ${{N}_{2}},$ ${{N}_{3}},$ ${{N}_{4}},$ ${{N}_{5}}$ на больших длинах взаимодействия ζ. На рис. 2 корреляционныe кривые ведут себя почти как периодические функции. При значениях ${{g}^{{\left( {3,4,5} \right)}}} > 1$ преобладают более парные коррелированные в 3, 4 и 5 модах фотоны, а при ${{g}^{{\left( {3,4,5} \right)}}} < 1$ – одиночные некоррелированные, аналогично тому, как в одиночной моде ${{g}^{{\left( 2 \right)}}} > 1$ соответствует группировке и суперпуассоновской статистике фотонов, а ${{g}^{{\left( 2 \right)}}} < 1$ – антигруппировке и субпуассоновской статистике [9, 10].

Рис. 2.

a – коэффициенты корреляции или фактор $g_{{jkl}}^{{\left( 3 \right)}}$ 3-го порядка; б – коэффициенты корреляции или фактор $g_{{jklm}}^{{\left( 4 \right)}},g_{{12345}}^{{\left( 5 \right)}}$ 4-го и 5-го порядков.

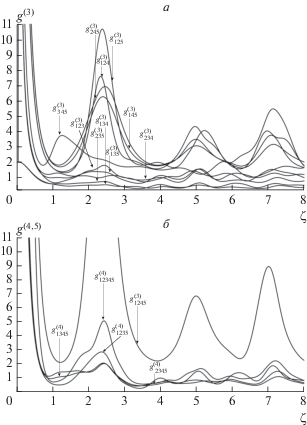
На рис. 2а также видно, что сначала реализуется процесс (1a), затем (1б) и (1в). На больших длинах взаимодействия все 3 процесса начинают конкурировать между собой, что следует из почти периодического характера этих кривых. Аналогичную ситуацию описывают другие кривые. Коэффициенты корреляции между 3 модами 1, 2 и 5; 1, 2 и 4; 2, 4 и 5; 3, 4 и 5; 1, 4 и 5 больше, чем парные, рассчитанные в [7]. Такие моды могут стать хорошими кандидатами для восстановления изображений методами компьютерной обработки информации по алгоритмам, аналогичным предложенным в [2]. Другие 3 моды 1, 2 и 3; 1, 3 и 5; 2, 3 и 4 не так сильно коррелированы, но проявляется эффект инверсии взаимной корреляции мод. Коэффициенты корреляция между 4 модами 1, 2, 4 и 5 больше, чем между 3 модами, а между модами 1, 2, 3 и 5; 1, 3, 4 и 5; 2, 3, 4 и 5, 1, 4 и 5 наоборот. Корреляция между 5 модами 1, 2, 3, 4 и 5 слабее, чем между 4 модами (1, 2, 4, 5). В обоих случаях наблюдается эффект инверсии взаимной корреляции мод. Отметим, что инверсия взаимной корреляции (или, другими словами, антикорреляция) наблюдается при значениях $g_{{Jkl}}^{{\left( 3 \right)}},$ $g_{{Jklm}}^{{\left( 4 \right)}}$ и $g_{{12345}}^{{\left( 5 \right)}}$ меньше единицы. Для реализации коррелированного и антикоррелированного режимов нужно выбирать соответствующую длину взаимодействия. Этот новый существенный эффект впервые нами выявлен на основании точного квантового расчета взаимодействия всех 5 мод.

ВЫВОДЫ

Получены результаты строгого квантового описания нелинейного интенсивного энергообмена между плоскими монохроматическими модами в РДС-кристаллах с учетом истощения накачки. Изучено поведение среднего числа фотонов взаимодействующих мод и их взаимных корреляций 3, 4 и 5-го порядков. Получен почти осциллирующий характер коэффициентов корреляции мод. Обнаружен новый эффект инверсии взаимной корреляции мод генерируемого излучения при определенных длинах взаимодействия.

Работа поддержана грантом РФФИ № 18-01-00598.

Список литературы

  1. Chirkin A.S., Saigin M.Yu., Shutov I.V. // J. Russ. Laser Res. 2008. V. 29. № 4. P. 336.

  2. Балакин Д.А., Белинский А.В., Чиркин А.С. // ЖЭТФ. 2017. Т. 152. № 2. С. 252.

  3. Balakin D.A., Belinsky A.V., Chirkin A.S. // J. Russ. Laser Res. 2017. V. 38. № 2. P. 164.

  4. Beskrovnyi V.N., Chirkin A.S. // In Quantum Comm. and Comp. Eds. Hirota O., Holevo A.S., Caves C.M.. New York: Plenum Press, 1997. 483 p.

  5. Люиселл У. Излучение и шумы в квантовой электронике. М: Наука, 1972. 403 с.

  6. Nikitin S.P., Masalov A.V. // Quantum Opt. 1991. V. 3. № 2. P. 105.

  7. Белинский А.В., Сингх Р. // Квантовая электроника. 2018. Т. 48. № 7. C. 611.

  8. Карасев В.П. // Теоретическая и математическая физика. 1993. Т. 95. № 1. С. 3.

  9. Смирнов Д.Ф., Трошин А.С. // УФН. 1987. Т. 153. № 10. С. 233.

  10. Клышко Д.Н., Масалов А.В. // УФН. 1995. Т. 165. № 11. С. 1249.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал