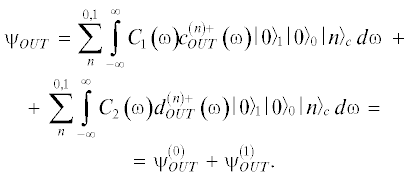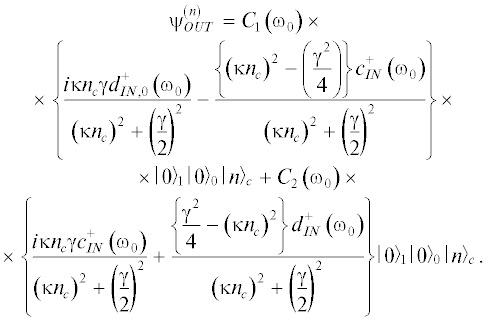Известия РАН. Серия физическая, 2019, T. 83, № 3, стр. 428-430

Квантовый вентиль контролируемого отрицания на основе четырехволнового смешения в резонаторе для поляризационных фотонных кубитов

С. Н. Андрианов^1, *, А. А. Калачев², О. П. Шиндяев¹, А. В. Шкаликов²

¹ Институт прикладных исследований Академии наук Республики Татарстан
Казань, Россия

² Казанский физико-технический институт им. Е.К. Завойского – обособленное структурное подразделение Федерального государственного бюджетного учреждения науки “Федеральный исследовательский центр “Казанский научный центр Российской академии наук”
Казань, Россия

^* E-mail: andrianovsn@mail.ru

Поступила в редакцию 03.09.2018
После доработки 10.09.2018
Принята к публикации 22.10.2018

DOI: 10.1134/S0367676519030323

Полный текст (PDF)

Аннотация

Исследована возможность эффективной реализации квантовых логических элементов на поляризационных фотонных кубитах с использованием среды с керровской нелинейностью в резонаторе. Показано, как реализуется квантовый логический вентиль контролируемого отрицания в ходе процесса четырехволнового смешения на таких кубитах. Построена теория функционирования этого вентиля с использованием формализма ввода-вывода и получены условия параметрического согласования, которые должны выполняться для эффективной работы вентиля.

ВВЕДЕНИЕ

Разработка масштабируемых квантовых компьютеров – одна из основных задач в области квантовых технологий [1, 2], решение которой приведет к беспрецедентному увеличению быстродействия вычислительных устройств, что имеет принципиальное значение для создания новых материалов, лекарств, обработки больших объемов данных и оптимизации сложных систем. Одним из перспективных подходов к реализации масштабируемых квантовых вычислений являются линейные оптические квантовые компьютеры [3, 4], в которых в качестве кубитов используют однофотонные состояния света, а квантовые логические операции являются вероятностными. Эффективность таких квантовых вентилей можно существенно увеличить за счет использования нелинейных оптических явлений, протекающих, например, в средах с керровской нелинейностью [5]. В работе [6] была предложена схема детерминированного квантового компьютера на поляризационных фотонных кубитах, использующая керровскую нелинейность в режиме четырехволнового смешения. Эффективность реализации двухкубитовых квантовых вентилей в таком компьютере можно повысить, поместив нелинейную среду в резонатор. Настоящая работа посвящена анализу этой возможности. Мы рассматриваем функционирование оптического квантового вентиля контролируемого отрицания в резонаторе в рамках формализма ввода–вывода [7] и находим оптимальные режимы его работы.

ГАМИЛЬТОНИАН И ПОСТАНОВКА ЗАДАЧИ

Рассмотрим электромагнитное поле в нелинейном диэлектрике. Энергия электромагнитного поля в диэлектрике может быть записана как

(1)

$\begin{gathered} H = \int {\frac{1}{{2{{\mu }_{0}}}}} {{{\vec {B}}}^{2}}\left( {\vec {r},t} \right){{d}^{3}}r + \\ + \,\,\int {{{d}^{3}}r} \int\limits_0^{\vec {D}\left( {\vec {r},t} \right)} {\vec {E}} \left( {\vec {r},t} \right)d\vec {D}\left( {\vec {r},t} \right), \\ \end{gathered} $

где $\vec {E}$ – электрическое поле, $\vec {B}$ – индукция, $\vec {D}$ – электрическое смещение [8]. В нелинейной среде для $\vec {D}$ можно записать

(2)

$\vec {D}\left( {\vec {r},t} \right) = {{\epsilon }_{0}}\vec {E}\left( {\vec {r},t} \right) + \vec {P}\left( {\vec {r},t} \right),$

где $\vec {P}\left( {\vec {r},t} \right)$ поляризация среды:

(3)

${{P}_{i}} = \chi _{{ij}}^{{\left( 1 \right)}}{{E}_{j}} + \chi _{{ij}}^{{\left( 2 \right)}}{{E}_{j}}{{E}_{k}} + \chi _{{ij}}^{{\left( 3 \right)}}{{E}_{j}}{{E}_{k}}{{E}_{l}},$

где $\chi _{{ij}}^{{\left( n \right)}}$ – тензор восприимчивости n-ого ранга. В одномерном случае при $\chi _{{ij}}^{{\left( 1 \right)}} = \chi _{{ij}}^{{\left( 2 \right)}} = 0$ будем иметь

(4)

$H = \int {\frac{1}{{2{{\mu }_{0}}}}} {{B}^{2}}\left( {z,t} \right)dz + \int {dz} \int\limits_0^{D\left( {z,t} \right)} {E\left( {z,t} \right)} dD\left( {z,t} \right),$

(5)

$D\left( {z,t} \right) = {{\epsilon }_{0}}E\left( {z,t} \right) + {{\chi }^{{\left( 3 \right)}}}{{E}^{3}}\left( {z,t} \right).$

Обращение выражения (5) при ${{\chi }^{{\left( 3 \right)}}}{{E}^{3}} \ll E$ дает

(6)

$E \cong \frac{D}{{{{\epsilon }_{0}}}} - {{\chi }^{{\left( 3 \right)}}}\frac{{{{D}^{3}}}}{{\epsilon _{0}^{4}}}.$

Подставляя (5) в (4), получим

(7)

$H = \int {\frac{1}{{2{{\mu }_{0}}}}} {{B}^{2}}\left( {z,t} \right)dz + \int {dz} \left( {\frac{{{{D}^{2}}}}{{2{{\epsilon }_{0}}}} - {{\chi }^{{\left( 3 \right)}}}\frac{{{{D}^{4}}}}{{4\epsilon _{0}^{4}}}} \right)dz.$

Квантование в среде с периодической восприимчивостью приводит к следующему выражению для гамильтониана [9]:

(8)

$\begin{gathered} H = \sum\limits_{mk} {\hbar {{\omega }_{{mk}}}} {{\left| {{{a}_{{mk}}}} \right|}^{2}} - \frac{{{{\hbar }^{2}}{{\epsilon }_{0}}}}{{16{{N}^{2}}\mu _{0}^{2}}}\int\limits_{{{ - L} \mathord{\left/ {\vphantom {{ - L} 2}} \right. \kern-0em} 2}}^{{L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}} {dz} \frac{{{{\chi }^{{\left( 3 \right)}}}\left( z \right)}}{{\epsilon _{0}^{4}\left( z \right)}} \times \\ \times \,\,\left[ {\prod\limits_{i = 1}^4 {\sum\limits_{{{m}_{i}}{{k}_{i}}} {\frac{{\left( {{{a}_{{{{m}_{i}}{{k}_{i}}}}}\theta _{{{{m}_{i}}{{k}_{i}}}}^{'} + c.c.} \right)}}{{\sqrt {{{\omega }_{{{{m}_{i}}{{k}_{i}}}}}} }}} } } \right]. \\ \end{gathered} $

Если две моды в разложении (8) равны друг другу, то это излучение является пробным и для взаимодействующей части гамильтониана можно записать

(9)

${{H}_{{int}}} = \xi {{a}^{ + }}a{{c}^{ + }}d + c.c.,$

что совпадает с гамильтонианом работы [6], в которой рассмотрен квантовый логический вентиль контролируемого отрицания на основе четырехволнового смешения поляризационных кубитов. Здесь c, ${{c}^{ + }}$ и d, ${{d}^{ + }}$ – операторы рождения и уничтожения фотонов в соответствующих поляризационных состояниях целевого кубита, a и ${{a}^{ + }}$ – операторы рождения и уничтожения фотонов контролирующего кубита.

Рис. 1.

Принципиальная схема эксперимента по четырехволновому смешению волн a, a, c и d для выполнения операции CNOT.

УРАВНЕНИЯ ДИНАМИКИ И РЕШЕНИЕ ЗАДАЧИ

В рамках формализма ввода–вывода [8] можно записать следующие уравнения:

(10)

$\frac{d}{{dt}}c(t) = - \frac{i}{\hbar }\left[ {c(t),H} \right] - \frac{\gamma }{2}c(t) + \sqrt \gamma {{c}_{{IN}}}(t),$

(11)

$\frac{d}{{dt}}d(t) = - \frac{i}{\hbar }\left[ {d(t),H} \right] - \frac{\gamma }{2}d(t) + \sqrt \gamma {{d}_{{IN}}}(t).$

Используя гамильтониан (9), получаем

(12)

$\frac{d}{{dt}}c(t) = - i{{\omega }_{0}}c - i\kappa dn - \frac{\gamma }{2}c(t) + \sqrt \gamma {{c}_{{IN}}}(t),$

(13)

$\frac{d}{{dt}}d(t) = - i{{\omega }_{0}}d - i\kappa cn - \frac{\gamma }{2}d(t) + \sqrt \gamma {{d}_{{IN}}}(t),$

где $\kappa = \frac{\xi }{\hbar },$ $n = {{a}^{ + }}a.$ Фурье-преобразование дает

(14)

$\begin{gathered} - i{{\omega }_{1}}c\left( \omega \right) = - i{{\omega }_{0}}c\left( \omega \right) - i\kappa d\left( \omega \right)n - \\ - \,\,\frac{\gamma }{2}c\left( \omega \right) + \sqrt \gamma {{c}_{{IN}}}\left( \omega \right), \\ \end{gathered} $

(15)

$\begin{gathered} - i\omega d\left( \omega \right) = - i{{\omega }_{0}}d\left( \omega \right) - i\kappa c\left( \omega \right)n - \\ - \,\,\frac{\gamma }{2}d\left( \omega \right) + \sqrt \gamma {{c}_{{IN}}}\left( \omega \right), \\ \end{gathered} $

откуда

(16)

$\begin{gathered} c\left( \omega \right) = \\ = \,\,\frac{{ - i\kappa n\sqrt \gamma {{d}_{{IN}}}\left( \omega \right) + \sqrt \gamma \left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right){{c}_{{IN}}}\left( \omega \right)}}{{{{{\left( {\kappa n} \right)}}^{2}} + {{{\left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right)}}^{2}}}}, \\ \end{gathered} $

(17)

$\begin{gathered} d\left( \omega \right) = \\ = \,\,\frac{{ - i\kappa n\sqrt \gamma {{c}_{{IN}}}\left( \omega \right) + \sqrt \gamma \left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right){{d}_{{IN}}}\left( \omega \right)}}{{{{{\left( {\kappa n} \right)}}^{2}} + {{{\left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right)}}^{2}}}}. \\ \end{gathered} $

Используя граничные условия

(18)

${{c}_{{IN}}}\left( \omega \right) + {{c}_{{OUT}}}\left( \omega \right) = \sqrt \gamma c\left( \omega \right),$

(19)

${{d}_{{IN}}}\left( \omega \right) + {{d}_{{OUT}}}\left( \omega \right) = \sqrt \gamma d\left( \omega \right),$

получим

(20)

$\begin{gathered} {{c}_{{OUT}}}\left( \omega \right) = \frac{{ - i\kappa n\gamma {{d}_{{IN}}}\left( \omega \right)}}{{{{{\left( {\kappa n} \right)}}^{2}} + {{{\left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right)}}^{2}}}} - \\ - \,\,\frac{{\left\{ {{{{\left( {\kappa n} \right)}}^{2}} - \left( {\frac{{{{\gamma }^{2}}}}{4} + {{{\left( {\omega - {{\omega }_{0}}} \right)}}^{2}}} \right)} \right\}{{c}_{{IN}}}\left( \omega \right)}}{{{{{\left( {\kappa n} \right)}}^{2}} + {{{\left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right)}}^{2}}}}, \\ \end{gathered} $

(21)

$\begin{gathered} {{d}_{{OUT}}}\left( \omega \right) = \frac{{ - i\kappa n\gamma {{c}_{{IN}}}\left( \omega \right)}}{{{{{\left( {\kappa n} \right)}}^{2}} + {{{\left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right)}}^{2}}}} + \\ + \,\,\frac{{\left\{ {\frac{{{{\gamma }^{2}}}}{4} - {{{\left( {\kappa n} \right)}}^{2}} + {{{\left( {\omega - {{\omega }_{0}}} \right)}}^{2}}} \right\}{{d}_{{IN}}}\left( \omega \right)}}{{{{{\left( {\kappa n} \right)}}^{2}} + {{{\left( {\frac{\gamma }{2} - i\left( {\omega - {{\omega }_{0}}} \right)} \right)}}^{2}}}}. \\ \end{gathered} $

Волновые функции состояния поля до и после преобразования можно записать в виде

(22)

$\begin{gathered} {{\psi }_{{IN}}} = \sum\limits_n^{0,1} {\int\limits_{ - \infty }^\infty {{{C}_{1}}\left( \omega \right)} } c_{{IN}}^{{\left( n \right) + }}\left( \omega \right){{\left| 0 \right\rangle }_{1}}{{\left| 0 \right\rangle }_{0}}{{\left| n \right\rangle }_{c}}d\omega + \\ \quad + \,\,\quad\sum\limits_n^{0,1} {\int\limits_{ - \infty }^\infty {{{C}_{2}}\left( \omega \right)} } d_{{IN}}^{{\left( n \right) + }}\left( \omega \right){{\left| 0 \right\rangle }_{1}}{{\left| 0 \right\rangle }_{0}}{{\left| n \right\rangle }_{c}}d\omega = \\ = \psi _{{IN}}^{{\left( 0 \right)}} + \psi _{{IN}}^{{\left( 1 \right)}}, \\ \end{gathered} $

(23)

Считая, что

(24)

$c_{{OUT}}^{{\left( n \right)}}\left( \omega \right) = c_{{OUT}}^{{\left( n \right)}}\delta \left( {\omega - {{\omega }_{0}}} \right),$

(25)

$d_{{OUT}}^{{\left( n \right)}}\left( \omega \right) = d_{{OUT}}^{{\left( n \right)}}\delta \left( {\omega - {{\omega }_{0}}} \right),$

получим

(26)

Тогда при выполнении условия согласования параметров $\kappa = \frac{\gamma }{2}$ получим

Наконец, осуществляя операцию фазового сдвига контролирующего кубита на ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2},$ приходим к результату

(28)

$\begin{gathered} {{\psi }_{{FIN}}} = {{C}_{1}}\left( {{{\omega }_{0}}} \right)c_{{IN}}^{ + }\left( \omega \right){{\left| 0 \right\rangle }_{1}}{{\left| 0 \right\rangle }_{0}}{{\left| 0 \right\rangle }_{c}} + \\ + \,\,{{C}_{2}}\left( {{{\omega }_{0}}} \right)d_{{IN}}^{ + }\left( \omega \right){{\left| 0 \right\rangle }_{1}}{{\left| 0 \right\rangle }_{0}}{{\left| 0 \right\rangle }_{c}} + \quad \\ \quad + \,\,{{C}_{1}}\left( {{{\omega }_{1}}} \right)d_{{IN}}^{ + }\left( \omega \right){{\left| 0 \right\rangle }_{1}}{{\left| 0 \right\rangle }_{0}}{{\left| 1 \right\rangle }_{c}} + \\ + \,\,{{C}_{2}}\left( {{{\omega }_{1}}} \right)c_{{IN}}^{ + }\left( \omega \right){{\left| 0 \right\rangle }_{1}}{{\left| 0 \right\rangle }_{0}}{{\left| 1 \right\rangle }_{c}}, \\ \end{gathered} $

что соответствует операции CNOT.

ЗАКЛЮЧЕНИЕ

Таким образом, показано, что на основе четырехволнового смешения в резонаторе возможна эффективная реализация квантового логического вентиля контролируемого отрицания на поляризационных фотонных кубитах. Получены условия параметрического согласования, обеспечивающие эффективную работу вентиля. Дополняя предложенную схему вентиля контролируемого отрицания схемами однокубитовых операций для фотонных кубитов на основе элементов сдвига фазы, делителей пучка и элементов вращения поляризации [10], можно построить эффективную схему детерминированного оптического квантового компьютера.

Список литературы

Ladd T.D., Jelezko F., Laflamme R.D. et al. // Nature. 2010. V. 464. No. 7285. P. 45.
Mohseni M., Read P., Neven H., et al. // Nature. 2017. V. 543. No. 7644. P. 171.
Knill E., Laflamme R., Milburn G. // Nature. 2001. V. 409. No. 6816. P. 46.
Kok P., Munro W.J., Nemoto K. et al. // Rev. Mod. Phys. 2007. V. 79. P. 135.
Nemoto K., Munro W.J. // Phys. Rev. Lett. 2004. V. 93. Art. no. 250502.
D’Ariano G.M., Macchiavello C., Maccone L. // Fortschr. Phys. 2000. V. 48. P. 573.
Walls D.F., Milburn G.J. // Quantum Optics. Berlin: Springer-Verlag, 2008. 424 p.
Мандель Л., Вольф Э. // Оптическая когерентность и квантовая оптика. М.: Физматлит, 2000, 896 с.
Pereira S., Sipe J.E. // Phys. Rev. 2002. V. 65. Art. no. 046601.
Kok P. // Lect. Notes Phys. 2010. V. 787. P. 187.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал