Известия РАН. Серия физическая, 2019, T. 83, № 4, стр. 469-472
Определение амплитуды рассеяния в ограниченной области расчетов
П. М. Красовицкий 1, 2, *, Ф. М. Пеньков 1
1 Институт ядерной физики
Алматы, Казахстан
2 Объединенный институт ядерных исследований
Дубна, Россия
* E-mail: pavel.kras@inp.kz
Поступила в редакцию 01.10.2018
После доработки 15.10.2018
Принята к публикации 19.11.2018
Аннотация
Для численного расчета задачи двумерного рассеяния предложен алгоритм, основанный на непосредственной дискретизации двумерного уравнения. Достигнуто сокращение асимптотического расстояния с помощью представления решения в виде суммы свободных волн. Продемонстрировано применение полученного алгоритма для решения задачи рассеяния на несферическом ядре.
ВВЕДЕНИЕ
Задача рассеяния на объекте, не обладающем сферической симметрией, как правило, решается в численном виде. В этом случае разложение по сферическим функциям теряет и физический, и математический смысл из-за несохранения углового момента в процессе рассеяния, т.е. стандартный подход, использующий запись амплитуды в явно унитарном виде, становится нерабочим инструментом. Для численного решения уже двумерной задачи рассеяния возникает проблема больших асимптотических расстояний, связанная с наличием дифракционной тени. Так, например, в задаче квантового рассеяния частицы на несферическом потенциале [1, 2] асимптотические расстояния должны выходить за область тени, которые при характерных значениях задачи составляют несколько сот единиц размеров собственно рассеивающего центра. Это влечет за собой необходимость длительных расчетов, использование большого количества машинных ресурсов и потерю точности расчетов из-за несовпадения асимптотик решения дифференциального уравнения и его дискретного аналога [2]. При этом очевидно, что для короткодействующих потенциалов все решения вне области взаимодействия представляют собой простые наборы свободных решений, которые могут быть определены уже за областью действия потенциала.
Целью настоящей публикации является демонстрация реализации идеи численного нахождения волновой функции в ограниченной области расчетов. В качестве иллюстрации был выбран пример с параметрами, характерными для ядерной физики. Основные характеристики были взяты для упругого рассеяния нейтрона на ядре 10Be. Это ядро известно как одно из наиболее деформированных и хорошо подходит в качестве исследования несферического объекта рассеяния. Вместе с тем это ядро долгоживущее, может быть образовано из устойчивого девятого изотопа захватом нейтрона, часто используемого в качестве нейтронного отражателя в ядерных реакторах. Исходя из особенностей метода исследования, был выбран только один аспект изучения этой реакции – различие рассеяния в модели несферического потенциала и в модели рассеяния на сферически-симметричном потенциале.
Заметим, что примеры рассеяния нейтрона на несферическом атомном ядре или задача дифракции составных частиц [1, 2] не исчерпывает актуальности предлагаемого здесь метода. Проблема, затронутая здесь, решается для частных случаев разными путями в теоретической физике, физике наноструктур и в связанных разделах химии, медицины и атомной интерферометрии [3–8].
ИДЕЯ ЧИСЛЕННОГО МЕТОДА РЕШЕНИЯ
Уравнение Шрёдингера в аксиально-симметричном случае для задачи рассеяния бесспиновой частицы может быть записано в виде:
(1)
$\begin{gathered} \Delta \Psi (r,\vartheta ) - V(r,\vartheta )\Psi (r,\vartheta ) = - {{k}^{2}}\Psi (\vec {r}), \\ \Delta = \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{2}{r}\frac{\partial }{{\partial r}} + \frac{1}{{{{r}^{2}}}}\frac{1}{{\sin (\vartheta )}}\frac{\partial }{{\partial \vartheta }}\sin (\vartheta )\frac{\partial }{{\partial \vartheta }}. \\ \end{gathered} $Здесь k2 = 2mE – волновое число, E – энергия системы, $\Psi (r,\vartheta )$ – волновая функция. Заметим, что в выбранной системе единиц энергия измеряется в единицах, обратных квадрату длины (здесь, используются система единиц, в которой постоянная Планка равна 1). Потенциал ограничен в некоторой области: $V = 0$ при $r > {{r}_{V}}.$
Асимптотический вид волновой функции
(2)
$\Psi \left( {r,\vartheta } \right) \to {{e}^{{ikr\cos \vartheta }}} + f\left( \vartheta \right)\frac{{{{e}^{{ikr}}}}}{r}\left( {1 + O\left( {\frac{1}{r}} \right)} \right),$определяет амплитуду рассеяния $f(\vartheta )$, которая подчиняется оптической теореме [9]
где $\sigma $ – полное сечение:Соотношение (3), т.е. условие сохранения вероятности, можно использовать как критерий точности численного решения задачи.
Идея метода базируется на том, что при $r > {{r}_{V}}$ справедливо свободное решение уравнения (1), которое удобно уже представить в виде разложения по полиномам Лежандра${{P}_{l}}\left( {\cos \vartheta } \right){\text{:}}$
(4)
$\begin{gathered} \Psi (r,\vartheta ) = \exp (ikr\cos \vartheta ) + \\ + \,\,\sum\limits_l {{{a}_{l}}} {{i}^{{l + 1}}}(2l + 1){{P}_{l}}\left( {\cos (\vartheta )} \right)h_{l}^{{(1)}}(kr), \\ \end{gathered} $с неизвестными коэффициентами ${{a}_{l}}$. Здесь $h_{l}^{{\left( 1 \right)}}\left( {kr} \right)$ − сферическая функция Бесселя третьего рода, выражаемая через функцию Ханкеля первого рода
Выбор радиального решения в форме этой функции определяется возможностью удовлетворить асимптотическому условию (2), поскольку:
и функция (4) имеет правильный асимптотический вид (2) с амплитудой:
(5)
$f(\vartheta ) = \frac{1}{k}\sum\limits_l {{{a}_{l}}} (2l + 1){{P}_{l}}\left( {\cos (\vartheta )} \right),$которая выражается через коэффициенты ${{a}_{l}}.$
Практически поиск неизвестных коэффициентов ${{a}_{l}}$ реализуется следующим образом. После стандартной замены $\Psi \left( {r,\vartheta } \right) = r\tilde {\Phi }\left( {r,\vartheta } \right),$ разделения падающей волны и рассеянной $\tilde {\Phi } = {{\Phi }_{0}} + \Phi ,$ приведения полученного из (1) уравнения к дискретному виду (на этом этапе алгоритм аналогичен [1]) используется метод матричной прогонки [10], который базируется на линейной связи
матриц-столбцов ${{\Phi }_{j}}$ = $\overline {(\Phi ({{r}_{j}},{{\vartheta }_{0}}),\Phi ({{r}_{j}},{{\vartheta }_{1}}),} $ $\overline { \ldots ,\Phi ({{r}_{j}},{{\vartheta }_{{{{m}_{{max}}}}}})),} $ ${{\vartheta }_{m}} = \Delta \vartheta m$ для любой точки ${{r}_{j}} = \Delta rj.$ Матричная запись дискретизированного уравнения с учетом граничного условия при $r = 0$ позволяет рекурентным образом определить матрицы $Z{}_{j}$ и ${{D}_{j}}$ для любого ${{r}_{j}}.$ На границе $r = {{r}_{{sh}}} > {{r}_{V}}$ соотношение (6) преобразуется в уравнение для неизвестных коэффициентов ${{a}_{l}},$ для чего используется разложение (4):
ПРИМЕРЫ РАСЧЕТОВ
С помощью программы, реализующей указанный алгоритм, была решена модельная задача, демонстрирующая возможные эффекты при рассеянии на несферическом потенциале. В качестве исходных данных для задачи были выбраны параметры рассеяния нейтрона на несферическом ядре 10Be. Для сравнения рассматривалось две модели: модель 1 с границей прямоугольной потенциальной ямы в виде поверхности эллипсоида вращения, модель 2 – сферически-симметричной прямоугольной потенциальной ямы. Потенциал взаимодействия нейтрона с ядром в модели 1 в сферических координатах записывался в виде
Параметры ${{V}_{0}},$ $b,$ $e$ определялись, исходя из условия равенства областей с ненулевым потенциалом в двух моделях. Это соответствует представлению о несжимаемости ядерной материи. Дополнительно для определения $b,$ $e$ был использован параметр деформации [11]: ${{1.06\left( {a - b} \right)} \mathord{\left/ {\vphantom {{1.06\left( {a - b} \right)} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}} = \beta ,$ $\beta = 1.22,$ $a$ – большая полуось, связанная с малой полуосью $b$ через эксцентриситет $e.$ Достаточно большая (87.036 МэВ) глубина потенциала (${{V}_{0}} < 0$) выбрана так, чтобы в прямоугольной сферически-симметричной яме размера ${{R}_{0}}$ (размер ядра 10Be взят из [12]) существовал уровень, соответствующий энергии развала ядра 11Be по каналу n + 10Be. Использование двумерного уравнения без азимутальной зависимости можно рассматривать как рассеяние нейтронов на спин-ориентированных мишенях.
Разумеется, использование описанных выше параметров потенциала взаимодействия моделирует процесс рассеяния нейтрона 10Be с большой степенью условности, поскольку в рассмотрение не включен гамильтониан ядра, в котором уже угловая часть восстанавливает сохранение углового момента. Но такая реалистическая задача описывается в пространстве с пятью измерениями в минимальной и сильно упрощенной постановке. Поэтому использование двумерного рассеяния на несферическом ядре является лишь частью описания полного процесса рассеяния с возможной передачей углового момента ядру бериллия. Тем не менее даже такой упрощенный анализ может показать, насколько деформация ядра влияет на угловую зависимость процесса рассеяния.
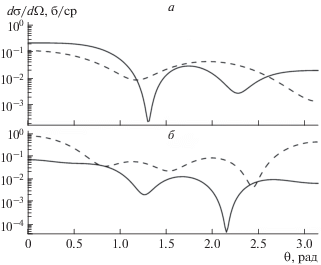
На рис. 1 приведена зависимость полного упругого сечения рассеяния нейтрона на ядре 10Be (ориентированном вдоль направления пучка нейтронов) от энергии в двух моделях. Видно, что рассеяние на эллипсоидальном потенциале (например, для спин-ориентированных мишеней) существенно отличаются от случая рассеяния на сферическом потенциале. Столь же радикальное отличие наблюдается и в дифференциальных сечениях рассеяния на рис. 2.
Рис. 1.
Зависимость полного упругого сечения рассеяния нейтрона на ядре 10Be от энергии для прямоугольной потенциальной ямы с границей в виде поверхности эллипсоида вращения (модель 1 – сплошная кривая) и для сферически симметричной прямоугольной потенциальной ямы (модель 2 – штрих).
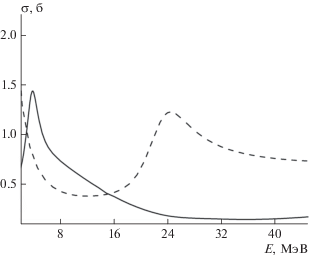
Рис. 2.
Дифференциальное сечение упругого рассеяния нейтронов на ядре 10Be для энергий нейтронов 11.5 (а) и 23 МэВ (б); обозначения кривых такие же как на рис. 1.
ЗАКЛЮЧЕНИЕ
В результате использования разложения решения по свободным решениям была модернизирована программа для расчета сечений двумерных уравнений в сферических координатах. Результатом модернизации является существенная экономия машинных ресурсов, уменьшение времени расчета, новые возможности расчета волновой функции в области геометрической тени.
Программа апробирована на модели эллипсоидального прямоугольного потенциала ядра 10Be. Расчеты рассеяния нейтронов показывают существенное отличие от рассеяния в модели сферически симметричного потенциала. Поэтому использование нуклон ядерного сферически симметричного взаимодействия для описания упругого рассеяния нейтронов на ядре 10Be (для спин-ориентированных мишеней) непригодно даже в качестве первого приближения.
Работа выполнена при финансовой поддержке гранта полномочного представителя Республики Казахстан в ОИЯИ № 434 2018 г.
Список литературы
Красовицкий П.М., Пеньков Ф.М. // Изв. РАН. Сер. физ. 2017. Т. 81. С. 806; Krassovitskiy P.M., Penkov F.M. // Bull. Rus. Acad. Sci. Phys. 2017. V. 81. P. 730.
Красовицкий П.М., Пеньков Ф.М. // Изв. РАН. Сер. физ. 2018. Т. 82. С. 1; Krassovitskiy P.M., Penkov F.M. // Bull. Rus. Acad. Sci. Phys. 2018. V. 82. P. 669.
Krassovitskiy P.M., Pen’kov F.M. // J. Phys. B. 2014. V. 47. Art. no. 225210.
Mathaes R., Winter G., Besheer A. et al. // Expert Opinion on Drug Delivery. 2015. V. 12. P. 481.
Ikot A.N., Akpan I.O., Abbey T.M. et al. // Comm. Theor. Phys. 2015. V. 65. P. 569.
Statt A., Virnau P., Binder K. // Molec. Phys. 2015. V. 113. P. 2556.
Cronin A.D., Schmiedmayer J., Pritchard D.E. // Rev. Mod. Phys. 2009. V. 81. P. 1051.
Chuluunbaatar O., Vinitsky S.I., Gusev A.A. et al. // Bull. Rus. Acad. Sci. Phys. 2018. V. 82. P. 654.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика (в 10 томах). Том III Квантовая механика (нерелятивистская теория). М.: Наука, 1989. 747 с.
Федоренко Р.П. Введение в вычислительную физику / Под ред. Лобанова А.И. Долгопрудный: Издательский дом “Интеллект”, 2008. 504 с.
Немец О.Ф. Гофман Ю.В. Справочник по ядерной физике. Киев: Наукова думка, 1975. 416 с.
Tanihata I. Measurements of interaction cross sections and nuclear radii in light p-shell region. Lawrence Berkeley National Laboratory. LBNL Report (1985).
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


