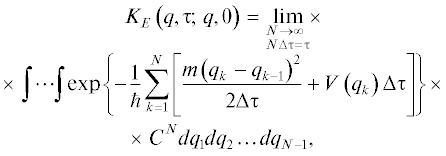Известия РАН. Серия физическая, 2019, T. 83, № 4, стр. 460-468
Изучение основных состояний ядер 6, 7, 9, 11Li методом фейнмановских континуальных интегралов
В. В. Самарин 1, 2, *, М. А. Науменко 1
1 Объединенный институт ядерных исследований
Дубна, Россия
2 Государственное бюджетное образовательное учреждение высшего образования Московской области
“Университет “Дубна”
Дубна, Россия
* E-mail: samarin@jinr.ru
Поступила в редакцию 01.10.2018
После доработки 15.10.2018
Принята к публикации 19.11.2018
Аннотация
Энергия и квадрат модуля волновой функции основного состояния ядер 6, 7, 11Li вычислены методом континуальных интегралов Фейнмана в модели взаимодействия ядерного остова и внешних нуклонов. Для энергии получено согласие с экспериментальными данными. Продемонстрировано проявление в структуре ядер 6Li и 7Li соответственно дейтронного и тритонного кластеров. Для ядер 7, 9, 11Li также были проведены расчеты в оболочечной модели деформированного ядра. Обе модели позволили объяснить сильную деформацию ядра 7Li.
ВВЕДЕНИЕ
Низкоэнергетические реакции с участием ядер трития, гелия, лития и бериллия [1] составляют значительную часть изученных и продолжающих изучаться в настоящее время ядерных реакций. Реакции с изотопами Li представляют значительный интерес с нескольких точек зрения. Ядра 6−11Li с отношением числа нейтронов к числу протонов, изменяющимся от 1 до 2.67, и, следовательно, с существенно различной структурой предоставляют уникальную возможность для проверки различных микроскопических моделей [2]. Знание свойств и волновой функции основного состояния нуклидов лития необходимо для теоретического описания реакций с их участием. В простейшей оболочечной модели конфигураций 6Li (n + p + α) и 7Li (n + n + + p + α) [1–6] внешние нуклоны в поле ядерного остова (α-кластера) занимают состояние 1p3/2 и проявляют свойства кластеров – дейтрона и тритона соответственно [7], поэтому ядра 6Li и 7Li можно рассматривать как системы трех и четырех тел. Ядро 11Li также можно рассматривать как систему трех тел: двух слабосвязанных нейтронов и ядерного остова, близкого по свойствам к ядру 9Li.
Уравнение Шредингера в рамках задачи трех тел с ортогональным проектированием впервые было решено для ядра 6Li в работе [8]. В работе [9] уравнение Шредингера для трехтельной системы n + n + α было решено с помощью разложений по гиперсферическим функциям (К-гармоникам). В работах [10, 11] волновые функции системы трех тел были получены с помощью гауссового базиса и численного решения системы интегральных уравнений Хилла–Уилера (Hill–Wheeler). Более простую возможность вычисления энергии ${{E}_{0}}$ и плотности вероятности ${{\left| {{{\Psi }_{0}}\left( {{{{\vec {r}}}_{1}}, \ldots ,{{{\vec {r}}}_{n}}} \right)} \right|}^{2}}$ для основного состояния n-частичной системы дает метод континуальных интегралов Фейнмана [12–18]. Его универсальность позволила в едином подходе выполнить расчеты для ряда малонуклонных ядер: 3H, 3, 4, 6He, 9Be [15‒18]. В данной работе многотельные расчеты проведены для ядер 6, 7, 11Li, представленных в виде системы из ядерного остова и двух-трех внешних нуклонов. Применение оболочечной модели деформированного ядра к перечисленным ядрам, а также к ядру 9Li дает для структуры ядер картину, близкую к результатам многотельных расчетов.
1. ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Энергия ${{E}_{0}}$ и квадрат модуля волновой функции основного состояния ${{\left| {{{\Psi }_{0}}} \right|}^{2}}$ частицы массой m с потенциальной энергией $V(q),$ зависящей от координаты q, могут быть найдены с помощью введенных Р. Фейнманом [12] континуальных интегралов (интегралов по траекториям) [12, 13] во мнимом (евклидовом) времени $t = - i\tau .$ Континуальные интегралы можно представить в виде предела многократного интеграла [13–15]
где(2)
$C = {{\left( {\frac{m}{{2\pi \hbar \Delta \tau }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$Здесь значения координаты ${{q}_{k}} = q({{\tau }_{k}}),$ τk = kΔτ, $k = \overline {0,N} ,$ ${{q}_{0}} = {{q}_{N}} = q$ задают “траекторию” частицы в виде ломаной линии в плоскости $\left( {q,\tau } \right)$ с вершинами $\left( {{{q}_{k}},{{\tau }_{k}}} \right),\,\,\,\,k = \overline {1,N - 1} ,\,\,\,\,N \geqslant 2,$ при этом $\left( {N - 1} \right)$-кратный интеграл соответствует усреднению по таким “траекториям”
(3)
$\begin{gathered} {{K}_{E}}\left( {q,\tau ;\,\,q,0} \right) \approx \\ \approx {{\left( {\frac{m}{{2\pi \hbar \tau }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\left\langle {\exp \left[ { - \frac{{\Delta \tau }}{\hbar }\sum\limits_{k = 1}^N {V({{q}_{k}})} } \right]} \right\rangle }_{{0,N}}}. \\ \end{gathered} $Здесь и далее угловыми скобками $\langle \ldots \rangle $ обозначено усреднение по случайным $\left( {N - 1} \right)$-мерным векторам $Q = \left\{ {{{q}_{1}}, \ldots ,{{q}_{{N - 1}}}} \right\}$ с законом распределения $W\left( {{{q}_{0}};\,\,{{q}_{1}}, \ldots ,{{q}_{{N - 1}}};\,\,{{q}_{N}} = {{q}_{0}} = q} \right)$
(4)
$\begin{gathered} W\left( {q;\,\,{{q}_{1}}, \ldots ,\,\,{{q}_{{N - 1}}};\,\,q} \right) = \\ = {{C}^{{N - 1}}}{{N}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\exp \left[ { - \frac{m}{{2\hbar \Delta \tau }}\sum\limits_{k = 1}^N {{{{\left( {{{q}_{k}} - {{q}_{{k - 1}}}} \right)}}^{2}}} } \right]. \\ \end{gathered} $Усреднение может быть вычислено методом Монте-Карло [16–18]. Алгоритм моделирования случайного вектора с законом распределения (4) описан в работе [16].
Энергии ${{E}_{0}},$ ${{E}_{1}}$ и квадраты модуля волновой функции ${{\left| {{{\Psi }_{0}}(q)} \right|}^{2}},$ ${{\left| {{{\Psi }_{1}}(q)} \right|}^{2}}$ основного и первого возбужденного состояний определяют первые члены асимптотики пропагатора в пределе $\tau \to \infty $ [14, 15]
(5)
$\begin{gathered} {{K}_{E}}\left( {q,\tau ;\,\,q,0} \right) \to {{\left| {{{\Psi }_{0}}(q)} \right|}^{2}}\exp \left( { - \frac{{{{E}_{0}}\tau }}{\hbar }} \right) + \\ + \,\,{{\left| {{{\Psi }_{1}}(q)} \right|}^{2}}\exp \left( { - \frac{{{{E}_{1}}\tau }}{\hbar }} \right) + \ldots ,\,\,\,\,\tau \to \infty . \\ \end{gathered} $Для значений q и $\tau $ таких, что
(6)
${{\left| {{{\Psi }_{0}}(q)} \right|}^{2}} \gg {{\left| {{{\Psi }_{1}}(q)} \right|}^{2}}\exp \left( { - \frac{{{{E}_{1}} - {{E}_{0}}}}{\hbar }\tau } \right),$энергию ${{E}_{0}}$ можно найти как угловой коэффициент линейной части графика зависимости $\hbar \ln {{K}_{E}}\left( {q,\tau ;\,\,q,0} \right)$ от $\tau $
(7)
$\hbar \ln {{K}_{E}}\left( {q,\tau ;\,\,q,0} \right) = \hbar \ln {{\left| {{{\Psi }_{0}}(q)} \right|}^{2}} - {{E}_{0}}\tau .$Для этого с учетом случайных погрешностей моделирования методом Монте-Карло в работах [16–18] была использована линейная регрессия. Формулы (1)−(7) естественным образом обобщаются на случаи большего числа степеней свободы. Приближенные значения квадрата модуля волновой функции основного состояния ${{\left| {{{\Psi }_{0}}(q)} \right|}^{2}}$ в точках $q$ ограниченной области финитного движения в работах [16–18] были найдены с помощью выражения
(8)
${{K}_{E}}\left( {q,\tau ;\,\,q,0} \right) = {{\left| {{{\Psi }_{0}}(q)} \right|}^{2}}\exp \left( { - \frac{{{{E}_{0}}\tau }}{\hbar }} \right)$при достаточно больших значениях $\tau $ > T, соответствующих линейной части графика зависимости $\hbar \ln {{K}_{E}}\left( {q,\tau ;\,\,q,0} \right).$ Поскольку волновая функция основного состояния не имеет узловых точек (линий или поверхностей) и не меняет знака, ненормированная волновая функция может быть найдена по формуле
Для удобства расчетов в масштабах действия ядерных сил удобно использовать безразмерные переменные $\tilde {q} = {q \mathord{\left/ {\vphantom {q {{{x}_{0}}}}} \right. \kern-0em} {{{x}_{0}}}},$ $\tilde {V} = {{V(q)} \mathord{\left/ {\vphantom {{V(q)} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}},$ ${{\tilde {E}}_{0}} = {{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}$, $\tilde {m} = {m \mathord{\left/ {\vphantom {m {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}},$ $\tilde {\tau } = {\tau \mathord{\left/ {\vphantom {\tau {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}},$ $\Delta \tilde {\tau } = {{\Delta \tau } \mathord{\left/ {\vphantom {{\Delta \tau } {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}},$ ${{\tilde {K}}_{E}} = {{K}_{E}}{{x}_{0}}$, где ${{x}_{0}} = 1$ фм, ${{\varepsilon }_{0}} = 1$ МэВ, ${{m}_{0}}$ − масса нейтрона, t0 = = ${{{{m}_{0}}x_{0}^{2}} \mathord{\left/ {\vphantom {{{{m}_{0}}x_{0}^{2}} \hbar }} \right. \kern-0em} \hbar } \approx 1.57 \cdot {{10}^{{ - 23}}}$ с, ${{b}_{0}} = {{{{t}_{0}}{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}{{\varepsilon }_{0}}} \hbar }} \right. \kern-0em} \hbar } \approx 0.02412,$ тогда в области линейной части графика зависимости пропагатора от $\tilde {\tau }$ (при $\tilde {\tau } > \tilde {T}$)
(10)
$b_{0}^{{ - 1}}\ln {{\tilde {K}}_{E}}\left( {\tilde {q},\tilde {\tau };\,\,\tilde {q},0} \right) \approx b_{0}^{{ - 1}}\ln {{\left| {{{\Psi }_{0}}(\tilde {q})} \right|}^{2}} - {{\tilde {E}}_{0}}\tilde {\tau },$(11)
$\begin{gathered} {{{\tilde {K}}}_{E}}\left( {\tilde {q},\tilde {\tau };\,\,\tilde {q},0} \right) \approx \\ \approx x_{0}^{{ - 1}}{{\left( {\frac{{\tilde {m}}}{{2\pi \tilde {\tau }}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\left\langle {\exp \left[ { - \Delta \tilde {\tau }{{b}_{0}}\sum\limits_{k = 1}^N {\tilde {V}({{{\tilde {q}}}_{k}})} } \right]} \right\rangle }_{{0,N}}}, \\ \end{gathered} $(12)
$\begin{gathered} W\left( {\tilde {q};\,\,{{{\tilde {q}}}_{1}}, \ldots ,{{{\tilde {q}}}_{{N - 1}}};\,\,\tilde {q}} \right) = \\ = {{{\tilde {C}}}^{{N - 1}}}{{N}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\exp \left[ { - \frac{1}{{2\Delta \tilde {\tau }}}\sum\limits_{k = 1}^N {{{{\left( {{{{\tilde {q}}}_{k}} - {{{\tilde {q}}}_{{k - 1}}}} \right)}}^{2}}} } \right], \\ \end{gathered} $(13)
$\tilde {C} = {{\left( {\frac{{\tilde {m}}}{{2\pi \Delta \tilde {\tau }}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$В общем случае эффективные парные центральные потенциалы нуклон-нуклонного взаимодействия нуклонов 1 и 2 могут быть представлены в виде [19]
(14)
$\begin{gathered} V(r) = {{v}_{0}}(r) + {{v}_{{\sigma }}}(r){{{\vec {\sigma }}}_{1}}{{{\vec {\sigma }}}_{2}} + \\ + \,\,{{v}_{{\tau }}}(r){{{\vec {\tau }}}_{1}}{{{\vec {\tau }}}_{2}} + {{v}_{{{\sigma \tau }}}}(r)\left( {{{{\vec {\sigma }}}_{1}}{{{\vec {\sigma }}}_{2}}} \right)\left( {{{{\vec {\tau }}}_{1}}{{{\vec {\tau }}}_{2}}} \right), \\ \end{gathered} $(15)
$V(r) = {{v}_{0}}(r) + {{v}_{\sigma }}(r){{\vec {\sigma }}_{1}}{{\vec {\sigma }}_{2}} + {{v}_{\tau }}(r){{\vec {\tau }}_{1}}{{\vec {\tau }}_{2}}$с тремя функциями ${{v}_{0}}(r),$ ${{v}_{\sigma }}(r),$ ${{v}_{{\tau }}}(r),$ для определения которых можно использовать значения энергии основного состояния ядер 2Н и 3Н. Для четного триплетного состояния протона и нейтрона в дейтроне потенциал
должен объяснять наличие единственного связанного состояния с энергией 2.225 МэВ и среднеквадратичным зарядовым радиусом 2.14 фм [3].
Известно, что спин основного состояния ядра 3Н равен ${1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ при этом по принципу Паули спины нейтронов должны быть антипараллельны. Для конфигурации ядра 3Н такой, что параллельны спины протона с радиусом-вектором ${{\vec {r}}_{3}}$ и нейтрона с радиусом-вектором ${{\vec {r}}_{1}},$ потенциальная энергия взаимодействия нуклонов в ядре 3Н может быть представлена в виде суммы парных взаимодействий нуклонов друг с другом
(17)
$V = V_{{n - n}}^{{({{0}^{ + }})}}\left( {\left| {{{{\vec {r}}}_{1}} - {{{\vec {r}}}_{2}}} \right|} \right) + V_{{p - n}}^{{({{1}^{ + }})}}\left( {\left| {{{{\vec {r}}}_{1}} - {{{\vec {r}}}_{3}}} \right|} \right) + V_{{p - n}}^{{({{0}^{--}})}}\left( {\left| {{{{\vec {r}}}_{2}} - {{{\vec {r}}}_{3}}} \right|} \right).$Здесь $V_{{p - n}}^{{({{0}^{--}})}}$ и $V_{{n - n}}^{{({{0}^{ + }})}}$ − синглетные потенциалы взаимодействия соответственно протона с нейтроном и нейтрона с нейтроном
Потенциалы (18), (19) не должны приводить к наличию связанных состояний.
Выражение (17) несимметрично по отношению к перестановке нейтронов. При его использовании в гамильтониане вместо общего выражения (14) оно привело бы к некоммутативности гамильтониана с оператором перестановки тождественных частиц. В подходе, примененном в данной работе, гамильтониан не используется явно, а свойство симметрии координатной волновой функции обеспечивается дополнительной процедурой симметризации (см. далее). Это позволяет в начальном приближении использовать выражение (17) при вычислении пропагатора для ядра 3Н.
Функции ${{v}_{0}}(r),$ ${{v}_{{\sigma }}}(r),$ ${{v}_{{\tau }}}(r)$ выражаются через перечисленные потенциалы
(20)
${{v}_{0}}(r) = \frac{3}{4}V_{{p - n}}^{{({{1}^{ + }})}}(r) - \frac{1}{2}V_{{p - n}}^{{({{0}^{--}})}}(r) + \frac{3}{4}V_{{n - n}}^{{({{0}^{ + }})}}(r),$(21)
${{v}_{{\sigma }}}(r) = \frac{1}{4}V_{{p - n}}^{{({{1}^{ + }})}}(r) - \frac{1}{4}V_{{p - n}}^{{({{0}^{--}})}}(r),$(22)
${{v}_{{\tau }}}(r) = - \frac{1}{4}V_{{p - n}}^{{({{0}^{--}})}}(r) + \frac{1}{4}V_{{n - n}}^{{({{0}^{ + }})}}(r).$В работах [16–18] при расчетах пропагатора ${{\tilde {K}}_{E}}\left( {\tilde {q},\tilde {\tau };\tilde {q},0} \right)$ для ядер 2, 3H, 3, 4He были использованы эффективные парные потенциалы сильного взаимодействия в виде линейных комбинаций гауссовых экспонент с отталкивательным кором, сходные с известным потенциалом M3Y (см., например, [20, 21])
(23)
$V_{{p - n}}^{{({{1}^{ + }})}}(r) = \sum\limits_{k = 1}^3 {{{u}_{k}}\exp \left( { - {{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {b_{k}^{2}}}} \right. \kern-0em} {b_{k}^{2}}}} \right)} ,$(24)
$V_{{p - n}}^{{({{0}^{--}})}}(r) = \sum\limits_{k = 1}^3 {{{u}_{k}}\exp \left( { - {{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {d_{k}^{2}}}} \right. \kern-0em} {d_{k}^{2}}}} \right)} ,$(25)
$V_{{n - n}}^{{({{0}^{ + }})}}(r) = \sum\limits_{k = 1}^3 {{{u}_{k}}\exp \left( { - {{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {c_{k}^{2}}}} \right. \kern-0em} {c_{k}^{2}}}} \right)} .$Для ядра 2Н потенциал (23) с набором параметров ${{u}_{1}} = 500$ МэВ, ${{u}_{2}} = - 102$ МэВ, ${{u}_{3}} = - 2$ МэВ, ${{b}_{1}} = 0.296$ фм, ${{b}_{2}} = {{c}_{2}} = {{d}_{2}} = 1.26$ фм, b3 = c3 = d3 = = 2.67 фм дает значения энергии ${{E}_{0}} = - 2.226$ МэВ и среднеквадратичного зарядового радиуса 1.92 фм, достаточно близкие к экспериментальным значениям. Числовые значения остальных параметров, ${{d}_{1}}$ и ${{c}_{1}},$ были определены в работе [16] из условия близости вычисленных значений энергий связи ядер 2, 3H, 3, 4He к экспериментальным значениям, в частности, для ядра 3Н энергия связи равна 8.48 МэВ. Примеры графиков эффективных потенциалов (23)−(25) и функций ${{\text{v}}_{0}}(r),$ ${{\text{v}}_{{\sigma }}}(r),$ ${{\text{v}}_{{\tau }}}(r)$ показаны на рис. 1.
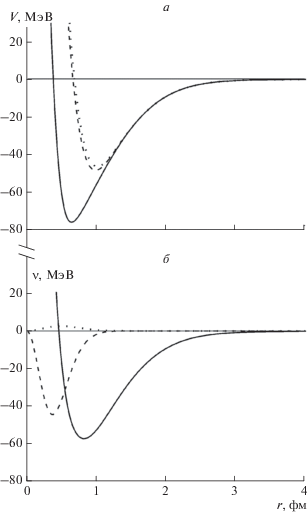
Рис. 1.
Графики: а – эффективных потенциалов (23) (сплошная линия), (24) (штриховая линия), (25) (точечная линия); б – функций ${{v}_{0}}(r)$ (сплошная линия), ${{v}_{{\sigma }}}(r)$ (штриховая линия), ${{\text{v}}_{{\tau }}}(r)$ (точечная линия).
Для основных состояний ядер, содержащих не более двух тождественных нуклонов, расчеты по формулам (10)−(12) можно проводить без учета принципа Паули. Принцип Паули можно не учитывать и для ядер 6, 7, 11Li, если рассматривать их как систему из остова и внешних нуклонов с конфигурациями {p, n}, {p, n, n} и {n, n}, соответственно. В ядрах 6, 7Li в качестве остова естественно выбрать α-кластер, остов ядра 11Li будем считать подобным ядру 9Li. В таком случае в рассматриваемых системах будет не более двух тождественных нуклонов.
Ядерную часть эффективного потенциала взаимодействия нуклона с ядерным остовом можно выбрать аналогичной псевдопотенциалу [22], используемому в физике металлов для описания взаимодействия внешних электронов (из зоны проводимости) с атомными остовами. Внутри атомного остова иона псевдопотенциал имеет простой вид (в частности, может быть постоянным), при этом вне атомного остова решения уравнения Шредингера с псевдопотенциалом и реальным потенциалом атома мало отличаются друг от друга. Энергия основного состояния электрона в псевдопотенциале близка к энергии самого верхнего занятого уровня атома. Наличие отталкивательных кóров в используемых в данной работе псевдопотенциалах объясняется наличием отталкивательных кóров в потенциалах нуклон-нуклонного взаимодействия. Энергия основного состояния в системе остов-нуклон оказывается близкой к энергии самого верхнего заполненного уровня оболочечной модели ядра. При этом состояния нуклонов ядерного остова, соответствующие нижележащим уровням, оказываются исключенными (запрещенными).
В работах [16–18] при расчетах пропагатора ${{\tilde {K}}_{E}}\left( {\tilde {q},\tilde {\tau };\,\,\tilde {q},0} \right)$ для ядер 6He, 6Li потенциалы сильного взаимодействия $\alpha $-кластера с нейтроном и протоном ${{V}_{{n - {\alpha }}}}(r) \equiv V_{{p - {\alpha }}}^{{(N)}}(r)$ были выбраны в виде линейных комбинаций функций типа Вудса–Саксона (фермиевского распределения)
В данной работе парный псевдопотенциал сильного взаимодействия $\alpha $-кластера с нейтроном и протоном ${{V}_{{n - {\alpha }}}}(r) \equiv V_{{p - {\alpha }}}^{{(N)}}(r)$ для ядер 6Li и 7Li и парный псевдопотенциал сильного взаимодействия ядерного остова с нейтроном для ядра 11Li были выбраны в виде функции
(27)
$\begin{gathered} U(r) = - {{U}_{1}}f(r;\,\,{{a}_{1}},{{B}_{1}}) + {{U}_{2}}f(r;\,\,{{a}_{2}},{{B}_{2}}) + \\ + \,\,{{U}_{3}}f(r;\,\,{{a}_{3}},{{B}_{3}})f(r;\,\,{{a}_{4}},{{B}_{4}}). \\ \end{gathered} $Примеры графиков парных псевдопотенциалов сильного взаимодействия $\alpha $-кластера и ядерного остова {9Li} с нейтроном показаны на рис. 2; их обсуждение приводится в следующем разделе. Потенциал взаимодействия протона с $\alpha $-кластером ${{V}_{{p - {\alpha }}}}(r)$ включал ядерную (N) и кулоновскую (C) части
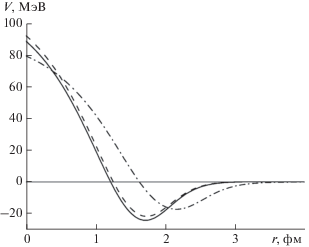
Рис. 2.
Графики псевдопотенциалов взаимодействия нейтрона с $\alpha $-кластером в ядрах 6Li (сплошная линия), 7Li (штриховая линия) и с ядерным остовом {9Li} (штрихпунктирная линия) в ядре 11Li.
Для кулоновской части взаимодействия использовалось известное выражение для энергии точечного заряда в поле равномерно заряженного шара.
Вычисления для ядер 3Н, 6Li и 11Li, рассматриваемых соответственно как системы n + n + p, n + + p + α и n + n + {9Li}, выполнялись в системе центра масс с использованием координат Якоби (см., например, [13]) для системы трех частиц с массами ${{m}_{1}},\,\,{{m}_{2}},$ ${{m}_{3}}$
(29)
$\vec {y} = {{\vec {r}}_{3}} - \frac{1}{2}\left( {{{{\vec {r}}}_{1}} + {{{\vec {r}}}_{2}}} \right).$Для ядер 3Н, 11Li в качестве ${{\vec {r}}_{1}},\,\,{{\vec {r}}_{2}}$ выбирались радиусы-векторы нейтронов с ${{m}_{1}} = {{m}_{2}} = m,$ для ядра 6Li − радиусы-векторы нейтрона и протона с равными массами ${{m}_{1}} \approx {{m}_{2}} = m.$ Для ядра 7Li, представленного как система n + n + p + α, использовались координаты Якоби для системы четырех частиц с массами ${{m}_{1}} = {{m}_{2}} = {{m}_{3}} = m,$ ${{m}_{3}} = M$
(30)
$\begin{gathered} \vec {x} = {{{\vec {r}}}_{2}} - {{{\vec {r}}}_{1}},\,\,\,\,\vec {y} = \frac{1}{2}\left( {{{{\vec {r}}}_{1}} + {{{\vec {r}}}_{2}}} \right) - {{{\vec {r}}}_{3}}, \\ \vec {z} = \frac{1}{3}\left( {{{{\vec {r}}}_{1}} + {{{\vec {r}}}_{2}} + {{{\vec {r}}}_{3}}} \right) - {{{\vec {r}}}_{4}}. \\ \end{gathered} $Вычисления по формулам (8), (9) с потенциальной энергией, несимметричной по отношению к перестановке нейтронов с радиусами-векторами ${{\vec {r}}_{1}},$ ${{\vec {r}}_{2}}$, дает координатную волновую функцию, также несимметричную по отношению к перестановке нейтронов
(31)
${{\Phi }_{0}}({{\vec {r}}_{1}},{{\vec {r}}_{2}},{{\vec {r}}_{3}}) = \sqrt {{{K}_{E}}\left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}},{{{\vec {r}}}_{3}},\tau ;\,\,{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}},{{{\vec {r}}}_{3}},0} \right)} .$Из-за асимметричности спиновой волновой функции по отношению к перестановке нейтронов с антипараллельными спинами координатная волновая функция должна быть симметрична по отношению к перестановке нейтронов. Такую (ненормированную) волновую функцию можно получить, образовав симметричную комбинацию
(32)
${{\Psi }_{S}}({{\vec {r}}_{1}},{{\vec {r}}_{2}},{{\vec {r}}_{3}}) = {{\Phi }_{0}}({{\vec {r}}_{1}},{{\vec {r}}_{2}},{{\vec {r}}_{3}}) + {{\Phi }_{0}}({{\vec {r}}_{2}},{{\vec {r}}_{1}},{{\vec {r}}_{3}})$или в координатах Якоби
(33)
${{\Psi }_{S}}(\vec {x},\vec {y}) = {{\Phi }_{0}}(\vec {x},\vec {y}) + {{\Phi }_{0}}( - \vec {x},\vec {y}).$Плотность вероятности в координатах Якоби $\rho (\vec {x},\vec {y}) = {{\left| {{{\Psi }_{S}}(\vec {x},\vec {y})} \right|}^{2}}$ имеет свойство симметрии по отношению к инверсии вектора $\vec {x}{\text{:}}$ $\rho (\vec {x},\vec {y}) = \rho ( - \vec {x},\vec {y}).$ Подобная симметризация по отношению к перестановке нейтронов нужна и для ядра 7Li. Для ядра 11Li взаимодействие внешних нейтронов с остовом в простейшем приближении будем считать не зависящим от спинов нейтронов, тогда симметричная по отношению к перестановкам нейтронов потенциальная энергия
(34)
$V = V_{{n - n}}^{{({{0}^{ + }})}}\left( {\left| {{{{\vec {r}}}_{1}} - {{{\vec {r}}}_{2}}} \right|} \right) + U\left( {\left| {{{{\vec {r}}}_{1}} - {{{\vec {r}}}_{3}}} \right|} \right) + U\left( {\left| {{{{\vec {r}}}_{2}} - {{{\vec {r}}}_{3}}} \right|} \right)$приводит к симметричной по отношению к перестановке нейтронов волновой функции основного состояния
2. РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Для реализации расчетов средних по случайным траекториям была использована технология CUDA параллельных вычислений на графических процессорах [23–25]. Расчеты были выполнены на гетерогенном кластере “HybriLIT” [26] Лаборатории информационных технологий Объединенного института ядерных исследований. Для определения энергии ${{E}_{0}}$ основного состояния ядер 3Н и 6, 7, 11Li численные расчеты пропагатора (11) проводились с числом траекторий $n\sim {{10}^{6}}{\text{--}}{{10}^{8}}$ и шагом сетки по мнимому времени $\Delta \tilde {\tau } = 0.003.$ Результаты показаны на рис. 3.
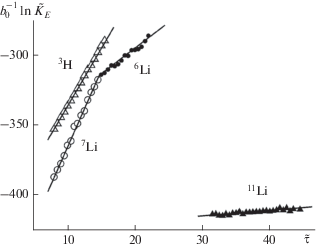
Рис. 3.
Линейные части графиков зависимости нормированного логарифма пропагатора $b_{0}^{{ - 1}}\ln {{\tilde {K}}_{{\text{E}}}}$ от мнимого времени $\tilde {\tau }$ для ядер 3Н (светлые треугольники), 7Li (кружки), 6Li (точки) и 11Li (черные треугольники): прямые – результаты линейной регрессии (расчет методом Монте-Карло для $n = 7 \cdot {{10}^{7}}$ траекторий с шагом сетки $\Delta \tilde {\tau } = 0.003$).
Графики потенциалов (23)–(25) и псевдопотенциалов (27) показаны соответственно на рис. 1 и 2. Значения параметров потенциалов и псевдопотенциалов были подобраны из условия совпадения с точностью до трех значащих цифр теоретического значения $\left( { - {{E}_{0}}} \right)$ c экспериментальной энергией разделения ядер 3Н, 7Li и 6Li на составляющие нуклоны (3Н) или внешние нуклоны и α-кластер (7Li и 6Li), соответственно 8.48, 10.9 и 3.70 МэВ [3]. Для ядра 11Li из-за малости энергии разделения (0.369 МэВ) на нейтроны и остов {9Li} совпадение ограничивалось двумя значащими цифрами. Относительная погрешность углового коэффициента в формуле (11) определялась с помощью линейной регрессии (см. рис. 3) и составляла несколько процентов. Для нуклон-нуклонных потенциалов (24), (25) были использованы незначительно измененные по сравнению с работой [16] значения параметров ${{d}_{1}} = 0.490$ фм, ${{c}_{1}} = 0.504$ фм. Для трех изотопов 6, 7, 11Li были использованы единые значения параметров U2 = = 55.8 МэВ, ${{B}_{1}} = 0.25$ фм, ${{B}_{2}} = 0.3$ фм, B3 = 0.5 фм, ${{B}_{4}} = 1$ фм; значения остальных параметров псевдопотенциалов (27) приведены в таблице. Небольшие различия графиков псевдопотенциалов взаимодействия нейтрона с $\alpha $-кластером (27) для ядер 6Li и 7Li можно объяснить поляризацией α‑кластера в различном поле внешних нуклонов. В частности, несколько больший радиус отталкивательного кора у ядра 7Li обусловлен бóльшим числом таких нуклонов.
Рассмотрим свойства волновой функции ${{\Psi }_{0}}$ и плотности вероятности ${{\left| {{{\Psi }_{0}}} \right|}^{2}}$ для ядер 6, 7, 11Li. Найденное по формуле (8) распределение ненормированной плотности вероятности ${{\tilde {K}}_{E}}\left( {\vec {x},\vec {y},\tilde {\tau };\,\,\vec {x},\vec {y},0} \right)$ = = ${{\tilde {K}}_{E}}\left( {x,y,\cos \theta ;\tilde {\tau }} \right)$ для трех значений угла $\theta $ трехтельной конфигурации ядра 6Li (n + p + α) показано на рис. 4а. Результаты для четырехтельной конфигурации ядра 7Li (n + n + p + α) в частном случае расположения нуклонов в вершинах правильного треугольника со стороной x и α-кластера на расстоянии z от центра треугольника приведены на рис. 5а. В работе [16] было показано, что подобное расположение нуклонов наиболее вероятно в ядре 3Н (см. также далее). Видно, что наиболее вероятными являются конфигурации с объединением внешних нуклонов соответственно в дейтронный кластер для 6Li (d + α, рис. 4в) и в тритонный кластер для 7Li (t + α, рис. 5в). Косвенным подтверждением этого является сравнительно небольшая энергия отделения этих кластеров – соответственно 1.47 и 2.47 МэВ, а также близость энергии отделения нейтрона от ядер 7Li и 3Н – соответственно 7.25 и 6.26 МэВ.
Рис. 4.
Плотность вероятности (а) в координатах Якоби x, y (б) с примерами положения нейтрона (светлые кружки), протона (темные малые кружки), α-кластера (темные большие кружки) и трехмерная модель (в) конфигурации ядра 6Li (n + p + α). Наиболее вероятной является конфигурация с объединением протона и нейтрона в дейтронный кластер (d + α).
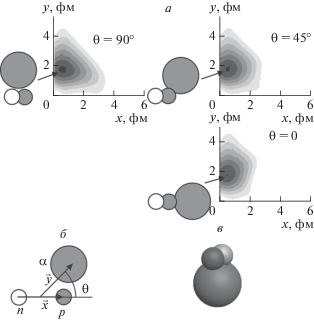
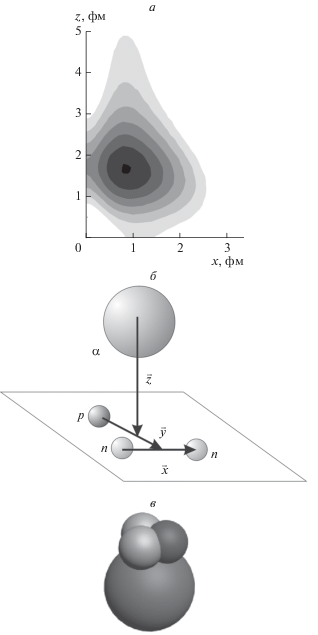
Рис. 5.
Плотность вероятности (а) в координатах Якоби x, y, z (б) и трехмерная модель (в) для четырехтельной конфигурации ядра 7Li (n + n + p + α). Наиболее вероятной является конфигурация с объединением протона и двух нейтронов в тритонный кластер (t + α). Обозначения такие же, как на рис. 4.
Представленная на рис. 5в модель согласуется с известными представлениями о форме ядер 7Li и 9Li. Из экспериментальных значений квадрупольных моментов были получены значения параметров квадрупольной деформации ${{\beta }_{2}}$ для 7Li от −0.9 до −1.5, для 9Li от −0.6 до −0.8 [27]. Сильно сплюснутая форма ядра 7Li может соответствовать усреднению по всевозможным поворотам системы t + α вокруг направления (оси симметрии), перпендикулярного межкластерной оси. Добавление двух внешних нейтронов делает ядро 9Li менее сплюснутым, что можно связать с поляризацией кластера в поле нейтронов. Некоторое уменьшение деформации до ${{\beta }_{2}} \approx - 0.6$ у ядра 11Li можно рассматривать как следствие влияния протяженной гало-оболочки внешних нейтронов на ядерный остов, подобный ядру 9Li. В качестве дополнительной модели ядер 7, 9, 11Li была использована оболочечная модель деформированного ядра с потенциалом Вудса–Саксона
(36)
$U(r,\cos \theta ) = - {{U}_{0}}{{\left\{ {1 + \exp \left[ {\frac{{r - {{R}_{U}}{{g}_{{\beta }}}(\cos \theta )}}{{{{a}_{U}}}}} \right]} \right\}}^{{ - 1}}},$Рис. 6.
а – схемы уровней нейтронов ядер 7Li, 9Li и 11Li в оболочечной модели деформированного ядра и в оболочечной модели сферического ядра 11Li (${{\beta }_{2}} = 0$), сплошные отрезки − занятые уровни, штриховые − свободные; б – плотности вероятности в цилиндрических координатах (по горизонтали − ось симметрии) для трех низших уровней нейтронов с квантовыми числами $\left| {{{m}_{j}}} \right| = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ $\left| {{{m}_{j}}} \right| = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},$ $\left| {{{m}_{j}}} \right| = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ в оболочечной модели деформированного ядра 9Li.
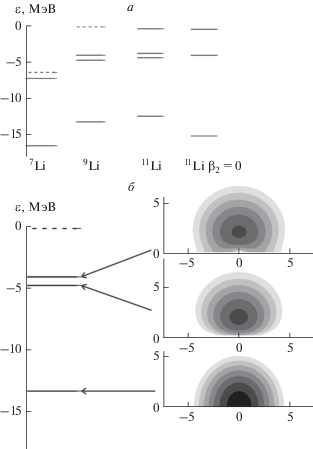
Таблица 1.
Параметры псевдопотенциала (27) сильного взаимодействия внешних нуклонов с остовами ядер 6, 7, 11Li
| Ядро | ${{U}_{1}}$, МэВ | ${{U}_{3}}$, МэВ | ${{a}_{1}}$, фм | ${{a}_{2}}$, фм | ${{a}_{3}}$, фм | ${{a}_{4}}$, фм |
|---|---|---|---|---|---|---|
| 6Li | 66.33 | 126 | 1.95 | 1.22 | 0.9 | 2.7 |
| 7Li | 63.54 | 126 | 1.95 | 1.22 | 0.9 | 2.7 |
| 11Li | 35.32 | 72 | 2.45 | 1.5 | 1 | 2.8 |
В деформированном ядре 11Li энергии подуровней с $\left| {{{m}_{j}}} \right| = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}$ и $\left| {{{m}_{j}}} \right| = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ соответствующих уровню 1p3/2 сферического ядра, оказываются близкими. Это позволяет с достаточной точностью использовать для ядра 11Li сферическую оболочечную модель с тремя заполненными нейтронными оболочками: $1{{s}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (в поляризованном альфа-кластерном остове), $1{{p}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ (первая внутренняя оболочка) и $1{{p}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ (внешняя гало-оболочка). Соответственно, остов ядра 11Li с достаточной точностью можно считать сферически симметричным, а псевдопотенциал взаимодействия остова с внешними нейтронами – центральным (см. рис. 2). Распределение плотности вероятности ${{\tilde {K}}_{E}}\left( {\vec {x},\vec {y},\tilde {\tau };\,\,\vec {x},\vec {y},0} \right)$ = ${{\tilde {K}}_{E}}\left( {x,y,\cos \theta ;\,\,\tilde {\tau }} \right)$ для трех углов $\theta $ трехтельной конфигурации ядра 11Li (n + + n + {9Li}) показано на рис. 7. Наиболее вероятна конфигурация с динейтронным кластером; линейная (сигарообразная) конфигурация имеет существенно меньшую вероятность. Для сравнения на рис. 8 приведена топография пропагатора ${{\tilde {K}}_{E}}\left( {\vec {x},\vec {y},\tilde {\tau };\,\,\vec {x},\vec {y},0} \right)$ = ${{\tilde {K}}_{E}}\left( {x,y,\cos \theta ;\,\,\tilde {\tau }} \right)$ для трех значений угла $\theta $ трехтельной конфигурации ядра 3Н (n + n + p). В показанной картине благодаря большой разнице между энергиями основного (−8.48 МэВ) и первого возбужденного (−2.22 МэВ) состояний заметно присутствие плотности вероятности двух состояний согласно формуле (5). Основному состоянию ядра 3Н отвечают треугольное и линейное (сигарообразное) расположение нуклонов. В области, где выполнено условие
(37)
$\begin{gathered} {{\left| {{{\Psi }_{0}}(x,y,\cos \theta )} \right|}^{2}} \ll {{\left| {{{\Psi }_{1}}(x,y,\cos \theta )} \right|}^{2}} \times \\ \times \,\,\exp \left( { - \frac{{{{E}_{1}} - {{E}_{0}}}}{\hbar }\tau } \right), \\ \end{gathered} $Рис. 7.
Плотность вероятности для трехтельной конфигурации ядра 11Li (n + n + {9Li}); обозначения те же, что на рис. 4. Наиболее вероятна конфигурация 1 с динейтронным кластером; линейная (сигарообразная) конфигурация 2 имеет существенно меньшую вероятность. Конфигурация 3 (n + {10Li}) еще менее вероятна.
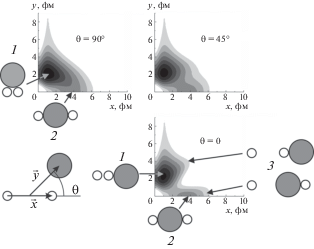
Рис. 8.
Топография пропагатора ${{\tilde {K}}_{E}}\left( {\vec {x},\vec {y},\tilde {\tau };\,\,\vec {x},\vec {y},0} \right)$ = ${{\tilde {K}}_{E}}\left( {x,y,\cos \theta ;\,\,\tilde {\tau }} \right)$ в координатах Якоби $\vec {x},\vec {y}$ для ядра 3Н (n + n + p); обозначения те же, что на рис. 4 и 7. Основному состоянию ядра 3Н отвечают треугольное 1 и линейное (сигарообразное) 2 расположения нуклонов; расположение нуклонов 3 соответствует первому возбужденному состоянию с разделением ядра 3Н на нейтрон и дейтрон n + d.
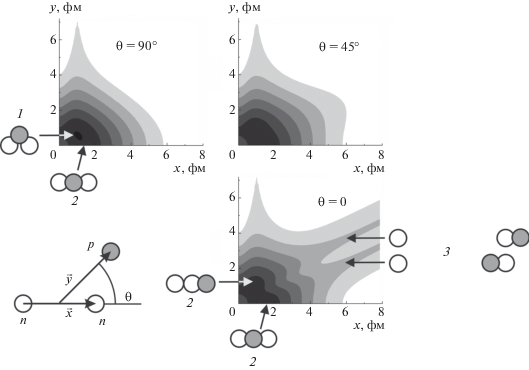
проявляется первое возбужденное состояние с разделением на нейтрон и дейтрон n + d.
ЗАКЛЮЧЕНИЕ
Предложенный поход к расчетам волновой функции основного состояния ядер 6, 7, 9, 11Li может служить полезным дополнением к существующим более сложным теоретическим методам. Он позволяет достаточно просто определить энергию основного состояния и установить ее зависимость от параметров нуклон-нуклонного потенциала. Анализ свойств плотности вероятности позволяет подобрать аналитические аппроксимации для волновой функции основного состояния и сделать более реалистичным выбор среднего поля оболочечной модели, а также распределения заряда и массы в ядрах. Все это может быть полезным при теоретическом описании реакций с участием изотопов лития и других легких ядер.
Список литературы
Пeниoнжкeвич Ю.Э. // ЯФ. 2011. T. 74. C. 1641; Penionzhkevich Yu.E. // Phys. Atom. Nucl. 2011. V. 74. P. 1615.
Пенионжкевич Ю.Э., Соболев Ю.Г., Самарин В.В. и др. // ЯФ. 2017. Т. 80. С. 525; Penionzhkevich Yu.E., Sobolev Yu.G., Samarin V.V. et al. // Phys. Atom. Nucl. 2017. V. 70. P. 928.
Загребаев В.И., Деникин А.С., Карпов А.В. и др. // Сетевая база знаний NRV по ядерной физике низких энергий. http://nrv.jinr.ru/;
Карпов А.В., Деникин А.С., Алексеев А.П. и др. // ЯФ. 2016. Т. 79. С. 520; Karpov A.V., Denikin A.S., Alekseev A.P. et al. // Phys. Atom. Nucl. 2016. V. 79. P. 749.
Karpov A.V., Denikin A.S., Naumenko M.A. et al. // Nucl. Instrum. Methods Phys. Res. Sect. A. 2017. V. 859. P. 112.
Соловьев В.Г. Теория атомного ядра: ядерные модели. М.: Энергоиздат, 1981. 296 с.
von Oertzen W., Freer M., Kanada En’yo Y. // Phys. Rep. 2006. V. 432. P. 43.
Voronchev V.T., Krasnopol’sky V.M., Kukulin V.I. // J. Phys. G. 1982. V. 8. P. 649.
Zhukov M.V., Danilin B.V., Fedorov D.V. et al. // Phys. Rep. 1993. V. 231. P. 151.
Кукулин В.И., Краснопольский В.М., Миселхи М.А. и др. // ЯФ. 1981. Т. 34. С. 21; Kukulin V.I., Krasnopol’sky V.M., Miselkhi M.A. et al. // Sov. J. Nucl. Phys. 1981. V. 34. P. 21.
Kukulin V.I., Krasnopol’sky V.M., Voronchev V.T. et al. // Nucl. Phys. A. 1986. V. 453. P. 365.
Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. М.: Мир, 1968. 382 с.
Блохинцев Д.И. Основы квантовой механики. М.: Наука, 1976. 664 с.
Шуряк Э.В. // УФН. 1984. Т. 143. С. 309; Shuryak E.V. // Sov. Phys. Usp. 1984. V. 27. P. 448.
Shuryak E.V., Zhirov O.V. // Nucl. Phys. B. 1984. V. 242. P. 393.
Самарин В.В., Науменко М.А. // ЯФ. 2017. Т. 80. С. 473; Naumenko M.A., Samarin V.V. // Phys. Atom. Nucl. 2017. V. 80. P. 877.
Самарин В.В., Науменко М.А. // Изв. РАН. Сер. физ. 2016. Т. 80. С. 314; Samarin V.V., Naumenko M.A. // Bull. Russ. Acad. Sci.: Phys. 2016. V. 80. P. 283.
Naumenko M.A., Samarin V.V. // Supercomp. Front. Innov. 2016. V. 3. P. 80.
Ву Т.Ю., Омура Т. Квантовая теория рассеяния. М.: Наука, 1969. 451 с.
Satchler G.R., Love W.G. // Phys. Rep. 1979. V. 55. P. 183.
Alvarez M.A.G., Chamon L.C., Pereira D. et al. // Nucl. Phys. A. 1999. V. 656. P. 187.
Харрисон У. Псевдопотенциалы в теории металлов. М.: Мир, 1968. 367 с.
NVIDIA CUDA. https://developer.nvidia.com/cuda-zone/.
Перепелкин Е.Е., Садовников Б.И., Иноземцева Н.Г. Вычисления на графич. процессорах (GPU) в задачах матем. и теор. физики. М.: Ленанд, 2014. 176 с.
Сандерс Д., Кэндрот Э. Технология CUDA в примерах: введение в программирование графических процессоров. М.: ДМК, 2011. 232 с.
Гетерогенный кластер “HybriLIT” ЛИТ ОИЯИ. http://hybrilit.jinr.ru/.
Centre for Photonuclear Experiments Data (Skobeltsyn Institute of Nuclear Physics, Lomonosov Moscow State University). http://cdfe.sinp.msu.ru/services/ radchart/radmain.html.
Загребаев В.И., Самарин В.В. // ЯФ. 2004. Т. 67. С. 1488; Zagrebaev V.I., Samarin V.V. // Phys. Atom. Nucl. 2004. V. 67. P. 1462.
Caмapин B.B. // ЯФ. 2015. T. 78. C. 133; Samarin V.V. // Phys. Atom. Nucl. 2015. V. 78. P. 128.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая