1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 10, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 10, стр. 1430-1439

R-матричный анализ реакций с возбуждением составного ядра 10B в области энергии 6.5‒19.5 МэВ

Л. Н. Генералов 1, С. М. Селянкина 1, *

1 Федеральное государственное унитарное предприятие Всероссийский научно-исследовательский институт экспериментальной физики
Саров, Россия

* E-mail: otd4@expd.vniief.ru

Поступила в редакцию 11.05.2020
После доработки 02.06.2020
Принята к публикации 26.06.2020

Полный текст (PDF)

Аннотация

Выполнен R-матричный анализ экспериментальных данных реакций 9Be(p,p0)9Be, 9Be(p,p1)9Be* (1.670 МэВ), 9Be(p,p2)9Be* (2.430 МэВ), 9Be(p,n0)9B, 9Be(p,d0)8Be, 9Be(p,α0)6Li, 9Be(p,α2)6Li* (3.5618 МэВ), 7Li(3He,p0)9Be для энергии возбуждения составного ядра 10B от 6.5 до 19.5 МэВ. В анализе использованы и наши экспериментальные данные: по дифференциальным, интегральным сечениям реакции 9Be(p,α2)6Li* (3.5618 МэВ, Jπ = 0 +) при энергии протонов Ep = 2.3–4.5 МэВ, и данные по дифференциальным сечениям реакции 9Be(p,n0)9B для угла 0° в интервале Ep = 2.2–3.5 МэВ. Определены новые уровни 10B и уточнены характеристики уже известных состояний.

ВВЕДЕНИЕ

Наше внимание к R-матричным исследованиям реакций привлекает возможность поиска новых, уточнения характеристик известных уровней ядер и выполнения оценки сечений ядерных реакций по ограниченным наборам экспериментальных данных. В качестве инструментария исследований выбран известный программный код AZURE2 [1, 2].

Основная причина настоящих исследований связана с появлением новых экспериментальных данных по дифференциальным сечениям пороговой реакции 9Be(p,α2)6Li* (3.5618 МэВ, Jπ = 0 +) с Q = –1.437 МэВ – угловым распределениям α2-частиц для энергии протонов Ep = 2.3‒4.5 МэВ, полученным [3] из описания результатов эксперимента [4] по изучению формы γ-линии с доплеровским уширением. При этом на основании экспериментальных исследований [5] и описываемых ниже, в данных [4] на 7.4 кэВ были увеличены энергии протонов.

В R-матричном анализе возможное количество реакций и область энергии возбуждения ядра 10B определяются тем, что при использовании стабильных ядер-мишеней (или пучков стабильных ядер) это ядро можно возбудить только в реакциях 6Li + α, 9Be + p и 7Li + 3He, начиная соответственно с энергий возбуждения Ex = 4.460, 6.585 и 17.79 МэВ. Количество каналов этих реакций огромно, большинство из них до сих пор экспериментально не изучено.

Во всех R-матричных исследованиях с образованием составного ядра 10B их авторы привлекали довольно ограниченный экспериментальный материал и по числу каналов реакций, и по энергии возбуждения, что связано с возрастающей сложностью анализа многоканальной задачи в широком энергетическом диапазоне, а также с бедностью и противоречивостью экспериментальных данных. В работах рассматривались выходные каналы реакции 9Be + p: при Ex = 6‒8 МэВ – p0, d0 и α0-каналы [6‒9]; при Ex = 8–10 МэВ [10‒13, 15‒17] – p0, n0 и α2-каналы; при Ex = 8.8–11.6 МэВ – p0, n0, α0, α2-каналы [14].

Наши исследования выполнены в области Ex = = 6.5–19.5 МэВ, использовались экспериментальные данные реакций 9Be(p,p0)9Be, 9Be(p,p1)9Be* (1.670 МэВ), 9Be(p,p2)9Be* (2.430 МэВ), 9Be(p,n0)9B, 9Be(p,d0)8Be, 9Be(p,α0)6Li, 9Be(p,α2)6Li* (3.5618 МэВ), 7Li(3He,p0)9Be. R-матричным расчетам предшествовала большая подготовительная работа по уточнению и экспертизе экспериментальных данных.

1. ЭНЕРГЕТИЧЕСКАЯ КАЛИБРОВКА УСКОРИТЕЛЯ ДЛЯ УТОЧНЕНИЯ ПОЛОЖЕНИЯ РЕЗОНАНСОВ РЕАКЦИЙ 9Be(p,n0)9B и 9Be(p,α2)6Li* В ОБЛАСТИ ЭНЕРГИИ ПРOТОНОВ 2.5–2.7 МэВ

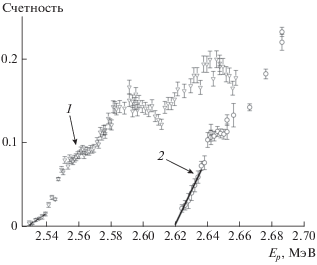
В наших исследованиях [3] реакции 9Be(p,α2)6Li* энергетическая калибровка ускорителя, выполненная по реперным точкам, относительно далеким от энергии ее резонанса в области Ep 2.56 МэВ (наблюдаемый максимум при 2.5665 МэВ), вызывала некоторое сомнение. В [5] мы по резонансной реакции 27Al(p,γ2)28Si* (4.618 МэВ) с реперной точкой 2.4883(10) МэВ получили другое положение наблюдаемого максимума при 2.5749(10) МэВ. Приведем результаты другого эксперимента, когда одновременно проводились регистрация γ-квантов и нейтронов под углом 0° к пучку протонов соответственно из реакций 9Be(p,α2)6Li*, 9Be(p,n0)9B и калибровка энергетической шкалы ускорителя по регистрации γ‑квантов из реакций 76Ge(n,n')76Ge* (563 кэВ), 74Ge(n,n')74Ge* (596 кэВ), 72Ge(n,n')72Ge* (691 кэВ), 72Ge(n,n')72Ge* (834 кэВ) [18]. Для регистрации нейтронов использовался всеволновой счетчик, а γ-квантов – HPGE-детектор REGE (диаметр 45 мм, высота 47.5 мм), находящийся на расстоянии 150 мм от бериллиевой мишени толщиной 24 мкг ⋅ см–2 (в энергетической шкале 2.7 кэВ для энергии протонов 2.5 МэВ) на танталовой подложке. Реакции на изотопах германия были вызваны в самом германиевом детекторе мишенными нейтронами из реакции 9Be(p,n0)9B. Нейтроны, как и γ‑кванты, падали на цилиндрическую поверхность детектора REGE. Для энергетической калибровки ускорителя по нейтронным порогам En,th реакций на изотопах германия были рассчитаны протонные пороговые энергии Ep,th, при превышении которых рождаются нейтроны с энергиями выше En,th. В расчетах по релятивистской кинематике Ep,th использовались значения масс p, n, ядер 9Be, 9B, определенные по дефектам масс [19–21] с учетом энергии связи атомных электронов. Наиболее отчетливо пороги образования γ-квантов проявились в реакциях 74Ge(n,n')74Ge*(596 кэВ) и 72Ge(n,n')72Ge*(691 кэВ) (рис. 1), значения Ep,th которых равны 2.5285(1) и 2.6201(1) МэВ соответственно. Среднее значение наблюдаемой резонансной энергии составило 2.5739(10) МэВ, которое на 7.4 кэВ больше оцениваемого максимума в данных [4]. В этих же исследованиях были измерены дифференциальные сечения реакции 9Be(p,n0)9B для угла 0°, в энергетической зависимости которых максимум находится при Ep = 2.571 МэВ (см. далее).

Рис. 1.

Счетность при регистрации γ-квантов из 74Ge(n,n')74Ge*(596 кэВ) и 72Ge(n,n')72Ge*(691 кэВ) (данные 1 и 2 соответствуют γ-квантам с энергиями 596 и 691 кэВ, прямые линии – экстраполяция в пороги).

2. ПОЛУЧЕНИЕ УГЛОВЫХ РАСПРЕДЕЛЕНИЙ α-ЧАСТИЦ РЕАКЦИИ 9Be(p,α2)6Li* ПО ФОРМЕ γ-ЛИНИИ

Дифференциальные сечения этой реакции впервые были получены косвенным методом в [10] при Ep = 2.4–2.6 МэВ из анализа формы γ-линии с доплеровским уширением. В этой же работе проведен R-матричный анализ c целью установления квантовых чисел практически совпадающих уровней составного ядра 10B, возбуждаемых в области Ep = 2.56 МэВ. Этим же методом при Ep = = 2.3–4.5 МэВ получены и наши данные [3]. Измерения зависимости формы γ-линии от энергии протона изложены в [4].

Использованная нами процедура получения угловых распределений в системе центра масс (с.ц.м.) заключалась в анализе спектров γ-квантов с доплеровским смещением, зарегистрированных [3] под нулевым углом относительно направления падающего на мишень пучка протонов. Ядро 6Li* (3.5618 МэВ) за время своей жизни 0.8 ⋅ 10–16 с. проходит путь 10–6 см, фактически испуская γ-кванты в месте своего рождения и, следовательно, можно не учитывать его торможение. Поэтому угол испускания γ-кванта θγ по отношению к направлению движения ядра 6Li* равен углу θL вылета этого ядра относительно движения пучка протонов. Приведем основные моменты вывода расчетных формул спектров.

Количество $d{{N}_{{{}^{6}{\text{Li}}*}}}$ ядер 6Li* (3.5618 МэВ), образующихся и вылетающих в телесный угол dΩ, определяется как

(1)
$d{{N}_{{{}^{6}{\text{Li*}}}}} = - 2{\pi }{{N}_{p}}C\frac{{d\sigma }}{{d\Omega }}({{{\theta }}_{L}})d\cos {{{\theta }}_{L}},$
где Np – количество протонов, упавших на мишень толщиной С, $\frac{{d\sigma }}{{d\Omega }}({{{\theta }}_{L}},{{\varphi }_{L}})$ – дифференциальное сечение реакции в лабораторной системе координат (л.с.к.) для полярного θL и азимутального φL углов. По количеству $d{{N}_{{{}^{6}{\text{Li}}*}}}$ (1) определяем количество dNγ зарегистрированных квантов:
(2)
$\begin{gathered} \frac{{d{{N}_{{\gamma }}}}}{{d{{E}_{{\gamma }}}}} = - 2\pi {{N}_{p}}C \cdot {{{\varepsilon }}_{{\gamma }}}\frac{1}{{{{E}_{{{\gamma 0}}}}{{{\beta }}_{c}}}}\frac{{d{\sigma }}}{{d\Omega }}({{{\theta }}_{c}}) \equiv \\ \equiv - 2{\pi }{{N}_{p}}C \cdot {{{\varepsilon }}_{{\gamma }}}\frac{1}{{{{E}_{{{\gamma 0}}}}{{{\beta }}_{c}}}}\sum\limits_l {{{A}_{l}}{{P}_{l}}({{{\theta }}_{c}})} , \\ \end{gathered} $
где ${{\varepsilon }_{\gamma }}$ – внутренняя эффективность регистрации, зависящая от энергии кванта Eγ, Eγ0 = 3.5618 МэВ, βc – скорость излучателя в с.ц.м., θc – угол вылета в с.ц.м., дифференциальное сечение разложено в ряд по полиномам Лежандра Pl(θc) с коэффициентами Al, l = 0, 1, 2… Для определения дифференциальных сечений образования $\alpha $-частиц надо выразить угол θc через угол вылета ${\theta }_{c}^{{\alpha }}$, ${{{\theta }}_{c}} = {\pi } - {\theta }_{c}^{{\alpha }}$:
(3)
$\begin{gathered} \frac{{d{{N}_{\alpha }}}}{{d{{E}_{{\gamma }}}}} = \\ = 2{\pi }{{N}_{p}}C \cdot {{t}_{m}} \cdot {{{\varepsilon }}_{{\gamma }}}\frac{1}{{{{E}_{{{\gamma 0}}}}{{{\beta }}_{c}}}}\sum\limits_l {{{A}_{l}}{{P}_{l}}(\cos {\theta }_{c}^{{\alpha }})} , \\ \end{gathered} $
где учтена энергетическая зависимость эффективности регистрации, dNα – количество альфа-частиц, tm = 1–1.03 – фактор мертвого времени.

Совсем недавно дифференциальные сечения этой реакции были измерены при Ep = 2.3‒6 МэВ прямым методом [14] – применялась обратная кинематика, когда на легкую мишень H налетало тяжелое ядро 9Be.

3. ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ ПО КАНАЛАМ РЕАКЦИЙ 9Be + p и 7Li + 3He, ИСПОЛЬЗОВАННЫЕ В R-АНАЛИЗЕ

Экспериментальные данные по каналам реакций, использованные в анализе, представлены в табл. 1. Характеристики остаточных ядер взяты из [22, 23].

Таблица 1.  

Экспериментальные данные, использованные в анализе

Реакция Энерговыделение реакции, МэВ Энергия налетающих частиц л.с.к., МэВ Тип данных Угол рассеяния в л.с.к., град Ошибка, % Работа
9Be(p,p0) 0 2.2–2.8 dσ/dΩ 163, 125*   [11]
2–3.8 dσ/dΩ 65–160* 13 [12]
2.49–2.64 dσ/dΩ 83, 120, 135, 145 3 [10]
9Be(p,p1) –1.684 4.2–6.1 dσ/dΩ 45, 125, 150   [24]
9Be(p,p2) –2.430 4.2–6.1 dσ/dΩ 45, 84, 115, 150   [24]
9Be(p,α0) 2.125 0.8–2.9 dσ/dΩ, σ 90 7 [6]
9Be(p,α2) –1.437 2.3–4.5 dσ/dΩ, σ 0–180* 5 [3, 4]
9Be(p,n0) –1.850 2–3.9 dσ/dΩ 0* 5 [13]
0* 5 Наст.
9Be(p,d0) 0.560 0.77–3.025 dσ/dΩ, σ 15–135 7 [6]
4–5.9 dσ/dΩ 50 4.5 [7]
0.29–0.89 dσ/dΩ, σ 90 7 [8]
0.03–0.7 σ   6 [9]
7Li(3He,p0) 11.200 0.9–2.5 dσ/dΩ 70, 130 5 [25]
2.2–3.2 dσ/dΩ 15–160* 7 [26]

* В с.ц.м.

В анализе использованы наши данные по дифференциальным и полным сечениям реакции 9Be(p,α2)6Li*, по дифференциальным сечениям реакции 9Be(p,n0)9B для угла 0°. Энергии протонов в этих данных соответствуют энергетической калибровке ускорителя (см. раздел 1), при выполнении которой также были получены относительные данные по реакции 9Be(p,n0)9B. Абсолютизация этих данных была выполнена в два этапа. Сначала по данным [15], с которыми в энергетической зависимости наши данные хорошо согласуются. Затем дифференциальные сечения были увеличены в 1.6 раза с учетом того, что данные [15] по полным сечениям образования нейтронов (где основной канал – реакция (p,n0)) занижены относительно “эталонных” данных [16]. Таким же путем были абсолютизированы данные [13], при этом смещенные в сторону увеличения энергии протонов на 19.3 кэВ.

В настоящем R-матричном анализе не использовались данные, полученные на поляризованных пучках, а также значения сечений из работ [14, 25, 26], существенно отличающиеся от наших данных.

4. РЕЗУЛЬТАТЫ АНАЛИЗА

R-матричное многоканальное описание части экспериментальных данных показано на рис. 2–4, где значения сечений представлены в с.ц.м., а энергии частиц, вызывающих реакции, в л.с.к. В табл. 2 приведены характеристики уровней составного ядра 10B, извлеченные в этом анализе: Ex, Jπ, Γ – энергия, спин, четность, полная ширина уровня возбуждения, соответственно, ${\Gamma }_{i}^{{sl}}$ – парциальная ширина i-канала с данными спином канала s и орбитальным моментом l.

Рис. 2.

Описания дифференциальных сечений реакции 9Be(p,p0)9Be при θc: ◻ –148.6° [10] (смещено на +50 мб ⋅ ср–1); △ – 139.5° [10]; ◼ – 163° [11]; ▼ – 89.3° [10] (смещено на –30 мб ⋅ ср–1; ◀ – 125.5° [10] (смещено на +120 мб ⋅ ср–1).

Рис. 3.

а, в – Описание дифференциальных сечений реакции 9Be(p,α2)6Li* (3.5618 МэВ, Jπ = 0 + ) при Ep = = 2.541‒2.631 МэВ (а) и Ep = 2.571 МэВ (в); б – полное сечение реакции 9Be(p,α2)6Li* (3.5618 МэВ, Jπ = 0 + ).

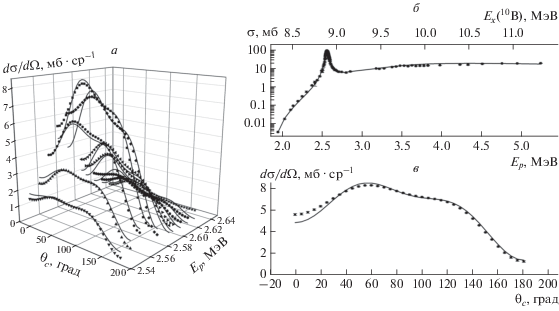
Рис. 4.

Описание дифференциальных сечений реакции 9Be(p,n0)9B (θc = 0°): ◻ –данные [13], ◼ – наши данные (смещено на + 7 мб ⋅ ср–1).

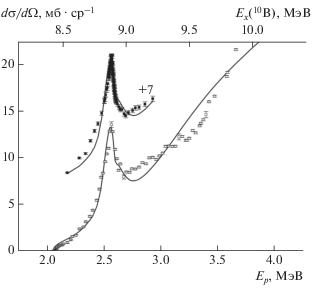
Таблица 2.  

Характеристики уровней составного ядра 10B, используемые в R-матричном анализе. Энергии уровней Ex даны в МэВ

Ex, Jπ Γ, кэВ канал ${\Gamma }_{i}^{{sl}}$, кэВ s l Ex, Jπ Γ, кэВ канал ${\Gamma }_{i}^{{sl}}$, кэВ s l
6.896, 1– 198.687 pp0 59.054 1 0 7.635, 2+ 323.896 pp0 20.169 1 1
4.841 · 10–3 1 2 240.231 · 10–3 1 3
34.066 · 10–3 2 2 117.140 · 10–3 2 1
pd0 88.820 1 1 7.132 · 10–3 2 3
pα0 50.774 1 1 pd0 119.970 1 2
7.235, 3– 65.813 pp0 2.284 1 2 pα0 183.393 1 2
187.093 · 10–3 2 2 7.806, 1+ 135.418 pp0 76.086 1 1
pd0 14.439 1 3 51.946 2 1
pα0 48.903 1 3 3.759 2 3
7.356, 2+ 166.963 pp0 2.443 1 1 pd0 3.122 1 0
364.102 · 10–3 1 3 385.114 · 10–3 1 2
1.081 2 1 pα0 120.651 · 10–3 1 2
204.462 · 10–3 2 3 8.525, 2– 1391.67 pp0 189.197 1 2
pd0 104.986 1 2 4.865 2 0
pα0 57.885 1 2 15.570 2 2
7.424, 2– 340.381 pp0 9.074 1 2 pd0 252.856 1 1
69.080 2 0 33.818 1 3
9.608 2 2 pα0 810.934 1 1
pd0 33.315 1 1 84.431 1 3
556.953 · 10–3 1 3 8.755, 2– 277.827 pp0 14.541 1 2
pα0 179.329 1 1 6.399 2 0
39.419 1 3 6.554 2 2
7.441, 1+ 119.016 pp0 1.893 1 1 pn0 768.273 · 10–3 1 2
93.764 2 1 12.124 2 0
360.133 · 10–3 2 3 6.509 2 2
pd0 15.237 1 0 pd0 29.163 1 1
676.273 · 10–3 1 2 201.769 1 3
pα0 7.086 1 2 8.838, 1– 819.064 pp0 481.338 1 0
7.499, 1– 391.394 pp0 223.663 1 0 39.354 1 2
19.885 1 2 83.616 2 2
9.822 2 2 pn0 166.697 1 2
pd0 179.082 · 10–3 1 1 11.380 1 2
4.596 2 2
pα2 32.083 0 1
Ex, Jπ Γ, кэВ канал ${\Gamma }_{i}^{{sl}}$, кэВ s l Ex, Jπ Γ, кэВ канал ${\Gamma }_{i}^{{sl}}$, кэВ s l
8.879, 1– 1523.962 pp0 1215.263 1 0 8.924, 1– 130.278 pp0 13.561 1 0
141.378 1 2 4.748 1 2
139.246 2 2 1.467 2 2
pn0 738.6 · 10–3 1 0 pn0 3.941 1 0
9.762 1 2 14.202 1 2
14.043 2 2 26.746 2 2
pα2 3.532 0 1 pα2 65.613 0 1
8.882, 3– 169.937 pp0 47.418 1 2 9.219, 1– 997.375 pp0 44.649 1 0
104.746 2 2 609.209 · 10–3 1 2
pn0 17.606 1 2 35.462 2 2
165.028 · 10–3 2 2 pn0 530.239 1 0
pα2 2.549 · 10–3 0 3 18.649 1 2
8.898, 2+ 55.972 pp0 717.079 · 10–3 1 1 8.024 2 2
532.820 · 10–3 1 3 pα2 359.743 0 1
9.871 2 1 9.995, 2+ 2628.50 pp0 583.596 1 1
1.070 2 3 54.823 1 3
pn0 12.480 1 1 657.938 2 1
261.219 · 10–3 1 3 64.897 2 3
9.762 2 1 pn0 304.051 1 1
68.986 · 10–3 2 3 11.146 1 3
pα2 21.121 1 2 796.490 2 1
8.928, 2+ 238.912 pp0 770.174 · 10–3 1 1 6.551 2 3
125.152 · 10–3 1 3 pα2 149.010 1 2
8.564 2 1 10.8, 2+ 483.453 pp0 29.907 1 1
183.140 · 10–3 2 3 4.735 1 3
pn0 209.152 1 1 276.138 2 1
279.163 · 10–3 1 3 3.877 2 3
1.418 2 1 pn0 42.786 1 1
157.937 · 10–3 2 3 pα2 11.983 0 2
pα2 18.264 0 2 pp1 2.766 · 10–3 0 2
3.663 1 2
pp2 66.361 2 1
617.628 · 10–6 2 3
44.985 3 1
Ex, Jπ Γ, кэВ канал ${\Gamma }_{i}^{{sl}}$, кэВ s l Ex, Jπ Γ, кэВ канал ${\Gamma }_{i}^{{sl}}$, кэВ s l
11.0, 2– 3065.263 pp0 659.423 1 2 11.359, 3+ 4168.757 pp0 206.122 1 3
1125.752 2 0 2847.46 2 1
199.060 2 2 263.124 2 3
1056.569 1 2 pp1 50.481 1 2
pp1 7.168 1 1 pp2 94.300 2 1
2.443 · 10–3 1 3 19.825 2 3
pp2 7.649 2 0 679.732 3 1
3.495 · 10–3 2 2 7.713 3 3
9.636 3 2 18.363, 2+ 492.815 pp0 17.312 1 1
11.05, 1– 5666.725 pp0 5485.349 1 0 43.675 1 3
191.584 1 2 393.395 2 1
3.284 2 2 37.973 2 3
pα2 1.159 0 1 3Hep0 2.77 · 10–3 1 1
pp1 81.382 · 10–3 0 1 98.8 · 10–3 1 3
319 · 10–3 2 1
453.506 · 10–3 1 1 38.3 · 10–3 2 3
18.796, 2– 473.237 pp0 17.949 1 2
pp2 3.395 · 10–3 2 2 387.541 2 0
66.431 2 2
1.182 · 10–3 3 2 3Hep0 5.35 · 10–3 1 2
1.282 2 0
11.1, 2– 1788.773 pp0 116.849 1 2 28.9 · 10–3 2 2
228.224 2 0 19.271, 1+ 416.808 pp0 367.228 1 1
1263.08 2 2 13.897 2 1
pp1 22.878 1 1 29.742 2 3
147.435 · 10–3 1 3 3Hep0 2.15 · 10–3 1 1
3.243 2 1
pp2 145.212 2 0 2.696 2 3
5.739 2 2 20.332, 1– 1959.283 pp0 426.366 1 0
6.644 3 2 1410.84 1 2
4.747 2 2
3Hep0 1.720 1 0
61.098 1 2
54.512 2 2

Реакция 9Be(p,p0)9Be

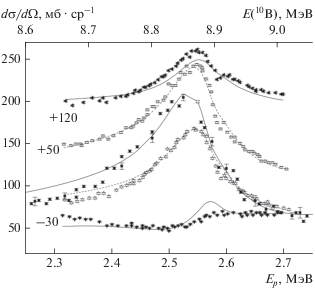
Наиболее хорошо описываются дифференциальные сечения при углах θc = 139.5°, 148.6°, 163° и несколько хуже при θc = 89.3°, 125.5° (рис. 2). Наибольший вклад вносят состояния с Ex = 8.525 (2–), 8.838 (1–), 8.882 (3–), 8.898 (2+ ), 8.924 (1–), 8.928 (2+ ) МэВ, а уровни с меньшими (возбуждаемые в реакции (p,d0)) и большими энергиями (возбуждаемые в реакциях (p,p1), (p,p2), (3He,p0)) являются “фоновыми” в этой области.

Реакция 9Be(p,α2)6Li* (3.5618 МэВ)

Хорошее описание дифференциальных сечений (рис. 3) получено при энергии Еp = 2.541–2.621 МэВ – в области возбуждения Ex = 8.876–8.946 МэВ, в которой проявляются два уровня с Jπ = 3– и 2 + [10], для которых мы получили значение энергии 8.882 и 8.898 МэВ соответственно. При Ep = 2.631–4.533 МэВ (Ex = 8.9–10.7 МэВ), расчетная кривая также неплохо согласуется с экспериментальными данными. Для Еp = = 2.384‒2.511 МэВ (Ex = 8.731‒8.845 МэВ) получено хорошее описание в интервале 50° ≤ θc ≤ 150°, однако для передних и задних углов наблюдаются расхождения в экспериментальных и расчетных данных. Функция возбуждения полного сечения хорошо воспроизводится при всех энергиях.

Реакция 9Be(p,n0)9B

Хорошее описание (рис. 4) получено в области энергии Еp = 2.5–2.8 МэВ (Ex = 8.85–9.1 МэВ), где наиболее сильно проявляются резонансы при 8.882 МэВ, 3– и 8.898 МэВ, 2+. При описании данных в области возбуждения Ex > 9 МэВ были обнаружены новые уровни с энергиями Ex = 8.928 (2+), 9.219 (1–), 9.995 (2+) МэВ, отсутствующие в [22, 23].

В анализе данных по реакциям 9Be(p,p1)9Be* (1.670 МэВ), 9Be(p,p2)9Be* (2.30 МэВ), 9Be(p,d0)8Be, 9Be(p,α0)6Li, 7Li(3He,p0)9Be обнаружены новые состояния (табл. 2), так как имеющихся уровней для описания этих данных было недостаточно.

В табл. 3 указаны характеристики уровней, определенные в результате нашего анализа (данные табл. 2) и имеющиеся в литературе. Состояния с близкими значениями энергии возбуждения объединены в одну строку таблицы.

Таблица 3.  

Уровни ядра 10B, используемые в нашем R-матричном анализе, и представленные в литературе

Ex, МэВ Jπ Γ, кэВ Работа Ex, МэВ Jπ Γ, кэВ работа
6.896 1– 198.687 Наст. 8.898 2+ 55.972 Наст.
6.875 1– 120 ± 5 [22, 23] 8.892 ± 0.005 2+ 36 ± 4 [12]
6.880 1– 145 [29] 8.895 ± 0.001 2+ 39 ± 1 [22, 23]
7.004 3+ 98 [22, 23] 8.894 ± 0.002 2+ 40 ± 1 [10]
7.235 3– 65.813 Наст. 8.89 2+ 38 ± 3 [17]
7.356 2+ 166.963 Наст. 8.89 2+ 90 ± 20 [11]
7.424 2– 340.381 Наст. 8.894 ± 0.002 2+ 34 ± 4 [14]
7.428 1– 94 [22, 23] 8.924 1– 130.278 Наст.
7.441 1+ 119.016 Наст. 8.928 2+ 238.912 Наст.
7.430 ± 10 2– 100 ± 10 [22, 23] 8.93 ± 0.01 1+ 45 ± 5 [12]
7.437 1– 130 ± 10 [29] 8.95 (1+ 3+) 40 ± 10 [11]
7.470 ± 4 2+ 65 [22, 23] 9.03 3– 45 ± 10 [11]
7.469 2+ 65 ± 10 [29] 9.219 1– 997.375 Наст.
7.479 ± 2 2– 74 ± 4 [22, 23] 9.58 ± 60   257 ± 64 [22, 23]
7.480 2– 80 ± 8 [29] 9.700   630 [22, 23]
7.499 1– 391.394 Наст. 9.995 2+ 2628.502 Наст.
7.5599 ± 0.4 0+ 2.65 ± 0.18 [22, 23] 10.00 ± 0.09 3– 450 ± 10 [12]
7.564 0+ 3.3 [29] 10.36 ± 0.09 2– 1000 ± 100 [12]
7.635 2+ 323.896 Наст. 10.8 2+ 483.453 Наст.
7.666 ± 0.027 1+ 247 [22, 23] 10.825 ± 9 (2+ 3+ 4+) 350 ± 7 [22, 23]
7.665 1+ 250 ± 20 [29] 10.83 ± 0.09 2+ 400 ± 100 [12]
7.750 ± 0.030 2– 210 [22, 23] 10.7 ± 0.1 2+ 300 ± 100 [14]
7.795 2– 265 ± 30 [29]
7.806 1+ 135.418 Наст. 11.0 2– 3065.263 Наст.
7.811 ± 0.017 1– 260 [22, 23] 11.0 0+ $3700_{{ - 600}}^{{ + 200}}$ [14]
7.960 ± 0.070   285 [28]
8.070 ± 0.050 2+ 800 [22, 23] 11.05 1– 5666.725 Наст.
8.07 2+ 800 [29] 11.1 2– 1788.773 Наст.
8.45 ± 0.010 2– 100 ± 20 [11] 11.359 3+ 4168.757 Наст.
8.525 2– 1391.67 Наст. 11.511 ± 0.030   316 ± 44 [22, 23]
8.66 2+ 200 ± 20 [12]
8.67 3– 35 ± 10 [11] 11.63 1– 480 ± 150 [14]
8.68 (1+ 2+ ) 220 [22, 23] 12.564 ± 0.026 (0+ 1+ 2+) 106 ± 26 [22, 23]
8.755 2– 277.827 Наст.
8.78 ± 0.010 3– 180 ± 10 [12] 13.494 ± 0.050 (0+ 1+ 2+) 300 ± 50 [22, 23]
8.79 3+ 50 ± 10 [11]
8.838 1– 819.064 Наст. 14.34   800 [22, 23]
8.879 1– 1523.962 Наст. 18.2   1500 [22, 23]
8.882 3– 169.937 Наст. 18.363 2+ 492.815 Наст.
8.880 ± 0.005 3– 105 ± 5 [12] 18.430 2– 340 [22, 23]
8.887 ± 0.003 3– 96 ± 4 [22, 23] 18.796 2– 473.237 Наст.
8.889 ± 0.006 3– 100 ± 20 [10] 18.8 (2+ 1+) 600 [22, 23]
8.89 3– 85 ± 10 [17] 19.271 1+ 416.808 Наст.
8.89 3– 30 ± 5 [11] 19.290 2– 190 [22, 23]
8.898 ± 0.010 3– 80 ± 10 [14] 20.1 1– 350 [22, 23]
20.332 1– 1959.283 Наст.

Для ранее известных состояний (6.875 (1–), 8.887 (3–), 8.895 (2+), 10.825 (2+) МэВ) получены новые значения энергий (6.895, 8.882, 8.898, 10.8 МэВ) и ширин. Для девяти уровней значения параметров, определенные нами, не совпадают с принятыми в литературе. Не подтверждено существование 16 уровней.

ЗАКЛЮЧЕНИЕ

Проведен многоканальный R-матричный анализ реакций с образованием составного ядра 10B при Ex от 6.5 до 19.5 МэВ. Был использован весь существующий экспериментальный материал. Определены новые уровни 10B и уточнены характеристики уже известных состояний. Наши численные данные по реакциям 9Be(p,n0)9B и 9Be(p,α2)6Li* (3.5618 МэВ) будут переданы в международную библиотеку экспериментальных данных EXFOR.

Авторы выражают благодарность одному из разработчиков кода AZURE2 Ричарду де Боеру (Richard de Boer) за помощь в освоении программы.

Список литературы

  1. Azuma R.E., Uberseder E., Simpson E.C. et al. // Phys. Rev. C. 2010. V. 81. Art. № 045805.

  2. Лейн А., Томас Р. Теория ядерных реакций при низких энергиях. М.: Издательство иностранной литературы, 1960.

  3. Генералов Л.Н., Селянкина С.М., Романихин В.П. // Сб. тез. “Ядро-2017" (Алма-Ата, 2017). С. 141.

  4. Генералов Л.Н., Абрамович С.Н., Звенигородский А.Г. и др. // Изв. РАН. Сер. физ. 2003. Т. 67. С. 1462; Generalov L.N., Abramovich S.N., Zvenogorodskii A.G. et al. // Bull. Russ. Acad. Sci. Phys. 2003. V. 67. P. 1616.

  5. Генералов Л.Н., Карпов И.А., Федотов Д.А. // Сб. тез. “Ядро-2014”. (Минск, 2014). С. 202.

  6. Weber G., Davis L.W., Marion J.B. // Phys. Rev. 1956. V. 104. № 5. P. 1307.

  7. Read F.H., Calvet J.M. // Proc. Phys. Soc. 1961. V. 77. P. 65.

  8. Bertrand F., Greiner G., Pornet J. // Rapport CEA-R-3575. 1968.

  9. Sierk A.J., Tombrello T.A. // Nucl. Phys. A. 1973. V. 210. P. 341.

  10. Kiss A., Koltay E., Szabo G. et al. // Nucl. Phys. A. 1977. V. 282. P. 44.

  11. Машкаров Ю.Г., Дейнеко А.С., Слабоспицкий Р.П. и др. // Изв. АН СССР. Сер. физ. 1976. Т. 40. С. 1218; Mashkarov Yu.G., Deineko A.S., Slabospitskii R.P. et al. // Bull. Acad. Sci. USSR. Phys. 1976. V. 40. P. 100.

  12. Allab M., Boucenna A., Haddad M. // J. Phys. 1983. V. 44. P. 579.

  13. Richards H.T., Smith R.V., Browne C.P. // Phys. Rev. 1950. V. 80. P. 524.

  14. Kuchera A.N., Rogachev G.V., Goldberg V.Z. et al. // Phys. Rev. C. 2011 V. 84. Art. № 054615.

  15. Marion J.B., Bonner T.W., Cook C.F. // Phys. Rev. 1955. V. 100. P. 91.

  16. Gibbons J.H., Macklin R.L. // Phys. Rev. 1959. V. 114. P. 571.

  17. Marion J.B. // Phys. Rev. 1956. V. 103. P. 713.

  18. Lister D., Smith A.B. // Phys. Rev. 1969. V. 183. P. 183.

  19. Firestone R.B. Table of Isotopes CD-ROM. 8th edition. 1998. Lawrence Berkeley Laboratory.

  20. Audi G., Bersillion O., Blachot J. et al. // Nucl. Phys. A. 2003. V. 729. P. 3.

  21. Wapstra A.H., Audi G., Thibauld C. // Nucl. Phys. A. 2003. V. 729. P. 129.

  22. Ajzenberg-Selove F. // Nucl. Phys. A. 1988. V. 490. P. 1.

  23. Tilley D.R., Kelley J.N., Godwin J.L. et al. // Nucl. Phys. A. 2004. V. 745. P. 155.

  24. Yasue M., Ohsawa T., Fuiwara N. et al. // J. Phys. Soc. Japan. 1972. V. 33. P. 265.

  25. Bondouk I.I., Asfour F., Saleh Z. et al. // Rev. Roum. Phys. 1975. V. 20. P. 1095.

  26. Lru Y.C. // Chin. J. Phys. 1972. V. 10. P. 76.

  27. Rath D.P., Boyd R.N., Hausman H.J. et al. // Nucl. Phys. A. 1990. V. 515. P. 338.

  28. Leask P.J., Freer M., Clarke N.M. et al. // Phys. Rev. C. 2001. V. 63. Art. № 034307.

  29. Tsan Mo, Hornyak W.F. // Phys. Rev. 1969. V. 187. P. 1220.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал