Известия РАН. Серия физическая, 2020, T. 84, № 12, стр. 1819-1821
Кинетика процессов ориентации и адсорбции в полимерных адгезивных материалах
А. В. Максимов 1, *, О. Г. Максимова 1, С. В. Осипов 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Череповецкий государственный университет”
Череповец, Россия
* E-mail: a_v_maximov@mail.ru
Поступила в редакцию 15.07.2020
После доработки 10.08.2020
Принята к публикации 26.08.2020
Аннотация
Рассмотрены механизмы отрывания адсорбированной макромолекулы от поверхности под действием эффективного среднего поля, формируемого межмолекулярными взаимодействиями с другими цепями. В этом приближении выведено кинетическое уравнение для параметра порядка и получены его решения. Для цепей конечной длины обнаружен эффект “критического замедления”, заключающийся в резком увеличении времен их релаксации в критической точке.
Изучение физико-химических свойств поверхностных полимерных структур: пленок, слоев и мембран, имеет не только теоретическое, но еще практическое значение, связанное с их уникальными характеристиками, важными для применения, например, в качестве защитных покрытий листового металлопроката [1]. Решение задачи об адсорбции макромолекул закладывает основу для построения теории адгезии полимеров на межфазных границах [2].
Для классических низкомолекулярных систем, совершающих фазовые переходы 1-го рода, описание обеих фаз и исследование эффектов, связанных с конечностью системы, представляет сложнейшую задачу [3, 4] и достигается только с помощью использования компьютерного моделирования. В данной работе в приближении среднего поля разработан динамический вариант модели “липкой ленты”, в рамках которой возможно получить описание как равновесное, так и релаксационное поведение обеих фаз.
Как и в обычной модели “липкой ленты” [3], в которой отдельная гибкая полимерная цепь находится в растворе вблизи некоторой адсорбирующей плоской поверхности, в данной модели [5] один участок цепи также закреплен на некоторой плоскости, а второй остается свободным (рис. 1а, 1б). Однако, в отличие от [3], где к свободному концу цепи приложена внешняя сила, в данной работе предполагается, что причиной вытягивания цепи является внутреннее эффективное среднее (молекулярное) поле μ, формируемое вследствие ее межмолекулярных взаимодействий со свободными концами других цепей с потенциальной энергией μVz, где z – длина вытянутого участка цепи, а V – константа взаимодействия (на единицу длины цепи), рис. 1в.
Рис. 1.
Одноцепная модель “липкой ленты” [3]. Состояния полимерной цепи, адсорбированной на плоскости (a) и почти полностью оторванной от нее (б) при малых и больших межмолекулярных взаимодействиях соответственно. Модель среднего поля [5], действующего на выделенную цепь со стороны других цепей (в)). Энергетические постоянные Ψ и V описывают соответственно взаимодействия с плоскостью и другими цепями (изображены штриховыми линиями).
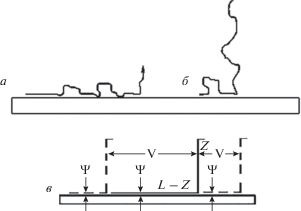
Другая часть цепи с числом мономерных звеньев L – z, адсорбированная на плоскости, имеет энергию Ψ(L – z), где L – суммарное число мономерных звеньев, образующих макромолекулу, а параметр Ψ характеризует энергию адсорбции для одного мономерного звена. Вероятность вытянутому участку цепи содержать z звеньев равна
(1)
$P{\text{(}}z{\text{)}}\sim {\text{exp[}}\mu qz + \chi {\text{(}}L - z{\text{)]}}\sim {\text{exp(}}tz{\text{)]}},$Величина μ = ❬z❭/L характеризует среднюю вытянутость цепей в направлении поля и рассчитывается с помощью распределения (1). Она является параметром порядка для данной модели, который при заданных значениях коэффициентов адсорбции χ = Ψ/kБT и молекулярного поля q = V/kБT можно определить из уравнения самосогласования [5]:
где функция(3)
$g\left( \mu \right) = {1 \mathord{\left/ {\vphantom {1 {\left[ {1--\exp \left( {--Lt\left( \mu \right)} \right)} \right]}}} \right. \kern-0em} {\left[ {1--\exp \left( {--Lt\left( \mu \right)} \right)} \right]}}--{1 \mathord{\left/ {\vphantom {1 {Lt\left( \mu \right)}}} \right. \kern-0em} {Lt\left( \mu \right)}}.$Свободная энергия цепи в среднем поле имеет вид [5]
(4)
$F = - {{k}_{{\text{Б}}}}T\ln Z - \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)\left\langle H \right\rangle {\text{,}}$(5)
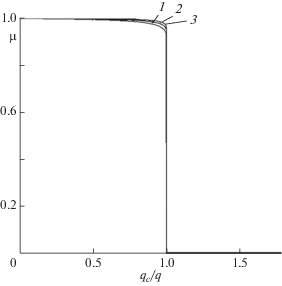
$f\left( \mu \right) = - {\text{ln}}\left\{ {{{\left[ {\mathop e\nolimits^{Lt\left( {\mu } \right)} - {\text{1}}} \right]} \mathord{\left/ {\vphantom {{\left[ {\mathop e\nolimits^{Lt\left( {\mu } \right)} - {\text{1}}} \right]} {Lt\left( \mu \right)}}} \right. \kern-0em} {Lt\left( \mu \right)}}} \right\} + {\text{(}}{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}{\text{)}}qL{{\mu }^{{\text{2}}}}{\text{,}}$Рис. 2.
Зависимости параметра порядка (степени вытянутости цепи) от перенормированного значения коэффициента молекулярного поля q = V/kБT при заданном значении коэффициента адсорбции χ = = Ψ/kБT = 0.2 (1), 0.4 (2), 0.8 (3) для полимерной цепи с заданным числом мономерных звеньев L = 800. qс – значение параметра q в критической точке.
Кинетическое уравнение для параметра порядка в этой модели выведено в приближении среднего поля на основе метода Кубо, который впервые был использован для модели Изинга [6]. Для модели, рассматриваемой в данной работе, этот метод приводит к уравнению
(6)
${{{{\tau }_{{\text{0}}}}d\mu } \mathord{\left/ {\vphantom {{{{\tau }_{{\text{0}}}}d\mu } {dt}}} \right. \kern-0em} {dt}} = - \mu + g(\mu ),$(7)
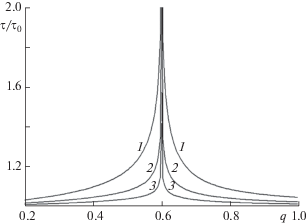
${t \mathord{\left/ {\vphantom {t {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}} = \int\limits_{\mathop {\mu }\nolimits_0 }^{\mu } {{{dx} \mathord{\left/ {\vphantom {{dx} {\left[ {g(x) - x} \right]}}} \right. \kern-0em} {\left[ {g(x) - x} \right]}}} ,$Рассчитаны зависимости времен релаксации от длины цепи и энергетических констант взаимодействия с поверхностью и межмолекулярных ориентационных взаимодействий с другими цепями (рис. 3). Для цепей с конечным числом сегментов L обнаружен эффект “критического замедления” [7, 8], заключающийся в резком увеличении времен их релаксации в критической точке (q = qс). Расчеты показали, что независимо от значения L максимальное значение τ/τ0 получается при одном и том же значении qt ≈ 0.6, как при фазовых переходах 1-го рода. Данный вывод подтверждаются результатами изучения методом броуновской динамики [8] адсорбционно-растягивающего перехода для полимерной цепи, привитой на адгезивную поверхность.
Рис. 3.
Зависимости перенормированного времени релаксации τ/τ0 от коэффициента молекулярного поля q = V/kБT для цепей с заданным числом мономерных звеньев L = 100 (1), 200 (2), 400 (3) и значении коэффициента адсорбции χ = Ψ/kБT = 0.3; μ0 = 0.5.
Таким образом, при отрывании достаточно длинной полимерной цепи, находящейся в молекулярном поле других цепей вблизи адсорбируемой поверхности, имеет место обычный фазовый переход 1-го рода, сопровождаемый резким ростом флуктуаций, наличием метастабильных состояний и скачками степени вытянутости, энергии, и теплоемкости цепей. Это отличает его от необычного перехода в обычной модели “липкой ленты” [3], имеющего черты переходов 1 и 2‑го рода одновременно. В обеих моделях возможно проследить аналитически, как по мере увеличения числа частиц (звеньев в цепи) в системе формируются скачки, характерные для фазовых переходов.
Данная динамическая модель, как и в работе [3], успешно описывает три различных режима поведения (адсорбированное, вытянутое и критическое) для цепей различной длины. Однако, в ней времена релаксации убывают с ростом длины цепей, а не возрастают, как в модели [8], что можно объяснить большой кооперативностью цепи вследствие самого приближения среднего поля.
Работа выполнена при поддержке РФФИ (проект № 19-42-350001-р_а).
Список литературы
Sanchez I.C., Fitzpatrick L.E. Physics of polymer surfaces and interfaces. Boston: Butterworth – Heinemann, 1992. P. 3.
Karim A., Kumar S. // Polymer surfaces, interfaces and thin films. Singapore: World Sci., 2000. P. 5.
Skvortsov A.M., Klushin L.I., Polotsky A.A. et al. // Phys. Rev. E. 2012. V. 85. № 5. Art. № 031803.
Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Т. 5. Ч. 1. М.: Наука, 1976. 484 с.
Максимов А.В., Максимова О.Г., Диордийчук Д.В. // Изв. РАН. Сер. физ. 2013. Т. 77. № 8. С. 1182; Maksimov A.V., Maksimova O.G., Diordiichuk D.V. // Bull. Russ. Acad. Sci. Phys. 2013. V. 77. № 8. P.1073.
Стенли Г. Фазовые переходы и критические явления. М.: Мир, 1973. 425 с.
Fleury P.A. // Science. 1981. V. 211. № 4478. P. 125.
Zhang Sh., Qi Sh., Klushin L.I. et al. // J. Chem. Phys. 2017. V. 147. Art. № 064902.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


