Известия РАН. Серия физическая, 2020, T. 84, № 9, стр. 1241-1245
Релаксационно-резонансные свойства диэлектрического отклика воды
А. А. Волков 1, А. А. Васин 1, *, А. А. Волков 2
1 Федеральное государственное бюджетное учреждение науки
Институт общей физики имени А.М. Прохорова Российской академии наук
Москва, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”
Москва, Россия
* E-mail: alexcampeones@yandex.ru
Поступила в редакцию 10.04.2020
После доработки 29.04.2020
Принята к публикации 27.05.2020
Аннотация
Широкополосные терагерцовые-инфракрасные спектры поглощения жидкой воды описаны в рамках нестандартной для воды газо-твердотельной модели Френкеля, дополненной взаимопревращением молекул и ионов, предполагающей в жидкостях смешанное трансляционно-колебательное движение молекул. Рассчитаны времена удержания молекул воды гидратной и ионной оболочками.
ВВЕДЕНИЕ
В ряду специфических свойств жидкой воды центральное место занимает диэлектрический отклик – реакция среды на зондирующее электромагнитное излучение в форме частотных спектров коэффициентов поглощения и рефракции. В силу электромагнитной природы вещества этот отклик напрямую информирует о происходящих в веществе процессах. В отношении воды информация огромна, но, несмотря на десятилетия исследований, на молекулярном уровне она в полной мере не расшифрована [1].
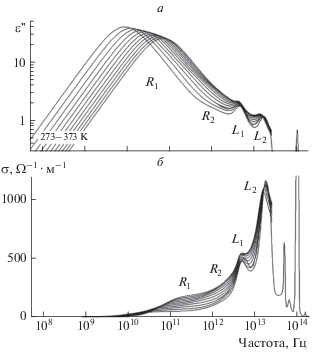
В настоящей работе мы обращаемся к спектру поглощения воды как проблемному. На рис. 1 он представлен в диапазоне частот – 109–1014 Гц (от микроволнового до оптического диапазона) в форме спектра мнимой ε"(ω) части диэлектрической проницаемости. В таком виде диэлектрические потери воды изучаются на протяжении десятилетий [2–12]. Результаты собирают в базы данных [13, 14].
Картину на рис. 1 формируют 4 полосы поглощения. На низких частотах доминирует полоса т.н. дебаевской релаксации, R1 (Relaxation-1) с максимумом на частоте νD ~ 20 ГГц при комнатной температуре. C этим поглощением cвязан нагрев воды под действием СВЧ-излучения (MW heating [15]). Эффект широко известен и используется для нагрева водосодержащих сред в бытовых и промышленных СВЧ печах [16].
Дебаевская релаксация дает большой вклад в статическую диэлектрическую проницаемость, ~90%. Высокое значение диэлектрической проницаемости (ε' ~ 80 при комнатной температуре) считается ответственным за высокую растворяющую способность воды. Предполагается, что большое ε' эффективно понижает энергию ион-ионного взаимодействия.
Со стороны высоких частот (в районе ν2 ~ 0.6 ТГц) к дебаевской релаксации прилегает слабая полоса поглощения R2 (Relaxation-2). На рис. 1 она сливается с R1 и практически не видна. Полоса R2 пользуется вниманием исследователей как неотъемлемая деталь релаксации-1 [9, 10].
Релаксационные полосы R1 и R2 продолжаются в высокочастотную область двумя пиками поглощения на частотах 5 и 18 ТГц. Оба пика – резонансные, L1 и L2 (Lorentzian-1 и Lorentzian-2), с одинаково сильным затуханием (с полушириной порядка собственной частоты пика). В спектрах они сильно перекрыты и, хотя составляют слитную пару, радикально различаются при протон-дейтронном замещении. Пик на частоте 5 ТГц к замещению не чувствителен. Пик на 18 ТГц вместе с высокочастотными ИК резонансами (на рис. 1 выше 18 ТГц они не видны) смещается вниз по частоте как корень из отношения масс протона и дейтрона (точнее, в 1.34 раза [18]).
Принято считать, что 5 ТГц пик как-то связан с трансляционными перемещениями молекул Н2О, а 18 ТГц пик – их либрациями (качаниями) [19]. Высокочастотные ИК резонансы интерпретируются как деформационные колебания индивидуальных молекул Н2О. В приведенной раскладке 5 ТГц пик разделяет в спектре поглощения внутримолекулярный и межмолекулярный отклики воды. Второй отклик малопонятен: в корне не ясно, каким образом молекулы воды, опутанные сеткой водородных связей, совершают трансляции. Считается, что для придания молекулам подвижности водородные связи с пикосекундными временами рвутся и восстанавливаются, что “молекулы непрерывно меняют своих соседей” [20]. В какой-то момент количество удерживающих связей уменьшается, и это делает молекулу способной к перемещению. Количество связей при таком подходе является важным объектом поиска. Сообщается как о достижении “мы получили среднее значение 1.74 ± 2.1% донорных и акцепторных связей на молекулу” [21]. Есть предложение рассматривать дебаевскую релаксацию как переход молекулы воды из угла в угол тетраэдра (Н2О)5 (“a translation of a water molecule from an occupied to an unoccupied corner of the cube bounding the (H2O)5 tetrahedron” [22]). Еще рассматривается механизм, при котором диэлектрическая релаксация в воде осуществляется миграцией дефектов (локальных отклонений структуры от считающегося базовым тетраэдрического вида) сквозь сетку водородных связей. В этом случае реориентация молекулы происходит, “когда она наталкивается на подходящий дефект сетки” [9]. В конечном счете, основу всех моделей составляет взаимодействие неделимых молекул Н2О с сеткой водородных связей [17].
В [23, 24] мы развили подход, в котором понятие водородной связи не используется. Он основан на идее Френкеля о газо-твердотельном устройстве жидкостей, предполагающем комбинированное диффузно-колебательное перемещение молекул [25]. Воду мы представили как плотный газ, состоящий из атомов кислорода с закрепленными на них одним, двумя или тремя протонами. Другими словами, модельную среду мы наполнили частицами трех сортов Н2О, Н3О+ и ОН–, а не одного, как принято, только молекулами Н2О. Молекулы и ионы в нашей модели совершают тепловое столкновительное движение, в результате которого обмениваются протонами и взаимопревращаются. За времена в масштабе 1–100 пикосекунд каждая молекула становится ионом, а ион – нейтральной молекулой.
Мгновенно среда представляет собой ансамбль дипольных (нейтральных Н2О) и заряженных (Н3О+ и ОН–) частиц. В результате соударений и протонного обмена положительный и отрицательный заряды хаотически (диффузно) перемещаются в объеме с собственной степенью свободы, то есть перемещаются надмолекулярно. Считаем, что биполярная диффузия зарядов осуществляется в режиме, описанном в [26], и проявляется в диэлектрических спектрах в форме дебаевской релаксации.
Диффузия зарядов происходит в условиях экранировки оболочкой из поляризованных молекул Н2О и облаком ближайших ионов противоположного знака. Предположительно, дисперсионные области R1, R2 и L1 в диэлектрических спектрах воды отражают процессы формирования гидратных оболочек и ионных облаков. Ниже мы проверим эту гипотезу путем модельной обработки диэлектрических спектров воды с применением модели, разработанной нами ранее для описания диэлектрического отклика суперионных проводников [27].
МОДЕЛЬ
Для воды как классического диэлектрика описание электродинамики традиционно проводится на языке диэлектрической проницаемости. В представлении диэлектрических потерь через ε"(ω) дебаевская релаксация R1 выражена столь ярко, что другие особенности отклика кажутся несущественными. С первых шагов ее изучения, век назад, ее связали с вращением молекулярных диполей. С годами вращательная модель усложнились, но удовлетворительного понимания динамики воды так и не дала: “the molecular interpretation of the Debye relaxation still remains vague” [22]. Проблема дебаевской релаксации в жидкой воде и в наши дни остается открытой, “puzzling” [28].
Давно известно, что за дебаевской релаксацией, могут скрываться механизмы, отличные от ориентационного [29]. В [23] релаксационный отклик воды мы интерпретировали как диффузное перемещение заряженной частицы в параболическом потенциале. В данном случае заряженной частицей создается ток, и его описание более удобно в терминах проводимости σ(ω). Язык проводимости не принят для описания свойств воды, но, на самом деле, ε- и σ-представления эквивалентны [30]. Спектр σ(ω) получается умножением ε"(ω) на частоту: σ(ω) = ωε0ε"(ω), где ε0 – диэлектрическая проницаемость вакуума. Умножение сильно упрощает работу с широкодиапазонными по частоте спектрами. Оно увеличивает вес высокочастотной, резонансной, части спектра и делает ее наблюдаемой наравне с более низкочастотной, релаксационной.
На рис. 1б диэлектрические спектры воды представлены проводимостью σ(ω). Считая, что спектры σ(ω) отражают трансляционную диффузию заряженных частиц, в [24] мы поставили полосам поглощения R1, R2 и L1 в соответствие частотный каскад диффузий D0, D1, D2 с длинами диффузии L, l, λ и характерными временами t0, t1 и t2. Физический смысл каскада определили как последовательное по мере увеличения времени наблюдения за диффузией (по мере понижения частоты) обрастание диффундирующей частицы экранирующими облаками – гидратной оболочкой и ионным окружением. В таких условиях трансляционное перемещение частиц тормозится задержками в квазилокализованных состояниях. Движение носит диффузно-колебательный характер, о котором писал Френкель [25].
Динамика этого типа смоделирована нами в приложении к суперионным проводникам в [27]. Следуя Такаги [32], мы распространили метод Онзагepa [33] на случай проводящих материалов, включив в число равновесных состояний, помимо $x = {\text{const}},$ состояние свободно движущейся частицы $\dot {x} = const$. Для проводимости такая модель дает
(1)
$\sigma (\omega ) = {{{{\omega _{P}^{2}\gamma } \mathord{\left/ {\vphantom {{\omega _{P}^{2}\gamma } {{{\varepsilon }_{0}}({{\omega }^{2}}{{\tau }_{R}}a + b)}}} \right. \kern-0em} {{{\varepsilon }_{0}}({{\omega }^{2}}{{\tau }_{R}}a + b)}}} \mathord{\left/ {\vphantom {{{{\omega _{P}^{2}\gamma } \mathord{\left/ {\vphantom {{\omega _{P}^{2}\gamma } {{{\varepsilon }_{0}}({{\omega }^{2}}{{\tau }_{R}}a + b)}}} \right. \kern-0em} {{{\varepsilon }_{0}}({{\omega }^{2}}{{\tau }_{R}}a + b)}}} {({{\omega }^{2}}{{a}^{2}} + {{b}^{2}})}}} \right. \kern-0em} {({{\omega }^{2}}{{a}^{2}} + {{b}^{2}})}},$Мы применили модель суперионной проводимости к описанию спектра поглощения воды. Формула (1) подбором параметров подгонялась к панорамному спектру проводимости, представленному на рис. 2. Подгонка проводилась в два этапа для двух полок проводимости σ0 и σ1 (отмечены штрих-пунктиром).
Рис. 2.
Динамическая проводимость воды σ(ω) в двойном логарифмическом масштабе (те же графики, что на рис. 1б (через 20 К), дополненные на низких частотах данными работы [34]). Толстая линия – расчет по формуле (1) для температуры 273 К.
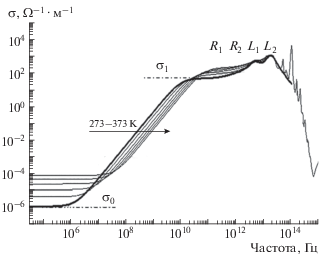
Ранее, в [24] полки σ0 и σ1 были связаны нами с молекулярной динамикой воды, зондируемой в двух режимах трансляционного перемещения иона – находящегося в гидратной оболочке (с откликом в форме σ1) и в двойной ион-гидратной оболочке (с откликом в форме σ0). При таком подходе динамику среды составляют два диффузионных процесса, в каждом из которых трансляционное перемещение иона сопровождается его задержками в локализованных состояниях – колебаниями внутри гидратной оболочки (с временем локализации τ1) и колебаниями его же гидратированного внутри ионной оболочки (с временем локализации τ0). Времена локализации τ1 и τ0 различаются на несколько порядков. Сильно различаются и определяемые ими проводимости σ1 и σ0, наблюдаемые на, соответственно, высоких (>1010 Гц) и низких частотах (<107 Гц): σ1 ≈ 80 Ом–1 ∙ м–1 и σ0 ≈ 5 ⋅ 10–6 Ом–1 ∙ м–1 [23, 24].
За отклики частиц, находящихся в локализованных состояниях с временами жизни τ1 и τ0, мы приняли полосы поглощения L1 и R1 на частотах, соответственно 5 и 0.2 ТГц. Полоса L1 выглядит как пик, переходящий на низких частотах (<1011 Гц) в полку проводимости σ1. Полоса R1 – дебаевская релаксация в форме переторможенного осциллятора с плоским максимумом σ1 (традиционно передаваемая дебаевским релаксатором с временем релаксации при комнатной температуре τD = 8.3 пс [22]). Контур R1 переходит на низких частотах (<107 Гц) в полку проводимости σ0. Полный спектр складывается из двух слагаемых вида (1) (индексы 1 и 2 для простоты не используются) передающих колебательно-диффузионные переходы L1 → σ1 и R1 → σ0. На этот спектр накладываются полосы поглощения R2 и L2, вторичные по важности, обусловленные перестройкой протонной подсистемы. Для учета полос R2 и L2 мы добавили в спектр два слабо зависящих от температуры лоренциана вида
(2)
$\sigma = {{{{\varepsilon }_{0}}\Delta \varepsilon (0)\omega _{0}^{2}{{\omega }^{2}}\gamma } \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}\Delta \varepsilon (0)\omega _{0}^{2}{{\omega }^{2}}\gamma } {\left[ {{{{\left( {{{\omega }_{0}}^{2} - {{\omega }^{2}}} \right)}}^{2}} + {{\omega }^{2}}{{\gamma }^{2}}} \right]}}} \right. \kern-0em} {\left[ {{{{\left( {{{\omega }_{0}}^{2} - {{\omega }^{2}}} \right)}}^{2}} + {{\omega }^{2}}{{\gamma }^{2}}} \right]}}$с одинаковыми диэлектрическими вкладами Δε(0)R2,L2 = 1 ± 0.3, частотами νR2 = 2.5 ± 0.5 и νL2 = = 18 ± 1 ТГц и затуханиями γR2 = 7 ± 1 и γL2 = 15 ± ± 1 ТГц (частоты и затухания в формуле (2) умножаются на 2π).
Расчетный график для температуры 273 K (толстая линия на рис. 2) с графической точностью передает экспериментальный спектр. Подгоночные параметры модели для крайних температур 273 и 373 К приведены в табл. 1.
Таблица 1.
Параметры динамики ионов, окруженных гидратной и гидратной + ионной оболочками, согласно модели (1). Время τD = ${\gamma \mathord{\left/ {\vphantom {\gamma {\omega _{0}^{{\text{2}}}}}} \right. \kern-0em} {\omega _{0}^{{\text{2}}}}}$ – характерное время переторможенного осциллятора, близкое по смыслу времени дебаевской релаксации при общепринятом описании [2–12]
| Гидратная оболочка | T, K | 273 | 373 | Гидратная + ионная оболочки |
T, K | 273 | 373 |
| ω0, ТГц | 33 | 35 | ω0, ТГц | 1.3 | 2.0 | ||
| γ, ТГц | 31 | 55 | γ, ТГц | 30 | 31 | ||
| τR, пс | 0.29 | 0.06 | τR, пс | 6.4 · 108 | 6.2 · 106 | ||
| σ1, Ω–1 · м–1 | 44 | 200 | τD, пс | 17.5 | 8.0 |
ОБСУЖДЕНИЕ
1. Первостепенно важным считаем сам факт воспроизведения моделью сложной дисперсионной картины. Количественное согласие расчетных кривых с экспериментальными спектрами из базы данных подтверждает предположение о совершении молекулами воды одновременно колебательного и трансляционного движении. По причине смешанного характера движения временные параметры модели ω0 τR и γ трудно сопоставимы с аналогичными по написанию литературными параметрами, полученными исключительно в рамках аддитивных моделей (с использованием аддитивного описания полос поглощения R1, R2, L1 и L2 с независимыми параметрами [2–12]).
Обычно спектральный анализ полос R1 и R2 проводится в представлении их куполообразным спектром ε"(ω) с единственным временным параметром – временем релаксации τ (рис. 1а). Частоте ω ~ 1/τ соответствует максимум ε". Выше максимума по частоте представление диэлектрических спектров функцией ε"(ω) в дебаевской форме, когда ε"(ω) ~ 1/ω, не корректно: интеграл проводимости σ(ω) = ωε0ε"(ω) = const по частоте расходится, что не отвечает соотношениям Крамерса–Кронига [30]. В нашей модели этот недостаток исключен заменой релаксационной формы описания полос R1, R2 на осцилляторную. Полосы R1, R2 передаются переторможенными лоренцианами с временными параметрами ω0 и γ, тесно связанными с новой для воды временной характеристикой τR.
2. Переход к проводимости подразумевает трансляционное перемещение зарядов. Появляются фундаментально новые для воды вопросы относительно происхождения зарядов, их концентрации, подвижности и времени жизни.
Из сравнения графиков на рис. 1а, 1б видно, как радикально изменяется форма спектра при переходе к новому представлению. Мощная релаксационная полоса на рис. 1а, накрывающая два слабых пика, на рис. 1б становится постаментом этих пиков, многократно увеличенных по интенсивности. Перекрытие контуров свидетельствует о сильном взаимодействия механизмов дебаевской релаксации и пиков ИК поглощения. Первая отражает трансляционное перемещение частиц, а вторые – локализованные осцилляции. Задачей моделирования – разделение контуров и нахождение времен пребывания молекул в трансляционном диффузном и локализованном колебательном состояниях.
3. При сильном затухании γ > 2ω0 выражение (1) сводится к разности двух друдевских релаксаторов. Принципиальное значение имеет сама возможность аналитически выразить проводимость σ(ω) (а не ε"(ω), как принято, в релаксационной форме. Это свидетельствует о присутствии в динамике проводящей системы эффектов экранирования. На микроскопическом уровне экранирование соответствует тому, что в системе подвижных кулоновски взаимодействующих частиц перемещение выделенной частицы с необходимостью сопровождается обратным по направлению током других частиц того же знака, стремящихся восстановить нарушенную зарядовую плотность. Динамические свойства такой системы определяются не только зарядом и инерцией одной частицы, как в друдевском случае, но и свойствами экранирующего облака.
4. В литературе уже отмечалась особая разделительная роль частоты ~1000 см−1 (3 ⋅ 1013 Гц) [35]. Из рис. 2 видно, что, действительно, моды R1, R2, L1 и L2, лежащие ниже 3 ⋅ 1013 Гц, всецело определяют контур спектра поглощения воды. Узкие ИК резонансы, расположенные на спадающем правом краю спектра поглощения, лишь придают контуру изрезанность. С позиций газо-твердотельной модели интенсивный полярный ИК спектр воды представляет собой фононный спектр протон-кислородной решетки. ИК спектры воды и льда практически одинаковы [36] и подобны спектрам ионного кристалла [37].
ЗАКЛЮЧЕНИЕ
Показана возможность полноценного описания диэлектрического отклика воды с позиций газо-твердотельной модели Френкеля в противовес принятой модели переориентации диполей в сетке водородных связей. Методом подгонки параметров модели под эксперимент найдены времена локализации молекул воды в гидратной и ионной оболочках. Полученные параметры могут составить базу для дальнейших теоретических разработок.
Работа выполнена при частичной поддержке РФФИ (проект № 19-02-00446-а).
Список литературы
Guillot B., Guissani Y. // J. Chem. Phys. 2001. V. 114. № 15. P. 6720.
Hasted J.B. // In Water: a comprehensive treatise. V. 1. Ed. Franks F. N.Y.: Plenum Press, 1972. P. 255.
von Hippel A. // IEEE Trans. Electr. Insul. 1988. V. 23. P. 801.
Kaatze U. // J. Chem. Eng. Data. 1989. V. 34. P. 371.
Fukasawa T., Sato T., Watanabe J. et al. // Phys. Rev. Lett. 2005. V. 95. Art. № 197802.
Yada H., Nagai M., Tanaka K. // Chem. Phys. Lett. 2009. V. 473. P. 279.
Møller U., Cooke D.G., Tanaka K. et al. // J. Opt. Soc. Am. B. 2009. V. 26. № 9. P. A113.
Sega M., Schroder C. // J. Phys. Chem. A. 2015. V. 119. P. 1539.
Popov I., Ben Ishai P., Khamzin A. et al. // Phys. Chem. Chem. Phys. 2016. V. 18. № 20. Art. № 13941.
Hansen J.S., Kisliuk A., Sokolov A.P., Gainaru C. // Phys. Rev. Lett. 2016. V. 116. Art. № 237601.
Arbe A., de Molina P.M., Alvarez F. et al. // Phys. Rev. Lett. 2016. V. 117. Art. № 185501.
Lunkenheimer P., Emmert S., Gulich R. et al. // Phys. Rev. E. 2017. V. 96. Art. № 062607.
Ellison W.J. // J. Phys. Chem. 2007. V. 36. P. 1.
Querry M.R., Wieliczka D.M., Segelstein D.J. // Handbook of optical constants of solids. Ed. Palik E.D. N.Y.: Acad. Press, 1991. P. 1059.
Huang W., Richert R. // J. Phys. Chem. B. 2008. V. 112. Art. № 9909.
Gabriel C., Gabriel S., Grant E.H. et al. // Chem. Soc. Rev. 1998. V. 27. P. 213.
Brini E., Fennell C.J., Fernandez-Serra M. et al. // Chem. Rev. 2017. V. 117. Art. № 12385.
Max J-J., Chapados C. // J. Chem. Phys. 2011. V. 134. Art. № 164502.
Sharma M., Resta R., Car R. // Phys. Rev. Lett. 2005. V. 95. Art. № 187401.
Маленков Г.Г. // ЖСХ. 2006. Т. 47. С. S5.
Niskanen J., Fondella M., Sahlec C.J. // PNAS. 2019. V. 116. № 10. P. 4058.
Agmon N. // J. Phys. Chem. 1996. V. 100. P. 1072.
Volkov A.A., Artemov V.G., Pronin A.V. // Eur. Phys. Lett. 2014. V. 106. Art. № 46004.
Volkov A.A., Artemov V.G., Volkov A.A. Jr., Sysoev N.N. // J. Mol. Liq. 2017. V. 248. P. 564.
Френкель Я.И. Кинетическая теория жидкостей. Л.: Наука. 1975. 592 с.
Stepisnik J., Mohoric A., Sersa I. // arXiv: 1010.1175v1. 2010.
Волков А.А., Козлов Г.В. Лебедев С.П., Ракитин А.С. // ФТТ. 1990. Т. 32. № 2. С. 329.
Hansen J.S., Kisliuk A., Sokolov A.P., Gainaru C. // Phys. Rev. Lett. 2016. V. 116. Art. № 237601.
Поуел Р., Эйринг Г. // УФН. 1945. Т. 27. № 2. С. 265.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 8. Электродинамика сплошных сред. М.: Наука, 1992. 661 с.
Саламон М.Б. Физика суперионных проводников. Рига: Зинатне, 1982. 315 с.
Takagi Y. // J. Phys. Soc. Jap. 1979. V. 47. № 2. P. 567.
Onsager L. // Phys. Rev. 1931. V. 37. № 4. P. 405.
Light T.S., Licht S., Bevilacqua A.C., Morash K.R. // Electrochem. Solid-State Lett. 2005. V. 8. P. E16.
Heyden M., Sun J., Funkner S., Mathias G. et al. // PNAS 2010. V. 107. № 27. Art. № 12068.
Marechal Y. // J. Mol. Struct. 2011. V. 1004. P. 146.
Peng Z., Yang L., Hui Y. et al. // Chin. Phys. B. 2014. V. 23. № 2. Art. № 026103.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая