1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 2, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 2, стр. 265-269

Перемежаемость вблизи границы обобщенной синхронизации в системах со сложной топологией аттрактора

В. А. Ханадеев 1, 2, *, О. И. Москаленко 1, 2, А. А. Короновский 1, 2

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского”
Саратов, Россия

2 Региональный научно-образовательный математический центр “Математика технологий будущего”
Саратов, Россия

* E-mail: v.a.hanadeev@gmail.com

Поступила в редакцию 28.08.2020
После доработки 25.09.2020
Принята к публикации 28.10.2020

Полный текст (PDF)

Аннотация

Исследованы характеристики перемежающегося поведения, имеющего место на границе обобщенной синхронизации в однонаправленно диссипативно связанных системах со сложной топологией аттрактора. На примере систем Лоренца и генераторов Чуа установлено, что и распределения длительностей ламинарных фаз, и зависимости средних длительностей ламинарных фаз от параметра надкритичности в данном случае подчиняются экспоненциальным законам.

ВВЕДЕНИЕ

Явление перемежаемости, возникающее при переходе от одного типа поведения к другому, хорошо известно в настоящее время [1]. Говоря о перемежаемости, подразумевают чередование регулярного (периодического или стационарного) и нерегулярного (хаотического) поведения или чередование различных хаотических режимов. Перемежаемость присутствует в разных динамических системах, в том числе физических, медицинских и биологических [1]. Она наблюдается также вблизи границ синхронных режимов, в связи с чем различают перемежающиеся полную синхронизацию, фазовую синхронизацию, обобщенную синхронизацию, синхронизацию с запаздыванием и синхронизацию, индуцированную шумом [2–6].

Одним из наиболее интересных типов перемежающегося синхронного поведения является режим перемежающейся обобщенной синхронизации [5]. Он наблюдается вблизи границы обобщенной синхронизации хаотических систем, связанных однонаправленно или взаимно [7], и подразумевает наличие функциональной связи (функционала) между состояниями этих систем только в определенные интервалы времени, называемые ламинарными фазами поведения, в то время как на фоне ламинарных фаз имеют место кратковременные турбулентные всплески, в течение которых функциональная связь между взаимодействующими системами не наблюдается.

Режим перемежающейся обобщенной синхронизации в настоящее время изучен достаточно хорошо, но только для ограниченного класса динамических систем. В частности, известно, что на границе этого режима в однонаправленно связанных системах с достаточно простой топологией аттрактора, как, например, у систем Ресслера, наблюдается перемежаемость типа “on-off”, характеризующаяся степенными распределениями длительностей ламинарных фаз и зависимостей средних длительностей ламинарных фаз от параметра надкритичности [5]. Однако, наряду с “простыми” системами достаточно широко распространены системы с так называемой сложной (двулистной) структурой аттрактора. Фазовое пространство таких систем состоит из двух различных подпространств W1, 2, имеющих малую общую область W0, внутри которой фазовые траектории могут переходить из подпространства W1 в подпространство W2 и наоборот. Так как каждое из подпространств визуально выглядит как гладкий лист (см. рис. 1), в данной работе будем называть эти осцилляторы системами с двулистной структурой аттрактора, а каждое из подпространств W1, 2 – листом. В том случае, если исследуемая система (в силу тех или иных причин) характеризуется только наблюдаемыми временными рядами (а оператор эволюции неизвестен), следует говорить о восстановленном фазовом пространстве с помощью метода Таккенса. К системам с двулистной структурой аттрактора относятся, например, такие классические модели как осцилляторы Лоренца, широко известные в метеорологии, или радиотехнические генераторы Чуа [8]. При определенном выборе значений управляющих параметров фазовые траектории таких систем как будто переходят с одного листа хаотического аттрактора на другой, фактически описывая двойную петлю на фазовой плоскости. Понятно, что специфика таких систем может привести к изменению механизмов возникновения синхронных режимов, в частности, обобщенной синхронизации, по сравнению со случаем систем с достаточно простой топологией аттрактора, а отличия в этих механизмах, в свою очередь, могут привести к отличиям в поведении систем вблизи границ соответствующих режимов. Иными словами, тип перемежаемости, наблюдаемый вблизи границы обобщенной синхронизации в системах с достаточно сложной топологией аттрактора, может отличаться от известных в настоящее время типов перемежаемости.

Рис. 1.

Фазовые портреты систем со сложной топологией аттрактора: система Лоренца (а), генератор Чуа (б).

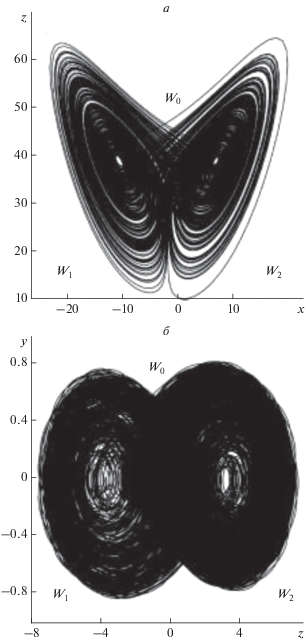
В настоящей работе проводится анализ характеристик перемежающегося поведения, наблюдаемого на границе обобщенной синхронизации в диссипативно связанных системах со сложной топологией аттрактора. В качестве объектов исследования выбраны однонаправленно связанные системы Лоренца и генераторы Чуа, находящие в хаотическом режиме с аттракторами типа двойной спирали. Как будет показано ниже, в обоих случаях распределения длительностей ламинарных фаз и зависимости средних длительностей ламинарных фаз от параметра связи таких систем подчиняются экспоненциальным законам, что не характерно для систем с достаточно простой топологией аттрактора.

ИССЛЕДУЕМЫЕ СИСТЕМЫ

Однонаправленно связанные системы Лоренца [9] описываются следующей системой обыкновенных дифференциальных уравнений:

(1)
$\begin{gathered} {{{\dot {x}}}_{1}} = {\sigma }\left( {{{y}_{1}} - {{x}_{1}}} \right),\,\,\,\,{{{\dot {y}}}_{1}} = {{r}_{1}}{{x}_{1}} - {{y}_{1}} - {{x}_{1}}{{z}_{1}}, \\ {{{\dot {z}}}_{1}} = - b{{z}_{1}} + {{x}_{1}}{{y}_{1}},\,\,\,\,{{{\dot {x}}}_{2}} = {\sigma }\left( {{{y}_{2}} - {{x}_{2}}} \right) + {\varepsilon }\left( {{{x}_{1}} - {{x}_{2}}} \right), \\ {{{\dot {y}}}_{2}} = {{r}_{2}}{{x}_{2}} - {{y}_{2}} - {{x}_{2}}{{z}_{2}},\,\,\,\,{{{\dot {z}}}_{2}} = - b{{z}_{2}} + {{x}_{2}}{{y}_{2}}, \\ \end{gathered} $
где ${{\vec {x}}_{{12}}}$ = (x1, 2, y1, 2, z1, 2) – векторы состояний взаимодействующих ведущей и ведомой систем, соответственно, σ = 10, b = 2, r1 = 40 и r2 = 35 – управляющие параметры, ε – параметр связи.

Уравнения для однонаправленно связанных генераторов Чуа записываются в виде [10]:

(2)
$\begin{gathered} {{{\dot {x}}}_{1}} = {{{\alpha }}_{1}}\left( {{{y}_{1}} - {{x}_{1}}^{3} - {\text{с}}{{x}_{1}}} \right),\,\,\,\,{{{\dot {y}}}_{1}} = {{x}_{1}} - {{y}_{1}} + {{z}_{1}}, \\ {{{\dot {z}}}_{1}} = - {\beta }{{y}_{1}},\,\,\,\,{{{\dot {x}}}_{2}} = {{{\alpha }}_{2}}\left( {{{y}_{2}} - {{x}_{2}}^{3} - с{{x}_{2}}} \right), \\ {{{\dot {y}}}_{2}} = {{x}_{2}} - {{y}_{2}} + {{z}_{2}} + {\varepsilon }\left( {{{y}_{1}} - {{y}_{2}}} \right),\,\,\,\,{{{\dot {z}}}_{2}} = - {\beta }{{y}_{2}}, \\ \end{gathered} $
где ${{\vec {x}}_{{12}}}$ = (x1,2, y1,2, z1,2) – векторы состояний взаимодействующих однонаправленно связанных генераторов, ${{{\alpha }}_{1}}$ = 10, ${{{\alpha }}_{2}}$ = 10.1, ${\beta }$ = 16 и с = –0.143 – управляющие параметры, ε – параметр связи. Система (2) является моделью реальной радиотехнической схемы, автономная динамика которой подробно исследована в [10].

Следует отметить, что при выбранных значениях управляющих параметров в обеих системах наблюдаются хаотические аттракторы со сходной двулистной структурой, что позволяет применять одинаковые методы и подходы для анализа поведения в таких системах.

МЕТОДЫ ИССЛЕДОВАНИЯ

Для определения наличия обобщенной синхронизации в исследуемых системах и анализа характеристик перемежающегося поведения, имеющего место вблизи ее границы, использовался метод вспомогательной системы [11], являющийся одним из классических подходов к анализу обобщенной синхронизации в системах с однонаправленной связью. Суть этого метода сводится к введению в рассмотрение дополнительной, так называемой, вспомогательной системы, идентичной ведомой системе по управляющим параметрам, но стартующей с других начальных условий, и сравнению состояний этих систем с течением времени. Если после завершения переходного процесса состояния ведомой и вспомогательной систем полностью совпадают, в исходной паре ведущей и ведомой систем наблюдается режим обобщенной синхронизации. Если же состояния этих систем всегда различны, режим обобщенной синхронизации отсутствует.

Промежуточным является режим перемежающейся обобщенной синхронизации [5], при котором режим обобщенной синхронизации наблюдается не всегда: при фиксированных значениях управляющих параметров во временных реализациях взаимодействующих систем происходит чередование участков с синхронной (ламинарные фазы) и асинхронной (турбулентные фазы) в смысле обобщенной синхронизации динамикой. Для определения типа перемежаемости, реализующегося в системе, необходимо проанализировать сигнал, представляющий собой временную зависимость разности состояний ведомой и вспомогательной систем, и рассчитать статистические характеристики длительностей ламинарных фаз – распределения длительностей ламинарных фаз и зависимости средних длительностей ламинарных фаз от параметра связи. При этом, под ламинарными фазами поведения понимаются временные интервалы, в течение которых модуль разности состояний ведомой и вспомогательной систем оказывается меньше некоторой наперед заданной константы Δ, величина которой мала по сравнению с амплитудой собственных колебаний в системе.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ

Применим метод вспомогательной системы для определения статистических характеристик перемежаемости в однонаправленно связанных системах Лоренца (1) и генераторах Чуа (2). Тип связи в обеих системах является диссипативным, что типично для режима обобщенной синхронизации.

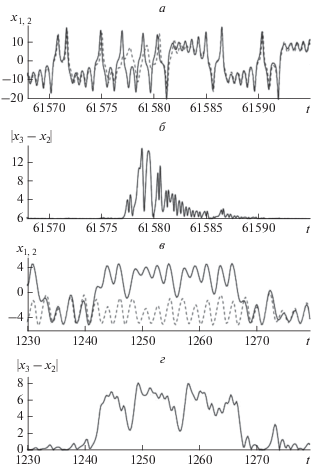
Рисунок 2 иллюстрирует фрагменты временных реализаций взаимодействующих систем Лоренца при ε = 9.6 и генераторов Чуа при ε = 1.5, соответствующих ламинарным и турбулентным фазам поведения, а также зависимости модуля разности состояний ведомой и вспомогательной систем в эти моменты времени. Из рисунков видно, что в обоих случаях в течение ламинарных фаз поведения состояния ведущей и ведомой систем оказываются близкими друг к другу, в то время как перед наступлением турбулентной фазы состояния этих систем расходятся на разные листы аттракторов, вновь сближаясь по окончании турбулентной фазы. Такая ситуация наблюдается и в системах Лоренца, и генераторах Чуа, что говорит о типичности такого поведения в системах со сложной топологией аттрактора с однонаправленным диссипативным типом связи, находящихся в режиме перемежающейся обобщенной синхронизации.

Рис. 2.

Фрагменты временных реализаций взаимодействующих систем Лоренца при ε = 9.6 (а) и Чуа (2) при ε = 1.5 (в), находящихся в режиме перемежающейся обобщенной синхронизации, и соответствующие им временные зависимости модуля разности состояний ведомой x2 и вспомогательной x3 систем Лоренца (б) и Чуа (г), соответственно.

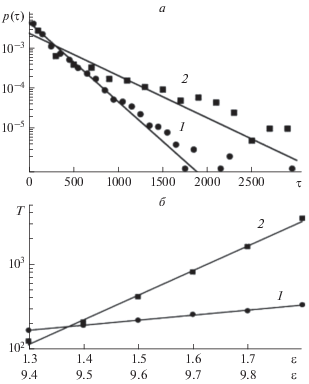
На рис. 3 представлены статистические характеристики длительностей ламинарных фаз для систем (1) и (2), находящихся в режиме перемежаемости. Рисунок 3а соответствует распределениям длительностей ламинарных фаз, рассчитанным для обеих систем при тех же значениях параметра связи, что и на рис. 2, а рис. 3б соответствует зависимостям средних длительностей ламинарных фаз для этих систем от параметра связи. На рисунках представлены численно полученные данные и их аппроксимации. Из рисунков видно, что для обеих рассмотренных систем и распределения длительностей ламинарных фаз p(τ), и зависимости средних длительностей ламинарных фаз T от параметра связи подчиняются экспоненциальным законам

$p\left( {\tau } \right) = \frac{1}{T}\exp \left( { - \frac{\tau }{T}} \right),$
Рис. 3.

Распределения длительностей ламинарных фаз при ε = 9.6 [при ε = 1.5] (а) и зависимости средних длительностей ламинарных фаз от параметра связи ε (б) для однонаправленно связанных систем Лоренца (1) – кружки (генераторов Чуа (2) – квадраты), находящихся в режиме перемежающейся обобщенной синхронизации, и их теоретические аппроксимации экспоненциальными законами (3) и (4). Параметры аппроксимации выбраны следующими: Т = 218.6, K = = 0.0005, α = 1.36 (Т = 410.4, K = 0.02, α = 6.64). Среднеквадратичные отклонения численно полученных данных от теоретических закономерностей (3) и (4) составляют σ = 0.0001 (σ = 0.0003) для рис. 1а, σm = = 0.0002 (σm = 0.0005) – для рис. 1б.

и

(4)
$T = K{\text{exp}}\left( {{\alpha \varepsilon }} \right),$

соответственно, где K и α – некоторые положительные константы (их значения указаны в подрисуночной подписи к рис. 3), что характерно также для взаимно связанных систем со сложной топологией аттрактора, находящихся вблизи границы обобщенной синхронизации [12].

ЗАКЛЮЧЕНИЕ

Таким образом, на примере двух однонаправленно диссипативно связанных систем Лоренца и радиотехнических генераторов Чуа проведено исследование характеристик перемежающегося поведения, имеющего место на границе обобщенной синхронизации в системах со сложной топологией аттрактора. Установлено, что тип перемежаемости, возникающий в данном случае, существенно отличается от перемежаемости типа “on–off”, имеющей место в системах с достаточно простой топологией аттрактора. Показано, что распределения длительностей ламинарных фаз и зависимости средних длительностей ламинарных фаз от параметра связи подчиняются экспоненциальным законам, что характерно также для аналогичных систем с взаимной связью, находящихся вблизи границы обобщенной синхронизации.

На основании проведенного рассмотрения можно утверждать, что тип перемежаемости, реализующейся вблизи границы обобщенной синхронизации, не зависит от типа связи между системами (однонаправленная или взаимная), а определяется, в первую очередь, топологией аттракторов взаимодействующих систем (простая она или сложная).

Работа выполнена при финансовой поддержке Совета по грантам Президента Российской Федерации для государственной поддержки молодых российских ученых – докторов наук (проект № МД-21.2020.2).

Список литературы

  1. Berge P., Pomeau Y., Vidal C. Order within chaos. New York: John Wiley and Sons, 1984.

  2. Ott E., Sommerer J.C. // Phys. Lett. A. 1994. V. 188. P. 39.

  3. Pikovsky A.S., Osipov G.V., Rosenblum M.G. et al. // Phys. Rev. Lett. 1997. V. 79 P. 47.

  4. Boccaletti S., Valladares D. // Phys. Rev. E. 2000. V. 62. P. 7497.

  5. Hramov A.E., Koronovskii A.A. // Europhys. Lett. 2005. V. 70. No 2. P. 169.

  6. Hramov A.E., Koronovskii A.A., Kurovskaya M.K. et al. // Phys. Rev. Lett. 2006. V. 97. Art. No 114101.

  7. Rulkov N.F., Sushchik M.M., Tsimring L.S. et al. // Phys. Rev. E. 1995. V. 51. P. 980.

  8. Кузнецов С.П. Динамический хаос. Москва: Физматлит. 2006. 356 с.

  9. Zheng Z., Wang X., Cross M.C. // Phys. Rev. E. 2002. V. 65. Art. No 056211.

  10. Huang A., Pivka L., Wu C.W. // Int. J. Bifurcat. Chaos. 1996. V. 6. P. 2175.

  11. Abarbanel H.D.I., Rulkov N.F., Sushchik M. // Phys. Rev. E. 1996. V. 53. P. 4528

  12. Москаленко О.И., Короновский А.А., Ханадеев В.А. // ЖТФ. 2019. Т. 89. С. 338.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал