1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 7, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 7, стр. 1017-1024

Напряженно-деформированное состояние трубы из гетерофазного сплава под действием внутреннего давления в неоднородном температурном поле

О. В. Матвиенко 1, 2, *, О. И. Данейко 1, Т. А. Ковалевская 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Томский государственный архитектурно-строительный университет”
Томск, Россия

2 Федеральное государственное автономное образовательное учреждение высшего образования “Национальный исследовательский Томский государственный университет”
Томск, Россия

* E-mail: matvolegv@mail.ru

Поступила в редакцию 25.01.2021
После доработки 25.02.2021
Принята к публикации 29.03.2021

Полный текст (PDF)

Аннотация

Исследовано влияние распределения температуры на напряженно-деформированное состояние нагруженной внутренним давлением трубы из дисперсно-упрочненного алюминия. Напряженное состояние обогреваемой трубы характеризуется наибольшими значениями тангенциального и осевого напряжений на внутренней стенке, а охлаждаемой – на внешней. Абсолютные значения радиальных напряжений монотонно уменьшаются по мере удаления от внутренней стенки трубы.

ВВЕДЕНИЕ

В настоящее время перед материаловедческими науками стоит задача создания новых материалов, обладающих не только повышенными прочностными и эксплуатационными характеристиками, но и обеспечивающих повышенную энергоэффективность и пониженную экологическую нагрузку на окружающую среду [1]. Одним из перспективных направлений в материаловедении в настоящее время является создание дисперсно-упрочненных сплавов и использование этих материалов в машиностроении, энергетике, авиационной и космической промышленности [2, 3].

В современной энергетике в качестве элементов теплообменных аппаратов широко применяются трубы, нагруженные внутренним и внешним давлением. Для определения надежности работы теплообменных аппаратов необходима информация о напряжениях и деформациях, возникающих в стенках теплообменных труб в результате приложенной нагрузки, а также в условиях неоднородного распределения температуры по толщине стенки трубы [4, 5].

Настоящая работа продолжает исследования воздействия поля давления на деформацию стенок трубы из сплава на основе алюминия, упрочненного некогерентными недеформируемыми наночастицами [6–8]. Целью работы является определение напряженно-деформированного состояния стенок трубы с учетом неоднородного распределения температуры.

Для определения напряжений в стенках трубы используется подход, подробно изложенный в работах [9–11]. В рамках этого подхода напряжения в стенках трубы находятся в результате решения уравнений механики деформируемого твердого тела [12, 13] с использованием условия упрочнения материала, выражающее связь между предельным напряжением сдвига и степенью деформации, которое получено на основе физической теории пластичности [14–17].

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДЕФОРМАЦИОННОГО УПРОЧНЕНИЯ

В основе модели пластической деформации дисперсно-упрочненных материалов с ГЦК-матрицей, содержащих некогерентную дисперсную фазу [18, 19], лежит концепция упрочнения и отдыха. В дисперсно-упрочнeнных материалах дефектная структура зоны сдвига сложнее, чем в чистых металлах и однофазных сплавах. Взаимодействие дислокаций с частицами в процессе пластической деформации помимо упрочняющего эффекта приводит к появлению ряда новых элементов дислокационной структуры [20–23]. Вместе с генерацией сдвигообразующих дислокаций в этом случае развиваются элементарные процессы, обусловленные взаимодействием дислокаций с частицами и порождающие кольца Орована [24–26], призматические петли [27–29], петли вторичного скольжения, дипольные конфигурации [30]. Между структурными элементами в ходе деформации и последующих релаксационных процессов возможны взаимные превращения. При этом характер и результат взаимодействий элементов дислокационной структуры с частицами может меняться с изменением соотношений масштабных характеристик упрочняющей фазы (размера частиц, расстояния между частицами) и расстояния между дислокациями [31]. Таким образом, при моделировании процесса пластической деформации и деформационного упрочнения предполагается, что в зоне сдвига образуются следующие типы деформационных дефектов: линейные – сдвигообразующие дислокации, призматические петли вакансионного и межузельного типа, дислокационные диполи вакансионного и межузельного типа, точечные деформационные дефекты – межузельные атомы, вакансии, бивакансии [14, 15].

Математическая модель включает уравнения баланса деформационных дефектов, в которых учтены следующие процессы: генерация и аннигиляция матричных сдвигообразующих дислокаций, генерация и аннигиляция призматических петель вакансионного и межузельного типа, а также генерация и аннигиляция дислокаций в дипольных конфигурациях [16]. Генерация и аннигиляция призматических петель происходит вблизи некогерентных упрочняющих частиц. В модели учтено, что при возрастании размера призматических петель в результате осаждения точечных дефектов соответствующего типа (например, в результате осаждения межузельных атомов на межузельные призматические петли) дислокации в призматических петлях могут терять устойчивость и переходить в разряд сдвигообразующих дислокаций. Учтено также, что при осаждении межузельных атомов на вакансионные призматические петли или вакансий и бивакансий на межузельные призматические петли размер призматических петель уменьшается вплоть до полной их аннигиляции.

МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛА

Результаты экспериментальных исследований показывают, что упрочнение алюминиевых сплавов дисперсными частицами практически не влияет на величину модуля упругости и модуля сдвига [32, 33]. Однако упругие свойства сплава изменяются в зависимости температуры. Для описания температурной зависимости модуля сдвига можно использовать формулу Белла [34, 35]:

(1)
$G = \left\{ {\begin{array}{*{20}{l}} {{{G}_{0}}}&{{\text{при}}}&{T < 0.06{{T}_{m}}} \\ {{{{\text{G}}}_{{\text{1}}}}\left( {1 - \frac{T}{{2{{T}_{m}}}}} \right)}&{{\text{при}}}&{0.06{{T}_{m}} < T < 0.57{{T}_{m}}.} \end{array}} \right.$

В (1) ${{T}_{m}} = 933$ К – температура плавления, ${{G}_{0}} = 35.017$ ГПа, ${{G}_{1}} = 36.1$ ГПа – параметры, характеризующие упругие свойства алюминия.

Для определения предела текучести использовалась физико-математическая модель пластической деформации дисперсно-упрочненных сплавов с некогерентными частицами.

Результаты математического моделирования, полученные на основе решения системы уравнений, описывающей эволюцию дефектной структуры [14, 16], показывают, что деформационное упрочнение материалов на основе алюминия с некогерентной упрочняющей фазой при одной и той же объемной доле увеличивается с уменьшением размера частиц и расстояния между ними при всех температурах деформации. Исследование влияния масштабных характеристик упрочняющей фазы на деформационное упрочнение материалов на основе алюминия с некогерентной упрочняющей фазой показало, что дислокационные диполи не образуются на протяжении всего процесса пластической деформации в материале с наноразмерными частицами.

На рис. 1 представлены зависимости интенсивности сдвиговых напряжений $\tau $ от степени пластической деформации ${{a}_{{pl}}} = a - {{{{\tau }_{0}}} \mathord{\left/ {\vphantom {{{{\tau }_{0}}} G}} \right. \kern-0em} G}$ материалов на основе алюминия с некогерентной упрочняющей фазой. Эти зависимости рассчитаны для различных значений масштабных характеристик упрочняющей фазы, а также различных температур материала.

Рис. 1.

Кривые упрочнения для сплава на основе алюминия при различных температурах: $T = 293$ К (кривые 1, 4), $T = 393$ К (кривые 2, 5), $T = 493$К (кривые 3, 6). Расстояние между частицами ${{\Lambda }_{p}} = 100$ нм, диаметр частиц $\delta = 10$ нм (кривые 1–3); ${{\Lambda }_{p}} = 200$ нм, $\delta = 20$ нм (кривые 4–6).

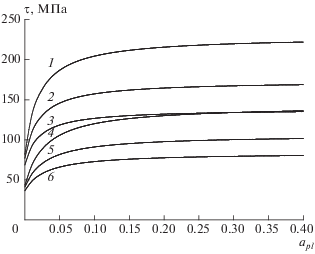
Пластическая деформация начинается, когда интенсивность напряжений в материале становится равной предельному напряжению сдвига ${{\tau }_{0}}.$ Кривые упрочнения характеризуются монотонной зависимостью предельного напряжения сдвига от степени деформации. При малых значениях степени пластической деформации ${{a}_{{pl}}}$ наблюдается заметное увеличение $\tau .$

Рассмотрение кривой упрочнения показывает, что в процессе пластического деформирования материал упрочняется, поскольку повышается предел пластичности. При больших пластических деформациях ${{a}_{{pl}}}$ кривая упрочнения выходит на горизонтальную асимптоту, соответствующую площадке текучести при $\tau = {{\tau }_{\infty }}.$

Результаты моделирования показывают, что упрочнение материала наночастицами существенно изменяет прочностные характеристики материала. Уменьшение расстояния между частицами для одной и той же объемной доли упрочняющей фазы приводит к более интенсивному торможению дислокаций, что вызывает упрочнение материала, приводящее к росту значений напряжения течения $\tau .$ С ростом температуры материал становится более пластичным, что сопровождается понижением напряжения течения материала:

(2)
${{\tau }_{s}} = {{\tau }_{0}} + {{\tau }_{1}}\frac{{a - {{{{\tau }_{0}}} \mathord{\left/ {\vphantom {{{{\tau }_{0}}} G}} \right. \kern-0em} G}}}{{{{a}_{*}} + a}}.$

В корреляции (2) $G$ – модуль сдвига матрицы, ${{\tau }_{0}}$ – предел текучести, ${{\tau }_{1}} = {{\tau }_{\infty }} - {{\tau }_{0}}$ – напряжение упрочнения, характеризующее максимальное увеличение напряжения течения в процессе упрочнения материала, $a$ – деформация, ${{a}_{*}}$ – эмпирический параметр, определяющий быстроту выхода кривой течения на асимптоту.

Результаты моделирования показывают, что с ростом температуры происходит уменьшение предела текучести и напряжения упрочнения. Это означает, что с ростом температуры пластическая деформация возникает при меньших напряжениях. Кроме того, уменьшение с ростом температуры ${{\tau }_{1}}$ свидетельствует об ослаблении способности материала к пластическому упрочнению. В рассматриваемом диапазоне изменения температуры зависимости ${{\tau }_{0}}$ и ${{\tau }_{1}}$ могут быть аппроксимированы функциями:

(3)
$\frac{{{{\tau }_{0}}}}{{{{\tau }_{{0*}}}}} = {{C}_{{00}}} + \frac{{{{C}_{{01}}}}}{{{{T}_{0}}}}T + \frac{{{{C}_{{02}}}}}{{T_{0}^{2}}}{{T}^{2}},$
(4)
$\frac{{{{\tau }_{1}}}}{{{{\tau }_{{1*}}}}} = {{C}_{{10}}} + \frac{{{{C}_{{11}}}}}{{{{T}_{0}}}}T + \frac{{{{C}_{{12}}}}}{{T_{0}^{2}}}{{T}^{2}}.$

В зависимостях (4), (5) ${{\tau }_{{0*}}}$ и ${{\tau }_{{1*}}}$ – предельное напряжение сдвига и упрочнения при температуре ${{T}_{0}} = 293$ К. Параметры аппроксимации имеют следующие значения: C00 = 0.8665, C01 = = 0.3479, ${{C}_{{02}}} = - 0.2144,$ ${{C}_{{10}}} = {\text{2}}{\text{.9817,}}$ ${{C}_{{11}}} = - {\text{2}}{\text{.7000,}}$ ${{C}_{{12}}} = {\text{0}}{\text{.7183}}{\text{.}}$ Значения материальных констант ${{\tau }_{{0*}}},$ ${{\tau }_{{1*}}},$ ${{a}_{*}}$ для различных размеров упрочняющих частиц $\delta ,$ а также расстояний между частицами ${{\Lambda }_{p}}$ представлены в табл. 1.

Таблица 1.  

Материальные константы ${{\tau }_{{0*}}},$ ${{\tau }_{{1*}}},$ ${{a}_{*}}$

Параметры упрочняющей фазы Материальные константы
${{\Lambda }_{p}} = 100$ нм
$\delta = 10$ нм 		${{\tau }_{{0*}}} = 81.08$ МПа
${{\tau }_{{1*}}} = 143.1$ МПа
${{a}_{*}} = 0.011$
${{\Lambda }_{p}} = 200$ нм
$\delta = 20$ нм 		${{\tau }_{{0*}}} = 43.13$ МПа
${{\tau }_{{1*}}} = 110.13$ МПа
${{a}_{*}} = 0.013$

НАПРЯЖЕННОЕ СОСТОЯНИЕ В СТЕНКЕ ТРУБЫ

Рассмотрим напряженно-деформированное состояние трубы из дисперсно-упрочненного алюминиевого сплава, нагруженной равномерным внутренним давлением ${{p}_{{in}}}$ и находящейся в неоднородном температурном поле (рис. 2).

Рис. 2.

Схема деформирования трубы.

Будем полагать, что внутренняя стенка трубы имеет постоянную температуру $T = {{T}_{{in}}},$ а внешняя – $T = {{T}_{{ex}}}.$ Отметим, что если торцевые стенки трубы теплоизолированы, то распределение температуры не будет зависеть от осевой координаты z. Кроме того, вследствие осевой симметрии рассматриваемой задачи температура не будет зависеть от угловой координаты $\varphi .$ Таким образом, уравнение стационарной теплопроводности может быть записано как [36]:

(5)
$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial T}}{{\partial r}}} \right) = 0.$

Граничные условия можно сформулировать в виде:

(6)
$r = {{R}_{{in}}}{\text{:}}\,\,T = {{T}_{{in}}};\,\,\,\,r = {{R}_{{ex}}}{\text{:}}\,\,T = {{T}_{{ex}}}.$

Интегрирование уравнения (5) с граничными условиями (6) позволяет определить зависимость температуры от радиальной координаты

(7)
$T = {{T}_{{in}}} + \left( {{{T}_{{ex}}} - {{T}_{{in}}}} \right)\frac{{\ln r - \ln {{R}_{{in}}}}}{{\ln {{R}_{{ex}}} - \ln {{R}_{{in}}}}}.$

В основе математической модели напряженного состояния лежат уравнения равновесия [37, 38]. Поскольку рассматривая задача является осесимметричной, нормальные напряжения не зависят от угловой координаты φ, касательное напряжение равно нулю ${{\sigma }_{{r{{\varphi }}}}} = 0.$ В случае плоской деформации компоненты вектора перемещения не зависят от координаты z. Следовательно будут равны нулю осевая деформация ${{\varepsilon }_{{zz}}} = 0,$ сдвиговые компоненты тензора деформации ${{\varepsilon }_{{{{\varphi }}z}}} = 0,$ ${{\varepsilon }_{{rz}}} = 0.$ Сдвиговые напряжения также будут равны нулю: ${{\sigma }_{{{{\varphi }}z}}} = 0,$ ${{\sigma }_{{rz}}} = 0.$ При этих предположениях баланс напряжений описывается уравнением

(8)
$\frac{{d{{\sigma }_{{rr}}}}}{{dr}} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{{{\varphi \varphi }}}}}}}{r} = 0.$

Сформулируем граничные условия для уравнения (8). На внутреннюю поверхность трубы $r = {{R}_{{in}}}$ действует однородное поле давления. Давление на внешнюю стенку трубы $r = {{R}_{{ex}}}$ полагаем отсутствующим. Таким образом, условия на границах принимают вид:

(9)
$r = {{R}_{{in}}}{\text{:}}\,\,{{\sigma }_{{rr}}} = - {{p}_{{in}}},\,\,\,\,r = {{R}_{{ex}}}{\text{:}}\,\,{{\sigma }_{{rr}}} = 0.$

Характер деформации стенок трубы определяется величиной приложенного давления ${{p}_{{in}}}.$ В рамках данного исследования будем рассматривать случай, когда достигнут предел пластического сопротивления (${{p}_{{in}}} = {{p}_{{pl}}}$), т.е. деформация всей стенки трубы является пластической. Таким образом, анализ напряженно-деформированного состояния можно провести на основе уравнений деформационной теории пластичности [39, 40].

Известно, что при пластической деформации упрочняющейся среды дополнительным условием, связывающим компоненты тензора напряжений, является условие пластического упрочнения [37]:

(10)
$\left| {{{\sigma }_{{rr}}} - {{\sigma }_{{{{\varphi \varphi }}}}}} \right| = {{\tau }_{s}}\left( a \right),$

Определим закон изменения интенсивности деформаций по радиусу трубы. В основе деформационной теории пластичности лежат представления [41], что изменения объема за счет пластических деформаций не происходит. Объемная деформация возникает только в результате упругих и температурных напряжений. Таким образом, при пластической деформации в неоднородном температурном поле объемная деформация равна:

(11)
${{\varepsilon }_{V}} = 3{{\alpha }_{T}}\left( {T - {{T}_{{in}}}} \right).$

При малых растяжениях или сжатиях и сдвигах величина объемной деформации равна:

(12)
${{\varepsilon }_{V}} = {{\varepsilon }_{{rr}}} + {{\varepsilon }_{{{{\varphi \varphi }}}}} + {{\varepsilon }_{{zz}}}.$

Компоненты тензора деформаций определяются соотношениями Коши и при наличии осевой симметрии и плоского деформированного состояния имеют вид:

(13)
${{\varepsilon }_{{rr}}} = \frac{{d{{u}_{r}}}}{{dr}},\,\,\,\,{{\varepsilon }_{{{{\varphi \varphi }}}}} = \frac{{{{u}_{r}}}}{r},\,\,\,\,{{\varepsilon }_{{zz}}} = 0.$

В уравнении (13) ${{u}_{r}}$ – радиальная составляющая вектора перемещения.

С учетом зависимостей (11)–(13) поле перемещения может быть найдено из решения уравнения:

(14)
$\frac{{\partial {{u}_{r}}}}{{\partial r}} + \frac{{{{u}_{r}}}}{r} = 3{{\alpha }_{T}}\left( {T - {{T}_{{in}}}} \right).$

Интенсивность сдвиговых деформаций, вызванная силовой нагрузкой, согласно [34, 37, 38] равна:

(15)
$a = \sqrt {2\left( {{{{\left( {\varepsilon _{{rr}}^{d}} \right)}}^{2}} + {{{\left( {\varepsilon _{{{{\varphi \varphi }}}}^{d}} \right)}}^{2}} + {{{\left( {\varepsilon _{{zz}}^{d}} \right)}}^{2}}} \right)} ,$
где компоненты девиатора деформаций определяются из условий:

(16)
$\varepsilon _{{rr}}^{d} = {{\varepsilon }_{{rr}}} - \frac{1}{3}{{\varepsilon }_{V}},\,\,\,\,\varepsilon _{{{{\varphi \varphi }}}}^{d} = {{\varepsilon }_{{{{\varphi \varphi }}}}} - \frac{1}{3}{{\varepsilon }_{V}},\,\,\,\,\varepsilon _{{zz}}^{d} = - \frac{1}{3}{{\varepsilon }_{V}}.$

АНАЛИЗ РЕЗУЛЬТАТОВ

Балансные уравнения для элементов дефектно-дислокационной структуры и механики деформируемого твердого тела решались численно с использованием метода пятого порядка Рунге–Кутта–Мерсона [42].

На рис. 3а показаны зависимости предела пластического сопротивления трубы ${{p}_{{pl}}}$ от температуры внешней стенки трубы. При нагреве внешней стенки материал наружных слоев трубы становится более пластичным. В результате этого величина давления, необходимого для достижения пластической деформации внешней стенки, уменьшается. Охлаждение внешней стенки, напротив, приводит к росту предела пластического сопротивления. Отметим, что при фиксированном значении ${{T}_{{in}}}$ варьирование температуры внешней стенки в диапазоне 200 К приводит к значительному изменению предела пластического сопротивления (для рассматриваемой геометрии это изменение составляет около 15%). Таким образом, для расчета прочностных характеристик теплообменника необходимо учитывать неоднородность распределения температуры в его стенках.

Рис. 3.

Зависимость предела пластического сопротивления от температуры стенок трубы: а – от внешней стенки (кривые 1, 4 – ${{T}_{{in}}} = 293$ К; кривые 2, 5 – ${{T}_{{in}}} = 393$ К; кривые 3, 6 – ${{T}_{{in}}} = 493$ К); б – от внутренней стенки (1, 4 – ${{T}_{{ex}}} = 293$ К, 2, 5 – ${{T}_{{ex}}} = 393$К, 3, 6 – ${{T}_{{ex}}} = 493$К). Радиусы трубы: ${{R}_{{in}}} = 0.1$ м, ${{R}_{{ex}}} = 0.105$ м. Масштабные характеристики упрочняющей фазы: ${{\Lambda }_{p}} = 100$ нм, $\delta = 10$ нм (кривые 1–3), ${{\Lambda }_{p}} = 200$ нм, $\delta = 20$ нм (кривые 4–6).

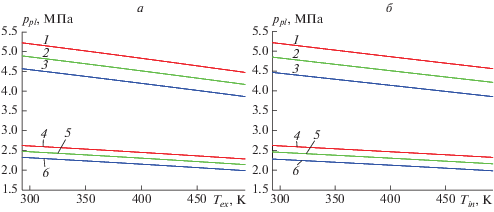
Аналогичные зависимости, характеризующие влияние температуры внутренней стенки на пластическую деформацию трубы, иллюстрирует рис. 3б. Увеличение температуры внутренней стенки при фиксированном значении ${{T}_{{ex}}}$ уменьшает сопротивляемость пластической деформации внутренних слоев трубы, что вызывает уменьшение ${{p}_{{pl}}}.$ При охлаждении внутренней стенки трубы предел пластического сопротивления увеличивается. Изменение ${{p}_{{pl}}}$ при вариации ${{T}_{{in}}}$ в диапазоне 200 К для рассматриваемых размеров трубы (${{R}_{{in}}} = 0.1$ м, ${{R}_{{ex}}} = 0.105$ м) также составляет 15%. Таким образом, для расчета прочностных характеристик теплообменника необходимо учитывать неоднородность распределения температуры в его стенках.

В сплавах с меньшими расстояниями между упрочняющими частицами при одной и той же объемной доле частиц требуется существенно большее давление для достижения пластической деформации стенок трубы. Таким образом, уменьшение расстояния между частицами вызывает упрочнение материала, приводящее к росту предела пластического сопротивления. Отметим, что для сплавов с различными параметрами упрочняющейся фазы характер зависимостей предела пластического сопротивления от температуры стенки трубы не изменяется.

На рис. 4 приведены зависимости радиального ${{\sigma }_{{rr}}},$ тангенциального ${{\sigma }_{{{{\varphi \varphi }}}}}$ и осевого ${{\sigma }_{{zz}}}$ напряжений от радиальной координаты, рассчитанные при различных значениях температуры внешней и внутренней стенки.

Рис. 4.

Распределение напряжений по стенке трубы: а – радиальных ${{\sigma }_{{rr}}},$ б – тангенциальных ${{\sigma }_{{{{\varphi \varphi }}}}},$ в – осевых ${{\sigma }_{{zz}}}.$ Радиусы трубы: ${{R}_{{in}}} = 0.1$ м, ${{R}_{{ex}}} = 0.105$ м. Масштабные характеристики упрочняющей фазы: ${{\Lambda }_{p}} = 100$ нм, $\delta = 10$ нм. Температура стенок трубы: 1, 4, 7 – ${{T}_{{{\text{in}}}}} = 493$ К; 2, 5, 8 – ${{T}_{{{\text{in}}}}} = 393$ К; 3, 6, 9 – ${{T}_{{{\text{in}}}}} = 293$ К; 1, 2, 3 – ${{T}_{{{\text{ex}}}}} = 493$ К; 4, 5, 6 – ${{T}_{{{\text{ex}}}}} = 393$ К; 7, 8, 9 – ${{T}_{{{\text{ex}}}}} = 293$ К.

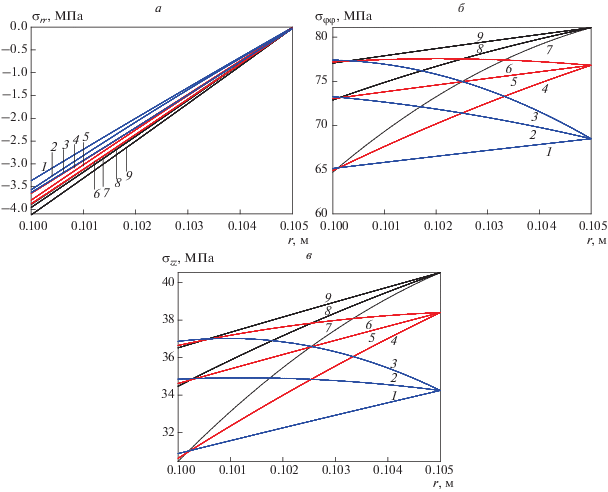
На рис. 4а приведена зависимость напряжения ${{\sigma }_{{rr}}}$ от радиальной координаты, рассчитанная для внутреннего давления, соответствующего пределу пластического сопротивления трубы ${{p}_{{in}}} = {{p}_{{pl}}}.$ Абсолютные значения напряжения ${{\sigma }_{{rr}}}$ монотонно уменьшаются от $\left| {{{\sigma }_{{rr}}}} \right| = {{p}_{{in}}}$ до 0 по мере удаления от внутренней стенки и приближении к внешней. Результаты проведенных исследований показывают, что распределение радиальных напряжений близко к линейному и может быть аппроксимировано зависимостью

(17)
${{\sigma }_{{rr}}} = - {{p}_{{in}}}\frac{{{{R}_{{ex}}} - r}}{{{{R}_{{ex}}} - {{R}_{{in}}}}}.$

Как уже отмечалось, увеличение температуры стенок трубы приводит к тому, что деформация стенки трубы по всей ее толщине становится пластической при меньшей величине приложенного давления. Таким образом, абсолютные значения радиальных напряжений при ${{p}_{{in}}} = {{p}_{{pl}}}$ с ростом температуры стенок трубы уменьшаются. Наиболее заметен этот эффект вблизи внутренней, нагруженной стенки трубы. Вблизи внешней стенки трубы этот эффект выражен слабо.

На рис. 4б представлено изменение напряжения ${{\sigma }_{{{{\varphi \varphi }}}}}$ по толщины стенки, рассчитанное для ${{p}_{{in}}} = {{p}_{{pl}}}.$ Величина тангенциальных напряжений на внутренней стенке трубы равна ${{\sigma }_{{{{\varphi \varphi }}}}}\left( {{{R}_{{in}}}} \right) = {{\tau }_{s}} - {{p}_{{in}}},$ а на внешней стенке трубы соответствует пределу текучести при $T = {{T}_{{ex}}}{\text{:}}$ ${{\sigma }_{{{{\varphi \varphi }}}}}\left( {{{R}_{{ex}}}} \right) = {{\tau }_{{\text{0}}}}\left( {{{T}_{{ex}}}} \right).$

Увеличение температуры внешней стенки приводит к уменьшению значений ${{\sigma }_{{{{\varphi \varphi }}}}}\left( {{{R}_{{ex}}}} \right),$ а нагрев внутренней стенки к уменьшению ${{\sigma }_{{{{\varphi \varphi }}}}}\left( {{{R}_{{in}}}} \right).$ Если температура внешней стенки превышает температуру внутренней, то ${{\sigma }_{{{{\varphi \varphi }}}}}\left( {{{R}_{{in}}}} \right) > {{\sigma }_{{{{\varphi \varphi }}}}}\left( {{{R}_{{ex}}}} \right).$ При этом зависимость ${{\sigma }_{{{{\varphi \varphi }}}}}\left( r \right)$ является убывающей. При ${{T}_{{ex}}} \leqslant {{T}_{{in}}}$ зависимость ${{\sigma }_{{{{\varphi \varphi }}}}}\left( r \right)$ становится возрастающей. Результаты расчетов показывают, что тангенциальные напряжения при достижении предела пластического сопротивления с ростом температуры стенки трубы уменьшаются. Отметим, что напряжения, связанные с деформацией стенки трубы в тангенциальном направлении ${{\sigma }_{{{{\varphi \varphi }}}}},$ более чем на порядок превосходят по абсолютной величине напряжения сжатия в радиальном направлении ${{\sigma }_{{rr}}}.$

Радиальное распределение осевого напряжения ${{\sigma }_{{zz}}}$ качественно повторяет распределение тангенциального напряжения ${{\sigma }_{{{{\varphi \varphi }}}}}$ (рис. 4в): при ${{T}_{{ex}}} \leqslant {{T}_{{in}}}$ зависимость ${{\sigma }_{{zz}}}\left( r \right)$ является возрастающей, а при ${{T}_{{in}}} < {{T}_{{ex}}}$ – убывающей. Таким образом, напряженное состояние обогреваемой трубы характеризуется наибольшими значениями осевого напряжения на внутренней стенке, а охлаждаемой – на внешней.

ЗАКЛЮЧЕНИЕ

Результаты математического моделирования показали, что охлаждение внешней стенки трубы приводит к росту предела пластического сопротивления. Увеличение температуры внутренней стенки уменьшает сопротивляемость пластической деформации внутренних слоев трубы. При охлаждении внутренней стенки трубы предел пластического сопротивления увеличивается. Для одной и той же абсолютной разности температур внешней и внутренней стенок предел пластического сопротивления тем меньше, чем выше температура внутренней стенки трубы. Абсолютные значения напряжения ${{\sigma }_{{rr}}}$ монотонно уменьшаются от $\left| {{{\sigma }_{{rr}}}} \right| = {{p}_{{in}}}$ до нуля по мере удаления от внутренней стенки и приближении к внешней. Абсолютные значения радиальных напряжений при ${{p}_{{in}}} = {{p}_{{pl}}}$ с ростом температуры стенок трубы уменьшаются. Тангенциальные напряжения при достижении предела пластического сопротивления с ростом температуры стенки трубы уменьшаются. Если температура внешней стенки превышает температуру внутренней, то зависимость тангенциальных напряжений от радиальной координаты является убывающей, в противном случае – возрастающей. Напряженное состояние обогреваемой трубы характеризуется наибольшими значениями осевого напряжения на внутренней стенке, а охлаждаемой – на внешней.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № FEMN-2020-0004).

Список литературы

  1. Березовский В.В., Шавнев А.А., Ломов С.Б., Курганова Ю.А. // Авиацион. матер. и технол. 2014. № 6. С. 17.

  2. Карабасов Ю.С. Новые материалы. М.: МИСиС, 2002. 736 с.

  3. Matvienko O., Daneyko O., Kovalevskaya T. // Acta Met. Sin. (Engl. Lett.). 2018. V. 31. No. 12. P. 1297.

  4. Saunders E.A.D. Heat exchangers: selection, design and construction. N.Y.: Longman Sci. and Techn., 1988. 568 p.

  5. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Фунд. пробл. совр. материаловед. 2020. Т. 17. № 3. С. 330.

  6. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2017. Т. 60. № 2. С. 35; Matvienko O.V., Daneiko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2017. V. 60. No. 2. P. 236.

  7. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2017. Т. 60. № 4. С. 7; Matvienko O.V., Daneyko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2017. V. 60. No. 4. P. 562

  8. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2017. Т. 60. № 7. С. 133; Matvienko O.V., Daneyko O I., Kovalevskaya T.A. // Russ. Phys. J. 2017. V. 60. No. 7. P. 1233.

  9. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2018. Т. 61. № 8. С. 138; Matvienko O.V., Daneyko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2018. V. 61. No. 8. P. 1520.

  10. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2019. Т. 62. № 4. С. 144; Matvienko O.V., Daneyko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2018. V. 62. No. 4. P. 720.

  11. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2019. Т. 62. № 10. С. 50; Matvienko O.V., Daneyko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2020. V. 61. No. 8. P. 1805.

  12. Matvienko O., Daneyko O., Kovalevskaya T. // MATEC Web Conf. 2018. V. 243. Art. No. 00022.

  13. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2020. Т. 63. № 5. С. 64; Matvienko O.V., Daneyko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2020. V. 63. No. 5. P. 779.

  14. Данейко О.И., Ковалевская Т.А., Матвиенко О.В. // Изв. вузов. Физ. 2018. Т. 61. № 7. С. 40; Daneyko O.I., Kovalevskaya T.A., Matvienko O.V. // Russ. Phys. J. 2018. V. 61. No. 7. P. 1229.

  15. Данейко О.И., Ковалевская Т.А., Кулаева Н.А. // Изв. вузов. Физ. 2017. Т. 60. № 3. С. 116; Daneyko O.I., Kovalevskaya T.A., Kulaeva N.A. // Russ. Phys. J. 2017. V. 60. No. 3. P. 508.

  16. Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2018. Т. 61. № 9. С. 120; Daneyko O.I., Kovalevs-kaya T.A. // Russ. Phys. J. 2018. V. 61. No. 9. P. 1687.

  17. Данейко О.И., Ковалевская Т.А., Кулаева Н.А. и др. // Изв. вузов. Физ. 2017. Т. 60. № 5. С. 69; Daneyko O.I., Kovalevskaya T.A., Kulaeva N.A. et al. // Russ. Phys. J. 2017. V. 60. No. 5. P. 821.

  18. Ковалевская Т.А., Данейко О.И. // Изв. вузов. Физ. 2019. Т. 62. № 12(744). С. 81; Kovalevskaya T.A., Daneyko O.I. // Russ. Phys. J. 2020. V. 62. No. 12. P. 2247.

  19. Ковалевская Т.А., Данейко О.И., Шалыгина Т.А. // Изв. вузов. Физ. 2020. Т. 63. № 4(748). С. 139; Kovalevskaya T.A., Daneyko O.I., Shalygina T.A. // Russ. Phys. J. 2020. V. 63. No. 4. P. 688.

  20. Arnhold V., Hummert K. New materials by mechanical alloying techniques. Oberursel: DGM Inform. Verlag, 1989. P. 263.

  21. Weber J.H., Schelleng R.D. Dispersion strengthened aluminum alloys. Warrendale: TMS, 1988. P. 468.

  22. Ashby M.F., Johnson K. Materials and design: the art and science of materials selection in product design. Oxford: Butterworth Heinemann, 2002. 390 p.

  23. Hymphreys F.J., Martin J.W. // Phil. Mag. 1967. V. 16. No. 143. P. 927.

  24. Orowan E. In: Symposium on internal stresses in metals and alloys. London: Inst. of Metals, 1948. P. 451.

  25. Ashby M.F. // Phil. Mag. 1966. V. 14. P. 1157.

  26. Ebeling R., Ashby M.F. // Phil. Mag. 1966. V. 13. P. 805.

  27. Hirsch P.B., Hymphreys F.J. // Scr. Met. 1973. V. 7. P. 259.

  28. Hazzledine P.M., Hirsch P.B. // Phil. Mag. 1974. V. 30. P. 1331.

  29. Humphreys F.J., Hirsch P.B. // Phil. Mag. 1976. V. 34. P. 373.

  30. Ковалевская Т.А., Виноградова И.В., Попов Л.Е. Математическое моделирование пластической деформации гетерофазных сплавов. Томск: Изд. ТГУ, 1992. 167 с.

  31. Humphreys F.J., Hirsch P.B. // Proc. Phys. Soc. 1973. V. 318(1532). P. 73.

  32. Луц А.Р., Галочкина И.А. Алюминиевые композиционные сплавы – сплавы будущего. Самара: СамГТУ, 2013. 82 с.

  33. Мэтьюз Ф., Ролингс Р. Композитные материалы. М.: Техносфера, 2004. 408 с.

  34. Горшков А.Г., Старовойтов Э.И., Тарлаковский Д.В. Теория упругости и пластичности. М.: Физматлит, 2002. 416 с.

  35. Polmear L.J. Light alloys: metallurgy of lights metals. John Willey and Sons, 1995. 235 p.

  36. Кутателадзе С.С. Основы теории теплообмена. М.: Атомиздат, 1979. 416 с.

  37. Малинин Н.Н. Прикладная теория пластичности и ползучести. М.: Машиностроение, 1975. 400 с.

  38. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2018. Т. 61. № 4. С. 113; Matvienko O.V., Daneyko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2018. V. 61. No. 4. P. 730.

  39. Timoshenko S.P., Goodier J.N. Theory of elasticity. N.Y.: McGraw Hill, 2010. 567 p.

  40. Матвиенко О.В., Данейко О.И., Ковалевская Т.А. // Изв. вузов. Физ. 2018. Т. 61. № 5. С. 140; Matvienko O.V., Daneyko O.I., Kovalevskaya T.A. // Russ. Phys. J. 2018. V. 61. No. 5. P. 962.

  41. Chakrabarty J. Theory of plasticity. N.Y., Hamburg, London, Paris, Sydney, Tokyo: Mc Graw Hill Book Company, 1987. 791 p.

  42. Chapra S. Numerical methods for engineers. N.Y.: McGraw, 2015. 518 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал