1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 8, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 8, стр. 1154-1158

Влияние трехспиновых групп на спад свободной индукции и первичное спиновое эхо в линейных полимерах со свободными концами

Т. П. Кулагина 1, *, Г. Е. Карнаух 1, И. Ю. Голубева 2

1 Федеральное государственное бюджетное учреждение науки Институт проблем химической физики Российской академии наук
Черноголовка, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

* E-mail: tan@icp.ac.ru

Поступила в редакцию 12.03.2021
После доработки 05.04.2021
Принята к публикации 28.04.2021

Полный текст (PDF)

Аннотация

Предложена теория сигналов спада свободной индукции и первичного спинового эха в линейных гибкоцепных полимерах, содержащих изолированные группы дипольно связанных трех спинов с произвольными константами диполь-дипольного взаимодействия. Предложен новый метод расчета сигналов первичного эха после воздействия двух радиочастотных импульсов в широком температурном интервале.

ВВЕДЕНИЕ

Наблюдаемые спектры ЯМР бывают более простые, чем спектры изолированной группы спинов, вследствие уширения под влиянием окружающих спинов и частичного усреднения [1, 2] дипольного взаимодействия спинов. Обычно трехпиновые группы рассматриваются в модели эквивалентных ядер, расположенных в вершинах равностороннего треугольника. Однако, представляет интерес исследование трехспиновой группы с различными константами диполь-дипольного взаимодействия (ДДВ).

До последнего времени аналитические выражения для спада свободной индукции (ССИ) и первичного спинового эха (СЭ) в работах и [1–5] не приведены, что затрудняет расчеты и получение информации о структуре и ориентации трехспиновых групп из сигналов ЯМР. В данной работе предложен новый метод расчета ССИ и СЭ в системе дипольно-связанных трех спинов 1/2 с произвольными константами ДДВ. В этом методе впервые использованы симметрии, определяемые спиновым обменом и операцией переворота всех спинов вокруг оси начальной поляризации и направлением импульсов при формировании солид-эха. Использование этих симметрий позволило свести расчеты с матрицей 8-го порядка к расчетам на двух матрицах 3 порядка [6–8]. Расчеты показали качественное соответствие теории и эксперимента [5] в твердом теле.

МЕТОДЫ ИССЛЕДОВАНИЯ

В работе предложена теория сигналов первичного эха (СЭ) в полимерах, содержащих группы дипольно связанных трех спинов 1/2 с произвольными константами диполь-дипольного взаимодействия (ДДВ). Предложен новый метод расчета сигналов СЭ A3(t, τ) после воздействия импульсной последовательности: ${{\left( {\frac{\pi }{2}} \right)}_{y}} - \tau - {{\left( {\frac{\pi }{2}} \right)}_{x}} - t$ [6].

В данной системе гамильтониан диполь-дипольного взаимодействия определяется формулой:

(1)
$\begin{gathered} \hat {H}_{d}^{z} = {{b}_{{12}}}(2\hat {S}_{1}^{z}\hat {S}_{2}^{z} - \hat {S}_{1}^{x}\hat {S}_{2}^{x} - \hat {S}_{1}^{y}\hat {S}_{2}^{y}) + \\ + \,\,{{b}_{{23}}}(2\hat {S}_{2}^{z}\hat {S}_{3}^{z} - \hat {S}_{2}^{x}\hat {S}_{3}^{x} - \hat {S}_{2}^{y}\hat {S}_{3}^{y}) + \\ + \,\,{{b}_{{31}}}(2\hat {S}_{3}^{z}\hat {S}_{1}^{z} - \hat {S}_{3}^{x}\hat {S}_{1}^{x} - \hat {S}_{3}^{y}\hat {S}_{1}^{y}). \\ \end{gathered} $

В расчете [6, 7] были использованы две симметрии, связанные со следующими операциями:

1. Переворот всех спинов вокруг оси x. Пространство всех состояний R разбивается на два подпространства четных Re и нечетных R0 относительно этого переворота состояний.

2. Спиновый обмен. Пространство всех состояний R разбивается на два подпространства симметрических Rs и антисимметрических Ra относительно спинового обмена состояний.

Проведены аналитические вычисления сигнала СЭ от изолированной группы трех спинов и получена следующая формула сигнала солид-эха A3(τ, t) [6]:

(2)
$\begin{gathered} {{A}_{3}}(\tau ,t) = \frac{1}{{64}}(27{{\cos }^{4}}\beta - 18{{\cos }^{2}}\beta + 7) + \frac{3}{{32}}({{\cos }^{2}}\beta + 2\cos \beta + 1)\cos {{\omega }_{{12}}}(\tau - t) + \\ + \,\,\frac{3}{{32}}({{\cos }^{2}}\beta - 2\cos \beta + 1)\cos {{\omega }_{{13}}}(\tau - t) + \frac{{27}}{{128}}({{\cos }^{4}}\beta - 2{{\cos }^{2}}\beta + 1)\cos {{\omega }_{{23}}}(\tau - t) + \\ + \,\,\frac{1}{{32}}( - 3{{\cos }^{2}}\beta - 2\cos \beta + 1)\cos {{\omega }_{{12}}}(\tau + t) + \frac{1}{{32}}( - 3{{\cos }^{2}}\beta + 2\cos \beta + 1)\cos {{\omega }_{{13}}}(\tau + t) + \\ + \,\,\frac{3}{{128}}(9{{\cos }^{4}}\beta - 10{{\cos }^{2}}\beta + 1)\cos {{\omega }_{{23}}}(\tau + t) - \frac{3}{{32}}({{\cos }^{2}}\beta - 1)(\cos ({{\omega }_{{13}}}\tau - {{\omega }_{{12}}}t) + \\ + \,\,\frac{3}{{64}}( - 3{{\cos }^{3}}\beta + {{\cos }^{2}}\beta + 3\cos \beta - 1)(\cos ({{\omega }_{{24}}}\tau - {{\omega }_{{12}}}t) + \cos ({{\omega }_{{23}}}t - {{\omega }_{{12}}}\tau )) + \\ + \,\,\frac{9}{{64}}({{\cos }^{3}}\beta - \cos \beta + 1)(\cos ({{\omega }_{{23}}}\tau - {{\omega }_{{13}}}t) + \cos ({{\omega }_{{23}}}t - {{\omega }_{{13}}}\tau )) + \frac{3}{{32}}({{\cos }^{2}}\beta - 1) \times \\ \times \,\,(\cos ({{\omega }_{{13}}}\tau + {{\omega }_{{12}}}t) + \cos ({{\omega }_{{12}}}t + {{\omega }_{{12}}}\tau )) + \frac{3}{{64}}(3{{\cos }^{3}}\beta + {{\cos }^{2}}\beta - 3\cos \beta - 1) \\ (\cos ({{\omega }_{{23}}}\tau + {{\omega }_{{13}}}t) + \cos ({{\omega }_{{23}}}t + {{\omega }_{{13}}}\tau )) - \frac{9}{{64}}({{\cos }^{3}}\beta + {{\cos }^{2}}\beta - \cos \beta - 1)(\cos ({{\omega }_{{23}}}\tau + {{\omega }_{{12}}}t) + \\ + \,\,\,\cos ({{\omega }_{{23}}}t + {{\omega }_{{12}}}\tau )) + \frac{1}{{32}}(9{{\cos }^{2}}\beta + 3{{\cos }^{2}}\beta - 5\cos \beta + 1)(\cos {{\omega }_{{12}}}\tau + \cos {{\omega }_{{12}}}t) - \\ - \,\,\frac{1}{{32}}(9{{\cos }^{3}}\beta - 3{{\cos }^{2}}\beta - 5\cos \beta + 1)(\cos {{\omega }_{{13}}}\tau + \cos {{\omega }_{{13}}}t) - \\ - \,\,\frac{3}{{64}}(9{{\cos }^{4}}\beta - 10{{\cos }^{2}}\beta + 1)(\cos {{\omega }_{{23}}}\tau + \cos {{\omega }_{{23}}}t), \\ \end{gathered} $
где ${{\sigma }_{1}} = {{b}_{{12}}} + {{b}_{{23}}} + {{b}_{{31}}},$ ${{\sigma }_{2}} = {{b}_{{12}}}{{b}_{{23}}} + {{b}_{{23}}}{{b}_{{31}}} + {{b}_{{31}}}{{b}_{{12}}},$

$\begin{gathered} {{\lambda }_{1}} = \frac{{{{\sigma }_{1}}}}{2},\,\,\,{{\lambda }_{2}}\frac{{ - {{\sigma }_{1}} - \chi }}{4},\,\,\,{{\lambda }_{3}} = \frac{{ - {{\sigma }_{1}} + \chi }}{4}, \\ \chi = \sqrt {9\sigma _{1}^{2} - 24{{\sigma }_{2}}} ,\,\,\,\cos \beta = \frac{{{{\sigma }_{1}}}}{{\sqrt {9\sigma _{1}^{2} - 24{{\sigma }_{2}}} }}, \\ {{\omega }_{{ij}}} = {{\lambda }_{i}} - {{\lambda }_{j}}. \\ \end{gathered} $

Вводя t = τ, получаем сигнал CЭ в трехспиновой группе с одинаковыми константами ДДВ b:

(3)
${{A}_{3}}(t) = \frac{5}{8} + \frac{1}{2}\cos \left( {\frac{{3bt}}{2}} \right) - \frac{1}{8}\cos (3bt).$

При σ1 = 0 введем ω = $\frac{{\sqrt { - 6{{\sigma }_{2}}} }}{2} = \sqrt {{M \mathord{\left/ {\vphantom {M 2}} \right. \kern-0em} 2}} ,$ М2 = $\omega _{{{\text{3}}loc}}^{{\text{2}}}$ = = ${\text{3/2}}\left( {b_{{12}}^{2} + b_{{12}}^{2} + b_{{23}}^{2}} \right)$ – второй момент трехспиновой системы. Тогда СЭ определяется как:

(4)
$\begin{gathered} {{A}_{3}}(t) = \frac{{41}}{{128}} + \frac{{11}}{{16}}\cos (\omega y) + \frac{5}{{32}}\cos (2\omega t) - \\ - \,\,\frac{3}{{16}}\cos (3\omega t) + \frac{3}{{128}}\cos (4\omega t) = \\ = \,\,1 - 4{{\sin }^{4}}\frac{{\omega t}}{2} + 3{{\sin }^{8}}\frac{{\omega t}}{2}. \\ \end{gathered} $

При t = τ формула (2) приобретает вид:

(5)
$\begin{gathered} {{A}_{3}}(t) = \frac{{65}}{{128}} - \frac{{33}}{{64}}{{\cos }^{2}}\beta + \frac{{81}}{{128}}{{\cos }^{4}}\beta + \,\,\frac{1}{{32}}(11 - 19\cos \beta - 3{{\cos }^{2}}\beta + 27{{\cos }^{3}}\beta )\cos ({{\omega }_{{12}}}t) \\ + \,\,\frac{1}{{32}}(11 + 19\cos \beta - 3{{\cos }^{2}}\beta - 27{{\cos }^{3}}\beta )\cos ({{\omega }_{{13}}}t) + \,\,\frac{3}{{32}}(1 + 8{{\cos }^{2}}\beta - 9{{\cos }^{4}}\beta )\cos ({{\omega }_{{23}}}t) + \\ + \,\,\frac{1}{{32}}(1 - 2\cos \beta - 3{{\cos }^{2}}\beta )\cos (2{{\omega }_{{12}}}t) + \,\,\frac{1}{{32}}(1 + 2\cos \beta - 3{{\cos }^{2}}\beta )\cos (2{{\omega }_{{13}}}t) + \\ + \,\,\frac{3}{{128}}(1 - 10{{\cos }^{2}}\beta + 9{{\cos }^{4}}\beta )\cos (2{{\omega }_{{23}}}t) + \,\,\frac{3}{{16}}( - 1 + {{\cos }^{2}}\beta )\cos (({{\omega }_{{12}}} + {{\omega }_{{13}}})t) + \\ + \,\,\frac{3}{{32}}( - 1 + 3\cos \beta + {{\cos }^{2}}\beta - 3{{\cos }^{3}}\beta )\cos (({{\omega }_{{12}}} - {{\omega }_{{23}}})t) + \\ + \,\,\frac{3}{{32}}( - 1 - 3\cos \beta + {{\cos }^{2}}\beta + 3{{\cos }^{3}}\beta )\cos (({{\omega }_{{13}}} + {{\omega }_{{23}}})t). \\ \end{gathered} $

Сигнал между первым и вторым импульсом выражает сигнал ССИ G3(t), который определяется следующей формулой [8]:

(6)
$\begin{gathered} {{G}_{3}}(t) = \frac{1}{8}(1 + 3{{\cos }^{2}}\beta ) + \frac{3}{8}{{\sin }^{2}}\beta \cos {{\omega }_{{32}}}t + \\ + \,\,\,\frac{1}{2}{{\cos }^{2}}\frac{\beta }{2}\cos {{\omega }_{{12}}}t + \frac{1}{2}{{\sin }^{2}}\frac{\beta }{2}\cos {{\omega }_{{13}}}t. \\ \end{gathered} $

В случае эквивалентных ядер c константой ДДВ b формула ССИ принимает вид:

(7)
${{G}_{3}}(t) = 1 - {{\sin }^{2}}\frac{{3bt}}{2}.$

ССИ в линейных полимерах без зацеплений рассчитываются в модели Андерсона–Вейса с соответствующими корреляционными функциями молекулярных движений ki(τ) [9]:

(8)
${{G}_{i}}(t) = \exp \left( { - \omega _{{loc}}^{2}\int\limits_o^t {(t - \tau ){{k}_{i}}(\tau )d\tau } } \right),\,\,\,i = 1,2,$
где ωloc – среднее локальное поле, создаваемое на любом спине как спинами, принадлежащими выделенному сегменту, так и всеми остальными спинами цепи.
(9)
$k(\tau ) = (1 - \alpha ){{k}_{1}}(\tau ) + \alpha {{k}_{2}}(\tau ),$
где α − доля крупномасштабного движения (эмпирический коэффициент), для сетчатой структуры и цепей со свободными концами α = 0.05.

k1(τ) = $\exp \left( { - \frac{\tau }{{{{\tau }_{c}}}}} \right)$ − корреляционная функция Бломбергена–Парселла–Паунда, характеризующая мелкомасштабные движения полимерной цепи в низкотемпературной области (Tc < T < Tc + + 50°), где τc – характерное время корреляции молекулярных движений, которое связано с температурой T по закону Аррениуса: τc = ${{\tau }_{0}}\exp \left( {\frac{E}{{kT}}} \right).$

k2(τ) = $\frac{1}{{{{N}_{0}}}}\sum\nolimits_{p = 1}^{{{N}_{0}}} {\exp \left( { - \frac{{{{p}^{2}}{{\pi }^{2}}\tau }}{{{{\tau }_{c}}N_{0}^{2}}}} \right)} $ − корреляционная функция Каргина–Слонимского–Рауза, характеризующая крупномасштабные движения сегментов полимерной цепи в среднетемпературном интервале (Tc + 50° < T < Tc + 100°) N0 – длина полимерной цепи в количестве длин сегментов.

Для цепей со свободными концами ССИ имеет вид [8]:

(10)
${{G}_{r}}(t) = {{G}_{1}}(t){{G}_{2}}(t).$

ССИ в линейном полимере, содержащем выделенные трехспиновые группы, выражается следующей формулой:

(11)
$G(t) = {{G}_{3}}(t){{G}_{r}}(t),$
где G3(t) – ССИ в системе трех спинов (6).

Аналогично выглядит выражение СЭ для всей спиновой системы:

(12)
$A(t,\tau ) = {{A}_{3}}(t,\tau ){{A}_{r}}(t,\tau ),$
где Ar(t, τ) – сигнал первичного эха в полимерах [9].

Формула для расчета первичного эха Ar(t, τ) – в полимерах получена на основе общего теоретического подхода, предложенного в работе [9], и связана со средним квадратом случайного изменения фазы $\left\langle {{{\delta }^{2}}{{\varphi }_{i}}} \right\rangle $ вследствие изменения локального магнитного поля на спине ядра соотношением:

(13)
${{A}_{{id}}} = \exp \left[ { - \frac{1}{2}\left\langle {{{\delta }^{2}}{{\varphi }_{i}}} \right\rangle } \right].$

Для определения связи $\left\langle {{{\delta }^{2}}{{\varphi }_{i}}} \right\rangle $ со средним квадратом смещения ядер получены формулы, справедливые для любых случайных процессов. По условию аддитивности смещений r(ti, tj) на отрезке времени [ti, tj] для каждой реализации случайного процесса справедливо равенство:

(14)
$r\left( {{{t}_{1}},{{t}_{2}}} \right) + r\left( {{{t}_{2}},{{t}_{3}}} \right) = r\left( {{{t}_{1}},{{t}_{3}}} \right).$

Для корреляции смещений стационарных процессов получена эквивалентная (14) формула:

(15)
$\begin{gathered} \left\langle {r\left( {{{t}_{1}},{{t}_{2}}} \right)r\left( {{{t}_{3}},{{t}_{4}}} \right)} \right\rangle = \frac{1}{2}(\left\langle {{{r}^{2}}\left( {{{t}_{1}},{{t}_{4}}} \right)} \right\rangle + \\ + \,\,\left\langle {{{r}^{2}}\left( {{{t}_{2}},{{t}_{3}}} \right)} \right\rangle - \left\langle {{{r}^{2}}\left( {{{t}_{1}},{{t}_{3}}} \right)} \right\rangle - \left\langle {{{r}^{2}}\left( {{{t}_{2}},{{t}_{4}}} \right)} \right\rangle ). \\ \end{gathered} $

С помощью формулы (15) получено выражение среднего квадрата смещений для эхо в стационарных условиях:

$\begin{gathered} \left\langle {{{{\left( {r\left( {0,\tau } \right) - r\left( {\tau ,\tau + t} \right)} \right)}}^{2}}} \right\rangle = \\ = \,\,2\left\langle {{{r}^{2}}\left( \tau \right)} \right\rangle + 2\left\langle {{{r}^{2}}\left( t \right)} \right\rangle - \left\langle {{{r}^{2}}\left( {\tau + t} \right)} \right\rangle . \\ \end{gathered} $

Величина $\left\langle {{{r}^{2}}\left( t \right)} \right\rangle $ задается уравнением

(17)
$\left\langle {{{r}^{2}}\left( t \right)} \right\rangle = 2\left\langle {\omega _{{loc}}^{2}\left( 0 \right)} \right\rangle \int\limits_0^t {\left( {t - t{\kern 1pt} '} \right)k\left( {t{\kern 1pt} '} \right)dt{\kern 1pt} '} ,$

Из формул (16), (17), (8) следует связь сигнала СЭ с ССИ:

(18)
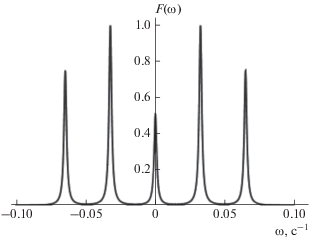
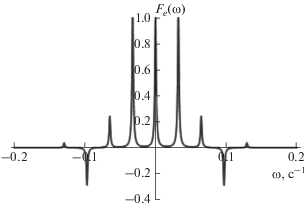
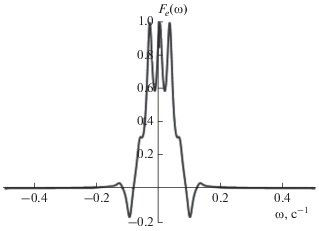
${{A}_{r}}(t,\tau ) = \frac{{{{G}_{r}}{{{(t)}}^{2}}{{G}_{r}}{{{(\tau )}}^{2}}}}{{{{G}_{r}}(\tau + t)}}.$

В данной работе рассматривалась модель при слабом влиянии спинов полимерной цепи на трехспиновую группу $({{\omega _{{{\text{3}}loc}}^{{\text{2}}}} \mathord{\left/ {\vphantom {{\omega _{{{\text{3}}loc}}^{{\text{2}}}} {\left( {\omega _{{{\text{l}}oc}}^{{\text{2}}} > {\text{1}}} \right)}}} \right. \kern-0em} {\left( {\omega _{{{\text{l}}oc}}^{{\text{2}}} > {\text{1}}} \right)}}$ и без учета подвижности спинов внутри группы. Проведено моделирование сигналов ССИ и СЭ в гибкоцепных линейных полимерах со свободными концами, содержащих изолированные группы трех спинов 1/2, по формулам (11), (18) с корреляционной функцией (9) при различных значениях времени корреляции τc (рис. 1–3). Из рис. 2 и 3 видно, что для расчетных параметров при уменьшении τc влияние спинов, принадлежащих полимерной цепи, уменьшается, и трехспиновая группа проявляется активнее.

Рис. 1.

Форма линии F(ω) при разных константах ДДВ σ1 = 0, σ2 = –7 ⋅ 10–4с2, N = 20, τc = 0.001c.

Рис. 2.

Фурье-преобразование СЭ Fe(ω) при различных константах ДДВ σ1 = 0, σ2 = –7 ⋅ 10–4с2, N = 20, τ1 = 10–5c, τc = 0.001c.

Рис. 3.

Фурье-преобразование СЭ Fe(ω) при различных константах ДДВ σ1 = 0, σ2 = –7 ⋅ 10–4с2, N = 20, a = 0.05, τ1 = 10–5c, τc = 0.001c.

ЗАКЛЮЧЕНИЕ

В работе развита теория сигналов ССИ и СЭ в линейных полимерах, содержащих изолированные трехспиновые группы с произвольными константами ДДВ. На основе предложенной ранее теории [9] получена формула первичного эха в линейных полимерах, содержащих выделенные трехспиновые группы, Проведены расчеты сигналов ССИ и СЭ в линейных полимерах с группой трех спинов 1/2 с эквивалентыми и произвольными константами ДДВ с использованием точной аналитической формулы [6, 7]. Расчеты сигналов ССИ указывают на то, что в форме линии при одинаковых константах ДДВ наблюдаются 3 пика, а при различных константах ДДВ – 5, 7 пиков.

Моделирование сигналов без учета внутригрупповой подвижности спинов показало существенное влияние трехспиновых групп при увеличении температуры. Это связано с более быстрым усреднением до нуля ДДВ спинов в полимерных цепях. В дальнейшем предполагается рассматривать ДДВ спинов в изолированной группе с учетом подвижности ядер.

Предложенная теория позволяет исследовать влияние трехспиновых групп на сигналы ССИ и СЭ в полимерах, содержащих выделенные трехспиновые группы, и получать информацию о структуре и константах ДДВ группы.

Работа выполнена как часть государственного задания (номер государственной регистрации АААА-А19-119071190017-7).

Список литературы

  1. Andrew E.R., Bersohn R. // J. Chem. Phys. 1950. V. 18. No. 2. P. 159.

  2. Gutowsky H.S., Pake G.E. // J. Chem. Phys. 1950. V. 18. P. 162.

  3. Powles J.G., Mansfield P. // Phys. Lett. 1962. No. 2. P. 58.

  4. Moskvich Yu.N., Sergeev N.A., Dotsenko G.I. // Phys. Stat. Sol. A. 1975. P. 409.

  5. Чижик В.И. Квантовая радиофизика. СПбГУ, 2004. 689 с.

  6. Kulagina T.P., Karnaukh G.E., Golubeva I.Yu. // Appl. Magn. Reson. 2020. V. 51. No. 2. C. 155.

  7. Кулагина Т.П., Карнаух Г.Е., Голубева И.Ю. // Хим. физ. 2020. Т. 39. № 4. С. 31; Kulagina T.P., Karnaukh G.E., Golubeva I.Yu. // Russ. J. Phys. Chem. В. 2020. V. 14. No. 2. P. 290.

  8. Кулагина Т.П., Карнаух Г.Е., Андрианов С.А. // Бутлеровск. сообщ. 2013. № 7. С. 35.

  9. Кулагина Т.П., Карнаух Г.Е., Кузина А.Н., Смирнов Л.П. // Хим. физ. 2013. Т. 32. № 3. С. 62; Kulagina T.P., Karnaukh G.E., Kuzina A.N., Smirnov L.P. // Russ. J. Phys. Chem. В. 2013. V. 7. No. 2. P. 170.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал