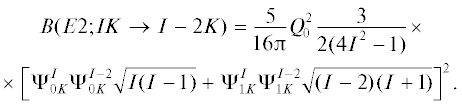Известия РАН. Серия физическая, 2022, T. 86, № 8, стр. 1112-1118
Исследование энергий и электромагнитных характеристик состояний отрицательной четности ядра 156Gd
П. Н. Усманов 1, *, А. И. Вдовин 2, А. Н. Нишонов 1
1 Наманганский инженерно-технологический институт
Наманган, Узбекистан
2 Международная межправительственная организация “Объединенный институт ядерных исследований”, Лаборатория теоретической физики имени Н.Н. Боголюбова
Дубна, Россия
* E-mail: usmanov1956.56@mail.ru
Поступила в редакцию 14.03.2022
После доработки 08.04.2022
Принята к публикации 22.04.2022
- EDN: YMXZKS
- DOI: 10.31857/S0367676522080257
Аннотация
В рамках феноменологической модели, учитывающей кориолисово взаимодействие состояний ротационных полос, исследуются свойств состояний отрицательной четности ядра. Рассматривается смешивание состояний октупольных полос на основаниях с ${}^{{156}}{\text{Gd}}{\text{.}}$ Рассматривается смешивание состояний октупольных полос на основаниях с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }},$ ${{{\text{1}}}^{ - }}.$ Для вычисления энергий, волновых функций и вероятностей $E{\text{1}}$-переходов получены аналитические выражения. Вычисленные значения энергий и отношений вероятностей $E{\text{1}}$-переходов хорошо согласуются с экспериментом.
ВВЕДЕНИЕ
По совокупности экспериментальных данных можно предположить, что в ядре ${}^{{156}}{\text{Gd}}$ обнаружены все или почти все уровни до энергии возбуждения 2 МэВ. Соответствующие экспериментальные данные оценены и систематизированы в работе [1]. Экспериментально известны развитые ротационные полосы с положительной четностью. В работах [2–5] нами проведены теоретические исследования состояний положительной четности этого ядра и обсуждены эффекты неадиабатичности, проявляющиеся в энергиях и электромагнитных характеристиках состояний полос. В спектре 156Gd выделены четыре ротационные полосы отрицательной четности с квантовыми числами оснований ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }},$ ${{{\text{1}}}^{ - }}$ и ${{2}^{ - }}.$ Нижайшая из указанных четырех полос – полоса с основанием ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ и энергией ${{E}_{x}} = {\text{1}}{\text{.2425}}$ МэВ. Эта полоса прослежена до спина ${{I}^{{{\pi }}}} = {\text{2}}{{{\text{5}}}^{ - }},$ в ней нарушена последовательность уровней с четными и нечетными спинами. Неадиабатичность видна также и в отношениях вероятностей $E{\text{1 - }}$переходов с уровней этой полосы на уровни основной полосы. В полосе с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и энергией основания 1.3665 МэВ известны три уровня с ${{I}^{{{\pi }}}} = {{{\text{1}}}^{ - }},{{3}^{ - }},{{5}^{ - }}.$ Две другие полосы построены на основаниях с ${{K}^{{{\pi }}}} = {{{\text{2}}}^{ - }}$ и энергиями 1.7805 МэВ и 1.9342 МэВ, в них известны по три уровня: ${{I}^{{{\pi }}}} = {{2}^{ - }},{{3}^{ - }},{{4}^{ - }}.$
В работе [6] рассматривалось смешивание полос с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }},$ ${{1}^{ - }},{{2}^{ - }},{{3}^{ - }}$ и численным методом определены энергии, волновые функции состояний. Описаны энергии полосы ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ до спина ${{I}^{{{\pi }}}} = {\text{1}}{{{\text{3}}}^{ - }}$ и изучены отношения вероятностей дипольных переходов. Экспериментально не были известны приведенные вероятности $E1$-переходов из октупольных состояний на уровни основной полосы. Головная энергия ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ полосы более близка расположена к ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ полосе, чем ${{K}^{{{\pi }}}} = {{{\text{2}}}^{ - }}.$ Поэтому в неадиабатичностях проявляющихся в состояниях ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ полосе, основную роль играет ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ полоса.
В настоящей работе для изучения свойств состояний отрицателъной четности ядра 156Gd предложена простая феноменологическая модель, которая учитывает смешивание состояний полос с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и ${{1}^{ - }}.$ Получены аналитические выражения для расчета энергий и волновых функций ротационных уровней. Исследуются неадиабатические эффекты, проявляющиеся в энергиях и вероятностях $E{\text{1 - }}$переходов из октупольно-колебательных полос. Модель хорошо описывает экспериментальные значения энергий. Нарушение четно-нечетной последовательности уровней в ротационной полосе с ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ и неадиабатичность в вероятностях $E{\text{1}}$-переходов объясняются смешиванием состояний октупольных полос ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и ${{1}^{ - }}.$
МОДЕЛЬ ЯДРА
Для изучения свойств низколежащих коллективных состояний в деформированных ядрах, гамильтониан ядра выбираем в следующем виде [7]
где(2)
$\begin{gathered} {{H}_{{KK{\kern 1pt} '}}}{\text{(}}I{\text{) = }}{{{{\omega }}}_{K}}{{{{\delta }}}_{{KK{\kern 1pt} '}}} - {{{{\omega }}}_{{rot}}}(I){{({{j}_{x}})}_{{KK{\kern 1pt} '}}}{{\chi }}(I,K){{{{\delta }}}_{{KK{\kern 1pt} ' \pm 1}}}, \\ {{\chi }}(I,0) = \frac{1}{2}{{\left[ {1 - {{{( - 1)}}^{I}}} \right]}^{{1{\text{/}}2}}},\,\,\,\,{{\chi }}(I,1) = {{\left[ {1 - \frac{2}{{I(I + 1)}}} \right]}^{{1{\text{/}}2}}}, \\ {{\chi }}(I,2) = {{\left[ {1 - \frac{6}{{I(I + 1)}}} \right]}^{{1{\text{/}}2}}}. \\ \end{gathered} $Волновую функцию ищем в виде:
(3)
$\begin{gathered} \left| {IMK} \right\rangle = \sqrt {\frac{{2I + 1}}{{16{{\pi }^{2}}}}} \sum\limits_{K{\kern 1pt} '} {\frac{{{{\psi }}_{{K{\kern 1pt} 'K}}^{I}}}{{\sqrt {1 + {{\delta }_{{K{\kern 1pt} ',0}}}} }}} \times \\ \times \,\,\left\{ {D_{{M,K{\kern 1pt} '}}^{I}(\theta )b_{{K'}}^{ + } + {{{( - 1)}}^{{I + K{\kern 1pt} '}}}D_{{M, - K{\kern 1pt} '}}^{I}(\theta )b_{{ - K{\kern 1pt} '}}^{ + }} \right\}\left| 0 \right\rangle , \\ \end{gathered} $Решая уравнение Шрёдингера
определяем собственные значения энергии и волновые функции состояний отрицательной четности. Полная энергия состояния определяется формулой Энергию вращающегося остова Erot(I) определяем, используя параметризацию Харриса(6)
${{E}_{{rot}}}(I) = \frac{1}{2}{{\Im }_{0}}\omega _{{rot}}^{2}(I) + \frac{3}{4}{{\Im }_{1}}\omega _{{rot}}^{4}(I),$(8)
$\begin{gathered} {{\omega }_{{rot}}}(I) = {{\left\{ {\frac{{\sqrt {I(I + 1)} }}{{2{{\Im }_{1}}}} + {{{\left[ {{{{\left( {\frac{{{{\Im }_{0}}}}{{3{{\Im }_{1}}}}} \right)}}^{3}} + \frac{{I(I + 1)}}{{4\Im _{1}^{2}}}} \right]}}^{{1{\text{/}}2}}}} \right\}}^{{1{\text{/}}3}}} + \\ + \,\,{{\left\{ {\frac{{\sqrt {I(I + 1)} }}{{2{{\Im }_{1}}}} - {{{\left[ {{{{\left( {\frac{{{{\Im }_{0}}}}{{3{{\Im }_{1}}}}} \right)}}^{3}} + \frac{{I(I + 1)}}{{4\Im _{1}^{2}}}} \right]}}^{{1{\text{/}}2}}}} \right\}}^{{1{\text{/}}3}}}. \\ \end{gathered} $ЧИСЛЕННЫЕ РАСЧЕТЫ
Расчеты проводились для изотопа $^{{156}}{\text{Gd}}{\text{.}}$ Спектр возбужденных уровней этого ядра получен в реакции ${\text{(}}n,n{\kern 1pt} '\gamma {\text{)}}$ [8]. Из двух полос с отрицательной четностью основание нижней полосы с ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ и энергией 1.2425 МэВ хорошо совпадает с рассчитанным в [9] коллективным октупольным состоянием. Будем рассматривать кориолисово смешивание состояний только известных из эксперимента полос с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и ${{{\text{1}}}^{ - }},$ что значительно упрощает теоретические расчеты. В этом случае для собственных значений энергии ε(I) в уравнении (5) имеем следующую формулу:
(9)
${{\varepsilon }}{{(I)}_{{0.1}}} = \frac{{{{{{\omega }}}_{{\text{0}}}} + {{{{\omega }}}_{{\text{1}}}}}}{2} \pm \sqrt {\frac{{{{{({{{{\omega }}}_{{\text{0}}}} - {{{{\omega }}}_{1}})}}^{2}} + 4{{\omega }}_{{rot}}^{2}(I)({{j}_{x}})_{{0.1}}^{2}}}{4}} .$При вычислении ${{E}_{{rot}}}\left( I \right)$ для инерционных параметров использовались значения ${{\Im }_{0}} = 42.739$ ${{{{\hbar }^{2}}} \mathord{\left/ {\vphantom {{{{\hbar }^{2}}} {{\text{МэВ}}}}} \right. \kern-0em} {{\text{МэВ}}}}$ и ${{\Im }_{1}} = 131.59$ ${{{{\hbar }^{4}}} \mathord{\left/ {\vphantom {{{{\hbar }^{4}}} {{\text{Мэ}}{{{\text{В}}}^{3}}}}} \right. \kern-0em} {{\text{Мэ}}{{{\text{В}}}^{3}}}},$ отличающиеся от значений, найденных по энергиям уровней основной полосы [2]. Наилучшее согласие вычисленных значений энергий с экспериментом получено при значениях ${{{{\omega }}}_{0}} = 1.33$ МэВ, ${{{{\omega }}}_{1}} = 1.235$ МэВ и (jx)0.1 = 2.142.
Рассчитанные энергии уровней представлены на рис. 1, где также приведены данные экспериментов. Кроме того, здесь же показаны состояния основной полосы (${{K}^{{{\pi }}}} = 0_{1}^{ + }$). Отметим, что в вычислениях энергий уровней основной полосы не учитывалось смешивание уровней основной полосы с другими полосами, т.е. на рисунке приведены адиабатические значения энергий состояний основной полосы. Как видно из рисунка, предложенная нами модель хорошо описывает экспериментальные энергии.
Рис. 1.
Сравнение теоретических и экспериментальных значений энергий состояний основной полосы и полос отрицательной четности с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и 1–.

На рис. 2 приведены зависимости внутренней энергии ${{\varepsilon }}(I)$ состояний полос с ${{K}^{{{\pi }}}} = {{1}^{ - }}$ и ${{K}^{{{\pi }}}} = {{0}^{ - }}$ от спина I. Из рисунка видно, что внутренняя энергия ${{\varepsilon }}(I)$ состояний с четными спинами полосы ${{K}^{{{\pi }}}} = {{1}^{ - }}$ является постоянной, т.е. не зависит от спина. Причина этого в том, что в нашей схеме они не смешиваются с состояниями полос с ${{K}^{{{\pi }}}} \geqslant {{2}^{ - }}.$ С ростом углового момента увеличивается кориолисова взаимодействия между полосами, поэтому энергии нечетных состояний ${{K}^{{{\pi }}}} = {{1}^{ - }}$ и ${{K}^{{{\pi }}}} = {{0}^{ - }}$ полос сильнее отталкиваются друг от друга.
В адиабатическом приближении приведенные вероятности E2 переходов внутри ротационной полосы имеют следующий вид:
(10)
$B(E2;IK \to (I - 2)K) = \frac{5}{{16\pi }}{{e}^{2}}Q_{0}^{2}{{\left[ {C_{{IK;20}}^{{I - 2,K}}} \right]}^{2}}.$В табл. 1 представлены сравнения экспериментальных [10, 11] и вычисленных значений приведенных вероятностей $B(E2;Igr \to (I - 2)gr)$ внутриполосных переходов в основной полосе, которые дают хорошие согласия. Отметим, что в вычислениях $B(E2)$ внутренний квадрупольный момент был взять равным ${{Q}_{0}} = 6.87$ барн [12].
В данной схеме для собственных функций состояний отрицательной четности с учетом взаимодействия Кориолиса имеем следующую формулу:
(11)
${{\psi }}_{{K,K{\kern 1pt} '}}^{I}(I) = \frac{{\Phi _{{K,K{\kern 1pt} '}}^{I}}}{{\sqrt {\sum\limits_{\nu = 0}^1 {{{{\left[ {\Phi _{{K,\nu }}^{I}} \right]}}^{2}}} } }},$(12)
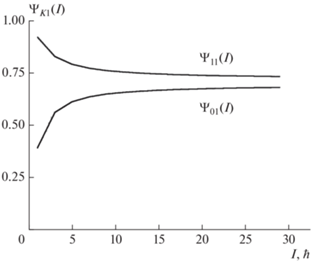
$\begin{gathered} {{{\text{Ф}}}_{{{\text{00}}}}} = {{{{\omega }}}_{{\text{0}}}} - {{{{\varepsilon }}}_{{\text{1}}}}{\text{(}}I{\text{),}}\,\,\,\,{{{\text{Ф}}}_{{{\text{11}}}}} = - {\text{ (}}{{{{\omega }}}_{{\text{1}}}} - {{{{\varepsilon }}}_{{\text{0}}}}{\text{(}}I{\text{)),}} \\ {{{\text{Ф}}}_{{{\text{01}}}}} = \frac{{\text{1}}}{{\sqrt {\text{2}} }}{{{{\omega }}}_{{rot}}}{\text{(}}I){{({{j}_{x}}{\text{)}}}_{{{\text{01}}}}},\,\,\,\,{{{\text{Ф}}}_{{{\text{10}}}}} = - \frac{{\text{1}}}{{\sqrt {\text{2}} }}{{{{\omega }}}_{{rot}}}{\text{(}}I){{({{j}_{x}}{\text{)}}}_{{{\text{01}}}}}. \\ \end{gathered} $На рис. 3 представлена структура состояний октупольной ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ полосы. Из рисунка видно, что даже при низких значениях спина кориолисово смешивание является заметным и больших значениях спина компоненты ${{\psi }_{{11}}}(I)$ и ${{\psi }_{{01}}}(I)$ имеют весы 60 и 40%, соответственно. Этот эффект должен проявляться в E2-переходах внутри октупольных полос и E1 переходах из них на состояния основной полосы.
В рамках данной модели для вероятностей $E1$-переходов из октупольных состояний на уровни основной полосы имеем:
(13)
$\begin{gathered} B(E1;I{{K}^{\pi }};(I \pm 1)gr) = \\ = \,\,{{\left[ {{{m}_{0}}{{\psi }}_{{0K}}^{I}C_{{I0;10}}^{{(I \pm 1)0}} - \sqrt 2 {{m}_{1}}{{\psi }}_{{1K}}^{I}C_{{I1;1 - 1}}^{{(I \pm 1)0}}} \right]}^{2}}, \\ \end{gathered} $Выписав явно выражения для коэффициентов Клебша–Гордана, получим:
(14)
$\begin{gathered} B(E1;I{{K}^{{{\pi }}}} \to (I - 1)gr) = \\ = {{\left\{ { - {{m}_{0}}\sqrt {\frac{I}{{2I + 1}}} {{\psi }}_{{0{\text{К}}}}^{I} - {{m}_{1}}\sqrt {\frac{{I + 1}}{{2I + 1}}} {{\psi }}_{{1{\text{К}}}}^{I}} \right\}}^{2}}, \\ \end{gathered} $(15)
$\begin{gathered} B(E1;I{{K}^{{{\pi }}}} \to (I + 1)gr) = \\ = {{\left\{ {{{m}_{0}}\sqrt {\frac{{I + 1}}{{2I + 1}}} {{\psi }}_{{0{\text{К}}}}^{I} - {{m}_{1}}\sqrt {\frac{I}{{2I + 1}}} {{\psi }}_{{1{\text{К}}}}^{I}} \right\}}^{2}}. \\ \end{gathered} $Отношения вероятностей $E1$-переходов из октупольных состояний на уровни основной полосы имеют вид:
(16)
$\begin{gathered} {{R}_{{IK}}} = \frac{{B(E1;IK \to (I + 1)gr)}}{{B(E1;IK \to (I - 1)gr)}} = \\ = {{\left| {\frac{{{{\psi }}_{{K,0}}^{I}(I)\sqrt {(I + 1)} - Z.{{\psi }}_{{K,1}}^{I}(I)\sqrt I }}{{{{\psi }}_{{K,0}}^{I}(I)\sqrt I + Z.{{\psi }}_{{K,1}}^{I}(I)\sqrt {(I + 1)} }}} \right|}^{2}}, \\ \end{gathered} $В табл. 2 представлены вычисленные значения отношений $R_{{IK}}^{{}}$ вероятностей $E1 - $переходов из состояний ${{K}^{{{\pi }}}} = {{1}^{ - }}$ полосы, которые сравниваются с экспериментальными данными [1, 13–17]. Экспериментальные значения отношений $R_{{IK}}^{{{\text{эксп}}}}$ отличаются от адиабатических значений $R_{{IK}}^{А}$ в 1.5–2 раза. Кроме того, с ростом спина адиабатические значения увеличиваются, тогда как для экспериментальных значений $R_{{IK}}^{{}}$ видна обратная тенденция. Наши расчеты такое неадиабатическое поведение $R_{{IK}}^{{}}$ воспроизводят.
Таблица 2.
Теоретические и эксприментальные значения отношений ${{R}_{{IK}}} = {{B(E1;{{I}^{{{\pi }}}}K \to I_{1}^{ + }gr)} \mathord{\left/ {\vphantom {{B(E1;{{I}^{{{\pi }}}}K \to I_{1}^{ + }gr)} {B(E1;{{I}^{\pi }}K \to I_{2}^{ + }gr)}}} \right. \kern-0em} {B(E1;{{I}^{\pi }}K \to I_{2}^{ + }gr)}}$ для E1-переходов с уровней Kπ = 1–-полос на уровни основной полосы
| IπK | $I_{1}^{ + }gr$ | $I_{2}^{ + }gr$ | Эксп. | Теория | |
|---|---|---|---|---|---|
| настоящая работа | правило Алаги | ||||
| 1–1 | 2+gr | 0+gr | 1.21(1) [1] 1.16(11) [16] 1.23(13) [9] |
1.40 | 0.5 |
| 3–1 | 4+gr | 2+gr | 0.81(3) [1] 0.80(12) [15] 0.5$\left( {_{{ - 0.3}}^{{ + \infty }}} \right)$ [17] 0.872(233) [18] 0.746(50) [19 ] |
1.07 | 0.75 |
| 5–1 | 6+gr | 4+gr | 0.75(7) [1] 0.5(3) [17] 0.746(67) [19 ] |
0.99 | 0.83 |
| 7–1 | 8+gr | 6+gr | 1.27(3) [1] 0.71(8) [17] |
0.96 | 0.88 |
| 9–1 | 10+gr | 8+gr | 0.42 (18) [1] 0.43(12) [17] |
0.93 | 0.90 |
| 11–1 | 12+gr | 10+gr | 0.63(7) [1] | 0.92 | 0.92 |
| 13–1 | 14+gr | 12+gr | – | 0.91 | 0.93 |
Вычисленные значения вероятностей $E1 - $переходов из состояний октупольных полос с ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ представлены в таблице 3 вместе с имеющимися экспериментальными данными [1]. Отметим, что вероятности $E1 - $переходов и их отношения вычислены при значениях m0 = 0.15$\sqrt {{\text{W}}{\text{.u}}.} $ и m1 = 0.0056$\sqrt {{\text{W}}{\text{.u}}.} $
Таблица 3.
Приведенные вероятности E1-переходов из состояний ${{K}^{{{\pi }}}} = {{1}^{ - }}$ полосы на состояния основной полосы (в ед. Вайскопфа W.u.)
| $I_{i}^{\pi }{{K}_{i}}$ | $I_{f}^{{}}{{K}_{f}}$ | $B(E1;{{I}_{i}}{{1}^{ - }} \to {{I}_{i}}gr)$ (W.u.) | |
|---|---|---|---|
| эксп. [1] | ${{m}_{0}} = 0.15$ ${{m}_{1}} = 0.0056$ |
||
| $1_{{}}^{ - }1$ | $0_{{}}^{ + }gr$ | 0.0018(7) | 0.0015 |
| $1_{{}}^{ - }1$ | $2_{{}}^{ + }gr$ | $0.0025_{{ - 18}}^{{ + 8}}$ | 0.0020 |
| $3_{{}}^{ - }1$ | $2_{{}}^{ + }gr$ | 0.00098(21) | 0.0034 |
| $3_{{}}^{ - }1$ | $4_{{}}^{ + }gr$ | 0.000777(16) | 0.0037 |
| $2_{{}}^{ - }1$ | $2_{{}}^{ + }gr$ | $ < {\kern 1pt} 3.2 \cdot {{10}^{{ - 5}}}$ | $3.1 \cdot {{10}^{{ - 5}}}$ |
| $5_{{}}^{ - }1$ | $4_{{}}^{ + }gr$ | $0.00085_{{ - 69}}^{{ + 15}}$ | 0.0042 |
| $4_{{}}^{ - }1$ | $4_{{}}^{ + }gr$ | $ < {\kern 1pt} 4.0 \cdot {{10}^{{ - 5}}}$ | $3.1 \cdot {{10}^{{ - 5}}}$ |
| $5_{{}}^{ - }1$ | $6_{{}}^{ + }gr$ | $0.00064_{{ - 52}}^{{ + 10}}$ | 0.0042 |
| $7_{{}}^{ - }1$ | $6_{{}}^{ + }gr$ | – | 0.0047 |
| $7_{{}}^{ - }1$ | $8_{{}}^{ + }gr$ | – | 0.0045 |
В рамках используемой модели приведенные вероятности $E2$-переходов внутри октупольных ротационных полос имеют следующий вид:
На рис. 4 представлены вычисленные по формуле (17) значения приведенных вероятностей Е2-переходов внутри ${{K}^{{{\pi }}}} = {{0}^{ - }}$ и ${{1}^{ - }}$ полосах, которые сравниваются с адиабатическими значениями. Из сравнения видно, что теоретические значения $B(E2)$ вычисленные с учетом кориолисова смешивания состояний отличаются от адиабатических значений. Учет смешивания полос приводит к уменьшению $B(E2;I{{0}^{ - }} \to (I - 2){{0}^{ - }})$ и увеличению $B(E2;I{{1}^{ - }} \to (I - 2){{1}^{ - }}).$ Это связано с тем, что учет взаимодействия полос приводит к увеличению энергий состояний ${{K}^{{{\pi }}}} = {{0}^{ - }}$ полосы (т.е. уменьшению эффективного момента инерции) и уменьшению энергий состояний полосы с ${{K}^{{{\pi }}}} = {{1}^{ - }}$ (т.е. увеличению эффективного момента инерции) (см. рис. 2). Полосы с большими моментами инерции имеют большие квадрупольные моменты$Q_{{\text{0}}}^{{}}$. Внутриполосные переходы прямо пропорциональны $Q_{{\text{0}}}^{{}}$ [18]. К сожалению, для данных переходов отсутствуют экспериментальные данные. Поэтому было бы интересно экспериментально исследовать $E2$-переходы внутри октупольных полос.
Рис. 4.
Приведенные вероятности Е2-переходов внутри полос с ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ и 0–. (${{B}^{A}}(E2;K = 1)$ – Адиабатические значения для ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ полосы; ${{B}^{A}}(E2;K = 0)$ – адиабатические значения для ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ полосы; $B(E2;K = 1)$ – вычисленные по формуле (17) для ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}$ полосы; $B(E2;K = 0)$ – вычисленные по формуле (17) для ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ полосы).

ЗАКЛЮЧЕНИЕ
Для изучения свойств октупольных состояний ядра $^{{156}}{\text{Gd}}$ предложена простая феноменологическая модель, которая учитывает смешивание состояний полос с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и ${{1}^{ - }}.$ Получены аналитические выражения для расчета энергий и волновых функций ротационных уровней.
Наши расчеты, проведенные с учетом кориолисова смешивания состояний отрицательной четности полос с ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и ${{1}^{ - }},$ удовлетворительно воспроизводят экспериментальные данные. Используемая модель качественно описывает нарушение четно-нечетной последовательности уровней в ротационной полосе ${{K}^{{{\pi }}}} = {{{\text{1}}}^{ - }}.$ Показано, что эффект смешивания полос приводит к существенным отклонениям от адиабатичности у вероятностей $E2$-переходов внутри ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и ${{1}^{ - }}$ полос и отношений приведенных вероятностей $E1$-переходов RIK = B(E1; IK → (I + 1)gr)/B(E1; IK → (I – 1)gr) из состояний ${{K}^{{{\pi }}}} = {{{\text{0}}}^{ - }}$ и ${{1}^{ - }}$ полос.
Проведенный расчет и анализ известных экспериментальных данных указывает: чтобы улучшить теоретические описание эксперимента, необходимо учитывать смешивание состояний полос с Kπ ≥ 2–. В ядре $^{{156}}{\text{Gd}}$ экспериментально известны две полосы с ${{K}^{{{\pi }}}} = {{{\text{2}}}^{ - }},$ но не обнаружены состояния с квантовой характеристикой ${{K}^{{{\pi }}}} = {{{\text{3}}}^{ - }}$ и не изучены внутриполосные переходы в октупольных полосах. Поэтому были бы интересны дополнительные экспериментальные и теоретические исследования для классификации высоко лежащих уровней по $K,$ где плотность состояний существенно высока.
Список литературы
Reich C.W. // Nucl. Data Sheets. 2012. V. 113. P. 2537.
Usmanov P.N., Yusupov E.K. // IIUM Engin. J. 2021. V. 22. No. 1. P. 167.
Усманов П.Н., Вдовин А.И., Юсупов Э.К. // Изв. РАН. Сер. физ. 2021. Т. 85. № 10. С. 1423; Usmanov P.N., Vdovin A.I., Yusupov E.K. // Bull. Russ. Acad. Sci. Phys. 2021. V. 85. No. 10. P. 1102.
Усманов П.Н., Вдовин А.И., Юсупов Э.К. // Сб. тезисов III Межд. науч. форума “Ядерн. наука и технологии” (Алматы, 2021). С. 67.
Михайлов И.Н., Усманов П.Н., Бриансон Ш. // ЯФ. 1991. Т. 54. С. 1239.
Громов К.Я., Усманов П.Н., Холматов А.Х. и др. // Изв. РАН. Сер. физ. 1993. Т. 57. С. 91.
Михайлов И.Н., Усманов П.Н., Бриансон Ш. // ЯФ. 1995. Т. 58. С. 1371.
Бондаренко В.А., Григорьев Е.П., Прокофьев П.Т. // Изв. АН СССР. Сер. физ. 1981. С. 2141.
Григорьев Е.П., Соловьев В.Г. Структура четных деформированных ядер. М.: Наука, 1974.
Sie S.H., Ward D., Geiger J.S. et al. // Nucl. Phys. 1977. V. A 291. P. 443.
Kearns F., Varley G., Dracoulis G.D. et al. // Nucl. Phys. 1977. V. A 278. P. 109.
Бегжанов Р.Б., Беленький В.М., Залюбовский И.И. Справочник по ядерной физике. Ташкент: Фан, 1989.
Backlin A., Hedin G., Fogelberg B. et al. // Nucl. Phys. 1982. V. A 380. P. 189.
McMillan D.J., Hamilton J.H., Pinajian J.J. // Phys. Rev. 1971. V. C 4. P. 542.
Konijn J., Be Boer F.W.N., Van Poelgeest A. et al. // Nucl. Phys. 1981. V. A352. P. 191.
McGowan F.K., Milner W.T. // Phys. Rev. 1981. V. C 23. P. 1926.
McGowan F.K. // Phys. Rev. 1981. V. 24. P. 1803.
Okhunov A.A., Hasan Abu Kassim, Usmanov Ph.N. // Sains Malays. 2011. V. 40. No. 1. P. 13.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая