Известия РАН. Серия физическая, 2023, T. 87, № 1, стр. 115-119

ВВЕДЕНИЕ

Обобщенная хаотическая синхронизация – одно из наиболее интересных явлений радиофизики [1, 2]. Данное явление характеризуется существованием связи между состояниями взаимодействующих осцилляторов в виде функционального соотношения (в общем виде – функционала) [2, 3]. Примечательно, что данная синхронизация наблюдается в системах самой различной природы и может возникать при однонаправленной и взаимной связи.

Обобщенная синхронизация обладает широким потенциалом для применения в различных сферах человеческой деятельности, от исследования взаимодействия систем различной природы [4] до скрытой передачи информации [5] и разработки медицинского оборудования [6].

В контексте данной работы явление мультистабильности заключается в том, что при фиксированных значениях управляющих параметров при определенных значениях безразмерного времени (в случае потоковых систем), либо при определенной итерации (в случае дискретных отображений) в зависимости от начальных условий обобщенная синхронизация может как наблюдаться, так и отсутствовать. Это возможно в режиме перемежающейся обобщенной синхронизации [7], характеризующейся чередованием временных интервалов синхронной и асинхронной динамики при фиксированных значениях управляющих параметров. Таким образом, мультистабильность следует рассматривать в контексте синхронизации, не связывая с определениями стабильности (устойчивости) фазовых траекторий.

На данный момент мультистабильность находится в процессе тщательного изучения. В нашей прошлой работе было показано, что данное явление наблюдается в хаотических системах с простой топологией аттрактора (с аттрактором ленточного типа) [8]. Целью данной работы является исследование возможности существования мультистабильности вблизи границы обобщенной синхронизации в хаотических системах со сложной (двулистной) топологией аттрактора [9].

МАТЕРИАЛЫ И МЕТОДЫ

В качестве исследуемой модели было выбрано множество пар систем Лоренца, связанных как однонаправленно, так и взаимно, описываемое следующей системой уравнений [10, 11]:

где $i = 1,2, \ldots ,N$ – индекс пары систем ($N \approx 4000$), $\sigma = 10,$ $b = 2,$ ${{r}_{1}} = 40,$ ${{r}_{2}} = 35,$ $\delta _{1}^{i} = 0,$ $\delta _{2}^{i} \in \left[ {0,{{{10}}^{{ - 10}}}} \right]$ – случайные числа, распределенные равномерно в указанном отрезке, характеризующие малую расстройку введенную между вторыми системами каждой пары. Расстройка $\delta _{2}^{i}$ введена для того, чтобы избежать ловушку численного счета. Параметры связи ${{{{\varepsilon }}}_{1}} = 0,$ ${{{{\varepsilon }}}_{2}} = {{\varepsilon }}$ в случае однонаправленной связи, и ${{{{\varepsilon }}}_{{1,2}}} = {{\varepsilon }}$ при взаимной связи. Значения этих параметров выбраны таким образом, чтобы после переходного процесса режим обобщенной синхронизации всегда возникал при некоторой критической величине параметра связи вне зависимости от начальных условий. Начальные условия для первых систем пары всегда выбирались одинаковыми, а для вторых – всегда разными, равномерно распределенными по аттракторам второй системы.

Данная система уравнений решалась при помощи классической интегрирующей схемы Рунге–Кутта (4 порядка) с шагом 0.001.

Обычно для исследования обобщенной синхронизации используется метод вспомогательной системы [12] в связи с простотой его реализации и достаточно высокой точностью. Недостатком данного подхода является невозможность его применения в случае взаимной связи [13]. В связи с этим, для исследования был использован более универсальный метод – расчет локальных показателей Ляпунова [14, 15].

Данный подход характеризуется расчетом показателей Ляпунова в скользящем ограниченном интервале безразмерного времени, что позволяет в зависимости от его размера устанавливать либо более точные значения показателей, соответствующие аттракторам систем в целом, либо следить за временной динамикой, что и требовалось в данном случае. В данной работе интервал был установлен равным 3500, как наибольший компромисс между точностью и динамикой исследуемой величины.

В качестве исследуемой величины выступает величина второго по старшинству локального ляпуновского показателя (условного, зависящего от параметра связи, при однонаправленной связи, либо обычного при взаимной). Обобщенная синхронизация наступает в момент, когда указанный показатель переходит из положительной области в отрицательную, тем самым указывая, что между системами наблюдается более устойчивая динамика.

На практике, в связи с небольшой погрешностью, обусловленной ограниченным временным интервалом и численным расчетом, используется менее строгий критерий. Системы можно считать синхронизованными, в контексте обобщённой синхронизации, если величина второго старшего локального показателя ${{\Lambda }}_{2}^{i}$ не превышает наперед заданную небольшую константу ${{\Delta :}}$ ${{\Lambda }}_{2}^{i} < {{\Delta ,}}$ ${{\Delta }} = 0.005.$

Для оценки мультистабильности по аналогии с работой [8] была рассчитана ее мера как вероятность детектирования асинхронных (в смысле обобщенной синхронизации) участков временной динамики, определяемая по формуле:

где $M \gg 1$ – число осцилляторов, участвующих в рассмотрении, $n\left( {{{\Lambda }}_{2}^{i}} \right)$ – количество систем, находящихся в синхронизме с i-м осциллятором.

Данная характеристика позволяет оценить степень асинхронной динамики, наблюдаемой при определенном значении безразмерного времени. Если при любых начальных условиях обобщенная синхронизация не возникает (например, при значении параметра связи ${{\varepsilon }} = 0$), то ${{P}_{a}} = 1.$ Напротив, если вне зависимости от начальных условий после переходного процесса всегда наблюдается синхронная динамика, то ${{P}_{a}} = 0.$ При ситуации, когда только какая-то часть начальных условий демонстрирует синхронную динамику, будет выполняться условие $1 > {{P}_{a}} > 0.$ Таким образом, в последнем случае будет наблюдаться явление мультистабильности, что и позволяет использовать данную характеристику в качестве оценки ее меры.

РЕЗУЛЬТАТЫ

Сперва были рассчитаны бассейны притяжения второй системы Лоренца (см. рис. 1). Данная характеристика строилась следующим образом. При фиксированных значениях управляющих параметров и начальных условий первой системы изменялись начальные условия второй системы (${{x}_{2}}$ и ${{y}_{2}}$). Затем, после переходного процесса при некотором значении безразмерного времени определялось наличие, либо отсутствие обобщенной синхронизации.

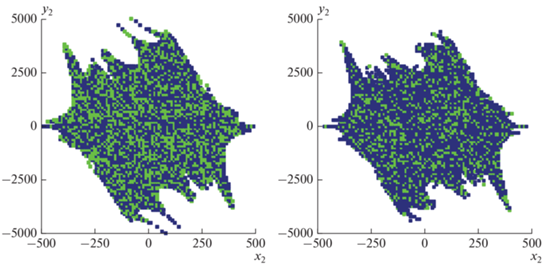
Из рис. 1 видно, что в зависимости от начальных условий обобщенная синхронизация может как присутствовать, так и отсутствовать, что подтверждает существование мультистабильности. Причем это утверждение справедливо как при однонаправленном типе связи, так и при взаимном.

Стоит отметить, что все же имеются различия в динамике указанной характеристики в зависимости от типа связи. При однонаправленной связи при небольшом отклонении параметра связи от критического значения с изменением безразмерного времени можно наблюдать чередование бассейнов, демонстрирующих преимущественно синхронную динамику, и бассейнов, характеризующихся в большей мере асинхронной динамикой.

В то же время, при взаимной связи этого не наблюдается. При увеличении безразмерного времени соотношение начальных условий, демонстрирующих асинхронную и синхронную динамику, остается практически неизменным. Это выражается в том, что получить при таком типе связи бассейны притяжения, меняющие в целом свою динамику в контексте обобщенной синхронизации, не предоставляется возможным для данной модели.

Наконец, в работе была численно рассчитана зависимость меры мультистабильности (2), усредненной по времени, от параметра связи при однонаправленной и взаимной связи (см. рис. 2).

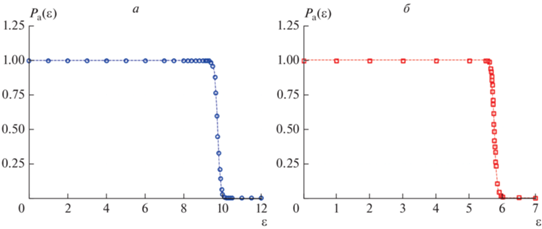
Видно, что при определенных значениях параметра связи (например, ${{\varepsilon }} > 10.2$ и ${{\varepsilon }} > 6$ в случае однонаправленной и взаимной связи, соответственно) мера мультистабильности ${{P}_{a}} \approx 0,$ что соответствует режиму, когда практически при любых значениях начальных условий после переходного процесса устанавливается режим обобщенной синхронизации и, соответственно, мультистабильность отсутствует. Кроме того, имеются интервалы значений параметра связи, при которых наблюдается мультистабильность, когда $0 \leqslant {{P}_{a}} \leqslant 1{\text{:}}$ ${{\varepsilon }} \in \left[ {9.3;10.0} \right]$ и ${{\varepsilon }} \in \left[ {5.55;6} \right]$ при однонаправленной и взаимной связи, соответственно. Это подтверждает выводы, сделанные после расчета бассейнов притяжения.

Данная характеристика также хорошо аппроксимируется функцией спадающего сигмоида вида $\frac{1}{{1 + {\text{exp}}\left( {\frac{{x - a}}{b}} \right)}},$ где $a,~b$ – некоторые вещественные параметры (см. пунктирные линии на рис. 2). В нашем случае параметры $a = 9.74,$ $b = 0.08$ при однонаправленной связи и $a = 5.749,$ $b = 0.04$ при взаимной.

Примечательно сходство между собой кривых в обоих случаях связи. Если для характеристики, соответствующей взаимной связи, уменьшить масштаб оси на 1.7, а затем аппроксимировать полученную зависимость, то ее коэффициенты будут $a = 9.774,$ $b = 0.068.$ Отметим, что при оценке коэффициентов аппроксимации ошибки не превысили 0.0015, а остаточная сумма квадратов оказалась не больше 0.011, что говорит о достоверности проведенной оценки. Сравнив между собой эти коэффициенты с параметрами аппроксимации, полученными в случае однонаправленной связи, можно убедиться, что данные кривые отличаются между собой незначительно и только численно. Однако, стоит отметить, что данный вывод справедлив конкретно для данной рассматриваемой модели и указанная характеристика может сильно отличаться в зависимости от типа связи при рассмотрении других нелинейных систем.

ЗАКЛЮЧЕНИЕ

Таким образом, на примере систем Лоренца при помощи метода локальных ляпуновских показателей установлено, что мультистабильность в контексте обобщенной синхронизации может возникать не только в системах с относительно простой (однолистной) топологией аттрактора (с аттрактором ленточного типа) [8], но и в системах со сложной (двулистной) структурой, причем как при однонаправленной связи, так и при взаимной. Сделанный вывод подтверждается численно рассчитанными характеристиками: бассейнами притяжения второй системы Лоренца и зависимостью меры мультистабильности, усредненной по времени, от параметра связи.

Из полученных результатов также следует, что тип перемежаемости вблизи границы обобщенной синхронизации не зависит от типа связи между системами (однонаправленной или взаимной), но определяется топологией аттракторов (простой или сложной) взаимодействующих систем. В системах со сложной топологией наблюдается перемежаемость перескоков [11], а в случае систем с простой топологией – “on-off” перемежаемость [8].

Полученные данные согласуются с результатами других работ, например критическое значение параметра связи соответствует значению, получаемому из спектра ляпуновских показателей [16].

Полученные результаты могут быть использованы при изучении систем со сложной топологией аттрактора на предмет наличия мультистабильности. Стоит отметить, что полученные выкладки можно также использовать при построении схемы для скрытой передачи информации, основанной на системах с взаимной связью. Если подобрать управляющие параметры так, чтобы при любых начальных условиях возникала обобщенная синхронизация, то при добавлении полезного сигнала к состоянию одного из осцилляторов (передатчика) в моменты ${{P}_{a}} = 0,$ по состоянию второго осциллятора (приемника) имелась бы возможность однозначного декодирования сигнала, который в необработанном виде выглядел бы как шум.

Работа выполнена при финансовой поддержке Совета по грантам Президента Российской Федерации для государственной поддержки молодых российских ученых и по государственной поддержке ведущих научных школ Российской Федерации (проект № МД-18.2022.1.2).