1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 84, № 3, 2022

Коллоидный журнал, 2022, T. 84, № 3, стр. 318-327

Эволюция статистических характеристик функций распределения частиц по размерам в микропорошках при их темпоральной обработке в шаровой планетарной мельнице

В. И. Савенко *

Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский проспект, 31, корп. 4, Россия

* E-mail: visavenko@rambler.ru

Поступила в редакцию 02.03.2022
После доработки 10.04.2022
Принята к публикации 11.04.2022

Полный текст (PDF)

Аннотация

В рамках стохастической динамической модели процесса механической обработки металлических микропорошков в шаровой планетарной мельнице получены теоретические темпоральные (изменяющиеся во времени) зависимости параметрических характеристик логарифмически нормальных функций распределения частиц по их размерам для ряда металлов, принадлежащих к группам IIA, IIIB, IVA и VIA таблицы Менделеева. На основе решений кинетического уравнения Фоккера-Планка-Колмогорова теоретически рассчитаны вариации во времени наиболее информативных моментов указанных функций распределения. Показано, что предложенная методика обладает достаточными прогностическими возможностями для правильного предсказания временнóго поведения основных статистических характеристик канонических ансамблей вышеперечисленных порошковых систем, а также для темпорального гранулометрического анализа состава этих систем при их механообработке в шаровых мельницах.

Ключевые слова: металлический микропорошок, шаровая планетарная мельница, функция распределения частиц по размерам, кинетическое уравнение Фоккера-Планка-Колмогорова

ВВЕДЕНИЕ

Как известно, металлические и полуметаллические порошки являются исходным сырьем для многих промышленных металлургических технологий [1, 2]. Такие технологии включают, как правило, стадию механической обработки (механоактивацию) порошковых материалов в мельницах различного типа [3]. Механообработка используется, в частности, для получения заранее заданных гранулометрических характеристик порошка, которые существенно зависят от физико-химических условий и продолжительности процесса [4–19].

В научной литературе опубликовано достаточное количество исследований, в которых этому вопросу уделяется должное внимание [4–10, 14, 17, 19]. Однако в большинстве из них рассматриваются лишь конкретные порошковые системы, а анализ временнóго поведения статистических характеристик этих систем (канонических ансамблей микрочастиц) носит узкоспециальный и эмпирический характер. Такой подход не позволяет заранее предсказать влияние условий механической обработки порошковых материалов в каждом новом случае и, в частности, оптимизировать длительность процесса, и/или заранее выбрать подходящую размольную среду.

Исключением в массиве таких исследований является цикл работ В.П. Малышева с сотрудниками (см. [20,21] и др.). В статьях, опубликованных этой группой, изложены результаты теоретических разработок вероятностно-статистической модели, которая описывает кинетику процесса измельчения руд и обладает немалыми прогностическими возможностями. Такая модель позволяет успешно предсказывать временные изменения фракционного состава статистического канонического ансамбля упруго-хрупких частиц при их механообработке в мельницах различного типа. Однако физико-механические характеристики обрабатываемого материала, а, следовательно, и вероятностные параметры, определяющие гранулометрический состав отдельных фракций и межфракционные кинетические переходы в таком ансамбле, предполагаются в данной модели не зависящими от времени механообработки. Такая модель не может служить для описания процесса механической обработки металлических микропорошков, если этот процесс включает пластическую моду изменения формы и/или объема микрочастиц. Влияние такой моды на процесс механообработки микропорошка зачастую приводит к заметному изменению физико-механических характеристик материала микрочастиц в этом процессе. Указанное обстоятельство, в свою очередь, может вызвать радикальные изменения динамики и режимов механообработки такого микропорошка.

Ранее в работе [22] для успешного решения вышеупомянутых проблем была предложена простейшая математическая анзац-модель (эвристическое кинетическое уравнение) процесса механообработки металлических и полуметаллических микропорошковых материалов, включающая в рассмотрение пластическую деформацию микрочастиц, а также учитывающая динамический и стохастический факторы процесса. Модель позволила на основе знания физико-химических, кинематических и граничных условий процесса механообработки описать и/или заранее предсказать вариации во времени статистических характеристик функций распределения микропорошковых частиц по их объемным, и/или линейным размерам. В рамках этой модели на основе анализа массива экспериментальных данных, полученных авторами [22], было установлено, что во всех случаях механической обработки металлических и полуметаллических микропорошков в шаровых планетарных мельницах статистические функции, описывающие распределения частиц по размерам в этих микропорошках, принадлежат к группе логнормальных (логарифмических гауссовых) функций [23].

В данной работе для достижения той же цели использован иной, более общий и универсальный подход. В основе этого подхода лежит получение и анализ решений кинетического уравнения Фоккера-Планка-Колмогорова (ФПК) [24–28], которое описывает темпоральное поведение соответствующих логнормальных функций распределения при заданных граничных и начальных условиях процесса механообработки микропорошков.

МАТЕРИАЛЫ И МЕТОДЫ

Экспериментально-теоретический анализ с применением уравнения ФПК базировался на результатах экспериментов по механообработке микропорошков металлов и полуметаллов, принадлежащих к IIА, IIIB, IVА и VIA группам таблицы Менделеева, которые были опубликованы ранее в работе [22]. Для полного понимания изложенных в данном сообщении новых результатов и выводов здесь необходимо напомнить, что в экспериментах, описанных в [22] использовали следующие кристаллические микропорошки промышленного производства: алюминий марки АСД-4 (средний объемно-взвешенный линейный размер (диаметр) частиц dv = 20–30 мкм), вольфрам ПВ-2 (dv = = 10–20 мкм), гафний ГФМ (dv = 10–20 мкм), магний МПФ-4 (dv = 150–250 мкм), никель ПНК-УТ3 (dv = 8–15 мкм), титан ПТМ-1 (dv = 50–60 мкм), цирконий ИМП (dv = 10–20 мкм), а также аморфный бор Б-99В (dv = 2–4 мкм).

Механообработка микропорошков проводилась в лабораторной планетарно-центробежной шаровой мельнице АГО-2У с водяным охлаждением. Мелющими телами служили изготовленные из сплава ШХ-15 шары диаметром 6 мм и общей массой М = 100 г. Масса порошковой пробы в индивидуальном эксперименте составляла m = 10 г. Круговая скорость вращения цилиндрических барабанов вокруг собственных осей – Ω = 1820 об/мин, круговая скорость орбитального вращения цилиндрических барабанов-контейнеров (круговая скорость водила) составляла ω = 1090 об/мин, частота этого вращения ${{v}_{0}}$ = ω/2π = 169 рад/мин. Продолжительность механообработки t индивидуальной порошковой пробы фиксировалась во временнóм интервале от 3 до 21 мин (в некоторых случаях – до 50 мин). В качестве размольной среды использовали очищенный неполярный гексан.

Гранулометрические характеристики микропорошков определяли с помощью жидкофазного (в среде пропанола) трехлазерного дифрактометрического анализатора высокого разрешения Microtrac S3500. Для разрушения агрегатов слабосвязанных микрочастиц, образующихся в порошковом материале в результате его “слеживания”, проводилось предварительное ультразвуковое вибрационное диспергирование уже загруженных в рабочий объем анализатора порошковых проб в течение 3–6 мин.

Для каждой исследованной порошковой пробы были построены интегральные и дифференциальные функции распределения микрочастиц по размерам и определены их статистические моменты, зависящие от длительности t механообработки: средний объемно-взвешенный диаметр 〈dv〉 ≡ mv(t), средний поверхностно-взвешенный диаметр 〈ds〉 ≡ ma(t), средний численно-взвешенный диаметр 〈dn〉 ≡ mn(t), а также стандартное среднеквадратичное отклонение sd(t) = D(t)0,5, где D(t) – дисперсия функции распределения. Вычисляли также медиану функций распределения Dia(t), а также асимметрию ski(t) и эксцесс kg(t) этих функций [23]. В рамках модели сферических микрочастиц рассчитывали удельную поверхность порошка cs(t).

Элементарные вероятностно-статистические пролегомены теории.

Рассмотрим одномодальную двухпараметрическую интегральную функцию распределения логарифмически нормального вида LN(x,μ,σ2) [23]:

(1)
$\begin{gathered} LN(x,\mu ,{{\sigma }^{2}}) = \tfrac{1}{{\sigma \sqrt {2\pi } }} \times \\ \times \,\,\int\limits_0^x {\exp \left[ { - \tfrac{1}{2}{{{\left( {\tfrac{{\ln {\kern 1pt} y - \mu }}{\sigma }} \right)}}^{2}}} \right]dy = \frac{1}{2} + \frac{1}{2}{\text{Erf}}\left[ {\frac{{\ln (x) - \mu }}{{\sigma \sqrt 2 }}} \right]} , \\ \end{gathered} $
со случайной безразмерной переменной х > 0, количественно характеризующей индивидуальную микрочастицу (ее приведенный объем х = $v$/${{v}_{0}}$, или приведенный диаметр х = d/d0). Здесь величины ${{v}_{0}}$ и d0 – заранее выбранные масштабирующие единицы объема и диаметра микрочастиц).

Функция LN(x,μ,σ) содержит два безразмерных параметра, изменяющихся в следующих пределах: −∞ < μ < +∞ и σ > 0. Соответствующая ей дифференциальная функция lnN(x,μ,σ2) (плотность вероятности фиксации конкретного значения переменной x такого распределения) имеет следующий вид:

(2)
$\ln N\left( {x,\mu ,{{\sigma }^{2}}} \right) = \frac{1}{{x\sigma \sqrt {2\pi } }}{{e}^{{ - {{{(\ln x - \mu )}}^{2}}{\text{/}}2{{\sigma }^{2}}}}}.$

Наиболее информативными статистическим характеристиками (моментами) этого распределения являются: математическое ожидание (среднее значение) случайной переменной:

(3)
$E[x]{\text{ }} = \left\langle x \right\rangle = {\text{exp}}\left( {\mu + 0.5{{\sigma }^{2}}} \right),$
медиана этого распределения: Dia[x] = еμ, его мода: Mo[x] = exp(μ – σ2) и дисперсия D[x]:

(4)
$D[x] = \left[ {\exp \left( {{{\sigma }^{2}}} \right) - 1} \right]\exp \left( {2\mu + {{\sigma }^{2}}} \right).$

Начальные моменты k-того порядка указанной функции распределения рассчитываются по общей формуле

(5)
$E\left[ {{{x}^{k}}} \right] = \exp \left( {k\mu + 0.5{{k}^{2}}{{\sigma }^{2}}} \right),\,\,\,\,k \in [N].$

В работе [22] для описания временнóго изменения объема любой микрочастицы, находящейся в микропорошковом ансамбле при его механообработке, было получено обобщенное стохастически-динамическое уравнение Ланжевена в безразмерных переменных:

(6)
$du(\tau ){\text{/}}d\tau = \alpha qu(\tau ) + b{{[u(\tau )]}^{{2/3}}} + \beta \Delta u(\tau ).$

Такими переменными в выражении (6) являются: безразмерное время τ = ν0t и безразмерный объем u(τ) = ${{v}_{i}}$(τ)/${{v}_{{i0}}}$, где ${{v}_{{i0}}}$ – реальный микрообъем некоторой случайно выбранной i-той порошковой микрочастицы перед механообработкой (т.е. при τ = 0), а ${{v}_{i}}$(τ) есть ее микрообъем в момент времени τ; наконец Δu = Δ${{v}_{i}}$(τ)/${{v}_{{i0}}}$, где Δ${{v}_{i}}$(τ) – флуктуирующая (стохастическая) добавка к микрообъему ${{v}_{i}}$(τ) выбранной i-той микрочастицы, зафиксированная в момент времени τ. При этом предполагается, что при темпоральных (зависящих от времени) изменениях этой добавки в общем случае выполняются условия Винеровского типа: 1) 〈Δ${{v}_{i}}$(τ)〉 = 0 и 2) [〈Δ${{v}_{i}}$(τ1)·Δ${{v}_{i}}$(τ2)〉]1/2 = Ф0δ(τ1–τ2) [26, 27]. В последнем соотношении величина Ф0 – не зависящая от времени механообработки τ характеристика стохастического процесса, имеющая размерность объема [м3] и носящая название интенсивности Ланжевеновского источника, а δ(τ1–τ2) – дельта-функция Дирака.

Коэффициентами в уравнении (6) являются следующие безразмерные комплексы и критерии подобия: комплекс α = Мν1/mν0 > 0, где ν1 – частота успешного (т.е. приводящего к изменению объема микрочастицы) квазирегулярного ударного воздействия инструмента (шаров) на выбранную микрочастицу; комплексный критерий Иоффе-Давиденкова-Фридмана (ИДФ): q = f(τP/τS) = (1 – τр/τs), где τр – предел текучести материала этой микрочастицы, а τs – предел его прочности;. Напомним здесь, что знак критерия ИДФ определяет вид разрушения материала микрочастицы (или характер изменения ее объема): хрупкий (при q < 0), или пластический (при q > 0) [29–31].

Комплекс b и симплекс β также являются безразмерными критериями подобия процесса [32–35] и выражаются, соответственно, в виде $b = \left\{ {{{\nu }_{2}}{{\gamma /}}\left[ {{{\lambda }}{{{({{v}_{{i0}}})}}^{{1/3}}}{{\nu }_{0}}} \right]} \right\} > 0$ и β = (ν3/ν0) > 0. Здесь ν2 – частота успешных (результативных) взаимных столкновений двух индивидуальных микрочастиц ансамбля между собой, обусловленных перемешиванием микропорошка при вращении мельницы и приводящих к их слипанию; γ – поверхностная энергия материала микрочастицы; λ – нормирующий множитель, характеризующий максимально возможную энергонапряженность упругого контакта микрочастиц [Дж/м3], или [Н/м2]; ν3 – основная частота в частотном спектре стохастического силового воздействия на микрочастицу. В соответствии с общепринятой формулировкой Ланжевеновского стохастического процесса ${{\nu }_{3}} \gg {\text{ }}{{\nu }_{1}}{\text{ и }}{{\nu }_{3}} \gg {\text{ }}{{\nu }_{2}}$ .

Результаты статистического анализа и их обсуждение.

Темпоральную (зависящую от времени) эволюцию среднего значения линейного размера микрочастиц 〈x(τ)〉 и дисперсии D(τ) = [sd(τ)]2 функции распределения lnN(x,μ,σ2) микрочастиц по их линейным размерам x = (u/θ)1/3, а также контемпоральные изменения моментов этой функции более высокого порядка – асимметрию ski(τ) и эксцесс kg(τ), можно выявить, применяя методику Г. Хакена [27], основанную на использовании синтеза уравнения ФПК и модифицированного соотношения (6). Такой синтез применительно к рассматриваемой задаче в рамках Винеровского приближения имеет вид:

(7)
$\begin{gathered} \frac{{df(x,\mu ,\sigma )}}{{d\tau }} = - \frac{\partial }{{\partial x}}\left[ {k(x)f(x,\mu ,\sigma )} \right] + \\ + \,\,\beta {{\Phi }_{0}}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}f(x,\mu ,\sigma ). \\ \end{gathered} $

В этом уравнении дифференциальная функция распределения f(x,μ,σ) ≡ ln N(x,μ,σ) по-прежнему определяется уравнением (2), а функционал $k(x) = [dx(\tau ){\text{/}}d\tau ] = \left[ {\alpha qx + b + \beta \Phi (\tau ){\text{/}}{{x}^{2}}} \right]{\text{/}}3$ представляет собой модифицированную сумму динамических и стохастического членов в обобщенном уравнении Ланжевена (6), переменная x в которых является безразмерным диаметром микрочастицы. Первый член уравнения (7) после знака равенства называется переносным, второй – диффузионным.

Дифференцируя левую и правую части уравнения (7) соответственно, по времени τ и линейному размеру микрочастиц х(τ), поделив затем результат на функцию f(x,μ,σ), появляющуюся в качестве сомножителя в каждом члене уравнения после такого дифференцирования, можно получить новое дифференциальное уравнение, содержащее степени переменной х вплоть до четвертой. Приравнивая члены, содержащие одинаковые степени х в левой и правой частях этого уравнения, нетрудно найти соответствующие выражения для характеристик dμ/dτ и dσ/dτ. Их интегрирование в условиях, когда переносный члена в уравнении (7) преобладает, приводит к временным зависимостям параметров μ(τ) и σ(τ). В нулевом приближении по переменной x они имеют следующий вид: $\mu (\tau ) = {{\mu }_{0}} + (2\alpha q\tau {\text{/}}3)$ и $\sigma (\tau ) = {{\sigma }_{0}}\exp ( - \alpha q\tau {\text{/}}3)$. При этом выражения для среднего значения распределения 〈x(τ)〉 и его дисперсии D(τ) принимают следующую форму:

(8.a)
$\begin{gathered} \left\langle {x(\tau )} \right\rangle = - b{\text{/}}(\alpha q) + (3{\text{/}}\alpha q) \times \\ \times \,\,\exp \left\{ {[(2\alpha q\tau {\text{/}}3) + {{\mu }_{0}}] + 0.5\sigma _{0}^{2}\exp ( - 2\alpha q\tau {\text{/}}3)} \right\}, \\ \end{gathered} $
(8.б)
$\begin{gathered} D(\tau ) = \left\{ {\exp \left[ {\sigma _{0}^{2}\exp ( - 2\alpha q\tau {\text{/}}3)} \right] - 1} \right\} \times \\ \times \,\,\exp \left\{ {(4\alpha q\tau {\text{/}}3 + 2{{\mu }_{0}}) + \sigma _{0}^{2}\exp ( - 2\alpha q\tau {\text{/}}3)} \right\}. \\ \end{gathered} $

Детальный анализ этих соотношений показывает, что ход временных зависимостей 〈x(τ)〉 и sd = [D(τ)]0.5 определяется в общем случае не только знаком и величиной управляющего параметра q(τ), но также величиной параметра $\sigma _{0}^{2}$ > 0 (или величиной параметра μ0 с учетом его знака). Кроме того, в большинстве случаев при анализе темпорального поведения величины 〈x(τ)〉 следует также обращать внимание на зависимость асимптотики решений (8.а) от предельных значений параметрического комплекса (2α|q|τ)/3. Действительно, при выполнении левостороннего предельного условия τ $ \ll $ τcr3 = 3/(2α|q|), т.е. при достаточно малых временах механообработки τ можно разложить обе экспоненты, присутствующие в выражении (8а), в ряд Тейлора, ограничиваясь при этом лишь первыми двумя его членами. Тогда после элементарных преобразований получим:

(9)
$\begin{gathered} \left\langle {x(\tau )} \right\rangle = - \frac{b}{{\alpha q}} + \\ + \,\,\frac{3}{{\alpha q}}\left\{ {\left[ {\exp \left( {{{\mu }_{0}} + \frac{{\sigma _{0}^{2}}}{2}} \right)} \right]\left[ {1 + \frac{1}{3}\alpha q\tau \left( {2 - \sigma _{0}^{2}} \right)} \right]} \right\}. \\ \end{gathered} $

Теперь очевидно, что для того, чтобы при условии τ $ \ll $ τcr3 осуществлялся процесс измельчения порошковых микрочастиц, необходимо и достаточно, чтобы $\sigma _{0}^{2} > 2$ при любом знаке критерия q. Минимальное значение 〈x(τ)〉min, которое может быть достигнуто в таком процессе, определяется величиной τcr3.

В то же время при τ ≥ τcr3 измельчение порошковых микрочастиц может смениться их агломерацией, если с самого начала механообработки соблюдается условие q = сonst > 0 (см. ниже).

Если же по-прежнему выполняются условия: τ $ \ll $ 3/(2α|q|), но $\sigma _{0}^{2} < 2$, то с самого начала механообработки микропорошка при росте безразмерного времени τ будет наблюдаться процесс агломерации микрочастиц. При достаточно большом значении τcr3 этот процесс может закончиться финальным образованием единственной мегачастицы, имеющей массу $m = \sum\nolimits_i {{{m}_{i}}} $. Однако это возможно лишь при условии, что общая масса m микропорошка не слишком велика.

В противоположном предельном случае, когда τ $ \gg $ 3/(2|q|) следует вернуться к анализу исходного решения (8.а). При этом оказывается, что независимо от величины параметра $\sigma _{0}^{2} > 2$ при q > 0 это решение предсказывает агломерацию порошковых микрочастиц, а при q < 0 – их измельчение до отрицательных размеров, что физически бессмысленно. Фактически речь здесь может идти лишь об измельчении микрочастиц до атóмных размеров.

Эти выводы уточняют и дополняют предварительное заключение о влиянии знака управляющего параметра q(τ) на ход процесса механообработки, которое было сделано при анализе предложенной ранее эвристической анзац-модели процесса (см. работу [22]). Однако вывод о том, что при τ $ \gg $ 3/(2|q|) и q < 0 возможно измельчение микрочастиц до атóмных размеров, не только не соответствует заключению, полученному при анализе анзац-модели, но также противоречит результатам многочисленных экспериментов (см. [22] и список цитируемых в ней источников). В действительности это противоречие легко разрешается, если принять во внимание то обстоятельство, что в рассматриваемом теоретическом варианте характеристика q(τ) не может быть константой процесса. В реальном процессе механообработки первоначальный режим измельчения микропорошка, характеризуемый значением q(τ)<0, при достаточно больших временах механообработки τ (т.е. при малых значениях <х(τ)> ~ ~ 10−7−10−9 м) прекращается из-за смены знака q(τ)<0 благодаря задействованию сверхпластичной моды деформирования материала микрочастиц [5].

Обобщая результаты вышеприведенного анализа, можно заключить, что темпоральная граница τcr3 между режимами агломерации и измельчения частиц микропорошков в общем случае – при анализе процесса механообработки на основе уравнения ФПК, определяется не только знаком критерия q, но также и численным значением нового критерия подобия – безразмерного комплекса τcr3 ≈ 3/(2α|q|). В реальном временнóм масштабе t [мин] эта граница определяется соотношением ${{t}_{{{\text{cr3}}}}} = {{\tau }_{{{\text{cr3}}}}}{\text{/}}{{\nu }_{0}} \cong 3m{\text{/}}\left[ {2{{\nu }_{1}}M\left. {\left| {(1 - {{\tau }_{p}}{\text{/}}{{\tau }_{s}}} \right.)} \right|} \right]$. В экспериментах, описанных в [22], при механообработке металлических микропорошков в шаровой планетарной мельнице в большинстве случаев выполнялись следующие условия: (m/M) = 0.1, (τр/τs) ≈ 1.01–1.1 и q = –0.01─0.1. Тогда tcr3 ≈ (1.5–15)/ν1. Найденный ранее в работе [22] диапазон возможных значений частоты ν1 ≈ 1.26–2.5 мин–1 позволяет теперь получить интервальную оценку граничного значения tcr3 ≈ 0.6–12 мин. Эта оценка не зависит от частоты ν0 и по порядку величины совпадает с многочисленными экспериментальными данными, ранее полученными при механообработке различных металлических микропорошковых систем [22].

Обратимся теперь к анализу временнóго поведения дисперсии D(τ) соответствующих распределений (см. определение (4)). При выполнении принятого ранее условия τ $ \ll $ τсr3 ≈ 3/(2α|q|) можно опять разложить входящие в выражение (8.б) для дисперсии D первую и третью экспоненты, содержащие член exp(σ2), в ряд Тейлора с точностью до 3-его члена разложения. При этом для дисперсии D(τ) получается следующее выражение (при q < 0):

(10)
$\begin{gathered} D(\tau ) = {{\left( { - \frac{3}{{\alpha {\kern 1pt} |{\kern 1pt} q{\kern 1pt} |}}} \right)}^{2}}\left\{ {\left[ {\sigma _{0}^{2}\left( {1 + \frac{{2\alpha {\kern 1pt} |{\kern 1pt} q{\kern 1pt} |{\kern 1pt} \tau }}{3}} \right)} \right]} \right. \times \hfill \\ \left. { \times \,\,\exp \left[ { - \frac{{4\alpha {\kern 1pt} |{\kern 1pt} q{\kern 1pt} |{\kern 1pt} \tau }}{3} + 2{{\mu }_{0}} + \sigma _{0}^{2}\left( {1 + \frac{{2\alpha {\kern 1pt} |{\kern 1pt} q{\kern 1pt} |{\kern 1pt} \tau }}{3}} \right)} \right]} \right\}. \hfill \\ \end{gathered} $

Очевидно, что экспоненциальный сомножитель в этом выражении будет уменьшаться с течением времени лишь в том случае, когда выполняется условие $\left. {\frac{{4\alpha {\kern 1pt} |{\kern 1pt} q{\kern 1pt} |{\kern 1pt} \tau }}{3} > \sigma _{0}^{2}\frac{{2\alpha {\kern 1pt} |{\kern 1pt} q{\kern 1pt} |{\kern 1pt} \tau }}{3}} \right)$, или $\sigma _{0}^{2} < 2$, как это уже потребовалось ранее при анализе поведения величины 〈x(τ)〉 для варианта, при котором τ $ \gg $ τсr3 и q < 0 (т.е. при измельчении порошковых микрочастиц). В то же время сомножитель $\sigma _{0}^{2}\left( {1 + \frac{{2\alpha {\kern 1pt} |{\kern 1pt} q{\kern 1pt} |{\kern 1pt} \tau }}{3}} \right)$, стоящий перед экспонентой в соотношении (10), будет при увеличении времени τ механообработки неограниченно возрастать. Таким образом, при возрастании времени τ в пределах 0 < τ < τcr3 между указанными сомножителями будет осуществляться конкуренция. Следовательно, при некотором значении 0 < τmax < τcr3 дисперсия D должна достичь своего экстремального значения Dmax(τmax). Этот экстремум в данном случае является максимумом, который действительно наблюдается на опыте (см. рис. 1, график зависимости величины sd(t) = [D(t)]0.5 от реального времени эксперимента t[мин]). Временнόе местоположение этого максимума определяется двумя общеизвестными условиями: $\partial D({{\tau }_{{\max }}}){\text{/}}\partial \tau = 0$ и ${{\partial }^{2}}D({{\tau }_{{\max }}}){\text{/}}\partial {{\tau }^{2}} < 0$. Подставляя в эти соотношения выражение (10) для функции D(τ), несложно найти уравнение, связывающее τmax с начальным параметром $\sigma _{0}^{2}$ логнормального распределения f(x,μ,σ) = ln N(x,μ0,$\sigma _{0}^{2}$). Это уравнение имеет следующий вид:

(11)
${{\tau }_{{\max }}} = \left[ {(3{\text{/}}2)\left( {1 - \sigma _{0}^{2}} \right)} \right]{\text{/}}\left[ {\left( {\sigma _{0}^{2} - 2} \right)\alpha |{\kern 1pt} q{\kern 1pt} |} \right].$
где по-прежнему $\alpha = {{\nu }_{1}}M{\text{/}}{{\nu }_{2}}m$. Естественное условие τmax > 0 позволяет дать интервальную оценку теоретически возможным значениям параметра $\sigma _{0}^{2}$: $1 < \sigma _{0}^{2} < 2$. При этом для реального времени t[мин] имеет место очевидное равенство tmax = τmax/ν0.

Рис. 1.

Темпоральные зависимости основных статистических характеристик дифференциальной функции распределения ln N(х,μ,σ2) микрочастиц порошкового вольфрама по их объемно-взвешенным линейным размерам при механообработке порошка в гексане: (а) – в размерных, (б) и (в) – в безразмерных переменных. По оси абсцисс отложено безразмерное время τ, связанное с реальным временем t соотношением τ = ν0t.

Для конкретизации результатов решения общей задачи в качестве типичного примера ограничимся пока анализом случая механообработки вольфрамового микропорошка.

Подставляя в найденное выражение для tmax соотношение (11) и экспериментальные значения входящих в него параметров задачи: m/M = 0.1, |q| ≅ 0.02 при q < 0, ν0 = 169 мин–1, а также вычисленное в работе [22] для процесса механообработки вольфрамового микропорошка значение ν1 = 2.5 мин–1, можно получить следующее выражение для tmax:

(12)
$\begin{gathered} {{t}_{{\max }}} = \left[ {m{\text{/}}\left( {M{{\nu }_{1}}|{\kern 1pt} q{\kern 1pt} |} \right)} \right]\left( {1 - \sigma _{0}^{2}} \right){\text{/}}\left( {\sigma _{0}^{2} - 2} \right) = \\ = 20.8\left( {1 - \sigma _{0}^{2}} \right){\text{/}}\left( {\sigma _{0}^{2} - 2} \right). \\ \end{gathered} $

Далее по экспериментально найденному для микропорошкового вольфрама значению tmax = = 4.5–5.0 мин (см. рис. 1, график функции sd(t)), при помощи соотношения (12) можно найти то фиксированное значение параметра $\sigma _{0}^{2}$ > 0, которое этот параметр должен принимать при наличии максимума, наблюдаемого на графике sd(t). Расчет показывает, что в этом случае $\sigma _{0}^{2}$= 1.62 ± 0.03.

Найденное значение параметра $\sigma _{0}^{2}$, обеспечивающее наличие tmax при наблюдаемом в экспериментах с вольфрамовым микропорошком значении tmax = (4.5–5.5) мин, позволяет получить соответствующую оценку параметра μ0 для данного случая. Действительно, при выполнении общего условия нормировки 〈хi0〉 = 1 и вытекающего из него соотношения $\mu = \left\{ {\ln \left[ {(\alpha q + b){\text{/}}3} \right] - \sigma _{0}^{2}{\text{/}}2} \right\}$, для значения $\sigma _{0}^{2}$/2 = 0.81 имеем: μ0 = ─7.71 ± 0.02. При этом расчете были использованы следующие, полученные на опытной основе, оценочные значения параметров процесса измельчения порошкового вольфрам: αq/3 ≅ ─5 × 10─4 при q ≅ ─0.02. и $b{\text{/}}3 = {{\nu }_{1}}\gamma {\text{/}}\left[ {3\lambda {{\nu }_{0}}{{{({{v}_{{i0}}})}}^{{1/3}}}} \right] = 1.5 \times {{10}^{{ - 3}}}$ (при экспериментально определенных нами значениях (${{v}_{{i0}}}$)1/3 = = 16 мкм и известных значениях величин λ ≈ σs = = 109 Н/м2, и γ ≈ 2.5 Дж/м2 для вольфрама [36])

Оценки параметров $\sigma _{0}^{2}$ и μ0 дифференциальной функции распределения ln N(x,μ0,$\sigma _{0}^{2}$), рассчитанные для других исследованных нами металлических микропорошков показывают, что область возможных изменений этих параметров во всех рассмотренных случаях ограничивается следующими неравенствами: $1 < \sigma _{0}^{2} < 2$ и ─8 ≤ μ0 ≤ ─5.

При столь широком интервале возможных значений $\sigma _{0}^{2}$ и μ0 величина tmax оказывается не всегда доступной для экспериментального наблюдения. Например, при достаточно большом, но теоретически допустимом значении $\sigma _{0}^{2}$ = 1.9 величина tmax ≈ 53 мин, и при ограничении продолжительности механообработки величиной t ≤ 21 мин перегиб на темпоральном графике sd(t) наблюдаться не будет.

С другой стороны, в достаточно часто встречающихся случаях, (например, при механообработке микропорошкового гафния) величина tmax ≤ 1–2 мин. В таких случаях обнаружить максимум на временнóй зависимости sd(t) экспериментально также не удается (см. график зависимости sd(t) на рис. 2а и 2б).

Рис. 2.

Темпоральные зависимости основных статистических характеристик дифференциальной функции распределения lnN(x,μ,σ2) микрочастиц порошкового гафния по их объемно-взвешенным линейным размерам при механообработке в гексане: (а) – в размерных, (б) – в безразмерных переменных. Отложенное по оси абсцисс безразмерное время τ по-прежнему связано с реальным временем t соотношением τ = ν0t.

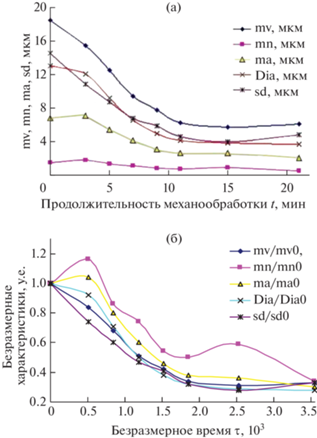
Зафиксированный с временным шагом Δt ≈ 2–3 мин темпоральный график для этой характеристики будет сразу меняться во времени симбатно (т.е. качественно одинаково) изменениям среднего значения 〈x(t)〉 (см. рис. 2б). При этом расчеты показывают, что возможное уменьшение значения tmax на порядок (с 1 мин до 0.1 мин) слабо влияет на значениях параметров $\sigma _{0}^{2}$ и μ0 логнормальной функции распределения.

Здесь также уместно отметить, что величина tmax формально не будет зависеть от значения μ0, если параметр μ0 является функцией заранее найденного аргумента $\sigma _{0}^{2}$, как это было принято при приведении ранее выполненных вычислений.

Поскольку начальные моменты более высокого порядка согласно определению (5) связаны со средним значением 〈x(τ)〉 (первым начальным моментом при k = 1) степенными показателями k, их временные зависимости будут симбатно повторять временнóе поведение первого начального момента (см. [22], рис. 7, 9 –11).

Возвращаясь к рассмотрению уравнения (7), следует отметить, что в тех случаях, когда условия механообработки микропорошка таковы, что в этом уравнении преобладает диффузионный член, оно становится стандартным уравнением одномерной диффузии. Тогда из его решения следует равенство 〈|x(τ)|〉 = (β│Φ0│τ)0.5, которое также является следствием известной формулы Эйнштейна-Смолуховского для броуновского движения. (см. например, монографии [28, 37]). При преобладании диффузионного члена в решении уравнения (7) указанное равенство в большей мере соответствует эксперименту, нежели полученное в работе [22] общее решение (13) эвристического уравнения (6):

(13)
$\begin{gathered} u(\tau ) = {{\left\{ {[(1 + b{\text{/}}\alpha q)\exp (\alpha q\tau {\text{/}}3)] - b{\text{/}}\alpha q} \right\}}^{3}} + \\ + \,\,\beta ({\text{sign}}{{\Phi }_{0}})\left. {\left| {{{\Phi }_{0}}} \right.} \right|, \\ \end{gathered} $
которое в таких условиях может сводиться лишь к линейному по времени τ соотношению 〈|x(τ)|〉 = = β│Ф0│τ.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Результаты экпкриментально-теоретического анализа процессов механообработки однокомпонентных микропорошков, изложенные в работе [22], а также в данном сообщении, свидетельствуют о принципиальных различиях в темпоральном поведении разнотипных микропорошков в указанных процессах. Эти различия обусловлены не только возможным несовпадением граничных и начальных условий процесса механообработки. Они коренятся главным образом в динамике изменения физико-химических свойств порошковых материалов и размольных сред. Отсюда проистекают различия и в стохастически-динамическом инструментарии, применяемом для темпорального описания механоактивационных процессов, и в конкретизации составляющего его основу математического аппарата, пригодного для решения поставленной задачи.

Также совершенно очевидно, что методические подходы и приемы, предложенные в работе [22] и в данной работе, не ограничиваются приведенными примерами однокомпонентных порошковых систем. Такие подходы можно успешно использовать для разработки моделей, пригодных для прогнозирования темпоральной эволюции гранулометрических характеристик иных, более сложных и практически гораздо более важных, многокомпонентных микропорошковых систем. Сказанное относится, в первую очередь, к таким композиционным микропорошковым системам, как полиметаллические, металлоуглеродные, или металополимерные микропорошковые смеси, потребность в прогнозировании темпорального поведения которых в настоящее время особенно актуальна.

Одним из преимуществ предлагаемой методики является ее универсальность. Применение ее в каждом конкретном случае позволяет решать как прямую, так и обратную задачи механообработки микропорошков.

Прямая задача механообработки состоит в прогнозировании темпорального поведения микропорошковой системы по заранее известным, наперед заданным энергосиловым параметрам процесса механообработки и микроструктурным характеристикам материала микрочастиц. К таким характеристикам относятся, в первую очередь, предел текучести, предел прочности, коэффициенты деформационного упрочнения и температурного разупрочнения, поверхностная энергия микропорошкового материала и т.п. Для прогнозирования темпорального поведения микропорошка необходимо также знание физико-химических и реологических характеристик заданной размольной среды.

Решение обратной задачи механообработки заключается в определении вышеуказанных характеристик материала микрочастиц и размольной среды по известному, экспериментально наблюдаемому темпоральному поведению гранулометрических характеристик анализируемой порошковой системы. Это не менее важная практическая задача, решение которой позволяет достаточно быстро разработать эффективную технологию промышленного производства соответствующих изделий.

ВЫВОДЫ

В рамках подхода, базирующегося на стохастическом уравнении Фоккера-Планка-Колмогорова, найдены решения, определяющие темпоральные вариации параметров σ(t) и μ(t) логнормальных функций распределения частиц по размерам, которые полностью описывают процесс механообработки микропорошков ряда металлов IIA, IIIB, IVA и VIA групп таблицы Менделеева в шаровой планетарной мельнице. Показано, что по найденным в рамках ФПК-подхода значениям параметрических характеристик $\sigma _{0}^{2}$ и μ0 соответствующих логнормальных функций распределения для вышеупомянутых металлических порошков можно рассчитать зависимости от времени основных начальных и центральных моментов указанных функций: среднее значение E[x1] = 〈x(τ)〉, D(τ) = [sd(τ)]2, а также темпоральные зависимости моментов более высокого (k-того) порядка $E[{{x}^{k}}] = \exp \left( {k\mu + 0.5{{k}^{2}}{{\sigma }^{2}}} \right),\,\,\,\,k \in [N].$ Обнаружено, что ход темпоральных зависимостей вышеназванных моментов определяется в общем случае не только знаком и величиной критерия ИДФ ≡ ≡ q(τ), но также численным значением параметра $\sigma _{0}^{2}$ > 0 (или численным значением параметра μ0 с учетом его знака). Показано, что временнáя граница между режимами агломерации и измельчения частиц микропорошков в общем случае – при анализе процесса механообработки на основе уравнения ФПК, определяется не только знаком критерия ИДФ, но также и численным значением нового темпорального критерия подобия – безразмерного комплекса τcr3 ≈ 3/(2α|q|).

Список литературы

  1. German R.M. Powder Metallurgy and Particulate Materials Processing. Princeton: Metal Powder Industries Federation, 2005.

  2. V International Conference “Fundamental Bases of Mechanochemical Technologies”, FBMT-2018. Book of Abstracts / Ed. by Lyakhov N., Šepelák V., Shakhtshneider T., Dudina D. Novosibirsk: IPC NSU-Publishing, 2018.

  3. Фундаментальные основы механической активации, механосинтеза и механохимических технологий / Отв. ред. Аввакумов Е.Г. Новосибирск: Изд-во СО РАН, 2009.

  4. Сметкин А.А., Ярмонов А.И. // Проблемы современных материалов и технологий. Вестник ПГТУ. 2001. № 7. С. 48.

  5. Васильев Л.С., Ломаева С.Ф. // Химия в интересах устойчивого развития. 2002. № 10. С. 13.

  6. Иванов Н.В., Ломаева С.Ф., Елсуков Е.П., Коныгин Г.Н. // Физика и химия обработки материалов. 2003. № 5. С. 59.

  7. Ломаева С.Ф. // Деформация и разрушение материалов. 2005. № 3. С. 9.

  8. Курзина И.А., Божко И.А., Калашников М.П., Ерошенко А.Ю., Шаркеев Ю.П. // Материаловедение. 2010. № 5. С. 48.

  9. Богатырева Е.В., Ермилов А.Г., Свиридова Т.А., Савина О.С., Подшибякина К.В. // Неорган. материалы. 2011. Т. 47. № 6. С. 877.

  10. Дорофеев Р.А., Стрелецкий А.Н., Повстугар И.В., Протасов А.В., Елсуков Е.П. // Коллоид. журн. 2012. Т. 74. № 6. С. 710.

  11. Григорьев О.К., Крячко Л.А., Бега Н.Д., Лаптев А.В., Головкова М.Е., Роженко Н.Н., Берсудский Е.И. // Электронная микроскопия и прочность материалов. 2013. № 19. С. 115.

  12. Peng T., Chang I. // J. Powder Technology. 2015. V. 284. P. 32. https://doi.org/10.1016/j.powtec.2015.06.039

  13. Kuzina A.A. // Russian Journal of Non-Ferrous Metals, 2016. V. 57. № 7. P. 710. https://doi.org/10.3103/S1067821216070129

  14. Стрелецкий А.Н., Борунова А.Б., Колбанев И.В., Сивак М.В., Долгобородов А.Ю. // Горение и взрыв. 2017. Т. 10. № 2. С. 100.

  15. Jalili F., Zhiani M., Kamali S. // Intern. Journ.of Hydrogen Energy. 2018. V. 43, № 46. P. 21187. DOI:. 2018.09.202https://doi.org/10.1016/J.IJHYDENE

  16. Pragatheeswaran A., Ravi R., Bakshi S.R. // Advanced Powder Technology. 2019. V. 30. № 11. P. 2759. https://doi.org/10.1016/j.apt.2019.08.023

  17. Малкин А.И., Клюев В.А., Рязанцева А.А., Савенко В.И. // Коллоид. журн. 2019. Т. 81. № 6. С. 703. https://doi.org/10.1134/S1061933X19060115

  18. Nguyen T.H., Nguyen B.M., Konyukhov Yu.V., Vvedenskaya V.V., Vasiliev A.A. // Materials Science. Power Engineering. 2020. V. 26. № 3. P. 90. https://doi.org/10.18721/JEST.26307

  19. Малкин А.И., Алиев А.Д., Клюев В.А., Савенко В.И., Ширяев А.А., Рязанцева А.А. // Коллоид. журн. 2020. Т. 82. № 4. С. 451. https://doi.org/10.1134/S1061933X20040079

  20. Малышев В.П., Бектурганов Н.С., Макашева А.М., Зубрина Ю.С. // Цветные металлы. 2016. № 2. С. 33.

  21. Malyshev V.P., Makasheva A.M., Zubrina Y.S. // Am. J. Phys. Chem. 2015. V. 4. № 6. P. 42.

  22. Савенко В.И., Клюев В.А., Малкин А.И. Гранулометрия металлических микропорошков, обработанных в шаровой планетарной мельнице // Колл. ж. 2022. Т. 84. № 1. С.84. https://doi.org/10.31857/S0023291222010116

  23. Balakrishnan N. and Chen W.W.S. Handbook of Tables for Order Statistics from Lognormal Distributions with Applications. Amsterdam: Kluwer. 1999.

  24. Белавин А.А., Кулаков А.Г., Тарнопольский Г.М. Лекции по теоретической физике. М.: МЦНМО. 2015.

  25. Gardiner C.W. Handbook of Stochastic Methods: for Physics, Chemistry and the Natural Sciences. Springer. 2004.

  26. Stepanov S.S. Stochastic World. (Series: Mathematical Engineering). Springer. 2013.

  27. Haken H. Sinergetics. Introduction and advanced topics. Berlin: Springer. 2004.

  28. Ефремов Ю.С. Статистическая физика и термодинамика. М.: Юрайт. 2019.

  29. Иоффе А.Ф. Избранные труды. Т. 1. Механические и электрические свойства кристаллов. Л.: Наука. 1974.

  30. Давиденков Н.Н. Избранные труды. В 2-х т. / Отв. ред. Г.С. Писаренко. Киев: Институт проблем прочности АН УССР. 1981.

  31. Фридман Я.Б. Механические свойства металлов. В двух частях. Издание 3-е, переработанное и дополненное. М.: Машиностроение. 1974.

  32. Гухман А.А. Введение в теорию подобия. М.: Высшая школа. 1973.

  33. Седов Л.И. Методы подобия и размерности в механике. 10-е стереотипное издание. М.: Наука. 1987.

  34. Архипов В.А., Коноваленко А.И. Практикум по теории подобия и анализу размерностей. Томск: Издательский Дом ТГУ. 2016

  35. Иванов И.Е., Ерещенко В.Е. Методы подобия физических процессов: М.: МАДИ. 2015.

  36. Физические величины. Справочник / Под редакцией Григорьева И.С., Мейлихова Е.З. М.: Энергоатомиздат. 1991.

  37. Квасников И.А. Термодинамика и статистическая физика. Том 3. Теория неравновесных систем. М.: УРСС. 2003.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал