Кристаллография, 2020, T. 65, № 4, стр. 522-527

Теория лауэ-дифракции рентгеновских лучей в толстом монокристалле с наклонной ступенькой на выходной поверхности. II. Аналитическое решение

В. Г. Кон¹, И. А. Смирнова^2, *

¹ Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

² Институт физики твердого тела РАН
Черноголовка, Россия

^* E-mail: irina@issp.ac.ru

Поступила в редакцию 24.10.2019
После доработки 26.11.2019
Принята к публикации 02.12.2019

DOI: 10.31857/S0023476120040128

Полный текст (PDF)

Аннотация

Получено аналитическое решение задачи о дифракции Лауэ рентгеновской сферической волны в монокристалле с наклонной ступенькой на выходной поверхности. Общие формулы применяются для конкретного случая дифракции плоской волны в толстом кристалле в условиях реализации эффекта Бормана. Показано, что при условии увеличения толщины со стороны отраженного пучка относительная амплитуда отраженной волны определяется тремя комплексными членами, что формально может приводить к интерференции с увеличением максимумов интенсивности до 9 раз по отношению к ее значению в кристалле без ступеньки. Формула для проходящего пучка содержит только два члена, и увеличение не может быть более чем в 4 раза. Результаты расчетов по аналитической формуле совпадают с результатами, полученными численным методом, рассмотренным в первой части работы.

ВВЕДЕНИЕ

В статье представлены результаты второй части работы, первая часть которой опубликована в [1]. Теоретически решается задача о распределении в пространстве (поперек пучка) интенсивностей проходящей и отраженной волн в случае дифракции Лауэ рентгеновских лучей в толстом монокристалле с наклонной ступенькой на выходной поверхности. В первой части работы задача была решена численно. Было показано, что в переходной области между границей ступеньки и границей треугольника Бормана с вершиной на нижней границе ступеньки имеет место эффект сильного перераспределения интенсивности отраженного пучка таким образом, что максимумы интенсивности увеличиваются более чем в 7 раз по сравнению с ее значением перед ступенькой. Одновременно средняя по области интерференции интенсивность проходящего пучка существенно уменьшается, как и суммарная интенсивность двух пучков, что свидетельствует о нарушении условий для эффекта Бормана.

В [1] было показано, что задачу удобно разбить на два этапа. На первом этапе рассматривают кристалл в форме пластины, и решение находят методом преобразования Фурье, как сделано в [2–6]. На втором этапе необходимо решать уравнения Такаги [7]. Если в образце нет деформации кристаллической решетки, но он имеет форму со сложной границей, то решение уравнений Такаги можно получить в интегральной форме [8–14]. Иногда интегральная форма уравнений не дает прямого решения задачи, а приводит к уравнению, которое в ряде случаев удается решить аналитически.

Именно такой случай реализуется в рассматриваемой задаче дифракции Лауэ в монокристалле с наклонной ступенькой на выходной поверхности. В работе представлен вывод аналитического решения для второго этапа задачи. Используется метод, который впервые был применен в [15].

ФОРМУЛИРОВКА ЗАДАЧИ И ЕЕ АНАЛИТИЧЕСКОЕ РЕШЕНИЕ

Схема численного эксперимента показана в первой части работы. Предполагается, что монохроматическая сферическая волна от точечного источника рентгеновского излучения, расположенного на расстоянии L от образца, падает на монокристалл в форме пластины толщиной t (максимальная толщина). На выходной поверхности кристалла имеется наклонная ступенька высотой t₀. Будем считать, что известны волновые функции E₀(x) и E_h(x) для проходящего и отраженного пучков на толщине z = t₁ = t – t₀.

На втором этапе необходимо решить уравнения Такаги [7]:

(1)

$\frac{2}{i}\frac{{\partial {{E}_{0}}}}{{\partial {{s}_{0}}}} = {{X}_{0}}{{E}_{0}} + {{X}_{{ - h}}}{{E}_{h}}\exp (i{\mathbf{hu}}),$

(2)

$\frac{2}{i}\frac{{\partial {{E}_{h}}}}{{\partial {{s}_{h}}}} = [{{X}_{0}} + 2{{\alpha }_{q}}]{{E}_{h}} + {{X}_{h}}{{E}_{0}}\exp ( - i{\mathbf{hu}}).$

Здесь X_0,h,–h = Kχ_0,h,–h, где K = 2π/λ – волновое число, χ₀, χ_h, χ_–h – компоненты Фурье поляризуемости кристалла для векторов обратной решетки 0, h, –h соответственно, координаты s₀ и s_h отсчитываются вдоль направлений проходящей и отраженной волн, u – вектор смещения из-за возможной деформации кристаллической решетки, параметр отклонения от условия Брэгга α_q = K(θ – ‒ θ₀)sin 2θ_B, λ – длина волны рентгеновского излучения. Угол θ–θ₀ описывает угловое положение кристалла относительно падающего излучения.

Рассмотрим случай, когда α_q = 0 и в кристалле нет деформаций (u = 0). В случае совершенного кристалла решение уравнений (1), (2) можно получить в интегральной форме через известные поля E₀ и E_h на некоторой границе внутри треугольника Бормана с вершиной в точке наблюдения и сторонами в направлениях проходящей (s₀) и отраженной (s_h) волн [8–14]. В [1] рассматривали случай, когда толщина плоской части кристалла t₁ велика по сравнению с толщиной дифракционной фокусировки [6, 16]: t_df = L|χ_h|F, где F = = 1/(sin θ_Bsin 2θ_B), θ_B – угол Брэгга. Тогда на толщине t₁ в области ступеньки на горизонтальной оси x волновая функция близка к константе, что соответствует плоской волне.

В отличие от [1] рассмотрим случай падающей плоской волны при точном выполнении условия Брэгга. Расстояние от точечного источника до кристалла должно быть значительно больше расстояния дифракционной фокусировки: L_df = t₁C, где С = (|χ_h|F)^–1. Для t₁ = 1 мм это расстояние равно L_d = 32.9 м. Заметим, что коллимацию падающего пучка на источниках синхротронного излучения третьего поколения легко выполнить с помощью составной преломляющей линзы [17].

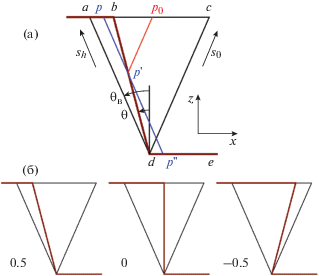
На рис. 1а показана форма образца в области ступеньки на выходной поверхности, а также треугольник Бормана, в котором хотя бы одна волновая функция зависит от координаты x. Используем прием, который впервые был предложен в [15]. Он состоит в рассмотрении вместо реальных волновых функций разности волновых функций для исследуемого образца E_k(r) и образца в форме пластины A_k(z). Заметим, что в случае плоской волны функция A_k(z) известна в аналитическом виде. Ясно, что интегральные уравнения для разностей будут такие же, однако граничные условия существенно различаются, потому что разность равна нулю там, где кристалл однороден по оси x.

Рис. 1.

Выходная граница кристалла в форме ступеньки и треугольник Бормана, в котором хотя бы одно поле зависит от координаты x (а). Различные варианты наклона ступеньки (б) при разных значениях параметра R = tg θ/tg θ_B (указаны на рисунке).

Итак, рассмотрим функции

(3)

${{e}_{k}}({\mathbf{r}}) = ({{E}_{k}}({\mathbf{r}}) - {{A}_{k}}(z))F_{0}^{{ - 1}}(z),\quad k = 0,h,$

где

(4)

${{A}_{k}}(z) = {{C}_{k}}{{F}_{0}}(z)F_{h}^{{ - 1}}(z),\quad {{F}_{{0,h}}} = \exp (i{{X}_{{0,h}}}z{\text{/}}2{{\gamma }_{0}}).$

Здесь γ₀ = cos θ_B, коэффициенты C_k зависят от нормировки. В случае плоской волны они равны ±0.5 для k = 0, h соответственно. Заметим, что поля e_k(r) отличны от нуля только внутри треугольника acd (рис. 1а).

Согласно интегральной формулировке теории [12] функцию e_h(p) в точке p на отрезке ab можно выразить через функции на линиях ad и db. Но разности полей на линии ad равны нулю, поэтому имеем решение в виде:

(5)

${{e}_{h}}(p) = {{e}_{h}}(p{\text{'}}) - \int\limits_{dp'} {d{{s}_{0}}} \frac{{\partial R}}{{\partial {{s}_{0}}}}{{e}_{h}} - \frac{i}{2}{{X}_{h}}\int\limits_{dp'} {d{{s}_{h}}} R{{e}_{0}},$

(6)

$R = {{J}_{0}}(X{{(({{s}_{{0p}}} - {{s}_{0}})({{s}_{{hp}}} - {{s}_{h}}))}^{{1/2}}}),$

где X = (X_hX_–h)^1/2, s_0p, s_hp – координаты точки p. Здесь и далее используем обозначения J_n(x) для функции Бесселя n-го порядка. С другой стороны, функция e₀(p') на линии db является решением интегрального уравнения

(7)

${{e}_{0}}(p{\text{'}}) = \int\limits_{dp'} {d{{s}_{h}}} \frac{{\partial R}}{{\partial {{s}_{h}}}}{{e}_{0}} + \frac{i}{2}{{X}_{{ - h}}}\int\limits_{dp'} {d{{s}_{0}}} R{{e}_{h}},$

если функция e_h(r) известна на этой линии. В рассматриваемом случае линия db является прямой. Введем координаты ξ и ξ_η для точек на линии dp' и в точке p'. Связь новых координат со старыми имеет вид

(8)

$\begin{gathered} z = \cos {{\theta }_{{\text{B}}}}({{s}_{0}} + {{s}_{h}}) = \xi x\cos \theta , \\ x = \sin {{\theta }_{{\text{B}}}}({{s}_{0}} - {{s}_{h}}) = --\xi x\sin \theta . \\ \end{gathered} $

Обозначим аргумент функции Бесселя в (6) буквой A. С учетом (8) легко получить, что на линии db

(9)

$\begin{gathered} {{s}_{0}} = {{\gamma }_{1}}\xi ,\quad {{s}_{h}} = {{\gamma }_{2}}\xi , \\ A = b({{\xi }_{\eta }} - \xi ),\quad b = X{{({{\gamma }_{1}}{{\gamma }_{2}})}^{{1/2}}}, \\ \end{gathered} $

где

(10)

${{\xi }_{\eta }} = {{\xi }_{0}} - \eta {{D}_{1}},\quad {{\xi }_{0}} = \frac{{{{t}_{0}}}}{\gamma },\quad {{D}_{1}} = \frac{{{{\gamma }_{0}}}}{{\sin ({{\theta }_{B}} - \theta )}},$

(11)

$\begin{gathered} {{\gamma }_{1}} = \frac{{\sin ({{\theta }_{{\text{B}}}} - \theta )}}{{\sin 2{{\theta }_{{\text{B}}}}}},\quad {{\gamma }_{2}} = \frac{{\sin ({{\theta }_{{\text{B}}}} + \theta )}}{{\sin 2{{\theta }_{{\text{B}}}}}}, \\ \gamma = \cos \theta . \\ \end{gathered} $

Здесь ξ_η – длина отрезка dp', η – длина отрезка pb. Найдем зависимость интенсивностей проходящей и отраженной волн от параметра η.

Интеграл в (7) вычисляется по координате ξ в пределах от нуля до ξ_η. С целью упрощения записи сделаем замену переменных ξ → ξ_η – ξ, которая не меняет пределов интегрирования. Тогда для производной можно записать выражение

(12)

$\frac{{\partial R}}{{\partial {{s}_{h}}}} = \frac{1}{2}X{{\left( {\frac{{{{s}_{0}}}}{{{{s}_{h}}}}} \right)}^{{1/2}}}{{J}_{1}}(A) = \frac{1}{2}X{{\left( {\frac{{{{\gamma }_{1}}}}{{{{\gamma }_{2}}}}} \right)}^{{1/2}}}{{J}_{1}}(b\xi ).$

В результате уравнение (7) после замены переменных принимает вид

(13)

$\begin{gathered} {{e}_{0}}({{\xi }_{\eta }}) = \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{0}}({{\xi }_{\eta }} - \xi ){{J}_{1}}(b\xi ) + \\ + \;\frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}({{\xi }_{\eta }} - \xi ){{J}_{0}}(b\xi ). \\ \end{gathered} $

Справа стоят интегралы в виде свертки. Для решения интегрального уравнения (13) применим к нему преобразование Лапласа

(14)

$e(q) = \int\limits_0^\infty {d\xi } \exp ( - q\xi ){{e}_{0}}(\xi )$

и используем его свойство, согласно которому свертка двух функций превращается в произведение их образов. Тогда имеем

(15)

${{e}_{0}}(q) = \frac{b}{2}{{e}_{0}}(q){{[{{J}_{1}}(b\xi )]}_{q}} + \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}{{e}_{h}}(q){{[{{J}_{0}}(b\xi )]}_{q}}.$

Квадратные скобки обозначают преобразование Лапласа функции внутри них, которое зависит от аргумента q. В справочнике [18] есть интеграл с номером 6.646.1, который можно преобразовать к виду

(16)

$\begin{gathered} {{\left[ {{{{\left( {\frac{\xi }{{\xi + a}}} \right)}}^{{n/2}}}{{J}_{n}}(b{{{[\xi (\xi + a)]}}^{{1/2}}})} \right]}_{q}} = \\ = \frac{{{{b}^{n}}\exp ({{a}_{2}}(q - u))}}{{u{{{(q + u)}}^{n}}}}, \\ \end{gathered} $

где

(17)

${{a}_{2}} = a{\text{/}}2,\quad u = {{({{q}^{2}} + {{b}^{2}})}^{{1/2}}}.$

Подставим (16) при a = n = 0 в (15) и выполним вычисления, используя обозначение W = iX_–hγ₁/2:

(18)

$\begin{gathered} {{e}_{0}}(q) = W{{e}_{h}}(q)\left( {\frac{{{{{[{{J}_{0}}(b\xi )]}}_{q}}}}{{1 - (b{\text{/}}2){{{[{{J}_{1}}(b\xi )]}}_{q}}}}} \right) = \\ = \;\frac{{W{{e}_{h}}(q)}}{{u - ({{b}^{2}}{\text{/}}2){{{(u + q)}}^{{ - 1}}}}}. \\ \end{gathered} $

Можно показать, что знаменатель в правой части (18) равен (u + q)/2, а обратная функция 2/(u + q) равна преобразованию Лапласа функции U(bξ), где

(19)

$U(x) = 2\frac{{{{J}_{1}}(x)}}{x}.$

Решение интегрального уравнения (13) после обратной замены переменных ξ → ξ_η – ξ имеет следующий вид:

(20)

${{e}_{0}}({{\xi }_{\eta }}) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } U(b[{{\xi }_{\eta }} - \xi ]){{e}_{h}}(\xi ).$

Рассмотрим уравнение (5). В данном случае ситуация сложнее, поскольку аргумент функции Бесселя зависит от координат точки p на линии ab. Эти координаты равны: z_p = t₀ = ξ₀cos θ, x_p = = ‒ξ₀sin θ – η, а для точки на отрезке dp' координаты определены в (8). В результате простых вычислений легко получить, что

(21)

$\begin{gathered} {{s}_{{op}}} - {{s}_{o}} = {{\gamma }_{1}}{{\xi }_{d}}, \\ {{s}_{{hp}}} - {{s}_{h}} = {{\gamma }_{2}}({{\xi }_{d}} + a),\quad {{\xi }_{d}} = {{\xi }_{\eta }} - \xi , \\ \end{gathered} $

(22)

$\begin{gathered} R = {{J}_{0}}(b{{\sigma }_{\xi }}),\quad \frac{{\partial R}}{{\partial {{s}_{0}}}} = \frac{{b{{\varsigma }_{\xi }}}}{{2{{\gamma }_{1}}}}{{J}_{0}}(b{{\sigma }_{\xi }}), \\ a = \varepsilon \eta ,\quad \varepsilon = {{D}_{1}} + {{D}_{2}}, \\ \end{gathered} $

(23)

$\begin{gathered} {{\sigma }_{\xi }} = {{\left( {{{\xi }_{d}}[{{\xi }_{d}} + a]} \right)}^{{1/2}}}, \\ {{\varsigma }_{\xi }} = {{\left( {\frac{{{{\xi }_{d}} + a}}{{{{\xi }_{d}}}}} \right)}^{{1/2}}},\quad {{D}_{2}} = \frac{{{{\gamma }_{0}}}}{{\sin ({{\theta }_{{\text{B}}}} + \theta )}}. \\ \end{gathered} $

С учетом описанных выше соотношений уравнение (5) имеет следующий вид:

(24)

$\begin{gathered} {{e}_{h}}(\eta ) = {{e}_{h}}({{\xi }_{\eta }}) - \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ){{\varsigma }_{\xi }}{{J}_{1}}(b{{\sigma }_{\xi }}) - \\ - \;\frac{i}{2}{{X}_{h}}{{\gamma }_{2}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{0}}(\xi ){{J}_{0}}(b{{\sigma }_{\xi }}). \\ \end{gathered} $

Интегралы снова представляют собой свертку двух функций, поэтому удобно использовать преобразование Лапласа, однако в данном случае имеем функции от более сложного аргумента. Применим преобразование Лапласа к третьему члену в (24) и подставим (18). Получаем с учетом формулы (16):

(25)

$\begin{gathered} \frac{b}{2}{{e}_{h}}(q)\frac{{b\exp ({{a}_{2}}(q - u))}}{{u(q + u)}} = \\ = \;\frac{b}{2}{{e}_{h}}(q){{\left[ {{{{\left( {\frac{\xi }{{\xi + a}}} \right)}}^{{1/2}}}{{J}_{1}}(b{{{[\xi (\xi + a)]}}^{{1/2}}})} \right]}_{q}}. \\ \end{gathered} $

Переходя из q-пространства обратно в ξ-пространство и прибавляя первый член, получаем для суммы второго и третьего членов выражение

(26)

$ - \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ){{J}_{1}}(b{{\sigma }_{\xi }})\left[ {{{{\left( {\frac{{{{\xi }_{d}} + a}}{{{{\xi }_{d}}}}} \right)}}^{{1/2}}} - {{{\left( {\frac{{{{\xi }_{d}}}}{{{{\xi }_{d}} + a}}} \right)}}^{{1.2}}}} \right].$

Выполняя вычисления для волновой функции отраженного пучка на линии ab, получаем вместо (24) более удобную формулу

(27)

$\begin{gathered} {{e}_{h}}(\eta ) = {{e}_{h}}({{\xi }_{\eta }}) - \frac{1}{4}{{b}^{2}}\varepsilon \eta \int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ) \times \\ \times \;U(b{{([{{\xi }_{\eta }} - \xi ][{{\xi }_{\eta }} - \xi + \varepsilon \eta ])}^{{1/2}}}). \\ \end{gathered} $

Эта формула выражает неизвестную функцию e_h(η) на линии ab через известную функцию e_h(ξ) на линии bd. Эта функция известна, так как функция E_h(r) на этой линии просто переносится с линии de в направлении отраженного пучка, т.е. ее значение в точке p' совпадает с ее значением в точке p'', а разность легко вычислить.

Формулу для функции e₀(η) на линии ab получим аналогично (24) с очевидными изменениями:

(28)

$\begin{gathered} {{e}_{0}}(\eta ) = \frac{b}{2}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{0}}(\xi )\frac{1}{{{{\varsigma }_{\xi }}}}{{J}_{1}}(b{{\sigma }_{\xi }}) + \\ + \;\frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{e}_{h}}(\xi ){{J}_{0}}(b{{\sigma }_{\xi }}). \\ \end{gathered} $

Применим преобразование Лапласа к первому члену в правой части с учетом (25) и подставим e₀(q) из (18). В результате получим выражение, равное второму члену, если заменить в нем J₀(bσ_ξ) на J₂(bσ_ξ)ζ$_{\xi }^{{ - 2}}$. Соответственно получаем в сумме:

(29)

$\begin{gathered} \frac{{{{J}_{0}}(b{{\sigma }_{\xi }})({{\xi }_{d}} + a) + {{J}_{2}}(b{{\sigma }_{\xi }}){{\xi }_{d}}}}{{{{\xi }_{d}} + a}} = \\ = \;\frac{{U(b{{\sigma }_{\xi }}){{\xi }_{d}} + {{J}_{2}}(b{{\sigma }_{\xi }})a}}{{{{\xi }_{d}} + a}}. \\ \end{gathered} $

Здесь использовано соотношение J₀ + J₂ = U. Ответ можно записать в виде

(30)

${{e}_{0}}(\eta ) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d\xi {{U}_{1}}({{\xi }_{\eta }} - \xi ,\eta ){{e}_{h}}(\xi )} ,$

где

(31)

$\begin{gathered} {{U}_{1}}(\xi ,\eta ) = \\ = \frac{{\xi U(b{{{[\xi (\xi + \varepsilon \eta )]}}^{{1/2}}}) + \varepsilon \eta {{J}_{0}}(b{{{[\xi (\xi + \varepsilon \eta )]}}^{{1/2}}})}}{{\xi + \varepsilon \eta }}. \\ \end{gathered} $

Функции на линии bc вычисляются проще. Так, поле E_h(r) на этой линии просто переносится с линии de в направлении отраженного пучка и в случае падающей плоской волны не зависит от x. А поле E₀(r) переносится с линии bd в направлении проходящего пучка. То есть поле в точке p₀ равно полю в точке p'. Поле E₀(r) на линии bd вычисляется по формуле (20).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Рассмотрим те же параметры, что и первой части работы, а именно: энергию фотонов E = ħω = = 10 кэВ, t₁ = 1 мм, кристалл кремния, отражение 220, угол Брэгга θ_B = 18.84°. Для функции e_h(ξ) на линии bd получим выражение с учетом (4):

(32)

${{e}_{h}}(\xi ) = {{C}_{h}}F_{h}^{{ - 1}}({{t}_{1}})[F_{0}^{{ - 1}}(\gamma \xi ) - F_{h}^{{ - 1}}(\gamma \xi )].$

Удобно анализировать отношение интенсивностей пучков на полной толщине t в кристалле со ступенькой к отношению в кристалле без ступеньки. Для этого рассмотрим отношение R_h(η) = = E_h(η)/A_h(t) на линии ab. Тогда из (27) с учетом (4) имеем

(33)

${{R}_{h}}(\eta ) = 1 + {{g}_{h}}(\gamma {{D}_{1}}\eta ) - {{G}_{h}}(\eta ),$

где

(34)

$\begin{gathered} {{G}_{h}}(\eta ) = \frac{1}{4}{{b}^{2}}\varepsilon \eta \int\limits_0^{{{\xi }_{\eta }}} {d\xi } {{g}_{h}}({{t}_{0}} - \gamma \xi ) \times \\ \times \;U(b{{([{{\xi }_{\eta }} - \xi ][{{\xi }_{\eta }} - \xi + \varepsilon \eta ])}^{{1/2}}}), \\ \end{gathered} $

(35)

${{g}_{h}}(x) = C{{F}_{0}}(x) - {{F}_{h}}(x),\quad C = {{F}_{h}}({{t}_{0}})F_{0}^{{ - 1}}({{t}_{0}}).$

В интеграле G_h(η) удобно сделать замену переменных ξ = ξ_η – ξ₁ без изменения пределов интегрирования, окончательно получим

(36)

$\begin{gathered} {{G}_{h}}(\eta ) = \frac{1}{4}{{b}^{2}}\varepsilon \eta \int\limits_0^{{{\xi }_{\eta }}} {d{{\xi }_{1}}} \times \\ \times \;{{g}_{h}}(\gamma {{D}_{1}}\eta + \gamma {{\xi }_{1}})U(b{{({{\xi }_{1}}[{{\xi }_{1}} + \varepsilon \eta ])}^{{1/2}}}). \\ \end{gathered} $

Заметим, что при η = η_m = t₀/γD₁ второй и третий члены в (33) равны нулю и отношение равно единице, т.е. решение непрерывно на границе треугольника Бормана. При η = 0 параметр R_h(0) = = F_h(t₀)/F₀(t₀), и относительная интенсивность очень слабо зависит от высоты ступеньки, однако реальная интенсивность от высоты ступеньки не зависит и равна интенсивности поля на толщине t₁.

Итак, формула для относительной интенсивности содержит три члена, причем второй и третий члены являются комплексными. Соответственно в сумме три члена формально могут увеличить интенсивность в 9 раз, если их модули примерно равны. В [1] было показано, что численный расчет приводит к увеличению максимумов интенсивности более чем в 7 раз. Формула (33) позволяет проанализировать, как это происходит.

Из формулы (30) с учетом (4) получаем формулу для отношения R₀(η) = E₀(η)/A₀(t) на линии ab:

(37)

${{R}_{0}}(\eta ) = 1 - {{G}_{{01}}}(\eta ),$

где

(38)

${{G}_{{01}}}(\eta ) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d{{\xi }_{1}}} {{g}_{h}}(\gamma {{D}_{1}}\eta + \gamma {{\xi }_{1}}){{U}_{1}}({{\xi }_{1}},\eta ).$

В формуле (37) всего два члена, т.е. формально максимум интенсивности может увеличиваться до четырех.

Рассмотрим отношение R₀(η) = E₀(η)/A₀(t) на линии bd. В этом случае координата η отсчитывается от точки b в сторону точки d, а ξ_η = ξ₀ – ηD₂. Точке p' соответствует точка p₀ на рис. 1а. Делая те же преобразования, что и раньше, получаем

(39)

${{R}_{0}}(\eta ) = F_{0}^{{ - 1}}(\gamma {{D}_{2}}\eta )[{{F}_{h}}(\gamma {{D}_{2}}\eta ) - {{G}_{{02}}}(\eta )],$

где

(40)

${{G}_{{02}}}(\eta ) = \frac{i}{2}{{X}_{{ - h}}}{{\gamma }_{1}}\int\limits_0^{{{\xi }_{\eta }}} {d{{\xi }_{1}}} {{g}_{h}}(\gamma {{D}_{2}}\eta + \gamma {{\xi }_{1}})U(b{{\xi }_{1}}).$

При выводе формулы (39) было учтено, что напряженность поля E₀ в точках η на отрезке bc и ξ_η на отрезке bd имеет одно и то же значение, а также что C_h = –C₀. При η = 0 формула (39) дает такое же значение, что и формула (37), а при η = η_m = t₀/γD₂ выражение равно F_h(t₀)/F₀(t₀), т.е. чуть больше единицы, так как на высоте t₀ реальное поле не поглощается, а знаменатель в отношении соответствует толщине t.

На рис. 1б показаны три типа наклона ступеньки, которые можно характеризовать разными значениями параметра R = tg θ/tg θ_B при отсчете угла θ, как на рис. 1а. На рис. 2 показаны распределения вычисленной по формулам (33), (37), (39) относительной интенсивности I/I₀ = = |R_0,h|² проходящего (T) и отраженного (R) пучков на всем основании ac треугольника Бормана для условий: t₀ = 0.2 мм, R = 0.5, 0, –0.5 соответственно. Результаты расчета численным методом [1] для тех же параметров совпадают с данными, полученными в настоящей работе. Интересно, что результат расчета [1] в случае L = 2 м не сильно отличается от того, который показан на рис. 2а. Дело в том, что толстый кристалл на малом расстоянии от точечного источника излучения сам создает расходящуюся сферическую волну, которая в области ступеньки почти совпадает с плоской волной.

Рис. 2.

Зависимость относительной интенсивности проходящего (T) и отраженного (R) пучка на участке выходной поверхности, совпадающей с основанием треугольника Бормана (линия ac на рис. 1а), x₀ = = 68.2 мкм, R: 0.5 (а), 0 (б), –0.5 (в).

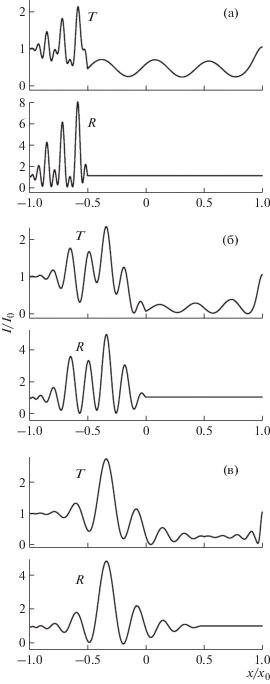
Как следует из расчетов, наиболее интересные результаты получаются при положительных значениях параметра R, когда отличие от единицы невелико. В этом случае интенсивность отраженного пучка осциллирует с малым периодом, достигая в максимумах наиболее высоких значений, близких к девяти. Но это происходит не всегда, а периодически зависит от высоты ступеньки.

Относительная интенсивность отраженного пучка остается больше, чем падающего пучка, для всех значений |R | < 1. При |R | > 1 формулы (33), (37), (39) не применимы, и расчет надо делать иначе. Отметим, что наблюдается некоторая корреляция между максимумами и минимумами интенсивности прошедшего и отраженного пучков в том смысле, что они возникают одновременно. В этом заключается отличие данных осцилляций от экстинкционных осцилляций интенсивности плоской волны в зависимости от толщины кристалла, когда интенсивность прошедшего пучка перетекает в интенсивность отраженного и обратно.

Список литературы

Кон В.Г., Смирнова И.А. // Кристаллография. 2020. Т. 65. № 4. С. 515.
Kato N. // Acta Cryst. 1961. V. 14. P. 526.
Kato N. // Acta Cryst. 1961. V. 14. P. 627.
Kato N. // J. Appl. Phys. 1968. V. 39. P. 2225.
Kato N. // J. Appl. Phys. 1968. V. 39. P. 2231.
Афанасьев А.М., Кон В.Г. // ФТТ. 1977. Т. 19. С. 1775.
Takagi S. // Acta Cryst. 1962. V. 15. P. 1311.
Слободецкий И.Ш., Чуховский Ф.Н., Инденбом В.Л. // Письма в ЖЭТФ. 1968. Т. 8. С. 90.
Uragami T.S. // J. Phys. Soc. Jpn. 1969. V. 27. P. 147.
Uragami T.S. // J. Phys. Soc. Jpn. 1970. V. 28. P. 1508.
Uragami T.S. // J. Phys. Soc. Jpn. 1971. V. 31. P. 1141.
Afanas’ev A.M., Kohn V.G. // Acta Cryst. A. 1971. V. 27. P. 421.
Saka T., Katagawa T., Kato N. // Acta Cryst. A. 1971. V. 28. P. 102.
Saka T., Katagawa T., Kato N. // Acta Cryst. A. 1971. V. 28. P. 113.
Афанасьев А.М., Кон В.Г. // Укр. физ. журн. 1972. Т. 17. С. 424. http://kohnvict.ucoz.ru/art/004r.pdf
Kohn V.G., Smirnova I.A. // Acta Cryst. A. 2018. V. 74. P. 699.
Snigirev A., Kohn V., Snigireva I., Lengeler B. // Nature. 1996. V. 384. P. 49.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматлит, 1963. 1100 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кристаллография

Архивы выпусков Информация о журнале Отправить рукопись в журнал