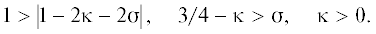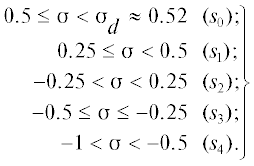Кристаллография, 2020, T. 65, № 6, стр. 933-938
Вырожденные отражения в акустике твердых тел. III. Кубические кристаллы
Д. А. Бессонов 1, В. Н. Любимов 1, *
1 Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
Москва, Россия
* E-mail: lyubvn36@mail.ru
Поступила в редакцию 29.01.2020
После доработки 29.05.2020
Принята к публикации 01.06.2020
Аннотация
Проанализированы особые случаи отражения объемных акустических волн от свободной поверхности кубического кристалла, когда и плоскость падения, и поверхность кристалла – плоскости симметрии, которым параллельны векторы поляризации падающей и отраженных волн. Описаны условия, когда при отражении возникает только одна объемная отраженная волна, а не две, как обычно. Сопутствующая отраженная волна (объемная или локализованная) исчезает – отражение оказывается вырожденным. Возникает либо чистое отражение (падающая и отраженная волны принадлежат одной и той же акустической ветви), либо конверсионное отражение (данные волны принадлежат к разным ветвям).
ВВЕДЕНИЕ
Когда акустическая объемная волна в кристалле отражается от его свободной границы с вакуумом, возникает, вообще говоря, несколько отраженных волн. Во-первых, могут возникнуть три отраженные объемные волны; во-вторых, две отраженные объемные волны вместе с сопутствующей, локализованной у границы; в-третьих – одна отраженная объемная волна вместе с двумя локализованными. Реализуемость конкретного варианта зависит от симметрии кристалла, его упругой анизотропии, ориентации границы и плоскости падения, от той акустической ветви, которой принадлежит падающая волна, и, наконец, от направления падающей волны [1–4].
При некотором угле падения волны амплитуда одной из отраженных объемных волн может оказаться нулевой. Отражение оказывается вырожденным. Это может реализоваться в кристаллах произвольной симметрии [5–7]. Для гексагональных кристаллов вырожденные отражения рассматривались в [8].
Если в отношении упругих свойств кристалл имеет плоскость симметрии и если рассматривать ее как плоскость падения, то “отщепляется” чисто поперечная SH-волна с вектором упругого смещения, ортогональным плоскости падения. Отражение волн данной ветви при любом угле падения происходит независимо от волн двух других акустических ветвей. Происходит “чистое” отражение. При этом векторы поляризации волн других двух ветвей параллельны выбранной плоскости падения. Данная ситуация реализуется во всех кристаллах, кроме триклинных. Участвующие в отражении волны с такими векторами поляризации связаны друг с другом. В этом случае падающая объемная волна может породить в качестве отраженных либо две объемные волны, либо одну объемную, сопровождаемую локализованной у границы волной. Подбирая угол падения, можно обеспечить ликвидацию одной из двух объемных отраженных волн или локализованной компоненты, сопровождающей объемную отраженную волну. Если при этом падающая и отраженная волны принадлежат одной и той же акустической ветви, то этот случай можно назвать чистым отражением, если разным – конверсионным отражением.
Анализ таких отражений проведен в [9] для случая ромбических кристаллов, когда и граница кристалла, и плоскость падения волны параллельны плоскостям симметрии. Плоскости симметрии ромбического кристалла совпадают с координатными плоскостями в стандартной кристаллографической системе координат [1]. Этим условиям удовлетворяют шесть различных конфигураций геометрии распространения. Ромбический кристалл характеризуется девятью независимыми модулями упругости. В каждой из шести различных по геометрии конфигураций отражения участвуют разные группы этих модулей. Описание отражений оказывается достаточно громоздким.
Такая громоздкость исчезает, если осуществить предельный переход от описания ромбических кристаллов [9] к кубическим, упругие свойства которых характеризуются только тремя независимыми модулями упругости. Описанию вырожденных отражений в кубических кристаллах и посвящена настоящая работа, развивающая подход к данной проблеме, предложенный в [10, 11].
ИСХОДНЫЕ ДАННЫЕ
Кубические кристаллы имеют два семейства симметрийно эквивалентных плоскостей симметрии. Одно из них – это плоскость (хz) и ей эквивалентные (оси координат $x$, $y$, $z$ параллельны осям симметрии 4). Другое семейство – плоскость ($х{\text{'}}z$) и ей эквивалентные (оси координат $x{\text{'}}$, $y{\text{'}}$ параллельны осям симметрии 2) [1]. В стандартной кристаллофизической системе координат $x$, $y$, $z$ кубические кристаллы характеризуются модулями упругости ${{c}_{{11}}}$, ${{c}_{{44}}}$, ${{c}_{{12}}}$ [1]. В матрице модулей упругости данных кристаллов можно выделить часть, отвечающую изотропному телу, которое характеризуется всего двумя модулями ${{c}_{{11}}}$, ${{c}_{{44}}}$ (вырожденные отражения в этом пределе описаны в [12]). При этом отличные от нуля компоненты матрицы модулей упругости кубического кристалла можно записать в следующей форме:
(1)
$\begin{gathered} {{c}_{{11}}} = {{с}_{{22}}} = {{с}_{{33}}}, \\ {{с}_{{12}}} = {{с}_{{13}}} = {{с}_{{23}}} = {{с}_{{11}}} - 2{{с}_{{44}}} - 2{{с}_{{cub}}}, \\ {{с}_{{44}}} = {{с}_{{55}}} = {{с}_{{66}}}. \\ \end{gathered} $(3)
$\begin{gathered} c_{{11}}^{'} = с_{{22}}^{'} = {{с}_{{11}}} - {{с}_{{cub}}},\quad с_{{33}}^{'} = {{с}_{{11}}}, \\ с_{{12}}^{'} = {{с}_{{11}}} - 2{{с}_{{44}}} - {{с}_{{cub}}}, \\ с_{{13}}^{'} = с_{{23}}^{'} = {{с}_{{11}}} - 2{{с}_{{44}}} - 2{{с}_{{cub}}}, \\ c_{{44}}^{'} = c_{{55}}^{'} = {{c}_{{44}}},\quad c_{{66}}^{'} = {{c}_{{44}}} + {{с}_{{cub}}}. \\ \end{gathered} $(4)
${{с}_{{11}}} > \left| {{{c}_{{12}}}} \right|,\quad {{c}_{{11}}} + 2{{c}_{{12}}} > 0,\quad {{c}_{{44}}} > 0.$Рис. 1.
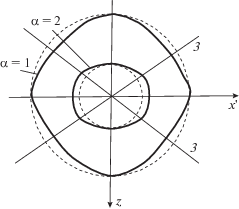
Сечение поверхности рефракции кубического кристалла плоскостью падения ($xz$). Показаны линии в сечении двух полостей ${\alpha } = 1,\;2$; ${{{v}}_{{L1}}}$, ${{{v}}_{{L2}}}$ – скорости предельных волн, ${{{v}}_{R}}$ – скорость рэлеевской волны, ${\omega }$ – частота; ${{({\mathbf{k}}_{1}^{i},{\mathbf{k}}_{1}^{r})}_{{{{{v}}_{0}}}}}$, ${{({\mathbf{k}}_{2}^{i},{\mathbf{k}}_{2}^{r})}_{{{{{v}}_{0}}}}}$ – чистые отражения, ${{({\mathbf{k}}_{1}^{i},{\mathbf{k}}_{2}^{r})}_{{{{{v}}_{I}}}}}$, ${{({\mathbf{k}}_{2}^{i},{\mathbf{k}}_{1}^{r})}_{{{{{v}}_{I}}}}}$ – конверсионные отражения, ${\mathbf{k}}_{{\alpha }}^{{i,r}}$ – волновые векторы падающих (i) и отраженных (r) волн. Окружности, показанные штрихами, отвечают изотропному пределу.
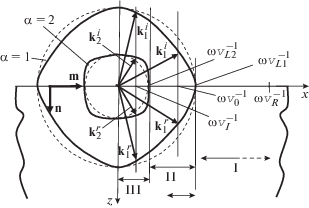
На рис. 1 единичный вектор n, ортогональный поверхности кристалла, задает ее ориентацию. Единичный вектор m (${\mathbf{m}} \bot {\mathbf{n}}$) задает общее направление распространения совокупного волнового поля вдоль выбранной поверхности. Плоскость векторов $({\mathbf{m}},{\mathbf{n}})$ является плоскостью падения. Параметр ${v}$ на рис. 1 – приведенная скорость, которая связана с волновым вектором ${\mathbf{k}}$ и частотой ${\omega }$: ${v} = {\omega /}{\mathbf{k}} \cdot {\mathbf{m}}$. Эта величина определяет углы падения (i) и отражения (r): $\angle \{ {{{\mathbf{k}}}^{{i,r}}}{\text{(}}{v}{\text{),}}{\mathbf{m}}\} $. На рис. 1 скорости предельных волн ${{{v}}_{{L1}}}$, ${{{v}}_{{L2}}}$ заданы соотношениями ${\rho }{v}_{{L1}}^{2} = {{с}_{{44}}}$, ${\rho }{v}_{{L2}}^{2} = {{c}_{{11}}}$, ${{c}_{{11}}} > {{c}_{{44}}}$ (${\rho }$ – плотность кристалла). Значения скоростей V объемных волн, распространяющихся вдоль осей симметрии, даны в табл. 1. Данные этой таблицы позволили графически представить сечения поверхности рефракции на рис. 1 и 2.
Таблица 1.
Векторы поляризации ${\mathbf{A}}$ и скорости V объемных волн, распространяющихся в плоскостях ($xy$) и ($х{\text{'}}z$) вдоль осей симметрии в кубических кристаллах
| Плоскость падения | ${\mathbf{k}}\,||$ | ${\mathbf{А}}\,||$ | ${\rho }{{V}^{2}}$ |
|---|---|---|---|
| ${\text{(}}xz{\text{)}}$ | x | x | ${{c}_{{11}}}$ |
| 2 | ${{c}_{{44}}}$ | ||
| $x{\text{'}}$ | $x{\text{'}}$ | ${{c}_{{11}}} - {{c}_{{cub}}}$ | |
| $y{\text{'}}$ | ${{c}_{{44}}} + {{c}_{{cub}}}$ | ||
| $(х{\kern 1pt} {\text{'}}z)$ | $x{\text{'}}$ | $x{\text{'}}$ | ${{c}_{{11}}} - {{c}_{{cub}}}$ |
| $z$ | ${{c}_{{44}}}$ | ||
| $z$ | $z$ | ${{c}_{{11}}}$ | |
| $x{\text{'}}$ | ${{c}_{{44}}}$ | ||
| 3 | 3 | ${{c}_{{11}}} - 4{{c}_{{cub}}}{\text{/}}3$ | |
| ${\mathbf{А}} \bot 3$ | ${{c}_{{44}}} + 2{{c}_{{cub}}}{\text{/}}3$ |
ВАРИАНТЫ ВЫРОЖДЕННЫХ ОТРАЖЕНИЙ
Все кристаллографически различные варианты (1, 2, 3, 4) выбора поверхности кристалла и соответствующих плоскостей падения, когда поверхность и плоскость падения совпадают с плоскостями симметрии кристалла, собраны в табл. 2.
Таблица 2.
Геометрия распространения, заданная векторами m и n; параметр чистого отражения ${\rho }{v}_{0}^{2}{\text{/}}{{c}_{{11}}}$ и коэффициенты (a, b, c, d) уравнения (7) – функции величин $\kappa $, ${\sigma }$ (5)
| Вариант | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| ${\mathbf{m}}\,||$ | $x$ | $x{\text{'}}$ | $x{\text{'}}$ | $z$ |
| ${\mathbf{n}}\,||$ | $y$ | $y{\text{'}}$ | $z$ | $x{\text{'}}$ |
| $\frac{{{\rho }{v}_{0}^{2}}}{{{{c}_{{11}}}}}$ | $2(\kappa + {\sigma })$ | $2\kappa $ | $\frac{\kappa }{{2(1 - \kappa - {\sigma })}}A$ | $\frac{{\kappa (1 - \kappa {\text{)}}}}{{2 - 2\kappa - 3{\sigma }}}A$ |
| a | $1 - {\kappa }$ | $\frac{{1 - \kappa - 2\sigma }}{{1 - \sigma }}$ | $1 - \kappa $ | $\frac{{{\text{1}} - \kappa - {\sigma }}}{{1 - {\sigma }}}$ |
| b | $ - 2A$ | $ - 2A$ | $ - 2A - {\sigma }$ | $ - 2A + \frac{{\sigma }}{{1 - {\sigma }}}$ |
| c | ${{A}^{2}} + 2A$ | |||
| d | $ - {{A}^{2}}$ | |||
| A | $\frac{{4(1 - \kappa - {\sigma })(\kappa + {\sigma })}}{\kappa }$ | $\frac{{4(1 - \kappa - {\sigma })\kappa }}{{{\text{(}}\kappa + {\sigma )(1} - {\sigma )}}}$ | $\frac{{4(1 - \kappa - {\sigma })(\kappa + {\sigma }) - {\sigma }}}{\kappa }$ | $\frac{{4(1 - \kappa - {\sigma })(\kappa + {\sigma }) - {\sigma }}}{{\kappa {\text{(1}} - {\sigma )}}}$ |
В табл. 2 приняты обозначения:
(5)
$\kappa = {{с}_{{44}}}{\text{/}}{{c}_{{11}}},\quad {\sigma } = {{с}_{{cub}}}{\text{/}}{{c}_{{11}}}.$Что касается параметра конверсионных отражений ${{{\xi }}^{{\text{2}}}} = {\rho }{{{v}}^{2}}{\text{/}}{{c}_{{{\text{44}}}}}$, то его величина определяется из бикубического уравнения
коэффициенты которого (a, b, c, d) приведены в табл. 2.Все характеристики кубических кристаллов в табл. 2 зависят всего от двух безразмерных переменных ${\kappa }$, ${\sigma }$. В то же время в ромбических кристаллах аналогичные характеристики для каждой из шести рассмотренных в [9] геометрий распространения зависят от трех независимых переменных – каждой геометрии соответствует своя тройка переменных. Размерность пространства, в котором существуют исследуемые характеристики для кубических кристаллов, оказалась меньше. Теперь в двумерном пространстве – на плоскости переменных ($\kappa $, ${\sigma }$) – в явном виде можно выявить и области существования, и все характеристики рассматриваемых волновых полей.
Характер корней уравнения (7) определяется знаком следующей функции [13]:
(8)
$D(\kappa ,{\sigma }) = {\text{ }}{{\left( {\frac{{{{b}^{3}}}}{{27}} - \frac{{abc}}{6} + \frac{{{{a}^{2}}d}}{2}} \right)}^{2}} + {\text{ }}{{\left( {\frac{{3ac - {{b}^{2}}}}{9}} \right)}^{3}}.$В области $D(\kappa ,{\sigma }) \leqslant 0$ другие два корня ${\xi }_{{\text{I}}}^{2}$ и ${\xi }_{{{\text{II}}}}^{2}$ уравнения (7) вещественные. Если они положительные, то отвечают конверсионным отражениям. В области $D(\kappa ,{\sigma }) > 0$ корни ${\xi }_{{\text{I}}}^{2}$ и ${\xi }_{{{\text{II}}}}^{2}$ комплексно сопряженные и отвечают нефизическим решениям. Области существования этих двух типов решений разделены условием $D(\kappa ,{\sigma }) = 0$, при котором из трех действительных корней уравнения (7) два совпадают: ${\xi }_{{\text{I}}}^{2} = {\xi }_{{{\text{II}}}}^{2} = {\xi }_{d}^{2}$, т.е. имеет место вырождение. Данное условие задает линию вырождения корней ${\xi }_{{\text{I}}}^{2}$, ${\xi }_{{{\text{II}}}}^{2}$ уравнения (7) ${{\kappa }_{d}} = {{\kappa }_{{d1,2}}}({\sigma })$. Эта линия – граница между областями принципиально различных типов корней ${\xi }_{{\text{I}}}^{2}$, ${\xi }_{{{\text{II}}}}^{2}$ уравнения (7). Для геометрии 1 данная линия представлена (в области устойчивости) на рис. 3.
Рис. 3.
Линия вырождения ${{\kappa }_{d}} = {{\kappa }_{{d1,2}}}({\sigma })$, отвечающая условию ${\xi }_{{\text{I}}}^{2} = {\xi }_{{{\text{II}}}}^{2} = {\xi }_{d}^{2}$, для геометрии варианта 1 (табл. 2).
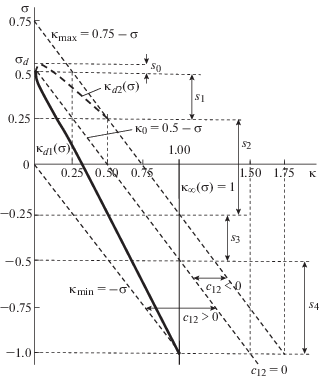
Линия вырождения имеет две ветви: ${{\kappa }_{{d1}}}({\sigma })$ и ${{\kappa }_{{d2}}}({\sigma })$. Вторая ветвь дана штриховой линией; она лежит в области устойчивости, но отвечает случаю ${{с}_{{12}}} \leqslant 0$. Конкретные представители кристаллов c таким свойством, насколько известно авторам, не обнаружены.
Кривая вырождения (рис. 3) определяет на плоскости 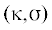 несколько областей (${{s}_{0}}$, ${{s}_{1}}$, ${{s}_{2}}$, ${{s}_{3}}$, ${{s}_{4}}$), в которых структура линий конверсионных отражений ${{{\xi }}^{{\text{2}}}} = {\xi }_{{{\text{I,II}}}}^{2}{{(\kappa )}_{{{\sigma } = {\text{const}}}}}$ (рис. 4) топологически различна.
несколько областей (${{s}_{0}}$, ${{s}_{1}}$, ${{s}_{2}}$, ${{s}_{3}}$, ${{s}_{4}}$), в которых структура линий конверсионных отражений ${{{\xi }}^{{\text{2}}}} = {\xi }_{{{\text{I,II}}}}^{2}{{(\kappa )}_{{{\sigma } = {\text{const}}}}}$ (рис. 4) топологически различна.
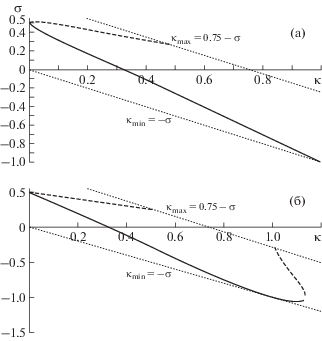
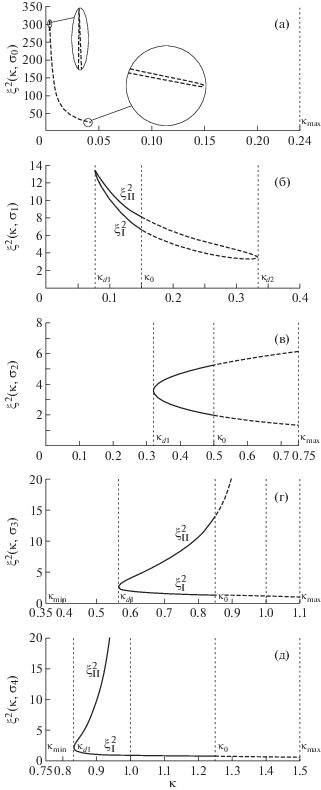
Рис. 4.
Линии конверсионных отражений ${{{\xi }}^{{\text{2}}}} = {\xi }_{{{\text{I,II}}}}^{2}{{(\kappa )}_{{{\sigma } = {\text{const}}}}}$ для геометрии 1 при различных значениях параметра ${\sigma } = {{{\sigma }}_{i}} = {\text{const}} \subset {{s}_{i}}$: а – ${{{\sigma }}_{{\text{0}}}} = 0.51$, б – ${{{\sigma }}_{{\text{1}}}} = 0.35$, в – ${{{\sigma }}_{{\text{2}}}} = 0$ (изотропный предел), г – ${{{\sigma }}_{{\text{3}}}} = - 0.35$, д – ${{{\sigma }}_{{\text{4}}}} = - 0.75$. В кружках на (а) показаны увеличенные фрагменты кривой.
Области ${{s}_{i}}$ на рис. 3 и 4 заданы неравенствами
Последовательность фрагментов рис. 4 отражает эволюцию представленных кривых при “включении” анизотропии кубического кристалла (изотропной среде отвечает рис. 4в). На рис. 4 приведены топологически различные картины поведения линий конверсионных отражений ${{{\xi }}^{{\text{2}}}} = {\xi }_{{{\text{I,II}}}}^{2}{{(\kappa )}_{{{\sigma } = {\text{const}}}}}$ (${\sigma } = {{{\sigma }}_{i}} = {\text{const}} \subset {{s}_{i}}$) во всех областях (9). Штриховые участки линий на рис. 3 и 4 отвечают случаям ${{с}_{{12}}} \leqslant 0$. Вся область ${{s}_{0}}$ отвечает вариантам ${{с}_{{12}}} \leqslant 0$.Из рис. 4 видно, что решения существуют в ограниченном диапазоне $\kappa $. При этом в зависимости от области и диапазона $\kappa $ возможны либо два, либо одно решение.
В областях ${{s}_{0}}$ и ${{s}_{1}}$, где ${\sigma > 0}$, линии являются замкнутыми. При этом во всей области существования решений присутствуют два корня, за исключением крайних точек, в которых происходит вырождение.
В области ${{s}_{2}}$, где ${\sigma = 0}$, правая из предельных точек вырождения пропадает (уходит из области устойчивости).
В областях ${{s}_{3}}$ и ${{s}_{4}}$, где ${\sigma < 0}$, величина ξII(κ) при ${\kappa = 1}$ стремится к бесконечности. При $\kappa {\text{ }} \to {\text{ 1}}$ коэффициент a при старшем члене уравнения (7) имеет особенность: a = κ – 1 → ±∞. В связи с этим в данных областях при $\kappa {\text{ > 1}}$ существует только одно решение уравнения (7), имеющее физический смысл – ξII (разумеется, решение, отвечающее рэлеевской волне ${\xi }_{R}^{2}$, по-прежнему остается).
Сопоставление вариантов 1, 2, 3, 4 показывает, что все линии вырождения на плоскости (κ, σ) идут очень близко друг к другу – в масштабе, принятом на рис. 3, их даже трудно разделить. Более того, следующие три точки на плоскости (κ, σ) (рис. 3):
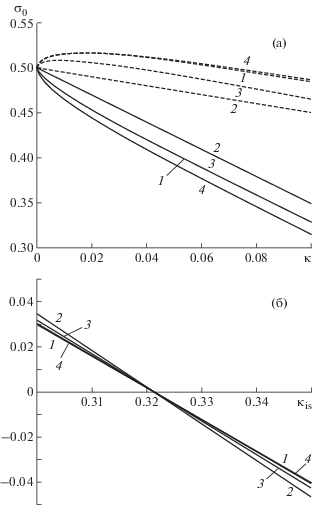
оказываются общими для всех четырех линий вырождения (последняя из этих точек отвечает пределу изотропной среды). Именно поэтому на рис. 3 представлен только вариант 1. Таким образом, топологически различные случаи, показанные на рис. 4, качественно могут иллюстрировать все рассматриваемые варианты (1, 2, 3, 4). В более крупном, чем на рис. 3, масштабе ход всех четырех линий вырождения в окрестности точек их пересечения (10) иллюстрирует рис. 5.Рис. 5.
Ход линий вырождения (варианты 1, 2, 3, 4) вблизи точек их пересечения на плоскости ($\kappa $, ${\sigma }$): а – вблизи точки (${\text{0}}$,${{{\sigma }}_{{\text{0}}}}$), ${{{\sigma }}_{{\text{0}}}} = 0.5$; б – вблизи точки изотропии (${{\kappa }_{{is}}}$, ${\text{0}}$), ${{\kappa }_{{is}}} \approx 0.321$.
Отметим особенность, возникающую в варианте 2, – здесь в области устойчивости появляется дополнительная ветвь, правда для ${{с}_{{12}}} \leqslant 0$ (рис. 6).
ЧИСЛЕННЫЕ ОЦЕНКИ
Численные оценки проведены для нескольких кубических кристаллов, модули упругости которых взяты из [18] (табл. 3). Конкретные значения ключевых параметров вырожденных отражений для этих кристаллов представлены в табл. 4.
Таблица 3.
Модули упругости ${{c}_{{{\alpha \beta }}}}$, ${{c}_{{cub}}}$ (в GPa) и безразмерные параметры $\kappa $, ${\sigma }$ (5) для нескольких кубических кристаллов
| Кристалл | ${{c}_{{11}}}$ | ${{c}_{{44}}}$ | ${{c}_{{12}}}$ | ${{c}_{{cub}}}$ | $\kappa $ | ${\sigma }$ |
|---|---|---|---|---|---|---|
| Алмаз | 107.6 | 57.6 | 12.5 | –10.1 | 0.535 | –0.093 |
| Si | 16.74 | 7.96 | 6.52 | –2.85 | 0.476 | –0.170 |
| GaAs | 11.88 | 5.94 | 5.38 | –2.69 | 0.500 | –0.226 |
Таблица 4.
Параметры вырожденных отражений и рэлеевской волны ряда кубических кристаллов. Номера 1, 2, 3, 4 задают геометрию распространения – ориентации m и n – согласно данным табл. 2
| Кристалл | Вариант | ${\rho }{v}_{0}^{2}{\text{/}}{{c}_{{11}}}$ | ${\rho }{v}_{{\text{I}}}^{2}{\text{/}}{{c}_{{44}}}$ | ${\rho }{v}_{{{\text{II}}}}^{2}{\text{/}}{{c}_{{44}}}$ | ${\rho }{v}_{R}^{2}{\text{/}}{{c}_{{44}}}$ |
|---|---|---|---|---|---|
| Алмаз | 1 | 0.884 | 1.88 | 5.32 | 0.742 |
| 2 | 1.07 | 2.06 | 4.09 | 0.691 | |
| 3 | 0.968 | 2.04 | 5.69 | 0.758 | |
| 4 | 0.893 | 1.87 | 4.78 | 0.750 | |
| Si | 1 | 0.612 | 2.18 | 3.91 | 0.711 |
| 2 | 0.952 | 2.46 | 3.37 | 0.592 | |
| 3 | 0.735 | 2.53 | 4.56 | 0.758 | |
| 4 | 0.654 | 2.16 | 3.50 | 0.742 | |
| GaAs | 1 | 0.548 | 2.15 | 3.54 | 0.656 |
| 2 | 1.00 | 2.47 | 3.10 | 0.513 | |
| 3 | 0.704 | 2.59 | 4.39 | 0.734 | |
| 4 | 0.609 | 2.12 | 3.10 | 0.711 |
ЗАКЛЮЧЕНИЕ
Заканчивая третью работу цикла, отметим, что описанные особенности акустических волн при их отражениях в кристаллах могут быть использованы при конструировании кристаллических звукопроводов. Существенно, что при описанных отражениях возникает только одна отраженная волна, а паразитные сопутствующие акустические поля заведомо отсутствуют.
Авторы выражают благодарность В.И. Альшицу за ряд полезных замечаний.
Список литературы
Федоров Ф.И. Теория упругих волн в кристаллах. М.: Наука, 1965. 388 с.
Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука, 1965. 204 с.
Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1973. 343 с.
Alshits V.I., Lothe J. // Wave motion. 1981. V. 3. P. 297.
Lothe J., Wang L. // Wave motion. 1995. V. 21. P. 163.
Wang L., Lothe J. // Wave motion. 1992. V. 16. P. 89.
Gundersen S.A., Wang L., Lothe J. // Wave motion. 1991. V. 14. P. 129.
Любимов В.Н., Альшиц В.И. // Кристаллография. 1982. Т. 27. Вып. 5. С. 851.
Любимов В.Н. // Кристаллография. 2019. Т. 64. № 3. С. 386.
Любимов В.Н., Филиппов В.В. // Акуст. журн. 1980. Т. 26. Вып. 2. С. 225.
Любимов В.Н., Филиппов В.В. // Изв. АН БССР. 1980. Вып. 5. С. 121.
Любимов В.Н. // Кристаллография. 2019. Т. 64. № 2. С. 270.
Бронштейн И.Н., Семендяев К.А. Справочник по математике. М.: Наука, 1981. 723 с.
Barnett D.M., Lothe J. // J. Phys. F. 1974. V. 4. P. 671.
Lothe J., Barnett D.M. // J. Appl. Phys. 1976. V. 47. P. 428.
Barnett D.M., Lothe J. // Proc. R. Soc. London. A. 1985. V. 402. P. 135.
Landolt H.H., Börnstein R. Zahlenwerte und Funktionen aus Naturwissenschaften und Technik. Neue Serie. Gruppe III. Band 11 / Ed. Hellwege K.-H. Berlin, Heidelberg, New York: Springer-Verlag, 1979. 854 s.
Сиротин Ю.И., Шаскольская М.П. Основы кристаллофизики. М.: Наука, 1975. 680 с.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография