Лесоведение, 2023, № 2, стр. 190-200

Анализ и прогноз динамики численности серой лиственничной листовертки при помощи модели Морана-Рикера с запаздыванием

Г. П. Неверова^a, *, Е. Я. Фрисман^b

^a Институт автоматики и процессов управления ДВО РАН
690041 Владивосток, ул. Радио, д. 5, Россия

^b Институт комплексного анализа региональных проблем ДВО РАН
679016 Биробиджан, ул. Шолом-Алейхема, д. 4, Россия

^* E-mail: galina.nev@gmail.com

Поступила в редакцию 06.07.2022
После доработки 17.08.2022
Принята к публикации 18.10.2022

EDN: AKRJWI
DOI: 10.31857/S0024114823020055

Полный текст (PDF)

Аннотация

Модель Морана–Рикера с запаздыванием 1 и 2 года, учитывающая внутрипопуляционные саморегуляторные механизмы, применяется к описанию динамики плотности двух популяций листовертки лиственничной (Zeiraphera griseana). Используются данные о популяциях, обитающих в Швейцарии в локациях Graubunden (the Global Population Dynamics Database: Data set 1525 (Baltensweiler, Fischlin, 1988)) и Oberengadin (Baltensweiler, 1991). Оценки значений параметров моделей находились путем минимизации суммы квадратов отклонений эмпирических и модельных траекторий. Показано, что найденные точечные оценки популяционных параметров удовлетворяют статистическим критериям и располагаются в области квазипериодических колебаний, как правило, соседствуя с другими динамическими режимами. Следовательно, вариация демографических параметров, например, в результате эволюционных процессов или же влияния модифицирующих факторов может привести к смене динамического режима. Чтобы проверить прогностические свойства этих моделей, часть данных была использована для оценок значений параметров, а оставшаяся часть – для сопоставления реальной динамики и модельного прогноза. Как оказалось, качество прогноза существенно зависит от характера динамики в конце обучающей выборки, используемой для оценки параметров. Наилучший прогноз будет получен, если обучающая выборка заканчивается на фазе пика численности. В случае фазы низкой численности прогноз может характеризоваться приемлемой ошибкой, однако характер прогнозируемой динамики может измениться: например, произойдет смещение пика численности. Для Data set 1525 проведено сопоставление точечных оценок, полученных по обучающей выборке разной длины, с динамическими режимами модели Морана–Рикера. Это позволило получить представление об эволюции динамических режимов в популяции листовертки лиственничной и выявить переходы от одних динамических режимов к другим.

Ключевые слова: плотностно-зависимая регуляция с запаздыванием, динамические режимы, оценка параметров, прогноз, смена режима динамики.

Анализу динамики численности популяций насекомых с последующим моделированием и сопутствующим прогнозом посвящено большое количество работ – от отдельных научных статей до монографий (Baltensweiler, Fischlin, 1988; Turchin, 1990, 2003; Baltensweiler, 1991; Kendall et al., 1999; Исаев и др., 2001, 2015; Turchin et al., 2003; Недорезова, Недорезов, 2011; Недорезов, 2015а, б; Nedorezov, Sadykova, 2015; Суховольский и др., 2015; Neverova et al., 2016; и др.). Интерес к данному объекту обусловлен тем, что многие виды насекомых имеют 1) выраженный годовой жизненный цикл, что позволяет использовать модели с неперекрывающимися поколениями, и 2) сложную флуктуирующую динамику вплоть до “вспышек” численности. Также немаловажную роль играют многочисленные ряды данных по динамике разных видов насекомых, накопленные научным сообществом за годы исследований. Существенный вклад в понимание динамических процессов популяциях лесных насекомых позволил получить феноменологический подход, учитывающий закономерности изменений плотности популяций в совокупности с влиянием модифицирующих и регулирующих факторов (Исаев и др., 2001, 2015; Суховольский и др., 2015). В частности, на основе данного подхода была предложена классификация типов динамики численности и типов вспышек массового размножения насекомых. В целом на сегодняшний день можно выделить следующие подходы, направленные на описание и анализ популяционной динамики насекомых: 1) применение классических одномерных моделей и их модификаций (Исаев и др., 2001, 2015; Недорезов, 2015а, б; Nedorezov, Sadykova, 2015); 2) разработка моделей различной степени детализации, охватывающих ключевые аспекты существования вида (Turchin, 1990, 2003); одной из разновидностей является имитационное моделирование; 3) использование авторегресионных моделей (Исаев и др., 2015; Суховольский и др., 2015).

Отметим, что излишне детализированные модели сложны как для исследования, так и интерпретации полученных результатов с точки зрения содержательности, но при этом хороши для достижения прогностических целей. С другой стороны, при использовании моделей, которые не являются имитационными и включают всего несколько переменных, введение дополнительных предположений может существенно изменить картину динамического поведения (Turchin et al., 2003; Недорезова, Недорезов, 2011). В этом контексте применение простых математических моделей с учетом небольшого числа регуляторных механизмов является весьма перспективным инструментарием для анализа популяционной динамики насекомых и построения прогнозов (Недорезова, Недорезов, 2011).

В данной работе к анализу и прогнозу реальной динамики листовертки лиственничной применяется модель Морана–Рикера (Moran, 1950; Ricker, 1954) с запаздыванием. Следует отметить, что уравнения с запаздыванием весьма успешно описывают динамику численности популяций насекомых (Turchin, 1990, 2003; Turchin et al., 2003; Kendall et al., 1999; Nedorezov, Sadykova, 2015; Neverova et al., 2016), поскольку они учитывают регулирующие факторы, а также инерционность системы (Исаев и др., 2015). В частности, в работе Л.В. Недорезова, Д.И. Садыковой (Nedorezov, Sadykova, 2015) модель Морана–Рикера при разных значениях лага была применена к описанию динамики плотности листовертки лиственничной (The Global Population Dynamics Database (GPDD): Data set 1525). Нередко внимание подобных исследований сосредоточено на оценке качественных и количественных показателей, характеризующих качество аппроксимации эмпирических данных модельными. При этом возможности математического моделирования для анализа динамики реальных популяций не всегда используются в полной мере. Модель Рикера–Морана с запаздыванием демонстрирует периодические и нерегулярные колебания, а также мультирежимность (Неверова, Фрисман, 2015; Neverova et al., 2016), когда при одних и тех же значениях демографических параметров наблюдается разная динамика: либо стабильная, либо периодическая, либо нерегулярная. При этом случайная вариация текущей численности популяции может привести к смене наблюдаемого динамического режима. В связи с этим при применении данной модели к описанию реальной динамики, помимо проверки точечной оценки модели на адекватность и соответствие объекту, возникает необходимость дополнительного исследования возможных динамических режимов модели в окрестности точечной оценки. Такое исследование позволяет идентифицировать динамические режимы, между которыми возможны переходы, вызванные влиянием факторов экзо- и эндогенной природы.

В данной работе модель Морана–Рикера с запаздыванием применяется к анализу и прогнозу динамики численности популяций серой лиственничной листовертки. Использованы данные о плотности (личинок на 1 кг хвои) популяций, обитающих в Швейцарии в локациях Graubunden (the Global Population Dynamics Database: Data set 1525 (Baltensweiler, Fischlin, 1988)) и Oberengadin (Baltensweiler, 1991). При этом изучаются не только динамические режимы модели, возникающие при значениях параметров, соответствующих найденной их точечной оценке, но и режимы, проявляющиеся при вариации параметров модели. Кроме того, в дальнейшем исследовании для оценок значений параметров моделей используются только части данных (части временных рядов), а оставшиеся части (“хвосты”) применяются для проверки прогностических свойств модели. На картах динамических режимов “новые” точечные оценки сопоставляются с оценками, полученными по всему временному ряду. Такое исследование позволяет получить представление о возможных динамических режимах и переходах между ними и, как следствие, делать выводы о предполагаемых сценариях развития популяции.

ОБЪЕКТЫ И МЕТОДИКА

Модель Морана–Рикера с запаздыванием в общем виде может быть представлена уравнением:

(1)

${{x}_{{n + 1}}} = a{{x}_{n}}\exp \left( { - \sum\limits_{i = 0}^{i = m} {{{b}_{i}}{{x}_{{n - i}}}} } \right),$

где – x_n численность популяции, с которой она вступает в n-ый период размножения, а – репродуктивный потенциал популяции. Множитель $\exp \left( { - \sum\nolimits_{i = 0}^{i = m} {{{b}_{i}}{{x}_{{n - i}}}} } \right)$ характеризует экологическое лимитирование роста численности популяции, m – величина временного лага – число поколений, в течение которых сказываются ограничения ресурсов жизнедеятельности. Подробное исследование динамических режимов модели (1) при различных значениях лага представлено в работе Г.П. Неверовой, Е.Я. Фрисмана (Неверова, Фрисман, 2015).

При $m = 0$ уравнение (1) сводится к классической и хорошо исследованной модели Рикера (Moran, 1950; Ricker, 1954)

${{x}_{{n + 1}}} = a{{x}_{n}}\exp ( - {{b}_{0}}{{x}_{n}}).$

Параметр b₀ играет роль масштабирующего коэффициента, определяется интенсивностью плотностно-зависимого экологического лимитирования и косвенно характеризует емкость экологической ниши, поскольку при x_n = 1/b₀ численность следующего поколения достигает максимума, возможного для данной популяции. Заметим, что здесь неявно предполагается, что каждое поколение “получает” одинаковый объем экологических ресурсов, необходимых для жизнедеятельности, независимо от предыдущей истории (динамики численности) популяции. Это может быть справедливо для тех видов, ресурсная база которых полностью восстанавливается за время, протекающее между периодами размножения. В противном случае необходимо явно учитывать уменьшение ресурсов, вызванное их потреблением предыдущими поколениями. В качестве одного из подходов здесь может быть рассмотрено уравнение (1), учитывающее влияние предыдущих поколений на изменение численности популяции.

Модель Морана–Рикера с однолетним и двухлетним запаздыванием применялась к описанию динамики двух популяций лиственничной листовертки, обитающих в Швейцарии в локациях Graubunden (Baltensweiler, Fischlin, 1988; Data set 1525 (GPDD)) и Oberengadin (Baltensweiler, 1991; Исаев и др., 2015). Коэффициенты модели оценивались методом подгонки начального условия (Безручко, Смирнов, 2005), для чего подбирались такие значений параметров модели, при которых модельная численность наилучшим образом аппроксимирует известную последовательность фактической численности популяции, т.е. решалась следующая задача

(2)

$L(u) = \sum\limits_{n + m}^n {{{{\left( {{{x}_{n}}\left( {u,x_{{m - i}}^{0}} \right) - {{z}_{n}}} \right)}}^{2}}} \to \min ,$

где $u = {{(a,{{b}_{i}})}^{T}}$ – вектор параметров системы, ($x_{{m - i}}^{0},$ $i = \overline {0,m} $) – начальное приближение, z_n – фактическая численность. Значение x_n(u, $x_{{m - i}}^{0}$) вычисляется по модели (1). Для минимизации целевого функционала преимущественно использовалась реализация метода Левенберга–Марквардта (Гилл и др., 1985) в программе MathCAD. Дополнительно применялся метод штрафных функций, который позволил наложить биологически значимые ограничения на искомые значения параметров (Гилл и др., 1985).

Анализ соответствия между эмпирическими данными и модельными траекториями проведен на основе стандартной методики (Draper, Smith, 2014; Nedorezov, Sadykova, 2015). Проверялись следующие гипотезы: 1) о равенстве нулю среднего арифметического отклонения эмпирических значений от модельных (тест Стьюдента); о нормальности распределения отклонений (критерий Колмогорова); об отсутствии автокорреляции в последовательности остатков (критерий Дарбина–Уотсона). Дополнительно вычислялся скорректированный коэффициент детерминации, который позволяет учесть при оценке качества модели соотношение количества наблюдений и числа оцениваемых параметров модели. Для каждого варианта модели рассчитывался информационный критерий Акаике (Akaike, 1974).

Далее найденная точечная оценка наносилась на карту динамических режимов модели (1) с соответствующим лагом. Карты получены следующим образом: в каждой точке (соответствующей одному пикселю) плоскости параметров выполнялось 5000 итераций отображения (1), по результатам последних 500 шагов определялся период предельного цикла, и эта точка окрашивалась в заданный цвет в соответствии с полученным периодом. Данные карты динамических режимов модели позволяют в значительной степени идентифицировать те динамические режимы, которые оказываются возможны при значениях параметров вблизи найденной точечной оценки.

Первоначально, чтобы максимально учесть имеющуюся информацию о динамике популяции, мы при поиске параметров модели использовали весь временной ряд, поскольку целью являлся анализ динамических режимов в окрестности полученной точечной оценки. В дальнейшем значения параметров моделей оценивались по укороченному ряду данных, а “хвосты” рядов использовались для проверки прогностических свойств модели.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Модель Морана–Рикера с различным значением лага применялась к описанию динамики двух популяций лиственничной листовертки. Полученные оценки параметров модели, включая начальное приближение, представлены в табл. 1. В первом столбце таблицы приведена точечная оценка и ее статистические характеристики, полученные в работе Л.В. Недорезова и Д.Л. Садыковой (Nedorezov, Sadykova, 2015) при применении модели Морана–Рикера с лагом 1 к описанию динамики плотности листовертки лиственничной (Baltensweiler, Fischlin, 1988; GPDD, Data set 1525), остальные оценки и статистические характеристики рассчитаны нами.

Таблица 1.

Значения статистических показателей и критериев, характеризующих качество описания реальных данных модельными

Источник данных динамики плотности Zeiraphera griseana	Graubunden (Baltensweiler, Fischlin, 1988) GPDD: Data set 1525		Oberengadin (Baltensweiler, 1991)
Лаг	m = 1	m = 2	m = 1	m = 2
Длина выборки	n=38		n=28
Точечная оценка параметров модели (1)	a = 8.2996, b₀ = 2.2 × 10⁻³, b₁ = 0.0214, x₁ = 0.1274, х₀ = 4.1 × 10⁻¹⁴ (Nedorezov, Sadykova, 2015)	a = 7.093, b₀= 4.923 × 10⁻³, b₁= 5.354 × 10⁻⁴, b₂= 0.014, x₂ = 2.504, x₁ = 0.121, x₀ = 0.326	a = 7.231, b₀ = 1.5 × 10⁻³, b₁ = 0.036, x₁ = 72.1, х₀ = 12.48	a = 8.989, b₀= 9.48 × 10⁻³, b₁= 9.33 × 10⁻⁴, b₂ = 0.026, x₂= 324.4, x₁= 81.4, x₀= 0.54
* Значение параметров ρ = b₁/b₀и β = b₂/b₀	ρ = 10.041	ρ = 0.109, β = 2.814	ρ = 23	ρ = 0.098, β = 2.734
Коэффициент детерминации	0.832	0.905	0.93	0.939
Скорректированный коэффициент детерминации	0.819	0.902	0.921	0.915
Значение теста Стьюдента при уровне значимости 1%, гипотеза принимается, если t < t_{α = 0.01}	t = 0.876 t_{α = 0.01} = 2.715	t = 0.67 t_{α = 0.01} = 2.715	t = 0.708 t_{α = 0.01} = 2.771	t = –0.34 t_{α = 0.01} = 2.771
Значение критерия Колмогорова при уровне значимости 1%, гипотеза принимается, если λ< λ _α	λ = 1.541 λ _{α = 0.01} = 1.63	λ = 1.59 λ _{α = 0.01} = 1.63	λ = 1.318 λ _{α = 0.01} = 1.63	λ = 1.78 λ _{α = 0.001} = 1.95
Значение критерия Дарбина-Уотсона при уровне значимости 5%; гипотеза принимается, если ${{d}_{}}$ < d < d	${{d}_{}}$ = 1.59 d = 1.838 d = 2.41	${{d}_{}}$ = 1.66 d = 1.979 d = 2.349	${{d}_{}}$ = 1.56 d = 2.22 d = 2.44	${{d}_{}}$_{= 1.41 d = 1.982 d = 2.59}
Критерий Акаике	8.466	7.739	6.7	6.32

На рис. 1а приведены результаты описания динамики плотности листовертки лиственничной по точечной оценке, полученной Л.В. Недорезовым и Д.Л. Садыковой (Nedorezov, Sadykova, 2015). Этим значениям параметров соответствует асимптотический режим, близкий к циклу длины 9, что, как отмечают авторы, хорошо согласуется с результатами наблюдений и является наилучшим результатом (Nedorezov, Sadykova, 2015). Отметим, что оценки параметров модели показывают, что b₁ значительно больше b₀, т.е. вклад предыдущего поколения в лимитирование воспроизводства популяции существенно больше вклада текущего поколения. Дополнительно нами была построена карта динамических режимов модели (1) при $m = 1;$ она представлена на рис. 1б.

Рис. 1.

(а) Результаты описания динамики плотности листовертки лиственничной при помощи модели Морана-Рикера с лагом 1. Оценка параметров получена Л.В. Недорезовым и Д.Л. Садыковой (Nedorezov, Sadykova, 2015). (б–в) Карты динамических режимов модели Морана–Рикера при m = 1, дополненные точечной оценкой, соответствующей реальной динамике. ρ = b₁/b₀. Числа – длины наблюдаемых циклов, Q – квазипериодическая динамика.

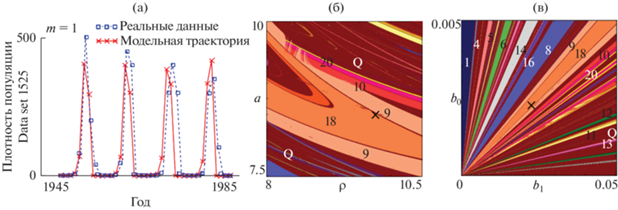
Как видно, точечная оценка параметров, полученная Л.В. Недорезовым и Д.Л. Садыковой, находится в окне периодичности, которое вклинивается в зону квазипериодической динамики и соответствует колебаниям с периодом 18. Цикл длины 18 возникает в результате бифуркации удвоения периода цикла 9, при этом раздвоившиеся элементы цикла близки друг к другу. В целом же оценка параметров лежит вблизи границы, разделяющей циклы 9 и 18, и, соответственно, небольшая флуктуация значений параметров может привести к смене режима динамики.

Следует отметить, что при несколько больших значениях репродуктивного потенциала и меньших значениях коэффициента ρ = b₁/b₀ наблюдается наложение языков Арнольда друг на друга. Так, на рис. 1б можно видеть характерные полосы цикла 9, лежащие поверх цикла длины 10 и его последующих бифуркаций (цикл 20, 40 и квазипериодическая динамика). Соответственно, цикл 9 сосуществует с перечисленными динамическими режимами и, в зависимости от выбора начального условия, может реализовываться либо цикл длины 9, либо сопутствующий режим (цикл длины 10 или его последующие бифуркации). Следовательно, если точечная оценка, соответствующая реальной динамике, будет находиться в области мультирежимности, то характер динамического режима будет определяться не только значениями демографических параметров, но и величиной текущей численности. Дополнительно в окрестности данной точечной оценки была построена карта динамических режимов в пространстве параметров b₁ и b₀ (рис. 1в). Как видно, карта пестрит различными близко соседствующими динамическими режимами. Это позволяет говорить о чувствительности динамических режимов к вариации значений коэффициентов, характеризующих интенсивность воздействия плотностно-зависимых факторов на процесс воспроизводства.

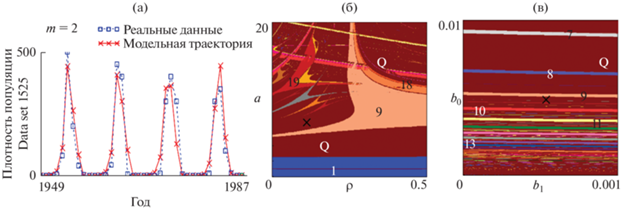
С другой стороны, модель Морана-Рикера с лагом 2 года несколько лучше аппроксимирует временной ряд: Data set 1525 (Baltensweiler, Fischlin, 1988). Такие выводы позволяют сделать рассчитанные значения статистических показателей и критериев, характеризующих качество описания фактических данных модельными, а также значение критерия Акаике (табл. 1). Результаты описания реальной динамики моделью (1) при т = 2 представлены на рис. 2. Как видно, модель в большинстве своем описывает характер динамики популяций и улавливает вспышки плотности несколько лучше. Точечная оценка, соответствующая данной модели, располагается в области квазипериодической динамики, где в случае небольших флуктуаций значений параметров a и ρ характер динамического режима сохраняется. Вместе с тем есть возможность точного попадания параметров в зону одного из языков Арнольда и перехода от квазипериодической динамики к строго периодической, соответствующей циклу 9, что вполне согласуется с результатами (Nedorezov, Sadykova, 2015). Также следует отметить чувствительность наблюдаемой динамики по отношению к значению параметра, характеризующего экологическое лимитирование в текущем году. Как видно, увеличение или уменьшении конкуренции за имеющиеся ресурсы может привести к смене динамического режима, в силу смещения текущей точечной оценки в зону одного из языков Арнольда и перехода от квазипериодической динамики к строго периодической (рис. 2в).

Рис. 2.

(а) Результаты описания динамики листовертки лиственничной моделью Морана–Рикера с лагом 2 года. (б‒в) Карты динамических режимов, дополненные точечной оценкой, соответствующей реальной динамике, ρ = b₁/b₀. Числа – длины наблюдаемых циклов, Q – квазипериодическая динамика.

Поведение реальных и модельных траекторий для лиственничной листовертки, обитающей на территории Oberengadin (Baltensweiler, 1991), при значениях лага 1 и 2 года представлено на рис. 3а, 3в. Как видно, модельные траектории улавливают особенности динамики реальной популяции. По аналогии с предыдущим случаем найденные точечные оценки были дополнены картами динамических режимов ( рис. 3в, 3г).

Рис. 3.

Результаты описания динамики Zeiraphera griseana моделью Морана–Рикера с лагом 1 (б) и 2 (в) года. (а, г) Карты динамических режимов, дополненные точечными оценками.

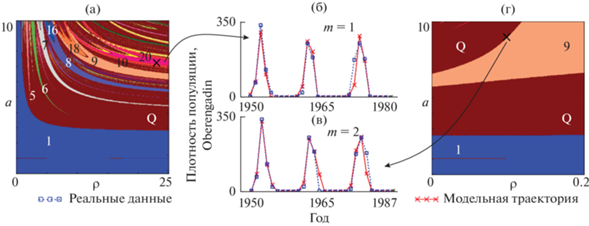
Точечная оценка модели (1) с лагом 1 располагается в области цикла 20 (рис. 3б). Оценка коэффициентов модели с двухлетним запаздыванием попадает в область квазипериодической динамики, близко соседствуя с языком Арнольда, соответствующего циклу длины 9 (рис. 3г). При этом видно, что в обоих случаях небольшая вариация значений параметров а и ρ может привести к цепочке изменений динамических режимов, звеньями которой будут являться квазипериодическая и периодическая динамика. Вследствие этого траектория реальной динамики вполне может представлять собой совокупность переходных процессов от одного режима к другому.

Отметим, что не всегда модели, дающие лучшую аппроксимацию данных, позволяют получить хороший прогноз изменения численности. Более того, модели, которые не соответствуют некоторым статистическим критериям и не дают удовлетворительную аппроксимацию данных, могут прогнозировать динамику лучше (Недорезова, Недорезов, 2011). Поэтому в рамках данной работы для построения прогноза динамики плотности популяции мы будем использовать оба варианта модели.

Перейдем теперь к исследованию прогностических возможностей рассматриваемых моделей. Разобьем имеющиеся ряды данных на две части: первую будем использовать в качестве обучающей выборки, а вторую – для оценки прогностических свойств моделей. Параметры моделей оценивались путем минимизации функционала (2) по обучающей выборке, длину которой мы варьировали (табл. 2). Отклонения эмпирических и модельных траекторий для первой части выборки проверялись на “нормальность” (критерий Колмогорова–Смирнова), а также на наличие сериальной корреляции (критерий Дарбина–Уотсона). Также рассчитывался скорректированный коэффициент детерминации $\left( {R_{j}^{2}} \right)$ между фактическими и модельными данными. Дополнительно анализировался характер динамики в конце фрагмента обучающей выборки, а также асимптотический динамический режим, который дает найденная точечная оценка. “Хвосты” рядов (вторая часть выборки) использовались для проверки прогностических свойств модели, для этого рассчитывались средняя абсолютная ошибка прогноза (MAE) и коэффициент детерминации R² между фактическими и прогнозными данными. Описанный блок исследований представлен в табл. 2, которая демонстрирует, что уменьшение обучающей выборки, сопровождающееся увеличением “хвоста” может приводить к росту качества прогноза (табл. 2).

Таблица 2.

Оценки значений параметров модели (1) и качества прогноза в зависимости от длины обучающей выборки

Длина обучающей выборки, Data set 1525		33	32	31	30	29	28	27	26	25	24	23	22	21	20
“Хвост”, l		5	6	7	8	9	10	11	12	13	14	15	16	17	18
Характер динамики в конце обучающей выборки*		↑	↓↑	↔	↔	↔	↔	↓↓	↓	↑↑	↑	↓↑	↔	↔	↔
Лаг т = 1	Параметр а	8.6	8.47	8.62	8.61	8.61	8.61	8.58	8.58	8.59	8.93	9.1	10.1	9.3	9.29
	Параметр ρ	9.7	10.3	10.0	9.97	9.97	9.97	10.12	10.1	10.1	9.7	9.8	8.45	9.29	9.37
	Статистические критерии**	+	+	+	+	+	+	+	+	+	+	+	+	+	+
	$R_{j}^{2}$	0.83	0.842	0.84	0.84	0.836	0.834	0.831	0.828	0.962	0.982	0.989	0.987	0.99	0.99
	MAE	71	71.1	61.8	54.3	48.2	43.4	39.4	36.6	56.6	109	81.3	70.2	103	89
	R²	0.93	0.76	0.75	0.75	0.75	0.75	0.75	0.756	0.525	0.35	0.595	0.64	0.34	0.39
	Асимптотическая динамика***	9	9	9	9	9	9	9	9	9	10	Q	Q	Q	Q
Лаг т = 2	Параметр а	7.196	7.03	7.03	7.027	7.027	7.037	7.207	6.973	8.601	9.66	8.857	10.71	8.68	9.36
	Параметр ρ	0.117	0.12	0.13	0.126	0.126	0.126	0.114	0.128	1.184	1.23	1.487	1.738	1.72	1.9
	Параметр β	2.851	2.92	2.9	2.92	2.92	2.919	2.905	2.925	2.943	2.896	2.905	2.765	2.85	2.74
	Статистические критерии**	+	+	+	+	+	+	+	+	+	+	+	+	+	+
	$R_{j}^{2}$	0.896	0.81	0.91	0.91	0.904	0.901	0.898	0.896	0.966	0.982	0.908	0.987	0.98	0.98
	MAE	45	66.4	60	53.4	48.1	43.7	40.14	37.4	49.6	76.54	80.81	110.6	65	78.5
	R²	0.996	0.91	0.81	0.81	0.808	0.808	0.807	0.806	0.605	0.504	0.509	0.327	0.57	0.43
	Асимптотическая динамика***	Q	Q	Q	Q	Q	Q	Q	Q	38	Q	Q	Q	Q	Q

Длина обучающей выборки, Oberengadin		23	22	21	20	19	18	17	16	15	14	13	12
“Хвост”, l		5	6	7	8	9	10	11	12	13	14	15	16
Характер динамики в конце обучающей выборки*		↓	↑↑	↑	↑	↓↑	↔	↔	↔	↔	↓↓	↓	↑↑
Лаг т = 1	Параметр а	7.216	8.49	8.37	8.27	8.56	7.89	8.37	8.14	8.14	8.14	8.14	9.22
	Параметр ρ	23.11	9.89	8.68	8.85	8.46	9.36	8.61	8.92	8.92	8.92	8.916	10.1
	Статистические критерии**	+	DW-	+	+	+	+	+	+	+	DW-	DW-	DW-
	$R_{j}^{2}$	0.913	0.984	0.927	0.929	0.992	0.992	0.992	0.992	0.991	0.991	0.99	0.993
	MAE	0.96	30	26	26.8	69	69.3	60.4	57	52.5	48.8	45.7	19.7
	R²	0.02	0.13	0.658	0.657	0.32	0.257	0.28	0.266	0.262	0.266	0.266	0.842
	Асимптотическая динамика***	20	9	18	18	18	9	18	9	9	9	9	Q
Лаг т = 2	Параметр а	8.8	9.46	8.3	10.9	9.08	9.2	9.04	9.22	9.302	9.29	10.7	9.34
	Параметр ρ	0.096	0.768	0.765	0.835	1.18	0.84	1.18	1.176	1.14	1.12	0.27	0.33
	Параметр β	2.743	0.99	3.014	2.94	2.81	2.81	2.8	2.74	2.74	2.75	2.88	2.9
	Статистические критерии**	+	DW-	+	DW-	DW-	DW-	DW-	DW-	DW-	DW-	DW-	DW-
	$R_{j}^{2}$	0.91	0.983	0.971	0.989	0.99	0.99	0.989	0.989	0.988	0.987	0.995	0.993
	MAE	0.86	24	21.7	29.4	34	36.3	29	34	31.8	28.6	21	17.9
	R²	0.613	0.9	0.79	0.78	0.708	0.667	0.703	0.598	0.594	0.611	0.784	0.859
	Асимптотическая динамика***	Q	4	Q	20	9	9	9	9	9	9	38	4

* ↑ фаза роста; ↑↑ пик численности; ↓ падение численности; ↓↓ начало фазы низкой численности; ↔ низкая численность; ↓↑ переход от низкой численности к фазе роста.

** + критерии Колмогорова–Смирнова и Дарбина–Уотсона выполняются; DW – зона неопределенности критерия Дарбина–Уотсона.

*** Числа – длины наблюдаемых циклов, Q – квазипериодическая динамика.

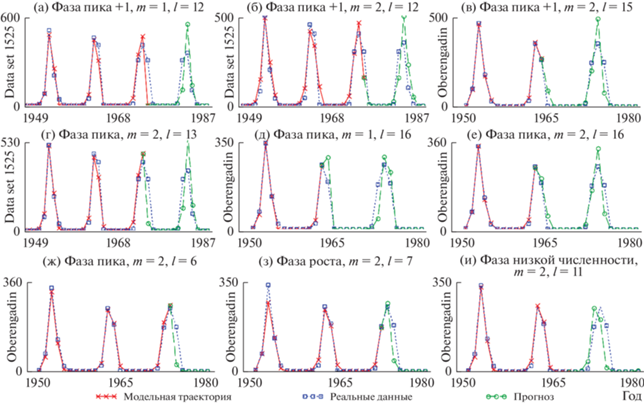
Динамика фактических и модельных данных, а также варианты прогноза приведены на рис. 4. Как видно, наилучший прогноз может быть получен, если обучающая выборка заканчивается на фазе пика численности (рис. 4г–4ж) или же на следующем за пиком численности элементе (рис. 4а–4в). Также в ряде случаев можно получить неплохие результаты прогноза для первой части временного ряда, завершающейся на стадии роста численности (рис. 4з).

Рис. 4.

Динамика популяций листовертки лиственничной и ее прогноз.

Модель (1) с лагом 2 года лучше описывает ряд данных, соответствующий динамике листовертки лиственничной, обитающей в Oberengadin (Baltensweiler, 1991) (табл. 2), что и отражают прогнозы, приведенные на рис. 4д, 4е. В целом же представленные на рис. 4а–4з варианты прогноза динамики плотности насекомых достаточно точно описывают фактические данные, повторяя тенденции изменения и улавливая пики. С другой стороны, прогноз, построенный по части выборки, завершающейся в фазе низкой численности, может характеризоваться приемлемой ошибкой, однако характер прогнозируемой динамики может измениться: например, может произойти смещение пика численности (рис. 4и).

Несмотря на то, что модель (1) при т = 1 несколько хуже описывает Data set 1525, качество ее прогноза сопоставимо с прогнозом модели (1) при т = 2 (табл. 2, рис. 4а, 4б, 4г). Более того, результаты применения модели (1) с лагом 1 удобно совместить с картой динамических режимов, что позволяет получить некоторое представление об эволюции динамики и переходных процессах, протекающих в реальной популяции (рис. 5б). Используемая модель косвенно учитывает влияние внешних факторов, поэтому изменение точечных оценок параметров и их “прыжки” по параметрическому пространству вполне могут быть проинтерпретированы как воздействие модифицирующих факторов, которые усиливают либо ослабляют процессы регуляции численности.

Рис. 5.

Карта динамических режимов модели (1) при т = 1, дополненная точечными оценками, полученными по обучающей выборке разной длины для Data set 1525. Найденные значения параметров приведены в табл. 2. * – а = 10.1, ρ = 8.45 – точечная оценка, не нанесенная на карту. Белыми стрелками показана эволюция точечных оценок с ростом обучающей выборки на единицу. Числа – длины наблюдаемых циклов, Q – квазипериодическая динамика.

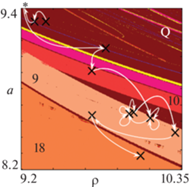
С этой точки зрения, популяция, которая развивается при слабо меняющихся внешних условиях, остается в диапазоне значений параметров, при которых наблюдаются схожие режимы, но в случае, когда условия существенно изменились, популяция, подстраиваясь под новую ситуацию, стремится выйти на принципиально другой режим. Так видно, что изначально в популяции в течение нескольких лет наблюдалась квазипериодическая динамика, которая некоторым образом модифицировалась в силу экологического лимитирования. Затем произошло достаточно резкое смещение оценок в область цикла 9 за счет падения скорости роста популяции. Отметим, что большинство найденных точечных оценок располагается в диапазоне девятилетних колебаний. Интересно, что здесь смещение точечных оценок относительно друг друга связано преимущественно с вариацией значений параметра ρ, характеризующего экологическое лимитирование. Изменение коэффициента рождаемости также происходит, но оно в значительной степени меньше и, скорее всего, обусловлено влиянием плотностно-зависимой регуляции с запаздыванием.

ЗАКЛЮЧЕНИЕ

Применение модели Морана–Рикера с запаздыванием к описанию динамики плотности двух популяций листовертки лиственничной оказалось вполне успешным, что позволяет уверенно предполагать влияние плотностно-зависимой регуляции с запаздыванием на развитие этого вида. Найденные точечные оценки популяционных параметров удовлетворяют статистическим критериям. Показано, что для анализа и описания динамики, помимо проверки модели (при значениях параметров, полученных на основе их точечной оценки) на адекватность и соответствие реальному объекту, необходимо дополнительное исследование возможных динамических режимов модели при значениях параметров, соседствующих с найденной точечной оценкой. Такое исследование позволяет как идентифицировать текущие динамические режимы, так и выявить новые режимы, к которым могут привести небольшие изменения параметров модели или случайные флуктуации численности. В частности, показано, что найденные точечные оценки демографических параметров, соответствующие динамике популяций листовертки лиственничной, располагаются в области квазипериодических колебаний и, как правило, соседствуют с другим динамическим режимом. Следовательно, вариация демографических параметров, например, в результате процессов эволюции или же влияния модифицирующих факторов может примести к смене динамического режима.

Показано, что предложенные модели динамики могут быть использованы для прогноза динамики популяций листовертки лиственничной. Как оказалось, качество прогноза существенно зависит от характера динамики в конце обучающей выборки, используемой для оценки параметров. Так, если в конце фрагмента временного ряда наблюдается фаза низкой численности, то, как правило, по оценкам, полученным на основе данного фрагмента, хорошо прогнозировать динамику численности оказывается достаточно проблематично. Однако если обучающий фрагмент временного ряда заканчивает на фазе пика численности или же на следующем за пиком численности элементе, то результаты прогноза существенно улучшаются. Отметим, что сопоставление точечных оценок, полученных по обучающим выборкам разной длины, с динамическими режимами модели Морана–Рикера с запаздыванием позволяет получить представление об эволюции динамических режимов в конкретной популяции и выявить переходы от одних динамических режимов к другим.

Работа выполнена в рамках государственных заданий Института автоматики и процессов управления ДВО РАН, Института комплексного анализа региональных проблем ДВО РАН.

Список литературы

Безручко Б.П., Смирнов Д.А. Математическое моделирование и хаотические временные ряды. Саратов: ГосУНЦ “Колледж”, 2005. 320 с.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир, 1985. 509 с.
Исаев А.С., Пальникова Е.Н., Суховольский В.Г., Тарасова О.В. Динамика численности лесных насекомых-филлофагов: модели и прогнозы. М.: Товарищество научных изданий КМК, 2015. 262 с.
Исаев А.С., Хлебопрос Р.Г., Недорезов Л.В., Киселев В.В., Кондаков Ю.П., Суховольский В.Г. Популяционная динамика лесных насекомых. М.: Наука, 2001. 347 с.
Неверова Г.П., Фрисман Е.Я. Математическое моделирование динамики локальных однородных популяций с учетом эффектов запаздывания // Математическая биология и биоинформатика. 2015. Т. 10. № 2. С. 309–324.
Недорезов Л.В. Динамика численности сосновой пяденицы в Нидерландах: оценка параметров обобщенной дискретной логистической модели // Евразиатский энтомологический журн. 2015а. Т. 14. № 1. С. 93–99.
Недорезов Л.В. Нетрадиционный подход к оценке параметров экологических моделей (на примерах динамики численности серой лиственничной листовертки и сосновой пяденицы) // Сибирский лесной журн. 2015 б. № 3. С. 70–82.
Недорезова Б.Н., Недорезов Л.В. Динамика численности сосновой пяденицы: прогноз с помощью дискретных математических моделей // Евразиатский энтомологический журн. 2011. Т. 10. № 3. С. 280–288.
Суховольский В.Г., Пономарев В.И., Соколов Г.И., Тарасова О.В., Красноперова П.А. Непарный шелкопряд Lymantria dispar L. на Южном Урале: особенности популяционной динамики и моделирование // Журн. общей биологии. 2015. Т. 76. № 3. С. 179–194.
Тютюнов Ю.В., Титова Л.И. От Лотки–Вольтерра к Ардити–Гинзбургу: 90 лет эволюции трофических функций // Журн. общей биологии. 2018. Т. 79. № 6. С. 428–448.
Akaike H. A new look at the statistical model identification // IEEE Transactions on Automatic Control. 1974. V. 19. № 6. P. 716–723.
Baltensweiler W. The folivore guild on larch (Larix decidua) in the Alps. Forest insect guilds: Patterns of interaction with host trees Radnor: US Forest Service General Technical Report NE-153, 1991. P. 145–164.
Baltensweiler W., Fischlin A. The Larch Budmoth in the Alps. Dynamics of Forest Insect Populations. Population Ecology. Springer, Boston, MA, 1988. https://doi.org/10.1007/978-1-4899-0789-9_17
Draper N.R., Smith H. Applied Regression Analysis Ed. 3. N.Y.: Wiley and Sons Inc., 2014. 736 p.
Kendall B.E., Briggs C.J., Murdoch W.W., Turchin P., Ellner S.P., McCauley E., Nisbet R.M., Wood S.N. Why do population cycle? A synthesis of statistical and mechanistic modeling approaches // Ecology. 1999. V. 80. P. 1789–1805.
Moran P.A.P. Some remarks on animal population dynamics // Biometrics. 1950. V. 6. № 3. P. 250–258.
Nedorezov L.V., Sadykova D.L. Dynamics of larch bud moth populations: application of Moran–Ricker models with time lag // Ecological Modelling. 2015. V. 297. P. 26–32.
Neverova G.P., Yarovenko I.P., Frisman E.Y. Dynamics of populations with delayed density dependent birth rate regulation // Ecological Modelling. 2016. V. 340. № 24. P. 64–73.
Ricker W.E. Stock and recruitment // Fisheries Research Board of Canada. 1954. V. 11. № 5. P. 559–623.
Turchin P. Complex Population Dynamics: A Theoretical/Empirical Synthesis. Princeton: Princeton University Press, 2003. P. 472.
Turchin P. Rarity of density dependence or population regulation with lags? // Nature. 1990. V. 344. P. 660–663.
Turchin P., Wood S.N., Ellner S.P., Kendall B.E., Murdoch W.W., Fischlin A., Casas J., McCauley E., Briggs C.J. Dynamical effects of plant quality and parasitism on population cycles of larch budmoth // Ecology. 2003. V. 84. № 5. P. 1207–1214.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Лесоведение

Архивы выпусков Информация о журнале Отправить рукопись в журнал