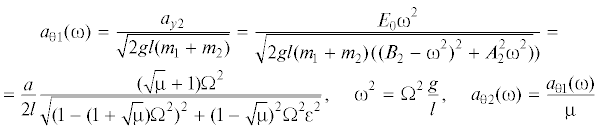Известия РАН. Механика твердого тела, 2022, № 5, стр. 93-102
О СУЩЕСТВОВАНИИ НОРМАЛЬНЫХ КООРДИНАТ ДЛЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ ЛИНЕЙНЫХ ДИССИПАТИВНЫХ СИСТЕМ
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: petrovipmech@gmail.com
Поступила в редакцию 18.08.2021
После доработки 25.10.2021
Принята к публикации 15.11.2021
- EDN: VVQNSI
- DOI: 10.31857/S0572329922050129
Аннотация
Линейная диссипативная механическая система с конечным числом степеней свободы определяется тремя квадратичными формами: кинетической и потенциальной энергией системы, а также диссипативной функцией Рэлея. Известно, что всегда можно ввести нормальные координаты, в которых кинетическая и потенциальная энергии приводятся к сумме квадратов с некоторыми коэффициентами. Третья же квадратичная форма при этом к сумме квадратов, вообще говоря, не приведется. В данном исследовании обсуждаются условия, при которых все три квадратичные формы одним преобразованием приводятся к сумме квадратов. Для таких систем можно ввести нормальные координаты, в которых система расщепляется на независимые системы второго порядка и их анализ существенно упрощается. Приводятся примеры анализа вынужденных колебаний линейных диссипативных систем для двух и трех степеней свободы.
1. Введение. Общая теория малых линейных колебаний систем с конечным числом степеней свободы для консервативных систем дана в 1762–1765 гг. Лагранжем. В этом случае механическая система определяется двумя квадратичными формами: кинетической и потенциальной энергией системы. Вейерштрас показал в 1858 г., что в силу положительной определенности кинетической энергии можно ввести нормальные координаты, в которых кинетическая энергия приведется к сумме квадратов, а потенциальную энергию к сумме квадратов с некоторыми множителями. В нормальных координатах уравнения расщепляются на независимые осцилляторы, решения которых выражаются через тригонометрические и показательные функции. Прежние исследователи (следуя Лагранжу) ошибочно предполагали, что в случае кратных корней характеристического уравнения нормальные координаты не будут существовать и что в окончательных интегралах уравнений движения время будет входить не только через тригонометрические и показательные функции. Соответствующие библиографические ссылки приведены в монографии [1].
Анализу колебаний механических систем посвящен ряд работ [2–4], в которых демонстрируется существенное упрощение при переходе к нормальным координатам. Одновременное приведение к диагональной форме двух вещественных симметричных матриц A и B всегда выполнимо [5], если одна из них соответствует знакоопределенной квадратичной форме. Поэтому квадратичные формы кинетической и потенциальной энергии консервативной системы всегда приводятся к диагональному виду и система дифференциальных уравнений расщепляется на независимые подсистемы второго порядка.
Для двух и более матриц [6, 7] не всегда возможно их одновременное приведение к диагональным. Известно несколько разновидностей условий, при выполнении которых это удается осуществить [8]. Наиболее общее условие приведения трех матриц $A$, $B$ и $C$ к диагональному виду получено в [9]. Для систем с $n$ степенями свободы оно состоит из равенства нулю n2 элементов матрицы
В данной работе показано, что n2 уравнений условия (1.1) сводятся к $n(n - 1){\text{/}}2$ независимых уравнений. Если квадратичные формы зависят от двух переменных, то 4 условия сводятся к одному равенству нулю определителя третьего порядка коэффициентов трех квадратичных форм. Вывод условия тоже упрощается и проводится, не опираясь на результат Новикова [9]. Для систем с тремя степенями свободы из условия Новикова получены три уравнения для билинейных по элементам матриц A и B форм.
Даны примеры применения полученного условия для анализа малых колебаний механической системы с двумя и тремя степенями свободы с учетом сил трения.
Другой подход исследования систем с двумя степенями свободы в случае двухкратной собственной частоты методом возмущений предложен в [11].
2. Независимые условия приведения трех квадратичных форм к каноническому виду. Матрица $M = (A{{B}^{{ - 1}}}C - C{{B}^{{ - 1}}}A)\det B$ антисимметрична: ${{M}_{{ij}}} = - {{M}_{{j{\kern 1pt} i}}}$, $i = 1, \ldots ,n$, j = 1, ..., n и имеет только $n(n - 1){\text{/}}2$ независимых коэффициента. Отсюда из критерия Новикова (1.1) вытекают $n(n - 1){\text{/}}2$ независимых условий:
Элементы матрицы ${{M}_{{ij}}}$ являются однородными полиномами переменных ${{a}_{{ij}}}$, ${\mkern 1mu} {{b}_{{ij}}}$, ${\mkern 1mu} {{c}_{{ij}}}$, линейными по ${{a}_{{ij}}}$.
3. Условие приведения трех квадратичных форм к каноническому виду. Теорема. Пусть даны три квадратичные формы двух переменных
Тогда для существования невырожденного преобразования
(3.1)
$Y = QX,\quad X = \left( {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \end{array}} \right),\quad Y = \left( {\begin{array}{*{20}{c}} {{{y}_{1}}} \\ {{{y}_{2}}} \end{array}} \right),\quad Q = \left( {\begin{array}{*{20}{c}} {{{q}_{{11}}}}&{{{q}_{{12}}}} \\ {{{q}_{{21}}}}&{{{q}_{{22}}}} \end{array}} \right)$Необходимо и достаточно, чтобы определитель, составленный из коэффициентов исходных квадратичных форм, обратился в ноль
(3.2)
$\Delta = \left| {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{22}}}} \\ {{{b}_{{11}}}}&{{{b}_{{12}}}}&{{{b}_{{22}}}} \\ {{{c}_{{11}}}}&{{{c}_{{12}}}}&{{{c}_{{22}}}} \end{array}} \right| = 0$Доказательство. Квадратичные формы от двух переменных образуют векторное пространство размерности 3 из векторов ${\mathbf{a}}({{a}_{{11}}},{{a}_{{12}}},{{a}_{{22}}})$, ${\mathbf{b}}({{b}_{{11}}},{{b}_{{12}}},{{b}_{{22}}})$, ${\mathbf{c}}({{c}_{{11}}},{{c}_{{12}}},{{c}_{{22}}})$. Если квадратичные формы f, ${{f}_{1}}$, ${{f}_{2}}$, ${{f}_{3}}$ одновременно приводятся к каноническому виду, то линейная оболочка этих форм является подпространством размерности 2 или меньше, а следовательно три формы линейно зависимы и определитель, составленный из координат векторов a, b, c равен нулю$\Delta = 0$. Это и есть условие теоремы 1.
Наоборот, если $\Delta = 0$, то ${{f}_{1}}$, ${{f}_{2}}$, ${{f}_{3}}$ линейно зависимы, и при этом ${{f}_{1}}$, ${{f}_{2}}$ линейно независимы, то ${{f}_{3}}$ линейно выражается через ${{f}_{1}}$, ${{f}_{2}}$, и тогда достаточно привести к каноническому виду две формы ${{f}_{1}}$, ${{f}_{2}}$. Если же ${{f}_{2}}$ пропорциональна ${{f}_{1}}$, то задача сводится к приведению двух форм ${{f}_{1}}$, ${{f}_{3}}$, что и требовалось доказать.
Второе доказательство. Теорема непосредственно вытекает из критерия Новикова (1.1) и тождества для матриц размерности 2 × 2
4. Малые колебания системы с двумя степенями свободы. Кинетическая $T$ и потенциальная энергии $\Pi $, диссипативная функция Рэлея D и работа внешних сил $N$ имеют вид
Запишем уравнения Лагранжа движения механической системы под действием сил, меняющихся по гармоническому закону
Предполагается, что внешние силы меняются по гармоническому закону с амплитудами U1, U2. Если определитель (3.2) коэффициентов квадратичных форм равен нулю $\Delta = 0$, то по доказанной теореме преобразованием (3.1) квадратичные формы приводятся к каноническому виду
Система уравнений расщепляется на два независимых уравнения второго порядка
(4.1)
$\begin{array}{*{20}{l}} {\frac{{{{d}^{2}}{{y}_{i}}}}{{d{{t}^{2}}}} + {{A}_{i}}\frac{{d{{y}_{i}}}}{{dt}} + {{B}_{i}}{{y}_{i}} = {{E}_{i}}\sin \omega t,\quad i = 1,\;2} \\ {{{E}_{1}} = {{U}_{1}}{{q}_{{11}}} + {{U}_{2}}{{q}_{{21}}},\quad {{E}_{2}} = {{U}_{1}}{{q}_{{12}}} + {{U}_{2}}{{q}_{{22}}}} \end{array}$Анализ такой системы значительно упрощается. Решение для установившихся колебаний
(4.2)
$\begin{gathered} {{y}_{i}} = {{P}_{i}}\sin \omega t - {{Q}_{i}}\cos \omega t \\ {{P}_{i}} = \frac{{{{E}_{i}}({{B}_{i}} - {{\omega }^{2}})}}{{{{{({{B}_{i}} - {{\omega }^{2}})}}^{2}} + A_{i}^{2}{{\omega }^{2}}}},\quad {{Q}_{i}} = \frac{{{{E}_{i}}{{A}_{i}}\omega }}{{{{{({{B}_{i}} - {{\omega }^{2}})}}^{2}} + A_{i}^{2}{{\omega }^{2}}}} \\ \end{gathered} $Имеет амплитуды
(4.3)
$\begin{array}{*{20}{l}} {{{a}_{i}} = \sqrt {P_{i}^{2} + Q_{i}^{2}} = \frac{{{{E}_{i}}}}{{\sqrt {{{{({{B}_{i}} - {{\omega }^{2}})}}^{2}} + A_{i}^{2}{{\omega }^{2}}} }},\quad i = 1,\;2} \end{array}$Для описания переходного процесса из состояния покоя до установления необходимо решить уравнение (4.1) с начальными условиями $y(0) = 0$, $\dot {y}(0) = 0$. Решение имеет вид
(4.4)
$\begin{array}{*{20}{c}} {{{y}_{i}}(t) = {{P}_{i}}\sin \omega \;t - {{Q}_{i}}\cos \omega t + {{J}_{i}}(t)} \\ {{{J}_{i}}(t) = {{e}^{{ - {{A}_{i}}t/2}}}\left( {\left( {\frac{{{{Q}_{i}} - 2{{P}_{i}}\omega }}{{2{{\omega }_{i}}}}} \right)\sin ({{\omega }_{i}}t) + {{Q}_{i}}\cos ({{\omega }_{i}}t)} \right),\quad {{\omega }_{i}} = \sqrt {{{B_{i}^{2} - A_{i}^{2}} \mathord{\left/ {\vphantom {{B_{i}^{2} - A_{i}^{2}} 4}} \right. \kern-0em} 4}} } \end{array}$Полезность полученных формул ниже демонстрируется на исследовании малых вынужденных колебаний двойного плоского маятника с учетом сил трения.
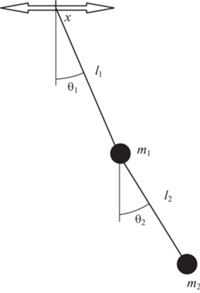
5. Двойной плоский маятник. Рассмотрим малые колебания около положения равновесия двойного плоского маятника, у которого точка подвеса движется по горизонтали по гармоническому закону $x = a\sin {{\omega }}t$ (рис. 1).
Запишем выражения T, $D$, $\Pi $ и N как функции обобщенных координат ${{{{\theta }}}_{{\text{1}}}}$, ${{{{\theta }}}_{{\text{2}}}}$ и скоростей ${{{{\dot {\theta }}}}_{{\text{1}}}}$, ${{{{\dot {\theta }}}}_{2}}$ [10]
Выпишем коэффициенты квадратичных форм функций T, $R$, $\Pi $
Из равенства нулю определителя (3.2) находим условие ${{r}_{2}}{\text{/}}{{r}_{1}} = {{m}_{2}}{\text{/}}{{m}_{1}}$приведения $T$, $R$, $\Pi $ к сумме квадратов, то есть коэффициенты трения должны быть пропорциональны массам. При найденном условии пропорциональности ${{r}_{1}} = r{\mkern 1mu} {{m}_{1}}$, ${{r}_{2}} = r{\mkern 1mu} {{m}_{2}}$ замена переменных
(5.1)
${{{{\theta }}}_{1}} = {{{{x}_{1}}} \mathord{\left/ {\vphantom {{{{x}_{1}}} {\sqrt {g{{l}_{1}}({{m}_{1}} + {{m}_{2}})} }}} \right. \kern-0em} {\sqrt {g{{l}_{1}}({{m}_{1}} + {{m}_{2}})} }},\quad {{{{\theta }}}_{2}} = {{{{x}_{2}}} \mathord{\left/ {\vphantom {{{{x}_{2}}} {\sqrt {g{{l}_{2}}{{m}_{2}}} }}} \right. \kern-0em} {\sqrt {g{{l}_{2}}{{m}_{2}}} }}$Построим ортогональное преобразование, приводящее первую матрицу к диагональному виду. Для этого надо найти собственное число ${{\lambda }_{1}}$ и единичный собственный вектор ${{e}_{1}},{{e}_{2}}$ из решения системы
Второе собственное число λ2 находится из аналогичного уравнения. Второй собственный вектор ортогонален первому. Они имеют вид
Преобразование
(5.2)
$\begin{array}{*{20}{l}} {{{x}_{1}} = {{e}_{{11}}}{{y}_{1}} + {{e}_{{12}}}{{y}_{2}},\quad {{x}_{2}} = - {{e}_{{12}}}{{y}_{1}} + {{e}_{{11}}}{{y}_{2}}} \end{array}$В преобразованных переменных функции $T$, $R$, $\Pi $ и $N$ примут вид
(5.3)
$\begin{gathered} {{A}_{1}} = \frac{r}{{{{l}_{1}}{{l}_{2}}}}\frac{{{{{{\lambda }}}_{{\text{2}}}}}}{{{{{{\lambda }}}_{{\text{1}}}}}},\quad {{A}_{2}} = \frac{r}{{{{l}_{1}}{{l}_{2}}}}\frac{{{{{{\lambda }}}_{{\text{1}}}}}}{{{{{{\lambda }}}_{{\text{2}}}}}},\quad {{B}_{1}} = \frac{{\text{1}}}{{{{{{\lambda }}}_{{\text{1}}}}}},\quad {{B}_{2}} = \frac{{\text{1}}}{{{{{{\lambda }}}_{{\text{2}}}}}} \\ {{E}_{1}} = \frac{{a{{{{\omega }}}^{2}}}}{{{{{{\lambda }}}_{1}}\sqrt g }}( - {{e}_{{12}}}\sqrt {{{l}_{2}}{{m}_{2}}} + {{e}_{{11}}}\sqrt {{{l}_{1}}({{m}_{1}} + {{m}_{2}})} ),\quad {{E}_{2}} = \frac{{a{{{{\omega }}}^{2}}}}{{{{{{\lambda }}}_{2}}\sqrt g }}({{e}_{{11}}}\sqrt {{{l}_{2}}{{m}_{2}}} + {{e}_{{12}}}\sqrt {{{l}_{1}}({{m}_{1}} + {{m}_{2}})} ) \\ \end{gathered} $Формулы (4.2)–(4.4), (5.1)–(5.3) определяют общее аналитическое решение задачи о вынужденных колебаниях двойного математического маятника при единственном условии пропорциональности диссипативных коэффициентов массам мятника: ${{r}_{2}}{\text{/}}{{r}_{1}} = {{m}_{2}}{\text{/}}{{m}_{1}}$
В частном случае ${{l}_{1}} = {{l}_{2}} = l$ формулы упрощаются
(5.4)
$\begin{gathered} {{{{\lambda }}}_{1}} = \frac{l}{g}(1 - \sqrt {{\mu }} ),\quad {{{{\lambda }}}_{2}} = \frac{l}{g}(1 + \sqrt {{\mu }} ) \\ {{A}_{1}} = \frac{r}{{{{l}^{2}}}}\frac{{1 + \sqrt {{\mu }} }}{{1 - \sqrt {{\mu }} }},\quad {{A}_{2}} = \frac{r}{{{{l}^{2}}}}\frac{{1 - \sqrt {{\mu }} }}{{1 + \sqrt {{\mu }} }},\quad {{B}_{1}} = \frac{g}{{l(1 - \sqrt {{\mu }} )}},\quad {{B}_{2}} = \frac{g}{{l(1 + \sqrt {{\mu }} )}} \\ {{E}_{1}} = {{E}_{2}} = {{E}_{0}}{{{{\omega }}}^{2}},\quad {{E}_{0}} = a\sqrt {\frac{g}{{2l}}({{m}_{1}} + {{m}_{2}})} ,\quad - {{e}_{{11}}} = {{e}_{{12}}} = \frac{1}{{\sqrt 2 }} \\ {{x}_{1}} = \frac{1}{{\sqrt 2 }}\left( { - {{y}_{1}} + {{y}_{2}}} \right),\quad {{x}_{2}} = - \frac{1}{{\sqrt 2 }}({{y}_{1}} + {{y}_{2}}) \\ \end{gathered} $По формуле (4.3) находим амплитуды переменных y1, y2
(5.5)
$\begin{array}{*{20}{l}} {{{a}_{{yi}}} = \frac{{{{E}_{0}}{{{{\omega }}}^{2}}}}{{\sqrt {{{{({{B}_{i}} - {{{{\omega }}}^{2}})}}^{2}} + A_{i}^{2}{{{{\omega }}}^{2}}} }},\quad i = 1,\;2} \end{array}$(5.6)
${\text{max}}({{a}_{{yi}}}) = \frac{{2{{B}_{i}}{{E}_{0}}}}{{{{A}_{i}}\sqrt {4{{B}_{i}} - {{A}_{i}}^{2}} }},\quad i = 1,\;2$(5.7)
${{{{\omega }}}_{{\text{1}}}} = \frac{{{{B}_{1}}}}{{\sqrt {{{B}_{1}} - A_{1}^{2}{\text{/}}2} }},\quad {{{{\omega }}}_{2}} = \frac{{{{B}_{2}}}}{{\sqrt {{{B}_{2}} - A_{2}^{2}{\text{/}}2} }}$.Подставляя в (5.6) значения ${{A}_{i}}$, ${{B}_{i}}$ (5.4), получим
Для отношения максимальных амплитуд имеем
При ${{{{\varepsilon }}}^{2}} < \frac{{2(1 - {{\mu }})}}{{3{{\mu }} + 1}} < 2$ максимальная амплитуда второй моды превосходит амплитуду первой моды. При этом выполнено условие $1 - {{{{\varepsilon }}}^{2}}\frac{{{{{(1 + \sqrt {{\mu }} )}}^{2}}}}{{4(1 - \sqrt {{\mu }} )}} > 0$ вещественности решения.
Интерес представляет диапазон параметров ${{\mu }} \in (1{\text{/}}2,\;1)$, ${{\varepsilon }} \in (0,\;1{\text{/}}2)$. Тогда ${\text{max}}({{a}_{{y2}}})$ превосходит ${\text{max}}({{a}_{{y1}}})$ более чем в 9 раз и амплитудные характеристики для углов θ1 и θ2 выражаются только через амплитудную характеристику второй нормальной моды ${{a}_{{y2}}}$, а первая мода вносит пренебрежимо малые поправки. С помощью (5.1), (5.4) и (5.5) находим амплитудно-частотные характеристики ${{a}_{{\theta 1}}}(\omega )$и ${{a}_{{{{\theta }}2}}}({{\omega }})$ для углов θ1 и θ2
Максимальные значения амплитуд углов и нормальной переменной y2 достигаются при одной и той же частоте ${{\omega }} = {{{{\omega }}}_{2}}$, которая находится с помощью (5.7) и (5.4)
Наибольшая амплитуда ${{{{\theta }}}_{2}}$ превосходит ${{{{\theta }}}_{1}}$в ${1 \mathord{\left/ {\vphantom {1 {\sqrt {{\mu }} }}} \right. \kern-0em} {\sqrt {{\mu }} }}$ раз. На параметры задачи следует наложить условие ${\text{max}}({{{{\theta }}}_{2}}) \ll 1$, чтобы линейная теория колебаний была применима.
6. Условия приведения трех квадратичных форм к каноническому виду при n = 3.
Три квадратичные формы приводятся к каноническому виду при выполнении уравнений (2.1). Из них при n = 3 получаем систему трех уравнений
Система линейна по коэффициентам aij и приводится к следующему матричному виду
(6.1)
$P\left( {\begin{array}{*{20}{l}} {{{a}_{{11}}}} \\ {{{a}_{{22}}}} \\ {{{a}_{{33}}}} \end{array}} \right) + Q\left( {\begin{array}{*{20}{l}} {{{a}_{{12}}}} \\ {{{a}_{{13}}}} \\ {{{a}_{{23}}}} \end{array}} \right) = 0$(6.2)
$P = \left( {\begin{array}{*{20}{c}} {\left| {{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{c}}}_{{\mathbf{2}}}}} \right|}&{\left| {{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{c}}}_{{\mathbf{1}}}}} \right|}&0 \\ {\left| {{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{c}}}_{{\mathbf{3}}}}} \right|}&0&{\left| {{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{c}}}_{{\mathbf{1}}}}} \right|} \\ 0&{\left| {{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{c}}}_{{\mathbf{3}}}}} \right|}&{\left| {{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{c}}}_{{\mathbf{2}}}}} \right|} \end{array}} \right)$(6.3)
$Q = \left( {\begin{array}{*{20}{c}} {{{Q}_{{11}}}}&{\left| {{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{c}}}_{{\mathbf{2}}}}} \right|}&{\left| {{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{c}}}_{{\mathbf{1}}}}} \right|} \\ {\left| {{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{c}}}_{{\mathbf{3}}}}} \right|}&{{{Q}_{{22}}}}&{\left| {{{{\mathbf{b}}}_{{\mathbf{1}}}},{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{c}}}_{{\mathbf{1}}}}} \right|} \\ {\left| {{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{c}}}_{{\mathbf{3}}}}} \right|}&{\left| {{{{\mathbf{b}}}_{{\mathbf{3}}}},{{{\mathbf{b}}}_{{\mathbf{2}}}},{{{\mathbf{c}}}_{{\mathbf{2}}}}} \right|}&{{{Q}_{{33}}}} \end{array}} \right)$Здесь прямыми скобками обозначены определители третьего порядка для матриц, составленных из векторов ${{{\mathbf{b}}}_{i}}({{b}_{{i1}}},{{b}_{{i2}}},{{b}_{{i3}}})$, ${{{\mathbf{c}}}_{i}}({{c}_{{i1}}},{{c}_{{i2}}},{{c}_{{i3}}})$.
Например
Разрешая систему (6.1) относительно ${{a}_{{11}}}$, ${{a}_{{22}}}$, ${{a}_{{33}}}$,найдем
(6.4)
$\left( {\begin{array}{*{20}{l}} {{{a}_{{11}}}} \\ {{{a}_{{22}}}} \\ {{{a}_{{33}}}} \end{array}} \right) = - {{P}^{{ - 1}}}Q\left( {\begin{array}{*{20}{l}} {{{a}_{{12}}}} \\ {{{a}_{{13}}}} \\ {{{a}_{{23}}}} \end{array}} \right).$Пример 1. Для трех квадратичных форм
Решение. Выпишем матрицы квадратичных форм ${{F}_{1}}$, ${{F}_{2}}$, ${{F}_{3}}$
С помощью формул (6.1) и (6.2) вычисляем матрицы $P$ и $Q$
По формуле (6.4) находятся требуемые коэффициенты
Используя известный алгоритм [5], находим преобразование
Все три формы в новых переменных имеют следующий канонический вид
Пример 2. В монографии [1] (стр. 252) рассмотрена задача определения нормальных колебаний твердого тела, имеющего закрепленную точку и колеблющегося под действием произвольной системы консервативных сил около положения равновесия. Кинетическая и потенциальная энергии в [1] приводятся к виду
Поставим вопрос: найти коэффициенты диссипативной функции
Решение. Выпишем матрицы квадратичных форм $D$, $T$ и $\Pi $
С помощью формул (6.1) и (6.2) вычисляем матрицы $P$ и $Q$
По формуле (6.1) находятся три линейных соотношения между диссипативными коэффициентами aij
Если коэффициенты aij удовлетворяют этой системе, то можно найти нормальные координаты, в которых динамические уравнения вынужденных колебаний расщепляются на три независимые уравнения второго порядка вида (4.1) с решением (4.2)–(4.4).
Заключение. Для вынужденных колебаний механических систем с двумя и тремя степенями свободы с учетом сил трения получены простые условия расщепления системы уравнений 4-го и 6-го порядков на две или три идентичные системы 2-го порядка типа (4.1). Они значительно проще исходной и позволяют получать простые аналитические решения системы в явном аналитическом виде.
Работа выполнена в рамках госзадания (номер госрегистрации АААА-А20-120011690138-6).
Список литературы
Whittaker E.T. A treatise on the analytical dynamics of particles and rigid bodies. Cambridge at the university press. Second edition, 1917. = Уиттекер Э. Аналитическая динамика. М.: URSS, 2004. 595 с.
Четаев Н.Г. Устойчивость движения. Работы по аналитической механике. М.: Изд-во АН СССР, 1962. 535 с.
Журавлев В.Ф. Основы теоретической механики. М.: Физматлит, 2008. 304 с.
Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука, 1976. 305 с.
Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967. 552 с.
Bellman R. Introduction to Matrix Analysis. N. Y.: McGraw-Hill, 1970. = Беллман Р. Введение в теорию матриц. М.: Наука, 1976. 352 с.
Johnson C.R., Horn R.A. Matrix Analysis. Cambridge: Cambridge Univ. Press, 1985. = Хорн Р., Джонсон Ч. Матричный анализ. M.: Мир, 1989. 665 с.
Kumar Mitra. Simultaneous diagonalization of rectangular matrices // Lin. Algebra Appl. 1982. V. 47. P. 139–150.
Новиков М.А. Одновременная диагонализация трех вещественных симметричных матриц // Изв. вузов. Математика. 2014. № 12. С. 70–82.
Ландау Л.Д., Лифшиц Е.М. Курс теоретической физики. Том I. Механика. М.: Наука, 1965. 204 с.
Журавлев В.Ф., Петров А.Г. Анализ действия возмущений линейных резонансных систем с двумя степенями свободы // Изв. РАН. МТТ. 2021. № 2. С. 42–50. https://doi.org/10.31857/S0572329921020185
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела