1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 6, 2022

Известия РАН. Механика твердого тела, 2022, № 6, стр. 127-139

ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ ПЛОСКИЕ ПРОДОЛЬНЫЕ ВОЛНЫ В СРЕДЕ СЛЕПЯНА–ПАЛЬМОВА

В. И. Ерофеев a, *, М. И. Корсаков a, **, А. В. Леонтьева a, ***

a Институт проблем машиностроения РАН – филиал Федерального государственного бюджетного научного учреждения “Федеральный исследовательский центр Институт прикладной физики Российской академии наук”
Нижний Новгород, Россия

* E-mail: erof.vi@yandex.ru
** E-mail: martyknight52@gmail.com
*** E-mail: aleonav@mail.ru

Поступила в редакцию 07.02.2022
После доработки 17.02.2022
Принята к публикации 21.07.2022

Полный текст (PDF)

Аннотация

Рассматриваются плоские продольные волны, распространяющиеся в среде Слепяна–Пальмова, состоящей из несущей среды и ансамбля нелинейных осцилляторов. Система уравнений динамики сводится к одному уравнению относительно продольного перемещения несущей среды. Проанализировано распространение гармонических волн в зависимости от изменения параметров системы, характеризующих относительную плотность и диссипацию в среде. Показано, что среди нелинейных стационарных волн могут существовать только периодические волны. Исследовано влияние параметров нелинейности и относительной плотности материала на пределы максимально возможной деформации, форму и длину волны.

Ключевые слова: модель Слепяна–Пальмова, продольная волна, гармоническая волна, дисперсия, диссипация, нелинейная периодическая волна

1. Введение. Известно, что одной из основных гипотез классической механики сплошных сред является принцип напряжений Коши, устанавливающий эквивалентность действия всех внутренних сил, приложенных к элементарной площадке, действию их равнодействующей, приложенной к центру площадки. Однако в общем случае действие произвольной системы сил эквивалентно действию главного вектора и главного момента. При этом в среде возникают не только напряжения, но и моментные напряжения, образующие, вообще говоря, несимметричные тензоры. Чтобы учесть эти факторы, необходимо допустить в среде наличие дополнительных степеней свободы и рассмотреть физически бесконечно малый объем (по которому ведется усреднение свойств среды) не как материальную точку, а как более сложный объект, обладающий новыми степенями свободы. Для расширения спектра свойств сплошной среды необходимо предположить у физически бесконечно малого объема существование внутренней структуры (микроструктуры), обусловленной зернистостью, волокнистостью или ячеистостью строения реальных материалов.

Таким образом, сегодня в механике деформируемого твердого тела широко применяются как модель классического континуума, так и модели обобщенных континуумов [1–22].

Кроме моделей сред с внутренними ротационными степенями свободы (континуум Коссера [23]. На русском языке эта теория опубликована в [24]. Комментарии можно найти в [25, 26]) и градиентных моделей (континуумы Леру [27, 28], Джеремилло [29], Тупина [30] и др.), известны модели сред с осцилляторными степенями свободы. Их появление связано, в первую очередь, с работами Л.И. Слепяна (одномерная система) [31] и В.А. Пальмова [32–34] (трехмерная система).

Модель Слепяна–Пальмова представляет собой линейно-упругую несущую среду и подвешенные в каждой точке невзаимодействующие осцилляторы (упругие или вязкоупругие). При формулировке этой модели постулируется, что динамическое поведение несущей среды описывается уравнениями Ламе, а собственные частоты, связанных с ней осцилляторов непрерывно распределены.

Динамика среды Слепяна–Пальмова описывается системой уравнений:

(1.1)
$\left( {\lambda + \mu } \right)grad\,div{\mathbf{u}} + \mu \Delta {\mathbf{u}} - \rho {\mathbf{\ddot {u}}} - \int\limits_0^\infty {m\left( q \right){{{{\mathbf{\ddot {v}}}}}_{q}}dq} + {\mathbf{K}} + {\mathbf{Q}} = 0$
(1.2)
$m\left( q \right){{{\mathbf{\ddot {v}}}}_{q}} + c\left( q \right)\left[ {1 + \tilde {R}\left( {\frac{\partial }{{\partial t}}} \right)} \right]\left( {{{{\mathbf{v}}}_{q}} - {\mathbf{u}}} \right) = {{{\mathbf{Q}}}_{q}}$
где $\rho $ – массовая плотность; $\lambda $ и $\mu $ – модули упругости Ламе; ${\mathbf{u}}$ – вектор перемещения точек несущей среды; K – интенсивность внешней массовой силы; ${{{\mathbf{v}}}_{q}}$ – вектор абсолютного перемещения массы осциллятора; ${{{\mathbf{Q}}}_{q}}$ – внешняя сила, приложенная к массе осциллятора; величина $m\left( q \right)dq$ равна массе всех осцилляторов, имеющих собственные частоты, лежащие в интервале $\left( {q,q + dq} \right)$, умноженной на единицу объема; m = = $\int\limits_0^\infty {m(q)dq} $ – полная массовая плотность всех осцилляторов, присоединенных к несущей среде; $c\left( q \right) = {{q}^{2}}m\left( q \right)$ – статическая жесткость подвески осцилляторов; величина $\tilde {R}\left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}}} \right)$ характеризует диссипацию энергии в подвесе осциллятора.

Даже при малом демпфировании осцилляторов, пространственное затухание вибраций в такой среде оказывается конечным [34]. Эта модель эффективно используется при расчетах вибрации летательных аппаратов, объектов ракетно-космической техники и подводного флота.

2. Нелинейная одномерная математическая модель. Предположим, что среда изолирована, то есть K = 0, ${{{\mathbf{Q}}}_{q}} = 0$. Будем рассматривать одномерный вариант системы (1.1), (1.2). Также внесем нелинейность в данную систему, считая, что она связана с нелинейностью несущей среды. Полученная система имеет вид:

(2.1)
$\left( {\lambda + 2\mu } \right)\frac{{{{\partial }^{2}}{{u}_{x}}\left( {x,t} \right)}}{{\partial {{x}^{2}}}} + \frac{\partial }{{\partial x}}\left[ {E{{{\left( {\frac{{\partial {{u}_{x}}}}{{\partial x}}} \right)}}^{2}}} \right] - \rho \frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial {{t}^{2}}}} - \int\limits_0^\infty {m\left( q \right)\frac{{{{\partial }^{2}}{{{v}}_{{qx}}}\left( {x,t} \right)}}{{\partial {{t}^{2}}}}dq} = 0$
(2.2)
$m\left( q \right)\frac{{{{\partial }^{2}}{{{v}}_{{qx}}}}}{{\partial {{t}^{2}}}} + c\left( q \right)\left[ {1 + \tilde {R}\left( {\frac{\partial }{{\partial t}}} \right)} \right]\left( {{{{v}}_{{qx}}} - {{u}_{x}}} \right) = 0$
где E – коэффициент, характеризующий нелинейность несущей среды.

Будем считать, что абсолютное перемещение осциллятора не зависит от его собственной частоты (${{{v}}_{{qx}}} = {{{v}}_{x}}$), то есть

$\int\limits_0^\infty {m\left( q \right)\frac{{{{\partial }^{2}}{{{v}}_{{qx}}}}}{{\partial {{t}^{2}}}}dq} = \frac{{{{\partial }^{2}}{{{v}}_{x}}\left( {x,t} \right)}}{{\partial {{t}^{2}}}}\int\limits_0^\infty {m\left( q \right)dq} $

Система (2.1), (2.2) сводится к одному уравнению относительно продольного перемещения несущей среды ux:

(2.3)
$\begin{gathered} \frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial {{t}^{2}}}} - c_{1}^{2}\frac{{{{\partial }^{2}}{{u}_{x}}}}{{\partial {{x}^{2}}}} - \frac{{c_{1}^{2}}}{{{{q}^{2}}}}\frac{{{{\partial }^{4}}{{u}_{x}}}}{{\partial {{x}^{2}}\partial {{t}^{2}}}} + \frac{1}{{{{a}^{2}}{{q}^{2}}}}\frac{{{{\partial }^{4}}{{u}_{x}}}}{{\partial {{t}^{4}}}} + \tilde {R}\frac{{{{\partial }^{3}}{{u}_{x}}}}{{\partial {{t}^{3}}}} - \tilde {R}c_{1}^{2}\frac{{{{\partial }^{3}}{{u}_{x}}}}{{\partial {{x}^{2}}\partial t}} - \\ \, - \frac{{c_{2}^{2}}}{{{{q}^{2}}}}\frac{{{{\partial }^{3}}}}{{\partial x\partial {{t}^{2}}}}\left[ {{{{\left( {\frac{{\partial {{u}_{x}}}}{{\partial x}}} \right)}}^{2}}} \right] - c_{2}^{2}\frac{\partial }{{\partial x}}\left[ {{{{\left( {\frac{{\partial {{u}_{x}}}}{{\partial x}}} \right)}}^{2}}} \right] - \tilde {R}c_{2}^{2}\frac{{{{\partial }^{2}}}}{{\partial x\partial t}}\left[ {{{{\left( {\frac{{\partial {{u}_{x}}}}{{\partial x}}} \right)}}^{2}}} \right] = 0 \\ \end{gathered} $
где введены следующие обозначения:

$\tilde {\rho } = \rho + \int\limits_0^\infty {m\left( q \right)dq} ,\quad c_{1}^{2} = \frac{{\lambda + 2\mu }}{{\tilde {\rho }}},\quad c_{2}^{2} = \frac{E}{{\tilde {\rho }}},\quad {{a}^{2}} = \frac{{\tilde {\rho }}}{\rho }$

Переход к безразмерным переменным

$U = \frac{{{{u}_{x}}}}{{{{u}_{0}}}},\quad z = \frac{{aq}}{{{{c}_{1}}}}x,\quad \tau = aqt$
(${{u}_{0}}$ – максимальное перемещение, при котором деформация несущей среды еще является упругой) преобразует уравнение (2.3) к виду:
$\begin{gathered} \frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - {{a}^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}}} \right) + \tilde {R}aq\frac{\partial }{{\partial \tau }}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}}} \right) - \\ \, - \tilde {N}\frac{\partial }{{\partial z}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}}} \right] - \tilde {N}{{a}^{2}}\frac{{{{\partial }^{3}}}}{{\partial {{\tau }^{2}}\partial z}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}}} \right] - \tilde {R}\tilde {N}aq\frac{{{{\partial }^{2}}}}{{\partial \tau \partial z}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}}} \right] = 0 \\ \end{gathered} $
где $\tilde {N} = {{c_{2}^{2}aq{{u}_{0}}} \mathord{\left/ {\vphantom {{c_{2}^{2}aq{{u}_{0}}} {c_{1}^{3}}}} \right. \kern-0em} {c_{1}^{3}}}$

или

(2.4)
$\begin{gathered} \frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - {{a}^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}}} \right) + R\frac{\partial }{{\partial \tau }}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}}} \right) - \\ \, - {{N}_{1}}\frac{\partial }{{\partial z}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}}} \right] - R{{N}_{1}}\frac{{{{\partial }^{2}}}}{{\partial \tau \partial z}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}}} \right] - {{N}_{2}}\frac{{{{\partial }^{3}}}}{{\partial {{\tau }^{2}}\partial z}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}}} \right] = 0 \\ \end{gathered} $

Здесь ${{{{N}_{2}}} \mathord{\left/ {\vphantom {{{{N}_{2}}} {{{N}_{1}}}}} \right. \kern-0em} {{{N}_{1}}}} = {{a}^{2}} > 1$.

3. Дисперсионные свойства системы. Отбросив нелинейные слагаемые уравнения (2.4)

(3.1)
$\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - {{a}^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}}} \right) + R\frac{\partial }{{\partial \tau }}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}}} \right) = 0$
исследуем дисперсионные свойства системы.

Рассмотрим сначала более простой случай, когда диссипация отсутствует. Уравнение (3.1) примет вид:

$\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{4}}U}}{{\partial {{\tau }^{4}}}} - {{a}^{2}}\frac{{{{\partial }^{4}}U}}{{\partial {{\tau }^{2}}\partial {{z}^{2}}}} = 0$

Распространение гармонической волны

$U\left( {z,\tau } \right) = {{U}_{0}}{{e}^{{i\left( {\omega \tau - kz} \right)}}} + к.с.$
где U0 – комплексная амплитуда волны, $\omega $ – частота, k – волновое число, $к.с.$ – комплексно-сопряженная величина, описывается следующим дисперсионным уравнением

(3.2)
${{\omega }^{4}} - (1 + {{a}^{2}}{{k}^{2}}){{\omega }^{2}} + {{k}^{2}} = 0$

Две дисперсионные ветви

$k = \pm \omega \sqrt {\frac{{{{\omega }^{2}} - 1}}{{{{a}^{2}}{{\omega }^{2}} - 1}}} $
в первой четверти изображены на рис. 1. Пунктиром отмечены асимптоты. При $a = 1$ дисперсионная кривая (3.2) вырождается в прямые $\omega = \pm 1$, $\omega = \pm k$.

Рис. 1.

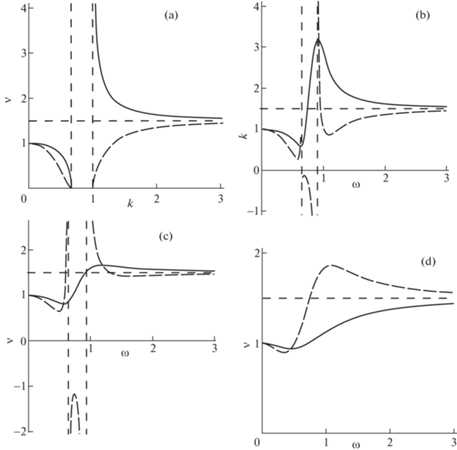
Зависимости $\omega \left( k \right)$ при изменении параметра a, $a = {{a}_{1}}$ (a), $a = {{a}_{2}}$ (b), $1 < {{a}_{1}} < {{a}_{2}}$.

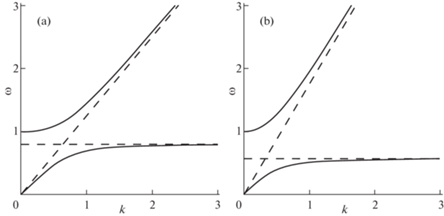
Верхняя ветвь дисперсионной кривой имеет частоту отсечки $\omega = 1$, нижняя ветвь исходит из нуля и ограничена сверху по частоте постоянной величиной $\omega = {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$.

Дисперсия отсутствует на низких частотах $\omega = k$ у низкочастотной ветви и на высоких частотах у высокочастотной ветви $\omega = ak$. Каждая из двух волн распространяется в своем частотном диапазоне, которые не пересекаются. Существует область непропускания по частоте, которая увеличивается при увеличении значения параметра $a$.

Динамика кривых фазовой скорости ${{{v}}_{{ph}}} = {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k}$ определяется уравнением:

${v}_{{ph}}^{4}{{k}^{4}} - (1 + {{a}^{2}}{{k}^{2}}){v}_{{ph}}^{2}{{k}^{2}} + {{k}^{2}} = 0$

Из последнего уравнения находим зависимость фазовой скорости от волнового числа

(3.3)
${{{v}}_{{ph}}} = \frac{{\sqrt 2 }}{{2k}}\sqrt {1 + {{a}^{2}}{{k}^{2}} \pm \sqrt {{{{(1 + {{a}^{2}}{{k}^{2}})}}^{2}} - 4{{k}^{2}}} } $

На основании формулы Рэлея [35]

${{{v}}_{{gr}}} = {{{v}}_{{ph}}} + k\frac{{d{{{v}}_{{ph}}}}}{{dk}}$
и (3.3) получим явные зависимости групповой скорости от волнового числа

(3.4)
${{{v}}_{{gr}}} = \frac{{{{a}^{2}}k \pm \frac{{{{a}^{2}}k + {{a}^{4}}{{k}^{3}} - 2k}}{{\sqrt {{{{(1 + {{a}^{2}}{{k}^{2}})}}^{2}} - 4{{k}^{2}}} }}}}{{\sqrt 2 \sqrt {1 + {{a}^{2}}{{k}^{2}} \pm \sqrt {{{{(1 + {{a}^{2}}{{k}^{2}})}}^{2}} - 4{{k}^{2}}} } }}$

Графическое изображение зависимостей фазовой (3.3) и групповой (3.4) скоростей от волнового числа представлено на рис. 2. Кривые скоростей, отмеченные “1” и “2”, соответствуют верхней и нижней ветвям дисперсионной кривой ω(k).

Рис. 2.

Зависимости ${{{v}}_{{ph}}}\left( k \right)$ (сплошная линия) и ${{{v}}_{{gr}}}\left( k \right)$ (длинный штриховой пунктир) при изменении параметра a, $a = {{a}_{1}}$ (a), $a = {{a}_{2}}$ (b), $1 < {{a}_{1}} < {{a}_{2}}$.

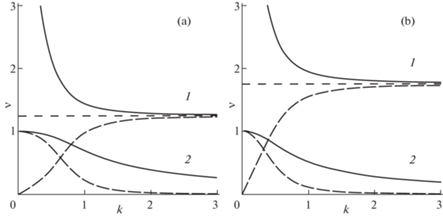
Во всем интервале частот и волновых чисел кривые фазовой скорости лежат выше соответствующих кривых групповой скорости.

При увеличении значения параметра a: значения фазовой и групповой скоростей, соответствующие высокочастотной ветви, – увеличиваются; значения скоростей, соответствующие низкочастотной ветви, – уменьшаются (для фиксированного значения волнового числа).

Дисперсионное уравнение, если диссипация присутствует

(3.5)
$\omega ({{\omega }^{2}} - {{k}^{2}})iR + {{\omega }^{2}} - {{k}^{2}} - {{\omega }^{4}} + {{a}^{2}}{{\omega }^{2}}{{k}^{2}} = 0$
где волновое число является комплексной величиной $k = {{k}_{1}} + i{{k}_{2}}$. Разделяя действительную и мнимую части в дисперсионном уравнении (3.5), получаем

$2R\omega {{k}_{1}}{{k}_{2}} + {{\omega }^{2}} - k_{1}^{2} + k_{2}^{2} - {{\omega }^{4}} + {{a}^{2}}{{\omega }^{2}}k_{1}^{2} - {{a}^{2}}{{\omega }^{2}}k_{2}^{2} = 0$
$R{{\omega }^{3}} - R\omega k_{1}^{2} + R\omega k_{2}^{2} - 2{{k}_{1}}{{k}_{2}} + 2{{a}^{2}}{{\omega }^{2}}{{k}_{1}}{{k}_{2}} = 0$

Зависимости действительной k1, мнимой k2 частей волнового числа, их отношения и скоростей от частоты приведены на рис. 3–5.

Рис. 3.

Зависимости ${{k}_{1}}\left( \omega \right)$ (сплошная линия) и ${{k}_{2}}\left( \omega \right)$ (длинный штриховой пунктир) при изменении параметра R, $R = 0$ (a), $R = {{R}_{1}}$ (b), $R = {{R}_{2}}$ (c), $R = {{R}_{3}}$ (d), $0 < {{R}_{1}} < {{R}_{2}} < {{R}^{{\left( 1 \right)}}} < {{R}^{{\left( 2 \right)}}} < {{R}_{3}}$.

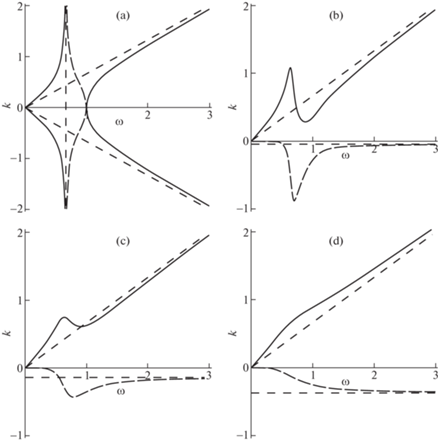
Рис. 4.

Зависимости $\gamma \left( \omega \right)$ при изменении параметра $R$, $R = {{R}_{1}}$ (сплошная линия), $R = {{R}_{2}}$ (длинный штриховой пунктир), $R = {{R}_{3}}$ (короткий штриховой пунктир), $0 < {{R}_{1}} < {{R}^{{\left( 3 \right)}}} < {{R}_{2}} < {{R}^{{\left( 1 \right)}}} < {{R}^{{\left( 2 \right)}}} < {{R}_{3}}$.

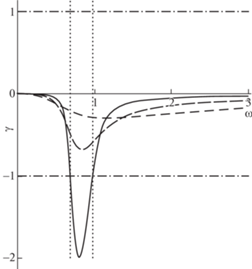
Рис. 5.

Зависимости ${{{v}}_{{ph}}}\left( \omega \right)$ (сплошная линия) и ${{{v}}_{{gr}}}\left( \omega \right)$ (длинный штриховой пунктир) при изменении параметра $R$, $R = 0$ (a), $R = {{R}_{1}}$ (b), $R = {{R}_{2}}$ (c), $R = {{R}_{3}}$ (d), $0 < {{R}_{1}} < {{R}^{{\left( 3 \right)}}} < {{R}_{2}} < {{R}^{{\left( 1 \right)}}} < {{R}^{{\left( 2 \right)}}} < {{R}_{3}}$.

На рис. 3,a дисперсионная кривая изображена в двух четвертях. В полосе непропускания волновое число является чисто мнимым. Коротким штриховым пунктиром на рис. 3 показаны асимптоты ${{k}_{1}} = \pm {\omega \mathord{\left/ {\vphantom {\omega a}} \right. \kern-0em} a}$, $\omega = {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$ ($R = 0$) и ${{k}_{1}} = {\omega \mathord{\left/ {\vphantom {\omega a}} \right. \kern-0em} a}$, ${{k}_{2}} = - {{R({{a}^{2}} - 1)} \mathord{\left/ {\vphantom {{R({{a}^{2}} - 1)} {2{{a}^{3}}}}} \right. \kern-0em} {2{{a}^{3}}}}$ ($R \ne 0$). Значения ${{k}_{1}}$, ${{k}_{2}}$ имеют разные знаки. Считаем, что ${{k}_{1}} > 0$.

При увеличении параметра $R$ кривые ${{k}_{1}}\left( \omega \right)$, ${{k}_{2}}\left( \omega \right)$ приобретают монотонность и меняют свое расположение относительно асимптот. Так действительная и мнимая ветви стремятся к асимптотам сверху, соответственно, при $R > {{R}^{{\left( 1 \right)}}}$, ${{R}^{{\left( 1 \right)}}} \approx {{2a} \mathord{\left/ {\vphantom {{2a} {\sqrt {{{a}^{2}} + 3} }}} \right. \kern-0em} {\sqrt {{{a}^{2}} + 3} }}$ и при $R > {{R}^{{\left( 2 \right)}}}$, ${{R}^{{\left( 2 \right)}}} \approx 2a\sqrt {{{({{a}^{2}} + 3)} \mathord{\left/ {\vphantom {{({{a}^{2}} + 3)} {({{a}^{4}} + 2{{a}^{2}} + 5)}}} \right. \kern-0em} {({{a}^{4}} + 2{{a}^{2}} + 5)}}} $, причем первая из них монотонно возрастает, а вторая – монотонно убывает.

На рис. 4 показано отношение мнимой части волнового числа к его действительной части $\gamma = {{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}$. Штрихпунктирной линией отмечены границы отрезка $\left| \gamma \right| \leqslant 1$. При R < R(3), ${{R}^{{(3)}}}$ = a – 1 зависимость $\gamma \left( \omega \right)$ имеет интервал частот $\left( {{{\omega }_{ - }};{{\omega }_{ + }}} \right)$, ω = = $({{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {2a}}} \right. \kern-0em} {2a}})\sqrt {1\, + \,{{a}^{2}}\, - \,{{R}^{2}}\, \pm \,\sqrt {{{{({{R}^{2}}\, - \,{{a}^{2}}\, - \,1)}}^{2}}\, - \,4{{a}^{2}}} } $ (точечный пунктир, рис. 4), где абсолютные значения коэффициента затухания больше единицы ($\left| \gamma \right| > 1$). На промежутке $\left( {{{\omega }_{ - }};{{\omega }_{ + }}} \right)$ затухание преобладает над распространением волны.

На рис. 5 изображены зависимости фазовой ${{{v}}_{{ph}}} = {\omega \mathord{\left/ {\vphantom {\omega {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}$ и групповой скоростей (вычисляется по формуле Рэлея) от частоты. При $0 < R < {{R}^{{\left( 1 \right)}}}$ график групповой скорости имеет разрывы. Здесь на небольшом участке частот фазовая и групповая скорости разных знаков. При $R > {{R}^{{\left( 1 \right)}}}$ график групповой скорости является непрерывным.

При R = 0, как было отмечено ранее, для любых допустимых значений частоты ω значения фазовой скорости больше значений групповой скорости ${{{v}}_{{ph}}} > {{{v}}_{{gr}}}$. При $R > 0$ появились промежутки частот, где значения фазовой скорости меньше абсолютных значений групповой скорости ${{{v}}_{{ph}}} < \left| {{{{v}}_{{gr}}}} \right|$.

При значении параметра $R = {{R}^{{\left( 1 \right)}}}$ кривые фазовой и групповой скоростей меняют свое расположение относительно асимптоты, но имеют пересечение в точке $\omega = \omega {\text{*}}$. При этом для значений частот из интервалов $0 < \omega < \omega {\text{*}}$ и $\omega > \omega {\text{*}}$ выполняются, соответственно, неравенства ${{{v}}_{{ph}}} > {{{v}}_{{gr}}}$ и ${{{v}}_{{ph}}} < {{{v}}_{{gr}}}$.

4. Нелинейные стационарные волны. Учтем нелинейность среды в отсутствие диссипации ($R = 0$, ${{N}_{1}} = 0$), тогда уравнение (2.3) примет вид:

(4.1)
$\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - \frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}} - {{a}^{2}}\frac{{{{\partial }^{2}}U}}{{\partial {{z}^{2}}}}} \right) - {{N}_{2}}\frac{{{{\partial }^{3}}}}{{\partial {{\tau }^{2}}\partial z}}\left[ {{{{\left( {\frac{{\partial U}}{{\partial z}}} \right)}}^{2}}} \right] = 0$

Уравнение (4.1) сводится к уравнению нелинейного осциллятора

(4.2)
$\frac{{{{d}^{2}}U}}{{d{{\xi }^{2}}}} + {{m}_{1}}{{m}_{2}}U\frac{{dU}}{{d\xi }} + {{m}_{1}}U = 0$
где коэффициенты равны
${{m}_{1}} = \frac{{1 - {{{v}}^{2}}}}{{{{{v}}^{2}}({{a}^{2}} - {{{v}}^{2}})}},\quad {{m}_{2}} = - \frac{{2{{N}_{2}}}}{{{{a}^{2}} - {{{v}}^{2}}}}$
$\xi = z - {v}\tau $ – бегущая координата, ${v}$ – скорость стационарной волны. Фазовые портреты уравнения (4.2) при различных значениях скорости представлены на рис. 6, $W = {{dU} \mathord{\left/ {\vphantom {{dU} {d\xi }}} \right. \kern-0em} {d\xi }}$.

Рис. 6.

Фазовые траектории волны на фазовой плоскости $\left( {U,W} \right)$ при $1 < {v} < a$ (a), ${v} > a$ (b).

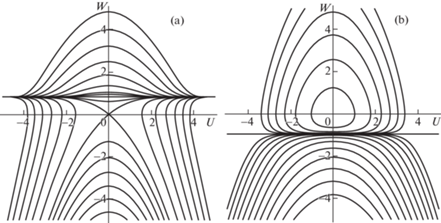
При скоростях $0 < {v} < 1$ фазовый портрет, изображенный на второй части рисунка (рис. 6,b) отображается симметрично относительно горизонтальной оси. В двух случаях, когда скорость принадлежит интервалам $0 < {v} < 1$ или ${v} > a$, фазовый портрет имеет замкнутые траектории. Если $1 < {v} < a$ фазовый портрет замкнутых фазовых траекторий не содержит (рис. 6,a), следовательно, стационарных волн не существует.

Рассмотрим случай ${v} > a$, константы ${{m}_{1}}$ и ${{m}_{2}}$ в уравнении (4.2) принимают положительные значения. Анализ уравнения (4.2) на фазовой плоскости $\left( {U,W} \right)$ показывает, что в начале координат имеется особая точка равновесия типа “центр”. Прямая $W = \varepsilon {\text{*}}$ определяет границу, разделяющую устойчивые движения (замкнутые фазовые траектории) и неустойчивые движения (незамкнутые фазовые траектории). Эта величина характеризует максимально возможную (в пределах упругости) деформацию:

$\varepsilon _{{}}^{*} = - \frac{1}{{{{m}_{2}}}} = \frac{{{{a}^{2}} - {{v}^{2}}}}{{2{{N}_{2}}}}$

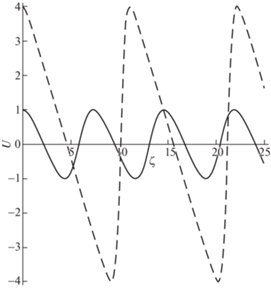
Профиль стационарной волны вблизи центра и при относительных деформациях, близких к ε* показан на рис. 7. При значениях деформации близких к максимально возможным $\varepsilon \to \varepsilon {\text{*}}$ зависимость имеет пилообразный вид, а при значениях деформации далеких от максимально возможных $\varepsilon \ll \varepsilon {\text{*}}$ зависимость имеет почти синусоидальный профиль.

Рис. 7.

Профиль волны при различных значениях $\varepsilon $, $\varepsilon \ll \varepsilon {\text{*}}$ (сплошная линия), $\varepsilon \to \varepsilon {\text{*}}$ (штриховая линия).

Зависимость между амплитудой нелинейной волны A и ее волновым числом $K$

$\frac{K}{{{{K}_{0}}}} = \frac{1}{{\sqrt {1 + {{{\left( {\frac{1}{{\pi \varepsilon {\text{*}}}}\frac{A}{{{{A}_{0}}}}} \right)}}^{2}}} }}$
где K0 и A0 – волновое число и амплитуда гармонической (линейной) волны, показана на рис. 8. Видно, что с ростом амплитуды волны относительное значение волнового числа уменьшается, длина волны растет.

Рис. 8.

Зависимость амплитуды нелинейной волны от волнового числа.

Рис. 9.

Зависимости U(ξ) при изменении параметров, соответственно, N2 (a) и a (b): $N_{2}^{{(1)}}$, a1 (сплошная линия), $N_{2}^{{(2)}}$, a2 (штриховой пунктир), $N_{2}^{{(1)}}$ < $N_{2}^{{(2)}}$, a1 < a2.

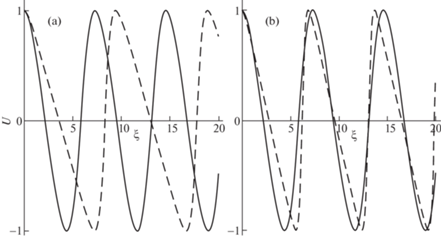
На рис. 9 изображены профили нелинейных волн фиксированных амплитуд и скоростей при различных значениях параметров среды N2 и a.

Увеличение значения параметра N2 уменьшает числовые значения максимально возможной деформации и увеличивает длину волны. Чем больше значение параметра a ($1 < a < {v}$), тем меньше длина волны и абсолютные значения максимальной деформации.

Влияние параметра a на волны, распространяющиеся со скоростями $0 < {v} < 1$, отличается. При увеличении значения параметра, увеличивается интервал допустимых деформаций и длина нелинейной волны.

5. Заключение. В отсутствие диссипации в среде распространяются быстрая и медленная волны, причем исключается их одновременное распространение. Дисперсия наблюдается вблизи двух частот дисперсионной кривой: частоты отсечки высокочастотной ветви и частоты, ограничивающей частотный интервал низкочастотной ветви. Во всем частотном диапазоне проявляется нормальная дисперсия.

Уменьшение значения параметра, характеризующего относительную плотность среды Слепяна–Пальмова, приводит к увеличению скоростей (фазовой, групповой) медленной волны, уменьшению скоростей быстрой волны и сокращению частотной зоны непропускания.

Наличие диссипации приводит к слиянию ветвей дисперсионной кривой, что обеспечивает непрерывный частотный диапазон распространения гармонических волн, а также способствует появлению аномальной дисперсии и эффекта обратной волны.

При превышении некоторого порогового значения параметра, характеризующего диссипацию в среде, аномальная дисперсия проявляется в высокочастотной области, в области низких частот сохраняется нормальная дисперсия.

Для нелинейных стационарных волн периодического типа показано, что чем больше амплитуда, тем больше длина волны при фиксированных параметрах системы. Для нелинейных стационарных волн равных амплитуд и скоростей установлено: при увеличении параметра нелинейности среды Слепяна–Пальмова, уменьшается значение максимально допустимой деформации и увеличивается длина волны; при увеличении значения параметра относительной плотности среды, область допустимой деформации сужается, длина волны уменьшается.

Работа выполнялась при поддержке Российского научного фонда (Грант № 21-19-00813).

Список литературы

  1. Mechanics of Generalized Continua: On Hundred Years After the Cosserats. Advances in Mathematics and Mechanics. V. 21 / Ed. by G. . Maugin, A.V. Metrikine. Berlin: Springer, 2010. 338 p. https://doi.org/10.1007/978-1-4419-5695-8

  2. Mechanics of Generalized Continua. Advanced Structured Matherials. V. 7 / Ed. by H. Altenbach, G.A. Maugin, V. Erofeev. Berlin-Heidelberg: Springer-Verlag, 2011. 350 p. https://doi.org/10.1007/978-3-642-19219-7

  3. Generalized Continua as Models with Multi-Scale Effects or Under Multi-Field Actions. Advanced Structured Matherials. V. 22 / Ed. by H. Altenbach, S. Forest, A. Krivtsov. Berlin-Heidelberg: Springer-Verlag, 2013. 332 p. https://doi.org/10.1007/978-3-642-36394-8

  4. Generalized Continua – from the Theory to Engineering Applications / Ed. by H. Altenbach, V.A. Eremeyev. Wien: Springer, 2013. 388 p. https://doi.org/10.1007/978-3-7091-1371-4

  5. Bagdoev A.G., Erofeyev V.I., Shekoyan A.V. Wave Dynamics of Generalized Continua. Advanced Structured Matherials. Vol. 24. Berlin-Heidelberg: Springer-Verlag, 2016. 274 p. https://doi.org/10.1007/978-3-642-37267-4

  6. Generalized Continua as Models for Classical and Advanced Materials. Advanced Structured Matherials. V. 42 / Ed. by H. Altenbach, S. Forest. Switzerland: Springer-Verlag, 2016. 458 p. https://doi.org/10.1007/978-3-319-31721-2

  7. Maugin G.A. Non-Classical Continuum Mechanics. Advanced Structured Matherials. V. 51. Singapore: Springer, 2017. 260 p. https://doi.org/10.1007/978-981-10-2434-4

  8. Advanced in Mechanics of Microstructured Media and Structures. Advanced Structured Matherials. V. 87 / Ed. by F. dell’Isola, V.A. Eremeyev, A. Porubov. Cham: Springer, 2018. 370 p. https://doi.org/10.1007/978-3-319-73694-5

  9. Generalized Models and Non-Classical Approaches in Complex Materials 1. Advanced Structured Matherials. V. 89 / Ed. by H. Altenbach, J. Pouget, M. Rousseau, B. Colle, T. Michelitsch. Cham: Springer, 2018. 760 p. https://doi.org/10.1007/978-3-319-72440-9

  10. Generalized Models and Non-Classical Approaches in Complex Materials 2. Advanced Structured Matherials. V. 90 / Ed. by H. Altenbach, J. Pouget, M. Rousseau, B. Collet, T. Michelitsch. Cham: Springer, 2018. 306 p. https://doi.org/10.1007/978-3-319-77504-3

  11. Erofeev V., Porubov A., Sargsyan S. (Editors). Nonlinear Wave Dynamics of Generalized Continua // Materials Physics and Mechanics. 2018. V. 35. № 1 (Spesial Issue dedicated to the memory E.L. Aero and G. Maugin). 190 p.

  12. Dynamical Processes in Generalized Continua and Structures. Advanced Structured Matherials. V. 103 / Ed. by H. Altenbach, A. Belyaev, V. Eremeyev, A. Krivtsov, A.V. Porubov. Cham: Springer, 2019. 525 p. https://doi.org/10.1007/978-3-030-11665-1

  13. Wave Dynamics, Mechanics and Physics of Microstructured Metamaterials. Advanced Structured Matherials. V. 109 / Ed. by M.A. Sumbatyan. Cham: Springer, 2019. 254 p. https://doi.org/10.1007/978-3-030-17470-5

  14. Higher Gradient Materials and Related Generalized Continua. Advanced Structured Matherials. V. 120 / Ed. by H. Altenbach, W.H. Muller, B.E. Abali. Cham: Springer, 2019. 231 p. https://doi.org/10.1007/978-3-030-30406-5

  15. Erofeev V.I., Pavlov I.S. Structural Modeling of Metamaterials. Advanced Structured Matherials. V. 144. Cham: Springer, 2021. 208 p. https://doi.org/10.1007/978-3-030-60330-4

  16. Лурье С.А. О парадоксе аномальной относительной изгибной жесткости сверхтонких балок в градиентной теории упругости // Изв. РАН. МТТ. 2020. № 3. С. 48–57. https://doi.org/10.31857/S0572329920030095

  17. Еремеев В.А., Лебедев Л.П. О разрешимости краевых задач теории упругих микрополярных оболочек с жесткими включениями // Изв. РАН. МТТ. 2020. № 6. С. 111–115. https://doi.org/10.31857/S0572329920050050

  18. Радаев Ю.Н. О факторизации основного гиперболического дифференциального оператора микрополярной теории упругости // Изв. РАН. МТТ. 2020. № 6. С. 24–32. https://doi.org/10.31857/S0572329920060136

  19. Тарлаковский Д.В., Нгуен Ван Лам. Оценка учета моментных свойств среды на примере нестационарной осесимметричной задачи // Изв. РАН. МТТ. 2021. № 6. С. 149–155. https://doi.org/10.31857/S0572329921060143

  20. Мурашкин Е.В., Радаев Ю.Н. Об одном обобщении алгебраической теории Гамильтона–Кэли // Изв. РАН. МТТ. 2021. № 6. С. 130–138. https://doi.org/10.31857/S0572329921060106

  21. Васильев В.В., Лурье С.А., Салов В.А. Новое решение задачи о трещине в растягиваемой ортотропной пластине // Изв. РАН. МТТ. 2021. № 6. С. 23–32. https://doi.org/10.31857/S0572329921060167

  22. Мурашкин Е.В., Радаев Ю.Н. К теории ориентированных тензорных элементов площади микрополярного континуума, погруженного во внешнее плоское пространство // Изв. РАН. МТТ. 2022. № 2. С. 3–13. https://doi.org/10.31857/S0572329922020155

  23. Cosserat E., Cosserat F. Theorie des Corps Deformables. Paris: Librairie Scientifique A. Hermann et Fils, 1909. 226 p. https://doi.org/10.1038/081067a0

  24. Коссера Э., Коссера Ф. Заметка о теории евклидовского действия / Аппель П. Руководство теоретической (рациональной) механики. Курс механики Парижского факультета наук. Том третий: равновесие и движение сплошных сред. М.: Изд-во “Кушнерев И.Н. и Ко”, 1911. С. 612–682 (Репринт: Радиоэлектроника. Наносистемы. Информационные технологии. 2013. Т. 5. № 1. С. 5–76).

  25. Ерофеев В.И. Братья Коссера и механика обобщенных континуумов // Вычислительная механика сплошных сред. 2009. Т. 2. № 4. С. 5–10. https://doi.org/10.7242/1999-6691/2009.2.4.28

  26. Ерофеев В.И., Герасимов С.И. Континуум Коссера сто лет спустя // Радиоэлектроника. Наносистемы. Информационные технологии. 2013. Т. 5. № 1. С. 3–4.

  27. Le Roux J. Etude geometrique de la torsion de la flexion, dans les deformations infinitesimaleg d’nn milien continu // Ann. Ecole Norm. Super. 1911. V. 28. P. 523–579. https://doi.org/10.24033/ASENS.643

  28. Le Roux J. Recherchesg sur la geometrie beg deformatios finies // Ann. Ecole Norm. Super. 1913. V. 30. P. 193–245. https://doi.org/10.24033/asens.659

  29. Jaramillo T.J. A Generalization of the Energy Function of Elasticity Theory. Dissertation. Departament of Mathematics. University of Chicago, 1929.

  30. Тупин Р.А. Теории упругости, учитывающие моментные напряжения // Механика. Сборник переводов. 1965. № 3. С. 113–140.

  31. Слепян Л.И. Волна деформации в стержне с амортизирующими массами // Инженерный журнал. Механика твердого тела. 1967. № 5. С. 34–40.

  32. Пальмов В.А. Об одной модели среды со сложной структурой // ПММ. 1969. Т. 33. № 4. С. 768–773.

  33. Пальмов В.А. Колебания упругопластических тел. М.: Наука, 1976. 328 с.

  34. Пальмов В.А. Приложение теории обобщенного континуума к проблеме пространственного затухания в сложных механических системах // Вычислительная механика сплошных сред. 2009. Т. 2. № 4. С. 105–110. https://doi.org/10.7242/1999-6691/2009.2.4.35

  35. Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.-Ижевск: НИЦ Регулярная и хаотическая динамика, 2005. 560 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал