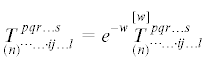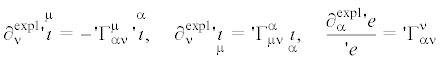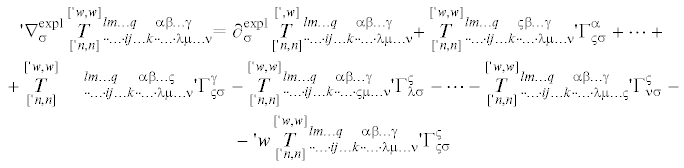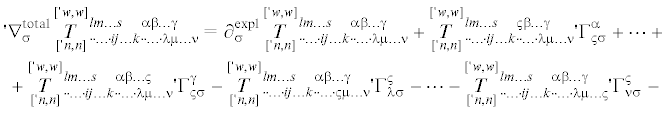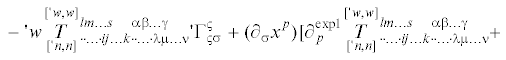Известия РАН. Механика твердого тела, 2022, № 6, стр. 104-113
К ТЕОРИИ КОВАРИАНТНОГО ДИФФЕРЕНЦИРОВАНИЯ ДВУХТОЧЕЧНЫХ ПСЕВДОТЕНЗОРНЫХ ПОЛЕЙ
Е. В. Мурашкин a, *, Ю. Н. Радаев a, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: evmurashkin@gmail.com
** E-mail: radayev@ipmnet.ru
Поступила в редакцию 09.06.2022
После доработки 10.07.2022
Принята к публикации 11.08.2022
- EDN: MZLHKD
- DOI: 10.31857/S0572329922060149
Аннотация
В настоящей работе обсуждаются вопросы ковариантного дифференцирования двухточечных псевдотензорных полей произвольных рангов и весов. Приводятся необходимые сведения из алгебры и анализа псевдотензоров. Вводится понятие двухточечного псевдотензорного поля, основанного на формуле его преобразования при замене систем координат. Приводится формула преобразования двухточечного псевдотензорного поля к двухточечному абсолютному тензорному полю. Вводятся определения полных и неполных операторов частного и ковариантного дифференцирования двухточечных псевдотензоров. Получены формулы для ковариантных производных двухточечного псевдотензорного поля. Отмечаются важные примеры двухточечных псевдотензорных полей из нелинейной механики деформируемого твердого тела.
Вводные замечания и предварительные сведения. Двухточечные тензоры играют исключительно важную роль в нелинейной механике континуума [1–4]. К таким тензорам относятся градиент деформации,11 тензор конечного поворота, тензор силовых напряжений Пиола–Кирхгофа и т.д. Некоторые из таких полей имеют псевдотензорную природу.22 Без последовательного использования псевдотензорного формализма двухточечных полей невозможно корректное построение моделей гемитропных микрополярных упругих континуумов [6–8]. Поиск сведений о правилах ковариантного дифференцирования двухточечных псевдотензорных полей представляет довольно сложную задачу. Цель настоящего исследования восполнить этот пробел.
В настоящей работе вначале приводятся минимально необходимые сведения из алгебры и анализа псевдотензоров. Вводится понятие двухточечного псевдотензорного поля, основанного на формуле его преобразования при замене систем координат. Приводятся определения полных и неполных операторов частного и ковариантного дифференцирования двухточечных псевдотензоров. Получены формулы для ковариантных производных двухточечного псевдотензорного поля. Более глубокое и полное изложение подходов псевдотензорного формализма можно найти в книгах по тензорному анализу и механике сплошных сред [1, 5, 9–12]. Основы алгебры и анализа абсолютных двухточечных тензорных полей (two-point (double) tensor fields) можно найти в дополнении к работе [1], написанном Эриксеном. В работах [6–8, 13, 14] рассматривались правила ковариантного дифференцирования одноточечных псевдотензорных полей, используемых к механике микрополярных континуумов и механике растущих тел.
Содержание статьи можно охарактеризовать следующим образом. В первом разделе работы приводятся основные сведения о псевдотензорах. Вводится понятие фундаментального ориентирующего псевдоскаляра. Даются определения обобщенной дельты Кронекера и символов перестановок. Приводится формула преобразования псевдотензора произвольного веса и ранга к абсолютному тензору того же самого ранга.
Второй раздел статьи посвящен понятию двухточечного псевдотензорного поля. Дается формальное определение двухточечного псевдотензорного поля, основанное на формуле его преобразования при замене обоих систем координат. Приводится формула преобразования двухточечного псевдотензорного поля к двухточечному абсолютному тензорному полю.
В третьем разделе статьи обсуждаются вопросы частного и ковариантного дифференцирований двухточечных псевдотензорных полей. Вводятся определения полных и неполных операторов Гамильтона, операторов частного и ковариантного дифференцирований двухточечных псевдотензоров. Обсуждаются формулы, связывающие полные и неполные ковариантные производные двухточечного псевдотензорного поля.
1. Необходимые сведения из алгебры и анализа псевдотензоров в евклидовом пространстве. Рассмотрим N-мерное евклидово пространство. Его единственной ориентационной характеристикой является фундаментальный ориентирующий псевдоскаляр e [6–8], который в N-мерном пространстве можно определить как косое произведение [15, c. 63–65] абсолютных векторов ковариантного базиса
(1.1)
$\mathop {\left| \!{\overline {\, \iota \,}} \right. }\limits_1 ,\mathop \iota \limits_2 , \ldots ,\mathop {\left. {\underline {\, \iota \,}}\! \right| }\limits_N = e$Ясно, что $e > \mathop 0\limits^{[ + 1]} $ для правоориентированной системы координат, а $e < \mathop 0\limits^{[ + 1]} $ – для левоориентированной, т.е. ${\text{sgn}}{\kern 1pt} e$ является единственным признаком, ориентирующим евклидово пространство.
Несложно показать, что в евклидовом пространстве справедливо соотношение
где g – детерминант, составленный из компонент метрического тензора.Одним из фундаментальных объектов многомерной геометрии является абсолютный тензор $\delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{M}}}}$, называемый обобщенной дельтой Кронекера. $\delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{M}}}}$ можно определить в N-мерном пространстве для $M \leqslant N$ согласно правилу
(1.3)
$\delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{M}}}} = \left\{ {\begin{array}{*{20}{l}} { + 1,}&{{\text{если}}\;{{j}_{1}},{{j}_{2}}, \ldots ,{{j}_{M}}{\kern 1pt} \;{\text{различные натуральные числа}}} \\ {}&{1,2, \ldots ,N\;{\text{и если}}\;{\kern 1pt} {{i}_{1}},{{i}_{2}}, \ldots ,{{i}_{M}}\;{\text{есть четная}}} \\ {}&{{\text{перестановка}}\;{{j}_{1}},{{j}_{2}}, \ldots ,{{j}_{M}}} \\ { - 1,}&{{\text{если}}\;{{j}_{1}},{{j}_{2}}, \ldots ,{{j}_{M}}{\kern 1pt} \;{\text{различные натуральные числа}}} \\ {}&{1,2, \ldots ,N\;{\text{и если}}\;{\kern 1pt} {{i}_{1}},{{i}_{2}}, \ldots ,{{i}_{M}}\;{\text{есть нечетная}}} \\ {}&{{\text{перестановка}}\;{{j}_{1}},{{j}_{2}}, \ldots ,{{j}_{M}}} \\ { - 0,}&{{\text{во всех остальных случаях}}} \end{array}} \right.$С помощью тензора $\delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{M}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{M}}}}$ можно легко вычислить символы перестановок:
1. относительный ковариантный N-вектор ${{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}}$ веса –1
(1.4)
${{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}} = \delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}^{{12 \ldots N}}$2. относительный контравариантный N-вектор ${{\varepsilon }^{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}}$ веса +1
(1.5)
${{\varepsilon }^{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}} = \delta _{{12 \ldots N}}^{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{N}}}}$В трехмерном пространстве справедливо
(1.6)
$e = {{\mathop e\limits^{[ + 1]} }_{{123}}} = \left| \!{\overline {\, {} \,}} \right. \mathop \iota \limits_1 ,\mathop \iota \limits_2 ,\mathop \iota \limits_3 \left. {\underline {\, {} \,}}\! \right| = (\mathop \iota \limits_1 \, \times \mathop \iota \limits_2 ) \cdot \mathop \iota \limits_3 $Псевдотензоры произвольного веса легко преобразовывать в абсолютные тензоры при помощи фундаментального ориентирующиего псевдоскаляра e (см. [6–8]. Для произвольного псевдотензора целого веса w и ранга n имеем
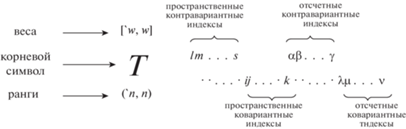
Здесь и далее в квадратных скобках сверху корневого символа будем указывать вес псевдотензорного поля, а в круглых скобках снизу – ранг.
Отметим, что равенство (1.7) позволяет обобщить алгебраическую теорему Гамильтона–Кэли, что было продемонстрировано в [14].
Заметим также, что (1.7) отнюдь не единственная схема приведения псевдотензора к абсолютному тензору см. например [9, c. 174].
2. Определение двухточечных псевдотензорных полей. Введем в евклидовом пространстве две системы координат ${{X}^{\alpha }}$ и xs. Обе системы координат считаются равноправными, однако, в дальнейшем, следуя терминологии нелинейной механики континуума, будем называть одну из них ${{X}^{\alpha }}$ отсчетной (лагранжевой), а вторую xs – пространственной (эйлеровой). Греческие и латинские индексы будут ассоциироваться с отсчетными ${{X}^{\alpha }}$ и пространственными xs координатами.33 Обозначим через $'{\kern 1pt} \mathop \iota \limits_\alpha $ и $\mathop \iota \limits_s $ векторы ковариантных базисов, а через $'{\kern 1pt} e$ и e – фундаментальные ориентирующие псевдоскаляры. Будем считать заданными метрические тензоры $'{\kern 1pt} {{g}_{{\alpha \gamma }}} = '{\kern 1pt} \mathop \iota \limits_\alpha \; \cdot '{\kern 1pt} \mathop \iota \limits_\gamma $ и ${{g}_{{sk}}} = \mathop \iota \limits_s \, \cdot \mathop \iota \limits_k $ соответственно введенным системам координат.
Двухточечный псевдотензор с корневым символом T рангов $'{\kern 1pt} n$ и n с весами $'{\kern 1pt} w$ и $w$ будет зависеть от пары переменных ${{X}^{\alpha }}$ и xs и его компоненты будут содержать как латинские, так и греческие индексы (см. рис. 1):
Для одноточечного псевдтензорного поля используется упрощенная запись
(2.1)
$\mathop {\mathop T\limits^{[w]} }\limits_{(n)} {\kern 1pt} _{{ \cdots \ldots \cdot ij \ldots l}}^{{pqr \ldots s}}$При переходе к другим системам координат ${{x}^{{\underline s }}}{\kern 1pt} (\underline s = 1,2, \ldots ,N)$ и ${{X}^{{\underline \alpha }}}{\kern 1pt} (\underline \alpha = 1,2, \ldots ,N)$ компоненты двухточечного псевдотензора преобразуются согласно правилу
(2.2)
$\begin{gathered} \mathop {\mathop {\underline T }\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot \underline i {\kern 1pt} \underline h \ldots \underline k \cdot \cdot \ldots \cdot \underline \lambda {\kern 1pt} \underline \kappa \ldots \underline \nu }}^{{\underline l {\kern 1pt} \underline m \ldots \underline s \;\;\;\;\underline \alpha {\kern 1pt} \underline \sigma \ldots \underline \tau }} = [\det ({{\partial }_{{\underline \beta }}}{{X}^{\gamma }}{{)]}^{{'{\kern 1pt} w}}}{{[\det ({{\partial }_{{\underline p }}}{{x}^{q}})]}^{w}} \times \\ \, \times ({{\partial }_{l}}{{x}^{{\underline l }}})({{\partial }_{m}}{{x}^{{\underline m }}}) \cdots ({{\partial }_{s}}{{x}^{{\underline s }}})({{\partial }_{{\underline i }}}{{x}^{i}})({{\partial }_{{\underline h }}}{{x}^{h}}) \cdots ({{\partial }_{{\underline k }}}{{x}^{k}}) \times \\ \, \times ({{\partial }_{\alpha }}{{x}^{{\underline \alpha }}})({{\partial }_{\sigma }}{{x}^{{\underline \sigma }}}) \cdots ({{\partial }_{\tau }}{{x}^{{\underline \tau }}})({{\partial }_{{\underline \lambda }}}{{x}^{\lambda }})({{\partial }_{{\underline \kappa }}}{{x}^{\kappa }}) \cdots ({{\partial }_{{\underline \nu }}}{{x}^{\nu }})\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ih \ldots k \cdot \cdot \ldots \cdot \lambda \kappa \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \sigma \ldots \tau }} \\ \end{gathered} $Двухточечные псевдотензоры преобразуются в абсолютные при помощи фундаментальных ориентирующих псевдоскаляров $'{\kern 1pt} e$ и e согласно правилу
(2.3)
$\mathop T\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}\, = '{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}{{e}^{{ - w}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}$3. Дифференцирование двухточечных псевдотензорных полей. Введем следующие обозначения для частных (неполных) производных по явному вхождению переменных ${{X}^{\alpha }}$ и xk:
С этого момента будем считать, что рассматриваемые системы координат связаны между собой с помощью преобразования деформации
Прямое описание деформации континуума соответствует преобразованию
а обратное описание44 задается преобразованиемРавноправие способов описания деформации мы будем отражать с помощью обозначения
Полное (total) дифференцирование подразумевает вычисление производных не только по явным (explicit) вхождениям переменных, но и по неявным, определяемым преобразованием деформации. Полные производные по переменным ${{X}^{\alpha }}$ и xk обозначим через
Отметим, что в теориях поля [16, 17] для сокращения записи уравнений поля для полных производных используют обычные обозначения
В частности для дивергенции одноточечного псевдотензорного поля заданного веса (например для тензора силовых напряжений Коши ($w = + 1$) [5, p. 142)] справедливо равенство:
Полные и неполные производные связаны соотношениями
(3.1)
$\partial _{\alpha }^{{{\text{total}}}} = \partial _{\alpha }^{{{\text{expl}}}} + ({{\partial }_{\alpha }}{{x}^{k}})\partial _{k}^{{{\text{expl}}}}$(3.2)
$\partial _{k}^{{{\text{total}}}} = \partial _{k}^{{{\text{expl}}}} + ({{\partial }_{k}}{{X}^{\alpha }})\partial _{\alpha }^{{{\text{expl}}}}$Неполные операторы Гамильтона определяются согласно
(3.3)
$'{\kern 1pt} {{\nabla }^{{{\text{expl}}}}} = '{\kern 1pt} \mathop \iota \limits^\alpha {\kern 1pt} \partial _{\alpha }^{{{\text{expl}}}}$(3.4)
${{\nabla }^{{{\text{expl}}}}} = \mathop \iota \limits^k {\kern 1pt} \partial _{k}^{{{\text{expl}}}}$Определим неполные отсчетный и пространственный градиенты двухточечного псевдотензорного поля произвольных рангов и весов $'w,w$ с помощью соотношений [13]:
(3.5)
$\begin{gathered} '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{\kern 1pt} '{\kern 1pt} {{\nabla }^{{{\text{expl}}}}} \otimes '{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}\mathop {\mathop {\mathbf{T}}\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} = '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{\kern 1pt} '{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes \partial _{\sigma }^{{{\text{expl}}}}('{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} \times \\ \times \mathop \iota \limits_l \, \otimes \cdots \otimes \mathop \iota \limits_s \, \otimes \mathop \iota \limits^i \, \otimes \cdots \otimes \mathop \iota \limits^k \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \cdots \otimes '{\kern 1pt} \mathop i\limits_\gamma \, \otimes '{\kern 1pt} \mathop i\limits^\lambda \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits^\nu ) \\ \end{gathered} $(3.6)
$\begin{gathered} {{e}^{w}}{{\nabla }^{{{\text{expl}}}}} \otimes {{e}^{{ - w}}}\mathop {\mathop {\mathbf{T}}\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} = {{e}^{w}}{\kern 1pt} \mathop \iota \limits^p \, \otimes \partial _{p}^{{{\text{expl}}}}({{e}^{{ - w}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} \times \\ \times \mathop \iota \limits_l \, \otimes \cdots \otimes \mathop \iota \limits_s \, \otimes \mathop \iota \limits^i \, \otimes \cdots \otimes \mathop \iota \limits^k \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits_\gamma \, \otimes '{\kern 1pt} \mathop \iota \limits^\lambda \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits^\nu ) \\ \end{gathered} $Преобразуем формулы (3.5) и (3.6) с учетом хорошо известных зависимостей
(3.8)
$\partial _{p}^{{{\text{expl}}}}\mathop \iota \limits^m = - \Gamma _{{sp}}^{m}\mathop \iota \limits^s ,\quad \partial _{p}^{{{\text{expl}}}}\mathop \iota \limits_m = \Gamma _{{mp}}^{s}\mathop \iota \limits_s ,\quad \frac{{\partial _{p}^{{{\text{expl}}}}e}}{e} = \Gamma _{{ps}}^{s}$В результате несложных преобразований получим
(3.9)
$\begin{gathered} \, \times \mathop \iota \limits^p \, \otimes \mathop \iota \limits_q \, \otimes \cdots \otimes \mathop \iota \limits_s \, \otimes \mathop \iota \limits^i \, \otimes \cdots \otimes \mathop \iota \limits^k \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits_\gamma \, \otimes '{\kern 1pt} \mathop \iota \limits^\lambda \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits^\nu \, + \cdots + \\ \, + \mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}\Gamma _{{sp}}^{q} \times \\ \end{gathered} $На основании (3.9) заключаем, что неполная ковариантная производная по координатам xp определяется согласно
(3.10)
$\begin{gathered} \nabla _{p}^{{{\text{expl}}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} = \partial _{p}^{{{\text{expl}}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} + \mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{qm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}\Gamma _{{qp}}^{l} + \cdots + \\ \, + \mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots q\;\;\;\;\alpha \beta \ldots \gamma }}\Gamma _{{qp}}^{s} - \mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot qj \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}\Gamma _{{ip}}^{q} - \cdots - \mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots q \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}\Gamma _{{kp}}^{q} - \\ \, - w\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}\Gamma _{{qp}}^{q} \\ \end{gathered} $Аналогично, вычисляется неполная ковариантная производная по координатам Xσ
Полные операторы Гамильтона определяются соотношениями
(3.12)
$'{\kern 1pt} {{\nabla }^{{{\text{total}}}}} = '{\kern 1pt} \mathop \iota \limits^\alpha {\kern 1pt} \partial _{\alpha }^{{{\text{total}}}},\quad {{\nabla }^{{{\text{total}}}}} = \mathop \iota \limits^k {\kern 1pt} \partial _{k}^{{{\text{total}}}}$Заметим, например, что для дивергенции одноточечного псевдотензорного поля (например, псевдотензора веса +1 силовых напряжений Коши) справедливы равенства
Полные отсчетный и пространственный градиенты двухточечного псевдотензорного поля произвольных рангов $'n,n$ и весов $'w,w$ определяются с помощью соотношений [13]:
(3.13)
$\begin{gathered} '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{{e}^{w}}'{\kern 1pt} {{\nabla }^{{{\text{total}}}}} \otimes '{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}{{e}^{{ - w}}}\mathop {\mathop {\mathbf{T}}\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} = '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{{e}^{w}}{\kern 1pt} '{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes \partial _{\sigma }^{{{\text{total}}}}('{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}{{e}^{{ - w}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} \times \\ \, \times \mathop \iota \limits_l \, \otimes \cdots \otimes \mathop \iota \limits_s \, \otimes \mathop \iota \limits^i \, \otimes \cdots \otimes \mathop \iota \limits^k \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits_\gamma \, \otimes '{\kern 1pt} \mathop \iota \limits^\lambda \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits^\nu ) \\ \end{gathered} $(3.14)
$\begin{gathered} '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{{e}^{w}}{{\nabla }^{{{\text{total}}}}} \otimes '{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}{{e}^{{ - w}}}\mathop {\mathop {\mathbf{T}}\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} = '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{{e}^{w}}\mathop \iota \limits^p \, \otimes \partial _{p}^{{{\text{total}}}}('{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}{{e}^{{ - w}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} \times \\ \, \times \mathop \iota \limits_l \, \otimes \cdots \otimes \mathop \iota \limits_s \, \otimes \mathop \iota \limits^i \, \otimes \cdots \otimes \mathop \iota \limits^k \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits_\gamma \, \otimes '{\kern 1pt} \mathop \iota \limits^\lambda \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits^\nu ) \\ \end{gathered} $В случае двухвалетного псевдотензора $\mathop {\mathop {\mathbf{S}}\limits^{['{\kern 1pt} w,w]} }\limits_{(1,1)} $ можно получить:
(3.15)
$\begin{gathered} '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{{e}^{w}}'{\kern 1pt} {{\nabla }^{{{\text{total}}}}} \otimes '{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}{{e}^{{ - w}}}\mathop {\mathop {\mathbf{S}}\limits^{['{\kern 1pt} w,w]} }\limits_{(1,1)} = '{\kern 1pt} {{e}^{{'{\kern 1pt} w}}}{\kern 1pt} '{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes \partial _{\sigma }^{{{\text{expl}}}}('{\kern 1pt} {{e}^{{ - '{\kern 1pt} w}}}\mathop {\mathop S\limits^{['{\kern 1pt} w,w]} }\limits_{(1,1)} {{{\kern 1pt} }^{{\alpha m}}}'{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \mathop \iota \limits_m ) + \\ \, + {{\partial }_{\sigma }}{{x}^{p}}{{e}^{w}}{\kern 1pt} '{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes \partial _{p}^{{{\text{expl}}}}({{e}^{{ - w}}}\mathop {\mathop S\limits^{['{\kern 1pt} w,w]} }\limits_{(1,1)} {{{\kern 1pt} }^{{\alpha m}}}'{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \mathop \iota \limits_m ) = ('{\kern 1pt} \nabla _{\sigma }^{{{\text{expl}}}}\mathop {\mathop S\limits^{['{\kern 1pt} w,w]} }\limits_{(1,1)} {{{\kern 1pt} }^{{\alpha m}}})'{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \mathop \iota \limits_m \, + \\ \, + ({{\partial }_{\sigma }}{{x}^{p}}\nabla _{p}^{{{\text{expl}}}}\mathop {\mathop S\limits^{['{\kern 1pt} w,w]} }\limits_{(1,1)} {{{\kern 1pt} }^{{\alpha m}}})'{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \mathop \iota \limits_m = ('{\kern 1pt} \nabla _{\sigma }^{{{\text{total}}}}\mathop {\mathop S\limits^{['{\kern 1pt} w,w]} }\limits_{(1,1)} {{{\kern 1pt} }^{{\alpha m}}})'{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \mathop \iota \limits_m \\ \end{gathered} $Отметим, что дивергентные слагаемые $^{'}\nabla _{\alpha }^{{{\text{total}}}}{{S}^{{\alpha m}}}$ возникают в записи уравнений баланса импульса в отсчетной конфигурации, где ${{S}^{{\alpha m}}}$ – первый тензор силовых напряжений Пиола–Кирхгофа.
Подставив выражение (3.1) в формулу (3.13) и найдем
(3.16)
$\begin{gathered} \, + {{\partial }_{\sigma }}{{x}^{p}}{{e}^{w}}{\kern 1pt} '{\kern 1pt} \mathop \iota \limits^\sigma \, \otimes \partial _{p}^{{{\text{expl}}}}({{e}^{{ - w}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{('{\kern 1pt} n,n)} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} \times \\ \, \times \mathop \iota \limits_l \, \otimes \cdots \otimes \mathop \iota \limits_s \, \otimes \mathop \iota \limits^i \, \otimes \cdots \otimes \mathop \iota \limits^k \, \otimes '{\kern 1pt} \mathop \iota \limits_\alpha \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits_\gamma \, \otimes '{\kern 1pt} \mathop \iota \limits^\lambda \, \otimes \cdots \otimes '{\kern 1pt} \mathop \iota \limits^\nu ) = \\ \, = ('{\kern 1pt} \nabla _{\sigma }^{{{\text{expl}}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} + {{\partial }_{\sigma }}{{x}^{p}}\nabla _{p}^{{{\text{expl}}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}) \times \\ \end{gathered} $Вычисляя (3.13) и (3.14) c учетом (3.1) и (3.2) получим выражения для полных ковариантных производных двухточечного псевдотензорного поля:55
(3.18)
$\, - w\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }}\Gamma _{{qp}}^{q} + ({{\partial }_{p}}{{X}^{\sigma }})[\partial _{\sigma }^{{{\text{expl}}}}\mathop {\mathop T\limits^{['{\kern 1pt} w,w]} }\limits_{['{\kern 1pt} n,n]} {\kern 1pt} _{{ \cdot \cdot \ldots \cdot ij \ldots k \cdot \cdot \ldots \cdot \lambda \mu \ldots \nu }}^{{lm \ldots s\;\;\;\;\alpha \beta \ldots \gamma }} + $Отметим, что выражения (3.17) и (3.18), можно записать в компактной форме, принимая во внимание (3.10) и (3.11):
(3.19)
$'{\kern 1pt} \nabla _{\sigma }^{{{\text{total}}}} = '{\kern 1pt} \nabla _{\sigma }^{{{\text{expl}}}} + ({{\partial }_{\sigma }}{{x}^{p}})\nabla _{p}^{{{\text{expl}}}}$(3.20)
$\nabla _{p}^{{{\text{total}}}} = \nabla _{p}^{{{\text{expl}}}} + ({{\partial }_{p}}{{X}^{\sigma }})'{\kern 1pt} \nabla _{\sigma }^{{{\text{expl}}}}$Заключение и выводы. В настоящей работе обсуждаются вопросы ковариантного дифференцирования двухточечных псевдотензоров произвольных рангов и весов.
1. Приводятся необходимые сведения из алгебры и анализа псевдотензоров в ориентированном евклидовом пространстве.
2. Вводится понятие двухточечного псевдотензорного поля, основанного на формуле его преобразования при замене обеих систем координат.
3. Приводится формула преобразования двухточечного псевдотензорного поля к двухточечному абсолютному тензорному полю.
4. Вводятся определения полных и неполных операторов частного и ковариантного дифференцирований двухточечных псевдотензоров.
5. Обсуждаются формулы, связывающие полные и неполные ковариантные производные двухточечного псевдотензорного поля (см. таблицу).
Благодарности. Работа выполнена в рамках государственного задания (№ госрегистрации АААА-А20-120011690132-4) и при поддержке Российского фонда фундаментальных исследований проект № 20-01-00666.
Таблица 1.
Операции частного и ковариантного дифференцирований двухточечных псевдотензоров
| отсчетные координаты Xα | пространственные координаты xk | |
|---|---|---|
| базисные векторы | $'\mathop \iota \limits_\alpha $ | $\mathop \iota \limits_s $ |
| частное (неполное) дифференцирование по явному вхождению переменной | $\partial _{\alpha }^{{{\text{expl}}}}$ | $\partial _{s}^{{{\text{expl}}}}$ |
| полное дифференцирование | $\partial _{\alpha }^{{{\text{total}}}}$ | $\partial _{s}^{{{\text{total}}}}$ |
| неполный оператор Гамильтона | $'{{\nabla }^{{{\text{expl}}}}} = '\mathop \iota \limits^\alpha {\kern 1pt} \partial _{\alpha }^{{{\text{expl}}}}$ | ${{\nabla }^{{{\text{expl}}}}} = \mathop \iota \limits^s {\kern 1pt} \partial _{s}^{{{\text{expl}}}}$ |
| полный оператор Гамильтона | $'{{\nabla }^{{{\text{total}}}}} = '\mathop \iota \limits^\alpha {\kern 1pt} \partial _{\alpha }^{{{\text{total}}}}$ | ${{\nabla }^{{{\text{total}}}}} = \mathop \iota \limits^s {\kern 1pt} \partial _{s}^{{{\text{total}}}}$ |
| цепное правило (chain rule) | $\partial _{\alpha }^{{{\text{total}}}} = ({{\partial }_{\alpha }}{{x}^{s}})\partial _{s}^{{{\text{total}}}}$ | $\partial _{s}^{{{\text{total}}}} = ({{\partial }_{s}}{{X}^{\alpha }})\partial _{\alpha }^{{{\text{total}}}}$ |
| цепное правило (chain rule) | $'\nabla _{\alpha }^{{{\text{total}}}} = ({{\partial }_{\alpha }}{{x}^{s}})\nabla _{s}^{{{\text{total}}}}$ | $\nabla _{s}^{{{\text{total}}}} = ({{\partial }_{s}}{{X}^{\alpha }})'\nabla _{\alpha }^{{{\text{total}}}}$ |
| полное дифференцирование | $\partial _{\alpha }^{{{\text{total}}}} = \partial _{\alpha }^{{{\text{expl}}}} + ({{\partial }_{\alpha }}{{x}^{s}})\partial _{s}^{{{\text{expl}}}}$ | $\partial _{s}^{{{\text{total}}}} = \partial _{s}^{{{\text{expl}}}} + ({{\partial }_{s}}{{X}^{\alpha }})\partial _{\alpha }^{{{\text{expl}}}}$ |
| полное ковариантное дифференцирование | $'\nabla _{\alpha }^{{{\text{total}}}} = '\nabla _{\alpha }^{{{\text{expl}}}} + ({{\partial }_{\alpha }}{{x}^{s}})\nabla _{s}^{{{\text{expl}}}}$ | $\nabla _{s}^{{{\text{total}}}} = \nabla _{s}^{{{\text{expl}}}} + ({{\partial }_{s}}{{X}^{\alpha }})'\nabla _{\alpha }^{{{\text{expl}}}}$ |
Список литературы
Truesdell C., Toupin R. The Classical Field Theories // Principles of Classical Mechanics and Field Theory / Prinzipien der Klassischen Mechanik und Feldtheorie. Ed. by S. Flügge. Berlin, Heidelberg: Springer Berlin Heidelberg. 1960. P. 226–858. https://doi.org/10.1007/978-3-642-45943-6_2.
Truesdell C., Noll W. The non-linear field theories of mechanics. Berlin, Heidelberg: Springer. 2004. 579 p. https://doi.org/10.1007/978-3-662-10388-3_1
Maugin G. Material inhomogeneities in elasticity. New York: Chapman and Hall/CRC. 2020. 292 p. https://doi.org/10.1201/9781003059882
Весоловский З. Динамические азадачи нелинейной теории упругости. Пер. с польского Киев: Наукова думка. 1981. 216 p.
Schouten J.A. Tensor Analysis for Physicist. Oxford: Clarendon Press. 1965. 434 p. [Схоутен Я.А. Тензорный анализ для физиков. М.% Наука. 1965. 456 с.].
Радаев Ю.Н., Мурашкин Е.В. Псевдотензорная формулировка механики гемитропных микрополярных сред // Проблемы прочности и пластичности. 2020. Т. 82. № 4. С. 399–412. https://doi.org/10.32326/1814-9146-2020-82-4-399-412
Murashkin E.V., Radayev Yu.N. On a micropolar theory of growing solids // Вестн. Сам. Гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. Т. 24. № 3. С. 424–444. https://doi.org/10.14498/vsgtu1792
Kovalev V.A., Murashkin E.V., Radayev Yu.N. On the Neuber theory of micropolar elasticity. A pseudotensor formulation // Вестн. Сам. Гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. V. 24. № 4. P. 752–761. https://doi.org/10.14498/vsgtu1799
Гуревич Г.Б. Основы теории алгебраических инвариантов. М., Л.: ГИТТД. 1948. 408 с. [Gurevich G.B. Foundations of the theory of algebraic invariants. Gröningen, P. Noordhoff, 1964. 429 p.].
Sokolnikoff I. Tensor Analysis: Theoryand Applications to Geometry and Mechanics of Continua. New York: John Wiley & Sons Inс. 1964. 361 p. [Сокольников И.С. Тензорный анализ. Теория и применения в геометрии и в механике сплошных сред. М.: Наука, 1971. 376 с.].
Synge J.L., Schild A. Tensor calculus. Toronto: Toronto University Press. 1949. V. 5. 334 p.
Мак-Коннел А.Дж. Введение в тензорный анализ. С приложениями к геометрии механике в физике. М.: Физматгиз. 1963. 411 с.
Radayev Y.N., Murashkin E.V., Nesterov T.K. On covariant non-constancy of distortion and inversed distortion tensors // Вестн. Сам. Гос. техн. ун-та. Сер. Физ.-мат. науки. 2022. V. 26. № 1. P. 36–47. https://doi.org/10.14498/vsgtu1891
Мурашкин Е.В., Радаев Ю.Н. Об одном обобщении алгебраической теории Гамильтона-Кэли // Изв. РАН. МТТ. 2021. № 6. С. 130–138. https://doi.org/10.31857/S0572329921060106
Розенфельд Б.А. Многомерные пространства. М.: Наука. 1966.
Ковалев В.А., Радаев Ю.Н. Элементы теории поля: вариационные симметрии и геометрические инварианты. М.: ФИЗМАТЛИТ. 2009. 156 с.
Ковалев В.А., Радаев Ю.Н. Волновые задачи теории поля и термомеханика. Саратов: Изд-во Сарат. ун-та. 2010. 328 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела