Известия РАН. Механика твердого тела, 2023, № 1, стр. 102-114
О ДЛИТЕЛЬНОМ РАЗРУШЕНИИ СОСТАВНОГО РАСТЯГИВАЕМОГО СТЕРЖНЯ В УСЛОВИЯХ ПОЛЗУЧЕСТИ
Л. В. Фомин a, *, Ю. Г. Басалов a, **
a НИИ механики МГУ имени М.В. Ломоносова
Москва, Россия
* E-mail: fleonid1975@mail.ru
** E-mail: basalov@yandex.ru
Поступила в редакцию 02.02.2022
После доработки 12.03.2022
Принята к публикации 14.03.2022
- EDN: KLPUYU
- DOI: 10.31857/S0572329922100087
Аннотация
Рассматривается напряженно-деформированное состояние и определяется время до разрушения составного растягиваемого стержня при ползучести. Стержень состоит из трех частей, расположенных симметрично по толщине. Принято дополнительное условие: все части составного стержня жестко, без проскальзывания соединены между собой. Ползучесть каждой части стержня описывается степенной моделью с различными параметрами. Для определения времени до разрушения используется кинетическое уравнение, которое описывает накопление повреждений в процессе ползучести. Для каждой части стержня принят одинаковый вид кинетического уравнения, но накопление повреждений происходит под действием напряжений, различных для каждой из частей. Анализируются распределения напряжений и процессы накопления повреждений во времени в различных частях составного стержня. Определяются значения материальных констант в степенных законах ползучести и длительного разрушения, приводящие к увеличению времени до разрушения составного стержня.
Введение. Современные материалы и элементы конструкций должны обеспечивать надежность и работоспособность изделий, выполненных из них, в течение всего срока службы. В связи с этим наукоемкие исследования высокотемпературной прочности материалов и конструкций достаточно актуальны. Наиболее часто для дополнительной защиты элементов конструкций от деструктивного воздействия внешней, часто рабочей, активной среды применяются типовые элементы составного типа. Внешний слой такой составной конструкции, как правило, контактирует с агрессивным веществом и защищает основные элементы конструкции от его разрушительного воздействия.
Данная статья посвящена исследованию напряженно-деформированного состояния и моделированию процессов разрушения такой типовой конструкции, как стержень, находящийся в условии ползучести [1–3] при растяжении. Изучение и моделирование таких процессов является предварительным опорным исследованием перспективной задачи о защитном эффекте внешних частей составного стержня при его контакте с рабочей активной средой в условиях длительного действия нагрузки и повышенных температур. В таких условиях (как в нейтральной среде, так и при воздействии активных сред) для металлических материалов и сплавов, как известно, проявляются свойства их ползучести, которые могут приводить к разрушению ответственных элементов конструкций.
Проблема изучения ползучести и длительного разрушения конструкций составного типа весьма актуальна. Приведем некоторый обзор известных научных работ и статей по указанной теме.
В работе [4] рассматривается кручение составных валов переменного сечения в условиях установившейся ползучести. При этом слои составных валов спаяны между собой. Решение рассматриваемой задачи ищется с помощью единой функции напряжений.
В работах [5–10] используется наследственная теория ползучести для описания поведения составных конструкций под нагрузкой. Так, в работе [5] рассматривается подход моделирования вязкоупругих свойств материала, который позволяет спрогнозировать перераспределение усилий во времени в слоях составных конструкций. Авторами статьи [5] определены новые ядра для описания ползучести стареющих материалов. Полученные в статье результаты являются теоретическим обоснованием решений нелинейных задач деформирования составных пластин и оболочек с учетом ползучести, что позволяет получить прогнозные оценки поведения конструкций в реальных условиях эксплуатации.
В статье [6] рассмотрена неустановившаяся ползучесть однородных и металлокомпозитных стержней (балок) нерегулярной слоистой структуры. Балки состоят из тонких стенок и прикрепленных к ним сверху и снизу полок (несущих слоев). Стенки и несущие слои изготовлены из однородных изотропных материалов. Механическое поведение этих материалов описывается нелинейной наследственной теорией ползучести Ю.Н. Работнова. На базе гипотез теории Тимошенко с привлечением идеи метода шагов по времени сформулирована задача неупругого изгибного деформирования таких стержней с учетом ослабленного сопротивления их стенок поперечному сдвигу. В исследовании показано, что в балках с усиленными несущими слоями ползучесть в основном развивается за счет деформаций поперечных сдвигов, которые активно накапливаются в стенках таких конструкций.
В работе [7] построено точное решение квазистатической задачи об определении напряженно-деформированного состояния толстостенной трубы, состоящей из любого количества (соединенных без натяга, ненапряженных) слоев нелинейно-вязкоупругих изотропных материалов, каждый из которых подчиняется определяющему соотношению Ю.Н. Работнова с разными парами произвольных материальных функций и постулату несжимаемости при нагружении давлениями на внутренней и внешней поверхностях трубы, медленно меняющимися во времени. Автором получено решение задачи о ползучести и длительной прочности многослойной трубы. Выведено уравнение для времени разрушения трубы при ползучести с использованием трех вариантов деформационного критерия разрушения: в качестве меры поврежденности выбраны максимальная деформация растяжения в каждом слое трубы, или интенсивность деформаций, или максимальная деформация сдвига.
В работе [8] методами строительной механики проведено моделирование напряженного состояния многослойных конструкций. Авторами проведены расчеты трехслойной цилиндрической оболочки (сталь, бетон, сталь).
В статье [9] на примере решения контактных задач ползучести предлагается обобщение модели основания Винклера на случай ползучести материала деформируемого покрытия. Использована наследственная теория ползучести. Рассматриваются вязкоупругое однородно стареющее однослойное, многослойное и композиционное покрытия, а также однослойные покрытия с нелинейной ползучестью.
В работе [10] исследована ползучесть гомогенных и гибридных композитных балок нерегулярной слоисто-волокнистой структуры. Балки состоят из тонких стенок и полок (несущих слоев). Стены могут быть усилены продольно или поперечно в плоскости, а несущие слои армированы в продольном направлении. Механическое поведение фазовых материалов описывается нелинейной наследственной теорией ползучести Работнова с учетом разной их устойчивости к растяжению и сжатию. На основе гипотез теории Тимошенко с использованием метода временных шагов сформулирована задача о неупругом изгибе таких балок с учетом ослабленного сопротивления их стенок поперечному сдвигу.
Интересный подход к оценке релаксации остаточных напряжений в поверхностно упрочненных лопатках газотурбинных двигателей при ползучести разработан авторами работ [11, 12]. В основе метода лежит гипотеза, позволяющая произвести декомпозицию лопатки на “тело” лопатки и тонкий упрочненный поверхностный слой, что дает возможность разбить рассматриваемую задачу на ряд краевых задач, которые решаются последовательно.
Аналогичный подход применен авторами [13] при разработке метода решения краевой задачи релаксации остаточных напряжений в поверхностно упрочненном сплошном цилиндре в условиях ползучести. В данной работе учитывается жесткая фиксация первоначально заданных осевой деформации и угле закручивания цилиндра. Разработанная авторами феноменологическая методика применяется при исследовании напряженно-деформированного состояния цилиндрического образца из сплава ЖС6КП после пневмодробеструйной обработки.
Известно, что поликристаллическое тело представляет собой совокупность сросшихся друг с другом хаотически ориентированных маленьких кристаллов – кристаллитов. Размеры кристаллитов (зерен), их форма и ориентация кристаллографических осей имеют случайный характер. На микроуровне и мезоуровне поликристаллическое тело можно считать составным, элементы которого состоят из множества ориентированных в разных направлениях кристаллитов. В работе [14] рассматривается вопрос оценки кинетики напряженно-деформированного состояния и процесса накопления повреждений поликристаллических конструкционных материалов при воздействии нестационарного длительного термосилового нагружения. При таком нагружении основным деградационным механизмом является ползучесть материала. Авторами [14] приведена математическая модель, построенная на базе концепций механики поврежденной среды и позволяющая описывать процессы при нестационарной ползучести в условиях сложного нагружения. Путем сопоставления результатов численного исследования с экспериментальными данными приводится доказательство применимости математической модели для одноосных и многоосных знакопеременных условий нагружения.
Ползучесть бетонов, армированных стальными стержнями [15, 16] и полимерными волокнами [17], и составных конструкций из них рассматриваются в условии длительного сжатия. В работе [16] произведен учет начальных напряжений и деформаций при оценке несущей способности сталежелезобетонных конструкций на эксплуатационные нагрузки.
Учет преднапряжений армирующих элементов и их влияние на ползучесть и длительные характеристики составных конструкций поперечно-клееных брусьев произведен в работах зарубежных авторов [18, 19]. В этих исследованиях учитываются реологические свойства древесины при продольном и поперечном сжатии [20].
Проведенный обзор показал, что в исследованиях ученых в основном изучается и моделируется напряженно-деформированное состояние (НДС) составных конструкций и их элементов. Изучению времени до разрушения таких составных конструкций в условии длительного действия нагрузок уделяется недостаточное внимание.
Настоящая статья посвящена как определению НДС, так и прогнозированию времени до разрушения составного металлического растягиваемого стержня, находящегося в условии ползучести. Исследование основывается на кинетической теории ползучести и длительной прочности Ю.Н. Работнова [1]. В качестве структурного параметра, описывающего накопление повреждений в процессе ползучести, в данной статье использован параметр поврежденности, который имеет смысл накопления пор и микронесплошностей в материале.
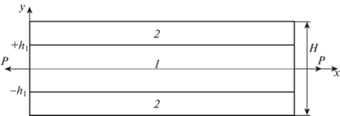
1. Постановка задачи. Рассматривается составной металлический стержень, находящийся в состоянии установившейся ползучести под действием постоянной растягивающей силы $P$, приложенной к его торцам. Стержень имеет прямоугольное поперечное сечение, длина стержня $L$, ширина стержня $H$ и толщина $b$ удовлетворяют двойному неравенству $L \gg H \gg b$. Расположение частей симметрично относительно срединной плоскости, проходящей через геометрическую середину ширины $H$. Центральная часть стержня выполнена из материала, обладающего одними свойствами ползучести, две крайние одинаковые части выполнены из другого материала, который обладает другими свойствами ползучести. Дополнительно примем следующее условие: все части составного стержня жестко, без проскальзывания соединены между собой. Расположение частей в стержне представлено на рис. 1.
На рис. 1 обозначение ${{h}_{1}}$ соответствует ординате границы первой (центральной) и вторых (крайних) частей в системе координат $x0y$. При этом ширина первой части равна $2{{h}_{1}}$.
При принятом условии жесткого соединения частей в составном стержне (без их взаимного проскальзывания) напряженные состояния вблизи мест соединения слоев становятся отличными от одномерных и неоднородными. Неоднородность напряженного состояния вблизи мест соединений частей может возникнуть, в том числе, и по причине естественных несовершенств технологических способов соединения частей между собой. Распространенными способами соединения являются диффузионная сварка, спайка, склейка, различные способы газодинамического напыления.
Общие тенденции развития методов исследования и определения напряженно-деформированного состояния типовых элементов конструкций (стержни, пластины, тонкостенные оболочки) приводят к сведению решения трехмерных задач к решению более простых задач – двумерных и одномерных. Иными словами, часто при соответствующих условиях размерность решаемой задачи понижается. Так, например, малый размер элемента конструкции в поперечном направлении может позволить исследователям избавиться от поперечной координаты в математических постановках задач и их решении. Кроме этого, используются методы упрощения, связанные с использованием гипотез и известных принципов. Реализация методов с использованием известных и принятых в механике гипотез, как правило, не содержит процедур регулярного уточнения решения.
Возвращаясь к постановке рассматриваемой задачи, учитывая малость поперечных размеров составного стержня по сравнению с его длиной, примем одномерный характер напряженного состояния. В процессе решения будем использовать гипотезу плоских сечений и обобщение принципа Сен-Венана для рассматриваемой задачи, что позволяет считать напряженное состояние однородным вдали от мест соединения частей составного стержня.
2. Определяющие и кинетические соотношения. Пусть соотношения (2.1) описывают скорость деформации ползучести, соответственно, первой (центральной) части и двух крайних частей
(2.1)
${{\dot {p}}_{1}} = {{B}_{1}}{{\left( {\frac{{{{\sigma }_{1}}}}{{1 - {{\omega }_{1}}}}} \right)}^{n}},\quad {{\dot {p}}_{2}} = {{B}_{2}}{{\left( {\frac{{{{\sigma }_{2}}}}{{1 - {{\omega }_{2}}}}} \right)}^{n}}$В соотношениях (2.1) на основе кинетической теории ползучести и длительной прочности Ю.Н. Работнова введен структурный параметр – параметр поврежденности $\omega $, который описывает накопление повреждений в процессе ползучести. Для каждой части составного стержня примем одинаковый вид кинетического уравнения для $\omega $, но поскольку в каждой части составного стержня действует свое механическое напряжение ${{\sigma }_{1}}$ и ${{\sigma }_{2}}$, то скорости накопления повреждений в них в процессе ползучести будут различными
(2.2)
$\frac{{d{{\omega }_{1}}}}{{dt}} = A{{\left( {\frac{{{{\sigma }_{1}}}}{{1 - {{\omega }_{1}}}}} \right)}^{m}},\quad {{\omega }_{1}} = {{\omega }_{1}}\left( t \right),\quad {{\omega }_{1}}\left( 0 \right) = 0,\quad \omega _{1}^{*} \equiv {{\omega }_{1}}(t = t_{1}^{*}) = 1$(2.3)
$\frac{{d{{\omega }_{2}}}}{{dt}} = A{{\left( {\frac{{{{\sigma }_{2}}}}{{1 - {{\omega }_{2}}}}} \right)}^{m}},\quad {{\omega }_{2}} = {{\omega }_{2}}\left( t \right),\quad {{\omega }_{2}}\left( 0 \right) = 0,\quad \omega _{2}^{*} \equiv {{\omega }_{2}}(t = t_{2}^{*}) = 1$Критерием разрушения каждой части стержня является условие достижения параметром поврежденности для соответствующей части значения, равного единице $\omega _{1}^{*} \equiv {{\omega }_{1}}(t = t_{1}^{*}) = 1$ и $\omega _{2}^{*} \equiv {{\omega }_{2}}(t = t_{2}^{*}) = 1$. Временем до разрушения всего составного стержня $t{\kern 1pt} *$ будем считать время минимальное из полученных времен до разрушения отдельных частей стержня: $t{\kern 1pt} * = \min \{ t_{1}^{*},t_{2}^{*}\} $.
Система, состоящая из уравнений (2.1), (2.2), (2.3), моделирует рассматриваемую полусвязанную задачу. Скорость накопления повреждений в процессе ползучести зависит от уровня напряжений. В свою очередь скорость деформации ползучести каждой части составного стержня зависит как от уровня механического напряжения в ней, так и от накопленной поврежденности, характеризуемой параметром $\omega $.
В силу осевой симметрии задачи, одинаковых законов установившейся ползучести двух крайних частей и симметрии процессов накопления поврежденности относительно геометрической оси стержня, внешние нагрузки распределяются между двумя крайними частями поровну, и напряжения ${{\sigma }_{2}}$ в них будут одинаковыми. Поскольку все части составного стержня жестко связаны между собой, то для дальнейшего решения примем гипотезу плоских сечений, т.е. деформация ползучести для сечений, ортогональных оси симметрии, для всех точек каждого сечения одинаковая, и она не зависит от поперечной координаты $y$.
Введем безразмерные переменные:
(2.4)
${{\bar {\sigma }}_{1}} = \frac{{{{\sigma }_{1}}}}{{{{\sigma }_{0}}}},\quad {{\bar {\sigma }}_{2}} = \frac{{{{\sigma }_{2}}}}{{{{\sigma }_{0}}}},\quad \bar {t} = {{B}_{1}}\sigma _{0}^{n}t,\quad \bar {\bar {t}} = {{B}_{2}}\sigma _{0}^{n}t$С учетом безразмерных напряжений в (2.4) определяющие соотношения (2.1) будут иметь следующий вид:
(2.5)
$\frac{{d{{p}_{1}}}}{{d\bar {t}}} = \frac{{\bar {\sigma }_{1}^{n}}}{{{{{\left( {1 - {{\omega }_{1}}} \right)}}^{n}}}},\quad \frac{{d{{p}_{2}}}}{{d\bar {\bar {t}}}} = \frac{{\bar {\sigma }_{2}^{n}}}{{{{{\left( {1 - {{\omega }_{2}}} \right)}}^{n}}}}$Выразим безразмерное время $\bar {\bar {t}}$:
Тогда определяющие соотношения (2.5) для центральной и двух крайних частей составного стержня будут иметь следующий вид:
(2.6)
$\frac{{d{{p}_{1}}}}{{d\bar {t}}} = \frac{{\bar {\sigma }_{1}^{n}}}{{{{{\left( {1 - {{\omega }_{1}}} \right)}}^{n}}}},\quad \frac{{d{{p}_{2}}}}{{d\bar {t}}} = \frac{{k\bar {\sigma }_{2}^{n}}}{{{{{\left( {1 - {{\omega }_{2}}} \right)}}^{n}}}}$Как отмечалось ранее, процессы накопления повреждений и разрушения определяются кинетическими уравнениями (2.2) и (2.3). Запишем кинетические уравнения накопления поврежденности с использованием единого для задачи безразмерного времени $\bar {t}$ и безразмерных напряжений:
(2.7)
$\frac{{d{{\omega }_{1}}}}{{d\bar {t}}} = {{С}_{1}}\frac{{\bar {\sigma }_{1}^{m}}}{{{{{\left( {1 - {{\omega }_{1}}} \right)}}^{m}}}},\quad \frac{{d{{\omega }_{2}}}}{{d\bar {t}}} = {{С}_{1}}\frac{{\bar {\sigma }_{2}^{m}}}{{{{{\left( {1 - {{\omega }_{2}}} \right)}}^{m}}}}$Начальные условия для уравнений (2.7): ${{\omega }_{1}}\left( 0 \right) = 0$, ${{\omega }_{2}}\left( 0 \right) = 0$.
В результате система уравнений для центральной части имеет вид:
Система уравнений для двух крайних частей:
Каждая из двух систем является не замкнутой. В каждой из них неизвестными величинами являются механическое напряжение, поврежденность и скорость деформации ползучести в рассматриваемой части стержня.
Принятое условие жесткого соединения частей стержня без проскальзывания и гипотеза плоских сечений дает возможность принять естественное условие равенства деформаций ползучести ${{p}_{1}} = {{p}_{2}}$ с учетом заданного начального условия $p\left( {t = 0} \right) = 0$.
Аналогично:
Из условия равенства деформаций ползучести ${{p}_{1}} = {{p}_{2}}$ следует:
Запишем уравнение равновесия
(2.8)
$P = 2\left[ {\int\limits_0^{{{h}_{1}}} {b{{\sigma }_{1}}dy + \int\limits_{{{h}_{1}}}^{{H \mathord{\left/ {\vphantom {H 2}} \right. \kern-0em} 2}} {b{{\sigma }_{2}}dy} } } \right] = 2b\left[ {{{h}_{1}}{{\sigma }_{1}} + \left( {\frac{H}{2} - {{h}_{1}}} \right){{\sigma }_{2}}} \right]$Введем величину $\Sigma \equiv \frac{P}{{bH}}$, тогда
С учетом выражений для безразмерных напряжений ${{\bar {\sigma }}_{1}}$ и ${{\bar {\sigma }}_{2}}$ уравнение равновесия (2.8) будет иметь вид:
(2.9)
${{\Sigma }_{0}} = \left[ {\alpha {{{\bar {\sigma }}}_{1}} + \left( {1 - \alpha } \right){{{\bar {\sigma }}}_{2}}} \right]$Выразим из (2.9) ${{\bar {\sigma }}_{2}}$:
(2.10)
${{\bar {\sigma }}_{2}} = \frac{{\left[ {{{\Sigma }_{0}} - \alpha {{{\bar {\sigma }}}_{1}}} \right]}}{{\left( {1 - \alpha } \right)}}$Таким образом, замкнутая система уравнений будет иметь следующий вид:
(2.11)
$\begin{gathered} \frac{{d{{\omega }_{1}}}}{{d\bar {t}}} = {{С}_{1}}\frac{{\bar {\sigma }_{1}^{m}}}{{{{{\left( {1 - {{\omega }_{1}}} \right)}}^{m}}}} \\ \frac{{d{{\omega }_{2}}}}{{d\bar {t}}} = {{С}_{1}}\frac{{{{{\left( {\left[ {{{\Sigma }_{0}} - \alpha {{{\bar {\sigma }}}_{1}}} \right]} \right)}}^{m}}}}{{{{{\left( {\left( {1 - \alpha } \right)\left( {1 - {{\omega }_{2}}} \right)} \right)}}^{m}}}} \\ \int\limits_0^{\bar {t}} {\frac{{\bar {\sigma }_{1}^{n}}}{{{{{\left( {1 - {{\omega }_{1}}} \right)}}^{n}}}}d\bar {t}} = k\int\limits_0^{\bar {t}} {{{{\left( {\frac{{\left[ {{{\Sigma }_{0}} - \alpha {{{\bar {\sigma }}}_{1}}} \right]}}{{\left( {1 - \alpha } \right)\left( {1 - {{\omega }_{2}}} \right)}}} \right)}}^{n}}} d\bar {t} \\ \end{gathered} $Начальные условия для кинетических соотношений в системе (2.11) имеют следующий вид: ${{\omega }_{1}}\left( 0 \right) = 0$, ${{\omega }_{2}}\left( 0 \right) = 0$.
В указанной системе из трех уравнений тремя неизвестными являются: поврежденность ${{\omega }_{1}} = {{\omega }_{1}}\left( {\bar {t}} \right)$ – в центральной части стержня, поврежденность ${{\omega }_{2}} = {{\omega }_{2}}\left( {\bar {t}} \right)$ – в двух крайних частях составного стержня, напряжение ${{\bar {\sigma }}_{1}} = {{\bar {\sigma }}_{1}}\left( {\bar {t}} \right)$. Напряжение ${{\bar {\sigma }}_{2}} = {{\bar {\sigma }}_{2}}\left( {\bar {t}} \right)$ определяется в соответствии с соотношением (2.10). Указанные характеристики напряженного состояния и поврежденности являются зависимыми от времени.
Необходимо отметить, что материальные параметры $A,{{B}_{1}},{{B}_{2}},m,n$, входящие в соотношения (2.1), (2.2), (2.3) и в систему уравнений (2.11), в общем случае можно определить на основе обработки экспериментальных данных по ползучести и длительной прочности стандартных образцов из материалов, из которых изготовлены рассматриваемые части составного стержня.
Критерием разрушения каждой части стержня является условие достижения параметром поврежденности для соответствующей части стержня значения, равного единице $\omega _{1}^{*} \equiv {{\omega }_{1}}(\bar {t} = \bar {t}_{1}^{*}) = 1$ и $\omega _{2}^{*} \equiv {{\omega }_{2}}(\bar {t} = \bar {t}_{2}^{*}) = 1$. Безразмерным временем до разрушения всего составного стержня $\bar {t}{\kern 1pt} *$ будем считать время минимальное из полученных безразмерных времен до разрушения отдельных частей стержня: $\bar {t}{\kern 1pt} * = \min \{ \bar {t}_{1}^{*},\bar {t}_{2}^{*}\} $.
3. Пример численного расчета. Анализ полученных результатов. В качестве примера численного расчета и дальнейшего анализа примем модельные значения констант в соотношениях системы (2.11): ${{С}_{1}} = 2,$ $k = 0.5,$ $\alpha = 0.5,$ ${{\Sigma }_{0}} = 0.5$. Значения $m = n$ примем равными друг другу, проанализируем кинетику накопления повреждений и распределения напряжений во времени при различных значениях m = n.
В первом варианте расчета примем $m = n = 3$. Тогда численным способом получим следующие распределения искомых характеристик. В этом случае зависимости ${{\omega }_{1}} = {{\omega }_{1}}\left( {\bar {t}} \right)$, ${{\omega }_{2}} = {{\omega }_{2}}\left( {\bar {t}} \right)$, ${{\bar {\sigma }}_{1}} = {{\bar {\sigma }}_{1}}\left( {\bar {t}} \right)$, ${{\bar {\sigma }}_{2}} = {{\bar {\sigma }}_{2}}\left( {\bar {t}} \right)$ от времени $\bar {t}$ представлены в виде соответствующих кривых 1 на рис. 2, 3, 4, 5. Необходимо отметить, что в данном случае параметр поврежденности ${{\omega }_{2}}$ достигает значения, равного единице, быстрее, чем параметр ${{\omega }_{1}}$. В связи с этим, согласно, принятому критерию разрушение части 1 и, соответственно, всего составного стержня наступает в момент времени $\bar {t}_{1}^{*} = 0.926$. В данный момент времени численный счет ${{\omega }_{1}} = {{\omega }_{1}}\left( {\bar {t}} \right)$ прекращается (при достижении ${{\omega }_{1}}(\bar {t}_{1}^{*}) = 0.5$), поскольку не имеет дальнейшего смысла.
Рис. 2.
Зависимости поврежденности ${{\omega }_{1}}$ в центральной части составного стержня от безразмерного времени $\bar {t}$ при различных параметрах $m = n$.
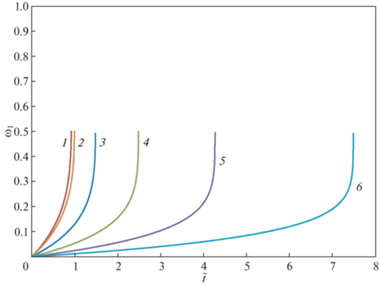
Рис. 3.
Зависимости поврежденности ${{\omega }_{2}}$ в крайних частях составного стержня от безразмерного времени $\bar {t}$ при различных параметрах $m = n$.
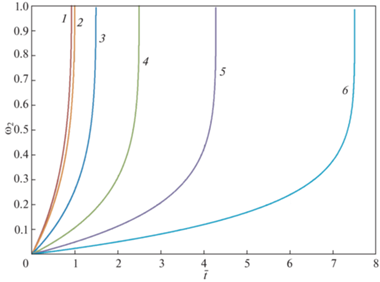
Рис. 4.
Зависимости напряжения ${{\sigma }_{1}}$ в центральной части составного стержня от безразмерного времени $\bar {t}$ при различных параметрах $m = n$.
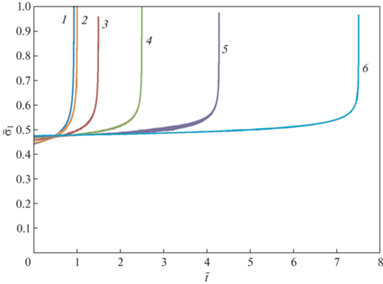
Рис. 5.
Зависимости напряжения ${{\sigma }_{2}}$ в крайних частях составного стержня от безразмерного времени $\bar {t}$ при различных параметрах $m = n$.
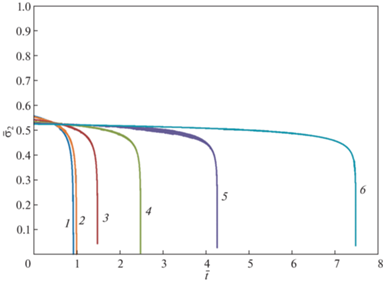
Аналогичный расчет (при ${{С}_{1}} = 2,$ $k = 0.5,$ $\alpha = 0.5,$ ${{\Sigma }_{0}} = 0.5$) был произведен для значений констант $m = n = 4,\,\,5,\,\,6,\,\,7$. На указанных рис. 2, 3, 4, 5 соответствующие кривые имеют номера 3, 4, 5, 6.
Здесь необходимо отметить следующие особенности. С течением времени с ростом напряжения ${{\bar {\sigma }}_{1}} = {{\bar {\sigma }}_{1}}\left( {\bar {t}} \right)$ в центральной части составного стержня напряжение ${{\bar {\sigma }}_{2}} = {{\bar {\sigma }}_{2}}\left( {\bar {t}} \right)$ в двух крайних частях уменьшается. При этом сумма ${{\bar {\sigma }}_{1}}$ и ${{\bar {\sigma }}_{2}}$ в любой момент времени одинакова и равна единице.
Показанные здесь результаты были получены при отношении констант в соотношениях ползучести (2.1) $k = {{B}_{2}}{\text{/}}{{B}_{1}} = 0.5$.
Примечания. На рис. 2, 3, 4, 5 введены следующие обозначения:
1 – расчетные кривые при $m = n = 3$; 2 – расчетные кривые при $m = n = 3.170$; 3 – расчетные кривые при $m = n = 4$; 4 – расчетные кривые при $m = n = 5$; 5 – расчетные кривые при $m = n = 6$; 6 – расчетные кривые при $m = n = 7$.
Представляет интерес проанализировать процессы накопления повреждений и распределения напряжений во времени при значениях k = 1 и k = 2.
Если составной стержень сделан из одинаковых материалов с равными друг другу материальными параметрами, в том числе ${{B}_{1}} = {{B}_{2}}$ в соотношениях (2.1), то $k\, = \,{{B}_{2}}{\text{/}}{{B}_{1}}$ = 1. В этом случае рассматриваемый составной стержень под действием растягивающей нагрузки при ползучести деформируется как единое целое. При этом вся площадь поперечного сечения стержня воспринимает внешнюю нагрузку “без чувствительности” к составному характеру этой конструкции. Здесь, как и ранее, дополнительно принято условие жесткого, без проскальзывания соединения между собой всех частей составного стержня.
Для определения времени до разрушения такой конструкции при k = 1 достаточно проинтегрировать первое уравнение системы (2.11) при значении ${{\bar {\sigma }}_{1}} = {{\Sigma }_{0}}$. В рассматриваемом случае ${{\bar {\sigma }}_{1}} = {{\Sigma }_{0}} = 0.5$
В результате зависимость ${{\omega }_{1}}\left( {\bar {t}} \right)$ имеет следующий вид:
С учетом условия ${{\omega }_{1}}\left( {\bar {t}{\kern 1pt} *} \right) = 1$ определяем $\bar {t}{\kern 1pt} *$ (при m = 3, ${{C}_{1}} = 2$):
Таким образом, при принятых параметрах ${{С}_{1}} = 2,$ $k = 1,$ $\alpha = 0.5,$ ${{\Sigma }_{0}} = 0.5,$ $n = m = 3$ время до разрушения составного стержня, который с учетом $k = {{B}_{2}}{\text{/}}{{B}_{1}} = 1$ ведет себя под нагрузкой как монолитная конструкция, равно единице $\bar {t}{\kern 1pt} * = 1$.
На основе проведенного анализа можно определять материалы частей составного стержня, в которых требуемые материальные параметры моделей ползучести и длительного разрушения приводят к увеличению времени до разрушения составного стержня по сравнению с монолитным. Такого рода исследования могут способствовать определению необходимых материалов составных конструкций, применение которых приведет к увеличению их длительной работоспособности.
Так, для расчетных данных, используемых при построении соответствующих кривых зависимостей ${{\omega }_{1}} = {{\omega }_{1}}\left( {\bar {t}} \right)$, ${{\omega }_{2}} = {{\omega }_{2}}\left( {\bar {t}} \right)$, ${{\bar {\sigma }}_{1}} = {{\bar {\sigma }}_{1}}\left( {\bar {t}} \right)$, ${{\bar {\sigma }}_{2}} = {{\bar {\sigma }}_{2}}\left( {\bar {t}} \right)$ от времени $\bar {t}$ на рисунках 2, 3, 4, 5, было определено значение $m = n = 3.170$, которое соответствует времени до разрушения $\bar {t}{\kern 1pt} * = 1$. Соответствующие кривые обозначены номером 2 на рис. 2, 3, 4 и 5.
Значения параметров $m = n\,\,\, > \,\,3.170$ приведет к увеличению времени до разрушения составных стержней по сравнению с монолитными.
Расчет и анализ процессов накопления повреждений и распределения напряжений во времени при значении $k = {{{{B}_{2}}} \mathord{\left/ {\vphantom {{{{B}_{2}}} {{{B}_{1}}}}} \right. \kern-0em} {{{B}_{1}}}} = 2$ показал интересный результат. Кривые накопления поврежденности и распределения напряжений при k = 2 меняются местами по сравнению с соответствующими кривыми при k = 0.5. Кривая зависимости ${{\omega }_{1}} = {{\omega }_{1}}\left( {\bar {t}} \right)$ от времени при k = 0.5 становится кривой ${{\omega }_{2}} = {{\omega }_{2}}\left( {\bar {t}} \right)$ при k = 2, в свою очередь кривая ${{\omega }_{2}} = {{\omega }_{2}}\left( {\bar {t}} \right)$ при k = 0.5 становится зависимостью ${{\omega }_{1}} = {{\omega }_{1}}\left( {\bar {t}} \right)$ при k = 2. Аналогичная ситуация наблюдается и для распределения напряжений ${{\bar {\sigma }}_{1}} = {{\bar {\sigma }}_{1}}\left( {\bar {t}} \right)$ и ${{\bar {\sigma }}_{2}} = {{\bar {\sigma }}_{2}}\left( {\bar {t}} \right)$. В результате при k = 2 поврежденность ${{\omega }_{1}} = {{\omega }_{1}}\left( {\bar {t}} \right)$ достигает предельного значения ${{\omega }_{1}} = 1$ быстрее, чем ${{\omega }_{2}} = {{\omega }_{2}}\left( {\bar {t}} \right)$. В случае при k = 0.5 наблюдается противоположная ситуация.
Заключение. Проведено исследование напряженно-деформированного состояния и процессов разрушения стержня (типовой элемент конструкции), находящегося в условии ползучести при растяжении. Изучение и моделирование таких процессов является предварительным опорным исследованием перспективной задачи о защитном эффекте внешних частей составного стержня при его контакте с рабочей активной средой в условиях длительного действия нагрузок и повышенных температур.
На основе кинетической теории ползучести и длительной прочности Ю.Н. Работнова получены зависимости накопления поврежденности от времени в центральной и двух крайних частях составного стержня.
Под действием растягивающей нагрузки при принятом условии жесткого, без проскальзывания соединения частей составного стержня в местах соединения частей происходит нарушение непрерывности (разрыв) механических напряжений при переходе от одной части составного стержня к другой.
В зависимости от констант в определяющих соотношениях ползучести и кинетических уравнениях накопления поврежденности напряжения в частях стержня с течением времени меняются. При этом сумма безразмерных напряжений в центральной и двух крайних частях в любой момент времени одинакова и равна единице.
В момент времени, предшествующий разрушению, наблюдается резкое изменение напряжений в частях стержня. Данный эффект объясняется резким нарастанием поврежденности в частях стержня и, как следствие, резким уменьшением площади эффективного сечения за счет увеличения микропор и микротрещин в процессе ползучести.
В результате проведенного исследования проанализировано влияние констант в моделях ползучести и длительного разрушения на время до разрушения составного стержня. Разработаны основы подхода для определения параметров указанных моделей, приводящих к увеличению времени до разрушения составного стержня по сравнению с монолитным. Такого рода исследования могут способствовать определению необходимых материалов составных конструкций, применение которых приведет к увеличению их длительной работоспособности.
Данная научная работа имеет как фундаментальный характер исследования определяющих и кинетических соотношений в механике деформируемого твердого тела, так и прикладное значение. Проведенное исследование может быть применено в энергетическом машиностроении, авиационно-космической отрасли, судостроении и нефтехимическом машиностроении.
Работа выполнена при частичной поддержке Российского фонда фундаментальных исследований, проект № 20-08-00387.
Список литературы
Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.
Локощенко А.М. Ползучесть и длительная прочность металлов. М.: Физматлит, 2016. 504 с.
Lokoshchenko A., Fomin L. Kinetic theory of creep and long-term strength of metals // Kinetic Theory / Ed. by G.Z. Kyzas, A.C. Mitropoulos. IntechOpen, 2017. https://doi.org/10.5772/intechopen.70768
Манукян М.Н. Кручение составных валов переменного сечения в условиях установившейся ползучести // Изв. aк. наук Армянской ССР. Физ.-мат. науки. 1961. V. XIV. № 1. С. 115–121.
Якубовский Ю.Е., Колосов В.И., Донкова И.А., Круглов С.О. Моделирование вязкоупругих свойств стареющего материала // Вестн. Тюменск. гос. ун-та. Физ.-мат. моделир. Нефть, газ, энергетика. 2018. Т. 4. № 4. С. 181–190. https://doi.org/10.21684/2411-7978-2018-4-4-181-190
Янковский А.П. Неустановившаяся ползучесть слоистых стержней нерегулярной структуры из нелинейно-наследственных материалов // Механика машин, механизмов материалов. 2016. № 3 (36). С. 86–97.
Хохлов А.В. Ползучесть и длительная прочность толстостенной трубы из нескольких слоев нелинейно-вязкоупругих материалов, нагруженной внутренним и внешним давлением // Мех. композ. матер. 2021. Т. 57. № 6. С. 1037–1064. https://doi.org/10.22364/mkm.57.6.02
Якубовская С.В., Красовская Н.И., Сильницкая Н.Ю., Иванова Е.Ю., Красовская О.В. Моделирование напряженного состояния многослойных конструкций при деформировании во времени // Науч.-тех. вестн. Поволжья. 2021. № 5. С. 115–118.
Кравчук А.С., Кравчук А.И. Моделирование ползучести по наследственной теории в простейшей модели деформируемого покрытия постоянной толщины // Аpriori. Cер.: естеств. тех. науки. 2014. № 2. С. 1–17.
Yankovskii A. P. Study on the unsteady creep of composite beams with an irregular laminar fibrous structure made from nonlinear hereditary materials // Mech. Compos Mater. 2017. V. 53. № 4. P. 457–470. https://doi.org/10.1007/s11029-017-9675-7
Саушкин М.Н., Радченко В.П. Приближенный метод оценки релаксации остаточных напряжений в поверхностно упрочненной лопатке в поле массовых сил в условиях ползучести // Пробл. машиностр. надежн. машин. 2013. № 3. С. 58–67.
Радченко В.П., Деревянка Е.Е. Влияние температурно-силового нагружения на релаксацию остаточных напряжений в поверхностно упрочненных элементах стержневой конструкции в условиях ползучести // Вестн. Самарск. гос. техн. ун-та. Сер. Физ.-мат. науки. 2019. Т. 23. № 3. С. 497–524. https://doi.org/10.14498/vsgtu1688
Деревянка Е.Е., Радченко В.П., Цветков В.В. Релаксация остаточных напряжений в поверхностно упрочненном цилиндре в условиях ползучести при жестких ограничениях на линейные и угловые деформации // Изв. РАН. МТТ. 2021. № 3. С. 118–127. https://doi.org/10.31857/S057232992103003X
Волков И.А., Игумнов Л.А., Шишулин Д.Н., Боев Е.В. Моделирование процессов нестационарной ползучести в условиях многоосного нагружения с учетом накопления повреждений в конструкционном материале // Изв. РАН. МТТ. 2022. № 2. С. 25–34. http://dx.doi.org/10.31857/S057232992103003X
Зараковская К.И., Захаров В.Ф. Напряженно-деформированное состояние составных железобетонных стержней с высокопрочной арматурой, подверженных длительному сжатию // Вестн. МГСУ. 2019. Т. 14. Вып. 9. С. 1121–1131. https://doi.org/10.22227/1997-0935.2019.9.1121-1131
Замалиев Ф.С. Учет начальных напряжений и деформаций при оценке несущей способности сталежелезобетонных конструкций на эксплуатационные нагрузки // Изв. КГАСУ. 2017. № 1 (39). С. 91–101.
Jonathon Tanks, Kimiyoshi Naito and Hisai Ueda. Characterization of the static, creep, and fatigue tensile behavior of basalt fiber/polypropylene composite rods for passive concrete reinforcement // Polymers. 2021. V. 13(18), 3136. https://doi.org/10.3390/polym13183136
Wanninger F., Frangi A., Fragiacomo M. Long-term behavior of posttensioned timber connections // J. Struct. Eng. 2014. V. 141. № 6. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001121
He M.J., Zheng X.Z., Lam F., Li Z. Potential loss in prestressing tendon forces under long-term service conditions: cross-laminated timber shear wall applications // J. Struct. Eng. 2022. V. 148. № 3. https://doi.org/10.1061/(ASCE)ST.1943-541X.0003272
Zheng X.Z., Li Z., He M.J., Lam F. Experimental investigation on the rheological behavior of timber in longitudinal and transverse compression // Construct. Building Mater. 2021. V. 304. P. 124633. https://doi.org/10.1016/j.conbuildmat.2021.124633
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела