1. На главную
  2. Электронные версии
  3. Микроэлектроника
  4. T. 49, № 2, 2020

Микроэлектроника, 2020, T. 49, № 2, стр. 116-132

Моделирование процессов электронно-лучевой литографии

А. Е. Рогожин a, *, Ф. А. Сидоров a,  b, **

a Физико-технологический институт имени К.А. Валиева Российской АН
117218 Москва, Нахимовский проспект, 36, корп. 1, Россия

b Московский физико-технический институт (НИУ)
141701 Долгопрудный, Институтский переулок, 9, Россия

* E-mail: rogozhin@ftian.ru
** E-mail: fedor.sidorov@phystech.edu

Поступила в редакцию 02.07.2019
После доработки 02.07.2019
Принята к публикации 02.07.2019

Полный текст (PDF)

Аннотация

Описаны методы моделирования этапов экспонирования и проявления в электронно-лучевой литографии. Представлены основные способы определения параметров процессов упругого и неупругого рассеяния электронов в структуре, а также алгоритмы моделирования распространения электронов в структуре – алгоритм на основе кинетической теории транспорта и алгоритм на основе метода Монте-Карло. Для процесса растворения резиста при проявлении приведены модели, позволяющие рассчитать растворимость проэкспонированных участков в зависимости от выделившейся в них энергии или количества неупругих взаимодействий электронного пучка с атомами резиста, вызвавших разрывы его молекул.

ВВЕДЕНИЕ

Профиль структур, получаемых с помощью электронно-лучевой литографии, во многом определяется процессами взаимодействия электронного пучка с резистом и сложным образом зависит от параметров экспонирования. За счет рассеяния первичных и вторичных электронов происходит нежелательное экспонирование областей, в которые электронный луч непосредственно не направлялся, что приводит к искажению изображения, получаемого в резисте (эффект близости) [1–3]. Задача определения оптимальных параметров экспонирования может быть решена путем проведения многочисленных экспериментов, что значительно усложняет процесс получения необходимого микрорельефа.

Процедуру подбора параметров экспонирования можно упростить за счет проведения моделирования взаимодействия электронного пучка со структурой. Для этого используются метод, основанный на кинетической теории транспорта и метод Монте-Карло. Метод моделирования на основе кинетической теории транспорта заключается в решении кинетического уравнения Больцмана для задачи распространения электронов в структуре. Такой подход эффективен в случае проведения моделирования для планарных структур с небольшим количеством слоев, однако, для структур с более сложной геометрией требуются существенные упрощения в вычислительном алгоритме. При использовании метода Монте-Карло траектории электронов в структуре моделируются отдельно друг от друга, и для определения их параметров используются случайные числа. Этот метод не имеет ограничений на геометрические параметры структуры, но при этом требует больших вычислительных мощностей.

В первой части этой статьи будет приведено описание моделей взаимодействия электронов с веществом. Во второй и третьей частях будет приведено описание алгоритмов моделирования на основе кинетической теории транспорта и Монте-Карло моделирования, соответственно. Четвертая часть будет посвящена описанию моделей, позволяющих на основе данных моделирования взаимодействия электронного пучка со структурой определить профиль, получаемый в резисте после экспонирования и проявления.

1. МОДЕЛИ ВЗАИМОДЕЙСТВИЯ ЭЛЕКТРОННОГО ПУЧКА С ВЕЩЕСТВОМ

Сталкиваясь с атомами структуры, налетающие электроны постепенно теряют свою энергию и многократно меняют направление движения. Траектории рассеиваемых электронов можно представить в виде ломаных линий, общий характер которых определяется упругими и неупругими взаимодействиями этих электронов с атомами вещества.

1.1. Упругое рассеяние

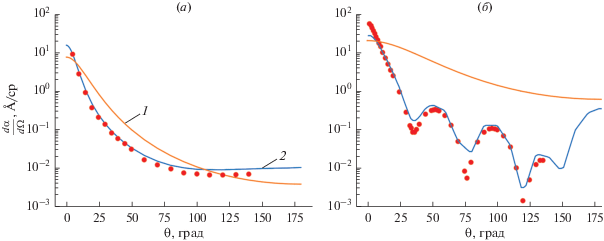
Упругое рассеяние происходит в основном в результате столкновения высокоэнергетических электронов с ядрами атомов, частично экранированными связанными электронами. При этом изменяется направление движения электрона, а его энергия остается практически неизменной. Азимутальный угол рассеяния $\varphi $ распределен равномерно в промежутке (0°, 360°), полярный угол рассеяния $\theta $ распределен в промежутке (0° до 180°) со средним значением 5°–10°.

Основной характеристикой упругого рассеяния электрона на атомах вещества является дифференциальное сечение рассеяния $\frac{{d\sigma }}{{d\Omega }},$ определяемое как отношение числа частиц, рассеянных мишенью в элемент телесного угла $d\Omega = d\varphi \sin \theta d\theta $ за единицу времени к плотности потока налетающих частиц. Интеграл от дифференциального сечения по полному телесному углу определяется как полное сечение упругого рассеяния:

(1.1)
${{\sigma }_{{{\text{el}}}}} = 2\pi \int\limits_0^\pi {\frac{{d\sigma }}{{d\Omega }}\sin \theta d\theta .} $

Полное сечение упругого рассеяния позволяет рассчитать среднее расстояние межу последовательными актами упругого рассеяния ${{\Lambda }_{{{\text{el}}}}}$ (длину свободного пробега):

(1.2)
${{\Lambda }_{{{\text{el}}}}} = \frac{1}{{n{{\sigma }_{{{\text{el}}}}}}},$
где $n$ – концентрация атомов вещества.

1.1.1. Формула Резерфорда

Для определения дифференциального сечения упругого рассеяния электронов на атомах вещества можно воспользоваться формулой Резерфорда [4]:

(1.3)
$\frac{{d{{\sigma }_{R}}}}{{d\Omega }} = \frac{{{{Z}^{2}}{{e}^{4}}}}{{4{{E}^{2}}{{{\left( {1 - \cos \theta + 2\beta } \right)}}^{2}}}},$
где $Z$ – зарядовое число атомов вещества, $e$ – заряд электрона, $E$ – энергия налетающего электрона, $\beta $ – параметр экранирования поля ядра атома-мишени атомными электронами [4–6]. Формула Резерфорда хорошо описывает сечения упругого рассеяния электронов на легких атомах, однако, ее точность снижается с ростом зарядового числа атомов, особенно, в области низких энергий электронов (<1 кэВ) (рис. 1) [7–10].

Рис. 1.

Сравнение дифференциальных сечений упругого рассеяния электронов на атомах аргона (а) и ртути (б), полученных на основе формулы Резерфорда-1 и моттовских сечений -2 с экспериментальными данными (точки) (а) [22], (б) [23].

1.1.2. Моттовские сечения упругого рассеяния

Более точные значения сечений упругого рассеяния (моттовские сечения [11]) могут быть получены за счет решения квантово-механического уравнения Дирака для движения рассеивающегося электрона в центральном статическом поле ядра атома-мишени. При этом дифференциальное сечение упругого рассеяния выражается через амплитуды рассеяния $f\left( x \right)$ и $g\left( x \right),$ получаемые при разложении решения уравнения Диракапо парциальным волнам [10]:

(1.4)
$\frac{{d{{\sigma }_{{{\text{Mott}}}}}}}{{d\Omega }} = {{\left| {f\left( \theta \right)} \right|}^{2}} + {{\left| {g\left( \theta \right)} \right|}^{2}},$
(1.5)
$f\left( \theta \right) = \frac{1}{{2ik}}\sum\limits_{l = 0}^\infty {\left[ {\left( {l + 1} \right)\left( {{{e}^{{2i\delta _{l}^{ + }}}} - 1} \right) + l\left( {{{e}^{{2i\delta _{l}^{ - }}}} - 1} \right)} \right]} {{P}_{l}}\left( {\cos \theta } \right),$
(1.6)
$g\left( \theta \right) = \frac{1}{{2ik}}\sum\limits_{l = 0}^\infty {\left( {{{e}^{{2i\delta _{l}^{ - }}}} - {{e}^{{2i\delta _{l}^{ + }}}}} \right)P_{l}^{1}\left( {\cos \theta } \right)} ,$
где $k$ – волновое число, соответствующее налетающей частице, ${{P}_{l}}\left( {\cos \theta } \right)$ – полиномы Лежандра, $P_{l}^{1}\left( {\cos \theta } \right)$ – присоединенные функции Лежандра, $\delta _{l}^{ + }$, $\delta _{l}^{ - }$ – фазовые сдвиги парциальных волн, соответствующие значениям проекции спина “вверх” и “вниз” соответственно. Алгоритм вычисления моттовских сечений упругого рассеяния достаточно сложен [12], и при моделировании часто используются дифференциальные сечения, полученные другими авторами для большого количества элементов в широком диапазоне энергий и углов рассеяния налетающего электрона [13–16]. Использование моттовских сечений для моделирования упругого рассеяния требует хранения в памяти компьютера большого двумерного массива, что долгое время накладывало серьезные ограничения на применения этого метода [17]. В настоящее время это не является серьезной проблемой, и моттовские сечения упругого рассеяния применяются в подавляющем большинстве работ [18–21].

1.2. Неупругие процессы

При неупругом рассеянии, представляющим собой взаимодействие между налетающим электроном и электронной оболочкой атома-мишени, энергия налетающего электрона частично передается атому и его электронам. Эти потери энергии обусловлены электронными, плазменными и фононными возбуждениями, ионизацией атомов и другими процессами. Акты потери энергии электроном носят дискретный характер, но во многих случаях бывает удобно использовать модель непрерывных потерь энергии величину $\frac{{dE}}{{ds}}$ – потери энергии на единицу длины пути электрона в веществе.

1.2.1. Формула Бете

При энергиях налетающего электрона выше 1 кэВ доминирующим видом неупругого рассеяния является однократная ионизация атомов вещества [24]. Удельные ионизационные потери энергии могут быть описаны формулой Бете [25]:

(1.7)
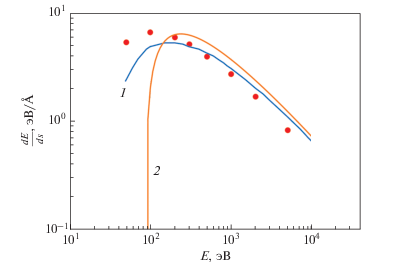
$ - {{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{Bethe}}}}} = 2\pi {{e}^{4}}{{N}_{{\text{A}}}}\frac{\rho }{Z}\frac{1}{E}\ln \left( {\frac{{1.66E}}{J}} \right),$
где ${{N}_{{\text{A}}}}$ – число Авогадро, $\rho $ – плотность вещества, $Z$ – его порядковый номер, соответственно, $e$ и $E$ – заряд и энергия движущегося в веществе электрона, соответственно. Средний потенциал ионизации $J$ определяется экспериментально [26] или вычисляется на основе порядкового номером атомов вещества одним из нескольких существующих способов [4, 27], например:

(1.8)
$\frac{J}{Z} = 9.76 + 58.8{{Z}^{{ - 1.19}}}.$

Формула Бете с высокой точностью описывает потери энергии в области высоких энергий налетающего электрона ($E \gg J$) [4, 28]. Однако, при приближении энергии налетающего электрона к среднему потенциалу ионизации точность формулы снижается, а в области потери энергии, рассчитываемые по ней, становятся отрицательными. Существуют модификации формулы Бете, позволяющие использовать ее в области низких энергий [29], в которых потери энергии описываются степенной функцией при $E \to 0$:

(1.9)
$ - \frac{{dE}}{{ds}}\,\,\infty \,\,\frac{1}{{\sqrt E }}.$

В таком виде формула Бете может быть использована, например, для оценки количества обратно отраженных и вторичных электронов, что дает правдоподобные результаты [30]. Однако, неограниченный рост потерь энергии при $E \to 0$ противоречит эмпирическим данным, согласно которым при уменьшении энергии электрона, его потери энергии достигают максимума при энергии в несколько сотен электрон вольт, затем стремятся к нулю [24].

1.2.2. Диэлектрическая функция

Потери энергии при прохождении электрона через вещество могут быть описаны в терминах диэлектрической функции $\varepsilon \left( {q,\omega } \right)$ [31]:

(1.10)
$\frac{{{{d}^{2}}\sigma }}{{d\left( {\Delta E} \right)dq}} = \frac{{m{{e}^{2}}}}{{\pi N{{\hbar }^{2}}E}}\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {q,\omega } \right)}}} \right]\frac{1}{q},$
где $\frac{{{{d}^{2}}\sigma }}{{d\left( {\Delta E} \right)dq}}$ – дифференциальное сечение процесса передачи налетающим электроном энергии $\Delta E = \hbar \omega $ и импульса $dq$ среде, m, e – масса и заряд электрона, $E$ – его энергия. Теоретический расчет диэлектрической функции $\varepsilon \left( {q,\omega } \right)$ возможен только для ряда металлов [32–34], однако, зависимость $\varepsilon \left( {q,\omega } \right)$ может быть определена методом спектроскопии характеристических потерь электронов [35–38]. При этом потери энергии могут быть определены из зависимости $\varepsilon \left( {q,\omega } \right)$ за счет ее продолжения в область $q > 0$ и последующего интегрирования [39, 40]:

(1.11)
$ - \frac{{dE}}{{ds}} = \frac{{m{{e}^{2}}}}{{\pi {{\hbar }^{2}}E}}\int\limits_0^{{E \mathord{\left/ {\vphantom {E 2}} \right. \kern-0em} 2}} {\operatorname{Im} \left[ {\frac{{ - 1}}{{\varepsilon \left( {0,\omega } \right)}}} \right]} {{G}_{e}}\left( {\frac{{\hbar \omega }}{E}} \right)\hbar \omega d\left( {\hbar \omega } \right),$
(1.12)
${{G}_{e}}\left( x \right) = \ln \left( {\frac{{1.166}}{x}} \right) - \frac{3}{4}x - \frac{x}{4}\ln \left( {\frac{4}{x}} \right) + \frac{1}{2}{{x}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} - \frac{{{{x}^{2}}}}{{16}}\ln \left( {\frac{4}{x}} \right) - \frac{{31}}{{48}}{{x}^{2}}.$

Этот метод позволяет точно определить потери энергии во всем диапазоне энергий электрона, в том числе, при низких энергиях. К тому же, его использование для веществ, в состав которых входит несколько атомов, позволяет избежать усреднения потенциалов ионизации различных атомов, что обеспечивает большую точность, чем подход на основе формулы Бете. В настоящее время данные спектроскопии характеристических потерь электронов доступны для большого количества материалов [36, 41, 42], что привело к широкому распространению метода определения потерь энергии из диэлектрической функции.

1.2.3. Гибридная модель потерь энергии

Вышеописанные методы позволяют определить полные потери энергии, исключая при этом возможность выделить вклады отдельных неупругих процессов. Главным недостатком такого подхода является невозможность описания процессов генерации вторичных электронов, которые в значительной степени объясняют уширение электронного пучка в резисте [30, 44, 45]. Для моделирования генерации вторичных электронов может быть использована гибридная модель потерь энергии [46]. В ее основе лежит предположение, что вторичные электроны возникают в результате однократной ионизации при рассеянии электронов пучка на электронах внешних оболочек атомов, энергии связи которых малы. Дифференциальное сечение ионизации рассчитывается по формуле Меллера [47, 48] для неупругого рассеяния на свободных электронах:

(1.13)
$\frac{{d\sigma }}{{d\varepsilon }} = \frac{{2\pi {{e}^{4}}}}{{m{{c}^{2}}{{\beta }^{2}}E}}\left[ {\frac{1}{{{{\varepsilon }^{2}}}} + \frac{1}{{{{{\left( {1 - \varepsilon } \right)}}^{2}}}} + {{{\left( {\frac{\tau }{{\tau + 1}}} \right)}}^{2}} - \frac{{2\tau + 1}}{{{{{\left( {\tau + 1} \right)}}^{2}}}}\frac{1}{{\varepsilon \left( {1 - \varepsilon } \right)}}} \right],$
где $\varepsilon $ – отношение потерянной энергии налетающего электрона к его энергии $E$ до столкновения,

$\tau = {E \mathord{\left/ {\vphantom {E {m{{c}^{2}}}}} \right. \kern-0em} {m{{c}^{2}}}},\,\,\,\,\beta = {v \mathord{\left/ {\vphantom {v c}} \right. \kern-0em} c} = \sqrt {1 - {{{\left( {1 + \tau } \right)}}^{{ - 2}}}} .$

Такой подход позволяет определить потери энергии на единицу длины пути за счет генерации вторичных электронов при однократной ионизации:

(1.14)
${{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{single}}}}} = \sum\limits_i {{{n}_{i}}{{Z}_{i}}\int\limits_{{{\varepsilon }_{c}}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} {E\varepsilon \frac{{d\sigma }}{{d\varepsilon }}d\varepsilon ,} } $
где ${{n}_{i}}$,${{Z}_{i}}$ – концентрация и порядковый номер отдельного элемента в веществе, ${{\varepsilon }_{c}}$ – отношение минимальной переданной электрону атома энергии, при которой возможна генерация вторичных электронов $\Delta {{E}_{c}}$, к энергии налетающего электрона E. В работе [46] описывается процесс его определения, который привел к значению 0.001.

Потери энергии, обусловленные остальными неупругими процессами, рассчитываются как разность полных потерь энергии (определяемых, например, с помощью формулы Бете) и потерь на ионизацию:

(1.15)
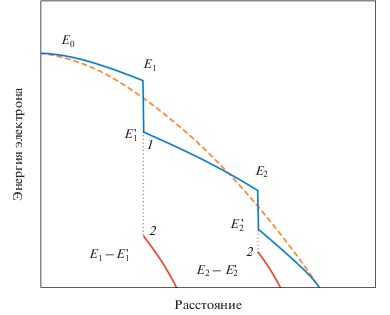
${{\left( {\frac{{dE}}{{ds}}} \right)}_{{{{\varepsilon }_{c}}}}} = {{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{Bethe}}}}} - {\text{\;}}{{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{single}}}}}.$

Это выражение используется для определения потерь энергии между последовательными актами ионизации и генерации вторичных электронов (рис. 2, 3). К недостаткам такого подхода следует отнести то, что он дает завышенную оценку для потерь энергии при низких значениях потерь энергий на ионизацию $\Delta E$ и используется в основном для моделирования высокоэнергетических вторичных электронов.

Рис. 2.

Сравнение значений потерь энергий электронов в оксиде алюминия Al2O3, рассчитанных по формуле Бете (кривая 1) и из диэлектрической функции [43] (кривая 2) с экспериментальными значениями (точки) [40].

Рис. 3.

Иллюстрация процесса изменения энергии электрона (кривая 1) и генерации вторичных электронов (кривые 2) в модели гибридных потерь энергии. Пунктирная линия – потери энергии, рассчитанные по формуле Бете.

1.2.4. Дискретные потери энергии

Как было отмечено, при энергиях налетающего электрона выше 1 кэВ доминирующим видом не упругого рассеяния является однократная ионизация атомов вещества. В силу этого, логичным подходом к описанию потерь энергии является введение не непрерывных, дискретных потерь энергии. В первых моделях дискретных потерь энергии [49, 50] было спользовано предположение, что все потери энергии обусловлены ионизацией различных оболочек атома. При этом была использована формула Гризинского для дифференциального сечения однократной ионизации электронов внутренних оболочек [51, 52]:

(1.16)
$\frac{{d\sigma }}{{d\Delta E}} = \frac{{\pi {{e}^{4}}}}{{\Delta {{E}^{3}}}}\frac{{{{E}_{B}}}}{E}{{\left( {\frac{E}{{E + {{E}_{B}}}}} \right)}^{{\frac{3}{2}}}}{{\left( {1 - \frac{{\Delta E}}{E}} \right)}^{{\frac{{{{E}_{B}}}}{{{{E}_{B}} + \Delta E}}}}}\left\{ {\frac{{\Delta E}}{{{{E}_{B}}}}\left( {1 - \frac{{{{E}_{B}}}}{E}} \right) + \frac{4}{3}\ln \left( {2.7 + {{{\left( {\frac{{{{E}_{0}} - \Delta E}}{{{{E}_{B}}}}} \right)}}^{{\frac{1}{2}}}}} \right)} \right\},$
где $E$ – энергия электрона перед столкновением, $\Delta E$ – потери энергии в данном столкновении, ${{E}_{B}}$ – энергия связи на $j$-й оболочки атома. Эта формула основана на предположении об изотропном распределении скоростей электронов оболочки, и поэтому в исходном виде не может быть использована для описания неупругого рассеяния на валентных электронах [51]. Для устранения этого ограничения может быть введена эффективная энергия связи валентных электронов ${{E}_{{{\text{valence}}}}},$ определяемая из соотношений:
(1.17)
${{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{valence}}}}} = {{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{Bethe}}}}} - {{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{core}}}}},$
(1.18)
${{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{valence}}}}} = \sum\limits_i {{{n}_{i}}{{N}_{i}}\int\limits_{{{E}_{{{\text{valence}}}}}}^E {\Delta E{{{\left( {\frac{{d\sigma }}{{d\Delta E}}} \right)}}_{i}}d\Delta E,} } $
где ${{n}_{i}}$ – концентрация атомов i-ого типа, ${{N}_{i}}$ – количество электронов на внешней оболочке атомов i-ого типа, ${{\left( {{{d\sigma } \mathord{\left/ {\vphantom {{d\sigma } {dE}}} \right. \kern-0em} {dE}}} \right)}_{i}}$ – дифференциальное сечение неупругого рассеяния, вычисляемое по формуле (1.16), ${{\left( {{{dE} \mathord{\left/ {\vphantom {{dE} {ds}}} \right. \kern-0em} {ds}}} \right)}_{{{\text{Bethe}}}}}$ – полные потери энергии, вычисляемые по формуле Бете,
(1.19)
${{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{core}}}}} = \sum\limits_i {{{n}_{i}}\sum\limits_j {{{N}_{{i,j}}}\int\limits_{{{E}_{{{{B}_{{i,j}}}}}}}^E {\Delta E{{{\left( {\frac{{d\sigma }}{{d\Delta E}}} \right)}}_{{i.j}}}d\Delta E.} } } $
Здесь ${{E}_{{{{B}_{{i,j}}}}}}$ – энергия связи электронов на j-й внутренней оболочки атомов i-ого типа, ${{\left( {{{d\sigma } \mathord{\left/ {\vphantom {{d\sigma } {d\Delta E}}} \right. \kern-0em} {d\Delta E}}} \right)}_{{i,j}}}$ – дифференциальное сечение неупругого рассеяния, вычисляемое по формуле Гризинского.

Однако, вычисляемое по формуле (1.18) значение ${{E}_{{{\text{valence}}}}}$ зависит от энергии налетающего электрона, что не имеет физического обоснования, а такжеприводит к необходимости использования различных значений ${{E}_{{{\text{valence}}}}}$ для различных диапазонов энергии [53]. Также в описанном методе не учитываются электронные возбуждения, сечение которых сравнимы с сечениями процессов ионизации при низких энергиях [54].

Использования параметра ${{E}_{{{\text{valence}}}}}$ можно избежать за счет применения формулы Меллера для определения дифференциальных сечений рассеяния на валентных электронах [55]. Это позволяет определить сечения и потери энергии за счет ионизации, далее разность полных потерь энергии, вычисляемых по формуле Бете и потерь энергии на ионизацию трактуется как потери энергии на электронные возбуждения:

(1.20)
${{\left( {\frac{{dE}}{{ds}}} \right)}_{{{{\varepsilon }_{c}}}}} = {{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{Bethe}}}}} - {{\left( {\frac{{dE}}{{ds}}} \right)}_{{{\text{ion}}}}}.$

Для определения сечения процессов возбуждения используется модифицированная формула Меллера [56], что позволяет определить соответствующую длину свободного пробега. Затем, дискретные потери энергии на возбуждения определяются из удельных потерь энергии на возбуждения и длины свободного пробега для процессов возбуждения.

2. МОДЕЛИРОВАНИЕ НА ОСНОВЕ КИНЕТИЧЕСКОЙ ТЕОРИИ

Моделирование на основе кинетической теории транспорта заключается в решении кинетического уравнения Больцмана, описывающего распространение электронов в структуре. Этот метод успешно применяется для моделирования электронного пучка в планарных структурах, состоящих из небольшого количества слоев [57–59]. Для задач с более сложной геометрией необходимо введение дополнительных граничных условий, что значительно усложняет расчет. Также данный метод неприменим для моделирования шероховатостей профиля, получаемого в структуре, поскольку в нем рассчитываются усредненные значения величин, определяющих растворимость резиста при проявлении.

2.1. Определение распределения электронов по глубине

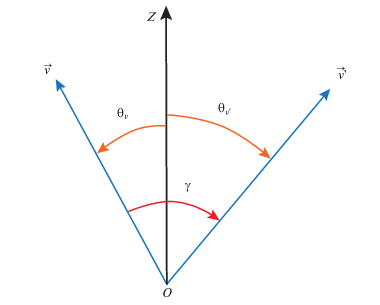
В большинстве случаев для упрощения расчетов, рассматривается точечный пучок электронов, направленный под прямым углом к поверхности (вдоль оси $z$). Распространение электронов в веществе по глубине может быть описано функцией распределения$f\left( {z,E,\cos {{\theta }_{v}}} \right),$ где $z$, $E$ – глубина проникновения электрона в образец и его энергия, ${{\theta }_{z}}$ – угол между скоростью электрона и осью $z$. В этом случае уравнение Больцмана принимает вид [60]:

(2.1)
$\frac{{dE}}{{ds}}\frac{{\partial f}}{{\partial E}} + \cos {{\theta }_{v}}\frac{{\partial f}}{{\partial z}} = \frac{1}{\Lambda }\int {w\left( {\cos \gamma } \right)} \left[ {f\left( {\cos {{\theta }_{{v{\kern 1pt} '}}}} \right) - f\left( {\cos {{\theta }_{v}}} \right)} \right]d{{\Omega }_{\gamma }},$
где $\frac{{dE}}{{ds}}$ – потери энергии на единицу длины пути, $\Lambda $ – длина свободного пробега для упругого рассеяния, $w\left( {\cos \gamma } \right)$ – нормированное дифференциальное сечение упругого рассеяния на угол между скоростями до и после рассеяния ($v$ и $v{\kern 1pt} '$), равный $\gamma $ (см рис. 4):

(2.2)
$w\left( {\cos \gamma } \right) = \frac{1}{{{{\sigma }_{{{\text{el}}}}}}}\frac{{d\sigma }}{{d{{\Omega }_{\gamma }}}}.$
Рис. 4.

Схема рассеяния электрона в веществе с указанием величин, используемых в уравнении (3.1).

Уравнение (2.1) может быть решено в диффузионном приближении [61], применимом в диапазоне энергий, характерных для электронно-лучевой литографии. Для этого функция распределения электронов раскладывается по полиномам Лежандра $P\left( {\cos \theta } \right){\kern 1pt} :$

(2.3)
$f\left( {z,E,\cos {{\theta }_{v}}} \right) = \sum\limits_0^\infty {{{C}_{n}}\left( {z,E} \right){{P}_{n}}\left( {\cos {{\theta }_{n}}} \right).} $

Подстановка (2.3) в (2.1) приводит к разностной дифференциальной схеме для коэффициентов ${{C}_{n}}$:

(2.4)
$\left( {\frac{{dE}}{{ds}}} \right)\frac{{\partial {{C}_{n}}}}{{\partial E}} + \frac{n}{{2n - 1}}\frac{{\partial {{C}_{{n - 1}}}}}{{\partial z}} + \frac{{n + 1}}{{2n + 3}}\frac{{\partial {{C}_{{n + 1}}}}}{{\partial z}} = - \frac{1}{{{{\lambda }_{n}}}}{{C}_{n}},$
где

(2.5)
$\frac{1}{{{{\lambda }_{n}}}} = \frac{1}{\Lambda }\int {\left[ {1 - {{P}_{n}}\left( {\cos \gamma } \right)} \right]} W\left( {\cos \gamma } \right)d{{\Omega }_{\gamma }}.$

Коэффициенты ${{C}_{0}}$ и ${{C}_{1}}$ пропорциональны плотности вероятности и проекции плотности потока вероятности на ось z, соответственно:

(2.6)
$\begin{gathered} \rho \left( {z,E} \right) = \int {f\left( {z,E,\cos {{\theta }_{v}}} \right)} d{{\Omega }_{v}} = 4\pi {{C}_{0}}\left( {z,E} \right), \\ {{J}_{z}}\left( {z,E} \right) = \int {v\cos {{\theta }_{v}}f\left( {z,E,\cos {{\theta }_{v}}} \right)} d{{\Omega }_{v}} = \frac{{4\pi }}{3}v{{C}_{1}}\left( {z,E} \right). \\ \end{gathered} $

Точное решение (2.1) возможно при отбрасывании в (2.3) коэффициентов ${{C}_{n}}$ с $n > 1,$ соответствующими турбулентному движению электронов. При этом (2.4) приводит к уравнению диффузии:

(2.7)
$\frac{\partial }{{\partial E}}\rho \left( {z,E} \right) = a\left( E \right)\frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}\rho \left( {z,E} \right),\,\,\,\,a\left( E \right) = {{\left( {\frac{{dE}}{{ds}}} \right)}^{{ - 1}}}\frac{{{{\lambda }_{1}}}}{3}.$

Его решение [62]:

(2.8)
$\rho \left( {z,E} \right) = \frac{1}{{\sqrt \pi \sigma \left( E \right)}}\exp \left( { - \frac{{{{z}^{2}}}}{{4{{\sigma }^{2}}\left( E \right)}}} \right)\left\{ {1 - \frac{{\sqrt \pi \sigma \left( E \right)}}{{\Delta {{\lambda }_{1}}\left( {{{E}_{0}}} \right)}}\exp \left( {{{\varsigma }^{2}}} \right){\text{erfc}}\left( {{{\varsigma }^{2}}} \right)} \right\},$
где

(2.9)
$\varsigma = \frac{z}{{2\sigma \left( E \right)}} + \frac{{\sigma \left( E \right)}}{{\Delta {{\lambda }_{1}}\left( {{{E}_{0}}} \right)}},\,\,\,\,{{\sigma }^{2}} = \int {a\left( E \right)dE,} \,\,\,\,\Delta = 0.71.$

Для описания функции распределения электронов в системе, состоящей из нескольких слоев, решение для предыдущего слоя используется как граничное условие для уравнения диффузии в новом слое.

2.2. Определение латерального распределения электронов

Латеральное распределение электронов описывается функцией плотности вероятности $\rho \left( {r,z,E} \right),$ определяющей вероятность нахождения электрона с энергией E в кольце радиуса r, имеющем объем $2\pi rdrdz$ и расположенном параллельно поверхности резиста на глубине $z$.Для определения продольного распределения электронов, необходимо решение уравнения Больцмана в более общем виде, чем (3.1) [63], и при этом отдельно учитывается вклад от электронов, рассеянных на малые углы (индекс f), обратного рассеянных электронов (индексы $bd$ и $bs$) и вторичных электронов (индекс s) [64]:

(2.10)
$\rho \left( {r,z,E} \right) = \rho \left( {z,E} \right)\left[ {{{\rho }_{f}}\left( {\left. r \right|z,E} \right) + {{\rho }_{{bd}}}\left( {\left. r \right|z,E} \right)} \right] + {{\rho }_{{bs}}}\left( {r,z,E} \right) + {{\rho }_{s}}\left( {r,z,E} \right).$

Здесь выражения вида $\rho \left( {\left. r \right|z,E} \right)$ означают плотность вероятности при известных значениях $z$ и E.

Слагаемое ${{\rho }_{f}}\left( {\left. r \right|z,E} \right)$ описывает вклад в продольное уширение пучка за счет малого количества актов рассеяния первичных электронов на малые углы в слое резиста:

(2.11)
${{\rho }_{f}}\left( {\left. r \right|z,E} \right) = \frac{{3{{\lambda }_{1}}}}{{2\pi {{z}^{3}}}}\exp \left( { - \frac{{3{{\lambda }_{1}}{{r}^{2}}}}{{2{{z}^{3}}}}} \right),$
где ${{\lambda }_{1}}$ определяется из соотношения (2.5).

Обратное рассеяние электронов происходит за счет малого количества актов рассеяния на большие углы вблизи границы резиста с подложкой (${{\rho }_{{bs}}}$), либо за счет диффузии электронов в структуре (${{\rho }_{{bd}}}$):

(2.12)
$\begin{gathered} {{\rho }_{{bs}}}\left( {r,z,E} \right) = \frac{1}{\pi }\int\limits_z^{{{z}_{d}}} {\beta \left( {1 + \beta } \right)} \rho \left( {z{\kern 1pt} ',E} \right)\frac{{z{\kern 1pt} ' - z}}{R}\frac{{{{dz{\kern 1pt} '} \mathord{\left/ {\vphantom {{dz{\kern 1pt} '} \Lambda }} \right. \kern-0em} \Lambda }}}{{{{{\left[ {\left( {1 + \beta } \right)R + z' - z} \right]}}^{2}}}},\,\,\,\,R = \sqrt {{{r}^{2}} + {{{\left( {z - z{\kern 1pt} '} \right)}}^{2}}} , \\ {{\rho }_{{bd}}}\left( {\left. r \right|z,E} \right) = \frac{A}{3}\int\limits_{{{z}_{d}}}^{{{z}_{{\max }}}} {{{{\left( {\frac{1}{{4\pi \sigma _{b}^{2}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\exp \left( { - \frac{{{{R}^{2}}}}{{4\sigma _{b}^{2}}}} \right)\frac{{z{\kern 1pt} ' - z}}{{{{z}_{{\max }}} - {{z}_{d}}}}dz{\kern 1pt} ',} \,\,\,\,\sigma _{b}^{2} = \int\limits_{E\left( {z'} \right)}^{E\left( z \right)} {a\left( {E{\kern 1pt} '} \right)dE{\kern 1pt} ',} \\ \end{gathered} $
где β – параметр экранирования в формуле Резерфорда для дифференциального сечения упругого рассеяния, Λ – длина свободного пробега для упругого рассеяния, $a\left( E \right)$ – коэффициент диффузии (2.7), $E\left( z \right),$ $E\left( {z{\kern 1pt} '} \right)$ – средние энергии электрона, получаемые за счет интегрировании функции $Ef\left( {z,E,\cos {{\theta }_{v}}} \right).$ Параметр ${{z}_{d}}$ выражает максимальную глубину проникновения электронов, рассеивающихся на большие углы вблизи границы резиста с подложкой, и его значение выбирается исходя из моделирования методом Монте-Карло. Значения параметров ${{z}_{{\max }}}$ и A, определяющих максимальную глубину, на которой могут находиться обратно отраженные электроны и коэффициент обратного отражения электронов соответственно, также выбираются исходя из соответствия результатам Монте-Карло моделирования. Например, для слоя полиметилметакрилата (ПММА) толщиной 0.5 мкм на кремниевой подложке выбираются следующие значения этих параметров: ${{z}_{d}} = 0.83$ мкм, ${{z}_{{\max }}} = 8.5$ мкм, $A = 0.19$ [64].

Вклад вторичных электронов в уширение пучка описывается плотностью вероятности вторичных электронов:

${{\rho }_{s}}\left( {r,z,E} \right) = \int\limits_{2E}^{{{E}_{0}}} {dE{\kern 1pt} '{{P}_{{{\text{inel}}}}}\left( {E{\kern 1pt} '} \right)\Phi \left( {E,E{\kern 1pt} '} \right)\int {{{d}^{3}}\vec {r}{\kern 1pt} '} \frac{1}{{8\pi {{S}^{3}}\left( E \right)}}\exp \left( {\frac{{ - \left| {\vec {r} - \vec {r}{\kern 1pt} '} \right|}}{{S\left( E \right)}}} \right)\rho \left( {r{\kern 1pt} ',z,E{\kern 1pt} '} \right).} $

Здесь ${{E}_{0}}$ – начальная энергия электронов, ${{P}_{{{\text{inel}}}}}$ – вероятность неупругого рассеяния, в котором возникает вторичный электрон, определяемая из выражений для сечения упругого и неупругого рассеяния:

(2.13)
${{P}_{{{\text{inel}}}}} = \frac{{{{\sigma }_{{{\text{inel}}}}}}}{{{{\sigma }_{{{\text{el}}}}} + {{\sigma }_{{{\text{inel}}}}}}},$
где сечения упругого (индекс el) и неупругого (индекс inel) рассеяния вычисляются по формуле Резерфорда и формуле Меллера, соответственно. Функция $\Phi \left( {E,E{\kern 1pt} '} \right)$ выражает дифференциальное сечение неупругого рассеяния, нормированное на полное сечение неупругого рассеяния. $S\left( E \right)$ – максимальная глубина проникновения электронов, выражающаяся через потери энергии на единицу пути:
(2.14)
$S\left( E \right) = \int\limits_{{{E}_{0}}}^{{{E}_{{\min }}}} {dE} {{\left( {\frac{{dE}}{{ds}}} \right)}^{{ - 1}}},$
где ${{E}_{{\min }}}$ – энергия, при которой электрон считается поглощенным.

Как и в Монте-Карло моделировании, основной характеристикой, получаемой в результате моделирования, является распределение энергии, выделенной в резисте. Плотность выделенной энергии в расчете на один электрон $I\left( {r,z} \right)$ может быть получена за счет интегрирования произведения плотности вероятности и функции потерь энергии [64].

3. МОНТЕ-КАРЛО МОДЕЛИРОВАНИЕ

При моделировании методом Монте-Карло для каждого электрона из пучка рассчитывается его траектория в структуре. Параметры траектории и потери энергии электрона определяются из дифференциальных сечений упругих и неупругих процессов с использованием случайных чисел из равномерного распределения на промежутке (0, 1). Данный метод требует больших вычислительных мощностей, но при этом его сложность практически не зависит от формы структуры и количества входящих в нее материалов. Также, в отличие от моделирования на основе кинетической теории транспорта, алгоритм расчета траектории электрона в структуре методом Монте-Карло позволяет воспроизвести стохастичность процессов рассеяния электрона, что может быть использовано для моделирования шероховатостей получаемого профиля.

3.1. Определение длины пробега электрона

Путем интегрирования дифференциальных сечений вычисляются значения полных сечений упругого и неупругого взаимодействий для каждого типа атомов, присутствующего в веществе:

(3.1)
$\sigma _{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}^{i}\left( E \right) = \int\limits_Q {\frac{{d\sigma _{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}^{i}\left( {E,q} \right)}}{{dq}}dq,} $
где индекс “el/inel” означает тип рассеяния – упругое рассеяние или неупругое, соответственно. Дифференциальные сечения рассеяния зависят как от энергии налетающего электрона, так и от второй переменной, которая здесь называется $q$. Для упругого рассеяния это полярный угол рассеяния $\theta $, для неупругого – энергия $\Delta E$, передаваемая налетающим электроном среде. Интегрирование в формуле (3.1) производится по области всех возможных значений $q$. Далее определяется полное сечение рассеяния на атомах всех типов:
(3.2)
${{\sigma }_{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}}\left( E \right) = \frac{1}{n}\sum\limits_{i = 1}^N {{{n}_{i}}} \sigma _{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}^{i}\left( E \right),$
где ${{n}_{i}}$ – концентрация атомов i-ого типа, $n = \sum\nolimits_{i = 1}^N {{{n}_{i}}} ,$ $N$ – количество типов атомов в веществе, для которого проводится моделирование. Длина свободного пробега между последовательными актами упругого или неупругого рассеяния определяется по формуле:

(3.3)
${{\Lambda }_{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}}\left( E \right) = {{\left( {n{{\sigma }_{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}}\left( E \right)} \right)}^{{ - 1}}}.$

Длина свободного пробега определяется по формуле:

(3.4)
${{\Lambda }^{{ - 1}}}\left( E \right) = \Lambda _{{{\text{el}}}}^{{ - 1}}\left( E \right) + \Lambda _{{{\text{inel}}}}^{{ - 1}}\left( E \right).$

Вероятность того, что на промежутке пути длиной $s$ не произойдет рассеяния ни на одном атоме равна [4]:

(3.5)
$p\left( s \right) = \Lambda {{\left( E \right)}^{{ - 1}}}\exp \left( { - \frac{s}{{\Lambda \left( E \right)}}} \right).$

При этом длина пробега электрона может быть определена по формуле:

(3.6)
$s = - \Lambda \left( E \right)\ln \left( {{{\xi }_{1}}} \right),$
где ${{\xi }_{1}}$ – случайное число из интервала (0, 1). Если пробег электрона начинается и заканчивается в слоях, состоящих из разного вещества (например, моделирование проводится для системы из $m$ слоев с толщинами ${{s}_{1}},~{{s}_{2}},~...,~{{s}_{m}}$ и длинами свободного пробега электронов ${{\Lambda }_{1}},~{{\Lambda }_{2}},~...,~{{\Lambda }_{m}}$), длина пробега электрона$s$должна быть пересчитана с условием пересечения границы между слоями. Например, она может быть вычислена как верхний предел интеграла в формуле [65]:
(3.7)
$\ln \left( {{{\xi }_{1}}} \right) = - \frac{{{{s}_{1}}}}{{{{\Lambda }_{1}}}} - \frac{{{{s}_{2}}}}{{{{\Lambda }_{2}}}}... + \int\limits_{{{s}_{k}}}^s { - \frac{{du}}{{{{\Lambda }_{k}}}},} $
где $k \leqslant m$.

3.2. Определение типа взаимодействия и атома

Далеена основе вероятностей упругого и неупругого рассеяния

(3.8)
${{p}_{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}} = {{{{\sigma }_{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}}} {\left( {{{\sigma }_{{{\text{el}}}}} + {{\sigma }_{{{\text{inel}}}}}} \right)}}} \right. \kern-0em} {\left( {{{\sigma }_{{{\text{el}}}}} + {{\sigma }_{{{\text{inel}}}}}} \right)}}$

определяется тип взаимодействия (упругое или неупругое рассеяние), в котором электрон примет участие после прохождения пути s:

(3.9)
$\begin{gathered} {{\xi }_{2}} < {{p}_{{{\text{el}}}}} \Rightarrow \,\,{\text{упругое}}\,\,{\text{рассеяние}} \\ {{\xi }_{2}} > {{p}_{{{\text{el}}}}} \Rightarrow \,\,{\text{неупругое}}\,\,{\text{рассеяние}}, \\ \end{gathered} $
где ${{\xi }_{2}}$ – новое случайное число из интервала (0, 1).

При известном типе взаимодействия определяется тип атома, на котором происходит рассеяние, согласно вероятностям:

(3.10)
${{p}_{i}} = \frac{{{{n}_{i}}\sigma _{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}^{i}\left( E \right)}}{{n{{\sigma }_{{{{{\text{el}}} \mathord{\left/ {\vphantom {{{\text{el}}} {{\text{inel}}}}} \right. \kern-0em} {{\text{inel}}}}}}}\left( E \right)}}.$

Определение типа атома производится аналогично определению типа процесса с использованием случайного числа ${{\xi }_{3}}$.

3.3. Определение нового направления электрона и потерь энергии

В случае упругого рассеяния, определяется новое направление рассеянного электрона, для чего используются случайные числа – ${{\xi }_{4}}$ и ${{\xi }_{5}}$. Азимутальный угол рассеяния$\varphi $считается равномерно распределенным на интервале $(0,2\pi )$ и определяется из выражения:

(3.11)
$\varphi = 2\pi {{\xi }_{4}}.$

Полярный угол рассеяния $\theta $ вычисляется на основе дифференциального сечения упругого рассеяния по формуле:

(3.12)
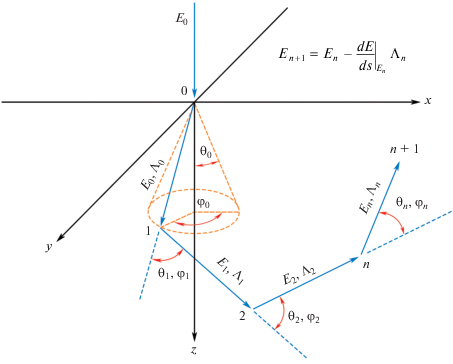
${{\xi }_{5}} = {{\int\limits_0^\theta {\frac{{d\sigma }}{{d\Omega }}\sin \vartheta d\vartheta } } \mathord{\left/ {\vphantom {{\int\limits_0^\theta {\frac{{d\sigma }}{{d\Omega }}\sin \vartheta d\vartheta } } {\int\limits_0^\pi {\frac{{d\sigma }}{{d\Omega }}\sin \vartheta d\vartheta .} }}} \right. \kern-0em} {\int\limits_0^\pi {\frac{{d\sigma }}{{d\Omega }}\sin \vartheta d\vartheta .} }}$

При известных углах n-ого акта упругого рассеяния ${{\varphi }_{n}}$ и ${{\theta }_{n}}$ новое направление движения электрона ${{\vec {x}}_{n}}$ определяется начальным направлением движения электронов в пучке ${{\vec {x}}_{0}}$ (часто принимается равным $\left( {0,0,1} \right)$) и комбинацией матриц поворота [18]:

(3.13)
${{\vec {x}}_{n}} = O_{n}^{T}{{\vec {x}}_{0}},\,\,\,\,{{O}_{n}} = {{W}_{n}}{{O}_{{n - 1}}},$
(3.14)
${{W}_{n}} = \left( {\begin{array}{*{20}{c}} {\cos {{\varphi }_{n}}}&{\sin {{\varphi }_{n}}}&0 \\ { - \sin {{\varphi }_{n}}\cos {{\theta }_{n}}}&{\cos {{\varphi }_{n}}\sin {{\theta }_{n}}}&{\sin {{\theta }_{n}}} \\ {\sin {{\varphi }_{n}}\sin {{\theta }_{n}}}&{ - \cos {{\varphi }_{n}}\sin {{\theta }_{n}}}&{\cos {{\theta }_{n}}} \end{array}} \right).$

При этом используются начальные значения ${{O}_{{ - 1}}} = E$ (единичная матрица) и ${{\varphi }_{0}} = {{\theta }_{0}} = 0.$

В случае неупругого рассеяния, определяются потери энергии. При использовании модели непрерывных потерь энергии, потери энергии на пути $s$, определяемом из выражения (2.6), вычисляются по формуле:

(3.15)
$\Delta E = \int\limits_0^s {\frac{{dE}}{{ds}}ds \approx \frac{{dE}}{{ds}}s.} $

При использовании модели дискретных потерь энергии, потери энергии $\Delta E$ определяются с помощью случайного числа ${{\xi }_{6}}$:

(3.16)
${{\xi }_{6}} = {{\int\limits_{{{E}_{{\min }}}}^{\Delta E} {\frac{{d\sigma }}{{d\left( {\Delta E{\kern 1pt} '} \right)}}d\left( {\Delta E{\kern 1pt} '} \right)} } \mathord{\left/ {\vphantom {{\int\limits_{{{E}_{{\min }}}}^{\Delta E} {\frac{{d\sigma }}{{d\left( {\Delta E{\kern 1pt} '} \right)}}d\left( {\Delta E{\kern 1pt} '} \right)} } {\int\limits_{{{E}_{{\min }}}}^{{{E}_{{\max }}}} {\frac{{d\sigma }}{{d\left( {\Delta E'} \right)}}d\left( {\Delta E{\kern 1pt} '} \right),} }}} \right. \kern-0em} {\int\limits_{{{E}_{{\min }}}}^{{{E}_{{\max }}}} {\frac{{d\sigma }}{{d\left( {\Delta E'} \right)}}d\left( {\Delta E{\kern 1pt} '} \right),} }}$
где дифференциальные сечения неупругого рассеяния ${{d\sigma } \mathord{\left/ {\vphantom {{d\sigma } {d\Delta E}}} \right. \kern-0em} {d\Delta E}}$ вычисляются по формуле Гризинского или из диэлектрической функции. В случае использования формулы Гризинского, ${{E}_{{\min }}}$принимается равным энергии связи нужной оболочки, ${{E}_{{\max }}}$ – энергии налетающего электрона $E$. В случае использования диэлектрической функции, ${{E}_{{\min }}} = 0,$ ${{E}_{{\max }}} = E - {{E}_{{\text{F}}}},$ где ${{E}_{{\text{F}}}}$ – энергия Ферми. Пример траектории электрона, рассчитываемой по методу Монте-Карло, приведен на рис. 5.

Рис. 5.

Схематическое изображение траектории электрона в веществе, получаемой при Монте-Карло моделировании при использовании модели непрерывных потерь энергии.

4. МОДЕЛИРОВАНИЕ РАЗРЫВА МОЛЕКУЛ РЕЗИСТА И ЕГО РАСТВОРЕНИЯ НА СТАДИИ ПРОЯВЛЕНИЯ ИЗОБРАЖЕНИЯ

Заключительным этапом моделирования процесса электронно-лучевой литографии является расчет профиля, получаемого на стадии проявлении изображения в жидких растворителях. Для этого необходимо сначала промоделировать разрыв молекул резиста при поглощении ими энергии, выделившейся в резисте при экспонировании, и затем – растворение проэкспонированных областей резиста. Существуют два подхода к решению этой задачи, основанные на анализе распределений, полученных из моделирования взаимодействий электронного пучка с резистом: в первом для определения параметров процессов разрыва молекул резиста и его растворения используется распределение выделившейся в резисте энергии, во втором – распределение процессов неупругого взаимодействия электронного пучка с атомами резиста.

4.1. Моделирование растворения резиста на основе распределения выделившейся в резисте энергии

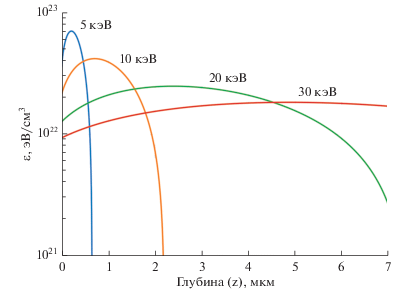
Данный подход к моделированию профиля в резисте, получающегося при его проявлении, основан на использовании эмпирических зависимостей скорости растворения областей резиста от плотности выделившейся в них энергии. На ранних этапах для определения плотности выделившейся энергии $\varepsilon $ использовалась формула (рис. 6) [66]

(4.1)
$\varepsilon = \frac{Q}{e}\frac{{{{E}_{0}}}}{{{{R}_{G}}}}\lambda \left( f \right),$
где $Q$ – доза экспонирования, $e$ – заряд электрона, ${{E}_{0}}$ – начальная энергия электронов в пучке, ${{R}_{G}}$ – глубина проникновения электронов, связанная эмпирической зависимостью с плотность резиста $\rho $ и начальной энергией электронов ${{E}_{0}}$ (в кэВ):

(4.2)
${{R}_{G}} = \frac{{4.6 \times {{{10}}^{{ - 6}}}}}{\rho }E_{0}^{{1.75}}.$
Рис. 6.

Зависимость плотности выделившейся в слое ПММА энергии от глубины, рассчитанная из функции (4.1) для дозы экспонирования 100 мкКл/см2 при различных значениях начальной энергии электронов.

Эмпирическая функция $\lambda \left( f \right)$ описывает зависимость плотности выделившейся энергии от глубины $z$ в слое резиста [67]:

(4.3)
$\lambda \left( f \right) = 0.74 + 4.7f - 8.9{{f}^{2}} + 3.5{{f}^{3}},\,\,\,\,f = \frac{z}{{{{R}_{G}}}}.$

В силу своей простоты такой способ определения плотности выделившейся в резисте энергии позволяет промоделировать профиль структуры лишь в одном измерении. Поэтому, с развитием вычислительной техники и методов моделирования электронных пучков в веществе, для расчета плотности выделившейся энергии стали использоваться результаты Монте-Карло моделирования и моделирования на основе кинетической теории транспорта.

Для моделирования разрывов молекул резиста при выделении в нем энергии была введена величина $g$, определяющая количество разрывов молекул резиста при выделении в нем энергии 100 эВ [68]. Это позволяло рассчитать локальную среднюю молекулярную массу резиста после экспонирования:

(4.4)
${{M}_{f}} = \frac{{{{M}_{n}}}}{{1 + g\varepsilon {{{{M}_{n}}} \mathord{\left/ {\vphantom {{{{M}_{n}}} {\rho {{N}_{{\text{A}}}}}}} \right. \kern-0em} {\rho {{N}_{{\text{A}}}}}}}}.$

Здесь ${{M}_{n}}$ – средняя молекулярная масса резиста до экспонирования, ${{N}_{{\text{A}}}}$ – число Авогадро. Далее, из распределения локальной молекулярной массы резиста определялась скорость растворения резиста по эмпирической формуле [69] (рис. 7):

(4.5)
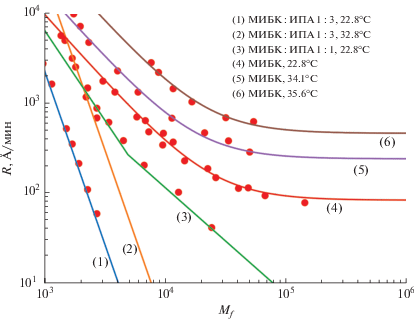
$R = \left( {{{R}_{0}} + \frac{\beta }{{M_{f}^{\alpha }}}} \right)\exp \left( {\frac{{{{E}_{a}}}}{{kT}}} \right),$
где ${{R}_{0}}$ – скорость растворения не проэкспонированных участков, ${{E}_{a}}$ – энергия активации, α, β – параметры. Для проявления изображения в ПММА в растворителе МИБК в диапазоне температур 23–36°C полученные экспериментально значения параметров, ${{R}_{0}},$ ${{E}_{a}},$ α и β составляют 4.33 × × 1019 Å/мин, 1.04 эВ, 1.5 и 1.62 × 1026 Å/мин, соответственно [69]. Наиболее часто значение параметра $g$ выбирается равным 1.9 [70], однако в различных работах приводятся значения, отличающиеся в несколько раз [68, 71, 72]. Помимо этого, было установлено, что значение $g$ может зависеть от энергии электронного пучка [72], также логично предположить, что оно зависит от температуры экспонирования. Несмотря на это, правильный подбор параметров описанной модели для конкретных условий экспонирования и проявления позволяет добиться хорошей точности моделирования профиля, получаемого в резисте после проявления.

Рис. 7.

Аппроксимация теоретической зависимостью (4.5) (сплошные линии) экспериментальных значения скорости растворения резиста [66] (точки) в зависимости от молекулярной массы резиста после экспонирования ${{M}_{f}}.$

4.2. Моделирование растворения резиста на основе распределения неупругих процессов в резисте

Более детальный подход к описанию разрыва молекул резиста и его последующего растворения основан на анализе распределения процессов неупругого взаимодействия электронного пучка с резистом. Это распределение может быть получено при использовании современных алгоритмов моделирования, таких как Direct Monte-Carlo [49, 73, 74] или алгоритма на основе кинетической теории транспорта, описанного в работах [59, 72]. Распределение процессов неупругого взаимодействия электронного пучка с резистом используется для определения распределения разрывов молекул резиста, что позволяет рассчитать локальную молекулярную массу резиста без усреднения и использования параметра $g$. Механизм разрыва молекул резиста при поглощения ими энергии, выделившейся врезисте при экспонировании, еще не изучен достаточно хорошо, вследствие чего моделирование разрывов молекул проводится на основе общих соображений. Приводящими к разрыву молекул резиста, считаются процессы неупругого взаимодействия электронного пучка с теми атомами резиста, которые отвечают за связь мономеров в полимерной молекуле. Доля этих процессов среди всех неупругих процессов, а также количество и вид атомов, взаимодействие электронного пучка с которыми приводит к разрыву молекул резиста, могут быть определены исходя из известных значений параметра $g$, либо из сравнения промоделированных массовых распределений резиста с распределениями, полученными с помощью эксклюзионной хроматографии [75].

Далее, проникновение растворителя в резист, приводящее к растворению проэкспонированных областей, описывается как диффузионный процесс с коэффициентом диффузии, зависящим от числа мономеров в молекулах резиста [76, 77]:

(4.6)
$D = {{D}_{0}}\exp \left( {{{ - A} \mathord{\left/ {\vphantom {{ - A} {kT}}} \right. \kern-0em} {kT}}} \right),\,\,\,\,{{D}_{0}}\sim {1 \mathord{\left/ {\vphantom {1 {{{n}^{\alpha }},}}} \right. \kern-0em} {{{n}^{\alpha }},}}$
где $n$ – число мономеров в полимерной молекуле, $A$ – энергия активации. Значение параметра $\alpha $ – может быть определено теоретически [78] или из моделирования методом молекулярной динамики [79] и примерно равно 2. Для определения энергии активации используется выражение [76]
(4.7)
${A \mathord{\left/ {\vphantom {A \alpha }} \right. \kern-0em} \alpha } = k\left[ {{{{{T}_{1}}{{T}_{2}}} \mathord{\left/ {\vphantom {{{{T}_{1}}{{T}_{2}}} {\left( {{{T}_{1}} - {{T}_{2}}} \right)}}} \right. \kern-0em} {\left( {{{T}_{1}} - {{T}_{2}}} \right)}}} \right]\ln \left( {{{d_{2}^{{clr}}} \mathord{\left/ {\vphantom {{d_{2}^{{clr}}} {d_{1}^{{clr}}}}} \right. \kern-0em} {d_{1}^{{clr}}}}} \right),$
где $d_{{1,2}}^{{clr}}$ – дозы, при которых было зарегистрировано полное проявление изображения при различных температурах ${{T}_{1}}$ и ${{T}_{2}}$. Для прямоугольных решеток с периодом 70 нм были получены значения ${A \mathord{\left/ {\vphantom {A \alpha }} \right. \kern-0em} \alpha }$ в промежутке 0.22–0.25 эВ, с периодом 50 нм – в промежутке 0.14–0.22 эВ [76]. С учетом $\alpha \approx 2$ это приводит к значению энергии активации, примерно равному 0.44 эВ.

Применение такого подхода к моделированию проявления ПММА в различных растворителях при получении прямоугольных решеток позволяет определить степень растворимости различных областей резиста в зависимости от количества мономеров во фрагментах его молекул. Например, было установлено, что в растворителе МИБК : : ИПА (1 : 1) растворяются области резиста, в которых содержатся фрагменты молекул, состоящие из 1–12 мономеров, при этом их относительная концентрация превышает 90–95% [72].

Такой метод моделирования проявления изображения в резисте является относительно новым, и в связанных с ним работах он описывается только в общих деталях. В отличие от метода моделирования скорости растворения резиста на основе распределения выделенной в нем энергии, он требует использования наиболее детальных и сложных алгоритмов моделирования взаимодействия электронного пучка с резистом. Однако, он позволяет избежать использования эмпирических формул и параметров, что может быть использовано для моделирования растворения резиста при параметрах процесса проявления, отличающихся от стандартных.

ЗАКЛЮЧЕНИЕ

В данной работе рассмотрены основные методы моделирования процессов электронно-лучевой литографии – взаимодействия электронного пучка со структурой и растворения проэкспонированных участков резиста при проявлении. В случае моделирования планарных структур с небольшим количеством слоев эффективно применяется метод моделирования на основе кинетической теории транспорта. За счет описания процесса распространения электронов в структуре в терминах функции распределения, этот метод не требует большого вычислительного времени. При этом существующие алгоритмы позволяют использовать его с учетом процессов, обеспечивающих существенный вклад в уширение электронного пучка в резисте, таких как рассеяние на большие углы и обратного отражения электронов, а также генерация вторичных электронов. Помимо распределения выделившейся в резисте энергии, этот метод может быть использован для получения более детальной информации о процессах, протекающих в резисте при экспонировании – распределения неупругих взаимодействий электронов с атомами резиста или распределения разрывов молекул резиста.

Более требовательный к вычислительным мощностям, метод Монте-Карло моделирования позволяет определить параметры траектории в произвольной структуре для каждого электрона отдельно. В зависимости от решаемой задачи, может быть использован один из множества существующих алгоритмов Монте-Карло моделирования – от наиболее простых, учитывающих только упругое рассеяние и общие потери энергии, до наиболее сложных, учитывающих дискретные потери энергии в различных процессах и генерацию вторичных электронов. Методы из последней категории предоставляют детальную информацию о процессах рассеяния электронов в структуре, что может быть использовано, например, для моделирования уширения линии за счет вторичных электронов или шероховатостей профиля структур.

Оба вышеописанных метода моделирования позволяют описать уширение пучка в резисте за счет процессов упругого и неупругого рассеяния и могут быть использованы для оптимизации параметров экспонирования.

Работа частично выполнена в рамках Государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки РФ по теме № 0066-2019-0004, поддержана РФФИ, грант № 18-37-00472.

Список литературы

  1. Chang T.H.P. Proximity effect in electron-beam lithography // J. Vac. Sci. Technol. 1975. V. 12. № 6. P. 1271–1275.

  2. Umbach C.P., Broers A.N. Proximity effect in electron beam patterned x-ray masks // Appl. Phys. Lett. 1990. V. 56. № 16. P. 1594–1596.

  3. Soe E., Choi B.K., Kim O. Determination of proximity effect parameters and the shape bias parameter in electron beam lithography // Microelectron. Eng. 2000. V. 53. № 1. P. 305–308.

  4. Dapor M. Electron-beam interactions with solids / ed. Dapor M. New York: Springer, Berlin, Heidelberg, 2003.

  5. Шейкин Е.Г. Модельное дифференциальное сечение упругого рассеяния электронов на атомах для моделирования прохождения электронов в веществе методом Монте-Карло // Журн. технической физики. Энергоатомиздат, 1991. T. 80. № 1. 3–11 c.

  6. Adesida I., Shimizu R., Everhart T.E. A study of electron penetration in solids using a direct Monte Carlo approach // J. Appl. Phys. 1980. V. 51. № 11. P. 5962–5969.

  7. Marrian C.R.K. Modeling of electron elastic and inelastic scattering // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 1996. V. 14. № 6. P. 3864.

  8. Schmoranzer H., Reisser M. Spatial energy deposition distribution by a keV-electron beam in resist layers for electron-beam lithography // Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms. 1995. V. 105. № 1–4. P. 35–41.

  9. Biewer T., Rez P. Energy deposition in thin films calculated using electron transport theory // J. Appl. Phys. 1994. V. 76. № 11. P. 7636–7638.

  10. Dapor M. Elastic scattering calculations for electrons and positrons in solid targets // J. Appl. Phys. 1996. V. 79. № 11. P. 8406–8411.

  11. Mott N.F., Massey H.S.W. Theory of Atomic Collisions. Springer, Berlin, Heidelberg, 1956.

  12. Czyzewski Z. et al. Calculations of Mott scattering cross section // J. Appl. Phys. 1990. V. 68. № 7. P. 3066–3072.

  13. Gregory D., Fink M. Theoretical electron scattering amplitudes and spin polarizations // At. Data Nucl. Data Tables. 2007. V. 14. № 1. P. 39–87.

  14. Reimer L., Lödding B. Calculation and tabulation of mott cross-sections for large-angle electron scattering // Scanning. 1984. V. 6. № 3. P. 128–151.

  15. Riley M.E., MacCallum C.J., Biggs F. Theoretical electron-atom elastic scattering cross sections // At. Data Nucl. Data Tables. 1975. V. 15. № 5. P. 443–476.

  16. Salvat F., Jablonski A., Powell C.J. Elsepa – Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules // Comput. Phys. Commun. 2005. V. 165.2. P. 157–190.

  17. Reimer L., Stelter D. FORTRAN 77 monte-carlo program for minicomputers using mott cross-sections // Scanning. 1986. V. 8. № 6. P. 265–277.

  18. Kuhr J.C., Fitting H.J. Monte-Carlo simulation of low energy electron scattering in solids // Phys. Status Solidi Appl. Res. 1999. V. 172. № 2. P. 433–449.

  19. Ding Z.-J., Shimizu R. A Monte Carlo modeling of electron interaction with solids including cascade secondary electron production // Scanning. 2006. V. 18. № 2. P. 92–113.

  20. Ivin V.V. et al. Modeling and simulation issues in Monte Carlo calculation of electron interaction with solid targets // Microelectron. Eng. 2003. V. 69. № 2–4. P. 594–605.

  21. Kieft E., Bosch E. Refinement of Monte Carlo simulations of electron-specimen interaction in low-Vtage SEM // J. Phys. D. Appl. Phys. 2008. V. 41. № 21.

  22. Iga I. et al. Elastic differential cross section measurements for electron scattering from Ar and O2 in the intermediate-energy range // J. Phys. B At. Mol. Phys. 1987. V. 20. № 5. P. 1095–1104.

  23. Holtkamp G. et al. Absolute differential cross sections for elastic electron scattering from mercury // J. Phys. B At. Mol. Phys. 1987. V. 20. № 17. P. 4543–4569.

  24. Shimizu R., Ze-Jun D. Monte Carlo modelling of electron-solid interactions // Reports Prog. Phys. 1992. V. 55. № 4. P. 487–531.

  25. Bethe H. Theory of the Passage of Fast Corpuscular Rays Through Matter // Ann. Phys. 1930. V. 5. № 5. P. 77–154.

  26. Seltzer S.M., Berger M.J. Evaluation of the collision stopping power of elements and compounds for electrons and positrons // Int. J. Appl. Radiat. Isot. 1982. V. 33. № 11. P. 1189–1218.

  27. Аккерман А.Ф. Моделирование траекторий заряженных частиц в веществе / Ред. Путилова Е.А. Москва: Энергоатомиздат, 1991.

  28. Tan Z. et al. Electron stopping power and mean free path in organic compounds over the energy range of 20–10 000 eV // Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms. 2004. V. 222. № 1–2. P. 27–43.

  29. Rao-Sahib T.S., Wittry D.B. X-ray continuum from thick elemental targets for 10–50-keV electrons // J. Appl. Phys. 1974. V. 45. № 11. P. 5060–5068.

  30. Joy D.C. A model for calculating secondary and backscattered electron yields // J. Microsc. 1987. V. 147. № 1. P. 51–64.

  31. Lindhard J. Stopping Power of Electron Gas // K. Dan. Vidensk. Selks. Mat. Phys. Medd. 1964. V. 34. № 4.

  32. Sorini A.P. et al. Ab initio calculations of electron inelastic mean free paths and stopping powers // Phys. Rev. B – Condens. Matter Mater. Phys. 2006. V. 74. № 16. P. 1–17.

  33. Ashley J.C., Tung C.J., Ritchie R.H. Electron inelastic mean free paths and energy losses in solids. I. Aluminum metal // Surf. Sci. 1979. V. 81. № 2. P. 409–426.

  34. Tung C.J., Ashley J.C., Ritchie R.H. Electron inelastic mean free paths and energy losses in solids II. Electron gas statistical model // Surf. Sci. 1979. V. 81. № 2. P. 427–439.

  35. Romanyuk O. et al. Dielectric response functions of the (0001–), (101–3) GaN single crystalline and disordered surfaces studied by reflection electron energy loss spectroscopy // J. Appl. Phys. 2011. V. 110. № 4.

  36. Tahir D., Tougaard S. Electronic and optical properties of selected polymers studied by reflection electron energy loss spectroscopy // J. Appl. Phys. 2012. V. 111. № 5.

  37. Tahir D. et al. Electronic and optical properties of La-aluminate dielectric thin films on Si (100) // Surf. Interface Anal. 2010. V. 42. № 10–11. P. 1566–1569.

  38. Tahir D. et al. Electronic and optical properties of Al2O3/SiO2 thin films grown on Si substrate // J. Phys. D. Appl. Phys. 2010. V. 43. № 25.

  39. Ashley J.C. Interaction of low-energy electrons with condensed matter: stopping powers and inelastic mean free paths from optical data // J. Electron Spectros. Relat. Phenomena. 1988. V. 46. № 1. P. 199–214.

  40. Ashley J.C. Energy loss rate and inelastic mean free path of low-energy electrons and positrons in condensed matter // J. Electron Spectros. Relat. Phenomena. 1990. V. 50. № 2. P. 323–334.

  41. Werner W.S.M., Glantschnig K., Ambrosch-Draxl C. Optical constants and inelastic electron-scattering data for 17 elemental metals // J. Phys. Chem. Ref. Data. 2009. V. 38. № 4. P. 1013–1092.

  42. Tanuma S., Powell C.J., Penn D.R. Calculations of electron inelastic mean free paths. IX. Data for 41 elemental solids over the 50 eV to 30 keV range // Surf. Interface Anal. 2011. V. 43. № 3. P. 689–713.

  43. Dapor M., Miotello A. Backscattering of electrons from selected oxides: MgO, SiO2, and Al2O3 // Eur. Phys. J. Appl. Phys. 1999. V. 5. № 2. P. 143–148.

  44. Samoto N., Shimizu R. Theoretical study of the ultimate resolution in electron beam lithography by Monte Carlo simulation, including secondary electron generation: Energy dissipation profile in polymethylmethacrylate // J. Appl. Phys. 1983. V. 54. № 7. P. 3855–3859.

  45. Pei X. The Monte Carlo Simulation of Secondary Electrons Excitation in the Resist PMMA // Appl. Phys. Res. 2014. V. 6. № 3. P. 1–7.

  46. Murata K., Kyser D.F., Ting C.H. Monte Carlo simulation of fast secondary electron production in electron beam resists // J. Appl. Phys. 1981. V. 52. № 7. P. 4396–4405.

  47. Mott N.F. The Collision between Two Electrons // Proc. R. Soc. A Math. Phys. Eng. Sci. 1930. V. 126. № 801. P. 259–267.

  48. Moller C. Uber den Stos zweier Teilchen unter Berucksichtigung der Retardation der Krafte // Zeitschrift fur Phys. 1931. V. 70. № 11–12. P. 786–795.

  49. Shimizu R. et al. A Monte Carlo approach to the direct simulation of electron penetration in solids // J. Phys. D. Appl. Phys. 1976. V. 9. № 1. P. 101–113.

  50. Ichimura S., Shimizu R. Backscattering correction for quantitative Auger analysis. I. Monte Carlo calculations of backscattering factors for standard materials // Surf. Sci. 1981. V. 112. № 3. P. 386–408.

  51. Gryziński M. Classical theory of atomic collisions. I. Theory of inelastic collisions // Phys. Rev. 1965. V. 138. № 2A.

  52. Gryziński M. Classical theory of atomic collisions. II. Low energy scattering // J. Chem. Phys. 1975. V. 62. № 7. P. 2620–2628.

  53. Shimizu R., Everhart T.E. A semiempirical stopping-power formula for use in microprobe analysis // Appl. Phys. Lett. 1978. V. 33. № 8. P. 784–786.

  54. Perkins S.T., Cullen D.E., Seltzer S.M. Tables and graphs of electron-interaction cross sections from 10 eV to 100 GeV derived from the LLNL Evaluated Electron Data Library (EEDL), Z = 1–100. Livermore, CA, 1991.

  55. Seltzer S.M. An Overview of ETRAN Monte Carlo Methods // Monte Carlo Transp. Electrons Photons. 2012. P. 153–181.

  56. Seltzer S.M. Electron-photon Monte Carlo calculations: The ETRAN code // Int. J. Radiat. Appl. Instrumentation. Part. 1991. V. 42. № 10. P. 917–941.

  57. Glezos N., Raptis I., Hatzakis M. LITHOS: A fast electron beam lithography simulator // Microelectron. Eng. 1995. V. 26. № 3–4. P. 131–140.

  58. Rosenbusch A., Glezos3 N., Raptis3 L. SELID: a new 3D Simulator for EBeam Lithography. V. 2884. P. 435–441.

  59. Stepanova M. et al. Simulation of electron beam lithography of nanostructures // J. Vac. Sci. Technol. B, Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2010. V. 28. № 6. P. C6C48–C6C57.

  60. Glezos N. Application of a new analytical technique of electron distribution calculations to the profile simulation of a high sensitivity negative electron-beam resist // J. Vac. Sci. Technol. B, Microelectron. Nanom. Struct. 1992. V. 10. № 6. P. 2606.

  61. Bethe H.A., Rose M.E., Smith L.P. The Multiple Scattering of Electrons // Proc. Am. Philos. Soc. 1938. V. 78. № 4. P. 573–585.

  62. Sommerfeld A. Lectures on theoretical physics. New York: Academic Press, 1950.

  63. Lewis H.W. Multiple scattering in an infinite medium // Phys. Rev. 1950. V. 78. № 5. P. 526–529.

  64. Glezos N., Raptis I. A fast electron beam lithography simulator based on the Boltzmann transport equation // IEEE Trans. Comput. Des. Integr. Circuits Syst. 1996. V. 15. № 1. P. 92–102.

  65. Han G. et al. Comprehensive model of electron energy deposition // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2002. V. 20. № 6. P. 2666.

  66. Greeneich J.S. Developer Characteristics of Poly-(Methyl Methacrylate) Electron Resist // J. Electrochem. Soc. 1975. V. 122. № 7. P. 970.

  67. Everhart T.E., Hoff P.H. Determination of kiloVt electron energy dissipation vs penetration distance in solid materials // J. Appl. Phys. 1971. V. 42. № 13. P. 5837–5846.

  68. Ku H.Y., Scala L.C. Polymeric Electron Beam Resists // J. Electrochem. Soc. 1969. V. 116. № 7. P. 980.

  69. Greeneich J.S. Time eVution of developed contours in poly-(methyl methacrylate) electron resist // J. Appl. Phys. 1974. V. 45. № 12. P. 5264–5268.

  70. Chapiro A. Radiation Chemistry of Polymeric Systems. New York: Wiley, 1962.

  71. Kyser D.F., Viswanathan N.S. Monte Carlo simulation of spatially distributed beams in electron-beam lithography // J. Vac. Sci. Technol. 2002. V. 12. № 6. P. 1305–1308.

  72. Aktary M., Stepanova M., Dew S.K. Simulation of the spatial distribution and molecular weight of polymethylmethacrylate fragments in electron beam lithography exposures // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2006. V. 24. № 2. P. 768.

  73. Venkattraman A., Alexeenko A.A. Direct simulation Monte Carlo modeling of e-beam metal deposition // J. Vac. Sci. Technol. A Vacuum, Surfaces, Film. 2010. V. 28. № 4. P. 916–924.

  74. Han G., Khan M., Cerrina F. Stochastic modeling of high energy lithographies // J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 2003. V. 21. № 6. P. 3166.

  75. Rogozhin A.E. et al. Simulation of dry e-beam etching of resist and experimental evidence // International Conference on Micro- and Nano-Electronics 2018 / ed. Lukichev V.F., Rudenko K. V. SPIE, 2019. P. 96.

  76. Mohammad M.A. et al. Interdependence of optimum exposure dose regimes and the kinetics of resist dissolution for electron beam nanolithography of polymethylmethacrylate // J. Vac. Sci. Technol. B, Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2010. V. 28. № 1. P. L1–L4.

  77. Miller-Chou B.A., Koenig J.L. A review of polymer dissolution // Prog. Polym. Sci. 2003. V. 28. № 8. P. 1223–1270.

  78. De Gennes P.G. Reptation of a polymer chain in the presence of fixed obstacles // J. Chem. Phys. 1971. V. 55. № 2. P. 572–579.

  79. Harmandaris V.A. et al. Crossover from the rouse to the entangled polymer melt regime: Signals from long, detailed atomistic molecular dynamics simulations, supported by rheological experiments // Macromolecules. 2003. V. 36. № 4. P. 1376–1387

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал