1. На главную
  2. Электронные версии
  3. Микроэлектроника
  4. T. 52, № 1, 2023

Микроэлектроника, 2023, T. 52, № 1, стр. 32-45

Расчет напряженности электрического поля и плотности тока внутри тонкого металлического слоя с учетом скин-эффекта

Э. В. Завитаев 1, *, О. В. Русаков 2, Е. П. Чухлеб 3

1 Мытищинский филиал Московского государственного технического университета им. Н.Э. Баумана
141005 Мытищи, Россия

2 Государственный гуманитарно-технологический университет
142611 Орехово-Зуево, Россия

3 Муниципальное учреждение дополнительного образования Центр дополнительного образования “Малая академия наук Импульс”
142432 Черноголовка, Россия

* E-mail: EduardZavitaev@yandex.ru

Поступила в редакцию 01.08.2022
После доработки 01.08.2022
Принята к публикации 15.09.2022

Полный текст (PDF)

Аннотация

Впервые решена задача о распределении электрического поля и электрического тока внутри тонкого металлического слоя при наличии скин-эффекта с учетом зеркально-диффузного характера отражения электронов от внутренних поверхностей слоя. Рассмотрены предельные случаи и проведено обсуждение полученных результатов.

Ключевые слова: тонкий слой, скин-эффект, электрическое поле

1. ВВЕДЕНИЕ

Научная проблема экранировки электрического поля внутри малых проводящих объектов, представляет значительный интерес в теоретической физике, микроэлектронике, оптоэлектронике и тонкопленочных технологиях [1–3]. Актуальность изучения данной проблемы обуславливается тем, что классические размерные эффекты, оказывающие существенное влияние на электрические и оптические свойства тонких пленок, проволок и мелких частиц, требуют детального кинетического расчета.

Практическая значимость изучения проблемы экранировки внешнего электрического поля обусловлена широким спектром применения тонких пленок, проволок и мелких частиц в микро- и оптоэлектронике. В частности, это связанно с важным прикладным значением тонких, в том числе поликристаллических и металлических пленок, поэтому к их параметрам и свойствам предъявляются довольно высокие требования. Например, тонкие пленки могут использоваться в качестве проводящих, светоотражающих, защитных покрытий.

В современных работах [4–6] впервые построена кинетическая теория высокочастотной электропроводности и постоянной Холла тонкой проводящей пленки с учетом различных коэффициентов зеркальности ее поверхностей. В работе [7] рассмотрено поведение электронной плазмы в тонкой металлической пластине в переменном электрическом поле. Особенность этих работ заключается в том, что расчеты базируются на применении уравнения Больцмана и с помощью введения соответствующих граничных условий позволяют учесть не только объемное, но и поверхностное рассеяние носителей заряда.

В перечисленных работах не учитывается проявление скин-эффекта из предположения, что толщина слоя мала по сравнению с характерной глубиной скин-слоя. Однако указанное условие может нарушаться, поэтому необходимо последовательное построение теории с учетом проявления данного размерного эффекта.

В настоящей работе моментным методом [8] рассчитана функция распределения, описывающая линейный отклик электронов в однородном металлическом слое на переменное электрическое поле, ориентированное параллельно его поверхности. По найденной функции распределения удается рассчитать зависимость напряженности электрического поля внутри слоя, плотности тока и полного тока через поперечное сечение слоя от “скин-параметра” (отношения толщины слоя к глубине скин-слоя), от отношения толщины слоя к длине свободного пробега электронов и частоты, а также от коэффициентов зеркальности поверхностей металла.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается тонкий металлический слой толщиной b и шириной L, к которому приложено переменное напряжение частоты ω. Электрическое поле параллельно слою и направлено вдоль координатной оси Z, ось X перпендикулярна слою. Напряженность поля Е может быть выражена в зависимости от времени t:

(1)
${\mathbf{E}} = {{{\mathbf{E}}}_{{\mathbf{0}}}}{\text{exp}}(--i\omega t).$

Исходя из того, что неравновесная функция Ферми-Дирака для электронов f(х,v) = f0(ε) + f1(x,v) удовлетворяет уравнению Больцмана [9], имеем:

(2)
${{v}_{x}}\frac{{\partial {{f}_{1}}}}{{\partial x}} + e{{v}_{z}}E\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }} - i{{\omega }}{{f}_{1}} = - \frac{{{{f}_{1}}}}{\tau },$
где e – заряд электронов, vz, vx – соответствующие проекции вектора их скорости на координатные оси, τ – электронное время релаксации.

Здесь $f_{0}^{'}\left( \varepsilon \right)$ = – δ(ε – εF), где δ – дельта-функция Дирака, εF – энергия Ферми, ε = mv2/2 – кинетическая энергия электронов, v – модуль вектора скорости электронов v, m – эффективная масса электронов.

Плотность высокочастотного тока j, вызванного приложенным напряжением, рассчитывается по формуле:

(3)
${\mathbf{j}} = en\left\langle {\mathbf{v}} \right\rangle = en{{\left[ {\int {{{f}_{0}}{{d}^{3}}{\mathbf{v}}} } \right]}^{{ - 1}}}\int {{{f}_{1}}{\mathbf{v}}{{d}^{3}}{\mathbf{v}}} .$

Здесь n – концентрация электронов проводимости, определяемая с помощью распределения Ферми-Дирака:

$n = 2{{\left( {\frac{m}{h}} \right)}^{3}}\int {{{f}_{0}}{{d}^{3}}{\mathbf{v}}} = 2{{\left( {\frac{m}{h}} \right)}^{3}}\frac{{4\pi v_{F}^{3}}}{3},$
где h – постоянная Планка, vF – скорость Ферми [10].

В формуле (3) использована стандартная нормировка функции распределения f, при которой плотность электронных состояний равна $2{\text{/}}{{h}^{3}}$.

Однозначное решение поставленной задачи возможно при выборе граничного условия для неизвестной функции ${{f}_{1}}$ на верхней и нижней границе металлического слоя. В качестве такого принимаем условия зеркально-диффузного отражения электронов от его поверхности:

(4)
$\left\{ {\begin{array}{*{20}{c}} {{{f}_{1}}\left( {{{v}_{x}},x} \right) = {{q}_{1}}{{f}_{1}}\left( { - {{v}_{x}},x} \right),\,\,{{v}_{x}} < 0,\,\,~x = b,} \\ {{{f}_{1}}\left( {{{v}_{x}},x} \right) = {{q}_{2}}{{f}_{1}}\left( { - {{v}_{x}},x} \right),\,\,~{{v}_{x}} > 0,~\,\,x = 0,} \end{array}} \right.$
где ${{q}_{1}}$ и ${{q}_{2}}$ – коэффициенты зеркальности (вероятности зеркального отражения): 0 ≤ ${{q}_{i}}$ ≤ 1 (i = 1, 2).

При ${{q}_{i}}$ = 0 получаем условие диффузного отражения электронов проводимости от внутренней поверхности металлического слоя, а при ${{q}_{i}}$ = 1 условие чисто зеркального отражения. При значениях ${{q}_{i}}$ ≠ 0 и ${{q}_{i}}$ ≠ 1 получаем различные варианты смешанного зеркально-диффузного отражения электронов.

Связь между E и j в случае, когда толщина слоя сравнима с длинной свободного пробега электронов в металле Λ (или меньше ее: b < Λ), оказывается существенно нелокальной. Взяв в уравнении (2) поле E в виде (1), найдем функцию распределения ${{f}_{1}}$ как решение этого уравнения. Затем, используя выражение (3), определим плотность тока j внутри слоя.

Кроме того, для решения поставленной задачи необходимо использовать уравнение для напряженности электрического поля внутри слоя. Такое уравнение получаем из системы уравнений Максвелла без учета тока смещения, который пренебрежимо мал по сравнению с током проводимости:

(5)
$\Delta {\mathbf{E}} = - i{{\omega }}{{{{\mu }}}_{0}}{\mathbf{j}}.$

3. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Подставив в уравнение (2) функцию

${{f}_{1}}(x,{\mathbf{v}}) = g(x,{\mathbf{v}})\delta (\varepsilon - {{\varepsilon }_{F}}){\text{exp}}( - i\omega t),$
получим
(6)
${{\nu }}g + {{v}_{x}}\frac{{\partial g}}{{\partial x}} - e{{v}_{z}}E\left( x \right) = 0,$
где ν = 1/τ – iω – комплексная частота рассеяния.

Решение уравнения (6) проведем с помощью моментного метода [8]:

(7)
$g = {{a}_{1}}\left( x \right){{v}_{z}} + {{a}_{2}}\left( x \right){{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right).$

С учетом (7) уравнение (6) принимает вид

(8)
$\begin{gathered} \nu \left( {{{a}_{1}}{{v}_{z}} + {{a}_{2}}{{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right)} \right) + {{v}_{x}}{{v}_{z}}\frac{{\partial {{a}_{1}}}}{{\partial x}} + \\ + \,\,{{v}_{x}}{{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right)\frac{{\partial {{a}_{2}}}}{{\partial x}} - e{{v}_{z}}E\left( x \right) = 0. \\ \end{gathered} $

Умножим выражение (8) на vz и проинтегрируем по пространству скоростей:

$\begin{gathered} \nu {{a}_{1}}\int {v_{z}^{2}{{d}^{3}}{\mathbf{v}} + \nu {{a}_{2}}} \int {v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} + \frac{{\partial {{a}_{1}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{{d}^{3}}{\mathbf{v}} + } } \\ + \,\,\frac{{\partial {{a}_{2}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{\text{sign}}v\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} - eE\left( x \right)} \int {v_{z}^{2}{{d}^{3}}{\mathbf{v}} = 0} . \\ \end{gathered} $

Далее вычислим значения всех четырех интегралов и подставим их в последнее равенство

$\begin{gathered} \int {v_{z}^{2}{{d}^{3}}{\mathbf{v}} = \mathop \smallint \limits_0^{{{v}_{F}}} {{v}_{ \bot }}d{{v}_{ \bot }}\mathop \smallint \limits_0^{2\pi } d\varphi \mathop \smallint \limits_{ - \sqrt {v_{F}^{2} - v_{ \bot }^{2}} }^{\sqrt {v_{F}^{2} - v_{ \bot }^{2}} } v_{z}^{2}d{{v}_{z}} = \frac{{4\pi }}{{15}}v_{F}^{5};} \\ \int {v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} = \mathop \smallint \limits_0^{{{v}_{F}}} {{v}_{ \bot }}\left( {\mathop \smallint \limits_{ - \sqrt {v_{F}^{2} - v_{ \bot }^{2}} }^{\sqrt {v_{F}^{2} - v_{ \bot }^{2}} } v_{z}^{2}d{{v}_{z}}} \right)d{{v}_{ \bot }} \times } \\ \times \,\,\mathop \smallint \limits_0^{2\pi } {\text{sign}}\left( {{\text{cos}}{\kern 1pt} \varphi } \right)d\varphi = 0; \\ \int {{{v}_{x}}v_{z}^{2}{{d}^{3}}{\mathbf{v}} = \mathop \smallint \limits_0^{{{v}_{F}}} v_{ \bot }^{2}d{{v}_{ \bot }}\mathop \smallint \limits_0^{2\pi } {\text{cos}}{\kern 1pt} \varphi d\varphi \mathop \smallint \limits_{ - \sqrt {v_{F}^{2} - v_{ \bot }^{2}} }^{\sqrt {v_{F}^{2} - v_{ \bot }^{2}} } v_{z}^{2}d{{v}_{z}} = 0} ; \\ \int {{{v}_{x}}v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} = \mathop \smallint \limits_0^{{{v}_{F}}} v_{ \bot }^{2}\left( {\mathop \smallint \limits_{ - \sqrt {v_{F}^{2} - v_{ \bot }^{2}} }^{\sqrt {v_{F}^{2} - v_{ \bot }^{2}} } v_{z}^{2}d{{v}_{z}}} \right)d{{v}_{ \bot }} \times } \\ \times \,\,\mathop \smallint \limits_0^{2\pi } {\text{cos}}{\kern 1pt} \varphi {\kern 1pt} {\text{sign}}\left( {{\text{cos}}{\kern 1pt} \varphi } \right)d\varphi = \frac{\pi }{{12}}v_{F}^{6}. \\ \end{gathered} $

В результате приходим к уравнению

(9)
$\frac{4}{5}\nu {{a}_{1}} + \frac{{{{v}_{F}}}}{4}\frac{{\partial {{a}_{2}}}}{{\partial x}} = \frac{4}{5}eE(x).$

Умножим выражение (8) на vz sign(vx) и проинтегрируем по пространству скоростей:

$\begin{gathered} \nu {{a}_{1}}\int {v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} + \nu {{a}_{2}}} \int {v_{z}^{2}{\text{sig}}{{{\text{n}}}^{2}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} + } \\ + \,\,\frac{{\partial {{a}_{1}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} + \frac{{\partial {{a}_{2}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{\text{sig}}{{{\text{n}}}^{2}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} - } \\ - \,\,eE\left( x \right)\int {v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} = 0} . \\ \end{gathered} $

Найдем выражения двух оставшихся интегралов

$\begin{gathered} \int {v_{z}^{2}{\text{sig}}{{{\text{n}}}^{2}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} = \int {v_{z}^{2}{{d}^{3}}{\mathbf{v}} = \frac{{4\pi }}{{15}}v_{F}^{5};} } \\ \int {{{v}_{x}}v_{z}^{2}{\text{sig}}{{{\text{n}}}^{2}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}} = \int {{{v}_{x}}v_{z}^{2}{{d}^{3}}{\mathbf{v}} = 0} .} \\ \end{gathered} $

Таким образом, приходим к уравнению

(10)
$\frac{4}{5}\nu {{a}_{2}} + \frac{{{{v}_{F}}}}{4}\frac{{\partial {{a}_{1}}}}{{\partial x}} = 0.$

Решая совместно систему уравнений (9) и (10), получим

(11)
$\frac{{{{\partial }^{2}}{{a}_{1}}}}{{\partial {{x}^{2}}}} - {{{{\lambda }}}^{2}}{{a}_{1}} = - \frac{{{{{{\lambda }}}^{2}}e}}{\nu }E\left( x \right).$

В уравнении (11) перейдем к безразмерной переменной ξ = x/b, $\partial $ξ = $\partial $x/b:

(12)
$\frac{{{{\partial }^{2}}{{a}_{1}}}}{{\partial {{\xi }^{2}}}} - {{{{\lambda }}}^{2}}{{b}^{2}}{{a}_{1}} = - \frac{{{{{{\lambda }}}^{2}}e{{b}^{2}}}}{\nu }E\left( \xi \right),$
где ντ = 1 – iωτ = 1 – iΩ${{v}_{F}}{{\tau /}}b = 1 - i\Omega {\text{/}}\Delta = \chi {\text{/}}\Delta $, ${{\lambda }} = 16\nu {\text{/}}\left( {5{{v}_{F}}} \right)$, Ω – безразмерная частота электрического поля, ∆ – безразмерная обратная длина свободного пробега электронов, χ = ∆ – iΩ – безразмерная комплексная частота рассеяния электронов.

Преобразуем уравнение (5) для напряженности электрического поля внутри слоя как

$\frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} = - i{{\omega }}{{{{\mu }}}_{0}}{{b}^{2}}{{j}_{z}}.$

Для полученного уравнения будем использовать граничные условия

(13)
$\left\{ {\begin{array}{*{20}{c}} {{{{\left. E \right|}}_{{\xi = 1}}} = {{E}_{0}},} \\ {{{{\left. E \right|}}_{{\xi = 0}}} = {{E}_{0}}.} \end{array}~} \right.$

Плотность тока внутри слоя определяется соотношением (3), которое после соответствующих преобразований примет вид [8]:

(14)
${{j}_{z}} = \frac{{ne}}{m}{\text{exp}}\left( { - i{{\omega }}t} \right){{a}_{1}}\left( \xi \right).$

Подставим (14) в полученное уравнение

$\frac{{{{\partial }^{2}}E}}{{{{\partial }^{2}}{{\xi }^{2}}}} = - i{{\omega }}{{{{\mu }}}_{0}}{{b}^{2}}\frac{{ne}}{m}{\text{exp}}\left( { - i{{\omega }}t} \right){{a}_{1}}\left( \xi \right),$
которое для амплитуды напряженности электрического поля внутри слоя можно записать в виде
$\frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} = - i{{\omega }}{{{{\mu }}}_{0}}{{b}^{2}}\frac{{ne}}{m}{{a}_{1}}\left( \xi \right),$
или
(15)
$\frac{{{{\partial }^{2}}E}}{{\partial {{\varepsilon }^{2}}}} = A{{a}_{1}}\left( \xi \right),$
где $A = - i{{\omega }}{{{{\mu }}}_{0}}{{b}^{2}}ne{\text{/}}m = - 2i{{b}^{2}}{\text{/}}\left( {{{\delta }^{2}}e\tau } \right) = - 2i{{\psi }^{2}}{\text{/}}\left( {e\tau } \right).$ Здесь учтено, что глубина скин-слоя δ связана с объемной статической удельной проводимостью металла σ0 = ne2τ/m соотношением $2{\text{/}}{{{{\delta }}}^{2}} = {{{{\sigma }}}_{0}}{{\omega }}{{{{\mu }}}_{0}}$, а “скин-параметр” ψ = b/δ.

Объединим в систему уравнения (12) и (15)

$\left\{ \begin{gathered} \frac{{{{\partial }^{2}}{{a}_{1}}}}{{\partial {{\xi }^{2}}}} - {{{{\lambda }}}^{2}}{{b}^{2}}{{a}_{1}} = - \frac{{{{{{\lambda }}}^{2}}e{{b}^{2}}}}{{{\nu }}}E\left( \xi \right), \hfill \\ \frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} = A{{a}_{1}}\left( \xi \right). \hfill \\ \end{gathered} \right.$

Обозначив константы

(16)
$\left\{ \begin{gathered} C = {{{{\lambda }}}^{2}}{{b}^{2}} = \frac{{{{{16}}^{2}}{{\nu }^{2}}{{b}^{2}}}}{{{{5}^{2}}v_{F}^{2}}} = \frac{{{{{16}}^{2}}}}{{{{5}^{2}}}}{{\chi }^{2}}, \hfill \\ B = - \frac{{{{{{\lambda }}}^{2}}e{{b}^{2}}}}{\nu } = - \frac{{{{{16}}^{2}}{{\nu }^{2}}{{b}^{2}}e}}{{{{5}^{2}}v_{F}^{2}\nu }} = - \frac{{{{{16}}^{2}}\nu {{b}^{2}}e}}{{{{5}^{2}}v_{F}^{2}}} = - \frac{{{{{16}}^{2}}\chi eb}}{{{{5}^{2}}{{v}_{F}}}}, \hfill \\ \end{gathered} \right.$
получим

(17)
$\left\{ \begin{gathered} \frac{{{{\partial }^{2}}{{a}_{1}}}}{{\partial {{\xi }^{2}}}} - C{{a}_{1}} = BE\left( \xi \right), \hfill \\ \frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} = A{{a}_{1}}\left( \xi \right). \hfill \\ \end{gathered} \right.$

Будем искать решение системы (17) в виде

(18)
$E\left( \xi \right) = k{{a}_{1}}\left( \xi \right),$
где k – некоторая константа.

Произведем замену в уравнениях (17), используя (18), тогда система примет следующий вид

(19)
$\left\{ \begin{gathered} \frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} - \left( {Bk + C} \right)E = 0, \hfill \\ \frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} = \frac{A}{k}E. \hfill \\ \end{gathered} \right.$

Откуда

(20)
$\frac{A}{k}E\left( \xi \right) - \left( {Bk + C} \right)E\left( \xi \right) = 0~~ \Rightarrow \frac{A}{k} = Bk + C,$
или
$B{{k}^{2}} + Ck - A = 0,$
следовательно

(21)
${{k}_{{1,2}}} = \frac{{ - C \pm \sqrt {{{C}^{2}} + 4BA} }}{{2B}}.$

Подставляя (21) в первое уравнение системы (19) получим

$\frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} - \left[ {\frac{C}{2} \pm \frac{1}{2}\sqrt {{{C}^{2}} + 4BA} } \right]E = 0,$
или
(22)
$\frac{{{{\partial }^{2}}E}}{{\partial {{\xi }^{2}}}} - {{\mu }}_{{1,2}}^{2}E = 0,$
где ${{\mu }}_{{1,2}}^{2} = \frac{C}{2} \pm \frac{1}{2}\sqrt {{{C}^{2}} + 4BA} = \frac{A}{{{{k}_{{1,2}}}}}$ в силу (20).

Запишем ${{\mu }}_{{1,2}}^{2}$ в безразмерной форме:

$\begin{gathered} {{\mu }}_{{1,2}}^{2} = \frac{{{{{16}}^{2}}{{\chi }^{2}}}}{{2 \times {{5}^{2}}}}\left( {1 \pm \sqrt {1 + \frac{{25i{{\psi }^{2}}b}}{{32{{\chi }^{3}}{{v}_{F}}\tau }}} } \right) = \\ = \,\,\left| {\Delta = \frac{b}{{{{v}_{F}}\tau }}} \right| = \frac{{{{{16}}^{2}}{{\chi }^{2}}}}{{2 \times {{5}^{2}}}}\left( {1 \pm \sqrt {1 + \frac{{25i{{\psi }^{2}}\Delta }}{{32{{\chi }^{3}}}}} } \right). \\ \end{gathered} $

Тогда

$\begin{gathered} {{k}_{{1,2}}} = \frac{A}{{{{\mu }}_{{1,2}}^{2}}} = \frac{{ - 2i{{\psi }^{2}}{\text{/}}\left( {e\tau } \right)}}{{\frac{{{{{16}}^{2}}{{\chi }^{2}}}}{{2 \times {{5}^{2}}}}\left( {1 \pm \sqrt {1 + \frac{{25i{{\psi }^{2}}\Delta }}{{32{{\chi }^{3}}}}} } \right)}} = \\ = \,\,\frac{\chi }{{2e\tau \Delta }}\left( {1 \mp \sqrt {1 + \frac{{25i{{\psi }^{2}}\Delta }}{{32{{\chi }^{3}}}}} } \right). \\ \end{gathered} $

Окончательно получим

(23)
$\begin{gathered} {{{{\mu }}}_{{1,2}}} = \frac{{16\chi }}{{5\sqrt 2 }}\sqrt {1 \pm \sqrt {1 + \frac{{25i{{\psi }^{2}}\Delta }}{{32{{\chi }^{3}}}}} } , \\ k_{{1,2}}^{*} = e\tau {{k}_{{1,2}}} = \frac{\chi }{{2\Delta }}\left( {1 \mp \sqrt {1 + \frac{{25i{{\psi }^{2}}\Delta }}{{32{{\chi }^{3}}}}} } \right). \\ \end{gathered} $

Решение дифференциального уравнения (22) можно представить как

(24)
$\begin{gathered} E\left( \xi \right) = {{C}_{1}}{\kern 1pt} \exp \left( {{{\mu }_{1}}\xi } \right) + {{C}_{2}}{\kern 1pt} \exp \left( { - {{\mu }_{1}}\xi } \right) + \\ + \,\,{{C}_{3}}{\kern 1pt} \exp \left( {{{\mu }_{2}}\xi } \right) + {{C}_{4}}{\kern 1pt} \exp \left( { - {{\mu }_{2}}\xi } \right). \\ \end{gathered} $

Тогда, с учетом (18),

(25)
$\begin{gathered} {{a}_{1}}\left( \xi \right) = \frac{{{{C}_{1}}}}{{{{k}_{1}}}}\exp \left( {{{\mu }_{1}}\xi } \right) + \frac{{{{C}_{2}}}}{{{{k}_{1}}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + \\ + \,\,\frac{{{{C}_{3}}}}{{{{k}_{2}}}}\exp \left( {{{\mu }_{2}}\xi } \right) + \frac{{{{C}_{4}}}}{{{{k}_{2}}}}\exp \left( { - {{\mu }_{2}}\xi } \right). \\ \end{gathered} $

Из (10), с учетом (25), найдем

(26)
$\begin{gathered} {{a}_{2}}\left( \xi \right) = - \frac{{5{{v}_{F}}}}{{16\nu b}}\frac{{\partial {{a}_{1}}\left( \xi \right)}}{{\partial \xi }} = - \frac{1}{{\lambda b}}\frac{{\partial {{a}_{1}}\left( \xi \right)}}{{\partial \xi }} = - \frac{1}{{\sqrt C }}\frac{{\partial {{a}_{1}}\left( \xi \right)}}{{\partial \xi }} = \\ = \,\, - \frac{1}{{\sqrt C }}\left( {\frac{{{{\mu }_{1}}{{C}_{1}}}}{{{{k}_{1}}}}\exp \left( {{{\mu }_{1}}\xi } \right) - } \right.\frac{{{{\mu }_{1}}{{C}_{2}}}}{{{{k}_{1}}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + \\ + \,\,\left. {\frac{{{{\mu }_{2}}{{C}_{3}}}}{{{{k}_{2}}}}\exp \left( {{{\mu }_{2}}\xi } \right) - \frac{{{{\mu }_{2}}{{C}_{4}}}}{{{{k}_{2}}}}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right). \\ \end{gathered} $

Тогда из выражений (7), (25) и (26) следует:

(27)
$\begin{gathered} g\left( \xi \right) = \left( {\frac{{{{C}_{1}}}}{{{{k}_{1}}}}\exp \left( {{{\mu }_{1}}\xi } \right) + \frac{{{{C}_{2}}}}{{{{k}_{1}}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + } \right. \\ + \,\,\frac{{{{C}_{3}}}}{{{{k}_{2}}}}\exp \left( {{{\mu }_{2}}\xi } \right) + \left. {\frac{{{{C}_{4}}}}{{{{k}_{2}}}}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right){{v}_{z}} - \\ - \,\,\frac{1}{{\sqrt C }}\left( {\frac{{{{\mu }_{1}}{{C}_{1}}}}{{{{k}_{1}}}}\exp \left( {{{\mu }_{1}}\xi } \right) - \frac{{{{\mu }_{1}}{{C}_{2}}}}{{{{k}_{1}}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + } \right. \\ + \,\,\frac{{{{\mu }_{2}}{{C}_{3}}}}{{{{k}_{2}}}}\exp \left( {{{\mu }_{2}}\xi } \right) - \left. {\frac{{{{\mu }_{2}}{{C}_{4}}}}{{{{k}_{2}}}}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right){{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right). \\ \end{gathered} $

Применим граничные условия (13) и (4) для нахождения коэффициентов C1, C2, C3 и C4:

(28)
$\left\{ {\begin{array}{*{20}{c}} {{{{\left. E \right|}}_{{\xi = 0}}} = {{E}_{0}},} \\ {{{{\left. E \right|}}_{{\xi = 1}}} = {{E}_{0}},} \end{array}~} \right.\,\,\,\,\left\{ {\begin{array}{*{20}{c}} {g\left( {{{v}_{x}},\xi } \right) = {{q}_{2}}g\left( { - {{v}_{x}},\xi } \right),\,\,{{v}_{x}} > 0,\,\,~\xi = 0,} \\ {g\left( {{{v}_{x}},\xi } \right) = {{q}_{1}}g\left( { - {{v}_{x}},\xi } \right),\,\,{{v}_{x}} < 0,\,\,~\xi = 1.} \end{array}} \right.$

Тогда из (28), с учетом (24) и (27), получим систему уравнений

$\left\{ \begin{gathered} {{C}_{1}} + {{C}_{2}} + {{C}_{3}} + {{C}_{4}} = {{E}_{0}},\,\,\,\,{{C}_{1}}\exp \left( {{{\mu }_{1}}} \right) + \hfill \\ + \,\,{{C}_{2}}{\kern 1pt} \exp \left( { - {{\mu }_{1}}} \right) + {{C}_{3}}{\kern 1pt} \exp \left( {{{\mu }_{2}}} \right) + {{C}_{4}}{\kern 1pt} \exp \left( { - {{\mu }_{2}}} \right) = {{E}_{0}}, \hfill \\ \frac{{{{C}_{1}}}}{{{{k}_{1}}}}\left[ {1 - {{q}_{2}} - \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right] + \frac{{{{C}_{2}}}}{{{{k}_{1}}}}\left[ {1 - {{q}_{2}} + _{{_{{^{{}}}}^{{^{{}}}}}}^{{_{{^{{}}}}^{{}}}}} \right. \hfill \\ \left. { + \,\,\frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right] + \frac{{{{C}_{3}}}}{{{{k}_{2}}}}\left[ {1 - {{q}_{2}} - \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right] + \hfill \\ + \,\,\frac{{{{C}_{4}}}}{{{{k}_{2}}}}\left[ {1 - {{q}_{2}} + \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right] = 0,\,\,\,\,\frac{{{{C}_{1}}{{e}^{{{{\mu }_{1}}}}}}}{{{{k}_{1}}}}\left[ {1 - {{q}_{1}} + _{{_{{^{{}}}}^{{^{{}}}}}}^{{_{{^{{}}}}^{{}}}}} \right. \hfill \\ \left. { + \,\,\frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right] + \frac{{{{C}_{2}}{{e}^{{ - {{\mu }_{1}}}}}}}{{{{k}_{1}}}}\left[ {1 - {{q}_{1}} - \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right] + ~ \hfill \\ + \,\,\frac{{{{C}_{3}}{{e}^{{{{\mu }_{2}}}}}}}{{{{k}_{2}}}}\left[ {1 - {{q}_{1}} + \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right] + \hfill \\ + \,\,\frac{{{{C}_{4}}{{e}^{{ - {{\mu }_{2}}}}}}}{{{{k}_{2}}}}\left[ {1 - {{q}_{1}} - \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right] = 0. \hfill \\ \end{gathered} \right.$

С учетом переобозначений

(29)
$\left\{ \begin{gathered} {{C}_{1}} + {{C}_{2}} + {{C}_{3}} + {{C}_{4}} = {{E}_{0}}, \hfill \\ {{e}_{1}}{{C}_{1}} + {{e}_{2}}{{C}_{2}} + {{e}_{3}}{{C}_{3}} + {{e}_{4}}{{C}_{4}} = {{E}_{0}}, \hfill \\ {{D}_{1}}{{C}_{1}} + {{D}_{2}}{{C}_{2}} + {{D}_{3}}{{C}_{3}} + {{D}_{4}}{{C}_{4}} = 0, \hfill \\ {{B}_{1}}{{C}_{1}} + {{B}_{2}}{{C}_{2}} + {{B}_{3}}{{C}_{3}} + {{B}_{4}}{{C}_{4}} = 0, \hfill \\ \end{gathered} \right.$
где обозначенные коэффициенты
$\left\{ \begin{gathered} {{e}_{1}} = \exp \left( {{{\mu }_{1}}} \right),~~{{e}_{2}} = \exp \left( { - {{\mu }_{1}}} \right),\,\,\,\,{{e}_{3}} = \exp \left( {{{\mu }_{2}}} \right), \hfill \\ {{e}_{4}} = \exp \left( { - {{\mu }_{2}}} \right);\,\,\,\,{{D}_{1}} = \frac{1}{{{{k}_{1}}}}\left[ {1 - {{q}_{2}} - \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right], \hfill \\ {{D}_{2}} = \frac{1}{{{{k}_{1}}}}\left[ {1 - {{q}_{2}} + \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right],\,\,\,\,{{D}_{3}} = \frac{1}{{{{k}_{2}}}}\left[ {1 - {{q}_{2}} - _{{_{{^{{}}}}^{{}}}}^{{_{{^{{}}}}^{{}}}}} \right. \hfill \\ \left. { - \,\,\frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right],\,\,\,\,{{D}_{4}} = \frac{1}{{{{k}_{2}}}}\left[ {1 - {{q}_{2}} + \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right]; \hfill \\ {{B}_{1}} = \frac{{{{e}^{{{{\mu }_{1}}}}}}}{{{{k}_{1}}}}\left[ {1 - {{q}_{1}} + \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right],\,\,\,\,{{B}_{2}} = \frac{{{{e}^{{ - {{\mu }_{1}}}}}}}{{{{k}_{1}}}}\left[ {1 - {{q}_{1}} - _{{_{{^{{}}}}^{{}}}}^{{_{{^{{}}}}^{{}}}}} \right. \hfill \\ \left. { - \,\,\frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right],\,\,\,\,{{B}_{3}} = \frac{{{{e}^{{{{\mu }_{2}}}}}}}{{{{k}_{2}}}}\left[ {1 - {{q}_{1}} + \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right], \hfill \\ {{B}_{4}} = \frac{{{{e}^{{ - {{\mu }_{2}}}}}}}{{{{k}_{2}}}}\left[ {1 - {{q}_{1}} - \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right], \hfill \\ \end{gathered} \right.$
или в безразмерной форме:
(30)
$\left\{ \begin{gathered} {{e}_{1}} = \exp \left( {{{\mu }_{1}}} \right),\,\,\,\,~{{e}_{2}} = \exp \left( { - {{\mu }_{1}}} \right), \hfill \\ {{e}_{3}} = \exp \left( {{{\mu }_{2}}} \right),\,\,\,\,{{e}_{4}} = \exp \left( { - {{\mu }_{2}}} \right); \hfill \\ D_{1}^{*} = \frac{{{{D}_{1}}}}{{e\tau }} = \frac{1}{{k_{1}^{*}}}\left[ {1 - {{q}_{2}} - \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right], \hfill \\ D_{2}^{*} = \frac{{{{D}_{2}}}}{{e\tau }} = \frac{1}{{k_{1}^{*}}}\left[ {1 - {{q}_{2}} + \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right], \hfill \\ D_{3}^{*} = \frac{{{{D}_{3}}}}{{e\tau }} = \frac{1}{{k_{2}^{*}}}\left[ {1 - {{q}_{2}} - \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right], \hfill \\ D_{4}^{*} = \frac{{{{D}_{4}}}}{{e\tau }} = \frac{1}{{k_{2}^{*}}}\left[ {1 - {{q}_{2}} + \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{2}}} \right)} \right]; \hfill \\ B_{1}^{*} = \frac{{{{B}_{1}}}}{{e\tau }} = \frac{{{{e}^{{{{\mu }_{1}}}}}}}{{k_{1}^{*}}}\left[ {1 - {{q}_{1}} + \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right], \hfill \\ B_{2}^{*} = \frac{{{{B}_{2}}}}{{e\tau }} = \frac{{{{e}^{{ - {{\mu }_{1}}}}}}}{{k_{1}^{*}}}\left[ {1 - {{q}_{1}} - \frac{{{{\mu }_{1}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right], \hfill \\ B_{3}^{*} = \frac{{{{B}_{3}}}}{{e\tau }} = \frac{{{{e}^{{{{\mu }_{2}}}}}}}{{k_{2}^{*}}}\left[ {1 - {{q}_{1}} + \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right], \hfill \\ B_{4}^{*} = \frac{{{{B}_{4}}}}{{e\tau }} = \frac{{{{e}^{{ - {{\mu }_{2}}}}}}}{{k_{2}^{*}}}\left[ {1 - {{q}_{1}} - \frac{{{{\mu }_{2}}}}{{\sqrt C }}\left( {1 + {{q}_{1}}} \right)} \right], \hfill \\ \end{gathered} \right.$
где $\frac{{{{\mu }_{1}}}}{{\sqrt C }} = \frac{1}{{\sqrt 2 }}{{\left( {1 + \sqrt {1 + \frac{{25i{{\psi }^{2}}\Delta }}{{32{{\chi }^{3}}}}} } \right)}^{{1/2}}},\,\,\,\,\frac{{{{\mu }_{2}}}}{{\sqrt C }} = \frac{1}{{\sqrt 2 }} \times $, $\,\,{{\left( {1 - \sqrt {1 + \frac{{25i{{\psi }^{2}}\Delta }}{{32{{\chi }^{3}}}}} } \right)}^{{1/2}}}$.

Проведем решение системы (29) стандартными методами. Для этого представим ее как

$\left\{ \begin{gathered} \left[ {\left( {1 - \frac{{{{B}_{2}}}}{{{{B}_{1}}}}} \right)\frac{{{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + 1 - \frac{{{{B}_{3}}}}{{{{B}_{1}}}}} \right]{{C}_{3}} + \hfill \\ + \,\,\left[ {\left( {1 - \frac{{{{B}_{2}}}}{{{{B}_{1}}}}} \right)\frac{{{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + 1 - \frac{{{{B}_{4}}}}{{{{B}_{1}}}}} \right]{{C}_{4}} = {{E}_{0}}, \hfill \\ \left[ {\frac{{{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + \frac{{{{e}_{3}}{{B}_{1}} - {{e}_{1}}{{B}_{3}}}}{{{{e}_{2}}{{B}_{1}} - {{e}_{1}}{{B}_{2}}}}} \right]{{C}_{3}} + \hfill \\ + \,\,\left[ {\frac{{{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + \frac{{{{e}_{4}}{{B}_{1}} - {{e}_{1}}{{B}_{4}}}}{{{{e}_{2}}{{B}_{1}} - {{e}_{1}}{{B}_{2}}}}} \right]{{C}_{4}} = \frac{{{{E}_{0}}}}{{{{e}_{2}} - {{e}_{1}}\frac{{{{B}_{2}}}}{{{{B}_{1}}}}}}, \hfill \\ {{C}_{2}} = \frac{{{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}}{{C}_{3}} + \frac{{{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}}{{C}_{4}}, \hfill \\ {{C}_{1}} = - \frac{{{{B}_{2}}}}{{{{B}_{1}}}}{{C}_{2}} - \frac{{{{B}_{3}}}}{{{{B}_{1}}}}{{C}_{3}} - \frac{{{{B}_{4}}}}{{{{B}_{1}}}}{{C}_{4}}.~ \hfill \\ \end{gathered} \right.$

С учетом новых обозначений система примет вид

(31)
$\left\{ \begin{gathered} {{A}_{1}}{{C}_{3}} + {{A}_{2}}{{C}_{4}} = {{E}_{0}}, \hfill \\ {{A}_{3}}{{C}_{3}} + {{A}_{4}}{{C}_{4}} = {{E}_{0}}, \hfill \\ {{C}_{2}} = \frac{{{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}}{{C}_{3}} + \frac{{{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}}{{C}_{4}}, \hfill \\ {{C}_{1}} = - \frac{{{{B}_{2}}}}{{{{B}_{1}}}}{{C}_{2}} - \frac{{{{B}_{3}}}}{{{{B}_{1}}}}{{C}_{3}} - \frac{{{{B}_{4}}}}{{{{B}_{1}}}}{{C}_{4}}, \hfill \\ \end{gathered} \right.$
где обозначенные коэффициенты

(32)
$\left\{ \begin{gathered} {{A}_{1}} = \left( {1 - \frac{{{{B}_{2}}}}{{{{B}_{1}}}}} \right)\frac{{{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + 1 - \frac{{{{B}_{3}}}}{{{{B}_{1}}}}, \hfill \\ {{A}_{2}} = \left( {1 - \frac{{{{B}_{2}}}}{{{{B}_{1}}}}} \right)\frac{{{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + 1 - \frac{{{{B}_{4}}}}{{{{B}_{1}}}}, \hfill \\ {{A}_{3}} = \left( {{{e}_{2}} - \frac{{{{e}_{1}}{{B}_{2}}}}{{{{B}_{1}}}}} \right)\left[ {\frac{{{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + \frac{{{{e}_{3}}{{B}_{1}} - {{e}_{1}}{{B}_{3}}}}{{{{e}_{2}}{{B}_{1}} - {{e}_{1}}{{B}_{2}}}}} \right], \hfill \\ {{A}_{4}} = \left( {{{e}_{2}} - \frac{{{{e}_{1}}{{B}_{2}}}}{{{{B}_{1}}}}} \right)\left[ {\frac{{{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}}}{{{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}}} + \frac{{{{e}_{4}}{{B}_{1}} - {{e}_{1}}{{B}_{4}}}}{{{{e}_{2}}{{B}_{1}} - {{e}_{1}}{{B}_{2}}}}} \right]. \hfill \\ \end{gathered} \right.$

После решения системы (31) получим следующие выражения для коэффициентов в безразмерной форме:

(33)
$\left\{ \begin{gathered} C_{4}^{*} = \frac{{{{C}_{4}}}}{{{{E}_{0}}}} = \frac{{{{A}_{3}} - {{A}_{1}}}}{{{{A}_{2}}{{A}_{3}} - {{A}_{1}}{{A}_{4}}}},\,\,\,\,C_{3}^{*} = \frac{{{{C}_{3}}}}{{{{E}_{0}}}} = \frac{{{{A}_{2}} - {{A}_{4}}}}{{{{A}_{2}}{{A}_{3}} - {{A}_{1}}{{A}_{4}}}}, \hfill \\ C_{2}^{*} = \frac{{{{C}_{2}}}}{{{{E}_{0}}}} = \frac{{\left( {{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}} \right)\left( {{{A}_{2}} - {{A}_{4}}} \right) + \left( {{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}} \right)\left( {{{A}_{3}} - {{A}_{1}}} \right)}}{{\left( {{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}} \right)\left( {{{A}_{2}}{{A}_{3}} - {{A}_{1}}{{A}_{4}}} \right)}}, \hfill \\ C_{1}^{*} = \frac{{{{C}_{1}}}}{{{{E}_{0}}}} = \frac{{\left( {{{B}_{3}}{{D}_{1}} - {{B}_{1}}{{D}_{3}}} \right)\left( {{{A}_{4}} - {{A}_{2}}} \right) + \left( {{{B}_{4}}{{D}_{1}} - {{B}_{1}}{{D}_{4}}} \right)\left( {{{A}_{1}} - {{A}_{3}}} \right)}}{{\left( {{{B}_{1}}{{D}_{2}} - {{B}_{2}}{{D}_{1}}} \right)\left( {{{A}_{2}}{{A}_{3}} - {{A}_{1}}{{A}_{4}}} \right)}}\frac{{{{B}_{2}}}}{{{{B}_{1}}}} - \,\, \hfill \\ - \left( {\frac{{{{A}_{2}} - {{A}_{4}}}}{{{{A}_{2}}{{A}_{3}} - {{A}_{1}}{{A}_{4}}}}\frac{{{{B}_{3}}}}{{{{B}_{1}}}} + \frac{{{{A}_{3}} - {{A}_{1}}}}{{{{A}_{2}}{{A}_{3}} - {{A}_{1}}{{A}_{4}}}}\frac{{{{B}_{4}}}}{{{{B}_{1}}}}} \right). \hfill \\ \end{gathered} \right.$

Для данной системы безразмерных коэффициентов выражения (24)–(26) примут вид:

(34)
$\begin{gathered} E\left( \xi \right) = {{E}_{0}}\left( {C_{1}^{*}\exp \left( {{{\mu }_{1}}\xi } \right) + C_{2}^{*}\exp \left( { - {{\mu }_{1}}\xi } \right) + } \right. \\ + \,\,\left. {C_{3}^{*}\exp \left( {{{\mu }_{2}}\xi } \right) + C_{4}^{*}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right), \\ \end{gathered} $
(35)
$\begin{gathered} {{a}_{1}}\left( \xi \right) = {{E}_{0}}e\tau \left( {\frac{{C_{1}^{*}}}{{k_{1}^{*}}}\exp \left( {{{\mu }_{1}}\xi } \right) + \frac{{C_{2}^{*}}}{{k_{1}^{*}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + } \right. \\ + \,\,\left. {\frac{{C_{3}^{*}}}{{k_{2}^{*}}}\exp \left( {{{\mu }_{2}}\xi } \right) + \frac{{C_{4}^{*}}}{{k_{2}^{*}}}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right), \\ \end{gathered} $
(36)
$\begin{gathered} {{a}_{2}}\left( \xi \right) = - \frac{{{{E}_{0}}e\tau }}{{\sqrt C }}\left( {\frac{{{{\mu }_{1}}C_{1}^{*}}}{{k_{1}^{*}}}{{e}^{{{{\mu }_{1}}\xi }}} - \frac{{{{\mu }_{1}}C_{2}^{*}}}{{k_{1}^{*}}}{{e}^{{ - {{\mu }_{1}}\xi }}} + } \right. \\ + \,\,\left. {\frac{{{{\mu }_{2}}C_{3}^{*}}}{{k_{2}^{*}}}{{e}^{{{{\mu }_{2}}\xi }}} - \frac{{{{\mu }_{2}}C_{4}^{*}}}{{k_{2}^{*}}}{{e}^{{ - {{\mu }_{2}}\xi }}}} \right), \\ \end{gathered} $
где коэффициент $C = \frac{{{{{16}}^{2}}}}{{{{5}^{2}}}}{{{{\chi }}}^{2}}$ (см. (16)).

Таким образом, система безразмерных коэффициентов (33) с учетом сделанных обозначений (23), (30) и (32), полностью определяет выражения (34)–(36), а значит, полностью определяет отклонение f1(x,v) функции распределения от равновесной в случае зеркально-диффузного отражения электронов на верхней и нижней границе слоя с учетом скин-эффекта.

4. РАСЧЕТ НАПРЯЖЕННОСТИ И ТОКА

Плотность тока внутри слоя определяется соотношением (14), с учетом (35) формула примет вид:

$\begin{gathered} {{j}_{z}} = \frac{{n{{e}^{2}}{{\tau }}{{E}_{0}}{{e}^{{ - i\omega t}}}}}{m}\left( {\frac{{C_{1}^{*}}}{{k_{1}^{*}}}\exp \left( {{{{{\mu }}}_{1}}\xi } \right) + \frac{{C_{2}^{*}}}{{k_{1}^{*}}}\exp \left( { - {{{{\mu }}}_{1}}\xi } \right)} \right. + \\ + \,\,\left. {\frac{{C_{3}^{*}}}{{k_{2}^{*}}}\exp \left( {{{{{\mu }}}_{2}}\xi } \right) + \frac{{C_{4}^{*}}}{{k_{2}^{*}}}\exp \left( { - {{{{\mu }}}_{2}}\xi } \right)} \right). \\ \end{gathered} $

Выражение для амплитуды плотности тока в слое можно записать следующим образом:

(37)
$\begin{gathered} {{j}_{z}} = {{j}_{{0z}}}\left( {\frac{{C_{1}^{*}}}{{k_{1}^{*}}}\exp \left( {{{\mu }_{1}}\xi } \right) + \frac{{C_{2}^{*}}}{{k_{1}^{*}}}\exp \left( { - {{\mu }_{1}}\xi } \right)} \right. + \\ + \,\,\left. {\frac{{C_{3}^{*}}}{{k_{2}^{*}}}\exp \left( {{{\mu }_{2}}\xi } \right) + \frac{{C_{4}^{*}}}{{k_{2}^{*}}}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right), \\ \end{gathered} $
здесь учтено, что ${{j}_{{0z}}} = {{\sigma }_{0}}{{E}_{0}}$, ${{\sigma }_{0}} = n{{e}^{2}}\tau {\text{/}}m$ – объемная статическая удельная проводимость металла.

Для удобства численных расчетов введем безразмерную величину амплитуды плотности тока

(38)
$\begin{gathered} J{\kern 1pt} *\left( {\Delta ,\Omega ,\xi ,{{q}_{1}},{{q}_{2}},\psi } \right) = \frac{{C_{1}^{*}}}{{k_{1}^{*}}}\exp \left( {{{\mu }_{1}}\xi } \right) + \\ + \,\,\frac{{C_{2}^{*}}}{{k_{1}^{*}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + \frac{{C_{3}^{*}}}{{k_{2}^{*}}}\exp \left( {{{\mu }_{2}}\xi } \right) + \frac{{C_{4}^{*}}}{{k_{2}^{*}}}\exp \left( { - {{\mu }_{2}}\xi } \right). \\ \end{gathered} $

Проинтегрировав выражение (37), определяем полный ток, текущий через поперечное сечение тонкого металлического слоя:

(39)
$\begin{gathered} I = \mathop \smallint \limits_0^b {{j}_{z}}dS = \mathop \smallint \limits_0^b {{j}_{z}}Ldx = Lb\mathop \smallint \limits_0^1 {{j}_{z}}d\xi = \\ = \,\,{{j}_{{0z}}}Lb\mathop \smallint \limits_0^1 \left( {\frac{{C_{1}^{*}}}{{k_{1}^{*}}}\exp \left( {{{\mu }_{1}}\xi } \right) + \frac{{C_{2}^{*}}}{{k_{1}^{*}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + } \right.\frac{{C_{3}^{*}}}{{k_{2}^{*}}} \times \\ \left. { \times \,\,\exp \left( {{{\mu }_{2}}\xi } \right) + \frac{{C_{4}^{*}}}{{k_{2}^{*}}}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right)d\xi = {{j}_{{0z}}}Lb\left( {\frac{{C_{1}^{*}}}{{{{\mu }_{1}}k_{1}^{*}}} \times } \right. \\ \times \,\,\exp \left( {{{\mu }_{1}}\xi } \right) - \frac{{C_{2}^{*}}}{{{{\mu }_{1}}k_{1}^{*}}}\exp \left( { - {{\mu }_{1}}\xi } \right) + \frac{{C_{3}^{*}}}{{{{\mu }_{2}}k_{2}^{*}}}\exp \left( {{{\mu }_{2}}\xi } \right) - \\ \left. {\left. { - \,\,\frac{{C_{4}^{*}}}{{{{\mu }_{2}}k_{2}^{*}}}\exp \left( { - {{\mu }_{2}}\xi } \right)} \right)} \right|_{0}^{1} = {{I}_{{0z}}}\left( {\frac{{C_{1}^{*}}}{{{{\mu }_{1}}k_{1}^{*}}}\left( {{{e}^{{{{\mu }_{1}}}}} - 1} \right) - } \right. \\ \left. { - \frac{{C_{2}^{*}}}{{{{\mu }_{1}}k_{1}^{*}}}\left( {{{e}^{{ - {{\mu }_{1}}}}} - 1} \right) + \frac{{C_{3}^{*}}}{{ + {{\mu }_{2}}k_{2}^{*}}}\left( {{{e}^{{{{\mu }_{2}}}}} - 1} \right) - \frac{{C_{4}^{*}}}{{{{\mu }_{2}}k_{2}^{*}}}\left( {{{e}^{{ - {{\mu }_{2}}}}} - 1} \right)} \right), \\ \end{gathered} $
где ${{I}_{{0z}}} = {{j}_{{0z}}}Lb$.

Также введем безразмерную величину полного тока и безразмерную величину напряженности:

(40)
$\begin{gathered} I{\kern 1pt} *\left( {\Delta ,\Omega ,{{q}_{1}},{{q}_{2}},\psi } \right) = \frac{{C_{1}^{*}}}{{{{\mu }_{1}}k_{1}^{*}}}\left( {{{e}^{{{{\mu }_{1}}}}} - 1} \right) - \\ - \,\,\frac{{C_{2}^{*}}}{{{{\mu }_{1}}k_{1}^{*}}}\left( {{{e}^{{ - {{\mu }_{1}}}}} - 1} \right) + \frac{{C_{3}^{*}}}{{{{\mu }_{2}}k_{2}^{*}}}\left( {{{e}^{{{{\mu }_{2}}}}} - 1} \right) - \frac{{C_{4}^{*}}}{{{{\mu }_{2}}k_{2}^{*}}}\left( {{{e}^{{ - {{\mu }_{2}}}}} - 1} \right), \\ \end{gathered} $
(41)
$\begin{gathered} E{\kern 1pt} *\left( {\Delta ,\Omega ,\xi ,{{q}_{1}},{{q}_{2}},\psi } \right) = C_{1}^{*}{{e}^{{{{\mu }_{1}}\xi }}} + \\ + \,\,C_{2}^{*}{{e}^{{ - {{\mu }_{1}}\xi }}} + C_{3}^{*}{{e}^{{{{\mu }_{2}}\xi }}} + C_{4}^{*}{{e}^{{ - {{\mu }_{2}}\xi }}}. \\ \end{gathered} $

В случае отсутствия скин-эффекта (ψ = 0) из (37) с помощью предельного перехода имеем

(42)
${{j}_{z}} = \frac{{{{j}_{{0z}}}\Delta }}{{{\chi }}}\left( {1 + U_{1}^{*}\exp \left( {\frac{{16{{\chi }}}}{5}\xi } \right) + U_{2}^{*}\exp \left( { - \frac{{16{{\chi }}}}{5}\xi } \right)} \right),$
где

$U_{1}^{*} = \frac{{\left( {{{q}_{1}} - 1} \right) + {{q}_{1}}\left( {{{q}_{2}} - 1} \right)\exp \left( { - \frac{{16\chi }}{5}} \right)}}{{2\exp \left( {\frac{{16\chi }}{5}} \right) - 2{{q}_{1}}{{q}_{2}}\exp \left( { - \frac{{16\chi }}{5}} \right)}},$
$U_{2}^{*} = \frac{{{{q}_{2}}\left( {{{q}_{1}} - 1} \right) + \left( {{{q}_{2}} - 1} \right)\exp \left( {\frac{{16\chi }}{5}} \right)}}{{2\exp \left( {\frac{{16\chi }}{5}} \right) - 2{{q}_{1}}{{q}_{2}}\exp \left( { - \frac{{16\chi }}{5}} \right)}}.$

Заметим, что результат (42), полученный после применения формулы (37) в случае отсутствия скин-эффекта, когда “скин-параметр” ψ = 0, совпадает с результатами работы [8] в случае отсутствия поправки к закону Видемана-Франца.

При неограниченном увеличении толщины слоя (∆ $ \gg $ 1) применение формул (34) и (37) позволяет получить результаты соответствующие классическому скин-эффекту в макроскопическом слое.

5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

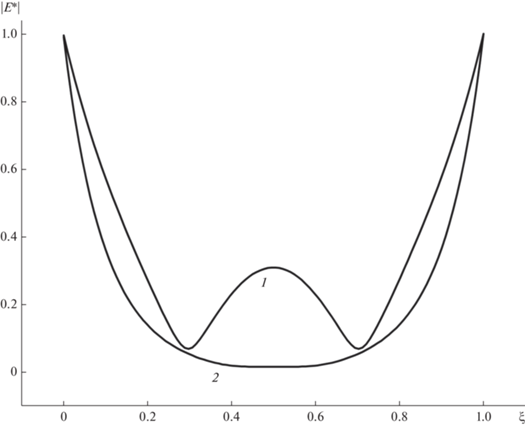
На рис. 1 представлена зависимость модуля амплитуды безразмерной напряженности электрического поля |E*(ξ)| от безразмерной координаты внутри слоя ξ. Обе кривые построены для случая сильного скин-эффекта (ψ = 10). Отличие состоит в том, что кривая 1 соответствует слою, у которого толщина b равна длине свободного пробега электронов Λ (∆ = 1), а кривая 2 соответствует макроскопическому слою (∆ $ \gg $ 1). Как видно из рисунка это обстоятельство заметно сказывается на величине модуля амплитуды безразмерной напряженности электрического поля |E*(ξ)|. Практически во всем объеме слоя ход кривой 1 носит некоторый осциллирующий характер, что связано с прохождением величины |E*(ξ)| через квазирезонансы – области, где вклад от различных траекторий электронов с одинаковыми фазами складывается, а с разными – уничтожается. Анализ хода кривой 2 напротив показывает, что в случае сильного скин-эффекта электрическое поле отсутствует практически во всем объеме макроскопического слоя, за исключением небольшого поверхностного слоя (назовем его слоем Кнудсена), глубина которого будет порядка длины свободного пробега электронов Λ. По мере роста размера слоя (увеличения ∆) осцилляции на кривой 1 будут сглаживаться. Это произойдет за счет увеличения объемного рассеяния электронов и преобладания его над поверхностным. При больших значениях безразмерной обратной длины свободного пробега электронов ∆ (∆ $ \gg $ 1) кривые 1 и 2 будут практически совпадать.

Рис. 1.

Зависимость модуля амплитуды безразмерной напряженности электрического поля от безразмерной координаты внутри слоя ξ. 1 – ψ = 10, ∆ = 1, Ω = 1, q1 = q2 = 0, 2 – ψ = 10, ∆ = 10, Ω = 1, q1 = q2 = 1.

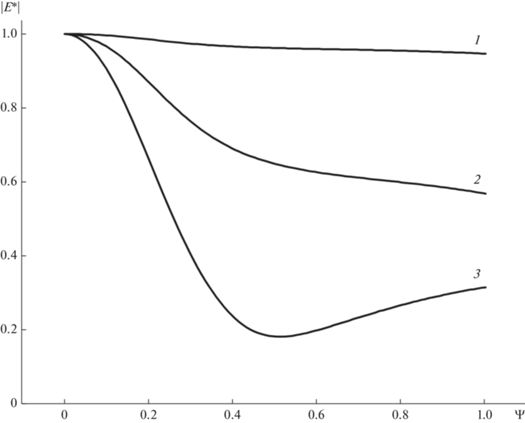
С помощью рис. 2, на котором представлена зависимость модуля амплитуды безразмерной напряженности электрического поля |E*(ψ)| от безразмерного “скин-параметра” ψ, можно выяснить особенности поведения электрического поля, когда проявляется его экранировка. Кривые на рисунке построены при различных значениях безразмерной координаты внутри слоя ξ. Из анализа хода кривых следует, что наличие скин-эффекта приводит к заметному изменению электрического поля в середине слоя по указанным выше причинам (см. описание рис. 1).

Рис. 2.

Зависимость модуля амплитуды безразмерной напряженности электрического поля от безразмерного “скин-параметра” ψ. 1 – ξ = 1, ∆ = 1, Ω = 1, q1 = q2 = 0.1, 2 – ξ = 0.9, ∆ = 1, Ω = 1, q1 = q2 = 0.1, 3 – ξ = 0.5, ∆ = 1, Ω = 1, q1 = q2 = 0.1.

На рис. 3 приведены графики зависимости модуля амплитуды безразмерной плотности тока |J*(ξ)| от безразмерной координаты внутри слоя ξ. Кривые 1 и 3 построены для случая сильного скин-эффекта (ψ = 10). Кривая 2 построена без учета скин-эффекта (ψ = 0). Наиболее интересно поведение хода этих кривых в слое Кнудсена вблизи поверхностей слоя. Анализ хода кривых 1 и 2 (результаты 1 и 2 получены с помощью кинетического подхода) показывает, что в приповерхностном слое имеет место некоторое увеличение плотности тока за счет поверхностного рассеяния электронов. Причем следует отметить наличие на кривой 1 максимума плотности тока. Анализ хода кривой 3, которая соответствует классическому скин-эффекту, показывает монотонное убывание безразмерной плотности тока |J*(ξ)| в слое Кнудсена.

Рис. 3.

Зависимость модуля амплитуды безразмерной плотности тока от безразмерной координаты внутри слоя ξ. 1 – ψ = 10, ∆ = 5, Ω = 1, q1 = q2 = 0, 2 – ψ = 0, ∆ = 5, Ω = 1, q1 = q2 = 0, 3 – ψ = 10, ∆ = 10, Ω = 1, q1 = q2 = 1.

На рис. 4 отображена зависимость модуля амплитуды безразмерной плотности тока |J*(ψ)| внутри слоя от безразмерного “скин-параметра” ψ. При малых значениях “скин-параметра” ψ (ψ $ \ll $ 1) графики 1 и 2, полученные с помощью кинетического подхода, совпадают, т.к. в этом случае скин-эффект практически не проявляется. По мере роста “скин-параметра” ψ кривая 1 асимптотически приближается к кривой 3, соответствующей классическому скин-эффекту в макроскопическом слое, когда ∆ $ \gg $ 1.

Рис. 4.

Зависимость модуля амплитуды безразмерной плотности тока от безразмерного “скин-параметра” ψ. 1 – ξ = = 0.1, ∆ = 1, Ω = 1, q1 = q2 = 0, 2 – ξ = 0.1, ∆ = 1, Ω = 1, q1 = q2 = 0, 3 – ξ = 0.1, ∆ = 10, Ω = 1, q1 = q2 = 1.

На рис. 5 показана зависимость модуля амплитуды безразмерной плотности тока |J*(∆)| внутри слоя от безразмерной обратной длины свободного пробега электронов ∆. При малых значениях толщины слоя (∆ $ \ll $ 1) кривые 1 и 2, полученные с помощью кинетического подхода, выходят из нуля. Плотность тока в этом случае крайне мала, т.к. ток в основном обусловлен поверхностным рассеянием электронов на границе слоя, а объемное рассеяние электронов практически отсутствует. Если толщина слоя достаточно большая (∆ $ \gg $ 1), то имеет место классический скин-эффект. При этом кривая 1 асимптотически приближается к кривой 3, построенной для макроскопического слоя.

Рис. 5.

Зависимость модуля амплитуды безразмерной плотности тока от безразмерной обратной величины длины свободного пробега электронов ∆. 1 – ψ = 3, ξ = 0.1, Ω = 1, q1 = q2 = 0, 2 – ψ = 0, ξ = 0.1, Ω = 1, q1 = q2 = 0, 3 – ψ = 3, ξ = 0.1, Ω = 1, q1 = q2 = 1.

Список литературы

  1. Ландау Л.Д., Лифшиц И.М. Электродинамика сплошных сред. М.: Физматлит, 2016. 656 с.

  2. Моисеев И.О., Юшканов А.А., Яламов Ю.И. Влияние скин-эффекта на поглощение электромагнитного излучения металлической частицей // ЖТФ. 2004. Т. 74. Вып. 1. С. 87–92.

  3. Завитаев Э.В., Русаков О.В., Юшканов А.А. Скин-эффект в тонкой цилиндрической проволоке из металла // ФТТ. 2012. Т. 54. Вып. 6. С. 1041–1047.

  4. Савенко О.В. Расчет высокочастотной электропроводности и постоянной холла для тонкой металлической пленки // Вестник МГОУ. Серия: Физика-Математика. 2016. № 4. С. 43–55.

  5. Кузнецова И.А., Романов Д.Н., Савенко О.В., Юшканов А.А. Расчет высокочастотной электропроводности тонкого полупроводникового слоя в случае различных коэффициентов зеркальности его поверхностей // Микроэлектроника. 2017. Т. 46. № 4. С. 275–283.

  6. Кузнецова И.А., Савенко О.В., Юшканов А.А. Влияние граничных условий на электрические и гальваномагнитные свойства тонкой металлической пленки // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 11. С. 52–60.

  7. Березкина С.В., Кузнецова И.А., Юшканов А.А. Поведение электронной плазмы в тонкой металлической пластине в переменном электрическом поле // ЖТФ. 2006. Т. 76. Вып. 5. С. 1–7.

  8. Завитаев Э.В., Русаков О.В., Чухлеб Е.П. Электрическая проводимость тонкого металлического слоя с учетом отклонения от закона Видемана–Франца // Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022. № 8. С. 36–42.

  9. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика, т. 10. Физическая кинетика. М.: Физматлит, 2007. 536 с.

  10. Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Часть 1. М.: Физматлит, 2010. 616 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал