1. На главную
  2. Электронные версии
  3. Неорганические материалы
  4. T. 58, № 11, 2022

Неорганические материалы, 2022, T. 58, № 11, стр. 1243-1248

Фрагильность и модули упругости халькогенидных стекол

А. А. Машанов 1, *, М. В. Дармаев 1, 2

1 Бурятский государственный университет им. Доржи Банзарова
670000 Улан-Удэ, ул. Смолина, 24а, Россия

2 Институт физического материаловедения СО Российской академии наук
670047 Улан-Удэ, ул. Сахьяновой, 6, Россия

* E-mail: Mashanov@bsu.ru

Поступила в редакцию 20.04.2022
После доработки 01.07.2022
Принята к публикации 06.07.2022

Полный текст (PDF)

Аннотация

Проведен расчет фрагильности двумя различными способами. Исследована корреляция между m и K/G, для системы As–S–Tl фрагильность линейно увеличивается, а для систем P–Se–Te, AsSe–TlSe и Sb–Ge–Se линейно уменьшается. Получена формула, связывающая фрагильность стекол с полосой температур δTg.

Ключевые слова: фрагильность, модули упругости, коэффициент Пуассона, халькогенидные стекла

ВВЕДЕНИЕ

Есть достаточно большая серия работ, посвященная классификации различных стекол на основе данных о т.н. фрагильности (хрупкости) m, которая представляет собой наклон кривой lgη – (Tg/T) при T = Tg, где η – коэффициент сдвиговой вязкости, Tg – температура стеклования жидкости [1–3]. Интерес к этой проблеме возрос в 2003–2006 годы после нахождения связи с параметром Грюнайзена и упругими постоянными стекол [4].

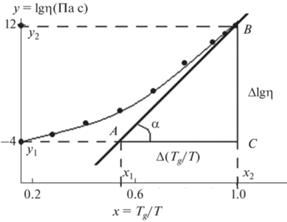
Фрагильность характеризует скорость уменьшения вязкости при повышении температуры и определяется тангенсом угла наклона кривой вязкости lg η – (Tg/T) вблизи температуры стеклования Tg (рис. 1) [1, 5]

(1)
$m = {{\left. {\frac{{\partial {\kern 1pt} \lg {\kern 1pt} \eta }}{{\partial ({{T}_{g}}{\text{/}}T)}}} \right|}_{{T = {{T}_{g}}}}}.$
Рис. 1.

Схема определения фрагильности стекол.

По значениям m можно классифицировать стекла. В первом приближении их делят на два больших класса: прочные и хрупкие. Это достаточно удобный способ классификации стекол, поскольку для них, как правило, известны экспериментальные данные о вязкости в области стеклования.

Настоящая работа посвящена определению фрагильности различными способами у халькогенидных стекол систем As–S–Tl, P–Se–Te, AsSe–TlSe и Sb–Ge–Se, а также исследованию взаимосвязи между фрагильностью m, упругими модулями стекол и коэффициентом Пуассона для данных стекол.

Экспериментальные данные о вязкости, модулях упругости и коэффициенте Пуассона взяты из электронной базы [6]; указанные халькогенидные стекла выбраны в связи с тем, что для них имеются экспериментальные данные о вязкости в достаточно широком диапазоне.

Цель работы – исследование взаимосвязи между фрагильностью (хрупкостью) m и соотношением модулей упругости K/G для халькогенидных стекол.

МЕТОДИКА ОПРЕДЕЛЕНИЯ ФРАГИЛЬНОСТИ

Для определения фрагильности строится график зависимости lg η от Tg/T (рис. 1) [7]. Следовательно, нужно иметь экспериментальные данные о вязкости η(T) в области стеклования вплоть до T = Tg. Обычно за значение Tg принимают температуру T13, соответствующую вязкости η(Tg) = 1013 Пз, lg η(Tg) = 13.

В точке кривой lg η – (Tg/T), соответствующей абсциссе x2 = (Tg/T) = 1, проводим касательную АВ. Затем строим произвольный треугольник АВС. Чем больше размер треугольника, тем точнее получится результат.

Отношение ВС/АС равно фрагильности m – тангенсу угла наклона кривой lgη – (Tg/T) в точке Tg/T = 1 (рис. 1).

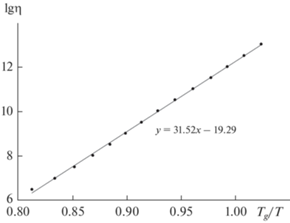
Отметим, что с использованием метода наименьших квадратов получается более точный результат и процесс определения фрагильности менее трудоемкий (рис. 2).

Рис. 2.

Определение фрагильности m для стекла Sb–Ge–Se с применением метода наименьших квадратов: Sb – 5, Ge – 15, Se – 80 мол. %.

ФРАГИЛЬНОСТЬ И МОДУЛИ УПРУГОСТИ СТЕКОЛ

Одним из интересных результатов, полученных по фрагильности стекол, является установление связи m с модулями упругости.

Новиков и Соколов [4] установили, что в первом приближении между фрагильностью m и отношением модуля объемного сжатия K к модулю сдвига G наблюдается линейная корреляция

(2)
$m \approx 29\left( {\frac{K}{G} - 0.41} \right).$

Из теории упругости известно, что отношение K/G является функцией коэффициента Пуассона μ

(3)
$\frac{K}{G} = \frac{2}{3}\left( {\frac{{1 + \mu }}{{1 - 2\mu }}} \right).$

Из соотношений (2) и (3) следует, что фрагильность является функцией коэффициента Пуассона.

В работе [4] отмечена важная роль коэффициента Пуассона в динамике сетки стекол. Фрагильность является характеристикой температурной зависимости вязкости стекла вблизи температуры стеклования. В свою очередь вязкость тесно связана со временем релаксации структуры стекла. Отсюда следует, что структурная релаксация зависит от упругих свойств, в частности, от коэффициента Пуассона.

Известно, что чем сильнее выражен ангармонизм колебаний решетки, тем легче протекает процесс релаксации структуры стекла. Отсюда понятно, почему фрагильность связана с ангармонизмом [3, 4].

На рис. 3 и 4 построены зависимости фрагильности m от отношения модулей упругости K/G. Для системы As–S–Tl наблюдается положительный наклон прямой, связанный с увеличением коэффициента Пуассона, для систем P–Se–Te, AsSe–TlSe и Sb–Ge–Se наблюдается отрицательный наклон прямых, объясняемый, в большей степени, уменьшением коэффициента Пуассона.

Рис. 3.

Зависимость фрагильности m от отношения модулей упругости (K/G) для стекол As–S–Tl (использованы данные справочника [6]).

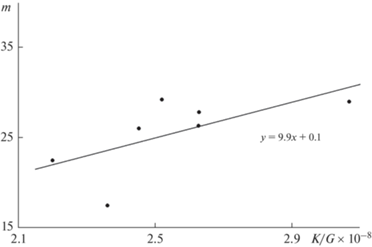
Рис. 4.

Зависимости фрагильности m от отношения модулей упругости (K/G) для стекол P–Se–Te, Sb–Ge–Se, AsSe–TlSe (использованы данные справочника [6]).

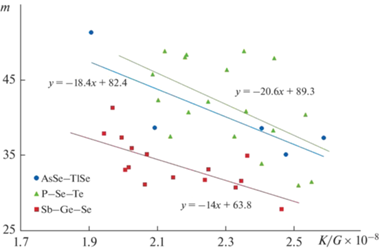
Полученные нами прямые m–K/G для стекол описываются следующими эмпирическими уравнениями:

$\begin{gathered} {\text{As}}{\kern 1pt} - {\kern 1pt} {\text{S}}{\kern 1pt} - {\kern 1pt} {\text{Tl: }}m = 9.9{K \mathord{\left/ {\vphantom {K G}} \right. \kern-0em} G} + 0.10, \\ {\text{P}}{\kern 1pt} - {\kern 1pt} {\text{Se}}{\kern 1pt} - {\kern 1pt} {\text{Te: }}m = - 20.6{K \mathord{\left/ {\vphantom {K G}} \right. \kern-0em} G} + 89.3, \\ {\text{AsSe}}{\kern 1pt} - {\kern 1pt} {\text{TlSe: }}m = - 18.4{K \mathord{\left/ {\vphantom {K G}} \right. \kern-0em} G} + 82.4, \\ {\text{Sb}}{\kern 1pt} - {\kern 1pt} {\text{Ge}}{\kern 1pt} - {\kern 1pt} {\text{Se: }}m = - 14{K \mathord{\left/ {\vphantom {K G}} \right. \kern-0em} G} + 63.8. \\ \end{gathered} $

Следует отметить, что формула (2) практически не выполняется для исследованных халькогенидных составов. В некоторых случаях зависимость m от отношения K/G оказывается достаточно сложной и не всегда описывается линейной корреляцией.

ФРАГИЛЬНОСТЬ И КОЭФФИЦИЕНТ ПУАССОНА

Фрагильность имеет следующую взаимосвязь с долей флуктуационного объема, замороженной при температуре стеклования fg = (Vf/V)Tg [7]

(4)
$m = \frac{{\lg (1{\text{/}}{{f}_{g}})}}{{{{f}_{g}}}}.$

Флуктуационный объем жидкостей и аморфных сред Vf обусловлен предельными смещениями возбужденных кинетических единиц из равновесных положений [8]

(5)
${{V}_{f}} = \left( {\pi {{r}^{2}}\Delta {{r}_{{{\text{max}}}}}} \right){{N}_{e}},$
где Ne – число возбужденных кинетических единиц, πr2 – площадь сечения частицы. Критическое смещение кинетической единицы Δrmax, соответствующее максимуму силы межатомного притяжения (предельной деформации межатомной связи Δrmax), оказывается функцией параметра Грюнайзена γL [9, 10]
(6)
$\frac{{\Delta {{r}_{{{\text{max}}}}}}}{{{{r}_{0}}}} = \frac{1}{{6{{\gamma }_{L}}}},$
что обусловлено проявлением нелинейности силы межатомного (межмолекулярного) притяжения при значительном смещении возбужденной частицы из равновесного положения. Из соотношений (5) и (6) видно, что флуктуационный объем Vf и, следовательно, его доля fg зависят от ангармонизма колебаний межатомных связей [11].

В свою очередь параметр Грюнайзена стеклообразных твердых тел оказывается функцией коэффициента Пуассона [10, 12, 13]

(7)
${{\gamma }_{L}} \cong \frac{2}{3}\left( {\frac{{1 + \mu }}{{1 - 2\mu }}} \right).$

Из соотношений (4)–(7) следует, что в первом приближении фрагильность должна быть пропорциональна параметру Грюнайзена и определяться функцией коэффициента Пуассона γL(µ)

(8)
$m \approx \frac{{\text{2}}}{{\text{3}}}\left( {\frac{{1 + \mu }}{{1 - 2\mu }}} \right).$

Исследованные в настоящей работе халькогенидные составы приближенно подчиняются корреляции (8) (рис. 5).

Рис. 5.

Зависимости фрагильности m от функции коэффициента Пуассона для стекол P–Se–Te, Sb–Ge–Se (использованы данные справочника [6]).

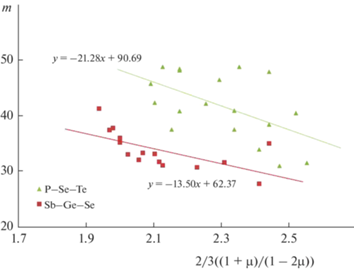
Интересно отметить, что нет физических оснований для существования универсальных корреляций между фрагильностью и коэффициентом Пуассона. Такие корреляции могут наблюдаться лишь для определенных групп стекол с взаимосвязанными структурами [5].

ФРАГИЛЬНОСТЬ И ТЕМПЕРАТУРНАЯ ПОЛОСА δТg

Взаимосвязь скорости охлаждения q и времени структурной релаксации τg выражается общим соотношением – уравнением стеклования

(9)
$q{{\tau }_{g}} = \delta {{T}_{g}},$
которое определяет появление стеклообразного состояния при температуре Tg в процессе охлаждения.

Величина δTg принимается равной интервалу температур, в котором вязкость η(T) меняется на порядок – от 1013 до 1012 Па с [14],

(10)
$\delta {{T}_{g}} = {{T}_{{12}}} - {{T}_{{13}}},$
где T12 и T13 – температуры, соответствующие lg η = = 12 и lg η = 13.

Легко убедиться, что подстановка в (1) уравнения Вильямса—Ландела–Ферри для зависимости $\eta (T)$ позволяет прийти к соотношению

(11)
$m = \frac{{{{C}_{1}}{{T}_{g}}}}{{{{C}_{2}}}}.$

С учетом δTg = C2/C1 для стекол одного класса вытекает следующее соотношение для определения фрагильности

(12)
$m = \frac{{{{T}_{g}}}}{{\delta {{T}_{g}}}}.$

Расчет m по этой формуле находится в удовлетворительном согласии с непосредственным определением фрагильности по формуле (1) (см. табл. 1).

Таблица 1.

  Расчет фрагильности стекол As–S–Tl, P–Se–Te, Sb–Ge–Se, AsSe–TlSe

Состав, мол. % tg, °С μ m m по формуле (12)
As S Tl  
40.00 60.00 – 172 0.306 17.43 15.34
36.90 57.93 5.17 134 0.309 22.45 18.50
33.90 55.93 10.17 128 0.311 29.21 22.91
32.26 54.84 12.90 120 0.317 26.00 21.24
31.06 54.04 14.91 115 0.324 27.81 20.97
28.17 52.11 19.72 107 0.337 26.34 22.35
25.00 50.00 25.00 94 0.344 28.95 22.94
P Se Te  
10.00 90.00 – 55 0.320 47.89 46.86
9.00 81.01 9.99 75 0.313 40.83 53.54
8.00 72.00 20.00 75 0.310 46.35 46.40
7.00 63.03 29.97 72 0.301 48.03 49.29
6.00 53.99 40.01 72 0.297 48.78 46.00
20.00 80.00 – 65 0.314 48.78 39.76
18.02 72.07 9.91 77 0.320 38.29 35.00
16.00 64.00 20.00 93 0.307 42.08 52.29
14.01 56.02 29.97 95 0.295 42.34 56.62
12.00 48.02 39.98 90 0.294 45.74 38.21
28.57 71.43 – 78 0.318 33.86 41.29
25.64 64.10 10.26 84 0.313 37.49 34.00
22.88 57.21 19.91 92 0.299 37.49 45.63
20.00 50.00 30.00 93 0.301 40.72 52.29
17.15 42.88 39.97 76 0.301 48.39 43.63
40.00 60.00 – 87 0.322 30.93 34.29
35.97 53.96 10.07 88 0.327 31.44 27.77
31.95 47.92 20.13 80 0.325 40.33 35.30
Sb Ge Se  
10 5 85 78 0.320 34.88 18.64
10 10 80 118 0.311 31.52 36.83
5 15 80 135 0.318 27.71 33.71
15 10 75 130 0.296 31.65 38.25
10 15 75 149 0.305 30.63 34.64
20 10 70 151 0.295 33.07 43.18
15 15 70 172 0.297 30.99 35.93
20 15 65 216 0.292 33.30 41.38
10 25 65 305 0.291 31.96 35.56
16 20 64 275 0.286 35.07 42.57
22 15 63 247 0.280 41.21 62.78
25 15 60 228 0.284 37.76 42.00
20 20 60 244 0.286 35.90 40.43
15 25 60 250 0.283 37.31 39.27
10 30 60 284 0.288 33.00 38.31
AsSe TlSe –  
100.00 –   162 0.310 35.11 39.55
90.00 10.00   136 0.300 38.58 45.44
80.00 20.00   134 0.320 38.54 50.88
66.60 33.40   121 0.320 37.29 39.40
40.00 60.00   69 0.310 51.28 57.00

ЗАКЛЮЧЕНИЕ

Анализ полученной взаимосвязи между m и K/G показывает, что фрагильность у исследуемых стекол системы As–S–Tl линейно растет, а у систем P–Se–Te, AsSe–TlSe и Sb–Ge–Se линейно уменьшается. В первом приближении фрагильность должна быть пропорциональна функции коэффициента Пуассона γL(µ) ≈ 2(1 + µ)/3(1 – 2µ). Из исследованных халькогенидных стекол этой закономерности подчиняются стекла систем P–Se–Te и Sb–Ge–Se. Полученные результаты согласуются с представлением Немилова [5] о том, что корреляции между m и µ могут наблюдаться лишь для определенных групп стекол.

Список литературы

  1. Angell C.A. Perspective on the Glass Transition // J. Phys. Chem. Solids. 1988. V. 49. № 8. P. 836–871.

  2. Novikov V.N. Vibration Anharmonicity and Fast Relaxation in the Region of Glass Transition // Phys. Rev. B. 1998. V. 58. P. 8367–8378.

  3. Sokolov A.P., Rossler E., Kisliuk A., Quitman D. Dynamics of Strong and Fragile Glassformers: Differences // Phys. Rev. Lett. 1993. V. 71. P. 2062–2065.

  4. Novikov V.N., Sokolov A.P. Poisson’s Ratio and the Fragility of Glass-Forming Liquids // Nature. 2004. V. 431. P. 961–963.

  5. Nemilov S.V. Structural Aspect of Possible Interrelation between Fragility (Length) of Glass Forming Melts and Poisson’s Ratio of Glasses // J. Non-Cryst. Solids. 2007. V. 353. P. 4613–4632.

  6. MDL ® SciGlass – 7.8 Institute of Theoretical Chemistry, Shrewsbury, MA, 2012.

  7. Сандитов Д.С., Машанов А.А., Сандитов Б.Д., Мантатов В.В. Фрагильность и ангармонизм колебаний решетки свинцовосиликатных и натриевоборатных стекол // Физика и химия стекла. 2008. Т. 34. № 4. С. 512–517.

  8. Сыдыков Б.С., Сандитов Д.С. Критерий плавления Линдемана и переход стекло-жидкость // Вестн. Бурятского гос. ун-та. Химия. Физика. 2014. Вып. 3. С. 126–130.

  9. Мантатов В.В. Модельная концепция в исследовании физических свойств неупорядоченных структур // Вестн. Бурятского гос. ун-та. Химия. Физика. 2022. Вып. 1. С. 3–17.

  10. Сандитов Б.Д., Мантатов В.В. Нелинейность силы межмолекулярного взаимодействия в некристаллических твердых телах. Улан-Удэ: Изд-во Бурятского гос. ун-та, 2001. 96 с.

  11. Аграфонов Ю.В., Сандитов Д.С., Цыдыпов Ш.Б. Физика классических неупорядоченных систем. Улан-Удэ: Изд-во Бурятского гос. ун-та, 2000. 234 с.

  12. Сандитов Д.С. Коэффициент поперечной деформации и структурно-чувствительные свойства стеклообразных материалов // Деформация и разрушение материалов. 2015. № 9. С. 2–16.

  13. Сандитов Д.С., Дармаев М.В. Упругие модули и параметр Грюнайзена стеклообразных твердых тел // Физика и химия стекла. 2022. Т. 48. № 1. С. 27–33.

  14. Nemilov S.V. Maxwell Equation and Classical Theories of Glass Transition as a Basis for Direct Calculation of Viscosity at Glass Transition Temperature // Glass Phys. Chem. 2013. V. 39. № 6. P. 609–623.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Неорганические материалы

Архивы выпусков Информация о журнале Отправить рукопись в журнал